Abstract
A beat-to-beat variation in the electric wave propagation morphology in myocardium is referred to as cardiac alternans and it has been linked to the onset of life threatening arrhythmias and sudden cardiac death. Experimental studies have demonstrated that alternans can be annihilated by the feedback modulation of the basic pacing interval in a small piece of cardiac tissue. In this work, we study the capability of feedback control to suppress alternans both spatially and temporally in an extracted rabbit heart and in a cable of cardiac cells. This work demonstrates real-time control of cardiac alternans in an extracted rabbit heart and provides an analysis of the control methodology applied in the case of a one-dimensional (1D) cable of cardiac cells. The real-time system control is realized through feedback by proportional perturbation of the basic pacing cycle length (PCL). The measurements of the electric wave propagation are obtained by optical mapping of fluorescent dye from the surface of the heart and are fed into a custom-designed software that provides the control action signal that perturbs the basic pacing cycle length. In addition, a novel pacing protocol that avoids conduction block is applied. A numerical analysis, complementary to the experimental study is also carried out, by the ionic model of a 1D cable of cardiac cells under a self-referencing feedback protocol, which is identical to the one applied in the experimental study. Further, the amplitude of alternans linear parabolic PDE that is associated with the 1D ionic cardiac cell cable model under full state feedback control is analyzed. We provide an analysis of the amplitude of alternans parabolic PDE which admits a standard evolutionary form in a well defined functional space. Standard modal decomposition techniques are used in the analysis and the controller synthesis is carried out through pole-placement. State and output feedback controller realizations are developed and the important issue of measurement noise in the controller implementation is addressed. The analysis of stabilization of the amplitude of alternans PDE is in agreement with the experimental results and numerical results produced by the ionic 1D cable of cardiac cells model. Finally, a discussion is provided in light of these results in order to use control to suppress alternans in the human myocardium.
Keywords: Cardiac Alternans, Action Potential Duration (APD), Proportional Perturbation Feedback (PPF), Dissipative Parabolic PDEs, State/Output Feedback Control
1 Introduction
Sudden cardiac death due to ventricular fibrillation (VF) is the most common and often the first manifestation of coronary heart disease. It is responsible for about 50% of the mortality from cardiovascular diseases in the United States and other developed countries [1]. In many cases VF is associated with, and may well be caused by, electrical alternans [2]. It has been shown experimentally that when cardiac tissue is stimulated by a rapid pacing protocol, the duration of the electrical excitation varies from beat to beat, and it is manifested as a variation in the action potential duration (APD), which may undergo a transition to the VF [3]. These period-doubling oscillations are referred to as “alternans” and on the scale of the whole heart these alternans are reflected in a beat-to-beat variation of the electrocardiogram (ECG) T-wave segments. In animal [4] and clinical human research studies [5] it has been shown that even hearts with a small level of T-wave alternans in the ECG where at a higher risk to develop VF and sudden cardiac death.
A well-known way to produce temporal alternans in a single cell or spatiotemporal alternans in the cardiac tissue is to start pacing of the cardiac cell/tissue with sufficiently large pacing period and then to slowly decrease the length of the pacing interval until the critical pacing period at which alternation in the APD emerges. Typically, the end of action potential is followed by a period of rest, called diastolic period (DI), until the next excitable stimuli that activates new action potential propagation occurs, see Fig.1. In the case of a short diastolic period, the cell/tissue does not have time to fully recover its resting electric properties before the next activation, which yields a shorter APD. Hence, these oscillations between patterns of a short DI → short APD → long DI → long APD are of period doubling nature and their analysis was first demonstrated in the pioneering works of Nolasco and Dahlen [6] where the basic mathematical analysis of alternans based on their analogy with electric systems was demonstrated. This instability of APD and DI patterns is crucially related to the onsets of VF, as it has been demonstrated by 2D numerical simulations in [7, 8]. Specifically, large oscillations in the APD induce spiral wave breakup and wave turbulence. In particular, if there is a large spatial gradient among the regions of different APDs, the length of the diastolic interval falls below a critical value that is necessary for the next wave propagation. This brings about propagation failure, as the next wave front encounters the regions of the tissue that are less prone to undergo wave propagation. Propagation failure then results in the local wave break that initiates a spiral, which can initiate a similar wave break and by this mechanism invade the entire domain of the cardiac tissue. Since cardiac alternans is believed to be a precursor to VF and sudden cardiac death, an important question to address is whether in principle spatiotemporal alternans in cardiac tissue can be annihilated by means of feedback control, as this can represent an effective antiarrhythmic strategy.
Figure 1.
Schematic of time evolution of transmembrane potential at a point along the cable with APD alternans.
In the past decade, most research efforts in the area of control of physiological systems were focused on the development of model-independent control techniques for chaotic systems, where the stabilization algorithm is based on the fact that there is an infinite number of unstable periodic orbits (UPO's) embedded in the chaotic attractor, so that small time-dependent perturbations to an accessible system parameter drive the system toward a desired UPO [9, 10, 11, 12, 13, 14]. In the same vein, Christini and Collins developed a novel real-time adaptive model independent (RTAMI) control technique [15, 16]. All aforementioned control algorithms are model independent and are based on the proportional perturbation feedback control paradigm which has been demonstrated to be suitable for some physiological systems. Specifically, experimental and theoretical works have demonstrated that simple closed-loop proportional perturbation feedback methods could be used to suppress the type of alternans that occur in a single cell, or in small pieces of tissue where significant spatiotemporal variations of repolarization and wave propagation dynamics do not take place [17, 12, 10, 18]. In the theoretical study of Echebarria et.al. [19] it has been demonstrated that alternans can be abolished in a small one-dimensional cable of cardiac cell tissue by applying pacing feedback produced by consecutive APD measurements at the pacing site. Analysis of this result is based on a small amplitude of alternans equation, which belongs to the class of parabolic partial differential equations (PDEs). However, this study did not provide an insight from a control point of view, which necessarily requires more detailed analysis of control-theoretic system properties (such as controllability and observability) and analysis of the closed-loop system under various feedback control laws. Specifically, the issues of implementing successful feedback control and handling inherent constraints present in the implementation of the feedback control algorithm need more careful and comprehensive examination. A possibility to suppress alternans by dynamic control methods in the human ventricles and possibly to prevent sudden cardiac death needs to be addressed from a control point of view accounting explicitly for the practical implementation of the controllers. Given that there is only a small number of electrodes that can be placed in the human ventricle for pacing purposes, and that there is only a small number of leads that can be placed in vivo in humans for the recording of cardiac activity, the main questions that need to be addressed are: 1) Can in principle cardiac alternans be controlled? 2) What are the possible limitations on the applied control action? and 3) Are there any improvements in the pacing control algorithm that can be made on the basis of insight obtained by the experimental and theoretical works?
In this work, we provide quantitative answers to these questions by demonstrating first, real-time control of cardiac alternans in an extracted rabbit heart; second, by providing a numerical demonstration of the features of the pacing protocols applied; and third, by addressing analytical features of the feedback-based alternans annihilation problem. In the ensuing section, we provide features of the experimentally implemented real-time control system. The real-time control is realized by the perturbation of the basic pacing cycle length (PCL). The pacing protocol uses the feedback gain based on modulated surface optical mapping measurements of the APD duration in the vicinity of the pacing electrode. Experimental results demonstrate a marked reduction of the amplitude of alternans in the rabbit heart with a novel pacing protocol that utilizes large values of feedback gain; the controller prevents conduction block at the pacing site by using only positive basic pacing cycle length perturbations. In this way, the pacing protocol differs from previously proposed self-referencing gain feedback protocols [12, 20, 18]. In addition, in numerical studies associated with the experiment, successful alternans stabilization has been demonstrated with the use of the novel pacing protocol in the case of a 1D cable of cardiac cells (2.5 cm in length), which exceeds the length of experimentally considered rabbit heart tissue. The novel pacing protocol in numerical studies uses the measurements of APD alternans at the boundary where the pacing is applied and at a distant site away from the pacing boundary. In this way, the pacing protocol accounts for the spatial evolution of APD alternans in order to prevent occurrence of a conduction block. In section 3, the experimental and numerical studies are complemented with an analysis of the associated amplitude of the alternans equation. Specifically, the amplitude of alternans linear parabolic PDE which includes a Sturm-Liouville spatial differential operator is considered [21]. First, a modal representation of the linear parabolic PDE is computed. The analysis demonstrates that the spatial operator of the amplitude of alternans contains a few unstable modes that can be stabilized by means of boundary control. Namely, only a few unstable modes are stabilized by the standard pole placement technique while the remaining infinite dimensional modal complement remains stable under feedback. In the same section, a basic condition for the controllability and observability required for an output feedback controller to achieve closed-loop stability is given. Simulation studies initially demonstrate agreement among results obtained by numerical simulations of 1D ionic cardiac cell cable model when the pacing protocol using the measurement of alternans along the cable is applied, and further results demonstrate exponential stabilization of the amplitude of alternans parabolic PDE by full state and output boundary feedback control. Finally, we point out critical features of the experimental, numerical and analytical study in order to use control to suppress alternans in the human myocardium.
2 Experimental and numerical study of pacing control
2.1 Cable of cardiac cells model and pacing control
The one-dimensional (1D) homogeneous cable of cardiac cells of length L paced at one end is considered, and it is described by the following parabolic PDE:
| (1) |
| (2) |
where the membrane current Iion(ζ, t) is given by the Noble model [22], Vp(t) = Istim/Cm represents the voltage that is supplied by the pacer which generates voltage pulses in the form of square pulses (amplitude-3.5mV , duration-1msec and period τ = 250 msec), D = 2.5e−4cm2/msec and Cm = 12μF/cm2. The membrane current Iion(ζ, t) is given by Iion(ζ, t) = INa + IK + Ileak, where INa = (gNamaxm3h + gNa)(V(t) − ENa), gNamax = 400 mmhol/cm2, gNa = 0.14 mmhol/cm2, ENa = 40 mV, gleak = 0, Vleak = −60 mV, GK1 = 1.2exp((−V(t) − 90)/50) + 0.015exp((V(t) + 90)/60), GK2 = 1.2n4, IK = (GK1 + GK2)(V(t) + 100), and Ileak = gleak(V(t) − Vleak). The inonic channel dynamics are given by , ι = m, h, n, where αm = 0.1(−V(t) − 48)/(exp((−V(t) − 48)/15) − 1), βm = 0.12(V(t)+8)/(exp((V(t)+8)/5) −1), αn = 0.0001 (−V(t) − 50)/(exp((−V(t)−50)/10)−1), βn = 0.002exp((−V(t) − 90)/80), αh = 0.17exp((−V(t) − 90)/20) and βh = 1/(exp((−V(t) − 42)/10) + 1). The voltage evolution in the cell cable model of Eqs.1-2 is calculated on the basis of the centered finite difference approximation of Eq.1 with a spatial discretization step size Δζ = 0.02, and with an explicit Euler time integration scheme (Δt = 0.05 msec).
When stimulated at ζ = 0 with the Vp(t) stimuli, membrane voltage at a paced cell crosses the threshold value of excitability which opens sodium channels and provides a large influx of sodium ions in the cell to create an effect of a depolarizing membrane. The depolarization of the membrane turns on the potassium channels that slowly recover the membrane potential by repolarization until the membrane reaches its resting negative potential. Due to diffusive coupling among cells this excitable wave travels in one direction along the cable, from cell to cell. This process is repeated at each time when action potential is elicited by the pacing stimulus. The action potential duration (APD) in the cells along the cable is the period of time during which the action potential is over the prespecified threshold value and the diastolic time interval (DI) is defined as the period of time during which the transmembrane potential is below a given value, see Fig.1. The restitution curve establishes a functional relationship between the APD generated by the (n + 1)-th stimulus and the diastolic time interval during which the tissue recovers its resting properties after the end of the previous (n)-th action potential, see Fig.2. This relationship is given by:
| (3) |
while the basic pacing interval is given by Tn = APDn +DIn. This one-dimensional discrete nonlinear map provides information of the critical diastolic period at which the slope of the function, f′, exceeds unity, which determines the onset of a period doubling bifurcation of alternans. The restitution curve, see Fig.2, given by Eq.3 is obtained by a so-called S1S2-pacing protocol [14]. The S1S2-pacing protocol is realized by applying a large number of “S1”-stimuli (≈ 50 − 100 beats) to a single cell at a sufficiently large basic pacing cycle length Tn, so that the last in the series of “S1” stimuli is followed by “S2” stimuli which is applied at a different time within the diastolic time period and which produces action potential duration that provides the restitution curve of Eq.3, see Figs.2-3.
Figure 2.
Restitution curve APDn+1 = f(DIn) of the Noble ionic model computed for a single cell.
Figure 3.
The S1S2-pacing protocol.
Under a short periodic pacing at one end of the cardiac cells cable, the propagating stimulus induces action potential along the cable and the action potential induced by two successive stimuli at a given point in space is characterized by different durations of the APD, a short APD is followed by a long one which follows a short one, etc. At a given point in space ζ, this alternantion of the APD defines the amplitude of alternans, an(ζ), for the n-th stimulus, or an(ζ) = (APDn(ζ) − APDn−1(ζ))(−1)n. In this way continuous voltage evolution is mapped through discrete APD measurements onto the amplitude of alternans an(ζ), where n = t/τ. This output mapping of the alternating APD length provides an evolution of the amplitude of alternans on a beat-to-beat basis at each point along the cable. Stabilization of alternans in the case of a single cell and in the case of a short cardiac cable given by Eqs.1-2 can be achieved by the boundary perturbation proportional feedback control law. The perturbation proportional feedback is realized by a boundary point measurement of APD, and perturbs the basic pacing period τ at a pacing site (we refer to Tn as an applied PCL period), or in other words:
| (4) |
where τ is the basic pacing cycle period and γ is a tunable parameter which defines the feedback gain of the APD alternation of the basic pacing cycle. It can be demonstrated that such a simple feedback-gain structure can annihilate alternans at the pacing site and up to a finite distance (≤ 1cm) from the pacing site [19, 18]. The stability analysis of a two-dimensional iterative map based on Eqs.3-4 applied to a single cell (or, in other words, zero length cable) yields the following system:
| (5) |
where the fixed point of the system is (APD* = Y*) with the property (APD* = Y*). The Jacobian of the system of Eq.5 is given by:
| (6) |
which yields the range of local stabilization gains γ = (0, 1). Stabilization of a two-dimensional iterative map is ensured when the Jacobian eigenvalues of Eq.6 lie within the unit circle. However, this iterative map stability analysis is valid only for a single paced cell and not for the cable of cells where diffusive coupling among cells and traveling wave morphology change the action potential duration characteristics. In the ensuing subsection, we demonstrate experimental alternans annihilation by feedback control given by Eq.4 in an extracted rabbit heart (Figure 4).
Figure 4.
Figure of the extracted rabbit heart.
2.2 Experimental procedure and results
An isolated rabbit heart, see Fig.4, is used for the experimental realization of pacing protocols that stabilize alternans. New Zealand White rabbits (female, 56 months old) weighing 3 – 5 kg were anesthetized with an intravenous injection of ketamine (10 mg) and xylazine (20 mg) containing 1000 units of heparin. After thoracotomy, the heart was rapidly isolated and the ascending aorta was cannulated and secured for retrograde perfusion with a warm (36.5 ± 0.5°C), oxygenated Tyrode's solution at a rate of 30 – 40 mL/min. To perform optical mapping of voltage V, hearts were stained with the voltage-sensitive dye di – 4 – ANEPPS (Molecular Probes, Eugene, OR). The hearts were illuminated with a solid-state, frequency-doubled laser (Verdi, Coherent, Santa Clara, CA) at a wavelength of 532 nm. The emitted fluorescence was transmitted through a 600-nm long-pass filter and acquired with a charge-coupled device camera (CA–D1–0128T, Dalsa, Waterloo, Canada) from 128 × 128 sites over a 20 × 20mm2 area the of epicardial ventricular surface at 2.0 ms/frame. Optical data were recorded to a personal computer using custom-designed software (LabVIEW, National Instruments, Austin, TX). Cytochalasin D (Sigma, St. Louis, MO; 5 M) was added to the perfusate to inhibit heart contraction. Stainless steel stimulating electrodes (tip diameter 0.20 mm) were placed on the ventricle. A 4 − cm2 stainless wire mesh situated on the left ventricle posterior wall served as a reference electrode. We applied two dynamic pacing protocols at a lateral location on the ventricle with a line array of recording sites of electrical activity placed at the heart surface in proximity to the pacing site:
P1. In the diastolic state (DI), 2× threshold current pulses were applied with the basic pacing cycle lengths (PCLs) of τ = [140, 160, 180, 200ms] with the applied protocol given by Eq.4, with various levels of the feedback gain γ;
P2. Identical protocol as P1, when only positive values of ΔTn = (APDn(ζ=0) − APDn−1(ζ=0)) > 0 are considered with various levels of the feedback gain γ.
In Fig.5 the evolution of the voltage dye sensitive signal in the neighborhood of the pacing site is provided along with APDs which are used by the pacing protocol given by Eq.4. In all experimental realizations, the recordings of the heart surface electric activity used in the pacing control law of Eq.4 were taken from the heart surface site which is closest to the pacing site. Our experimental findings demonstrate for the first time that alternans stabilization can be realized in the rabbit heart tissue. Specifically, Figs.6-7 show the evolution of the amplitude of alternans at four aligned recording sites which undergo stabilization after the control is turned on at 1500msec. One can notice in Fig.7 that before the control is applied, the amplitude of alternans is almost uniform across the length of four recording sites in the case of the shorter pacing cycle length τ = 160msec. Also, the applied control through the perturbation of the basic pacing cycle length of Eq.4 is not robust with respect to noise and to mismatch between pacing and recording sites. Namely, the pacing site is within the tissue since the electrode is attached to the heart muscle, while the recording site used for feedback control is at the heart surface close to the pacing electrode. This mismatch among recording and pacing sites results in a time delay in Eq.4 that may produce destabilizing effects that propagate along with the action potential wave front which propagates at the speed of ≈ 50 − 60 cm/sec. Since the demonstrated experimental findings are realized in an extremely noisy recording environment of electrical closed-loop system activity at the heart surface, small oscillations of the amplitude of alternans (less than 5msec, see Fig.6) appear due to both the inherent noise of our experimental setup and mismatch among the recording and pacing site location. Also, it has been observed that the pacing protocol (P1.) with the basic pacing cycle length of 160msec and 140msec with a feedback gain in the range γ = [0, 1] was more prone to initiate ventricular fibrillation, mainly due to the conduction block induction at the pacing site, compared to the pacing protocol (P2.) with the same basic pacing cycle length and γ values. In the Fig.6-7, it is also shown that the recording site that is more than (1cm) away from the pacing site can not undergo successful alternans annihilation, as the amplitude of alternans exceeds 5msec. This inability to annihilate alternans beyond a certain small characteristic length by model independent self-referencing pacing protocol will be elaborated in the ensuing sections.
Figure 5.
Recorded evolution of the voltage dye signal V(t) (blue line), filtered voltage signal (green line), (Vthreshold = 1367) and associated APD's in the vicinity of the pacing site under the pacing protocol given by Eq.4 with γ = 0.75 and τ = 180msec.
Figure 6.
Evolution of the amplitude of alternans a(nτ) = APDn − APDn−1 at four sites placed in an array 3mm apart from the pacing site under the pacing protocol given by Eq.4 with γ = 0.75 and τ = 180msec (blue solid line-close to the pacing site, red dashed-dotted line-middle recording site, green dashed line-remote site, black line-the most distant recording site from the pacing site ≈ 1.3cm).
Figure 7.
Evolution of the amplitude of alternans a(nτ) = APDn − APDn−1 at four sites placed in an array 4mm apart from the pacing site under the pacing protocol given by Eq.4 with γ = 1 and τ = 160msec (blue solid line-close to the pacing site, red dashed-dotted line-middle recording site, green dashed line-remote site, black line-the most distant recording site from the pacing site ≈ 1.5cm).
2.3 Numerical simulation
In the alternans stabilization numerical simulation study of the model given by Eqs.1-2, we used an identical control law as in the experimental realization which is given by Eq.4. However, in the numerical simulation study we were interested in understanding the effects of large gain perturbation values of basic PCL and to explore the possibility of alternans annihilation in a domain larger than 1cm (which is bigger than the corresponding domain in the experimental system). We constructed a novel pacing protocol that explores the spatial evolution of alternans and uses measurements of alternans far from the pacing site in order to achieve stabilization of alternans in a cable of over 1 cm without inducing the conduction block (e.g., the preceding wave's back collides with the following wave's front). It can be demonstrated that the increase in the feedback parameter γ increases the size of the perturbation around the fixed basic pacing cycle period τ, so that high gain values of negative perturbations are prone to produce a conduction block at the pacing site, see Fig.8 (a stimuli will be applied on the wave back of the preceding wave which is in excitable state and not in the resting state so it will not elicit excitable wave propagation along the cable). Also, the pacing algorithm that takes only positive ΔTn perturbation values, and in the case where the ΔTn is negative, it applies only basic (PCL) τ, may produce a conduction block away from the pacing site (see Fig.9, the 9-th beat in Fig.9 is blocked to propagate along the cable since by its front it encounters less excitable area, which inevitably leads into wave front dissipation).
Figure 8.
Conduction block at the pacing site.
Figure 9.
Evolution of the voltage V(ζ, t) in the cable model of Eqs.1-2 under the pacing protocol given by Eq.4 with γ = 0.4. Note that the 9-th beat propagation along the cable is blocked since its front encounters an 8-th beat wave back.
Therefore, in order to avoid the block at the pacing site and far from the pacing site, one needs to change the basic pacing protocol given by Eq.4 and include a condition that accounts for the conduction block. In order to prevent conduction block, an appropriate measure of the APD at the distant site is obtained. The voltage threshold value for the APD measurements in our numerical simulation is given as −40mV, while the threshold voltage value of Vblock(ζci) = −75 mv is used at a location ζci where conduction block is prevented. Under the assumption that the propagation wave velocity does not vary significantly, which is a reasonable assumption for the length of cardiac relevant tissue size (1 – 5cm), the difference in the APD at the pacing site and far away will create a necessary condition to prevent the block away from the pacing site; in other words the quantity that delays a pacer is defined as ΔT̄ (that is, ΔT̄n(ζci) = APD(−40mV)n−1(ζ=0) − APD(−75mV)n−1(ζci)). Namely, for a short cable length of up to 2.5 cm and τ = 250 msec the pacing protocol that achieves stabilization of amplitude of alternans is defined as follows:
| (7) |
| (8) |
with ΔTn = γ(APDn(ζ=0) − APDn−1(ζ=0)) and ΔT̄n(ζci) = APD(−40mV)n−1(ζ=0) − APD(−75mV)n−1(ζci). When the pacing protocol given by Eqs.7-8 is applied, the pacing algorithm provides a pacing stimuli which does not induce a conduction block (i.e., see Fig.10 where the 9-th beat propagates along the cable, compered to the 9-th beat propagation along the cable in Fig.9 which is blocked since its front encounters an 8-th beat wave back). The conduction block demonstrated in the Fig.9 can not be allowed by any means as it generates spiral wave that may lead into ventricular fibrilation. Therefore, since the pacing algorithm of Eqs.7-8 ensures conduction block prevention at the pacing and away from the pacing site the entire alternans profile is stabilized at the spatially uniform steady state an(ζ) = 0, (where n = t/τ), see Fig.11. In the Fig.10, the voltage evolution in the cable of first 10 beats is presented, while Fig.11 demonstrates that it takes effectively about 30 – 40 beats to bring the amplitude of alternans close to the spatially uniform unstable steady state an(ζ) = 0. Still, it is important to emphasize two points: First, that the pacing protocol constructed in this way prevents conduction block at both the pacing site and at a desired location away from the pacing site. This is achieved by not allowing the shortening of the basic pacing period in the case of a prevention block at the pacing site (Eq.7), while for the prevention of a conduction block at a desired location away from the pacing site, this is achieved by measuring the difference in APDs at the pacing site and at the distant site ζci (Eq.8); see also the 9-th beat wave front in the Fig.10 which just passes close to the 8-th beat wave back. Second, since only positive perturbations are considered in Eqs.7-8, the constrained ability of the control action essentially reduces the space of available control values and places a natural constraint on the length of the cable that can undergo successful alternans annihilation by model-independent cycle-length-perturbation pacing protocol. Therefore, it is clear that model independent pacing protocols which do not incorporate any spatial features in their realization have limited ability in achieving alternans annihilation.
Figure 10.
Evolution of the voltage V(ζ, t) in the cable model of Eqs.1-2 under the pacing protocol given by Eqs.7-8 with γ = 0.71. Note that the 9-th beat propagates along the cable and by its front passes an 8-th beat wave back.
Figure 11.
Boundary stabilization of alternans in the case of cable equation (Eqs.1-2) where the pacing protocol given by Eqs.7-8 is applied with γ = 0.71 and ζc = 1.9 , (n = t/τ).
Remark 1
In light of the experimental implementation, the pacing protocol in the numerical study given by Eqs.7-8 differs by the term ΔT̄n(ζci) from the experimentally applied pacing protocols P1 and P2. In experimental protocols only Eq.7 is used and the term ΔT̄n(ζci) is set to zero. Also, it is important to emphasize that the Noble cardiac cell model used in numerical simulations belongs to the Purkinje fibers cells which conduct the electric pulse faster than the cells of the ventricular walls used in the experiment. In addition, the heart tissue in the experimental setup may exhibit some memory effects.
3 Analysis and control of amplitude of alternans PDE
3.1 Analysis of amplitude of alternans PDE
In this section, we provide an analysis of the amplitude of alternans equation by analyzing the structure of the alternans equation and studying the ability of model-based control to suppress alternans. Namely, associated with Eqs.1-2 is the small amplitude of APD alternans PDE which was developed by Echebarria and Karma [19]. The small amplitude of alternans parabolic PDE is linearized around the spatially uniform steady-state a(ζ, t) = 0 and takes the following form:
| (9) |
| (10) |
| (11) |
where the parameters Da and w are taken to be and w ≈ 2D/c̄ where APDc is the APD evaluated at onset of alternans, and c̄ is the value obtained from a standard dispersion curve that links the propagation speed of the wave front with a local diastolic interval, that is c̄ = fd(DIc), see [23]. Note that in Eq.9 there is no term that accounts for small oscillations of alternans along the cable due to differences in propagation velocity of two consecutive waves. This contribution in Eq.9 can be neglected when the tissue cable length is between 1 – 5 cm, which is the size of a cardiac ventricle of human myocardium that varies within these limits as a function of age [24].
The term v(t) in the PDE of Eq.9 can be inserted into the PDE [21], to yield:
| (12) |
| (13) |
| (14) |
where a(ζ, t) is the state of the PDE, v(t)/τ = v̄(t) ∈ ℝ is the manipulated input, and the parameters D̄a = Da/τ = 0.182/τ, w̄ = w/τ = 0.045/τ, σ̄ = σ/τ = log(1.5)/τ and τ = 250msec are taken as in [19]. We proceed by seeking solution of Eqs.12-13 in the following form , which allows us to formulate the following abstract evolutionary equation:
| (15) |
| (16) |
where the domain of the Sturm-Liouville-operator 𝒜 is defined as follows:
| (17) |
where ℒ2(0, L) denotes, the Hilbert space of measurable square-integrable real-valued functions f : [0, L] → ℝ, such that , with weighted inner product and norm on ℒ2(0, L) defined, respectively, by and . The input operator ℬ is given by inner product as follows
| (18) |
where δ(ζ − ζ0) is an approximated delta function . The function δ(ζ − ζ0) is taken to be nonzero in a finite spatial interval of the form [ζ0 − ε, ζ0 + ε], where ε is a small positive real number, and zero elsewhere. The output operator is parameterized by the locations where measurements of amplitude of alternans are obtained. The point sensor function is given by approximated delta function as , and it is taken to be nonzero in a finite spatial interval of the form [ζc − ε, ζc + ε], where ε is a small positive real number, and zero elsewhere. The output operator is given as:
| (19) |
It can be demonstrated that the Sturm-Liouville operator is a self-adjoint operator on ℒ2(0, L) with respect to an appropriately weighted inner product (ϕi, ϕj)η [21, 25]. Namely, the operator 𝒜 is given, for any function in the domain 𝒟(𝒜) by:
| (20) |
where are continuously differentiable functions on [0, L]. The spectrum of eigenvalues of the operator 𝒜 consists of isolated eigenvalues with finite multiplicity and it is given by
| (21) |
where αn is the solution to the following transcendental equation:
| (22) |
The eigenfunctions and adjoint eigenfunctions for all n ≥ 1, are given by:
| (23) |
where An are nonzero constants, which are calculated by the orthogonality condition (where δij is the Kronecker delta), and are given by,
| (24) |
In the case of a small amplitude oscillation of Eqs.9-10-11 and given parameters, the spectrum of the operator 𝒜 reveals that for L = 2.5 cm, the first three eigenvalues of the operator 𝒜 are unstable (λ1 = 0.0015527, λ2 = 0.0012787, λ3 = 0.00064788), while the remaining infinite eigenvalues are stable (Fig.12). It can also been seen from Fig.12 that the increase in the cable length increases the number of unstable modes of the operator 𝒜 so that for the maximal anatomical length considered which is approximately ≈ 5 cm, five eigenvalues are unstable. Also, in relation to experimental and numerical studies, the tissue characteristic length of approximately 1cm has one eigenvalue unstable which confirms experimental and numerical studies that have demonstrated successful alternans annihilation at this characteristic length.
Figure 12.
Distribution of eigenvalues on the basis of Eq.21 for different lengths of the cable L (1 cm, 2.5 cm, 5 cm); APD profiles of two consecutive beats calculated by Eqs.1-2 and eigenfunctions of unstable eigenmodes of the operator 𝒜 given by Eq.23 for L=2.5.
3.2 State feedback control
In this section, we address the problem of constructing model-based state feedback controllers which can stabilize alternans in the model given by Eqs.9-10. In particular, the eigenspectrum of the dissipative operator of the parabolic PDE of Eqs.12-13-14 provides beneficial structure that can be exploited by a state feedback controller that can achieve the stabilization of the unstable modes, while the stable modes remain invariant under the state feedback control structure. Namely, due to the partitioning of the operator eigenspectrum Ω {𝒜} = Ω+{𝒜s} ∪ Ω−{𝒜f} into a finite dimensional part Ω+{𝒜s} and an infinite dimensional complement Ω−{𝒜f} the formulated control algorithm is finite dimensional and places eigenmodes of the operator 𝒜s at desired locations in the left half of the complex plane. In order to proceed, it is important to assume approximate modal controllability which holds of , for all n ≥ 1 [25]. Hence, it can be easily verified by simple vector algebra that the approximate controllability of the reduced system (𝒜s, ℬs) is satisfied by checking the rank of (that is rank(𝒜s) = rank(Cctrb)). Accordingly, there exists a similarity transformation so that all three unstable states can be controlled from a single input [26]. In other words, by applying the transformation a(t) = T′z(t), Ās = T 𝒜sT′, and B̄s = Tℬs, the linear finite-dimensional system dynamics given by:
| (25) |
can be transformed into a controllable form that couples all three states and provides control from a single input, and is given by:
| (26) |
The simple pole placement gain state feedback control law given by v̄(t) = −Kz(t) places all three eigenmodes at desired locations in the closed-loop, so that λcl = eig {Ās − B̄sK} and the desired locations of the stabilized eigenmodes are given as λcl = [−0.0019 − 0.0025 − 0.0029]. The feedback gain K is given as K = [−0.5845 0.0804 − 0.0080] and the similarity transformation T = [−0.6754 0.7113 −0.1949; 0.5793 0.3482 −0.7370; −0.4563 −0.6106 −0.6472], so that the manipulated input v̄(t) = −KTa(t) = −𝒦a(t) in Eq.25 places the unstable eigenvalues in the closed-loop system at λcl. Therefore, by stabilizing the unstable modes of a finite dimensional subsystem the exponential stabilization of alternans is achieved. However, even though this state feedback controller achieves exponential stability of the closed-loop system, it does excite the evolution of the higher modes of the operator 𝒜. This is reflected in a high excursion of the state from the spatially uniform equilibrium state a(ζ, t) = 0 at both the boundary and far away from the boundary where the control is applied. Fig.13 shows that the amplitude of alternans increases at both the pacing site and far away from it and as a consequence a propagation failure (conduction block) may be created as the amplitude of alternans in neighboring cells undergoes significant value changes (see detailed analysis of the conduction block dynamics in [27]). In particular, the propagation failure at the pacing site may happen as a consequence of a large negative perturbation of the basic pacing cycle length that may place an excitation stimuli at the wave back of the preceding wave which is not in the complete refractory state, see for demonstration Fig.8. Such a stimuli will not elicit a wave to propagate from the pacing site along the cable. Similarly, the propagation failure away from the pacing site may happen as the preceding wave's back can collide with the following wave's front, see for demonstration Fig.9. Another important notion that is revealed from Fig.12 is that the increase in the cable length results in an increase of the number of unstable modes of the operator 𝒜 which needs to be stabilized in order to achieve stabilization along the entire cable length. Moreover, Fig.12 demonstrates that increase of the cable length strengthens the convective nature of the underlying PDE, since the necessary “gap” condition, i.e. that consecutive stable eigenvalues have a sufficiently large separation (see [28], and the appendix of [29]), fails to hold. This condition is difficult to satisfy in systems with strong convective terms and/or a small diffusion parameter. The amplitude equation Eqs.12-13-14 given in the modal form is solved by Galerkin's method (40 eigenfunctions are considered, , see for details [29]) using an explicit Euler time integration scheme (Δt = 1/2max {eig {𝒜}}).
Figure 13.
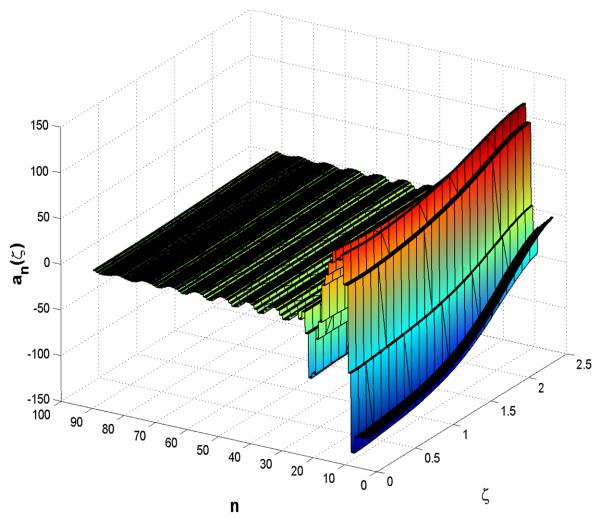
Boundary stabilization of the amplitude equation (Eqs.9-10-11) under state feedback control with initial condition a1(0) = 0.1.
3.3 Output feedback control
A natural extension of the state feedback controller is to extend the synthesis in the cases where only output measurements are used in the feedback structure. In order to do this a state observer of the Luenberger type is considered [30]. Under the assumption of approximate modal observability [25], which holds if , for all n ≥ 1, a linear Luenberger type observer is constructed of the form:
| (27) |
where 𝒞s is the matrix of appropriate dimensions corresponding to the dimensions of the unstable eigenspace Ω+(𝒜) and the number of measurement sensors. In this simulation study, three measurements are used at , where ζci = [0 1.1364 2.2727]. In the case of cable length of L = 2.5 cm there are three unstable eigenvalues. Finally, due to the approximate controllability and observability of (𝒜s, ℬs, 𝒞s), there exist 𝒦 and ℒo such that 𝒜s + ℬs𝒦 and 𝒜s + 𝒞sℒo are exponentially stable. The control gain is chosen to be K = [−0.5845 0.0804 −0.0080] and the closed-loop poles are λcl = [−0.0019 −0.0025 −0.0029]. The gain ℒo is chosen to be ℒo = [0.0015 0.0016 0.0004; 0.0023 − 0.0001 − 0.0006; 0.0014 −0.0010 0.0003] and the estimation error poles are chosen as λℒo = −[0.0025 0.003 0.0035]. In the Fig.14 the successful stabilization of amplitude of alternans is demonstrated by the output feedback control law. The effect of noise in the output feedback controller realization is demonstrated in the Fig.15 which demonstrates that the presence of even small noise prevents successful alternans annihilation.
Figure 14.
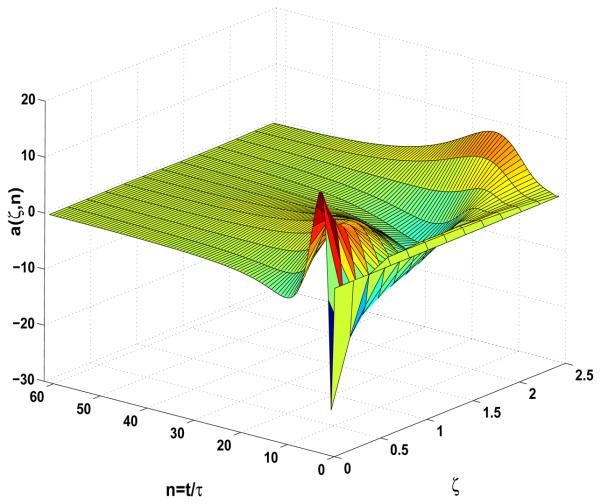
Boundary stabilization of the amplitude equation Eqs.9-10-11 under the output feedback v(t) = −𝒦â(t) with initial condition a1(0) = 0.1.
Figure 15.
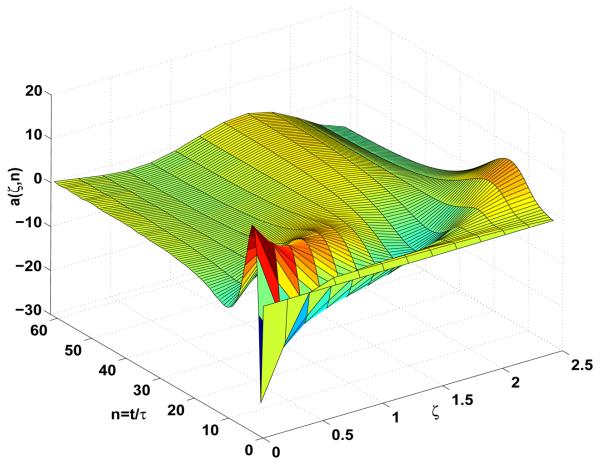
Boundary stabilization of the amplitude equation of Eqs.9-10-11 under the output feedback v̄(t) = −𝒦â(t) with a measurement noise level of ϱ(t) ≤ 0.02 and with initial condition a1(0) = 0.1.
Remark 3
Above we demonstrated alternans annihilation by full state feedback control and output feedback control, where it was assumed that the evolution of alternans is known in the case of state feedback control, while in the output feedback control case alternans were measured at three appropriately chosen locations. In light of experimental and numerical studies, our controller design which is based on the model of Eqs.9-10-11 is a special case of the single point measurement gain based output feedback controller of the form v(t) = −γa(ζm, t). The amplitude of alternans is measured in the case of the experimental study in the vicinity of the pacing cite while in the numerical study it is obtained at the pacing site. In this case, it is obvious that a single measurement provides a gain based feedback that can only stabilize a single unstable mode and as unstable modes appear as a function of the length of the tissue size considered, see Eq.21 and Fig.12, such a local feedback fails to stabilize cable tissue longer than 1cm. Therefore, it is important to point out that any feedback control law must utilize more measurements in order to achieve successful stabilization, or the number of measurements applied must be at least equal to the number of the unstable modes. Only under this condition of observability of unstable modes subsequent stabilizability of the system can be ensured. Previous studies failed to address that inherent limitation of the collocated recording and pacing site control law feature in the perturbation feedback control law of Eq.4.
Remark 4
It is important to address the issue of noise in the framework of the output feedback controller design. Namely, the sensitivity of the closed-loop system to noisy measurements is very high. Specifically, a small amount of noise introduced at the boundary where the control is applied will generate perturbations that will form a standing wave, which is usually a crude approximation of a linear combination of the eigenfunctions corresponding to the unstable modes. This effect is indeed observed in the experimental realization of pacing protocols that measure the amplitude of alternans at the pacing site and apply a self-referencing gain feedback close to the pacing site. In the simulation studies, it is demonstrated that the noise level that will produce the unstable standing wave solution under output feedback control is very low, see Fig.15. Therefore, when the impact of noisy measurements at the output is included in the output feedback controller realization, simulation studies demonstrate that the stabilization of spatially uniform steady-state of cardiac alternans can not be achieved. Namely, for the random noise perturbation with magnitude ϱ(t) ≤ 0.02, that is yϱ(t) = y(t) + ϱ(t) in Eq.27, the output feedback fails to stabilize alternans, giving rise to a standing wave solution instead, see Fig.15. This strongly advocates that the current collocated pacing and measurement site experimental realizations of pacing protocols, can produce small perturbations which will be amplified, and subsequently produce failure of alternans stabilization. Small destabilizing perturbations in the closed-loop system may be attributed to two factors: the first is inherent noise due to the finite accuracy in the measurements, and the second is small time delay in the realization of close but different locations of measuring and pacing cites. Therefore, one can regard that these two effects when combined may be responsible for the creation of destabilizing effects in the closed-loop system.
Remark 5
One important point from a controller synthesis perspective is to connect the diffusion-reaction mechanism of voltage propagation given by Eqs.1-2 with the amplitude of alternans equation given by Eqs.9-10-11. In the diffusive coupled cardiac cell model of Eqs.1-2 excitable waves are traveling from the pacing site along the cable and the amplitude of alternans is generated by two consecutive beats; this property of the model of Eqs.1-2 does not have a corresponding feature in the amplitude of alternans PDE equation of Eqs.9-10-11. The discrete nature of the amplitude of alternans an(ζ) is approximated with the continuous representation a(ζ, t) in Eqs.9-10-11. Hence, the amplitude of alternans PDE of Eqs.9-10-11 does not provide enough information on how to apply control and handle the presence of constraints in the system (e.g., conduction block) as it is the case for the amplitude of alternans an(ζ) generated from the cardiac cell model of Eqs.1-2. However, since constraints are naturally present, the controller synthesis based on the model given by Eqs.9-10-11 must include them in its realization in order to be relevant for implementation in the cell cable model of Eqs.1-2. This implies that a model-based optimal constrained controller synthesis needs to be invoked in order to successfully achieve alternans control. In particular, the model predictive control (MPC) methods for parabolic PDEs [31, 32, 33, 34] can be used in the alternans control problem since it can explicitly account for state and input constraints in its formulation.
4 Concluding remarks
Our experimental work has demonstrated real time stabilization of the cardiac alternans in an intact rabbit heart. Although our experimental work addresses only alternans stabilization that is recorded at the surface of the optically mapped rabbit heart, we believe that the interior of the heart close to the recording sites also undergoes successful alternans stabilization. In our experimental findings the alternans annihilation is demonstrated with model-independent self referencing proportional perturbation feedback of the basic pacing cycle length that is successful in alternans annihilation up to a certain length of the cardiac tissue. Our results are in agreement with other similar experimental [18] and theoretical results [19]. However, our experimental findings are obtained by a novel pacing protocol that prevents the occurrence of the conduction block at the pacing site. Complementary numerical analysis for the ionic 1D cardiac cell cable model supports the experimental findings in that when only positive perturbations are applied in the feedback control law the negative effect of possible conduction block or fibrillation induction may be prevented.
Furthermore, the analysis of the associated amplitude of alternans linear PDE reveals that the boundary stabilization of the parabolic PDE can be easily achieved by stabilizing the unstable modes of the dissipative evolutionary operator, provided that the entire state measurement is utilized in the feedback control structure. The analysis demonstrates that the boundary input injection has an effect on all modes of the evolutionary operator and that it is not selective since the operator's eigenfunctions do not vanish at the boundary where the pacing is applied, (i.e., ). This finding that the boundary input injection has an effect on all modes of the evolutionary operator is contrary to the findings in [19] where the claim was made that only the first eigenvalue of the evolutionary operator can be stabilized. In addition, this finding advocates that the stabilization of the alternans amplitude can be achieved in a longer cable when the entire state and not only point-measurement point-control feedback structure is used. The knowledge of the entire state of alternans can be reconstructed from the real-time measurements and used in a model-based control algorithm.
Furthermore, the pacing control algorithm that uses the pacing site measurement of the amplitude of alternans achieves stabilization only in a certain size domain tissue, since increase in the gain parameter γ can not achieve stabilization of alternans in cables of arbitrary lengths. This is due to the fact that the number of measurements which must be used in the feedback realization must be at least equal to the number of unstable modes. That is why the boundary point measurement of the amplitude of alternans can stabilize only a single mode and confirms that when we increase the length of the tissue beyond the length of 1 cm (see eigenvalue distribution in Fig.12), a model-based control algorithm that is realized with more measurements must be used in order to annihilate alternans. We also demonstrated state and output feedback control that achieve alternans stabilization in the cardiac relevant cable length.
Finally, the current inability of pacing algorithms to control alternans in the longer tissue size stems from neglecting the spatial evolution of alternans. Another factor that also impacts the ability of the controller to suppress alternans is the need to account for the occurrence of the conduction block and the limited ability to measure and utilize the relevant evolution of the alternans in the entire domain in the pacing based alghorithms (a single point measurement of APDs leads to a feedback signal which allows stabilization of only one unstable mode). Therefore, this strongly advocates that the spatiotemporal control of cardiac alternans must be posed as a model-based optimal constrained control problem that accounts for the rate of stabilization and for the constraints imposed on the available control input and spatial evolution of alternans.
Figure 16.
Manipulated input profiles under output feedback control with the additive noise (dotted-line) and under full state feedback control (solid-line). Both controllers are applied to the amplitude of alternans equation of Eqs.9-10.
References
- 1.Zipes DP, Wellens HJ. Sudden cardiac death. Circulation. 1998;98:2334–2351. doi: 10.1161/01.cir.98.21.2334. [DOI] [PubMed] [Google Scholar]
- 2.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrilation. Circulation. 1999;99:1385–1395. doi: 10.1161/01.cir.99.10.1385. [DOI] [PubMed] [Google Scholar]
- 3.Cao JM, Qu Z, Kim YH, Wu TJ, Garfinkel A, Weiss JN, Karagueuzian HS, Chen PS. Spatiotemporal heterogenity in the induction of ventricular fibrillation by rapid pacing: importance of cardiac restitution properties. Circulation Research. 1999;84:1318–1331. doi: 10.1161/01.res.84.11.1318. [DOI] [PubMed] [Google Scholar]
- 4.Pastore JM, Girouard SD, Laurita KR, Akar FG, Rosenbaum DS. Mechanism linking T-wave alternans to the genesis of cardiac fibrilation. Circulation. 1999;99:1385–1394. doi: 10.1161/01.cir.99.10.1385. [DOI] [PubMed] [Google Scholar]
- 5.Rosenbaum DS, Jakson LE, Smith JM, Garam H, Ruskin JN, Cohen RJ. Electrical alternans and vulnerability to ventricular arrhythmias. The New England Journal of Medicine. 1994;330:235–241. doi: 10.1056/NEJM199401273300402. [DOI] [PubMed] [Google Scholar]
- 6.Nolasco JB, Dahlen RW. Journal of Applied Physiology. 1968;25:191. doi: 10.1152/jappl.1968.25.2.191. [DOI] [PubMed] [Google Scholar]
- 7.Karma A. Electrical alternans and spiral wave breakup in cardiac tissue. Chaos. 1994;4(3):461–472. doi: 10.1063/1.166024. [DOI] [PubMed] [Google Scholar]
- 8.Qu ZL, Garfinkel A, Chen PS, Weiss JN. Mechanism of discordant alternans and induction of reentry in simulated cardiac tissue. Circulation. 2000;102(14):1664–1679. doi: 10.1161/01.cir.102.14.1664. [DOI] [PubMed] [Google Scholar]
- 9.Ott E, Grebori C, York J. Controlling chaos. Physical Review Letters. 1990;64:1196. doi: 10.1103/PhysRevLett.64.1196. [DOI] [PubMed] [Google Scholar]
- 10.Hall GM, Gauthier DJ. Experimental control of cardiac muscle alternans. Physical Review Letters. 2002;88:198102. doi: 10.1103/PhysRevLett.88.198102. [DOI] [PubMed] [Google Scholar]
- 11.Hall GM, Gauthier DJ. Stabilizing unstable periodic orbits in fast dynamical systems. Physical Review E. 1994;50:3234. doi: 10.1103/physreve.50.3245. [DOI] [PubMed] [Google Scholar]
- 12.Hall K, Christini DJ, Tremblay M, Collins JJ, Glass L, Billette J. Dynamic control of cardiac alternans. Physical Review Letters. 1997;78:4518–4521. [Google Scholar]
- 13.Socolar JE, Gauthier DJ. Analysis and comparison of multiple-delay schemes for controlling unstable fixed points of discrete maps. Physical Review E. 1998;57:6589. [Google Scholar]
- 14.Tolkaceva EG, Romeo MM, Guerraty M, Gauthier D. Condition for alternans and its control in a two-dimensional mapping model of paced cardiac cells. Physical Review E. 2004;69:031904. doi: 10.1103/PhysRevE.69.031904. [DOI] [PubMed] [Google Scholar]
- 15.Christini DJ, Collins JJ. Real-time, adaptive, model-independent control of low-dimensional chaotic and nonchaotic dynamical systems. IEEE Transactions on Circuits and Systems. 1997;44:1027. [Google Scholar]
- 16.Jordan PN, Christini DJ. Adaptive diastolic interval control of cardiac action potential duration alternans. Journal of Cardiovascular Electrophysiology. 2004;15:1177. doi: 10.1046/j.1540-8167.2004.04098.x. [DOI] [PubMed] [Google Scholar]
- 17.Garfinkel A, Spano M, Ditto WL, Weiss JN. Controlling cardiac chaos. Science. 1992;257:1230–1235. doi: 10.1126/science.1519060. [DOI] [PubMed] [Google Scholar]
- 18.Christini DJ, Riccio ML, Culianu CA, Fox JJ, Karma A, Gilmour RF. Control of electric alternans in canine cardiac purkinje fibers. Physical Review Letters. 2006;96:104101. doi: 10.1103/PhysRevLett.96.104101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Echebarria B, Karma A. Spatiotemporal control of cardiac alternans. Chaos. 2002;12:923–930. doi: 10.1063/1.1501544. [DOI] [PubMed] [Google Scholar]
- 20.Hall G, Gauthier D. Experimental control of cardiac muscle alternans. Physical Review Letters. 2002;88:198102. doi: 10.1103/PhysRevLett.88.198102. [DOI] [PubMed] [Google Scholar]
- 21.Ray W. Advanced Process Control. McGraw-Hill; New York, New York: 1981. [Google Scholar]
- 22.Noble D. A modification of the Hodgkin-Huxley equations applicable to purkinje fibre action and pace-maker potentials. Journal of Physiology. 1962;160:317–352. doi: 10.1113/jphysiol.1962.sp006849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Echebarria B, Karma A. Instability and spatiotemporal dynamics of alternans in paced cardiac tissue. Physical Review Letters. 2002;88:208101. doi: 10.1103/PhysRevLett.88.208101. [DOI] [PubMed] [Google Scholar]
- 24.Oh JK, Seward JB, Tajik AJ. The Echo Manual. Lippincott Williams & Wilkins; 1999. [Google Scholar]
- 25.Curtain RF, Zwart H. An Introduction to Infinite-Dimensional Linear Systems Theory. Springer-Verlag; New York: 1995. [Google Scholar]
- 26.Antsaklis PJ, Michel AN. Linear Systems. McGraw-Hill; New-York: 1997. [Google Scholar]
- 27.Henry H, Rappel W-J. Dynamics of conduction block in a model of paced cardiac tissue. Physical Review E. 2005;71:051911. doi: 10.1103/PhysRevE.71.051911. [DOI] [PubMed] [Google Scholar]
- 28.Temam R. Infinite-Dimensional Dynamical Systems in Mechanics and Physics. Springer-Verlag; New York: 1988. [Google Scholar]
- 29.Christofides PD. Nonlinear and Robust Control of PDE Systems: Methods and Applications to Transport-Reaction Processes. Birkhäuser; Boston: 2001. [Google Scholar]
- 30.Dochain D. State observation and adaptive linearizing control for distributed parameter (bio)chemical reactors. International Journal of Adaptive Control and Signal Processing. 2001;15:633–653. [Google Scholar]
- 31.Dubljevic S, El-Farra NH, Mhaskar P, Christofides PD. Predictive control of parabolic PDEs with state and control constraints. International Journal of Robust and Nonlinear Control. 2006;16:794–772. [Google Scholar]
- 32.Dubljevic S, P. M, El-Farra NH, Christofides PD. Predictive control of transport-reaction processes. Computers & Chemical Engineering. 2006;29:2335–2345. [Google Scholar]
- 33.Dubljevic S, Christofides PD. Predictive output feedback control of parabolic PDEs. Industrial & Engineering Chemistry Research. 2006;45(25):8421–8429. [Google Scholar]
- 34.Dubljevic S, Christofides PD. Predictive control of parabolic PDEs with boundary control actuation. Chemical Engineering Science. 2006;61:6239–6248. [Google Scholar]