Abstract
Phase response curves (PRCs) have been widely used to study synchronization in neural circuits comprised of pacemaking neurons. They describe how the timing of the next spike in a given spontaneously firing neuron is affected by the phase at which an input from another neuron is received. Here we study two reciprocally coupled clusters of pulse coupled oscillatory neurons. The neurons within each cluster are presumed to be identical and identically pulse coupled, but not necessarily identical to those in the other cluster. We investigate a two cluster solution in which all oscillators are synchronized within each cluster, but in which the two clusters are phase locked at nonzero phase with each other. Intuitively, one might expect this solution to be stable only when synchrony within each isolated cluster is stable, but this is not the case. We prove rigorously the stability of the two cluster solution and show how reciprocal coupling can stabilize synchrony within clusters that cannot synchronize in isolation. These stability results for the two cluster solution suggest a mechanism by which reciprocal coupling between brain regions can induce local synchronization via the network feedback loop.
Keywords: neuronal networks, synchronization, clustering, phase response curves, pulse coupled oscillators
Introduction
There are many examples of synchronization in the nervous system. Transiently synchronized assemblies of neurons are believed to underlie cognitive functions (Buzsaki, 2006). Central pattern generating networks (Marder and Calabrese, 1996) that underlie repetitive motor behavior frequently exhibit phase-locking between synchronized groups of neurons. Locking between clusters of similar or disparate populations may be widespread in the nervous system. There are two major motivations for studying phase locking between synchronized clusters. The first is that transitions between one and two cluster states may be a general mechanism for shifts in population rhythms. The second is that reciprocal coupling between two disparate brain regions may result in local synchrony within each of the two populations.
In a population of similar neurons, a single, globally-synchronous cluster would produce a population frequency as measured by the local field potential that is equal to the frequency of a single neuron. On the other hand, two synchronized clusters in which the two clusters are out of phase with each other would produce a local field potential at a population rhythm that is twice that of an individual neuron. Pervouchine et al. (2006), postulate that a synchronized population of entorhinal stellate cells breaks up into two similar clusters, with each cluster firing at theta frequency in anti-phase with the other cluster. This hypothesis was invoked to explain a beta peak observed by Cunningham et al. (2004) in slices of entorhinal cortex in which the individual neurons presumably fired at theta frequency. Similarly, Terman et al. (1996), proposed that the frequency of sleep spindles is twice that of the delta rhythm because the thalamocortical cells, which fire individually at delta frequencies, split into two clusters firing in anti-phase during sleep spindles.
The two cluster analysis can also apply to two populations that are not similar to each other. It has been proposed that a population of synchronized inspiratory neurons in the preBotzinger Complex phase lock with a population of synchronized expiratory neurons in the para-facial expiratory group during normal respiratory rhythmogenesis (Janczewski and Feldman, 2006; Joseph and Butera, 2005; Mellen et al., 2003). For a pathological example, phase-locking between a locally synchronized population of cortical neurons and a population of locally synchronized thalamic neurons has been proposed as a mechanism for absence epileptic seizures (Velasquez et al., 2007).
A phase resetting curve (PRC) keeps track of how an input to a periodically firing neuron advances or delays the next action potential depending upon the phase at which the input arrives. In order to apply the PRC to the analysis of a network, a simplifying assumption is required. Usually, the coupling between neurons is assumed to be either weak (Ermentrout and Kopell, 1991; Rinzel and Ermentrout, 1998) or pulsatile (Achuthan and Canavier, 2009; Acker et al., 2003; Canavier et al., 1997; Dror et al., 1999; Goel and Ermentrout, 2002; Netoff et al., 2005b; Oprisan et al., 2004; Sieling et al., 2009). Since neurons communicate via discrete, all or nothing signals called action potentials or spikes, here we approximate their coupling as pulsatile. Under the assumption of pulsatile coupling, the input used to generate the PRC in an isolated neuron should be similar to that received within the network.
The immediate motivation for this study was the counterintuitive empirical discovery that the two cluster solution can be stable in a four neuron all to all network in which two isolated neurons cannot synchronize (Achuthan and Canavier, 2009). This study also identified cluster solutions in which the isolated cluster could exhibit stable synchrony. The latter result was not surprising and was predicted using an analysis that treated interactions within a cluster and those between clusters as independent. Although this approach generally succeeded for the case in which the isolated cluster could be synchronized, it failed in some cases in which the isolated cluster could not synchronize itself. The analysis in this study uses PRCs and the assumption of pulsatile coupling to correctly predict the stability of the two cluster solution by considering between and within cluster interactions simultaneously during a perturbation of a single neuron within one cluster from the phase locked two cluster solution. Although the analysis was developed to explain a two cluster solution in a neural circuit, it is applicable to any system of pulse coupled oscillators (Goldsztein and Strogatz, 1995; Peskin, 1975; Wu and Chen, 2007).
Methods
Application of the open loop PRC to the analysis of circuits with pulsatile coupling
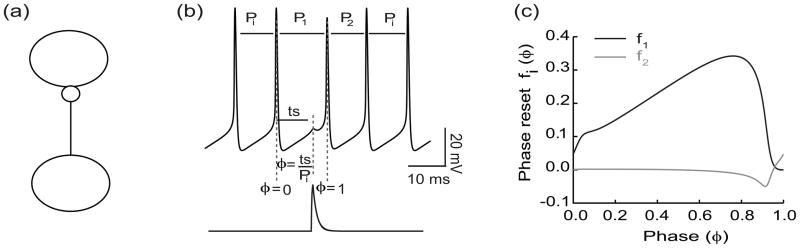
Phase resetting theory was developed in the context of limit cycle oscillators (Glass and Mackey, 1988; Winfree, 2001), that are externally perturbed. The perturbations are presumed to affect only the phase and not the amplitude of the oscillation; the phase is advanced if a perturbation causes motion along the limit cycle in the direction of the trajectory, whereas it is delayed if the motion is in the opposite direction. We define the phase modulo 1, such that it is zero at the beginning of a cycle and 1 at the end. In a neural context, we assign a phase of zero to each upward crossing of the spike threshold. Each type of input that a neuron will receive in a network is used as the perturbation to measure a PRC (Fig. 1) in the open loop configuration with no feedback. The unperturbed cycle length is Pi, the length of the cycle that contains the perturbation is P1 and the subsequent cycle length is P2. The open loop stimulus interval ts is the elapsed time between the most recent firing of the oscillator and the time that the perturbation is applied. The phase φ is the normalized stimulus interval ts/Pi. The first order phase resetting is given by the equation f1(φ) = (P1 − Pi)/Pi and the second order resetting is denoted by f2(φ) = (P2 − Pi)/Pi. The total, or permanent resetting is presumed to be the sum of the first and second order resetting and to be periodic in phase.
Fig. 1.
Direct Measurement of the PRC. a) Open loop configuration without feedback. b) Lower trace depicts the activation of a postsynaptic conductance resulting from a spike in the presynaptic neuron. Upper trace shows the response to the input (perturbation) is delivered at a phase of φ= ts/Pi, which is an open loop stimulus interval (ts) after the reference spike normalized by the intrinsic period Pi. A phase of zero is taken as an upward crossing of a threshold (−14 mV in this example). C) The kth order phase resetting is given by fk(φ) = (Pk − Pi)/Pi.
We make the following assumptions in order to apply the PRCs for isolated neurons to the analysis of a network in which the neurons are coupled. 1) Each component of the network is a pacemaker (Winfree, 1967), that is, a limit cycle oscillator, and remains so in the circuit. 2) The effect of a single perturbation dies out before the next input is received. This implies that a perturbed oscillator returns rapidly to the limit cycle, otherwise the phase would be undefined at the time the input is received, because the PRC as measured is only defined on the limit cycle. 3) The perturbations that the oscillator receives in a closed circuit are similar to the ones used to generate the appropriate open loop PRCs. By similar, we mean that the synaptic conductance waveform evoked by an action potential in the closed circuit is similar in shape (duration, amplitude, etc.) to that evoked by a free running action potential. Physiologically, this implies that the time course of transmitter release is similar in the closed circuit as in the open circuit. With spiking neurons, this is very likely, as the duration and amplitude of an action potential are not likely to be sufficiently altered by feedback in a circuit to make much difference.
Existence criteria for the two cluster solution
The key idea with respect to our analysis of pulse coupled networks of oscillators is that all information required to predict the activity of the network is contained in the phase resetting curves (PRC) measured for each isolated oscillator in response to each input perturbation that it is likely to receive in the network. For a given specific firing pattern, the PRC can be used to construct a discrete map of the firing intervals.
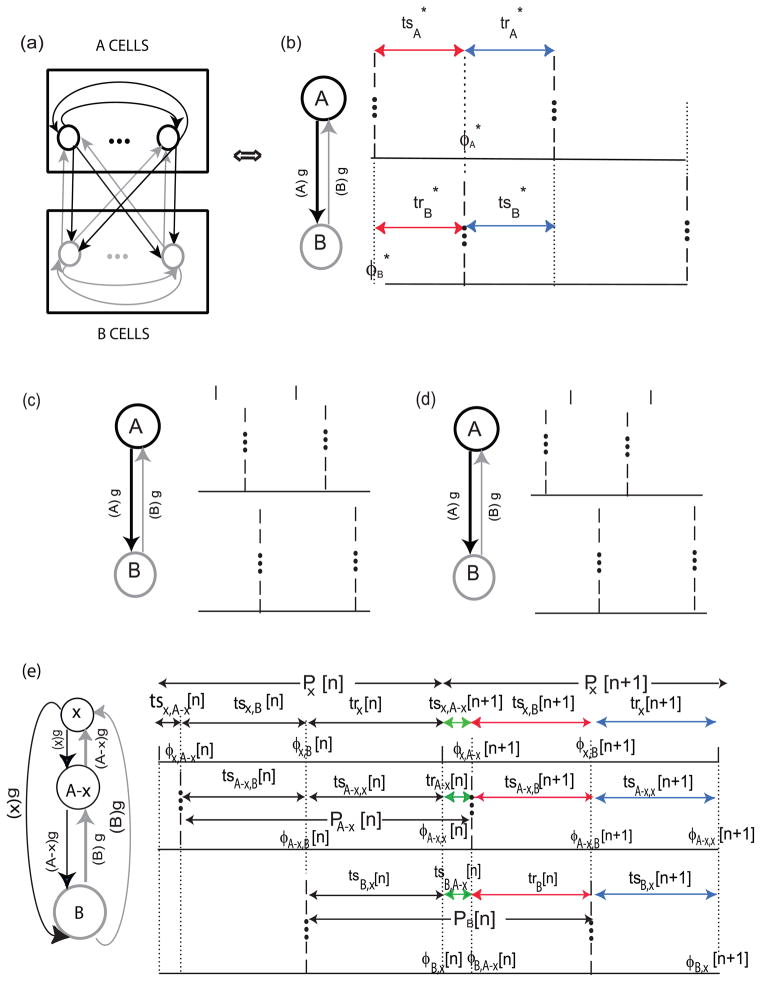
We assume two clusters that we will call cluster A and cluster B (Fig. 2a). The neurons within each cluster are assumed to be identical and identically coupled. However, neurons in one cluster are not necessarily identical to those in the other cluster nor is the coupling necessarily identical, that is, the synapses that emanate from neurons in one cluster do not have to be the same type as those emanating from the other cluster indicated by connections in black and grey. We assume a 1 : 1 phase locked firing pattern in which the cells within each cluster fire synchronously with respect to one another, but out of phase with respect to the other cluster (Fig. 2b). In order to identify possible two cluster modes, we consider each cluster as a single oscillator. In the inset to Fig. 2b, the labels (A)g and (B)g indicate that the synaptic conductance activated in each cluster when the other cluster fires is equal to the number of neurons (A or B) in the other cluster times the conductance of a single synapse g. In practice (Achuthan and Canavier, 2009), the PRC for the cluster can be approximated (see Fig. 3) by the PRC for a single neuron within the cluster (Pervouchine et al., 2006) in response to the aggregate input from the other cluster. This approximation is not critical to the analysis because for computational models at least, the PRC of the entire cluster could be measured if desired.
Fig. 2.
Two Cluster Mode Firing Pattern. (a) All to all circuit with identical coupling strength g. Each neuron within cluster A synapses (black arrows) on every other neuron in cluster A as well as on each neuron in cluster B. Similarly, each neuron within cluster B synapses (grey arrows) on every other neuron in cluster B as well as on each neuron in cluster A. The dots represent an unspecified number of additional neurons in each cluster. (b) Unperturbed firing pattern. In order to find the fixed point ), each cluster is considered as a single oscillator receiving a single synchronous synaptic input whose conductance strength g is scaled by the number of neurons in the other cluster: (A)g or (B)g. The stimulus (ts) and recovery (tr) intervals indicated in the same color (red or blue) are equal by definition. (c,d) Perturbation of the Firing Pattern. A group of neurons in cluster A is presumed to be slightly advanced (c) or slightly delayed (d) from the firing of the rest of cluster A − x. (e) A map of the perturbed firing pattern, with the perturbed sub-cluster x considered as a separate oscillator. There are nine named intervals on each cycle and six phases at which inputs are received on each perturbed cycle φij[n] (shown as dashed vertical lines) which denotes the phase at which neuron or cluster i receives input from neuron or cluster j. The three different colors (red, green or blue) indicate the equivalency of each set of intervals. These are used to reduce the complexity of the map as described in the text.
Fig. 3.
The PRC of a Cluster Approximated by the PRC of a group of neurons x. The input perturbation is the same in all three cases, to cluster A, cluster A minus x neurons and perturbed neurons x from cluster A. Within cluster effect on the PRC are neglected to simplify analysis.
The firing pattern in Fig. 2b represents a steady firing pattern after the transients due to initial conditions have dissipated and the resetting experienced by each oscillator leads to a common network period. In this firing pattern, the neurons in cluster A ( or B) receive an input from the other cluster at a phase . The stimulus interval (tsi) is the time elapsed between when oscillator i fires and when it received an input, and the recovery interval (tri) is time elapsed between when an input is received and the next time that the oscillator fires. By definition, the recovery interval in each neuron is equal to the stimulus interval in the other.
| (1) |
| (2) |
We now make use of the assumption of pulsatile coupling, that the effect of one input has died out before the next is received, in order to express the firing intervals in terms of the PRCs. The recovery interval is the time remaining until the end of the unperturbed cycle plus the first order resetting from the input received from the partner cluster at phase . The stimulus interval in the closed loop network is the open loop stimulus interval plus the first order resetting at zero due to all the other neurons in the same cluster firing simultaneously, as well as the second order resetting from the most recent firing of the partner cluster at phase . In this scheme, the second order resetting from the input in one cycle must be complete by the end of the stimulus interval in the next. Together the stimulus and recovery intervals in each oscillator constitute a cycle period, and the expressions for each of them is given below where PA and PB are the intrinsic periods of oscillators A and B respectively.
| (3) |
| (4) |
| (5) |
| (6) |
where fk,i,j is the kth order resetting in the ith cluster produced by an input from the jth cluster.
A graphical method (Oprisan et al., 2004; Sieling et al., 2009) can be used to find the possible phase locked modes by setting up curves comprised of (tsA, trA) and (trB, tsB) pairs and finding the intersections at which the existence criteria are satisfied for the alternating between cluster firing pattern. These intersections yield the pairs used in the next section. Since we have assumed that all neurons within a cluster are identical and identically coupled, the existence of within cluster synchrony is assured by symmetry, in that identical neurons receiving an identical input at phase 0 are guaranteed to have the same cycle length.
Criteria for stability of the two cluster solution
In this section, we analyze the stability of the cluster mode in which the phasic relationships are given by as determined above. In order for any phase locked mode to be stable, it must be robust to small perturbations. There are multiple ways in which to perturb the two cluster solution and to ensure stability the solution should be robust to all perturbations. In previous work (Achuthan and Canavier, 2009), two perturbations were applied separately to determine within and between cluster stability. For the former, a single oscillator was perturbed from each isolated cluster, and for the latter, each cluster was perturbed slightly from the steady phases while assuming neurons within a cluster remained synchronized if synchrony was stable in the isolated cluster. As stated in the introduction, this approach did not give correct stability results for cluster modes in which the isolated clusters could not synchronize. Therefore we took a different approach here. Cluster B was assumed to remain synchronized, as shown by the firing pattern in Fig. 2(c and d), but a group of neurons was perturbed from one cluster A such that we now have two sub-clusters x and A − x. There are two variants of this perturbation, one in which cluster x leads and one in which cluster A − x leads. We used linear systems theory to determine whether the perturbation grows indicating that the mode is unstable, or decays indicating stability. The logic is similar to that of the proof previously given for global synchrony (Achuthan and Canavier, 2009).
We do not determine a steady state or fixed point for the perturbed firing pattern directly, but simply assume that the fixed point is the one determined for the unperturbed one (Fig. 2(b)), hence we ignore the change in the inter-cluster effects in cluster A-x in the perturbed pattern. Each neuron or cluster receives two inputs per cycle. Two stimulus intervals and a single recovery interval are therefore defined for each oscillator, which can in this instance contain x, A − x or B neurons, for a total of nine intervals per cycle as shown in Fig. 2(e). All stimulus intervals are subscripted such that the first subscript reflects the postsynaptic oscillator and the second subscript denotes the presynaptic oscillator. In the recovery intervals, the subscript indicates the postsynaptic oscillator. The following equations define the time intervals in Fig. 2(e) in terms of the PRCs under the assumption of pulsatile coupling.
| (7) |
| (8) |
| (9) |
In contrast to the intervals in Fig. 2b, the intervals are not assumed to be at steady state, but a map is constructed from the intervals indexed by cycle [n] to those indexed by cycle [n + 1] accounting for the evolution of the intervals in time. The recovery intervals are defined as the time remaining in the unperturbed cycle when the last (second) input is received in cycle [n], plus the first order resetting due to the last input. The first stimulus interval is the elapsed time between the previous firing time of the oscillator and the first input, plus the second order resetting due to the last input in the previous cycle. However, the xth and (A − x)th oscillators fire nearly synchronously, and thus one will get an input very late in the cycle when second order resetting is at its maximum. On the other hand, firing between clusters is not presumed to be nearly synchronized, so second order resetting terms from the other cluster will always be ignored. In order to honor the assumption that the effect of one input dies out before the next one is received, the second order resetting due to the first input in each cycle is always ignored no matter the source. Thus the expression for the second stimulus interval is simply the period times the difference in the phases at which the two inputs are received plus the first order resetting due to the first input. Therefore we end up with a single second order term, which occurs in the expression for tsA−x,B[n] and is due to the second order resetting due to the effect of the leading subcluster on the lagging subcluster within the perturbed subcluster A.
Additionally the following expression for the length of each cycle in the ith cluster results from summing the three intervals for each oscillator described above:
| (10) |
Pi refers to the intrinsic period of the neurons in the ith cluster. In a one to one locking, by definition the network period is the same for both neurons. fk(φij[n]) refers to the kth order reset in the ith neuron/cluster produced by firing of the jth neuron/cluster in the nth cycle. The ‘ij’ indices are only omitted from f if they are obvious from the argument.
The following equations give a discrete map of the time intervals from one cycle to the next for the firing pattern shown in Fig. 2(e). This is the simplest formulation we could obtain to analyze stability. Other, equivalent derivations are possible but will yield the same unique stability results.
The map is as follows:
| (11) |
| (12) |
| (13) |
| (14) |
Of the nine intervals that are defined on each cycle, three sets of three of these intervals are equal by definition. Equal intervals are indicated in the same color (red, brown, or green) in Fig. 2(e). As the green intervals go to zero, the firing pattern in Fig. 2(b) is recovered as indicated below:
| (15) |
| (16) |
| (17) |
Fig. 2e shows a perturbation in which cluster x receives an input at 0+ and cluster A − x receives an input at 1−, but the case in which the firing order is reversed must also be considered as shown in Fig. 2d. Therefore we evaluate the phasic relationship between the perturbed cluster x and the cluster to which it belongs at 0+ and 1− (and 1− and 0+) to determine the stability of the cluster mode. The phases between the clusters are evaluated at and as described in the previous section.
Results
In the firing mode given in Fig. 2(e) since each cluster receives two inputs, there are six phase variables φx,A−x, φx,B, φA−x,B, φA−x,x, φB,x, φB,A−x. These variables are not all independent, and the system can be reduced to two phase variables using algebraic substitutions. The stability criteria for the two cluster solution can be obtained by expressing the perturbations of the phase variables in their [n + 1]th cycle in terms of the perturbations of the phases variables in the [n]th cycle. First we assume a perturbation about the fixed point determined as described in the previous section: . We substitute for each φij[n] the linearized quantity . We then linearize each PRC about the fixed point such that and cancel the steady state terms to obtain the linear system as shown below. We denote by the slope term mkij where mkij is the slope of fk at phase , for the kth order resetting of cluster i when it receives input from cluster j.
As explained in detail in Appendix C, we can reduce the original six dimensional problem to two dimensions in terms of the phase variables φx,B and φA−x,B only:
| (18) |
| (19) |
Note that the intrinsic periods of the individual neurons do not appear in the above two equations because they cancel out (see Appendix C). The two equations (18) and (19) constitute a discrete time linear system of the form
where S is a 2 × 2 matrix and Δ[n + 1] = [Δφx,B[n + 1], ΔφA−x,B[n + 1]]T. The matrix S can be expressed as follows,
| (20) |
where
The characteristic polynomial corresponding to the matrix is quadratic and is given by,
| (21) |
The eigenvalues of the matrix S determine the stability of the cluster mode. If |λmax| is less than one we can conclude that the clustered solution is stable implying that the applied perturbation decays to zero. In the sub-section below, we will analyze the cluster interaction terms and show that under certain conditions, it is possible to simplify our analysis and thereby factorize the characteristic polynomial and obtain analytical expressions for the eigenvalues.
Analysis of the cluster interaction terms
The perturbed sub-cluster x and the sub-cluster A− x receive the same input from the unperturbed cluster B. The sub-cluster is comprised of neurons that are identical to perturbed sub-cluster x, but their phase resetting in response to an input from cluster B could potentially differ from that of a single neuron due to the effect of neurons within a cluster on each other. We approximate the PRC for a cluster of identical neurons with the PRC for an individual neuron (Pervouchine et al., 2006) as illustrated in Fig. 3. We presume that all postsynaptic oscillators comprised of the same type of neuron have the same resetting whether they are comprised of one or more neurons. Thus we no longer keep track of the resetting separately for the A − x oscillator and perturbed sub-cluster x from the cluster, denote both by fk,A,j(φ), which represents the kth order PRC for the entire cluster A or any single neuron or sub-cluster within A in response to an input from cluster, sub-cluster, or single neuron j. Note that we do keep track of the size of the presynaptic cluster because its size dictates the strength of the conductance pulse delivered to the postsynaptic cluster. We use all three subscripts for f here because the actual phases such as 1− and 0+ will be used as the argument, hence the latter two subscripts can no longer be inferred from the argument.
| (22) |
As a result of (22), the slopes m1,A−x,B and m1,x,B are equal and can be denoted m1,A,B. Although the expression (21) is more general, the assumption in (22) allows a simpler and more intuitive determination of stability because the characteristic polynomial (21) can then be factorized as:
where λ1 and λ2 evaluated at the phase locked points are,
| (23) |
| (24) |
or if we consider that the single neuron lags rather than leads its cluster as shown in Fig. 2(d),
| (25) |
If between and within cluster interactions are considered separately (Achuthan and Canavier, 2009; Dror et al., 1999; Oprisan et al., 2004), the between cluster stability is given by :
| (26) |
and the within cluster stability is given by :
| (27) |
and
| (28) |
The key observation is that the λ2 derived in our current study has an additional term (see (25)) that represents the effect of between cluster interactions on within cluster synchrony. This term scales the eigenvalue that is obtained for synchrony in the isolated cluster, and may therefore change the stability results as described in the next section. The between cluster interaction term also differs slightly in the two cases, with replacing .
Test Cases with Homogeneous networks
We used four neuron networks for our examples because these are the smallest networks that can exhibit a two cluster solution. For these networks, A-x and x are both equal to 1. In this section, we use as an example a network in which all neurons are identical and identically connected. Multiple two cluster solutions are possible in this case because the neurons comprising the two clusters are interchangeable (Hansel et al., 1993). Here we re-examine two previously published (Achuthan and Canavier, 2009) examples of the two cluster mode in all to all networks of four identical model neurons identically coupled via inhibition. The two examples differ in the excitability type of the component model neurons, which results in different PRC shapes (Ermentrout, 1996). Type I excitable neurons generally synchronize via mutual inhibition, but Type II in general do not (Achuthan and Canavier, 2009; Hansel and Mato, 2003; Hansel et al., 1993, 1995; Ermentrout, 1996). Type I excitability is characterized by a gradual transition from quiescence to repetitive spiking as the applied depolarizing current is increased, whereas Type II excitability is characterized by an abrupt transition from quiescence to repetitive spiking (Hodgkin, 1948). The Type I neuron used is a Wang and Buzsaki (WB) (Wang and Buzsaki, 1996) model neuron, and the Type II is a Morris-Lecar (ML) (Morris and Lecar, 1981) model neuron. The model equations and parameter values are given in Appendices A and B. Parameters were chosen to ensure that each uncoupled model neuron oscillated spontaneously and that the coupling was approximately pulsatile. The synaptic decay time constants were set to less than a quarter of the intrinsic period, which also makes it likely that the effect of an input will die out within a network period. Specifically, for the Type I WB neuron model network, the synaptic decay time constant was set to 1 ms compared to an intrinsic period of 17 ms, and for the Type II ML neuron model network, the synaptic decay time constant was set to 10 ms compared to an intrinsic period of 44 ms. Further constraints imposed were that the third order resetting was negligible (not shown) and the first order resetting at zero equals the second order resetting at one. The latter two quantities are the same by definition if the effect of a single input dies out before next one received. Finally, the action potential waveforms were not significantly changed by the coupling in the network, satisfying the assumption of similar inputs in the open and closed loop conditions.
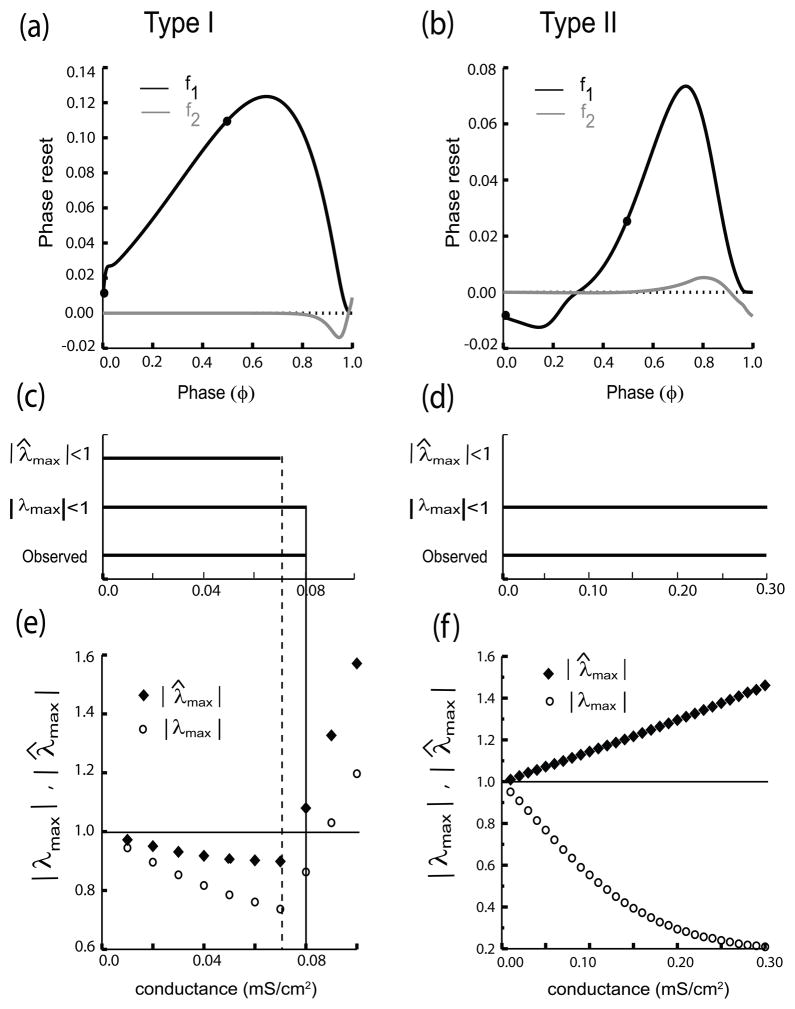
The initial slope of the first order phase resetting (black) is positive for a representative Type I PRC Fig. 4(a) but negative for Type II Fig. 4(b). A positive slope at phase zero stabilizes synchrony and a negative one destabilizes synchrony, which explains the different synchronization tendencies of the isolated clusters. The second order resetting (grey) is prominent only at late phases. The circles on the PRC indicate the phases at the fixed point calculated using the existence criteria for the between cluster mode. The two clusters are identical, and the locked phases are also identical such that for an exact anti-phase mode. The full system of differential equations was numerically integrated until all transients had dissipated in order to determine the range of coupling conductances that support a stable two cluster mode. Fig. 4(c) compares the observed range to the range predicted to support a stable cluster mode based on |λmax| < 1 (open circles) or |λ̂max| < 1 (filled diamonds). For the Type I case in (c) and (e), the criterion of |λmax| < 1 predicts the actual value at which the cluster mode loses stability (solid vertical line) more accurately than the criterion of |λ̂max| < 1 (dashed vertical line). At the conductance value of 0.08mS/cm2, the slope in (a) has a small positive value of about 0.3 which causes the factor to reduce the absolute value of the maximum eigenvalue by a factor of 0.7, thus reducing it below one and stabilizing the two cluster mode. For the example in Figure 4a, c and e global synchrony was shown to be bistable with the two cluster mode at gsyn values of 0.01 to 0.03 mS/cm2, thus if the conductance were increased from 0.03 to 0.04 mS/cm2, it would force a single synchronous cluster to break up into two clusters (as illustrated in Fig. 9(A2), Achuthan et. al 2009).
Fig. 4.
Stability Results for Two Clusters in Homogenous All to All Network Example. Representative shapes for first (f1(φ)) and second order (f2(φ)) PRCs (a) Type I and (b) Type II excitable cells in response to inhibition with gsyn = .08 mS/cm2. The slope of the first order resetting (black curve) near phase 0 is positive for the Type I PRC (a) but negative for Type II PRC (b). Filled circles indicate the phase locked points at which the two cluster solution exists. Parameter values for both the ML and WB models are given in Appendix A and B, respectively. Stability results for the two cluster solution in Type I (c) and Type II (d) inhibitory networks. Horizontal bars indicate the conductance values for which the cluster mode is stable based on observing the solutions obtained by integrating the full system of differential equations, compared to the range predicted based on |λmax| < 1 or |λ̂max| < 1 (see text for description of these eigenvalues). (e) The absolute value of the maximum eigenvalues |λmax| (open circles) and λ̂max (filled diamonds) are plotted versus conductance (e) Type I example. Dotted vertical line from horizontal bar in (c) shows where λ̂max crosses the stability boundary (horizontal line at a maximum absolute value of one) whereas the bold vertical line show the crossing for |λmax| more closely agrees with the point at which the full system ceased to exhibit this mode. (f) Same analysis as (e) for the Type II example. |λmax| (filled diamonds) is greater than one for all values of conductance examined, indicating that synchrony in an isolated cluster is unstable and incorrectly predicted that the two cluster mode will not be observed. However, |λmax| is less than one for all values of conductance showing that the analysis based on Fig. 2 is required for correct predictions in this case.
The effect of the additional scaling term in λ2 that incorporates the between cluster interactions is much more dramatic in the Type II case Fig. 4(d) and (f). At all values of conductance, |λ̂max| > 1, as indicated by the absence of a horizontal bar in (c). This is largely because the initial slope of the first order PRC is negative, which in this case renders synchrony in an isolated cluster unstable at all values of the conductance. However, the slope in this example increases in steepness as the conductance is increased from near zero to near one, causing the factor to reduce the absolute value of the maximum eigenvalue with increasing effectiveness such that the criterion |λmax| < 1 correctly predicts that the two cluster mode will be stable at all conductance values shown (horizontal bars). In fact, increasing the conductance beyond the range shown does not change the PRC much more. The very strong but pulsatile inhibitory synaptic input reverses at a potential of −75 mV, and has the effect of briefly clamping the membrane potential to very near the reversal potential. Increasing the conductance only brings the postsynaptic potential during the input slightly closer to the synaptic reversal potential causing the PRC to saturate. Consequently, the value for the maximum eigenvalue does not change further. This in turn causes the mode to retain stability as the conductance is strengthened arbitrarily.
Importance of second order resetting
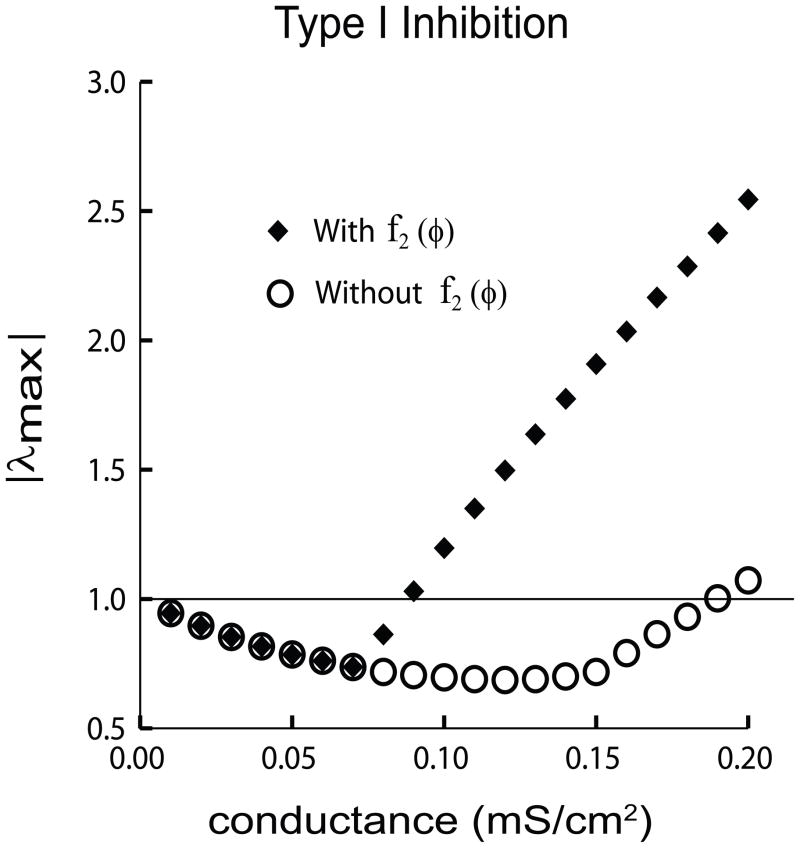
Frequently (Goel and Ermentrout, 2002; Netoff et al., 2005b) the second order resetting terms are neglected. We re-examined the stability results presented in Fig. 4(e) for the case of a Type I inhibitory network with the second order resetting term m2,A−x,x set to zero wherever it appears in the matrix S (see Eq. (20)). The eigenvalues for this reduced system (circles in Fig. 5) do not give the correct stability results, as the maximum absolute value does not cross one until .19 mS/cm2. For comparison, the correct prediction for the maximum eigenvalue crossing is replotted from Fig. 4(e) as the filled diamonds. For conductance values from 0 mS/cm2 to .07 mS/cm2 the eigenvalue |λ1| = |λmax| for both the circles and black diamonds. Since the second order reset term has no effect on λ1 (see Eq. (23)) the circles and diamonds overlay in this range. Beyond .07 mS/cm2, if the second order reset term f2(φ) is considered, the eigenvalue λ2 becomes greater than λ1. Therefore |λ2| = |λmax| for this case (diamonds) and diverges from the case in which f2(φ) is neglected (open circles), in which |λ1| remains the maximum eigenvalue. For the Type I case, considering second order resetting was necessary to obtain correct stability results; on the other hand, neglecting second order resetting did not qualitatively affect the stability results for the Type II example (figure not shown). Neglecting second order resetting may produce correct results in some cases but not all, and therefore it should not in general be neglected.
Fig. 5.
Importance of Second Order Resetting. Comparison of |λmax| for the case in which f2(φ) is neglected (without f2(φ), open circles) and the case in which it is considered (with f2(φ), filled diamonds) plotted against the synaptic conductance strength. For both cases, |λmax| is less than one up to .07 mS/cm2, predicting stability for the two cluster solution. In this range, the eigenvalue with the largest absolute value is |λ1|, which does not include a contribution from f2(φ). Beyond .07 mS/cm2 when f2(φ) is considered (filled diamonds), the eigenvalue with the the largest absolute value is λ2, which correctly predicts that the cluster mode loses stability for conductances greater than .08 mS/cm2. This diverges from the case where f2(φ) is ignored (open circles); neglecting f2(φ) incorrectly predicts stability up to .18 mS/cm2 (circles).
Test case with a Heterogenous network
The two clusters in the previous test case were identical, but the results presented here are not limited to that case. We also analyzed a two cluster mode of all to all ML neurons in a four neuron network coupled by inhibition in which one cluster has Type I excitability and the other has Type II excitability. The major difference is that since the clusters are not identical, it is not sufficient to perturb only one, instead each cluster must be considered as cluster A and the analysis performed twice. Another difference is that the intrinsic periods of the neurons in clusters A and B (PA and PB) are included in the analysis but do not appear in the final stability results because they cancel out. Calculations are given in Appendix C.
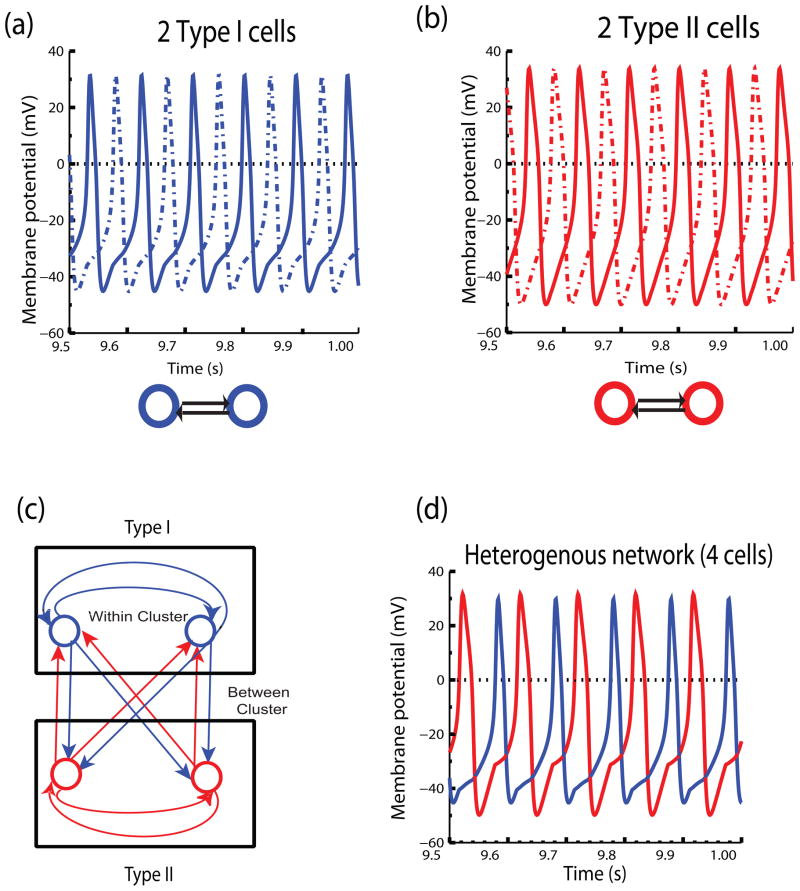
We first consider the cases of uncoupled clusters and analyze their individual cluster network behavior. Figure 6(a) shows that the isolated two neuron network with Type I excitable cells coupled via inhibition does not synchronize despite the general tendency of Type I to synchronize when coupled via inhibition, but instead exhibits a stable anti-phase mode (solid and dotted blue voltage traces corresponding to the two cells). Figure 6(b) shows that the isolated two neuron network with Type II excitable cells, as expected, also does not synchronize with inhibition but instead exhibits a stable anti-phase mode (solid and dotted red voltage traces). The action potential waveforms are not significantly changed by the coupling in the network, satisfying assumption of similar inputs in the open and closed loop conditions.
Fig. 6.
Two Heterogenous Clusters. (a) Isolated network of Type I excitable neurons coupled with inhibition. Dotted and bold blue voltage traces show that the isolated network does not synchronize, but instead displays an anti-phase mode. (b) Isolated network of Type II excitable neurons coupled with inhibition. Red dotted and dashed voltage traces show that the isolated network does not synchronize, but instead exhibits an anti-phase mode. Synaptic time constant parameter for both (a) and (b) is τsyn = 8 ms and gsyn = .16 mS/cm2. Istim value for (a) is 50.0 μA/cm2 and for (b) is 102 μA/cm2 (c) A heterogenous network of two clusters, one of Type I excitability and the other belonging to Type II excitable class where the coupling is all to all, identical and inhibitory. (d) When the two clusters are reciprocally coupled to each other as shown in (c) they give rise to a stable two cluster solution as shown by the red and blue voltage traces with exact synchrony within the clusters.
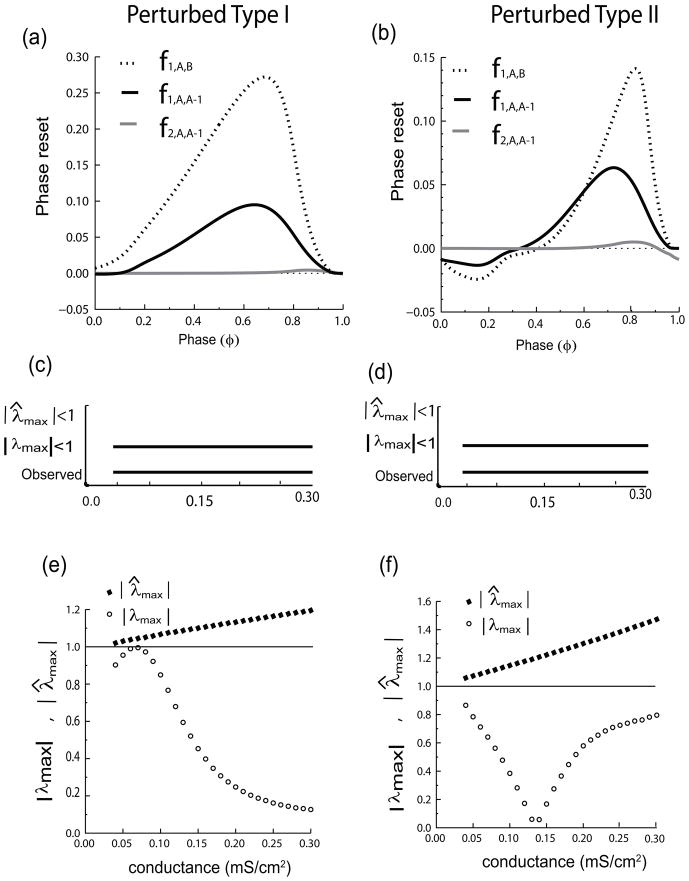
Next, we consider the all to all coupled network, in which the clusters are coupled via inhibition ( Fig. 6(c)). We find that when the two clusters are reciprocally coupled to each other they give rise to a stable two cluster mode as shown in (d) (red and blue voltage traces) with exact within-cluster synchrony. Again we see that reciprocal coupling can stabilize synchrony within clusters that cannot synchronize in isolation, as we saw in the Type II excitable homogenous test case as well. Figure 7 shows the stability analysis considering the Type I cluster as the perturbed cluster A on the left hand side, and the stability analysis considering the Type II cluster as the perturbed cluster A on the right hand side. The PRCs required for the analysis depend upon which cluster is being perturbed; representative PRCs are shown in Fig. 7(a) and (b), respectively. Although Type I first order PRCs typically have only delays in response to inhibition, it is possible to have a small anomalous region of advances for perturbations applied during the action potential (Rinzel and Ermentrout, 1998; Oprisan and Canavier, 2002), which causes the initial slope to be negative rather than positive. This is the case for the PRC describing the effect of the perturbed cluster A − 1 on the single neuron that is not firing with the others (indicated by the solid line in Fig. 7(a)). This initial negative slope explains why within-cluster synchrony is unstable, despite the generally tendency of Type I clusters to synchronize with inhibition. The corresponding PRC for the perturbed Type II cluster (Fig. 7(b), solid curve), also has an initial negative slope indicative of unstable within cluster synchrony, but this is typical for Type II neurons coupled by inhibition. Therefore if the uncorrected |λ̂max| is used to predict the stability of the two cluster mode, this mode is not predicted to be stable at any conductance value, which is indicated by the absence of a horizontal bar next to |λ̂max| < 1 in Fig. 7(c) or (d). Figure 7(e) and (f) shows that |λ̂max| (black diamonds) is always greater than one for the conductance range in which a two cluster mode is predicted to exist. On the other hand, the |λmax| derived in this study correctly predicts the stability as evidenced by the match between the horizontal bars in Fig. 7(c) and (d) indicating the predicted versus observed range of conductance values that support a stable two cluster mode. In order to correctly interpret the results in Fig. 7(e) and (f), six distinct possible eigenvalues must be considered for the two cluster mode when the two clusters are not identical: |λ1| must be calculated with each cluster taken as cluster A (two distinct values), whereas for each perturbed cluster |λ2| must be calculated in two ways depending upon whether the single neuron or the perturbed cluster fires first (four more distinct values) for a total of six. If any one of these six has an absolute value greater than one, the cluster mode will be destabilized. The open circles in Fig. 7(e) and (f) correspond to |λmax| for perturbing the Type I and Type II clusters respectively. Since all eigenvalues are less than one at all values of conductance shown, the two cluster mode is correctly predicted. Comparing these values to the |λ̂max| values, it is clear that only when between cluster interactions are correctly calculated can we account for the phenomenon of stabilization (by reciprocal connectivity) of otherwise unstable within-cluster synchrony.
Fig. 7.
Perturbation Analysis of each of the Two Heterogenous Clusters example as in Fig. 6. In (a, c, and e) the perturbed cluster A is Type I and the unperturbed cluster B is Type II, whereas in (b, d, and f) the perturbed cluster A is Type II and the unperturbed cluster B is Type I. (a) and (b) Representative PRCs required for the stability analysis, which include the first order PRC of any group of neurons from cluster A in response to input from the entire cluster B (dotted line, gsyn = .16 mS/cm2), the first (solid black, gsyn = .08 mS/cm2) and second (grey) order PRC of neurons from cluster A in response to input from the other neurons in cluster A. Horizontal bars that are labeled ‘observed’ in (c) and (d) are the same and indicate the conductance values for which the heterogenous two cluster mode is stable based on observing the solutions obtained by integrating the full system of differential equations. Note |λmax| (or |λ̂max|) must be below one in a range of parameter values as indicated by the presence of a horizontal bar labeled |λmax| < 1 (or |λ̂max| < 1) in both (c) and (d) in order for a stable mode to be predicted. This is because the mode must be robust to both types of perturbations in order to persist. The absence of a bar labeled in (c) and (d) corresponding to |λ̂max| < 1 means that at no conductance value was |λ̂max| less than one in either (e) or (f), as illustrated by the filled black diamonds. This indicates that synchrony in each isolated cluster is unstable and incorrectly predicts that the two cluster mode will not be observed. However, |λmax| in both (e) and (f) is less than one for all values of conductance at which a two cluster mode was observed in (c) and (d), again showing that the analysis based on Fig. 2 is required for correct predictions in this case.
Discussion
Significance
Our approach to the analysis of clustering was derived and presented in a neural context; however, it is applicable to any two clusters of pulse coupled oscillators. Other systems of pulse coupled oscillators include digital phase locked loops (Goldsztein and Strogatz, 1995), fireflies displaying synchronous flashing patterns (Mirollo and Strogatz, 1990), and cardiac pacemaking cells (Peskin, 1975). One example of clustering in a non-neural system is given by a species of fireflies (Photinus pyralis) that rarely synchronize while flashing but instead exhibit flashing in clusters (Wu and Chen, 2007).
In this study we presented a rigorous analysis of the conditions under which a homogeneous population of oscillators can form two clusters and under which reciprocal coupling between disparate clusters can lead to synchronization in both populations, even if one or both populations do not synchronize when not coupled to the other population. One possible example of the synchronizing effect of one population on another is provided by modeling studies in which global synchrony of model oriens-lacunosum moleculare (OL-M) interneurons can only be obtained robustly in networks that also contain fast spiking (FS) basket interneurons (Rotstein et al., 2005). Pervouchine et al. (Pervouchine et al., 2006) showed in a highly reduced model how the reciprocal coupling between FS cells and O-LM cells can promote synchronization between O-LM cells, but the methods in this study may provide a more complete explanation of the synchronizing effects of one population of cells on another. In a neural context, we suggest that the effective coupling between brain regions or sub-populations within a region can be altered as a result of attention or other factors, providing a mechanism to turn synchronization within neural assemblies off and on quickly. We also suggest pathological reciprocal connectivity may be responsible for excessive synchronization in epilepsy (Velasquez et al., 2007) and other dynamical diseases.
Novelty
The analysis of two pulse coupled oscillators is straightforward (Acker et al., 2003; Dror et al., 1999; Goel and Ermentrout, 2002), but the analysis of networks of arbitrary size is more complicated. The novelty of the approach presented herein is in how to set up the problem in terms of the appropriate perturbation in order to correctly account for the stability of the solution. In general, stability results for pulse coupled oscillators rely on the construction of a map of the firing intervals in a specified firing order. For two neurons, only two 1: 1 locked modes are possible: synchrony or an alternating firing order. In the case of the alternating firing order, small perturbations in general leave the firing order intact, so it is sufficient to linearize the map about the fixed point to determine stability. For synchrony, the map for the alternating firing pattern is linearized as it approaches 0+ in one neuron and 1− in the other (Goel and Ermentrout, 2002; Oprisan and Canavier, 2001). The problem is more complex for N all to all coupled neurons: the perturbation of any subset of the N neurons can be advanced and any subset can be delayed so there are many permutations of possible perturbations.
One previous approach to determining the stability of global synchrony in a cluster of all to all oscillators, linearized about a sequential (splay) firing pattern (Goel and Ermentrout, 2002) and ignored the absorption of single neurons into clusters as global synchrony is approached. Here we consider the final absorption of the last remaining non-synchronous cluster into a cluster as the stability limiting step. Although our approach here is general and can be applied to all perturbations, we suspect that it is sufficient to examine the absorption of the last remaining unsynchronized neuron (a cluster of one). In our experience, the most common route to destabilization is when any one of the 1−m1,i terms containing the first order resetting becomes negative, and this usually happens first with the m1,A−x term because the synaptic conductance increases with the size of the cluster, and the magnitude and slope of the resultant PRC also increase. Thus the most destabilizing perturbation is likely to result from the steepest PRC, which corresponds to the largest conductance, meaning the input from the largest (A − 1) cluster to the smallest cluster of a single neuron (Achuthan and Canavier, 2009). However, this is not a rigorous result, and there may be counterexamples.
Alternate Approaches
The results obtained herein could not be derived under the assumptions of weak coupling (Ermentrout and Kopell, 1991) for two reasons. First, weak coupling averages the effect of an input over one cycle period starting from the point at which the input is applied. Thus the effects both before and after the next spike are considered together rather than separately as first and second order resetting, whereas in our analysis it was sometimes critical to track these effects separately (see Fig. 5). Second, the stability of the results obtained using weak coupling assumptions do not in general depend upon the strength of the coupling, however we examine coupling regimes in which increasing the coupling strength destabilizes the two cluster mode (see Fig. 4(c) and (e)). One attempt to analyze clustering using weak coupling assumptions (Li et al., 2003) assumed that between cluster stabilizing and within cluster destabilizing influences summed linearly. Our approach is more general in the sense that it does not require weak coupling but less general in the sense that it does require pulsatile coupling. Therefore our methods are only valid for synaptic interactions that die out within a network period. For example, in the case presented of two heterogenous clusters in Fig. 7, the stability results begin to produce small mismatches with observations for synaptic time constants greater than 8 ms because the second order reset contributions due to the between cluster interactions become significant. Another approach (Orosz et al., 2009; Hansel et al., 1993; Tass, 2007) studies clustering in networks that arises due to complex coupling terms that include multiple Fourier modes that do not have a simple biophysical interpretation. Yet another approach to clustering treated component oscillators as relaxation oscillators with active and silent states (Rubin and Terman, 2000) and constructed a map of the jumps between states. Our methods are simpler to apply to spiking neurons, but the relaxation oscillator based-maps may be complementary to PRC-based maps for bursting neurons (Oprisan et al., 2004; Sieling et al., 2009). The idea that one population can synchronize another is not novel. Under certain conditions (Hansel and Mato, 2003), a population of interneurons can synchronize an excitatory population, which may occur in interneuron-driven gamma rhythm (Borgers and Kopell, 2003). The novelty here is the rigorous derivation of the stability criterion in the case that the clusters can be approximated as pulse coupled oscillator, as well as the idea that neither of the reciprocally coupled clusters need be capable of synchronizing on its own.
Summary
Although the analysis presented herein treats individual oscillators within a single cluster as identical and identically coupled, this requirement is not absolute as cluster solutions persist in the presence of some degree of heterogeneity (Achuthan and Canavier, 2009b; Achuthan et al., 2011). Although these results do not generalize immediately to the case of three or more sub-clusters, in practice it is difficult to observe more than two clusters in a large network (Hansel et al., 1993; Achuthan and Canavier, 2009; Golomb and Rinzel, 1994) so the two cluster solution is likely to have the greatest physiological relevance. Our results may help explain population frequencies that are twice the frequency of the component neurons (Pervouchine et al., 2006; Terman et al., 1996) as well as phase-locking between synchronous populations in distinct brain areas (Joseph and Butera, 2005; Velasquez et al., 2007). We have shown that, in theory, reciprocal connectivity can synchronize populations that de-synchronize in its absence.
Acknowledgments
This research was supported by NIH grants NS054281 and MH085387 under the CRCNS program. We are grateful to S. Wang for useful discussions.
Appendices
Appendix A: Type I WB model
The differential equations for the Wang and Buzsaki (Wang and Buzsaki, 1996) and Morris-Lecar (Morris and Lecar, 1981) networks were simulated by using a variable step size implicit fifth order Runge-Kutta method (Hairer and Wanner, 1991). Here is the current balance equation for each WB model neuron:
where the capacitance is given by C = 1 μF/cm2. V is the membrane voltage given in millivolts and t is the time with units as milliseconds. IL denotes the leak current and is given by IL = gL(V − EL). INa is the sodium current and is given by, . The activation gating variable for sodium is m and its steady state value is defined by m∞ = αm/(αm + βm), where αm(V) = −.1(V + 35)/e−.1(V +35)−1 and βm(V) = 4e−(V +60)/18. The rate equation for the inactivation variable h is given by,
where ϕ = 5. Following are the rate constants for the inactivation variable h, αh(V) = .07e−(V +58)/20 and βh(V) = 1/e−.1(V +28)+1. The potassium current is denoted by IK = gKn4(V − EK), where the activation variable n satisfies the following equation,
The rate constants for n are given by αn(V) = −.01(V +34)/e−.1(V +34)−1 and βn(V) = .125e−(V +44)/80. The parameter values used in the simulations for the reversal potentials are: ENa = 55 mV, EK = −90 mV and EL = −65 mV. The maximum sodium, potassium and leak conductances are, gNa = 35 mS/cm2, gK = 9 mS/cm2 and gL = .1 mS/cm2. The applied current Istim is set to .5 μA/cm2.
The synaptic current is given by Isyn = gsyns(V − Esyn), where gsyn denotes the maximum synaptic conductance and Esyn = −75 mV for inhibitory synaptic connectivity and equals 0 mV for excitatory synaptic connectivity. The rate of change of the gating variable s is given as follows,
where T(Vpre) = 1/(1 + e−Vpre/2) where Vpre denotes the presynaptic voltage, α = 6.25 ms−1 is the synaptic activation rate constant (Bartos et al., 2001). The synaptic decay time constant τsyn, is set to 1.0 ms. The following sets of four initial conditions for V, h, n and s in each neuron were used to determine whether the antiphase two cluster mode could be observed:
−14.000000 0.246847 0.283832 0.000000, −14.000000 0.256847 0.283832 0.000000, −60.695787 0.715586 0.110823 0.000000, −60.695787 0.725586 0.110823 0.000000. Note that the clusters were perturbed from exact synchrony within a cluster by varying the value for h.
Appendix B: Type I/II ML model
The equation for each ML neuron model is given as,
where capacitance is C = 20 μF/cm2. The membrane voltage V has units of millivolts and t, the time is in milliseconds. The calcium current is given by ICa = gCam∞(V)(V − ECa). The leak current is given by IL = gL(V − EL). The steady state activation variable m has the following value,
where V1 = −1.2 mV and V2 = 18 mV. The following equation describes the rate of change of the gating variable for potassium activation,
where ϕ is set to .04. The equation for the steady-state activation for w is given by,
The rate of activation is as follows,
where V3 = 2 mV and V4 = 30 mV. The parameter values for the reversal potentials are as follows, ECa = 120 mV, EK = −84 mV and EL = −60 mV. The maximal conductances are set to gK = 8.0 mS/cm2, gL = 2.0 mS/cm2, gCa = 4.4 mS/cm2. The applied current is set to Istim = 102 μA/cm2. All these values for the parameters used in our simulation for Type II ML neuron model were taken from (Rinzel and Ermentrout, 1998) and hold good unless otherwise stated. τsyn, which is the synaptic decay time constant is set to 10.0 ms for the case with homogenous clusters. τsyn is chosen to be equal to 8ms in order to analyze the heterogenous cluster example.
A Type I ML neuron model has the following parameters- Istim = 50.0μA/cm2, ϕ = .0666667, gCa = 4.0 mS/cm2, V3 = 12 mV, V4 = 17.4 mV which is used in the heterogenous cluster example.
Appendix C: Derivation of Stability Results
Substituting for stimulus and recovery intervals in equation (11) and eliminating the steady state components gives:
| (29) |
Note that, in the above expression Δφx,B[n + 1] is expressed in terms of ΔφB,x[n], ΔφB,A−x[n] and Δφx,A−x[n + 1]. We use the map in (14) to find an expression for Δφx,A−x[n + 1] in (29) such that,
| (30) |
The term (m2,A−x,x)ΔφA−x,x[n − 1] can be expressed as in terms of Δφx,A−x[n], Δφx,B[n] and ΔφA−x,B[n] in the following way. Consider tsA−x,B[n] and equate it to tsx,B[n] to obtain,
| (31) |
The above equality of terms in (31) yields the following expression for (m2,A−x,x)ΔφA−x,x[n − 1] after elimination of the steady state components,
| (32) |
We substitute for (m2,A−x,x)ΔφA−x,x[n − 1] in equation (30) which yields,
| (33) |
Note, that now Δφx,A−x[n + 1] can be substituted for in (29) using expression in (33). Similarly, we use the periodicity constraint given in (12) to express ΔφA−x,B[n + 1] as follows,
| (34) |
Note that (m2,A−x,x)ΔφA−x,x[n] is the second order reset term. Therefore from (29), (33) and (34) we have two equations of the form Δφ[n + 1] expressed in terms of Δφ[n].
As a next step, we eliminate the phase variables φ1,A−x and φB,x as follows. We use constraint (13) to eliminate the variable ΔφB,x[n]. Substituting the expressions for the stimulus and recovery intervals and eliminating the steady state components gives,
| (35) |
To summarize, so far we have expressed two variables namely Δφx,B and ΔφA−x,B in their [n + 1]th cycle as a function of variables in the [n]th cycle (see equations 29, 33, 34). Also we have shown that it is possible to express the perturbed variables Δφx,A−x and ΔφB,x in terms of Δφx,B and ΔφA−x,B and other variables (see equations (33) and (35)). At this stage, we have reduced the six dimensional problem to four dimensions. Below, we will show that it is possible to further reduce the dimensionality of the problem to two by using alternate constraints to express the perturbed variables ΔφA−x,x and ΔφB,A−x in the nth cycle in terms of the other variables.
We compute ΔφA−x,x[n], by considering the stimulus interval tsx,A−x[n + 1] and equating it to trA−x[n] (see Fig. 2(e)), such that,
After eliminating steady state components we get the following expression,
| (36) |
Substituting the expression for Δφx,A−x[n + 1] from equation (33) in the above equation gives us the following,
| (37) |
Similarly we compute ΔφB,A−x[n], by considering the interval tsx,A−x[n + 1] and equating it to tsB,A−x[n], such that,
Therefore, after elimination of steady state components, in the above equation we obtain,
| (38) |
Note that ΔφB,A−x[n] has been expressed as a function of Δφx,A−x[n + 1] and ΔφB,x[n].
Substituting for the terms Δφx,A−x[n + 1], ΔφB,x[n] and ΔφB,A−x[n] using equations (33), (35) and (38) in equation (29) gives,
Similarly using equations (35), (37) and (38) in the expression for ΔφA−x,B[n + 1] in (34) we obtain the following,
References
- Achuthan S, Canavier CC. Phase-resetting curves determine synchronization, phase locking and clustering in networks of neural oscillators. Journal of Neuroscience. 2009;29:5218–5233. doi: 10.1523/JNEUROSCI.0426-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Achuthan S, Canavier CC. Prediction of phase locked neuronal network activity in the presence of heterogeneity and noise using phase resetting curves. Society for Neuroscience. 2009b Abstract no. 321.5. [Google Scholar]
- Achuthan S, Sieling F, Prinz A, Canavier CC. Phase resetting curves in presence of heterogeneity and noise. In: Glanzman D, Ding M, editors. Neuronal Variability and its Functional Significance. New York: Oxford University Press; 2011. [Google Scholar]
- Acker CD, Kopell N, White JA. Synchronization of strongly coupled excitatory neurons:relating network behavior to biophysics. Journal of Computational Neuroscience. 2003;15:71–90. doi: 10.1023/a:1024474819512. [DOI] [PubMed] [Google Scholar]
- Bartos M, Vida I, Frotscher M, Geiger JRP, Jonas P. Rapid signaling at inhibitory synapses in a dentate gyrus interneuron network. Journal of Neuroscience. 2001;21:2687–2698. doi: 10.1523/JNEUROSCI.21-08-02687.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borgers C, Kopell N. Synchronization in networks of excitatory and inhibitory neurons with sparse, random connectivity. Neural Computation. 2003;15:509–538. doi: 10.1162/089976603321192059. [DOI] [PubMed] [Google Scholar]
- Buzsaki G. Rhythms of the brain. Oxford University Press; 2006. [Google Scholar]
- Canavier CC, Butera RJ, Dror RO, Baxter DA, Clark JW, Byrne JH. Phase response characteristics of model neurons determine which patterns are expressed in a ring circuit model of gait generation. Biological Cybernetics. 1997;77:367–380. doi: 10.1007/s004220050397. [DOI] [PubMed] [Google Scholar]
- Dror RO, Canavier CC, Butera RJ, Clark JW, Byrne JH. A mathematical criterion based on phase response curves for stability in a ring of coupled oscillators. Biological Cybernetics. 1999;80:11–23. doi: 10.1007/s004220050501. [DOI] [PubMed] [Google Scholar]
- Ermentrout B. Type I membranes, phase resetting curves, and synchrony. Neural Computation. 1996;8:979–1002. doi: 10.1162/neco.1996.8.5.979. [DOI] [PubMed] [Google Scholar]
- Ermentrout GB, Kopell N. Multiple pulse interactions and averaging in systems of coupled neural oscillators. Journal of Mathematical Biology. 1991;29:195–217. [Google Scholar]
- Glass L, Mackey MC. From clocks to chaos: the rhythms of life. Princeton University Press; Princeton, N.J: 1988. [Google Scholar]
- Goel P, Ermentrout GB. Synchrony, stability and firing patterns in pulse coupled oscillators. Physica D. 2002;63(3-4):191–216. [Google Scholar]
- Goldsztein G, Strogatz SH. Stability of synchronization in a network of digital phase locked loops. International Journal of Bifurcations and Chaos. 1995;5:983–990. [Google Scholar]
- Golomb D, Rinzel J. Clustering in globally coupled inhibitory neurons. Physica D. 1994;72:259–282. [Google Scholar]
- Hairer E, Wanner G. Springer series in computational mathematics. Springer; Berlin: 1991. Solving ordinary differential equations II. Stiff and differential-algebraic problems. [Google Scholar]
- Hansel D, Mato G. Asynchronous states and emergence of synchrony in large networks of interacting excitatory and inhibitory neurons. Neural Computation. 2003;15:1–56. doi: 10.1162/089976603321043685. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Clustering and slow switching in globally coupled phase oscillators. Physical Review E. 1993;48(5):3470–3477. doi: 10.1103/physreve.48.3470. [DOI] [PubMed] [Google Scholar]
- Hansel D, Mato G, Meunier C. Synchrony in excitatory neural networks. Neural Computation. 1995;7:307–337. doi: 10.1162/neco.1995.7.2.307. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL. The local electric changes associated with repetitive action in a non-medullated axon. Journal of Physiology. 1948;107:165–181. doi: 10.1113/jphysiol.1948.sp004260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janczewski WA, Feldman JL. Distinct rhythm generators for inspiration and expiration in the juvenile rat. Journal of Physiology. 2006;570:407–420. doi: 10.1113/jphysiol.2005.098848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joseph IMP, Butera RJ. In: IEEE, Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference. Zhang YT, Piscataway NJ, editors. Shanghai, China: 2005. [Google Scholar]
- Li Y, Wang Y, Miura R. Clustering in small networks of excitatory neurons with heterogenous coupling strengths. Journal of Computational Neuroscience. 2003;14:139–159. doi: 10.1023/a:1021902717424. [DOI] [PubMed] [Google Scholar]
- Marder E, Calabrese R. Principles of rhythmic motor pattern generation. Physiological Reviews. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- Mellen NM, Janczweski WA, Bocchiaro CM, Feldman JL. Opioid-induced quantal slowing reveals dual networks for respiratory rhythm generation. Neuron. 2003;37:821–826. doi: 10.1016/s0896-6273(03)00092-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirollo RE, Strogatz SH. Synchronization of pulse coupled biological oscillators. SIAM Journal on Applied Mathematics. 1990;50:1645–1662. [Google Scholar]
- Morris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophysical Journal. 1981;35:193–213. doi: 10.1016/S0006-3495(81)84782-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Netoff TI, Banks M, Dorval A, Acker C, Haas J, Kopell NJ, White JA. Synchronization in hybrid neuronal networks of the hippocampal formation. Journal of Neurophysiology. 2005b;93:1197–1208. doi: 10.1152/jn.00982.2004. [DOI] [PubMed] [Google Scholar]
- Oprisan S, Canavier CC. The influence of limit cycle topology on the phase resetting curve. Neural Computation. 2002;14:1027–1057. doi: 10.1162/089976602753633376. [DOI] [PubMed] [Google Scholar]
- Oprisan SA, Canavier CC. Stability analysis of rings of pulse coupled oscillators: The effect of phase-resetting in the second cycle after the pulse is important at synchrony and for long pulses. Differential Equations and Dynamical Systems. 2001;9:243–258. [Google Scholar]
- Oprisan SA, Prinz AA, Canavier CC. Phase resetting and phase locking in hybrid circuits of one model and one biological neuron. Biophysical Journal. 2004;87:2283–2298. doi: 10.1529/biophysj.104.046193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orosz G, Moehlis J, Ashwin P. Designing the dynamics of globally coupled oscillators. Progress of Theoretical Physics. 2009;122(3):611–630. [Google Scholar]
- Pervouchine DD, Netoff TI, Rotstein HG, White JA, Cunningham MO, Whittington WA, Kopell NJ. Low-dimensional maps encoding dynamics in entorhinal cortex and hippocampus. Neural Computation. 2006;18:1–34. doi: 10.1162/neco.2006.18.11.2617. [DOI] [PubMed] [Google Scholar]
- Peskin C. Courant Institute of Mathematical Sciences. Vol. 5. NYU; New York: 1975. Mathematical aspects of heart physiology; pp. 268–278. [Google Scholar]
- Rinzel J, Ermentrout B. Methods in neuronal modeling from ions to networks. Cambridge, MA: MIT; 1998. Analysis of neural excitability and oscillations. [Google Scholar]
- Rotstein HG, Pervouchine DD, Acker CD, Gillies MJ, White JA, Buhl EH, Whittington MA, Kopell N. Slow and fast inhibition and an H-current interact to create a theta rhythm in a model of CA1 interneuron network. Journal of Neurophysiology. 2005;94:1509–1518. doi: 10.1152/jn.00957.2004. [DOI] [PubMed] [Google Scholar]
- Rubin J, Terman D. Analysis of clustered firing patterns in synaptically coupled networks of oscillators. Journal of Mathematical Biology. 2000;41:513–545. doi: 10.1007/s002850000065. [DOI] [PubMed] [Google Scholar]
- Sieling F, Canavier CC, Prinz AA. Predictions of phase-locking in excitatory hybrid networks: excitation does not promote phase-locking in pattern generating networks as reliably as inhibition. Journal of Neurophysiology. 2009;102:69–84. doi: 10.1152/jn.00091.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tass PA. Phase resetting in Medicine and Biology. Springer-Verlag; Berlin Heidelberg: 2007. [Google Scholar]
- Terman D, Kopell N, Bose A. Functional reorganization in thalamocortical networks: Transition between spindling and delta sleep rhythms. Proceedings of National Academy of Sciences, USA. 1996;93(26):15417–15422. doi: 10.1073/pnas.93.26.15417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velasquez JLP, Galan RF, Dominguez LG, Leshchenko Y, Lo S, Belkas J, Guevara ER. Phase response curves in the characterization of epileptiform activity. Physical Review E. 2007;76:061912. doi: 10.1103/PhysRevE.76.061912. [DOI] [PubMed] [Google Scholar]
- Wang XJ, Buzsaki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. Journal of Neuroscience. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winfree AT. Biological rhythms and the behavior of populations of coupled oscillators. Journal of Theoretical Biology. 1967;16:15–42. doi: 10.1016/0022-5193(67)90051-3. [DOI] [PubMed] [Google Scholar]
- Winfree AT. The geometry of biological time. Springer-Verlag; New York: 2001. [Google Scholar]
- Wu W, Chen T. Desynchronization of pulse coupled oscillators with delayed excitatory coupling. Nonlinearity. 2007;20:789–808. [Google Scholar]