Identification of protein oligomerization states by analysis of interface conservation

Abstract

The discrimination of true oligomeric protein–protein contacts from nonspecific crystal contacts remains problematic. Criteria that have been used previously base the assignment of oligomeric state on consideration of the area of the interface and/or the results of scoring functions based on statistical potentials. Both techniques have a high success rate but fail in more than 10% of cases. More importantly, the oligomeric states of several proteins are incorrectly assigned by both methods. Here we test the hypothesis that true oligomeric contacts should be identifiable on the basis of an increased degree of conservation of the residues involved in the interface. By quantifying the degree of conservation of the interface and comparing it with that of the remainder of the protein surface, we develop a new criterion that provides a highly effective complement to existing methods.

The true oligomerization state of a protein is often difficult to ascertain, even though its correct identification may be critical to an understanding of the protein's physiological function. Studies in dilute solution conditions often underestimate the size of oligomers because the true in vivo oligomer is held together by relatively weak interactions that require either high protein concentrations for stability or the presence of other components that are absent from the solution. On the other hand, artificially large oligomers may also be incorrectly deduced from examination of the protein–protein contacts in the crystalline environment: many of these interactions are nonspecific and simply reflect facile ways of arranging the macromolecule in a regularly ordered lattice (1). Until very recently, efforts to discriminate between crystal and true oligomeric contacts have been based more or less exclusively on examination of the size of the interface, with greater amounts of buried solvent accessible surface area (SASA) being interpreted as indicating a greater probability that the contact is a true oligomeric contact. From an analysis of a database of protein–protein contacts, Janin has devised a simple statistical expression that can be used to estimate the probability that a contact is a crystal (i.e., nonspecific) contact (2). Similarly, the Protein Quaternary Structure (PQS) Server (http://pqs.ebi.ac.uk) uses (among other criteria) a buried SASA of 400 Ų as an arbitrary lower-limit criterion for defining an oligomeric contact (3). More recent work by the same authors has found that a cutoff of ≈850 Ų is more appropriate, at least for discriminating monomeric from homodimeric proteins (4).

Nevertheless, as both sets of authors have pointed out (2, 4), there are clear cases where the simple SASA criterion fails. In particular, there are examples where a large buried SASA is found, but the interaction is considered unlikely to be physiologically relevant (2, 3). In contrast, there are also several cases where an interaction that is of clear physiological importance is characterized by only a small buried SASA. Because of these problems, efforts have continued to develop more discriminating criteria capable of making correct assignments with greater frequency. Thornton's group has shown recently that the use of a scoring function based on statistical potentials can slightly out-perform the SASA criterion in predicting the oligomerization states of a large number of monomeric and homodimeric proteins (4). Although it has been encouraging that several of the proteins incorrectly assigned by the statistical potential scoring function can be correctly assigned by the SASA criterion, a number of cases have been wrongly assigned by both methods.

Our purpose in the present work is to investigate whether the correct assignment of oligomerization states can be facilitated by the use of a new criterion on the basis of the degree of conservation of the interface residues across a series of homologous proteins. Our hypothesis is simple (and appears also to have occurred to Thornton and colleagues: ref. 4): if the interaction observed in the crystal is a true oligomeric contact (so the interaction is in some way important to function), then the residues comprising the interface should be subject to evolutionary conservation (5). We define the degree of conservation of each residue in a sequence in terms of its sequence entropy (see Methods), with lower sequence entropies being associated with residues that are more highly conserved. By comparing the mean sequence entropy of the interface with that calculated for the remainder of the protein surface, we are able to devise a simple but effective criterion for discriminating between crystal and oligomeric contacts.

Methods

Multiple Sequence Alignments.

Multiple sequence alignments for each protein studied were obtained from the Homology Derived Secondary Structure of Proteins database (ref. 6; ftp://ftp.embl-heidelberg.de/pub/databases/hssp); the alignments were used without further manipulation.

Calculation of Sequence Entropy.

The HSSP database includes calculations of the sequence entropy s, at each position i in the sequence by using the following expression (6):

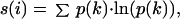1

where p(k) is the probability that the position in the sequence is occupied by a residue of type k. Because the HSSP database considers each amino acid to be a unique type, the summation is over the 20 amino acids. Although this is a straightforward definition, it is in some respects too restrictive: conservative changes such as the exchange of the hydrophobic residue ile by another hydrophobic residue such as val are given the same weight in calculating the entropy as distinctly nonconservative changes such as the replacement of ile by arg. To circumvent this problem, we follow the suggestion of Mirny and Shakhnovich (7) and divide the 20 amino acids into the following 6 groups: (1) Arg, Lys; (2) Asp, Glu; (3) His, Phe, Trp, Tyr, Val; (4) Asn, Gln, Ser, Thr; (5) Ala, Ile, Leu, Met, Val; (6) Gly, Pro. We retain Eq. 1 for calculating the sequence entropy, but now the summation is over 6 residue groups instead of over the 20 residue types.

Calculation of Mean Interface and Noninterface Surface Entropies.

To calculate a mean sequence entropy for the interface, we use the following expression.

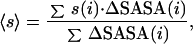2

where ΔSASA(i) is the SASA of residue i that becomes buried when the interface forms, and s(i) is the sequence entropy (defined above) associated with the residue. Note that this expression correctly weights the contribution of each residue by its relative contribution to the total interface area. SASAs were calculated by using the program uhbd (8).

In applying Eq. 2, we make one exception that is especially important to note. Consider an interface comprised entirely of contacts between main chain atoms (e.g., in a β-sheet type interaction). Such an interface will be completely immune to side-chain mutations, except in the extreme case (not considered here) where mutation of the side chain causes a conformational change in the main chain. Such an interface should really be assigned a mean entropy of zero, because it is in effect completely conserved. To ensure that these situations are treated correctly, we take special care in the treatment of contributions from main chain atoms: their contributions to the numerator are set to zero, but their contribution to the denominator is retained.

To calculate the mean entropy of the remainder of the protein surface, we use an expression identical to Eq. 2 but where the summation is now over all of the SASA not involved in the interface. Having calculated mean interface and noninterface entropies, we can define an interface-to-noninterface entropy ratio: it is this quantity that we use as our criterion for discriminating true oligomeric contacts from crystal contacts. Values less than 1.0 indicate that the interface residues are more highly conserved than the rest of the surface residues. Values greater than 1.0 indicate that the interface is actually less conserved than the remainder of the surface. The idea behind using this ratio is that it provides a simple mechanism for normalizing the results with respect to the number of sequences involved in the analysis, because these can vary widely between proteins. Simply comparing the mean entropies of interfaces of different proteins would not yield meaningful results, because the absolute values of the entropies will depend on the number and evolutionary distance of sequences used in the analysis.

Results

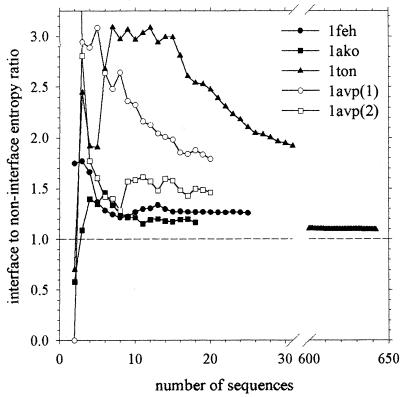
We concentrate initially on the recalcitrant cases noted by Thornton's group (4). We consider first the five monomeric proteins that are incorrectly assigned by their statistical potential scoring function as dimeric and that we identify here by their Protein Data Bank codes: 1feh, 1ckm, 1ako, 1avp and 1ton. Of these, 1ckm cannot be tested with our method because of a lack of data: as of this moment, the HSSP database entry (6) for this protein contains no homologous sequences other than the original sequence itself. For the other four proteins, the mean sequence entropies in the interface and over the remainder of the protein surface are listed in Table 1; notice that for 1avp, there are two entries because the interface is nonsymmetric and is therefore composed of different residues on the two partners. For all four proteins, the average sequence entropy in the interface is higher than for the remainder of the protein surface; as a result, the interface-to-noninterface entropy ratio (see Methods) is in all cases greater than 1.0. Because these results indicate that the interfaces are subject to somewhat lower evolutionary pressure than experienced by the rest of the protein surface, they provide a compelling signal indicating that these interfaces should not be considered true oligomeric contacts but should instead be considered (correctly) as crystal contacts. This result is especially important to note for the case of 1feh, which, because of its large buried SASA (1,575 Ų), is considered (incorrectly) to be dimeric according to both the SASA and scoring function criteria (4). Encouragingly, these qualitative results are independent of the number of sequences used in the analyses: when the number of sequences in the analysis is reduced (by removing more distant sequences), the calculated ratios remain greater than 1.0 (Fig. 1).

Table 1.

Comparison of mean sequence entropies of interface residues and noninterface residues for proteins known to be monomeric

Protein Data Bank code	Number of sequences*	Interface area†	〈s〉interface‡	〈s〉noninterface§	Ratio¶
1feh	25	1,575	0.98	0.78	1.26
1ako	18	845	1.05	0.90	1.16
1ton	642	704	1.17	1.07	1.09
1avp (1)	20	401	1.07	0.60	1.78
1avp (2)	20	383	0.88	0.60	1.47

^*The number of unique sequences may differ from that specified in the .hssp files because the latter includes redundancies. 

^† Buried solvent accessible surface area in the interface is measured in Ų. 

^‡ Mean sequence entropy calculated over interfacial residues (see Methods). 

^§ Mean sequence entropy calculated over all surface residues not involved in the interface. 

^¶ Ratio of interface to noninterface sequence entropy. 

Figure 1.

Calculated interface-to-noninterface entropy ratio for known monomeric proteins plotted as a function of the number of sequences used in the analysis.

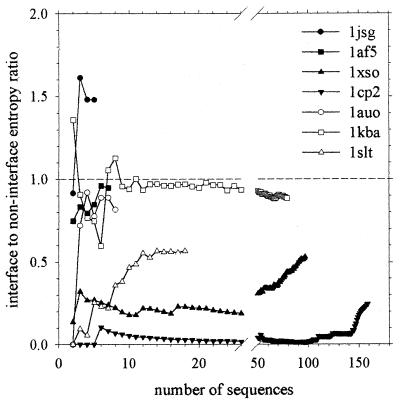
Next we consider the cases in which the statistical potential scoring function incorrectly labeled dimeric proteins as monomeric (4). For six of these seven proteins, the calculated interface-to-noninterface entropy ratio is less than 1.0 (Table 2), indicating that the interface is subject to greater evolutionary constraints than the remainder of the protein's surface, exactly as would be expected of a true dimeric interface. Again, these qualitative results are insensitive to the number of sequences used in the analysis: only for 1kba and 1jsg does the calculated ratio ever rise above 1.0 (Fig. 2). The one truly exceptional case, 1jsg, is also the case for which we have the fewest homologous sequences (only five): with such a small number of sequences, it may not be possible to extract any truly meaningful information (see Methods). In any case, as has been pointed out (4), the experimental evidence for 1jsg being dimeric is actually rather weak (9); that our method does not assign this protein as dimeric does not therefore necessarily represent a conspicuous failure. Of the remaining six proteins, it is again worth noting that four (1xso, 1auo, 1kba, and 1slt) were wrongly assigned as monomeric by both the statistical potential scoring function and the SASA-based criteria (4).

Table 2.

Comparison of mean sequence entropies of interface residues and noninterface residues for proteins known to be dimeric

Protein Data Bank code	Number of sequences	Interface area	〈s〉interface	〈s〉noninterface	Ratio
1cp2	159	962	0.17	0.68	0.24
1af5	8	857	0.50	0.52	0.95
1jsg	5	792	0.78	0.53	1.48
1xso	97	679	0.44	0.83	0.53
1auo	8	658	0.61	0.72	0.84
1slt	18	550	0.41	0.80	0.52
1kba	79	491	0.70	0.83	0.85

Figure 2.

Calculated interface-to-noninterface entropy ratio for known dimeric proteins plotted as a function of the number of sequences used in the analysis.

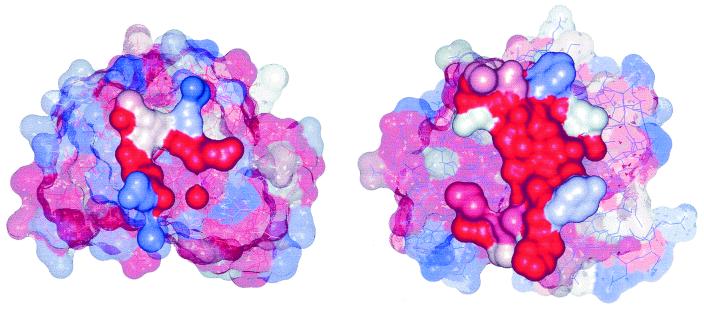
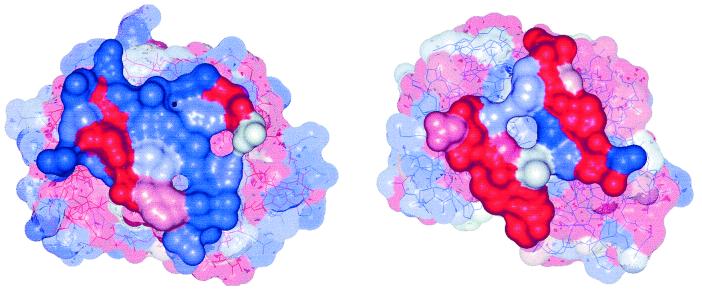
One potential concern with the use of a method based on measurements of sequence conservation is that it may not be able to discriminate between cases in which close homologues adopt different oligomerization states. To demonstrate that this need not be a problem, we have examined three proteins for which there are both monomeric and dimeric homologues (Table 3). In all three cases, there is a striking difference in the interface-to-noninterface entropy ratios, with the ratios for the monomeric proteins being not only greater than 1.0 but also much larger than the values obtained for the dimeric proteins (all less than 0.80; Table 3). The first two of the three examples, 1slt and 1xso, were examined because they were previously incorrectly assigned by the statistical potential scoring function (ref. 4; see Figs. 3 and 4 for a graphical representation of the interface conservation of these proteins). The third example, 1bsr, is an example of dimerization through domain swapping (10) and was selected because it represents a taxing test for the method: the sequence identity of the monomeric and dimeric forms is very high (81%; ref. 4), yet they can be safely separated on the basis of the sequence entropy ratio.

Table 3.

Comparison of mean sequence entropies of interface residues and noninterface residues for proteins for which there are both monomeric and dimeric homologues

Protein Data Bank code	Number of sequences	Interface area	〈s〉interface	〈s〉noninterface	Ratio
1bkz	42	751	0.97	0.90	1.07
1slt	18	550	0.41	0.80	0.52
1eso	44	248	1.02	0.83	1.23
1xso	97	679	0.44	0.83	0.53
1afk*	130	404	0.88	0.71	1.25
1bsr	130	1,898	0.55	0.70	0.79

 The monomeric form is tabulated first. 

^*Values obtained when 1afk monomers are superimposed on the 1bsr monomer structures. Analysis of the monomer-monomer interface present in the original 1afk pdb file gives a smaller interface (303 Ų) with an even higher interface to noninterface entropy ratio (1.45). 

Figure 3.

Surfaces of (Left) 1eso and (Right) 1xso, with residues colored according to their sequence entropy. Residues forming the interface are drawn solid, others transparent. Colors are graduated from red (indicating zero entropy) to blue (indicating highest entropy found in the sequence).

Figure 4.

Surfaces of (Left) 1bkz and (Right) 1slt, with residues colored according to their sequence entropy. Residues forming the interface are drawn solid, others transparent. Colors are graduated from red (indicating zero entropy) to blue (indicating highest entropy found in the sequence).

Having shown that the method is useful for identifying recalcitrant cases that evade correct assignment through established methods, we have proceeded with a larger-scale analysis. We have applied the method to the full set of 76 proteins described by Ponstingl et al. as being unambiguously dimeric (Table 1 of ref. 4). Of the 52 cases for which there are 10 or more sequences with which to conduct analyses, we find that 43 (83%) have interface-to-noninterface entropy ratios less than 0.90 and are therefore strong candidates to be dimeric. Examination of the remaining 9 proteins, which have ratios higher than 0.90 (Table 4), raises two interesting issues. First, for two of the proteins we have found that there is in fact strong evidence in the literature that the monomeric form is the physiologically relevant one. Proaerolysin (1pre), for example, has been shown to exist in a monomer–dimer equilibrium, with the monomer being fully capable of receptor binding (11). For interleukin 8 (1icw), on the other hand, variants that exist primarily as monomers have been shown to be functionally equivalent to the wild-type protein (12, 13). For these two cases, then, the prediction given by our ratio test appears actually to be correct. Second, the simplest implementation of our method appears to produce artificially high ratios for several proteins that are known to interact with other molecules. For DNA-binding proteins, for example, a substantial part of the protein surface that is not involved in the monomer–monomer interface will instead be involved in binding DNA and so will also be subject to strong evolutionary conservation. Therefore, the degree of conservation of the monomer–monomer interface may not actually appear to be particularly great when compared with the remainder of the protein surface. This will certainly be true for the transcriptional repressors tet (2tct) and Smtb (1smt) but is also likely to be true for cytochrome c3 (1czj) and aldehyde ferredoxin oxidoreductase (1aor), both of which must interact with electron transfer partners.

Table 4.

“Known” dimeric proteins with calculated sequence entropy ratios greater than 0.90

Protein Data Bank code	Number of sequences	Interface area	〈s〉interface	〈s〉noninterface	Ratio
1aor	20	1,243	1.18	0.80	1.49
1icw	68	1,061	0.60	0.52	1.15
1czj	12	830	0.78	0.71	1.09
1pre	19	2,291	0.25	0.23	1.09
2tct	27	2,674	0.57	0.54	1.07
1afw	154	2,387	0.87	0.89	0.99
1smt	60	1,961	0.92	0.94	0.98
1alk	70	3,813	0.81	0.84	0.97
1a3c	28	1,000	0.41	0.46	0.90

Finally, we have conducted a much larger analysis of 1,151 proteins identified as symmetric dimers by the PQS server and for which 10 or more sequences are present in the corresponding sequence alignment files. Because of the potential problems with proteins that form interactions with other molecules and because of difficulties in correctly interpreting ratio values close to 1.0, we have used the following more stringent criteria for assigning the oligomeric states:

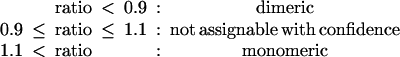Of the 1,151 proteins, 233 are assigned as crystal contacts by the PQS server and so are considered monomeric. Using our method with the above criteria, we find that 131 of these 233 proteins are considered monomeric, 57 have intermediate ratios and are therefore unassignable, and the remaining 45 have ratios less than 0.90 and therefore, according to our criteria, have the potential to be dimeric (or higher oligomers). The discrepancies between our predictions and the predictions of the PQS server therefore amount to 45/(45 + 131) × 100% = 26%. The PQS server assigns 918 of the 1,151 proteins as truly dimeric. We find that 548 of these proteins have ratios less than 0.90 and can therefore be assigned as dimeric with confidence, and 222 are unassignable, whereas the remaining 148 are calculated as being monomeric. Again, the discrepancies between the two prediction methods amount to 148/(148 + 548) × 100% = 21%. Our results, which constitute a set of predictions that can be used to further assess the method in future, are accessible at our web site: (ftp://ftp.biochem.uiowa.edu/incoming/PQS.monomers.predictions and ftp://ftp.biochem.uiowa.edu/incoming/PQS.dimers.predictions).

Discussion

The use of sequence analysis methods to identify functionally important residues in macromolecules is a well established idea, and it has been known for some time that such methods have potential for identifying protein–protein binding sites (14). Here, however, we have shown that similar methods can also be used in two ways: (i) to identify interfaces that, on the basis of other criteria, appear to be perfectly reasonable binding orientations as crystal contacts, and (ii) to identify small or otherwise low-scoring interfaces as being true oligomeric contacts. It is in the former use that we can have most confidence in the method: if an interface contains many residues that are not subject to any evolutionary conservation, it is clearly unlikely to represent a true oligomeric contact. In the latter use, that of demonstrating that an otherwise unpromising interface is a legitimate oligomeric contact, it is less simple to have complete confidence in the method. The reason for this is straightforward: the residues in an interface may be conserved for a number of reasons that are unrelated to oligomerization. The most obvious examples would be surface residues that play important structural roles or, in the case of enzymes, residues that are important for catalytic function. There is however another possibility: that the interface residues are conserved because they are involved (physiologically) in interactions with other molecules (2). Although it might seem somewhat unlikely that the same surface can form an interface with multiple molecules, it is clearly not unprecedented, and a particularly good example of this phenomenon has recently been reported: DeLano et al. (15) have shown that the same site on an antibody can adapt its shape to bind to a number of very different macromolecular ligands.

Our approach rests on the simple idea of comparing the evolutionary behavior of the interface residues with those of the remaining surface residues. In the present applications, we have considered all surface residues not involved in the interface as contributing to the latter, but this will not always be appropriate: several of the proteins listed in Table 4, for example, appear to have artificially high calculated ratios because much of their exposed surface is involved in binding other molecules. Obviously, one way around this problem is to simply exclude any residues known to be involved in binding other molecules from calculations of the entropy of the noninterface surface. Although this is simply stated and can be implemented easily on a case-by-case basis (assuming that the residues involved in binding other molecules are known), it is not straightforward to implement in an automated fashion (for large-scale analyses) unless structures of the protein's complexes with other molecules are available. This problem should be borne in mind in evaluating predictions made in an automated fashion.

In application to the known dimeric proteins investigated by Ponstingl et al. (4), the entropy ratio test appears to be of more or less identical accuracy to the SASA and scoring function criteria (86% vs. 85% and 88%, respectively). Moreover, it correctly assigns almost all of the cases that are incorrectly assigned by the other methods, although, of course, because the overall accuracies of the different methods are comparable, this must mean that several cases correctly assigned by other methods are incorrectly assigned by the sequence entropy test. The real use of the method is therefore likely to be as a complement to the existing techniques. In particular, in cases where there is clear agreement between the predictions of the different techniques, it should be possible to assign the oligomeric state with greatly increased confidence.

Abbreviations

SASA

solvent accessible surface area

PQS

Protein Quaternary Structure