Abstract
Class Ia ribonucleotide reductase (RNR) subunit R2 contains a diiron active site. In this paper, active site models for the intermediate X-Trp48+· and X-Tyr122·, the active Fe(III)Fe(III)-Tyr122·, and the met Fe(III)Fe(III) states of E. coli R2 are studied, using broken-symmetry density functional theory (DFT) incorporated with the conductor like screening (COSMO) solvation model. Different structural isomers and different protonation states have been explored. Calculated geometric, energetic, Mössbauer, hyperfine, and redox properties are compared with available experimental data. Feasible detailed structures of these intermediate and active states are proposed. Asp84 and Trp48 are most likely the main contributing residues to the result that the transient Fe(IV)Fe(IV) state is not observed in wild-type class Ia E. coli R2. Asp84 is proposed to serve as a proton transfer conduit between the diiron cluster and Tyr122 in both the tyrosine radical activation pathway and in the first steps of the catalytic proton coupled electron transfer pathway. Proton coupled and simple redox potential calculations show that the kinetic control of proton transfer to Tyr122· plays a critical role in preventing reduction from the active Fe(III)Fe(III)-Tyr122· state to the met state, which is potentially the reason that the Tyr122· in the active state can be stable over very long period.
1. Introduction
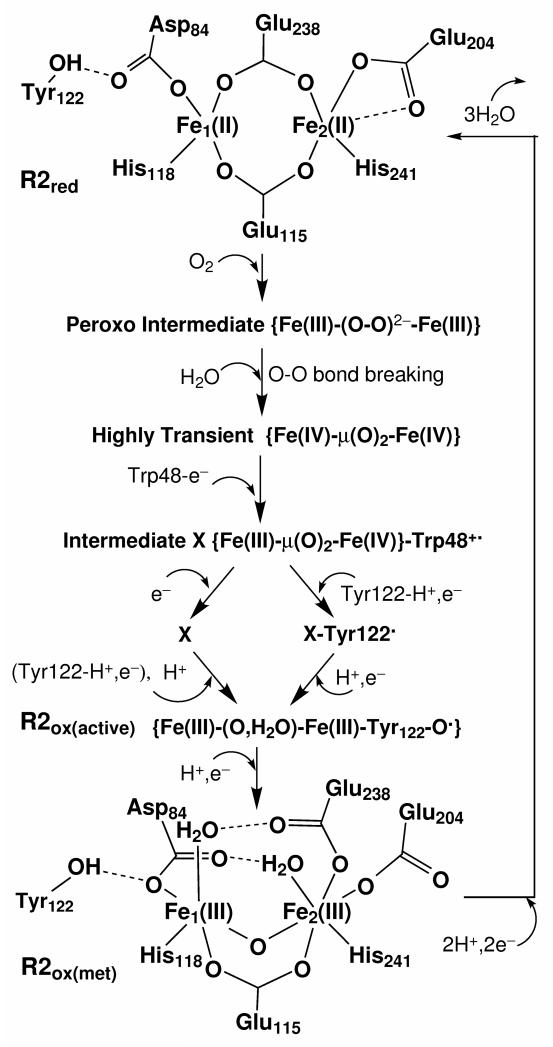
Ribonucleotide reductases (RNRs) catalyze the reduction of ribonucleotides to deoxyribonucleotides providing the required building blocks for DNA replication and repair.1,2 Class Ia RNRs consist of two dissimilar protein subunits: R1 and R2, each a homodimer in an overall α2β2 architecture. The ribonucleotide-to-deoxyribonucleotide reactions occur by a long range radical (or proton-coupled-electron-transfer) propagation mechanism initiated by a fairly stable tyrosine radical (Tyr122 in E. coli) in subunit R2, where a dinuclear iron cluster initially generates and stabilizes this tyrosine radical. The subunit R1 contains the substrate binding site, and catalyzes the dehydroxylation of the 2′-hydroxyl group of the ribose ring. The tyrosine radical in R2 has been identified in the neutral deprotonated form with the oxidized Fe(III)Fe(III) active site and is stable for days at room temperature.1 Once this tyrosine radical is lost, the enzyme becomes inactive. The active form can be regenerated by a complicated sequence of steps involving changes in oxidation state and structural rearrangement with coupled electron and proton transfers (see Figure 1). First the resting oxidized diferric met form of R2 (R2ox(met))3 is reduced by 2 electrons from a reductase protein to the diferrous form, R2red.4 Next, molecular oxygen (O2) binds to the diiron center of R2red and the O-O bond breaks. Then a high-oxidation intermediate state of RNR-R2, called X, is kinetically and spectroscopically observed.5-10 A combination of Q band ENDOR (electron-nuclear double resonance) and Mössbauer data on Y122F-R2 mutant indicate the iron centers of X are high spin Fe(III) (S = 5/2) and high spin Fe(IV) (S = 2) sites that antiferromagnetically couple to give an Stotal = 1/2 ground state.10 The formation of X requires an extra electron, evidently coming from a tryptophan residue, since a transient, broad absorption band centered near 560 nm develops upon reaction of O2 with the Fe(II)Fe(II) cluster and is ascribed to a tryptophan cation radical.11,12 Such a transient 560 nm absorption is not observed in the reaction of E. coli W48F mutant R2, which provides strong evidence that Trp48 in E. coli is the donor of the extra electron.12 Further evidence for the assignment of Trp48+· is the acceleration of decay of the 560-nm-absorbing species by ascorbate, free Fe(II), and 2-mercaptoethanol,11 since Trp48 is near the surface of the protein and is in the H-bonding network of Tyr122⋯Asp84⋯Fe1⋯His118⋯Asp237⋯Trp48, where Fe1 is the iron site closer to Tyr122.
Figure 1.
Schematic drawing of the processing cycle of reproducing Tyr122· from the met diferric state of E. coli R2.
If Trp48+· is reduced by a nearby reductant, the intermediate X-Fe(III)Fe(IV) is the species that oxidizes Tyr122 to Tyr122·. RNR-X has captured the attention of many researchers over the past decade to elucidate its chemical and structural nature.5-35
In the absence of a reductant near Trp48+·, Tyr122· can be produced by an electron transfer reaction to the Trp48+· and this Tyr122· forms faster than that produced by X alone.11 The generation of Tyr122· by Trp48+· of the X-Trp48+· species then produces an intermediate containing both X and Tyr122·. A related species accumulates in the electron deficient W48F-R2 reaction, enough to allow its spectroscopic characteristics to be determined.12
Presently, the detailed structures for the intermediates X-Trp48+· and X-Tyr122·, and the active diferric form of R2 which contains the tyrosine radical are not known. However, the reduced diferrous4 and met oxidized diferric3 (without Tyr122·) states of E. coli R2 have been crystallized, and their X-ray structures were determined at 1.7 and 2.2 Å resolution, respectively. In this paper, based on the active site crystal structures of the Fe(II)Fe(II) and Fe(III)Fe(III) clusters, and earlier proposed RNR-X active site models,27,30 we will study feasible active site structures of the X-Trp48+·, X-Tyr122·, and the active Fe(III)Fe(III)-Tyr122· states using broken-symmetry36-38 density functional theory (DFT) calculations.
2. Active Site Models
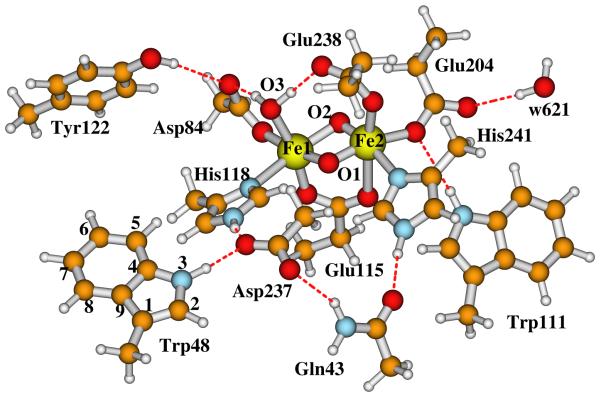
The diiron centers of the reduced and oxidized (met) E. coli R2 X-ray crystal structures are schematically shown in Figure 1. In both states, the −OH group of Tyr122 H-bonds with the Asp84 sidechain. Fe1 (which is closer to Tyr122) is ligated to the sidechains of Asp84 and His118, and the other iron (Fe2) is ligated to Glu204 and His241. In the reduced diferrous cluster, both carboxylate groups from Glu238 and Glu115 exist in a bridging position between the two irons. In the diferric (met) center, the carboxylate of Glu238 changes from the bidentate position to monodentate binding with only Fe2, and each iron site has a terminally binding water molecule, which also H-bonds with Glu238 and Asp84, respectively. In the outer ligand shells, the main H-bonding interactions between the residue sidechains are (see Figure 2): Trp111⋯Glu203, His118⋯Asp237⋯Trp48, and Asp237⋯Gln43⋯His241. The Tyr122⋯Asp84-Fe1-His118⋯Asp237⋯Trp48 pathway is designed for the electron transfer and creation of the Trp48+· and Tyr122· radicals.
Figure 2.
Our previously proposed E. coli RNR-X active site structure with di-μ-oxo bridge.27 This is also our currently proposed structure for the X-Trp48+· state, and for the possible Fe1(IV)Fe2(IV) state.
Upon O2 binding to the Fe(II)Fe(II) center, a diferric peroxo intermediate state (P) was observed in the D84E mutant39 and W48F/D84E double mutant R2.40 Very recently, Jensen et. al performed a series of DFT calculations and proposed that O2 binds to the diferrous center in a cis-μ-1,2 mode,41 which is consistent with our previous calculations for the peroxo-intermediate P of methane monooxygenase (MMO).42 Structural changes along with electron/proton transfers should occur after the O2 binding with Fe(II)Fe(II). A water molecule is proposed to enter along with O2 and binds to the Fe1 site, which causes the opening of the bridging carboxylate of Glu238 to monodentate binding position with Fe2 and H-bonding with this H2O.41 Meanwhile Asp84 sidechain rotates, so that one of its oxygen atoms H-bonds to both Tyr122 and the terminal water on Fe1. This process possibly generates another peroxo-type intermediate state P’ proposed by Jensen et. al,41 which falls between intermediate P and X and has been observed in the RNR W48A/Y122F double mutant.43 Next, the O-O bond breaks, an electron transfers from Trp48 to one of the iron sites, and X{Fe(III)Fe(IV)}-Trp48+· is formed.
In recent years, our group has been studying the properties of a set of active site model clusters for RNR-X using broken-symmetry DFT methods,25-31 and have compared them with the available experimental data, including Mössbauer,10 57Fe, 1H, 17O2, and H2 17O ENDOR17,19,20, EXAFS (extended X-ray absorption fine structure),18 and MCD (magnetic circular dichroism).21 We have performed these calculations on a wide variety of RNR-X model systems (many with both Fe1(III)Fe2(IV) and Fe1(IV)Fe2(III) comparisons) including “open” systems with a single μ-oxo bridge or a μ-oxo and μ-1,1 carboxylate bridge (in addition to the μ-1,3 carboxylate bridge from Glu115 usually present), and on more “closed” complexes with either a (μ-oxo)2 or a (μ-oxo)(μ-hydroxo) bridge. The open systems display a very long Fe-Fe bond length > 2.9 Å (much longer than that from EXAFS analysis), and poor 57Fe Mössbauer properties, and poor 17O and 1H parameters compared to observed ENDOR spectra.19 Based on the detailed analysis and comparisons, the model we studied that can best reproduce most of the experimentally observed properties, in particular the ENDOR experiments,19,20 contains (Figure 2) two μ-oxo bridges (O1 and O2), plus one terminal water (O3) which binds to Fe1(III) and also H-bonds to both sidechains of Asp84 and Glu238, and one bidentate carboxylate group from the sidechain of Glu115.27,29
On the other hand, Miti et. al performed Fe(IV)-d-d transition calculations using time-dependent density functional theory (TD-DFT) on their RNR-X models and compared with their MCD experiments.35 They found that the assignment of the Fe(IV) d-d transitions in wild-type RNR-X best correlates with the Fe(III)(μ-O)(μ-OH)Fe(IV) structure, which differs from the di-μ-oxo model only by having a proton on the bridging oxygen labeled O2. However, the newly performed ENDOR experiments by Shanmugam et al.20 ruled out the μ-hydroxo bridge in X. The authors have proposed that X contains a μ-oxo bridge and a terminal hydroxo bound to Fe(III).20 A model of this type in our previous calculations27 shows poor 57Fe Mössbauer parameters and also poor 1H hyperfine compared to 1H ENDOR.19 In the current paper, we therefore started from our previously calculated X(di-μ-oxo) model (Figure 2) to establish the current X-Trp48+· and X-Tyr122· models. Also, in our proposed reaction pathway, the external proton enters the active site after X (Figure 1, left hand side).
Since X-Trp48+· state is 1+ more positive than the net charge of X, if the active site of X contains as alternative states di-μ-oxo (Figure 2) or (μ-oxo, μ-hydroxo), the center of X-Trp48+· is likely to have the di-μ-oxo structure. We note that the total cluster charge including only the first shell ligands is −1 for the di-μ-oxo and 0 for the (μ-oxo, μ-hydroxo) structure. To test this idea, we will first calculate the energetics of the X{Fe(III)(di-μ-oxo)Fe(IV)}-Trp48+· and X{Fe(III)(μ-oxo, μ-hydroxo)Fe(IV)}-Trp48+· structures. The initial geometries are taken from our previously optimized X model calculations,31 which were originally constructed from chain A of the oxidized E. coli R2 (met) diferric (Fe(III)Fe(III)) X-ray crystal structure (PDB code: 1RIB),3 by breaking the Cβ-Cα, Cγ-Cβ or Cδ-Cγ bonds and adding a linking hydrogen atom along the C-C direction to fill the open valence of the terminal carbon atom.44 The reason for starting from the diferric X-ray crystal structure is that, the overall protein structure and the orientations of most of the carboxylate ligands of X should be closer to the diferric state than the diferrous state. The sizes of the active site models in the current study are as shown in Figure 2, which is also the structure of the current X{Fe(III)(di-μ-oxo)Fe(IV)}-Trp48+· model. Note that the X-Trp48+· model studied by Siegbahn is the same as our X{Fe(III)(di-μ-oxo)Fe(IV)}-Trp48+· model but Siegbahn’s model has a smaller size and an Fe1(IV)Fe2(III) assignment,23,24 reversed from ours Fe1(III)Fe2(IV), with the latter based on Bollinger’s Mössbauer and kinetics experiments.45 The X{Fe(III)(μ-oxo, μ-hydroxo)Fe(IV)}-Trp48+· model is then constructed by adding a proton to the bridging oxygen O2.
The models of the X-Tyr122· and the active Fe(III)Fe(III)-Tyr122· states from our current calculations will be given in section 4 — Results and Discussion.
3. Computational Methodology
All density functional spin-unrestricted calculations have been performed using the Amsterdam Density Functional (ADF) package.46-48 The parametrization of Vosko, Wilk and Nusair (VWN)49 is used for the local density approximation term, and the OPBE50-52 functional is used for the non-local exchange and correlation terms. OPBE is the combination of Handy’s optimized exchange (OPTX)52 and PBE correlation (PBEc) functionals.50,51
In previous work,25-29 we used the PW91 exchange-correlation potential,53 and established that by comparison with experimental 57Fe Mössbauer (isomer shift and quadrupole splitting parameters) and also 57Fe ENDOR hyperfine parameters, the PW91 potential displays the experimentally correct high-spin Fe(III) and Fe(IV) sites in RNR-X. This correct spin state character is also found in lower oxidation states for RNR, MMO, and related synthetic complexes. However, for the Fe(IV)Fe(IV) oxidation state of MMO (intermediate state Q), some structural models show incorrect spin-crossover behavior.54 We addressed this problem by using OPBE for high oxidation state problems involving RNR and MMO. OPBE shows considerably improved spin state crossover energy balance for this class of systems.30,54
Swart et al. have reported a systematic study on the performance of several exchange-correlation functionals for seven different iron complexes which are experimentally found to have either a low, intermediate, or high spin ground state.55 They found that the Handy’s optimized exchange (OPTX) functional performs well, and the OPBE functional performs the best among GGA(general gradient approximation)-type potentials. These authors have also tested different functionals in calculating the atomization energies for the G2-set of up to 148 molecules, six reaction barriers of SN2 reactions, geometry optimizations of 19 small molecules and 4 metallocenes, and zero-point vibrational energies for 13 small molecules.56 Their examination shows that the OPTX containing functionals perform better than the regular GGAs like PBE,50,51 BLYP,57,58 and BP,57,59,60 and OPBE performs exceptionally well in all cases. Recently, new functionals like the double-hybrid B2PLYP61 and hybrid meta-GGA functional TPSSh62 have been demonstrated to outperform the hybrid B3LYP58,63,64 and nonhybrid functionals for predicting certain properties for test sets of transition metal systems.65-68 However Mössbauer isomer shift parameters for the latter potentials have not yet been fitted for the Fe-oxo complexes. The extensive family of geometry optimizations within the dielectric continuum solvation model in the current study are also difficult with hybrid functionals, since our models are large (over 140 atoms), and hybrid or meta-hybrid methods require about three times the computer time of regular GGA methods. We therefore continue to use the OPBE potential in the current study for both geometry optimization and Mössbauer property calculations.
Bollinger et al. proposed that site Fe1 which is closer to Tyr122 is the ferric site in RNR-X based on their two-iron-isotope reactions and Mössbauer spectroscopy experiments.45 This conclusion is supported by our previous 1H and 17O hyperfine A-tensor calculations for the water ligand (bound to Fe1) in X active site models,27,29 and is consistent with the internal electron transfer from Trp48 along the Trp48⋯Asp237⋯His118⋯Fe1 H-bonding pathway. In the current study, we will only perform calculations on the Fe1(III)Fe2(IV) high-spin antiferromagnetically (AF) coupled { S1 = 5/2, S2 = 2, SX = ½} state for the X center. X-Trp48+· and X-Tyr122· are diradicals. The total spin of these diradicals can be either 0 or 1. As in previous work, we will perform “broken-symmetry” (BS)36-38 calculations to represent these spin states. First we construct a ferromagnetically (F) spin-coupled (Stotal = 10/2 for X-Trp48+· or X-Tyr122·) determinant, where the spins on both irons and on Trp48+· or Tyr122· are aligned in a parallel fashion. Then we rotate the spin vector located on atom Fe1(III) or atom Fe2(IV) by interchanging the α and β fit density blocks on site Fe1 or Fe2 from the output file TAPE21 created by this F-coupled calculation in ADF to get the starting spin density for the Stotal = 0 (flip Fe1(III)) or Stotal = 1 (flip Fe2(IV)) diradical state. These BS states are not pure Stotal = 0 or Stotal = 1 states. Instead, these BS states (and their energies) are weighted averages of the pure spin states, strongly weighted toward the lower Stotal states based on the spin coupling algebra.36-38 We have not included spin projection corrections in the current work since we have estimated that these will make only very small differences in the DFT calculated relative energies of different states. The properties of BS states can be directly connected to the hyperfine properties of corresponding pure spin states using the Wigner Eckart theorem.36-38,67
3.1. Geometry Optimization
All models are optimized within the conductor-like screening (COSMO)69-72 solvation model with dielectric constant ε = 20. In COSMO, the quantum cluster is embedded in a molecular shaped cavity surrounded by a continuum dielectric medium. There is no universal dielectric constant for COSMO-like solvation calculations. Although the dielectric value ε = 4 is commonly used for the protein interior, since this is the value of the dielectric constants of crystalline and polymeric amides73 and dry protein and peptide powders,74-77 many studies show that higher effective dielectric constant values (4-30) for protein interiors are needed in reproducing the pKa values of certain internal ionizable groups.77-84 Very recently,31 we have studied quantum cluster size and solvent polarity effects on the geometries and Mössbauer properties of RNR-X(di-μ-oxo) models. Our calculations show that certain Fe-ligand distances (especially Fe1-N(His118) in X), Mössbauer quadruple splittings, and Heisenberg J coupling constant are sensitive to both the quantum cluster size and the polarity of the environment, while the calculated Mössbauer isomer shift and various hyperfine A-tensor properties change very little with the model size and ε.31 ε = 4 appears too small when studying the diiron active site geometry with only the first-shell ligands as seen by comparison with larger models. In the current study, the diradical state can be difficult to obtain, and geometry optimizations are time consuming. We therefore choose a medium model size for the quantum cluster (Figure 2), which contains up to the second-shell residue sidechains (and including also Trp48 and Gln43, 3rd shell residue sidechain) around the diiron center. Accordingly, we choose a larger dielectric constant (ε = 20) for the current calculations in COSMO. The van der Waals radii for atoms Fe, C, O, N, and H are taken as 1.5, 1.7, 1.4, 1.55, and 1.2 Å, respectively. The probe radius for the contact surface between the cluster and solvent is set to 2.0 Å. The triple-ζ polarization (TZP) Slater-type basis sets with frozen cores (C(1s), N(1s), O(1s) and Fe(1s,2s,2p) are frozen) are applied for geometry optimizations. The link-H atoms on Tyr122, Gln43, Trp48, and Trp111 are fixed during geometry optimizations. The broken-symmetry state energies obtained after COSMO geometry optimizations are used to compare the relative energies and calculate the redox potentials and pKa’s in the current paper. We understand that depending on the systems and the DFT functionals employed, the entropy terms may also be significant in determining the relative free energies and the spin state.85-87 However, frequency calculations within COSMO solvation model for our current active site clusters are very demanding. Further, the vibrational entropy terms obtained from frequency calculations are not accurate since the positions of certain link-H atoms are fixed during geometry optimizations. Unlike zero point energies, vibrational entropies are most sensitive to low frequency modes, which are more difficult to calculate accurately. The constraints applied for geometry optimizations would need to be released or somehow modelled. We therefore did not calculate the entropy terms in the current study.
3.2. Mössbauer Isomer Shift and Quadrupole Splitting Calculations
For certain models and states, we have applied single-point Mössbauer isomer shift and quadruple splitting calculations at the optimized geometries using all-electron (i.e. without frozen core approximation) TZP Slater-type basis sets. First, a high-spin F-coupled single-point energy calculation (in COSMO) is performed at the BS optimized geometry. Its TAPE21 file is then modified accordingly by interchanging the α and β fit density blocks on site Fe1 or Fe2. Starting from the modified TAPE21, a BS state single-point energy calculation in COSMO again with all-electron TZP Slater-type basis sets is performed to obtain the electron density (ρ(0)) and the electric field gradient (EFG) at the Fe nucleus.
The Mössbauer isomer shifts δ are calculated based on ρ(0):
| (1) |
In our previous studies,54,88 the parameters α and C have been fitted separately for the Fe2+,2.5+ and Fe2.5+,3+,3.5+,4+ complexes for PW91, OPBE, and OLYP, with all-electron TZP Slater type basis sets. For the Fe2.5+,3+,3.5+,4+ complexes, we have obtained A = 11877.0, α = −0.312, and C = 0.373 mm s−1 for OPBE potential.
For calculating the Mössbauer quadrupole splittings (ΔEQ), the EFG tensors V are diagonalized and the eigenvalues are reordered so that |Vzz| ≥ |Vxx| ≥ |Vyy|. The asymmetry parameter η is defined as
| (2) |
Then the ΔEQ for 57Fe of the nuclear excited state (I = 3/2) can be calculated as
| (3) |
where e is the electrical charge of a positive electron, Q is the nuclear quadrupole moment (0.15 barns) of Fe.89
3.5. pKa Calculations
Several pKa calculations are performed in the current paper. For example, to examine whether the (di-μ-oxo) or (μ-oxo)(μ-hydroxo) model for X-Trp48+· is energetically more favored, we need to calculate the pKa value for the bridging site O2. For the following process,
| (4) |
the pKa value for the bridging OH− group at site O2 is calculated by
| (5) |
For the current study, the energies E[X(di-μ-oxo)-Trp48+·] and E[X(μ-oxo)(μ-hydroxo)-Trp48+·] are taken from the broken-symmetry state energies after the COSMO geometry optimizations. ΔGsol(H+,1atm) is the solvation free energy of a proton at 1 atm pressure. We will use −263.98 kcal mol−1 90-92 for this term since so far it is the best measured value (note that previously we have used −262.11 kcal mol−1 which was obtained from experimental and theoretical analysis27). E(H+) = 12.6416 eV is the calculated energy of a proton (in gas-phase with OPBE potential) with respect to a spin restricted hydrogen atom. The translational entropy contribution to the gas-phase free energy of a proton is taken as −TΔSgas(H+) = −7.76 kcal mol−1 at 298 K and 1 atm pressure.93 5/2RT includes the proton translational energy 3/2RT and PV = RT.93 The zero point energy difference term ΔZPE is estimated as ΔZPE = −7.29 kcal mol−1 taken from previous frequency calculations for small X models.30 Later when we calculate the pKa for Tyr122 sidechain, the ΔZPE is calculated separately, and will be given in the text.
4. Results and Discussion
4.1. Calculated Properties of Models X(di-μ-oxo)-Trp48+· and X(μ-oxo)(μ-hydroxo)-Trp48+·, and the Possible Fe1(IV)Fe2(IV) State
Table 1 shows the main calculated properties for X(di-μ-oxo)-Trp48+· and X(μ-oxo)(μ-hydroxo)-Trp48+·models, including the Fe-Fe and main Fe-ligand distances (Å), the net spin populations (NSP) of Fe1(III), Fe2(IV) and Trp48+·, and the broken-symmetry state energies E (eV) after COSMO optimizations.
Table 1.
Calculated Fe-Fe and Fe-ligand distances (Å), the net spin populations (NSP) of Fe1(III), Fe2(IV) and Trp48+·, the broken-symmetry state energies E (eV), and the pKa value of the bridging O2 site for models X(di-μ-oxo)-Trp48+· and X(μ-oxo)(μ-hydroxo)-Trp48+· and similar calculated properties for Fe1(IV)(di-μ-oxo)Fe2(IV)a
| X(di-μ-oxo)-Trp48+· | X(μ-oxo)(μ-hydroxo)-Trp48+· | Fe1(IV)(di-μ-oxo)Fe2(IV) | ||
|---|---|---|---|---|
| Stotal = 0 | Stotal = 1 | Stotal = 0 | Stotal = 0 | |
| Fe1-Fe2 | 2.792 | 2.794 | 2.959 | 2.731 (2.744) b |
| Fe1-O1 | 1.886 | 1.926 | 1.934 | 1.765 (1.772) |
| Fe2-O1 | 1.748 | 1.732 | 1.708 | 1.815 (1.808) |
| Fe1-O2 | 1.937 | 1.968 | 2.153 | 1.832 (1.809) |
| Fe2-O2 | 1.758 | 1.753 | 1.960 | 1.769 (1.786) |
| Fe1-O3 | 2.119 | 2.130 | 2.092 | 2.125 (2.095) |
| Fe1-N-His118 | 2.345 | 2.368 | 2.196 | 2.180 (2.212) |
| Fe2-N-His241 | 2.180 | 2.192 | 2.154 | 2.102 (2.155) |
| Fe1-O-Asp84 | 2.081 | 2.117 | 2.019 | 1.958 (2.001) |
| Fe1-O-Glu115 | 1.985 | 1.995 | 1.980 | 2.020 (2.012) |
| Fe2-O-Glu115 | 2.592 | 2.598 | 2.350 | 2.349 (2.344) |
| Fe2-O-Glu204 | 1.964 | 1.986 | 1.922 | 1.923 (1.910) |
| Fe2-O-Glu238 | 2.065 | 2.075 | 2.013 | 2.049 (2.037) |
| NSP(Fe1) | 3.83 | 4.04 | 4.09 | 3.15 (3.14) |
| NSP(Fe2) | −3.24 | −3.23 | −3.28 | −3.17 (−3.16) |
| NSP(C1-Trp48+·) | −0.24 | 0.24 | −0.43 | 0.00 |
| NSP(C2-Trp48+·) | −0.07 | 0.07 | −0.14 | 0.00 |
| NSP(N3-Trp48+·) | −0.09 | 0.09 | −0.14 | 0.00 |
| NSP(C4-Trp48+·) | −0.01 | 0.01 | −0.03 | 0.00 |
| NSP(C5-Trp48+·) | −0.04 | 0.04 | −0.05 | 0.00 |
| NSP(C6-Trp48+·) | −0.08 | 0.09 | −0.16 | 0.00 |
| NSP(C7-Trp48+·) | 0.03 | −0.03 | 0.06 | 0.00 |
| NSP(C8-Trp48+·) | −0.12 | 0.13 | −0.22 | 0.00 |
| NSP(C9-Trp48+·) | 0.05 | −0.05 | 0.10 | 0.00 |
| E | −880.6840 | −880.5995 | −880.4384 | −880.9702 (−880.8538) |
| pKa c | 6.06 | |||
Model of X(di-μ-oxo)-Trp48+·and Fe1(IV)(di-μ-oxo)Fe2(IV) was shown in Figure 2. The difference between X(di-μ-oxo)-Trp48+· and X(μ-oxo)(μ-hydroxo)-Trp48+·is that the bridging site O2 is protonated in X(μ-oxo)(μ-hydroxo)-Trp48+·.
Data in parenthesis are for the geometry which was optimized starting from the Stotal = 0 state X(di-μ-oxo)-Trp48+· optimized geometry, and all the H-linking atoms were fixed according to the initial geometry during the optimization process.
The optimized geometries of X(di-μ-oxo)-Trp48+· in Stotal = 0 and Stotal = 1 states are very similar, except the Fe1-O1 and Fe1-O2 distances in Stotal = 1 state are by 0.03 – 0.04 Å longer than the corresponding ones in the Stotal = 0 state, resulting a little larger net spin population (NSP) of Fe1 in the Stotal = 1 state.
The net spin populations are the main indication of the iron spin state and the free radical location. In the ideal ionic limit, the net unpaired spin populations are 5 and 4 for the high-spin Fe1(III) (five d-electrons) and Fe2(IV) (four d-electrons) sites, respectively. The absolute calculated net spins in Table 1 are only smaller by about 1e− than the ionic limit, indicating that the expected oxidation states of the Fe sites with substantial Fe-ligand covalency are correctly predicted. The opposite signs for the spin densities of Fe1 and Fe2 confirm the AF-coupling.
The calculated NSP’s do show that the free radical is located at Trp48 for the X-Trp48+· models. For model X(di-μ-oxo)-Trp48+· in Stotal = 0 and Stotal = 1 state, the total net spin on all the C plus N atoms of the Trp48 ring is −0.57 (spin down) and 0.59 (spin up), respectively, clearly indicating Trp48 is in the cation radical state. Since the diiron center is far from Trp48 by ~10 Å, the coupling between X and Trp48+· is expected to be weak.11 Our broken-symmetry calculations do show X(di-μ-oxo)-Trp48+· model in Stotal = 0 and Stotal = 1 states having similar energies, with Stotal = 0 state a little more stable than Stotal = 1 state by about 2 kcal mol−1.
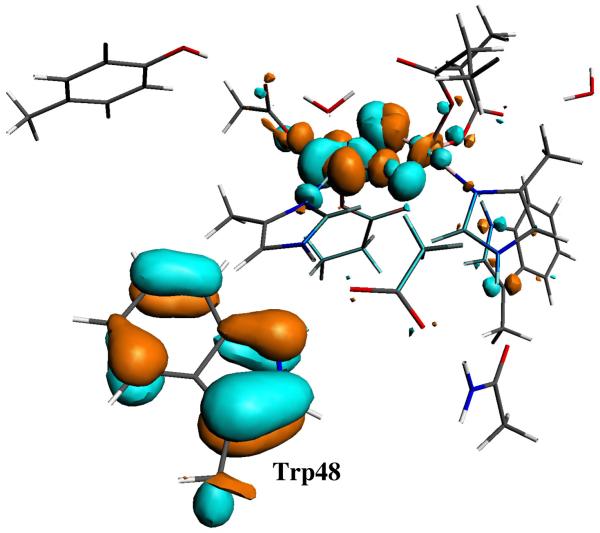
The atomic orbital’s contribution to the α-LUMO (lowest unoccupied molecular orbital) in the Stotal = 0 state and β-LUMO in the Stotal = 1 state of the X(di-μ-oxo)-Trp48+· model calculations also show that the electron hole mainly comes from Trp48 (see Figure 3).
Figure 3.
Molecular orbital plot for the virtual α-LUMO of the X(di-μ-oxo)-Trp48+· model in Stotal = 0 state. 50% of this orbital is located at Trp48.
We failed to converge the Stotal = 1 state calculations for the X(μ-oxo)(μ-hydroxo)-Trp48+· model. In Table 1, only the Stotal = 0 state X(μ-oxo)(μ-hydroxo)-Trp48+· calculated results were presented. It is reasonable to assume that its Stotal = 0 state also has lower energy than (or very similar energy to) the Stotal = 1 state. Comparing with the X(di-μ-oxo)-Trp48+· structures, the protonation of the bridging O2 site in X(μ-oxo)(μ-hydroxo)-Trp48+· elongates the Fe-Fe distance, weakens the Fe1-O1 and Fe-O2 interactions, and strengthens all other Fe-ligand interactions. In X(μ-oxo)(μ-hydroxo)-Trp48+· model, the total NSP on the C and N atoms of the Trp48 ring is calculated to be −1.01 (spin down), indicating a very localized electron hole at Trp48.
According to equations 4 and 5, we calculated the pKa value for the bridging O2 site using the Stotal = 0 state broken-symmetry energies after the COSMO geometry optimizations. The pKa value 6.06 is obtained and is also given in Table 1. It is therefore the X(di-μ-oxo)-Trp48+·model in Stotal = 0 state that is more likely to represent the X-Trp48+· active site structure. This is also in agreement with the analysis of the 2H ENDOR measurements that X does not contain a μ-hydroxo bridge.20
Experimentally it has been observed that the formation of X-Trp48+· is kinetically first order in both O2 and Fe(II)-R2 complex with a formation rate constant ~200 s−1.11 This implies that precursors to the X-Trp48+· diradical species do not accumulate to greater than ~10% of the initial Fe(II)-R2 reactant concentration.11
It is well known that the hydroxo component of methane monooxygenase (MMOH) has a similar diiron active site to RNR-R2.94 However in MMOH, a glutamic acid residue, rather than aspartic acid (Asp84) binds to Fe1 (see Figure 2). Upon reaction with dioxygen, the O-O bond cleavage rate is only about 1 s−1,95 and an intermediate state Q in MMOH has been kinetically and spectroscopically observed.96-99 Q is proposed to be in the AF-coupled high-spin Fe1(IV)Fe2(IV) state with two di-μ-oxo bridges and one terminal water ligand, just as in the diiron center shown in Figure 2.42,54,100,101 In MMOH, an arginine residue is in the place of Trp48 in E. coli R2.94 Siegbahn performed the O-O bond cleavage calculations for the active sites of RNR-R2 and MMOH, and concluded that the electron transfer from Trp48 to the diiron center decreases the O-O cleavage barrier by approximately 3 kcal mol−1 for RNR compared to MMOH.23,24 This electron transfer therefore possibly occurs sometime during the O-O bond cleavage, which explains the faster O-O cleavage rate in wild-type R2 than in MMOH. However, although with a slower rate, O-O bond still can be cleaved in the W48F mutant R2.12 It has been observed that after O-O cleavage, a species which was proposed as the Fe(IV)O2Fe(IV) state,12 is accumulated at the 80 s−1 rate.12 Therefore, there is still some probability that the Fe(IV)Fe(IV) state, like intermediate Q in MMOH, is formed before the electron is transferred from Trp48 to the diiron center in wild-type R2. We present results on the structural, electronic and energetic properties of the Fe(IV)Fe(IV) state and discuss why it is not observed in wild-type R2.
The Fe1(IV)Fe2(IV) state possibly has the similar structure to MMOH-Q42,54 and to X-Trp48+· shown in Figure 2. We therefore also optimized the geometry of the broken-symmetry (Stotal = 0) state of Fe1(IV)(di-μ-oxo)Fe2(IV), starting from the Stotal = 0 X(di-μ-oxo)-Trp48+· structure. The geometric and energetic properties of the COSMO optimized Fe1(IV)(di-μ-oxo)Fe2(IV) structure are also given in Table 1 (the last column outside the parenthesis). In this structure, each iron has one short Fe-O distance (1.77 Å for Fe1-O1 and Fe2-O2), which was also reported for the MMOH-Q structure from EXAFS experiments.98
The COSMO optimized structure of the Fe1(IV)(di-μ-oxo)Fe2(IV) cluster is by 6.6 kcal mol−1 (0.286 eV) lower in energy than the Stotal = 0 state of X(di-μ-oxo)-Trp48+· structure. This energy gap is surprisingly large. The lower energy Fe1(IV)(di-μ-oxo)Fe2(IV) state should be observable, unless there is a large kinetic barrier to attain the diferryl state. In fact, reorganization energies of about 1 eV (23 kcal mol−1) are quite common in biological electron transfer, so kinetics need not fully track the lowest energy states. We notice that the Fe-Fe and most of the Fe-ligand distances in the optimized Fe1(IV)(di-μ-oxo)Fe2(IV) geometry are shorter than the corresponding ones in X(di-μ-oxo)-Trp48+· structures. The earlier Fe(II)-Fe(II) state of R2 has the longest Fe-Fe distance, 3.94 Å of all known intermediates.4 Upon O2 binding and the O-O bond breaking, the Fe-Fe distance should diminish and the first-shell ligands, especially the sidechains of Asp84, His118, His241, and Glu204 should follow this decrease, in order to arrive at the Fe1(IV)(di-μ-oxo)Fe2(IV) state geometric minimum. Since the Fe-Fe distance of the X(di-μ-oxo)-Trp48+· state is longer than that of Fe1(IV)(di-μ-oxo)Fe2(IV), the central diiron geometry on the reaction pathway should first arrive at a geometry similar to that of the X(di-μ-oxo)-Trp48+· state. Then vertical electron transfer from Trp48 to Fe1 may happen at this stage. According to Marcus theory, the crossing point(s) for electron transfer will occur at a geometry (geometries) intermediate to both X(di-μ-oxo)-Trp48+· and Fe1(IV)(di-μ-oxo)Fe2(IV).
The α and β molecular orbital energy (eV) levels around HOMO and LUMO for the optimized Fe1(IV)(di-μ-oxo)Fe2(IV) cluster are shown in Figure 4. Simple one-electron orbital energy differences (εiLUMO − εjHOMO) do not represent total excitation energies well, because electron self-interaction energies in orbitals i, j are not included properly and electron relaxation effects upon excitation are not included either. Bearing this in mind, here we only qualitatively compare the energy gaps between the molecular orbitals of the optimized Fe1(IV)(di-μ-oxo)Fe2(IV) structure. In Figure 4, the sum of the atomic orbital contributions (which are larger than 1%) to the molecular orbital shows the location of the molecule orbital. Both α and β LUMO’s mainly locate at site Fe1. Fe2 also has a large contribution to α-LUMO. Both α and β HOMO’s are localized at the Trp48 sidechain. The molecular orbital one-electron energy difference between α-HOMO and α-LUMO is only 1.3 kcal mol−1, while the β-HOMO and β-LUMO are degenerate. Therefore, it is very likely that the LUMO’s and HOMO’s exchange positions at some point (as mentioned above) when the central active site compresses to a geometry which is similar to that of the X(di-μ-oxo)-Trp48+· state. In Figure 4, both α and β HOMO-3 orbitals localize at the Tyr122 sidechain, and are ~11 kcal mol−1 below the corresponding HOMO’s, which also provides an explanation for why the “extra” electron comes from Trp48 and not Tyr122 in wild-type E. coli R2, even though Tyr122 is closer to the diiron center. As seen in next section, this relative energy difference changes when Tyr122 deprotonates.
Figure 4.
α and β molecular orbital energy (eV) levels around HOMO and LUMO for the Fe1(IV)(di-μ-oxo)Fe2(IV) model cluster. The atomic orbital contributions to the molecular orbital, which are larger than 1% and are located at the same residue sidechain or at one of the iron sites, are added up to show the location of the molecular orbital. Majority spin is α on Fe1 and β on Fe2 (see Table 1).
Considering the oxidation process, where O2 binds to Fe(II)-Fe(II) and the subsequent reaction causes an overall compression, the “restraining” force or “steric strain” of the protein backbone may well increase the energy of the Fe1(IV)(di-μ-oxo)Fe2(IV) state. In our geometry optimizations described in section 3.1, only the link-H atoms on the second- and third-shell residue sidechains were fixed. All atoms in the first-shell ligands were allow to move. In order to test how the steric strain of the first-shell protein backbone will influence the structure and energy of the Fe1(IV)(di-μ-oxo)Fe2(IV) state, we started from the optimized X(di-μ-oxo)-Trp48+· (Stotal = 0) state geometry and fixed all link-H atoms according to this geometry, then optimized the rest of the atoms in the Fe1(IV)(di-μ-oxo)Fe2(IV) state. The main Fe-Fe and Fe-ligand distances and broken-symmetry energy of this “more strained” Fe1(IV)(di-μ-oxo)Fe2(IV) state structure are also given in Table 1 (the last column in the parenthesis). By also fixing the first-shell link-H atoms according to the X(di-μ-oxo)-Trp48+· (Stotal = 0) state geometry, the Fe1(IV)(di-μ-oxo)Fe2(IV) state energy is increased by 2.7 kcal mol−1 (0.116 eV). This energy is expected to increase more if the strain is exerted according to the Fe(II)-Fe(II) state geometry (or corresponding to the met Fe(III)Fe(III) state geometry where the Fe-Fe distance is 3.42 Å observed in the X-ray crystal structure).3 This may qualitatively explain that the formation rate constant of X-Trp48+· is high (~200 s−1),11 and no accumulation of the diferryl state is observed even if the O-O cleavage occurs before the electron transfer from Trp48 to Fe1.
Comparing the geometries between the two optimized Fe1(IV)(di-μ-oxo)Fe2(IV) state structures (data outside and inside the parenthesis of the last column of Table 1), the significant Fe-ligand distance changes are for Fe1-O-Asp84, Fe1-N-His118, and Fe2-N-His241, which lengthen by 0.04, 0.03, and 0.05 Å, respectively, when fixing the link-H atoms on Asp84, His118, and His241 sidechains. Asp84 has a shorter and therefore more stiff sidechain comparing with Glu sidechains, and it is the only difference between the first shell structures of RNR-R2 and MMOH active sites. In MMOH, the site where Asp84 sits in R2 is also a Glu.94 It is likely that the strain of Asp84 is another reason which prevents the accumulation of the Fe1(IV)(di-μ-oxo)Fe2(IV) state in E. coli R2. Later we will see that the Fe-O-Asp84 bond breaks when the proton from Tyr122 transfers to Asp84 in the X(di-μ-oxo)-Tyr122· structure.
4.2. Calculated Properties of Models X(di-μ-oxo)-Asp84H-Tyr122· and X(μ-oxo)(μ-hydroxo)-Tyr122·
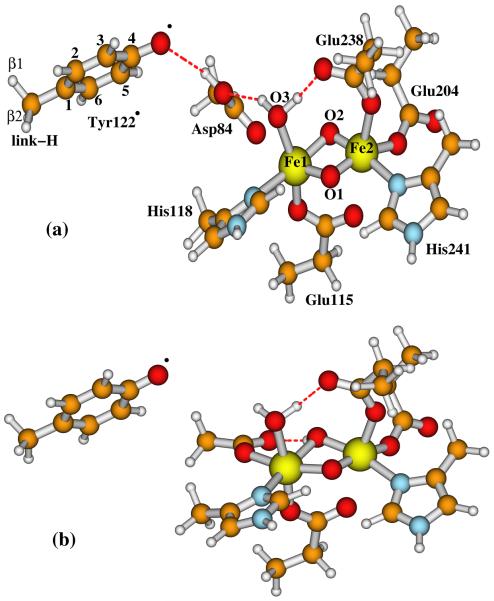
In the absence of a reductant near Trp48+·, Tyr122 will then donate an electron to Trp48+·, and the X-Tyr122· diradical will be formed.11,12 Since Tyr122· is found in the neutral deprotonated form, the electron transfer from Tyr122 to Trp48+· is coupled with proton transfer, and the proton transfer may even happen prior to the electron transfer. The direct proton acceptor of this proton transfer would be the carboxylate group of Asp84, which has H-bonding interaction with the −OH group of Tyr122 in X-Trp48+·. Starting from the optimized Stotal = 0 state X(di-μ-oxo)-Trp48+· structure, we simply moved the proton from Tyr122 to Asp84, and optimized the geometry with the same charge and spin state as X(di-μ-oxo)-Asp84H-Trp48+·. During the optimization, the proton stayed on Asp84 and H-bonded to the oxygen of Tyr122, the Fe1-O(Asp84) bond was gradually elongated and finally was broken at a distance 2.817 Å, and importantly, the X-Tyr122· state was automatically obtained. The center of the optimized X(di-μ-oxo)-Asp84H-Tyr122· model is shown in Figure 5a, and the main calculated properties of this model are given in Table 2. The total net spin on the C and O atoms of the Tyr122 ring is −1 (spin down), definitely showing the Tyr122· radical state.
Figure 5.
Active site models for (a) X(di-μ-oxo)-Asp84H-Tyr122· and (b) X(μ-oxo)(μ-hydroxo)-Tyr122·. Asp84 sidechain is protonated in (a) and not in (b). The outer-shell residue sidechains shown in Figure 2, including Gln43, Trp48 (or Phe48), Trp111, Asp237, and water-627, are also included in calculations but not shown here.
Table 2.
Calculated Fe-Fe and Fe-ligand distances (Å), net spin populations (NSP) of Fe1(III), Fe2(IV) and Tyr122·, broken symmetry state energies E (eV), 57Fe Mössbauer isomer shift (δ, mm s−1), quadrupole splittings (ΔEQ, mm s−1) and η, and proton hyperfine coupling constants (Axx, Ayy, Azz, MHz) for Tyr122· in models X(di-μ-oxo)-Asp84H-Tyr122· and X(μ-oxo)(μ-hydroxo)-Tyr122· in wild-type and in W48F variant, and compared with experimental (exp) results
| Wild-type | W48F | ||||
|---|---|---|---|---|---|
| X(di-μ-oxo)- Asp84H-Tyr122· |
X(μ-oxo)(μ- hydroxo)-Tyr122· |
X(di-μ-oxo)- Asp84H-Tyr122· |
X(μ-oxo)(μ- hydroxo)-Tyr122· |
exp a | |
| Fe1-Fe2 | 2.724 | 2.912 | 2.749 | 2.909 | |
| Fe1-O1 | 1.860 | 1.928 | 1.877 | 1.928 | |
| Fe2-O1 | 1.777 | 1.712 | 1.758 | 1.712 | |
| Fe1-O2 | 1.942 | 2.049 | 1.949 | 2.046 | |
| Fe2-O2 | 1.735 | 1.927 | 1.744 | 1.957 | |
| Fe1-O3 | 2.097 | 2.191 | 2.119 | 2.174 | |
| Fe1-N-His118 | 2.252 | 2.196 | 2.255 | 2.162 | |
| Fe2-N-His241 | 2.145 | 2.153 | 2.143 | 2.169 | |
| Fe1-O-Asp84 | 2.817 | 2.014 | 2.495 | 1.999 | |
| Fe1-O-Glu115 | 1.963 | 1.975 | 1.973 | 2.006 | |
| Fe2-O-Glu115 | 2.591 | 2.454 | 2.603 | 2.246 | |
| Fe2-O-Glu204 | 1.957 | 1.914 | 1.961 | 1.916 | |
| Fe2-O-Glu238 | 2.094 | 2.032 | 2.100 | 2.063 | |
| NSP(Fe1) | 4.01 | 4.07 | 4.02 | 4.07 | |
| NSP(Fe2) | −3.23 | −3.28 | −3.24 | −3.29 | |
| NSP(C1-Tyr122·) | −0.39 | −0.39 | −0.39 | −0.39 | |
| NSP(C2-Tyr122·) | 0.09 | 0.10 | 0.10 | 0.10 | |
| NSP(C3-Tyr122·) | −0.22 | −0.24 | −0.22 | −0.23 | |
| NSP(C4-Tyr122·) | −0.05 | −0.03 | −0.04 | −0.03 | |
| NSP(O-Tyr122·) | −0.30 | −0.31 | −0.30 | −0.31 | |
| NSP(C5-Tyr122·) | −0.25 | −0.25 | −0.25 | −0.26 | |
| NSP(C6-Tyr122·) | 0.10 | 0.10 | 0.10 | 0.11 | |
| E | −880.5871 | −880.7229 | −849.8933 | −850.0994 | |
| δ(Fe1, Fe2) | (0.50, 0.22) | (0.51, 0.31) | (0.52, 0.21) | (0.51, 0.32) | (0.47, 0.22) |
| ΔEQ(Fe1, Fe2) | (0.54, −0.33) | (−0.43, −0.64) | (0.46, −0.35) | (0.54, −0.59) | (−0.7, −0.64) |
| η(Fe1, Fe2) | (0.77, 0.66) | (0.53, 0.44) | (0.76, 0.80) | (0.88, 0.42) | (0.5, 2.7) |
| 1H(Axx, Ayy, Azz) for Tyr122·: | |||||
| H-3 | (23.9, 6.8, 19.4) | (25.1, 7.6, 20.0) | (24.2, 6.9, 19.6) | (24.6, 7.3, 19.7) | (26.9, 7.8, 19.6) |
| H-5 | (26.1, 7.1, 21.0) | (26.3, 7.6, 21.3) | (26.2, 7.0, 21.0) | (27.2, 7.6, 21.9) | (26.9, 7.8, 19.6) |
| H-β1 | −(69.6, 62.9, 64.5) | −(80.9, 74.2, 75.9) | −(73.2, 66.6, 68.1) | −(69.5, 63.1, 64.6) | (57.8, 52.1, 54.9) |
| H-2 | −(6.4, 0.7, 3.1) | −(6.7, 1.2, 3.5) | −(6.5, 0.8, 3.9) | −(6.8, 1.2, 3.5) | ~( 0, 0, 0) |
| H-6 | −(6.5, 0.6, 3.0) | −(6.8, 1.0, 3.5) | −(6.6, 0.6, 3.1) | −(7.0, 1.2, 3.7) | ~( 0, 0, 0) |
| H-β2 | (−3.8, 1.3, 0.9) | −(11.6, 6.0, 6.9) | (−4.8. −0.09, 0.4) | (−4.4, 0.3, 0.9) | ~ (0, 0, 0) |
| H-link | −(57.4, 50.5, 52.0) | −(36.5, 30.5, 31.7) | −(52.8, 46.1, 47.6) | −(53.9, 47.3, 48.8) | |
Experimental data are for W48F mutant E. coli R2, taken from Ref. 12.
If Trp48+· is reduced by a nearby reductant, then X alone will oxidize Tyr122 to Tyr122·, with a slower rate (0.85 ± 0.15 s−1) than the oxidation by X-Trp48+· (6.2 ± 1.2 s−1).11 Siegbahn studied the pathway of X → Fe(III)Fe(III)-Tyr122·, and proposed that a water molecule goes between Tyr122 and Asp84 (and also H-bonds with the terminal H2O ligand) in X as a bridge for the proton transfer from Tyr122 to Asp84.23 A water molecule between the Tyr and Asp is commonly observed in class Ib RNRs, where Tyr and Asp are far from each other.102 However, no such a water molecule has ever been observed between Tyr122 and Asp84 in class Ia E. coli R2 crystal structures, including the iron-free form.103 We therefore did not have such a water molecule in the X-Trp48+· → X-Tyr122· pathway.
Experimentally 57Fe Mössbauer isomer shifts (δ) and quadrupole splittings (ΔEQ) for X and the proton hyperfine coupling constants (Axx, Ayy, Azz) for Tyr122· were determined for the X-Tyr122· diradical state in mutant W48F E. coli R2.12 Our calculated properties are compared with those experimental data in Table 2. For the current X(di-μ-oxo)-Asp84H-Tyr122· model, the calculated δ(Fe1, Fe2) = (0.50, 0.22 mm s−1) are highly consistent with the observed values (0.47, 0.22 mm s−1). The absolute values of the ΔEQ’s are also reasonably reproduced. Our previous calculations show that the correct sign of ΔEQ is difficult to predict when η is close to 1. The sign of the calculated ΔEQ can vary with the chosen computational methods, atomic basis sets, dielectric constant of the environment, different model structures, and the size of the quantum cluster.31 The standard deviation (SD) of ΔEQ for OPBE potential on the test set of synthetic complexes is 0.25 mm s−1,54 so the absolute values of our calculated ΔEQ here (0.54, 0.33 mm s−1) are about 1SD from experiment (0.7, 0.64 mm s−1).
From the ADF output, we extracted the local Tyr122· 1H hyperfine A-tensors corresponding to Tyr radical spin S1 = ½ and the spin Hamiltonian term(∑i S1·(Ai) ·(IH)i).12 We cross checked that these Ai are the same when computed either for Stotal = 1 or Stotal = 0. (It also turned out that the energies of the Stotal = 1 and Stotal = 0 states are almost the same.) The calculated 1H hyperfine A-tensors for H-3 and H-5 of Tyr122· (see Figure 5a for notations) are very similar and agree with the corresponding experimental values very well. One of the calculated β protons (Hβ1) has a large A-tensor (> 50 MHz) as observed in experiment. Experimentally, the hyperfine couplings for protons H-2, H-6, and the other H-β were very weak and were not reported.12 Correspondingly, our calculated A-tensors for these protons are also small.
We recall that in met Fe(III)Fe(III) E. coli R2 crystal structure (see R2ox(met) in Figure 1) (PDB code: 1RIB),3 the bridging site O2 changes to a terminally bound water molecule which H-bonds with the carboxylate group of Asp84. Therefore another possible conformation for X-Tyr122· state would have the protonated Asp84 sidechain in X(di-μ-oxo)-Asp84H-Tyr122· model (Figure 5a) rotating and donating the proton to site O2. See Figure 5b for this new structure, which is named X(μ-oxo)(μ-hydroxo)-Tyr122· hereafter. The calculated properties of this model are also given in Table 2.
When site O2 is protonated, the central geometry of the model X(μ-oxo)(μ-hydroxo)-Tyr122· is different from that of X(di-μ-oxo)-Asp84H-Tyr122·. The Fe-Fe and Fe-O2 distances are much longer in X(μ-oxo)(μ-hydroxo)-Tyr122·, resulting in different Mössbauer properties. The predicted quadrupole splitting values still do not agree well with experiment. The calculated δ(Fe1) = 0.51 mm s−1 for X(μ-oxo)(μ-hydroxo)-Tyr122· is similar to that (0.50 mm s−1) for X(di-μ-oxo)-Asp84H-Tyr122·, and is close to the observed value of 0.47 mm s−1. However, the predicted δ(Fe2) = 0.31 mm s−1 for X(μ-oxo)(μ-hydroxo)-Tyr122· is larger (by 0.09 mm s−1) than that for X(di-μ-oxo)-Asp84H-Tyr122· and the experimental value (both are 0.22 mm s−1). Therefore the calculated Mössbauer isomer shifts for model X(di-μ-oxo)-Asp84H-Tyr122· are closer to experimental results than for model X(μ-oxo)(μ-hydroxo)-Tyr122·. On the other hand, the broken-symmetry state electronic energy of X(μ-oxo)(μ-hydroxo)-Tyr122· is by 3 kcal mol−1 lower than that of X(di-μ-oxo)-Asp84H-Tyr122·. However, considering the accuracy of DFT and solvation calculations, this is not a large energy difference. The change of the active site structure from the isomer X(di-μ-oxo)-Asp84H-Tyr122· (where Asp84 is protonated) to X(μ-oxo)(μ-hydroxo)-Tyr122· will be determined by the rotational potential energy barrier of the protonated Asp84 sidechain, and a potential energy barrier for Asp84(O)-Fe1 rebinding and Asp84(OH) to O2 proton transfer. The calculated hyperfine A-tensors for H-3 and H-5 of Tyr122· in X(μ-oxo)(μ-hydroxo)-Tyr122· are essentially the same as those in X(di-μ-oxo)-Asp84H-Tyr122·.
We note that the 57Fe Mössbauer and 1H-Tyr122· hyperfine experimental data were obtained for the W48F mutant R2, while our calculations so far were performed on the wild-type X-Tyr122· cluster models. In order to see if the mutation will influence the calculated properties, we changed the Trp48 sidechain to Phe48 sidechain (assuming the Cα and Cβ positions of Trp48 and Phe48 are the same) in both X(di-μ-oxo)-Asp84H-Tyr122· and X(μ-oxo)(μ-hydroxo)-Tyr122· models. The geometries of the W48F models were also optimized in COSMO. The calculated properties are also given in Table 2 for comparison. Overall the properties of the mutant models are very similar to the corresponding wild-type models. Still the predicted δ(Fe2) = 0.21 mm s−1 in W48F-X(di-μ-oxo)-Asp84H-Tyr122· model reproduces the observed value of 0.22 mm s−1 very well, and δ(Fe2) in W48F-X(μ-oxo)(μ-hydroxo)-Tyr122· model is too large (0.32 mm s−1). Therefore, the X(di-μ-oxo)-Asp84H-Tyr122· model is more likely to represent the X-Tyr122· active site structure.
4.3. Feasible Active Site Conformations in the Fe1(III)Fe2(III)-Tyr122· Active State of E. coli R2
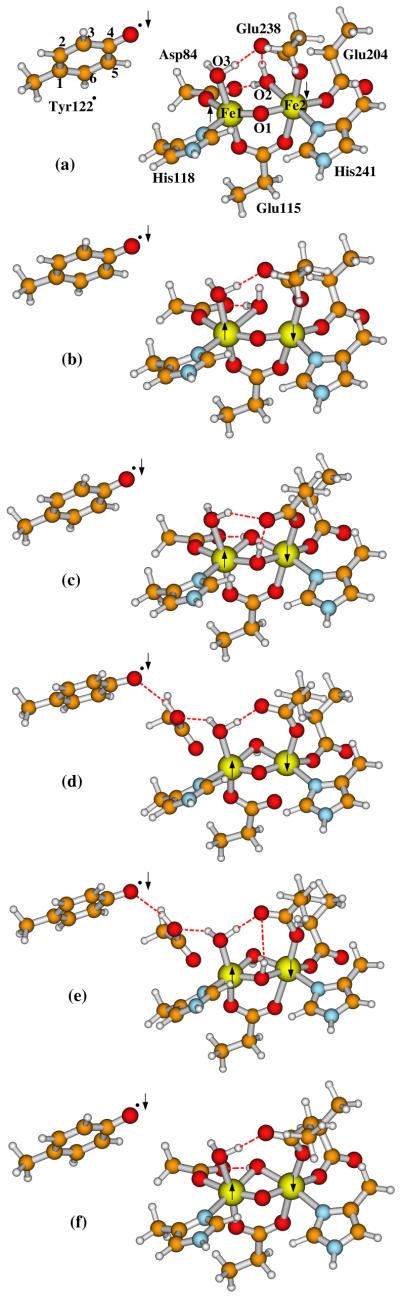
The active state of Fe1(III)Fe2(III)-Tyr122· is formed by an electron transfer to the X-Tyr122· center or by Tyr122 being oxidized by X. The complex can also pick up a proton as well. So far as we know, no X-ray crystal structure is available for the active state of R2. 57Fe Mössbauer spectra for the active state of R2 were first reported 30 years ago,104 and later were redone and checked by Que’s group.105 Mössbauer, 1H NMR, optical and resonance Raman experiments show that the major spectroscopic properties of the active site do not change when the tyrosyl radical is reduced,104-106 indicating similar structures of the active and inactive (met) diferric center of R2. Based on the met Fe1(III)Fe2(III) crystal structure (R2ox(met) in Figure 1) and the X-Tyr122· models studied above, we constructed six active site models for the active form of R2, in order to investigate the feasible conformations of R2 in the active state by comparing the relative energies of these model clusters and their calculated Mössbauer properties with experiments.
The diiron centers of the six active state model clusters are shown in Figure 6a-f. The names of these models are given as:
A(Obr,H2Ot2) (Figure 6a), where “A” represents the active Fe1(III)Fe2(III)-Tyr122· state, Obr is the bridging (br) oxo at site O1, H2Ot2 represents the H2O at site O2, and t2 means terminally binding to Fe2. This structure is basically the same as the met diferric (R2ox(met) in Figure 1) form as seen in the X-ray crystal structure, but with the neutral deprotonated Tyr122·. Starting from the X(di-μ-oxo)-Tyr122· state (Figure 5a), this A(Obr,H2Ot) may be formed in the following process: first an electron has to transfer to Fe2(IV), then the protonated Asp84 sidechain rotates to donate the proton to O2 (see Figure 5b), and meanwhile another proton also needs to transfer to O2. Site O2 then becomes a water molecule, which H-bonds to Asp84 sidechain. The Fe1-O2 distance elongates and the H2O terminally binds only to Fe2(III). This process is similar to the X → Fe(III)Fe(III)-Tyr122· pathway proposed by Siegbahn with smaller models.23 The main difference is that, in Siegbahn’s model, a water molecule is inserted between Tyr122 and Asp84, X is in Fe1(IV)Fe2(III) state rather than Fe1(III)Fe2(IV) state, and the bridging O2 site in X is a hydroxo rather than a μ-oxo.
A(Obr,H2Ot1) (Figure 6b). The difference between this model and A(Obr,H2Ot2) is the position of the H2O at site O2. The initial purpose for studying this model is to test if the water molecule at site O2 would stay in the bridging (br) position between Fe1(III) and Fe2(III) like the bridging hydroxo in Figure 5b. However, after geometry optimization, the Fe2-O2 bond breaks. Therefore the H2O at site O2 terminally binds to Fe1 (t1). Alternatively, this complex can be considered a weak bridging structure with the H2O bridge between Fe1 and Fe2.
A(OH−br,OH−br) (Figure 6c). Although the ligand residue sidechains in the diiron centers of E. coli R2 and MMOH are very similar, their X-ray crystal structures for both Fe(II)Fe(II) and Fe(III)Fe(III) states are different. The Fe(III)Fe(III) state of MMOH contains two μ-OH− species,94 rather than the one μ-oxo and one H2Ot in met diferric R2. The model A(OH−br,OH−br) is constructed in order to see whether the active form of R2 would favor the di-μ-OH− structure energetically.
A(Obr,OH−br)-Asp84H (Figure 6d). This model is constructed to see if the protonated Asp84 in the active state will stay in the position as in X(di-μ-oxo)-Tyr122· (Figure 5a), and the protonated site O2 becomes a μ-OH−.
A(OH−br,OH−br)-Asp84H (Figure 6e). Comparing with A(Obr,OH−br)-Asp84H, site O1 is also protonated and becomes a μ-OH− in this model.
A(Obr,OH−br) (Figure 6f). This structure is evaluated to see if it is possible that the active form stays in an analogous protonation state to the X(μ-oxo)(μ-hydroxo)-Tyr122· structure (Figure 5b). Even if not, later when we calculate the redox potential for X(di-μ-oxo)-Tyr122· + H+ + e− → Active-Form, we will also need the energy of this structure. This structure is similar to Figure 5b, but with binding at Fe2-O-Glu115, making Glu115 bidentate to Fe1 and Fe2.
Figure 6.
Active site models for the active (A) state Fe1(III)Fe2(III)-Tyr122· of E. coli R2 studied in the current paper. The following names are given for these models and discussed in the text: (a) A(Obr,H2Ot2; (b) A(Obr,H2Ot1); (c) A(OH−br,OH−br); (d) A(Obr,OH−br)-Asp84H; (e) A(OH−br,OH−br)-Asp84H; and (f) A(Obr,OH−br), where “br” means the oxygen species is in the “bridging” position between Fe1 and Fe2, “t2” and “t1” in models (a) and (b) represent the ligand water molecule at site O2 “terminally” binding to Fe2 and Fe1, respectively, and Asp84H means the sidechain of Asp84 is protonated in that model. The arrows indicate the directions of the net spins on Fe1, Fe2, and Tyr122·. The outer-shell residue sidechains shown in Figure 2, including Gln43, Trp48, Trp111, Asp237, and water-627, are also included in calculations but not shown here.
All geometries of these models were optimized within COSMO according to section 3.1. The main Fe-ligand distances, net spin populations on Fe1(III), Fe2(III), and Tyr122·, broken-symmetry state energies after geometry optimizations, and the calculated and experimental 57Fe Mössbauer properties are given in Table 3.
Table 3.
Calculated Fe-Fe and Fe-ligand distances (Å), net spin populations (NSP) of Fe1(III), Fe2(III) and Tyr122·, broken symmetry state energies E (eV), 57Fe Mössbauer isomer shift (δ, mm s−1), quadrupole splittings (ΔEQ, mm s−1) and η for the Fe1(III)Fe2(III)-Tyr122· active site modelsa
| (a) A(Obr,H2Ot2) |
(b) A(Obr,H2Ot1) |
(c) A(OH−br,OH−br) |
(d) A(Obr,OH−br)- Asp84H |
(e) A(OH−br,OH−br)- Asp84H |
(f) A(Obr,OH−br) |
exp b | |
|---|---|---|---|---|---|---|---|
| Fe1-Fe2 | 3.151 | 3.131 | 3.053 | 2.881 | 3.079 | 2.889 | |
| Fe1-O1 | 1.782 | 1.795 | 1.959 | 1.781 | 1.933 | 1.785 | |
| Fe2-O1 | 1.826 | 1.818 | 2.046 | 1.848 | 2.159 | 1.847 | |
| Fe1-O2 | 2.744 | 2.412 | 2.003 | 2.084 | 1.993 | 2.016 | |
| Fe2-O2 | 2.278 | 2.506 | 2.023 | 2.111 | 2.081 | 2.075 | |
| Fe1-O3 | 2.215 | 2.196 | 2.345 | 2.129 | 2.103 | 2.248 | |
| Fe1-N-His118 | 2.123 | 2.152 | 2.238 | 2.207 | 2.148 | 2.276 | |
| Fe2-N-His241 | 2.206 | 2.150 | 2.220 | 2.238 | 2.167 | 2.239 | |
| Fe1-O-Asp84 | 2.041 | 2.090 | 2.011 | 3.032 | 2.962 | 2.065 | |
| Fe1-O-Glu115 | 1.995 | 2.006 | 2.001 | 1.975 | 1.946 | 2.033 | |
| Fe2-O-Glu115 | 2.245 | 2.165 | 2.153 | 2.427 | 2.224 | 2.271 | |
| Fe2-O-Glu204 | 2.014 | 2.013 | 1.966 | 2.023 | 1.916 | 2.066 | |
| Fe2-O-Glu238 | 2.042 | 2.037 | 2.060 | 2.032 | 1.994 | 2.060 | |
| NSP(Fe1) | 4.05 | 4.04 | 4.16 | 4.02 | 4.20 | 3.85 | |
| NSP(Fe2) | −4.05 | −4.04 | −4.14 | −4.06 | −4.13 | −4.04 | |
| NSP(C1-Tyr122·) | −0.39 | −0.39 | −0.39 | −0.38 | −0.39 | −0.29 | |
| NSP(C2-Tyr122·) | 0.10 | 0.10 | 0.10 | 0.09 | 0.09 | 0.08 | |
| NSP(C3-Tyr122·) | −0.24 | −0.24 | −0.24 | −0.22 | −0.22 | −0.18 | |
| NSP(C4-Tyr122·) | −0.03 | −0.03 | −0.03 | −0.04 | −0.05 | −0.02 | |
| NSP(O-Tyr122·) | −0.31 | −0.31 | −0.31 | −0.30 | −0.30 | −0.25 | |
| NSP(C5-Tyr122·) | −0.25 | −0.25 | −0.25 | −0.24 | −0.25 | −0.19 | |
| NSP(C6-Tyr122·) | 0.10 | 0.10 | 0.10 | 0.10 | 0.10 | 0.08 | |
| E | −885.6346 | −885.7093 | −885.5971 | −885.2601 | −884.7301 | −885.3473 | |
| δ(Fe1, Fe2) | (0.47, 0.54) | (0.50, 0.53) | (0.48, 0.53) | (0.48, 0.54) | (0.50, 0.54) | (0.44, 0.56) | (0.45, 0.55) |
| ΔEQ(Fe1, Fe2) | (−1.72, −1.78) | (−1.63, −1.70) | (0.98, 0.64) | (−0.64, −1.46) | (2.50, 0.65) | (−1.06, −1.30) | (−2.44, −1.62) |
| η(Fe1, Fe2) | (0.44, 0.14) | (0.38, 0.26) | (0.53, 0.82) | (0.71, 0.63) | (0.54, 0.51) | (0.36, 0.56) | (0.2, 0.6) |
| pKa: c | |||||||
| (e) → (d) + H+ | 1.27 | ||||||
| (a) → (f) + H+ | 15.03 | ||||||
| (b) → (f) + H+ | 16.29 | ||||||
| (c) → (f) + H+ | 14.40 | ||||||
The diiron centers of these models are shown in Figures 6a-f
Taken from Ref. 105
Calculated according to equation 5, with the relevant broken-symmetry state energies given in this table.
The calculated net spin populations for all six models are nearly the same. All are clearly in the Fe1(III)↑-Fe2(III)↓-Tyr122·↓ state (the arrows represent the net spins up or down). It is reasonable to see that with a terminally bound H2O to Fe2 (Figure 6a), the model A(Obr,H2Ot2) yields the longest Fe1-Fe2 distance. In model A(Obr,H2Ot1) (Figure 6b), the H2O at site O2 is actually far from Fe1 (2.412 Å), but even further from Fe2 (2.506 Å). This model turned out to have the lowest broken-symmetry state energy among the first four models (a)-(d), which have the same number of atoms. Models (a)-(d) are tautomeric states, so their energies can be directly compared.
Model A(Obr,OH−br)-Asp84H (Figure 6d) has the highest energy of models (a)-(d), which is 10.4 kcal mol−1 higher than that of A(Obr,H2Ot1). Since this is a comparatively large energy difference, the model A(Obr,OH−br)-Asp84H is probably not the ground state structure of E. coli R2 in the Fe1(III)Fe2(III)-Tyr122· active state. Model A(OH−br,OH−br) (Figure 6c) also has higher energy than A(Obr,H2Ot1), by 2.6 kcal mol−1. According to this energy difference alone, one cannot rule out this active site structure. However, since the X-ray crystal structure for met diferric R2 shows the active site in (Obr,H2Ot2) form, the active state of R2 may not stay in the (OH−br,OH−br) conformation either. Next model A(Obr,H2Ot2) (Figure 6a), which was constructed according to the met diferric R2 crystal structure, is only 1.7 kcal mol−1 higher in energy than A(Obr,H2Ot1). Considering the very similar conformations of A(Obr,H2Ot2) and A(Obr,H2Ot1), both structures may represent the active site of the active state R2, meaning that the H2O ligand at site O2 either binds to Fe1 or Fe2, or in a bridging position because of the shallow potential energy surface.
Model A(OH−br,OH−br)-Asp84H (Figure 6e) has one more proton than the first four models (a)-(d). For comparing the energetic stability between this model and A(Obr,OH−br)-Asp84H (Figure 6d), we calculated the pKa for the process A(OH−br,OH−br)-Asp84H → A(Obr,OH−br)-Asp84H + H+ according to equation (5) by replacing E[X(di-μ-oxo)-Trp48+·] and E[X(μ-oxo)(μ-hydroxo)-Trp48+· with E[A(Obr,OH−br)-Asp84H] and E[A(OH−br,OH−br)-Asp84H], respectively, and obtained the value 1.27. Therefore, the A(Obr,OH−br)-Asp84H structure is energetically more stable than A(OH−br,OH−br)-Asp84H. Since A(Obr,OH−br)-Asp84H has substantially higher energy than A(Obr,H2Ot1) and A(Obr,H2Ot2), A(OH−br,OH−br)-Asp84H is ruled out for the active state structure of E. coli R2.
By contrast, model A(Obr,OH−br) (Figure 6f) has one less proton than the first four models (a)-(d). In the similar way, we also calculated the pKa’s for the processes
| (6) |
| (7) |
| (8) |
and obtained pKa values 15.0, 16.3, and 14.4, respectively. Therefore energetically model A(Obr,OH−br) (Figure 6f) is also far less stable than models (a)-(c), and about 2.4 kcal mol−1 less stable than model (d) at pH = 7 (equivalently, the calculated pKa for Asp84H in model (d) is 8.7, assuming the same ΔZPE given in Eq. 5).
The calculated Mössbauer isomer shifts for the six active state models (in Table 3) are very consistent with the experiment. Models (a), (c), (d), and (f) almost exactly reproduce the observed δ values. However, the predicted Mössbauer quadrupole splittings for (c), (d), and (f) are far off from the experimental results. The very large observed |ΔEQ(Fe1)| = 2.44 mm s−1 is only reproduced by model (e) (2.50 mm s−1). However, the calculated |ΔEQ(Fe2)| = 0.65 mm s−1 for model (e) is too small compared with experiment (1.62 mm s−1). Models (a) and (b) yield very similar quadrupole splittings. Although the calculated |ΔEQ(Fe1)|’s for (a) and (b) are not as large as 2.44 mm s−1, both predicted |ΔEQ(Fe1)| and |ΔEQ(Fe2)| are relatively large and closer to the experiment than other models. Therefore, based on the calculated energetic and Mössbauer properties, models (a) and (b) are the best among the six models in representing the ground state structure of E. coli R2 in the Fe1(III)Fe2(III)-Tyr122· active state. Model A(Obr,OH−br)-Asp84H (Figure 6d), having higher energy than models (a) and (b), is a likely intermediate for the radical (hole) transfer pathway from subunit R2 to R1, since the close proximity of the proton on Asp84H to Tyr122· will facilitate the coupled 1e−/1H+ reduction of Tyr122· with a transient hole then appearing on Trp48+·.
4.4. Met Diferric Fe1(III)Fe2(III) Active Site Structures
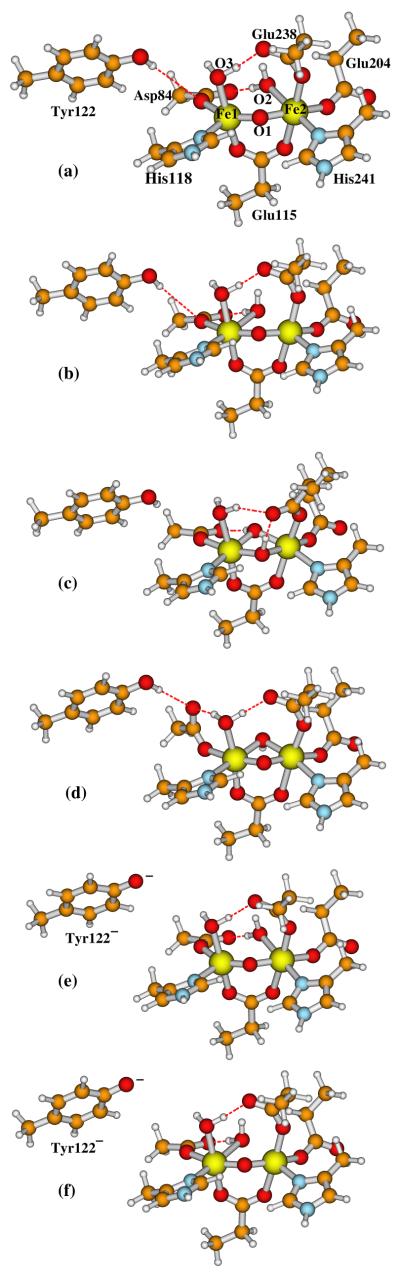
We already know that the X-ray crystal structure shows the (Obr,H2Ot2) type active site for met diferric active site. Our calculations in the section above shows that the active state model A(Obr,H2Ot1) (Figure 6b) is a little lower and model A(OH−br,OH−br) (Figure 6c) is higher in energy than model A(Obr,H2Ot2) (Figure 6a). In this section, we will examine the relative energies from OPBE calculations for these three structures in met diferric Fe1(III)Fe2(III) state. Adding a H atom to Tyr122· in models A(Obr,H2Ot2), A(Obr,H2Ot1), and A(OH−br,OH−br), we obtained the initial geometries for the corresponding met (M) diferric Fe1(III)Fe2(III) state models M(Obr,H2Ot2), M(Obr,H2Ot1), and M(OH−br,OH−br). These structures were then optimized as described in section 3.1, and are shown in Figures 7(a)-(c), respectively. The calculated geometric and Mössbauer properties are given in Table 4 and compared with the experimental results.
Figure 7.
Active site models for the met (M) diferric Fe1(III)Fe2(III) state of E. coli R2 studied in the current paper. The following names are given for these models and discussed in the text: (a) M(Obr,H2Ot2); (b) M(Obr,H2Ot1); (c) M(OH−br,OH−br); (d) M(Obr,OH−br); (e) M(Obr,H2Ot2)-Tyr122−; and (f) M(Obr,H2Ot1)-Tyr122−. The outer-shell residue sidechains shown in Figure 2, including Gln43, Trp48, Trp111, Asp237, and water-627, are also included in calculations but not shown here.
Table 4.
Calculated Fe-Fe and Fe-ligand distances (Å), Fe net spin populations (NSP), broken symmetry state energies E (eV), 57Fe Mössbauer isomer shift (δ, mm s−1), quadrupole splittings (ΔEQ, mm s−1) and η for the met (M) diferric Fe1(III)Fe2(III) active site modelsa
| (a) M(Obr,H2Ot2) |
(b) M(Obr,H2Ot1) |
(c) M(OH−br,OH−br) |
(d) M(Obr,OH−br) |
(e) M(Obr,H2Ot2)- Tyr122− |
(f) M(Obr,H2Ot1)- Tyr122− |
exp b | |
|---|---|---|---|---|---|---|---|
| Fe1-Fe2 | 3.192 | 3.141 | 3.052 | 2.919 | 3.176 | 3.137 | 3.422 |
| Fe1-O1 | 1.786 | 1.798 | 1.960 | 1.806 | 1.783 | 1.798 | 2.170 |
| Fe2-O1 | 1.822 | 1.814 | 2.043 | 1.815 | 1.825 | 1.815 | 2.060 |
| Fe1-O2 | 2.819 | 2.382 | 1.999 | 2.151 | 2.808 | 2.405 | 3.105 |
| Fe2-O2 | 2.372 | 2.585 | 2.027 | 2.090 | 2.329 | 2.550 | 2.264 |
| Fe1-O3 | 2.204 | 2.181 | 2.340 | 2.162 | 2.220 | 2.190 | 2.109 |
| Fe1-N-His118 | 2.120 | 2.171 | 2.241 | 2.265 | 2.119 | 2.161 | 2.146 |
| Fe2-N-His241 | 2.182 | 2.148 | 2.220 | 2.280 | 2.190 | 2.150 | 2.292 |
| Fe1-O-Asp84 | 2.064 | 2.135 | 2.029 | 2.132 | 2.036 | 2.090 | 2.159 |
| Fe1-O-Glu115 | 1.990 | 2.001 | 1.999 | 2.029 | 1.997 | 2.006 | 1.829 |
| Fe2-O-Glu115 | 2.205 | 2.157 | 2.150 | 2.333 | 2.234 | 2.161 | 1.951 |
| Fe2-O-Glu204 | 2.015 | 2.005 | 1.964 | 2.092 | 2.016 | 2.012 | 2.122 |
| Fe2-O-Glu238 | 2.029 | 2.028 | 2.066 | 2.042 | 2.030 | 2.030 | 2.119 |
| NSP(Fe1) | 4.05 | 4.03 | 4.16 | 4.02 | 4.05 | 4.04 | |
| NSP(Fe2) | −4.05 | −4.03 | −4.14 | −4.02 | −4.05 | −4.04 | |
| E | −890.4791 | −890.5096 | −890.3996 | −890.2911 | −890.0441 | −890.0860 | |
| δ(Fe1, Fe2) | (0.48, 0.54) | (0.51, 0.52) | (0.48, 0.53) | (0.50, 0.53) | (0.47, 0.54) | (0.50, 0.52) | (0.45, 0.55) |
| ΔEQ(Fe1, Fe2) | (−1.68, −1.69) | (−1.53, −1.70) | (0.92, 0.66) | (−1.32, −1.48) | (−1.70, −1.72) | (−1.63, −1.73) | (−2.44, −1.62) |
| η(Fe1, Fe2) | (0.51, 0.22) | (0.45, 0.28) | (0.44, 0.85) | (0.25, 0.57) | (0.43, 0.17) | (0.39, 0.30) | (0.2, 0.6) |
| pKa: c | |||||||
| (a) → (d) + H+ | 13.36 | ||||||
| (b) → (d) + H+ | 13.87 | ||||||
| (a) → (e) + H+ | 16.98 d | ||||||
| (b) → (f) + H+ | 16.78 d | ||||||
The diiron centers of these models are shown in Figures 7a-f
Geometry is taken from chain-A of the met diferric crystal structure (PDB code: 1RIB, resolution 2.2 Å),3 and the Mössbauer data are taken from Ref. 105
Calculated according to equation 5, with the relevant broken-symmetry state energies given in this table
The main calculated Fe-ligand distances, calculated isomer shifts and quadrupole splittings of models M(Obr,H2Ot2), M(Obr,H2Ot1), and M(OH−br,OH−br) are very similar to the corresponding values for A(Obr,H2Ot2), A(Obr,H2Ot1), and A(OH−br,OH−br), respectively. This further supports the experimental demonstration that the Tyr122· radical has very little effect on Mössbauer spectra of 57Fe in R2,104 and that the active site geometries of the active form and the met diferric form are very similar.
The broken-symmetry state energy of model M(OH−br,OH−br) is still higher than those of M(Obr,H2Ot2) and M(Obr,H2Ot1). Therefore, as observed in the crystal structure, the met diferric center is not in the (OH−br,OH−br) form. The calculated broken-symmetry energies of models M(Obr,H2Ot2) and M(Obr,H2Ot1) are almost degenerate (the difference is only 0.7 kcal mol−1). From energetic point of view, both M(Obr,H2Ot2) and M(Obr,H2Ot1) may coexist. Since the calculated isomer shifts of M(Obr,H2Ot2) are closer to experiment than M(Obr,H2Ot1), it is also possible that the met-diferric active site only exists in the M(Obr,H2Ot2) form, depending on the detailed structral changes during the Tyr122· radical reduction and proton transfer processes.
In Figure 7(d) and column (d) of Table 4, we present another met diferric model M(Obr,OH−br), which contains a μ-oxo bridge at site O1, and a μ-hydroxo bridge at site O2. This model has one proton less than the met models (a)-(c) mentioned above. Considering the catalytic cycle of radical transfer starting from the transient intermediate state A(Obr,OH−br)-Asp84H (Figure 6d) by an electron transfer (from Trp48) and the proton transfer from Asp84H to Tyr122·, M(Obr,OH−br) is then the immediate Fe(III)Fe(III) structure after the Tyr122· is reduced. The calculated pKa’s for the processes
| (9) |
and
| (10) |
are 13.36 and 13.87, respectively, showing that M(Obr,OH−br) is less stable than M(Obr,H2Ot2) and M(Obr,H2Ot1). Later the energy of the M(Obr,OH−br) structure will be used to calculate the redox potential for reducing Tyr122· starting from the transient A(Obr,OH−br)-Asp84H active state.
Further, in Figures 7(e) and 7(f), and columns (e) and (f) in Table 4 we present two more met diferric structures with deprotonated (negatively charged) Tyr122−. Their diiron centers have the (Obr,H2Ot2) and (Obr,H2Ot1) forms, respectively, M(Obr,H2Ot2)-Tyr122− (Figure 7e) and M(Obr,H2Ot1)-Tyr122− (Figure 7f). The purpose of these two model calculations is to obtain the pKa values of the −OH group of the Try122 sidechain for the following processes:
| (11) |
and
| (12) |
To better estimate the zero point energy difference term ΔZPE in equation (5) for the above processes, we optimized the geometries of the Tyr122 sidechain alone in neutral and anion deprotonated forms within COSMO solvation model (ε = 20), and performed frequency calculations at the two optimized geometries. ΔZPE = −8.03 kcal mol−1 was obtained. The calculated pKa’s for processes (11) and (12) are given in Table 4, and will be used for calculating the coupled redox potential for reducing the Tyr122· radical from the active state to met diferric state in the following section.
The Fe-Fe distance of model M(Obr,H2Ot2) (3.192 Å) is by 0.04 Å longer than that of A(Obr,H2Ot1), and it is the longest among the met diferric models. The Fe-Fe distance in chain-A of the X-ray crystal (2.2 Å resolution) structure is 3.42, and in chain-B 3.29 Å.3 Therefore our calculated Fe-Fe distances in these met diferric models are at least 0.1 Å shorter than experiment. One possible rationale for this and other geometric differences is that we did not fix the positions of the link-H atoms to the first-shell ligands in these geometry optimizations.
4.5. Relative Energies and Redox Potentials between Different States
Through experiments using various redox mediators, Silva et al. found that the (proton coupled) redox potential (E0′) for the active Tyr122· radical (at pH 7.6 and 4 °C) is more positive than +0.64 V and more negative than +1.33 V vs. SHE.107 The redox potentials for amino acids in aqueous solutions and in peptides have also been measured.108-110 In this section we will present the relative energies and redox potentials between the different radical and oxidation states studied above to see if we can produce reasonable results by our current DFT-OPBE calculations. First, we examine the coupled redox potentials for the following processes:
| (13) |
and
| (14) |
Each of them can be considered as two processes in series,
| (13a) |
| (13b) |
and
| (14a) |
| (14b) |
The simple redox potential of Eq.13a and Eq.14a can be calculated as in Eq.13c and Eq.14c, respectively:
| (13c) |
and
| (14c) |
The broken-symmetry state energies (E) of models A(Obr,H2Ot2), M(Obr,H2Ot2)-Tyr122−, A(Obr,H2Ot1), and M(Obr,H2Ot1)-Tyr122− were given in Tables 3 and 4. ΔSHE is the standard hydrogen electrode potential. Lewis, et al. calculated ΔSHE = −4.28 V based solely on experimental data.91,92 They had included the experimental free energy (−6.2 kJ mol−1 = −0.06 eV) of an electron at room temperature in their calculations. However, the reference energy in our redox calculations always sets the electron energy threshold to be zero. The important point here is to be consistent in using the same reference energy. By setting ΔG°f,298(e−) = 0, the ΔSHE calculated by Lewis, et al. is then shifted by −0.06 V. That is, ΔSHE = −4.34 V, which is used in our current redox potential calculations. We then obtain that E0(Eq.13a) = 0.07 V and E0(Eq.14a) = 0.04 V.
The coupled redox potentials of Eq.13 and Eq.14 are then calculated according to Eq.13d and Eq.14d, respectively:111
| (13d) |
and
| (14d) |
where pKa(Eq.13b) =16.98 and pKa(Eq.14b) = 16.78 have been given in Table 4. When pH = 7.6, we have: E0′(Eq.13) = 0.63 V and E0′(Eq.14) = 0.59 V. Combining the chemical reduction/oxidation observations with different redox mediators and the known ability of hydroxyurea (redox potential +0.73 V vs. SHE) to reduce Tyr122· yields an experimental redox potential range from +0.73 V to +1.33 V (at pH = 7.6 and 4 °C).107 Our calculated redox potential range for the “resting” active states A(Obr,H2Ot2) and A(Obr,H2Ot1) is less positive than the lower bound by about 0.1 to 0.15 V.
On the other hand, if the A(Obr,OH−br)-Asp84H (Figure 6d) model represents the transient intermediate state facilitating the coupled 1e−/1H+ reduction of Tyr122· for the radical (hole) transfer from subunit R2 to R1, the redox process (Eq. 15) starting from A(Obr,OH−br)-Asp84H provides another relevant coupled redox potential for reducing Tyr122· in E. coli R2:
| (15) |
Again, this process can be written in the following two steps:
| (15a) |
| (15b) |
The simple redox potential of Eq. 15a can be calculated as:
| (15c) |
The pKa of process 15b is 13.87 (Table 4). Therefore the coupled redox potential for process 15 at pH = 7.6 is:
| (15d) |
This value agrees very well with the expected redox potential range typical for tyrosine.107
Other simple or coupled redox potentials which can be calculated are:
| (16) |
and
| (17) |
The model cluster X(di-μ-oxo) shown in Figure 2 was already calculated and presented in our previous paper, Ref. 31, where it was named Model-B. The calculated geometric and Mössbauer properties of X(di-μ-oxo) with dielectric constant ε = 20 were given in Figure 4 of Ref. 31. Here we simply use this X(di-μ-oxo) model to calculate the redox potential of equation 16 (without protonation). The broken-symmetry state energy of X(di-μ-oxo) directly after geometry optimization is E[X(di-μ-oxo)] = −885.6781 eV, which was not given in Ref. 31. With this energy and the Stotal = 0 state X(di-μ-oxo)-Trp48+· energy E[X(di-μ-oxo)-Trp48+·] = − 880.6840 eV given in Table 1, the simple redox of Eq.16 can be calculated as:
| (16a) |
The experimental amino acid redox potential for trpH+·/trpH couple in peptides and in aqueous solution is around 1.15 V at pH = 2 or 3.108-110 However, this experimental value may not closely represent the redox potential of process (16) in protein R2.
Similar to processes (13) and (14), (17) can also be written in the following two steps:
| (17a) |
| (17b) |
The energies of X(di-μ-oxo)-Asp84H-Tyr122· and A(Obr,OH−br) were given in Tables 2 and 3 respectively, and the pKa(Eq.17b) = 16.29 was given in Table 4. Then the simple redox potential of (17a) can be calculated as:
| (17c) |
and the coupled redox potential of Eq. 17 at pH = 7.6 can be obtained as:
| (17d) |
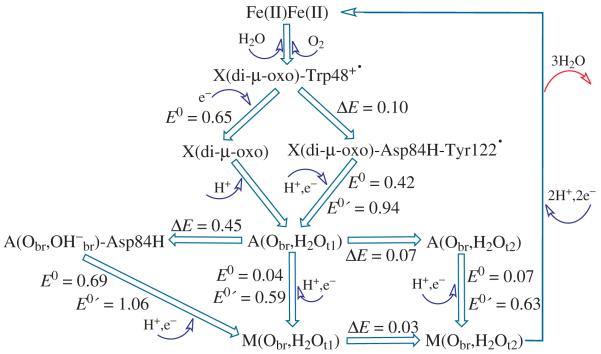
In Figure 8, we show the calculated relative energies (ΔE, eV), simple redox potentials (E0, V), and coupled redox potentials (E0′, V, at pH = 7.6) between various oxidation and radical states during the catalytic cycle (starting with X(di-μ-oxo)-Trp48+· and ending with the met-Fe(III)Fe(III) state) in E. coli R2 obtained in the current study. The current calculations do not include vibrational entropy terms or the extended protein environment. However, the calculated redox potentials are still in reasonably good agreement with the experimental range.
Figure 8.
Schematic reaction cycle in E. coli RNR R2 shown with calculated relative energy (ΔE, eV), simple redox potential (E0, V), and coupled redox potentials (E0′, V, at pH = 7.6) between the typical oxidation and radical states. Both model X(di-μ-oxo) and model X(di-μ-oxo)-Trp48+· are shown in Figure 2. Model X(di-μ-oxo)-Asp84H-Tyr122· is shown in Figure 5a with protonated Asp84 sidechain.
4.6. Reaction Pathway Mechanisms and Energetics — Comparisons with Earlier Models
One important question is: what accounts for the stability of the tyrosine radical (Tyr122·) within subunit R2? In this respect, our model for X and for the activation reaction pathway producing the Tyr122· radical are different from Siegbahn’s.23 Both proposals utilize Asp84 in proton transfer, but in Siegbahn’s there is an intervening added H2O molecule. Siegbahn proposes in Ref. 23 that the high exothermicity to go from X to the active (Tyr122·) state explains the stability of Tyr122. In our view, this result is only suggestive and not at all sufficient, since this proposal does not address the coupled electron/proton reduction proceeding from the active form (A, having Fe(III)Fe(III)-Tyr122·) to the met state (M, having Fe(III)Fe(III)-Tyr122-OH). We think that the comparative redox potentials for the activation process (1) X-Trp48+· + e− + H+ → A versus (2) A + e− + H+ → M are more relevant, since for (2) the redox potential E0′ is about 0.25 V less positive than for (1), so the driving force for reduction from an external one electron donor (external reductant) is less (Figure 8). Probably even more important is the control on redox potential by limiting proton access into the active site, since the redox potential is about 0.5 V less positive for E0 (without proton transfer) compared to E0′ (with proton transfer). Therefore, kinetic control of protons entering the active site can keep the active state A from being reduced to M(met). We do not know all the conformational changes between A and M, and the electron tunneling as well as the proton transfer barriers may be different. Therefore, the kinetics of proton transfer can play an important role in the stability of Tyr122·. The hyperactive state A(Obr,OH−br)-Asp84H (Figure 6d) has a higher redox potential to M, which makes it more vulnerable to reduction, but its equilibrium concentration is correspondingly much less than A, by a calculated factor of about 10−7.6. In Stubbe and coworkers’ model112 for the kinetic mechanism of the catalytic cycle, most steps involve subunit R2 docked to R1, and therefore these will provide considerable protection of the Tyr122· against electron transfer from external reductants. However, the substrate free form of subunit R1, after disulfide re-reduction, is proposed to require dissociation of R2 from R1, leaving the Tyr122· much more accessible to reductant once per turnover. In the activation cycle as well, R2 is separated from R1, but this is a much rarer event.
A second important question is: why and how does radical transfer occur on the catalytic pathway starting from Tyr122· (on subunit R2) when the substrate is bound to subunit R1? This question has two parts, the first involving long range electron transfer via a combined multistep electron tunneling process, and the second involving the local initiation of radical transfer within subunit R2. We will address only the second part here, noting that there are long range effects also from the driving force of Cys439 thiolate oxidation, from subunit R2 binding to R1, and from conformational changes, affecting both the dielectric environment and charge distribution. In any event, we will consider the initial steps in radical transfer on the catalytic pathway from the active Tyr122· state to generate the Trp48+· cation radical. Here our proposed mechanism differs even qualitatively from Siegbahn’s.23 We propose that Asp84 acts as a proton transfer conduit from the bridging H2O providing a preorganized, although transient state for coupled e−/H+ transfer to Tyr122· from Trp48. This is essentially like the reverse of our proposed Tyr122· activation pathway. Siegbahn proposes instead a proton transfer pathway from a H2O bound terminal to Fe1 after an initial external proton transfer to the diferric cluster, so these mechanisms are quite different. In Stubbe’s kinetic model,112 the estimated rate constant for the electron transfer from Cys439 to Tyr122 is greater than 1000 s−1, which is consistent (at 300 K) with a barrier or series of barriers of about 14 kcal mol−1 or less based on standard transition state theory. (This result will be modified by the electron transfer rate prefactor which includes the electron tunneling factor 2π3/2(HAD2)/[λ1/2(RT)3/2].113) Our predicted equilibrium energy for the hyperactive state A(Obr,OH−br)-Asp84H (Figure 6d) is about 10.4 kcal/mol above that of the resting Tyr122· state A(Obr,H2Ot1) (Figure 6b). The barrier to A(Obr,OH−br)-Asp84H must be higher than this value, but we have not yet evaluated it, or the net barrier and net energy change for the coupled electron/proton transfer generating the Trp48+· and Tyr122-OH. In Siegbahn’s proposed pathway, the ΔE for producing the Trp48+· and Tyr122-OH is 3.9 kcal mol−1 with the external proton transfer and 11.8 kcal mol−1 without it. The cost of initial external proton transfer to the active site cluster is not determined. We think that our mechanism is simpler and more direct than the one Siegbahn has proposed, and in our mechanism the Asp84 acts as a proton conduit in both the tyrosine radical activation and in the catalytic radical transfer pathways. However, there are many open questions about the catalytic radical transfer pathway, and considerable additional work is needed to attain a more complete picture of this mechanism.
5. Conclusions
Active site models for class Ia E. coli R2 in X{Fe1(III)Fe2(IV)}-Trp48+·, X{Fe1(III)Fe2(IV)}-Tyr122·, active Fe1(III)Fe2(III)-Tyr122·, and met Fe1(III)Fe2(III) states have been examined for structures, energies, and properties, using density functional broken-symmetry methodology. Different structural isomers and different protonation states have been explored. The proposed transient Fe(IV)Fe(IV) state is also examined.
Combining our current and Siegbahn’s previous calculations, and experimental observations,23,24 both Trp48 and Asp84 in E. coli R2 are the important contributing factors for class Ia RNR and MMOH behaving differently upon O2 binding with the Fe(II)Fe(II) center. The steric strain of the short Asp84 sidechain in RNR generates an energy cost when Fe1 and Fe2 move closer, which is likely why the cis-μ-1,2 type41,42 peroxo intermediate state is not observed in wild-type R2, but observed in MMOH42,95,114 and in the D84E mutant R2.39 Because of the long Fe(II)-Fe(II) distance, the peroxo intermediate in wild-type R2 would easily change from cis to trans or μ-η2,η2 form to facilitate the O-O bond cleavage. In fact, O2 may directly bind in a trans or μ-η2,η2 form in wild-type R2 since the peroxo-Fe(III)Fe(III) complex has to decay rapidly.11 The electron transfer from Trp48 to Fe1 in R2 possibly occurs some time during the O-O bond cleavage, which explains why the O-O bond cleavage in the W48F mutant is much slower (80 s−1 for formation of the Fe(IV)Fe(IV) species)12 than in wild-type R2 (200 s−1 for formation of the X-Trp48+· state).11 For the portion of the O-O bond cleavage which happens before the electron transfer from Trp48 to Fe1, the steric strain of Asp84 hinders the decrease of the Fe1-Fe2 distance to attain the lowest-energy structure of the Fe(IV)Fe(IV) state. Rather, the active site compresses to a geometry which is similar to that of the X(di-μ-oxo)-Trp48+· state, where one electron transfers from Trp48 to Fe1. This provides another reason that the Fe(IV)Fe(IV) state is not observed in wild-type E. coli R2, in contrast to methane monooxygenase.
Turning now to the X, active, and met species, we develop a detailed assessment of tautomeric states as shown in Figures 5, 6, 7, and 8. Protonated Asp84H plays a critical role as a proton transfer conduit between the diiron cluster and Tyr122·. Asp84 is essential both in the activation process for generating the Tyr122· radical state, and in the catalytic pathway after activation. There are three particularly important active states: (a) A(Obr,H2Ot2), (b) A(Obr,H2Ot1), and (d) A(Obr,OH−br)-Asp84H (Figures 6a,b,d and Table 3). The first two are low-lying “resting” active states corresponding to the stable Tyr122· radical observed spectroscopically. The last (d) A(Obr,OH−br)-Asp84H is calculated to lie 0.45 eV (10.4 kcal mol−1) higher in energy than active model (b). Model (d) is a highly transient, hyperactive catalytic species ready to oxidize Trp48 to Trp48+· to start the catalytic cycle of hole transfer from subunit R2 to the catalytic substrate binding site on subunit R1 where a Cys radical is generated. The proton on Asp84H is very well positioned for immediate proton transfer for the reduction of Tyr122·. From the calculated energy difference between A(Obr,OH−br)-Asp84H (model A(d)) and A(Obr,H2Ot1) (model A(b)), we can estimate a relative equilibrium constant of [A(d)]/[A(b)] = 10−7.6. So while structure A(b) is stable, A(d) is present only about 100 μs per hour.
In Figure 8, the calculated proton coupled redox potential (E0′) for X(di-m-oxo)-Asp84H-Tyr122· → A(Obr,H2Ot1) and the three E0′s from active (A) to met-RNR-R2 (M) are 0.4-0.6 V more positive than the corresponding simple electron transfer redox potentials (E0). Therefore, kinetic control of proton transfer to the diiron center or to the Tyr122· plays a critical role for the occurrence of these processes. When the Tyr122· has been generated in the “resting” active state(s) (A(a),(b)), it is blocked by the sidechain of Phe208. There is possibly no available proton transfer source and path nearby. Therefore the Tyr122· in the active state can stay for days at room temperature.1 It is likely that, since the docking of R1 and R2 provides the source and pathway of the proton (and electron) transfer, the Tyr122· is then reduced and the radical transfers to R1.23 The proposed electron coupled proton transfer pathway between Tyr122· in R2 and Cys439 in R1 contains the residues His118, Asp237, Trp48, and Tyr356 in R2, and Tyr731 and Tyr730 in R1.115
The current work provides a clear framework for further progress in understanding the intricate mechanisms of radical activation and catalysis in diiron RNR.
Supplementary Material
Acknowledgements
We thank NIH for financial support (GM43278 to L.N.). The support of computer resources of the Scripps Research Institute is also gratefully acknowledged.
Footnotes
Supporting Information
Some optimized active site model geometries are given as the Supporting Information.
References
- (1).Wallar BJ, Lipscomb JD. Chem. Rev. 1996;96:2625–2658. doi: 10.1021/cr9500489. [DOI] [PubMed] [Google Scholar]
- (2).Sjöberg BM. Struct. Bond. 1997;88:139–173. [Google Scholar]
- (3).Nordlund P, Eklund H. J. Mol. Biol. 1993;232:123–164. doi: 10.1006/jmbi.1993.1374. [DOI] [PubMed] [Google Scholar]
- (4).Logan DT, Su XD, Aberg A, Regnstrom K, Hajdu J, Eklund H, Nordlund P. Structure. 1996;4:1053–1064. doi: 10.1016/s0969-2126(96)00112-8. [DOI] [PubMed] [Google Scholar]
- (5).Bollinger JM, Jr., Edmondson DE, Huynh BH, Filley J, Norton JR, Stubbe J. Science. 1991;253:292–298. doi: 10.1126/science.1650033. [DOI] [PubMed] [Google Scholar]
- (6).Bollinger JM, Jr., Stubbe J, Huynh BH, Edmondson DE. J. Am. Chem. Soc. 1991;113:6289–6291. [Google Scholar]
- (7).Ravi N, Bollinger JM, Jr., Huynh BH, Edmondson DE, Stubbe J. J. Am. Chem. Soc. 1994;116:8007–8014. [Google Scholar]
- (8).Ravi N, Bominaar EL. Inorg. Chem. 1995;34:1040–1043. [Google Scholar]
- (9).Bollinger JM, Jr., Tong WH, Ravi N, Huynh BH, Edmondson DE, Stubbe J. In: Methods in Enzymology. Klinman JP, editor. Academic Press; New York: 1995. p. 258. [DOI] [PubMed] [Google Scholar]
- (10).Sturgeon BE, Burdi D, Chen SX, Huynh BH, Edmondson DE, Stubbe J, Hoffman BM. J. Am. Chem. Soc. 1996;118:7551–7557. [Google Scholar]
- (11).Baldwin J, Krebs C, Ley BA, Edmondson DE, Huynh BH, Bollinger JH. J. Am. Chem. Soc. 2000;122:12195–12206. [Google Scholar]
- (12).Krebs C, Chen SX, Baldwin J, Ley BA, Patel U, Edmondson DE, Huynh BH, Bollinger JM. J. Am. Chem. Soc. 2000;122:12207–12219. [Google Scholar]
- (13).Bollinger JM, Tong WH, Ravi N, Huynh BH, Edmondson DE, Stubbe J. J. Am. Chem. Soc. 1994;116:8015–8023. [Google Scholar]
- (14).Bollinger JM, Tong WH, Ravi N, Huynh BH, Edmondson DE, Stubbe J. J. Am. Chem. Soc. 1994;116:8024–8032. [Google Scholar]
- (15).Burdi D, Sturgeon BE, Tong WH, Stubbe JA, Hoffman BM. J. Am. Chem. Soc. 1996;118:281–282. [Google Scholar]
- (16).Veselov A, Scholes CP. Inorg. Chem. 1996;35:3702–3705. [Google Scholar]
- (17).Willems JP, Lee HI, Burdi D, Doan PE, Stubbe J, Hoffman BM. J. Am. Chem. Soc. 1997;119:9816–9824. [Google Scholar]
- (18).Riggs-Gelasco PJ, Shu LJ, Chen SX, Burdi D, Huynh BH, Que L, Stubbe J. J. Am. Chem. Soc. 1998;120:849–860. [Google Scholar]
- (19).Burdi D, Willems J-P, Riggs-Gelasco P, Antholine WE, Stubbe J, Hoffman BM. J. Am. Chem. Soc. 1998;120:12910–12919. [Google Scholar]
- (20).Shanmugam M, Doan PE, Lees NS, Stubbe J, Hoffman BM. J. Am. Chem. Soc. 2009;131:3370–3376. doi: 10.1021/ja809223s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (21).Mitić N, Saleh L, Schenk G, Bollinger JMJ, Solomon EI. J. Am. Chem. Soc. 2003;125:11200–11201. doi: 10.1021/ja036556e. [DOI] [PubMed] [Google Scholar]
- (22).Siegbahn PEM. Inorg. Chem. 1999;38:2880–2889. doi: 10.1021/ic981332w. [DOI] [PubMed] [Google Scholar]
- (23).Siegbahn PEM. Q. Rev. Biophys. 2003;36:91–145. doi: 10.1017/s0033583502003827. [DOI] [PubMed] [Google Scholar]
- (24).Siegbahn PEM. Chem. Phys. Lett. 2002;351:311–318. [Google Scholar]
- (25).Han W-G, Lovell T, Liu T, Noodleman L. Inorg. Chem. 2003;42:2751–2758. doi: 10.1021/ic020465l. [DOI] [PubMed] [Google Scholar]
- (26).Han W-G, Lovell T, Liu T, Noodleman L. Inorg. Chem. 2004;43:613–621. doi: 10.1021/ic0206443. [DOI] [PubMed] [Google Scholar]
- (27).Han WG, Liu TQ, Lovell T, Noodleman L. J. Am. Chem. Soc. 2005;127:15778–15790. doi: 10.1021/ja050904q. [DOI] [PubMed] [Google Scholar]
- (28).Han W-G, Liu T, Lovell T, Noodleman L. Inorg. Chem. 2006;45:8533–8542. doi: 10.1021/ic060566+. [DOI] [PubMed] [Google Scholar]
- (29).Han W-G, Liu T, Lovell T, Noodleman L. J. Inorg. Biochem. 2006;100:771–779. doi: 10.1016/j.jinorgbio.2006.01.032. [DOI] [PubMed] [Google Scholar]
- (30).Han W-G, Noodleman L. Dalton Trans. 2009:6045–6057. doi: 10.1039/b903847g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (31).Han W-G, Noodleman L. Theor. Chem. Accounts. 2010;125:305–317. doi: 10.1007/s00214-009-0566-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (32).Younker JM, Krest CM, Jiang W, Krebs C, Bollinger JM, Green MT. J. Am. Chem. Soc. 2008;130:15022–15027. doi: 10.1021/ja804365e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Jiang W, Yun D, Saleh L, Bollinger JM, Krebs C. Biochemistry. 2008;47:13736–13744. doi: 10.1021/bi8017625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (34).Jiang W, Saleh L, Barr EW, Xie JJ, Gardner MM, Krebs C, Bollinger JM. Biochemistry. 2008;47:8477–8484. doi: 10.1021/bi800881m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (35).Mitić N, Clay MD, Saleh L, Bollinger JMJ, Solomon EI. J. Am. Chem. Soc. 2007;129:9049–9065. doi: 10.1021/ja070909i. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (36).Noodleman L. J. Chem. Phys. 1981;74:5737–5743. [Google Scholar]
- (37).Noodleman L, Case DA. Adv. Inorg. Chem. 1992;38:423–470. [Google Scholar]
- (38).Noodleman L, Lovell T, Han W-G, Liu T, Torres RA, Himo F. Density Functional Theory. In: Lever AB, editor. Comprehensive Coordination Chemistry II, From Biology to Nanotechnology. Vol. 2. Elsevier Ltd; 2003. pp. 491–510. [Google Scholar]
- (39).Moenne-Loccoz P, Baldwin J, Ley BA, Loehr TM, Bollinger JM. Biochemistry. 1998;37:14659–14663. doi: 10.1021/bi981838q. [DOI] [PubMed] [Google Scholar]
- (40).Baldwin J, Voegtli WC, Khidekel N, Moenne-Loccoz P, Krebs C, Pereira AS, Ley BA, Huynh BH, Loehr TM, Riggs-Gelasco PJ, Rosenzweig AC, Bollinger JM. J. Am. Chem. Soc. 2001;123:7017–7030. doi: 10.1021/ja002114g. [DOI] [PubMed] [Google Scholar]
- (41).Jensen KP, Bell CB, Clay MD, Solomon EI. J. Am. Chem. Soc. 2009;131:12155–12171. doi: 10.1021/ja809983g. [DOI] [PubMed] [Google Scholar]
- (42).Han W-G, Noodleman L. Inorg. Chem. 2008;47:2975–2986. doi: 10.1021/ic701194b. [DOI] [PubMed] [Google Scholar]
- (43).Saleh L, Krebs C, Ley BA, Naik S, Huynh BH, Bollinger JM. Biochemistry. 2004;43:5953–5964. doi: 10.1021/bi036099e. [DOI] [PubMed] [Google Scholar]
- (44).Han W-G, Tajkhorshid E, Suhai S. J. Biomol. Struct. Dyn. 1999;16:1019–1032. doi: 10.1080/07391102.1999.10508311. [DOI] [PubMed] [Google Scholar]
- (45).Bollinger JM, Chen SX, Parkin SE, Mangravite LM, Ley BA, Edmondson DE, Huynh BH. J. Am. Chem. Soc. 1997;119:5976–5977. [Google Scholar]
- (46).SCM . ADF2008.01 Amsterdam Density Functional Software. Theoretical Chemistry, Vrije Universiteit; Amsterdam, The Netherlands: http://www.scm.com. [Google Scholar]
- (47).te Velde G, Bickelhaupt FM, Baerends EJ, Guerra CF, Van Gisbergen SJA, Snijders JG, Ziegler T. J. Comput. Chem. 2001;22:931–967. [Google Scholar]
- (48).Guerra CF, Snijders JG, te Velde G, Baerends EJ. Theor. Chem. Acc. 1998;99:391–403. [Google Scholar]
- (49).Vosko SH, Wilk L, Nusair M. Can. J. Phys. 1980;58:1200–1211. [Google Scholar]
- (50).Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- (51).Perdew JP, Burke K, Ernzerhof M. Phys. Rev. Lett. 1997;78:1396–1396. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- (52).Handy NC, Cohen AJ. Mol. Phys. 2001;99:403–412. [Google Scholar]
- (53).Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, Singh DJ, Fiolhais C. Phys. Rev. B. 1992;46:6671–6687. doi: 10.1103/physrevb.46.6671. [DOI] [PubMed] [Google Scholar]
- (54).Han WG, Noodleman L. Inorg. Chim. Acta. 2008;361:973–986. doi: 10.1016/j.ica.2007.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (55).Swart M, Groenhof AR, Ehlers AW, Lammertsma K. J. Phys. Chem. A. 2004;108:5479–5483. [Google Scholar]
- (56).Swart M, Ehlers AW, Lammertsma K. Mol. Phys. 2004;102:2467–2474. [Google Scholar]
- (57).Becke AD. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- (58).Lee CT, Yang WT, Parr RG. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- (59).Perdew JP. Phys. Rev. B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- (60).Perdew JP. Phys. Rev. B. 1986;34:7406–7406. [PubMed] [Google Scholar]
- (61).Grimme S. J. Chem. Phys. 2006;124:034108. doi: 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
- (62).Staroverov VN, Scuseria GE, Tao JM, Perdew JP. J. Chem. Phys. 2003;119:12129–12137. [Google Scholar]
- (63).Becke AD. J. Chem. Phys. 1993;98:5648–5652. [Google Scholar]
- (64).Hertwig RH, Koch W. Chem. Phys. Lett. 1997;268:345–351. [Google Scholar]
- (65).Jensen KP. Inorg. Chem. 2008;47:10357–10365. doi: 10.1021/ic800841t. [DOI] [PubMed] [Google Scholar]
- (66).Furche F, Perdew JP. J. Chem. Phys. 2006;124:044103. doi: 10.1063/1.2162161. [DOI] [PubMed] [Google Scholar]
- (67).Orio M, Pantazis DA, Petrenko T, Neese F. Inorg. Chem. 2009;48:7251–7260. doi: 10.1021/ic9005899. [DOI] [PubMed] [Google Scholar]
- (68).Ye SF, Neese F. Inorg. Chem. 2010;49:772–774. doi: 10.1021/ic902365a. [DOI] [PubMed] [Google Scholar]
- (69).Klamt A, Schüürmann G. J. Chem. Soc. Perkin Trans. II. 1993:799–805. [Google Scholar]
- (70).Klamt A. J. Phys. Chem. 1995;99:2224–2235. [Google Scholar]
- (71).Klamt A, Jonas V. J. Chem. Phys. 1996;105:9972–9981. [Google Scholar]
- (72).Pye CC, Ziegler T. Theor. Chem. Acc. 1999;101:396–408. [Google Scholar]
- (73).Gregg EC. Handbook of Chemistry and Physics. Chemical Rubber Company; Cleveland, OH: 1976. Dielectric Constants of Solids; pp. E55–E60. [Google Scholar]
- (74).Harvey SC, Hoekstra P. J. Phys. Chem. 1972;76:2987–2994. doi: 10.1021/j100665a011. [DOI] [PubMed] [Google Scholar]
- (75).Bone S, Pethig R. J. Mol. Biol. 1982;157:571–575. doi: 10.1016/0022-2836(82)90477-6. [DOI] [PubMed] [Google Scholar]
- (76).Bone S, Pethig R. J. Mol. Biol. 1985;181:323–326. doi: 10.1016/0022-2836(85)90096-8. [DOI] [PubMed] [Google Scholar]
- (77).Dwyer JJ, Gittis AG, Karp DA, Lattman EE, Spencer DS, Stites WE, Garcia-Moreno B. Biophys. J. 2000;79:1610–1620. doi: 10.1016/S0006-3495(00)76411-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (78).Sham YY, Muegge I, Warshel A. Biophys. J. 1998;74:1744–1753. doi: 10.1016/S0006-3495(98)77885-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (79).Bashford D, Karplus M. Biochemistry. 1990;29:10219–10225. doi: 10.1021/bi00496a010. [DOI] [PubMed] [Google Scholar]
- (80).Fitch CA, Karp DA, Lee KK, Stites WE, Lattman EE, Garcia-Moreno B. Biophys. J. 2002;82:3289–3304. doi: 10.1016/s0006-3495(02)75670-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (81).Antosiewicz J, McCammon JA, Gilson MK. Biochemistry. 1996;35:7819–7833. doi: 10.1021/bi9601565. [DOI] [PubMed] [Google Scholar]
- (82).Simonson T, Brooks CL. J. Am. Chem. Soc. 1996;118:8452–8458. [Google Scholar]
- (83).Karp DA, Gittis AG, Stahley MR, Fitch CA, Stites WE, Garcia-Moreno B. Biophys. J. 2007;92:2041–2053. doi: 10.1529/biophysj.106.090266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (84).Harms MJ, Schlessman JL, Chimenti MS, Sue GR, Damjanovic A, Garcia-Moreno B. Protein Science. 2008;17:833–845. doi: 10.1110/ps.073397708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (85).Oglezneva IM. Russ. J. Coord. Chem. 2009;35:711–719. [Google Scholar]
- (86).Paulsen H, Trautwein AX. J. Phys. Chem. Solids. 2004;65:793–798. [Google Scholar]
- (87).Jensen KP, Cirera J. J. Phys. Chem. A. 2009;113:10033–10039. doi: 10.1021/jp900654j. [DOI] [PubMed] [Google Scholar]
- (88).Han W-G, Liu T, Lovell T, Noodleman L. J. Comput. Chem. 2006;27:1292–1306. doi: 10.1002/jcc.20402. [DOI] [PubMed] [Google Scholar]
- (89).Martinez-Pinedo G, Schwerdtfeger P, Caurier E, Langanke K, Nazarewicz W, Sohnel T. Physical Review Letters. 2001;87:062701, 1–4. doi: 10.1103/PhysRevLett.87.062701. [DOI] [PubMed] [Google Scholar]
- (90).Tissandier MD, Cowen KA, Feng WY, Gundlach E, Cohen MH, Earhart AD, Coe JV, Tuttle TR. J. Phys. Chem. A. 1998;102:7787–7794. [Google Scholar]
- (91).Lewis A, Bumpus JA, Truhlar DG, Cramer CJ. J. Chem. Edu. 2004;81:596–604. [Google Scholar]
- (92).Lewis A, Bumpus JA, Truhlar DG, Cramer CJ. J. Chem. Edu. 2007;84:934. [Google Scholar]
- (93).Tawa GJ, Topol IA, Burt SK, Caldwell RA, Rashin AA. J. Chem. Phys. 1998;109:4852–4863. [Google Scholar]
- (94).Elango N, Radhakrishnan R, Froland WA, Wallar BJ, Earhart CA, Lipscomb JD, Ohlendorf DH. Protein Sci. 1997;6:556–568. doi: 10.1002/pro.5560060305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (95).Lee SY, Lipscomb JD. Biochemistry. 1999;38:4423–4432. doi: 10.1021/bi982712w. [DOI] [PubMed] [Google Scholar]
- (96).Lee SK, Fox BG, Froland WA, Lipscomb JD, Münck E. J. Am. Chem. Soc. 1993;115:6450–6451. [Google Scholar]
- (97).Liu KE, Valentine AM, Wang DL, Huynh BH, Edmondson DE, Salifoglou A, Lippard SJ. J. Am. Chem. Soc. 1995;117:10174–10185. [Google Scholar]
- (98).Shu LJ, Nesheim JC, Kauffmann K, Munck E, Lipscomb JD, Que L. Science. 1997;275:515–518. doi: 10.1126/science.275.5299.515. [DOI] [PubMed] [Google Scholar]
- (99).Hsu HF, Dong YH, Shu LJ, Young VG, Que L. J. Am. Chem. Soc. 1999;121:5230–5237. [Google Scholar]
- (100).Gherman BF, Dunietz BD, Whittington DA, Lippard SJ, Friesner RA. J. Am. Chem. Soc. 2001;123:3836–3837. doi: 10.1021/ja0055108. [DOI] [PubMed] [Google Scholar]
- (101).Baik MH, Newcomb M, Friesner RA, Lippard SJ. Chem. Rev. 2003;103:2385–2419. doi: 10.1021/cr950244f. [DOI] [PubMed] [Google Scholar]
- (102).Högbom M, Huque Y, Sjöberg BM, Nordlund P. Biochemistry. 2002;41:1381–1389. doi: 10.1021/bi011429l. [DOI] [PubMed] [Google Scholar]
- (103).Åberg A, Nordlund P, Eklund H. Nature. 1993;361:276–278. doi: 10.1038/361276a0. [DOI] [PubMed] [Google Scholar]
- (104).Atkin CL, Thelande L, Reichard P, Lang G. J. Biol. Chem. 1973;248:7464–7472. [PubMed] [Google Scholar]
- (105).Lynch JB, Juarez-Garcia C, Münck E, Que L., Jr. J. Biol. Chem. 1989;264:8091–8096. [PubMed] [Google Scholar]
- (106).Sahlin M, Ehrenberg A, Graslund A, Sjoberg BM. J. Biol. Chem. 1986;261:2778–2780. [PubMed] [Google Scholar]
- (107).Silva KE, Elgren TE, Que L, Stankovich MT. Biochemistry. 1995;34:14093–14103. doi: 10.1021/bi00043a014. [DOI] [PubMed] [Google Scholar]
- (108).Harriman A. J. Phys. Chem. 1987;91:6102–6104. [Google Scholar]
- (109).Defelippis MR, Murthy CP, Broitman F, Weinraub D, Faraggi M, Klapper MH. J. Phys. Chem. 1991;95:3416–3419. [Google Scholar]
- (110).Stubbe J, van der Donk WA. Chem. Rev. 1998;98:705–762. doi: 10.1021/cr9400875. [DOI] [PubMed] [Google Scholar]
- (111).Han W-G, Lovell T, Noodleman L. Inorg. Chem. 2002;41:205–218. doi: 10.1021/ic010355z. [DOI] [PubMed] [Google Scholar]
- (112).Stubbe J, Nocera DG, Yee CS, Chang MCY. Chem. Rev. 2003;103:2167–2201. doi: 10.1021/cr020421u. [DOI] [PubMed] [Google Scholar]
- (113).Reece SY, Nocera DG. Annu. Rev. Biochem. 2009;78:673–699. doi: 10.1146/annurev.biochem.78.080207.092132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (114).Valentine AM, Stahl SS, Lippard SJ. J. Am. Chem. Soc. 1999;121:3876–3887. [Google Scholar]
- (115).Stubbe J, Riggs-Gelasco P. Trends Biochem. Sci. 1998;23:438–443. doi: 10.1016/s0968-0004(98)01296-1. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.