Abstract
We studied the effect of titin-based passive tension on sarcomere structure by simultaneously measuring passive tension and low-angle x-ray diffraction patterns on passive fiber bundles from rabbit skinned psoas muscle. We used a stretch-hold-release protocol with measurement of x-ray diffraction patterns at various passive tension levels during the hold phase before and after passive stress relaxation. Measurements were performed in relaxing solution without and with dextran T-500 to compress the lattice toward physiological levels. The myofilament lattice spacing was measured in the A-band (d1,0) and Z-disk (dZ) regions of the sarcomere. The axial spacing of the thick-filament backbone was determined from the sixth myosin meridional reflection (M6) and the equilibrium positions of myosin heads from the fourth myosin layer line peak position and the I1,1/I1,0 intensity ratio. Total passive tension was measured during the x-ray experiments, and a differential extraction technique was used to determine the relations between collagen- and titin-based passive tension and sarcomere length. Within the employed range of sarcomere lengths (∼2.2–3.4 μm), titin accounted for >80% of passive tension. X-ray results indicate that titin compresses both the A-band and Z-disk lattice spacing with viscoelastic behavior when fibers are swollen after skinning, and elastic behavior when the lattice is reduced with dextran. Titin also increases the axial thick-filament spacing, M6, in an elastic manner in both the presence and absence of dextran. No changes were detected in either I1,1/I1,0 or the position of peaks on the fourth myosin layer line during passive stress relaxation. Passive tension and M6 measurements were converted to thick-filament compliance, yielding a value of ∼85 m/N, which is several-fold larger than the thick-filament compliance determined by others during the tetanic tension plateau of activated intact muscle. This difference can be explained by the fact that thick filaments are more compliant at low tension (passive muscle) than at high tension (tetanic tension). The implications of our findings are discussed.
Introduction
The striated muscle sarcomere is comprised of myosin-based thick filaments that interdigitate and interact with actin-based thin filaments to cause active tension development (1). In addition, the sarcomere contains a third myofilament made up of the giant elastic protein titin, also known as connectin (2,3), with single molecules spanning the half sarcomere from the edge of the sarcomere (Z-disk) to the middle of the sarcomere (4). It is now well established that the majority of titin in the I-band region of the sarcomere is extensible and functions as a molecular spring that provides the passive tension of sarcomeres that are stretched beyond their slack length (5,6). Certain titin isoforms vary in the length of their molecular springs (7,8), with short and therefore stiff springs in cardiac muscle (9,10), and longer and thus more compliant springs in skeletal muscle (11,12).
Although titin is typically considered to function independently of actomyosin interaction, several studies have shown that titin's passive tension increases the calcium sensitivity of active tension development (13–19). It has been proposed that this interplay between titin and active tension is due to an effect of titin on myofilament lattice spacing (the lateral distance between thin and thick filaments), with myofilament lattice spacing in turn influencing calcium sensitivity (13). An alternative mechanism is that the likelihood of cross-bridge interaction is enhanced by passive tension-induced thick-filament strain (13–15,18,19). Thus, the interplay between passive tension (titin) and active tension (thin and thick filaments) may involve a change in sarcomeric structure.
In this work, we performed a comprehensive study of the effects of passive tension on the sarcomeric structure of skeletal muscle. We chose to use skeletal muscle in these experiments because it is much better ordered than cardiac muscle, and therefore any sarcomeric structural changes induced by passive tension would be more likely to be detected. We performed low-angle x-ray diffraction studies on rabbit skinned psoas muscle fibers and measured 1), the myofilament lattice spacing in the A-band (d1,0); 2), the lateral spacing of thin filaments in and near the Z-disk (dZ); and 3), the spacing of the thick-filament backbone using the sixth myosin meridional (M6) reflection. In vertebrate muscle, the intensity of the M6 reflection (∼7.2 nm) is thought to arise primarily from periodic features within the thick-filament backbone itself (for reviews, see Reconditi (20) and Huxley (21)) and thus has a straightforward interpretation as strain in the thick filament. We also determined the equilibrium position of myosin heads from the fourth myosin layer line (M4) peak position as well as the intensity ratio of the 1,1 and 1,0 equatorial peaks, I1,1/I1,0 (for details, see below). Skinned fibers in relaxing solution were stretched to various sarcomere lengths (SLs) and then held to allow stress relaxation to occur. X-ray exposures were taken before and after 20 min of stress relaxation. Because the myofilament lattice is expanded in skinned fibers compared with intact fibers, we also performed measurements in the presence of dextran T-500 to compress the lattice.
Our findings indicate that titin-based passive tension causes changes in the thick-filament length, A-band lattice spacing, and Z-disk lattice spacing. Although the changes in thick-filament length appear to be elastic, both the Z-band and A-band lattices show viscoelastic behavior when the fibers are swollen after skinning, and elastic behavior when the lattice is reduced with dextran. Passive tension did not correlate with changes in the radial position of the myosin heads, as estimated by either I1,1/I1,0 or by the position of peaks on M4. A surprising finding was that the compliance of the thick filament, over the range of passive tensions we examined, was much larger than previously reported for maximally activated muscle. We discuss the implications of our findings in terms of the mechanisms by which titin might influence cell signaling processes and active tension development.
Materials and Methods
Muscle specimens
Fiber bundles were dissected from psoas muscle of 6-month-old male rabbits (New Zealand White) and then skinned. All mechanical experiments were carried out in relaxing solution, some of which contained 1.5% dextran T-500. For details, see the Supporting Material.
X-ray diffraction
Small-angle x-ray diffraction experiments were performed at the BioCAT beamline 18ID (Argonne National Laboratory, Argonne, IL) as described previously (22). Muscle bundles were mounted horizontally in a small trough with windows allowing simultaneous collection of the x-ray patterns and viewing of the striation pattern on a video-equipped inverted microscope. The fiber was held by aluminum clips on hooks between a tension transducer and a servo-motor. The x-ray exposure times were ∼0.5 s and the x-ray diffraction patterns were collected with the use of a CCD-based area detector. For details, see the Supporting Material.
Data acquisition and SL measurement
We measured the SLs immediately before and after x-ray exposure by performing a fast Fourier transform analysis of digitized striation images as described previously (22). The SLs were monitored and did not change during stress relaxation. Tension, muscle length, and x-ray beam intensity were digitized by means of an A/D converter (model PCI-1200; National Instruments, Austin, TX) that was installed in the same computer used to digitize the striation images.
Analysis of lattice spacing
The lattice spacing and SLs were measured in relaxed preparations as described previously (22). Separations of the 1,0 and 1,1 equatorial reflections measured from the diffraction pattern were converted to d1,0 lattice spacing via Bragg's law, which can be converted to inter-thick-filament spacing by multiplying d1,0 by 2/√3 (23). The intensities of the 1,0 and 1,1 equatorial reflections, as well as any other equatorial reflections, were determined from one-dimensional (1D) projections along the equator and analyzed as described by Irving and Millman (24). The I1,1/I1,0 intensity ratios can be used to estimate shifts of mass due to the movement of cross-bridges from the region of the thick filament to region of the thin filament (25).
Analysis of 7.2 nm (M6) meridional reflections
Positions, axial widths, and intensities were obtained from axial projections of the intensity using the projection tool in FIT2D and analyzed as described previously (26). Briefly, the smooth background underneath the peaks was subtracted from the 1D intensity traces by means of a convex hull algorithm. The position of the M6 reflection was estimated as the centroid of the M6 peak without any assumptions regarding the peak shape.
Myosin layer lines
Before we performed the analysis, we subtracted a radially symmetric background using the 2D background fitting routines in FIBERFIX (http://www.small-angle.ac.uk/small-angle/Software/FiberFix.html). We made radial projections along the unsampled fourth myosin layer lines using the projection tool in FIT2d (http://www.esrf.eu/computing/scientific/FIT2D/) and fit them using the nonlinear least-squares routines in the Origin software suite (OriginLab, Northampton, MA) assuming a Gaussian shape for the layer line maxima (only one peak was visible on this layer line), an additional peak for the M4 meridional reflection, and a polynomial for the residual background. The difference between the two fit peak positions divided by two was taken as the radial distance of the first intensity maxima from the meridian.
Protocols
Rabbit psoas fiber bundles were stretched at 0.1 slack length per second from the slack SL (typically ∼2.2 μm) to various predetermined SLs (2.6–3.3 μm), held for 20 min, and then released at the same velocity. Two-dimensional (2D) x-ray diffraction patterns were collected at various times during the stretch-hold-release protocol. We measured the total passive tension during the x-ray experiments, and then estimated the titin-based passive tension from the total tension as follows: We first extracted titin's anchors in the sarcomere by incubating them first in 0.6 M KCl and then in 1.0 M KI, for 45 min each (5,27,28). We then remeasured the passive tension-SL relation to estimate the collagen-based passive tension. The difference in tension before and after extraction of titin was assumed to be titin-based passive tension.
Statistics
We assigned significant differences using a paired or unpaired Student's t-test as appropriate (verified at p < 0.05), and performed a regression analysis using the least-squares method. All data are expressed as the mean ± SE, with n representing the number of experiments.
Results
Passive tension in skinned rabbit psoas muscle
Skinned psoas fiber bundles in relaxing solution were stretched from their slack SL, held for 20 min, and then released. Passive tension was analyzed at the beginning of the hold phase (t = 0) and 0.5 and 20 min later (see Fig. 1 A). The velocity of stretch and release was controlled at 0.1 slack length per second, and the maximal SL was restricted to <3.4 μm to avoid overstretching the sarcomere and causing irreversible damage by pulling titin off the ends of the thick filament (27,29). Due to the viscoelasticity of passive muscle, the passive tension decreased during the hold (stress relaxation), and after 20 min the passive tension was only ∼1/3 of the peak passive tension (Fig. 1 B). To determine the origin of passive tension, we extracted fibers with KCl/KI solution (see Materials and Methods) to abolish titin-based tension by removing titin's anchors in the sarcomere, and imposed identical stretch, hold, and release protocols. The KCl/KI insensitive tension, which is assumed to be due to collagen, is shown in Fig. 1 D. The difference in tension before and after extraction, which is assumed to be due to titin, is shown in Fig. 1 C. The results in Figs. 1, B–D, were used to calculate the relative contribution of titin and collagen to the total passive tension, and the results are shown in Fig. 1 E. Our findings indicate that within the SL range used here, titin was the main contributor to passive tension. Collagen's contribution increased with SL but stayed below ∼20%. These findings are consistent with previous work in rabbit psoas fiber bundles by Prado et al. (11), who degraded titin with the protease trypsin and observed similar large contributions of titin to passive tension. Thus, the majority of passive tension in the skinned psoas fiber bundles is due to titin; the value is >90% at SL < 2.8 μm and then gradually decreases at longer SLs to ∼80% at 3.4 μm. Because titin's tension is generated intrasarcomerically, we plotted the relationship between titin-based tension and x-ray diffraction-based structural parameters.
Figure 1.
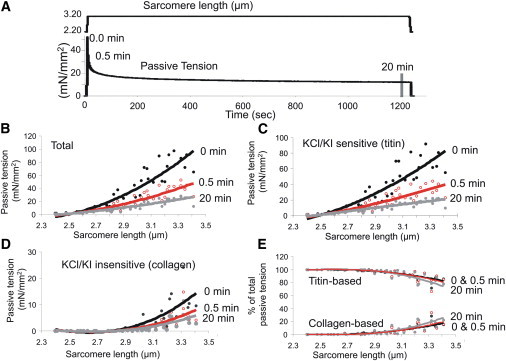
Mechanical protocol and functional dissection of passive tension in rabbit skinned psoas muscle fibers. (A) Explanation of the stretch-hold-release protocol, indicating the times when passive tensions were measured. (B) Total passive tension. (C) KCL/KI extraction-sensitive passive tension (titin-based). (D) KCL/KI-insensitive passive tension (collagen-based). (E) Relative contribution of titin-based and collagen-based passive tension during the hold phase, at three different times after completion of the stretch.
Features of 2D x-ray patterns
X-ray patterns were collected at various times during the mechanical protocol imposed on the skinned passive fiber bundle before stretch, twice after the stretch during the hold phase (0.5 and 20 min after completing the stretch), and after release. A representative 2D x-ray diffraction pattern from a skinned skeletal muscle bundle is shown in Fig. 2. The axial projection of the intensity along the meridian is shown in Fig. 2 B (upper right), and a more detailed profile of the M6 (7.2 nm) reflection on which we focused in this work is shown at bottom right. Fig. 2 C shows a radial projection of the intensity along the equator. The positions of the 1,0 and 1,1 A-band lattice reflections are shown along with Z reflections, which give a measure of the actin filament separation at or near the Z-disk (30). These high-quality 2D x-ray patterns allowed us to study the dependence of structural parameters on passive tension.
Figure 2.
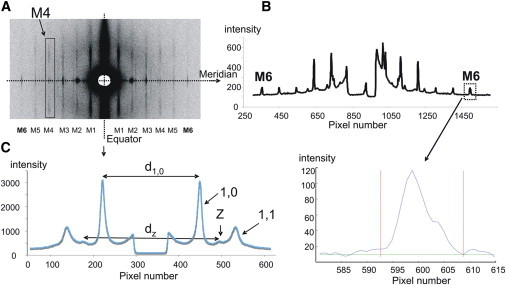
Features of x-ray diffraction patterns from passive rabbit psoas fibers. (A) 2D x-ray pattern indicating the meridian of the pattern (parallel to the fiber axis) and the equator (perpendicular to the fiber axis). Note layer lines that are orders of 1/42.9 nm repeat. M4 indicates the fourth myosin layer line. (B) 1D trace of the intensity along the meridian with myosin-based meridional reflections M6 as indicated. Bottom right: Intensity profile of the M6 meridional reflection after background subtraction. (C) 1D trace of the intensity along the equator. Note the 1,0 and 1,1 equatorial peaks and the reflection attributed to the thin filaments at and near the Z-band (Z).
A-band and Z-band lattice spacings as a function of titin-based passive tension
The relation between A-band interfilament lattice spacing, d1,0, and titin-based passive tension is shown in Fig. 3 A. At t = 0 min (high passive tension (HPT)), there is a linear relation between spacing and passive tension (y = −0.08x + 40.0, r2 = 0.6, with the p-value of the slope being nonzero (<0.001)). Of interest, the relation after 20 min of stress relaxation when passive tension is low (LPT) is still linear, but it has a much steeper slope (y = −0.30x + 41.3, r2 = 0.6, p < 0.001). We interpret this to mean that the lattice does not behave purely elastically (in which case the two curves would overlap); rather, it behaves viscoelastically (see also Discussion). We repeated these experiments in the presence of 1.5% dextran. Fig. 3 B shows the interfilament lattice spacing, d1,0, as a function of titin-based passive tension. As expected, dextran greatly decreased the lattice spacing, but now the data before and after 20 min of stress relaxation overlap (HPT y = −0.10x + 35.6, r2 = 0.5, p < 0.001; LPT y = −0.17x + 36.7, r2 = 0.6, p < 0.001), indicating that 1.5% dextran abolishes the viscoelastic effect. It is clear that d1,0 varies with passive tension.
Figure 3.
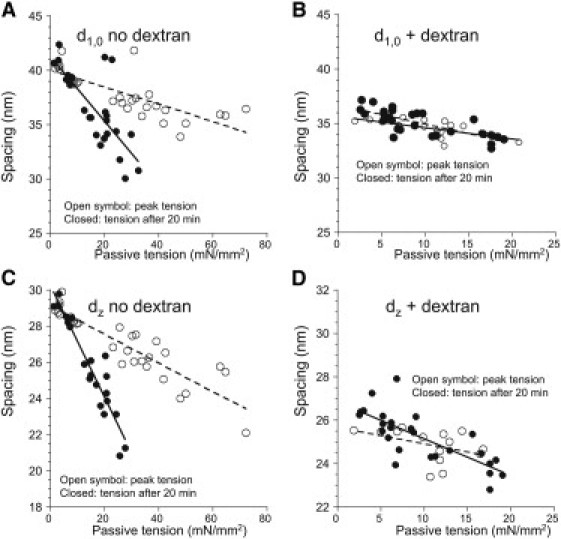
Passive tension dependence of A-band and Z-band lattice spacing. (A) A-band lattice spacing (d1,0) as a function of titin-based passive tension with measurements at peak tension (open symbols) and after 20 min of stress-relaxation (solid symbols). Note the large difference in slopes of the best-fit lines. (B) A-band lattice spacing (d1,0) as a function of titin-based passive tension in the presence of 1.5% dextran. Note the similarity of the slopes of the best-fit lines. (C) Z-band lattice spacing (dz) as a function of titin-based passive tension. Note the large difference in the slopes of the best-fit lines for peak tension data and steady-state tension after 20 min of stress relaxation. (D) Z-band lattice spacing (dz) as a function of titin-based passive tension in the presence of 1.5% dextran. The slopes of the best-fit lines are similar.
Fig. 3 C shows the relation between Z-disk lattice spacing, dz, and titin-based passive tension. At peak passive tension, there is a linear relation that changes to a different linear relationship after 20 min of stress relaxation (HPT y = −0.08x + 29.1, r2 = 0.8, p < 0.001; LPT y = −0.31x + 30.2, r2 = 0.9, p < 0.001). Fig. 3 D shows dz as a function of titin-based passive tension in the presence of 1.5% dextran. The data before and after 20 min of stress relaxation now overlap (HPT y = −0.08x + 25.7, r2 = 0.2, NS; LPT y = −0.17x + 26.8, r2 = 0.8, p < 0.001). Thus, in similarity to the A-band lattice, the viscoelastic character of the Z-disk lattice is also abolished by 1.5% dextran.
We also measured d1,0 and dz after the release of fibers that had been stretched for 20 min. Table 1 shows that in the absence of dextran, both d1,0 and dz were initially smaller than they were before the stretch, and that within ∼3 min the lattices expanded toward the prestretch value. In the presence of dextran, this effect was absent, i.e., the first exposure taken after the release had already recovered to the prestretch value. Thus, the lattice behaviors during the hold phase (stress relaxation) and after the release (stress recovery) both indicate that these lattices are viscoelastic in the absence of dextran, and elastic when the lattice is compressed with dextran.
Table 1.
Spacings of d10, dz, and dm6 before stretch and after release
| Dextran | SL (μm) | Before stretch | 1 min post rel. | 3 min post rel. | |
|---|---|---|---|---|---|
| d10 (nm) | 0 | 2.30 ± 0.01 (17) | 42.8 ± 0.05 (17) | 41.36 ± 0.26(19) | 41.66 ± 0.23 (9) |
| d10 (nm | 1.5% | 2.28 ± 0.01 (16) | 38.7 ± 0.24 (9) | 38.7 ± 0.88 (16) | 38.7 ± 0.25 (9) |
| dz (nm) | 0 | 2.30 ± 0.01 (17) | 30.4 ± 0.03 (17) | 29.8 ± 0.16 (18) | 30.2 ± 0.18 (8) |
| dz (nm) | 1.5% | 2.28 ± 0.01 (16) | 27.7 ± 0.19 (13) | 27.7 ± 0.10 (12) | 27.1 ± 0.68 (6) |
| dm6 | 0 | 2.27 ± 0.01 (9) | 7.18 ± 0.001 (7) | 7.19 ± 0.004 (4) | 7.19 ± 0.002 (4) |
| dm6 | 1.5% | 2.23 ± 0.08 (4) | 7.19 ± 0.002 (9) | 7.19 ± 0.005 (4) | 7.19 ± 0.002 (4) |
Thick-filament strain and titin-based passive tension
We also measured the thick-filament strain induced by titin-based passive tension and analyzed the meridional myosin-based reflections. In vertebrate muscle, the intensity of the meridional reflection at 7.2 nm (M6) is thought to arise primarily from periodic features within the thick-filament backbone itself (20,21) and thus has a straightforward interpretation as strain in the thick filament. (The intensity of the M3 meridional reflection is dominated by contributions from the myosin heads and does not faithfully report thick-filament backbone strain (20).) An example of a detailed profile of the M6 reflection is shown in Fig. 2 B (bottom right). Note the presence of a stronger low-angle peak and a weaker high-angle shoulder. This substructure in the M6 is likely due to interference effects from the two sides of the A-band (20,31). Although we originally attempted to analyze the location of the main peak and the shoulder separately, in many cases the shoulder was small, which made analysis challenging. We therefore elected to use the centroid of the entire M6 peak as a conservative measure of the M6 reflection position. We measured this at various times during the stretch-hold-release protocol as shown in Fig. 4 (top). (An example of an M6 reflection superimposed at HPT and LPT is shown in Fig. 5 A.) The M6 spacing as a function of SL is shown at the bottom of Fig. 4. Note the steep increase in spacing with increasing SL beyond ∼2.8 μm, which becomes less steep after 20 min of stress-relaxation. Therefore, it appears that strain stored in the thick filament during peak stretch dissipates with time during stress relaxation, in proportion to the reduction in passive tension.
Figure 4.
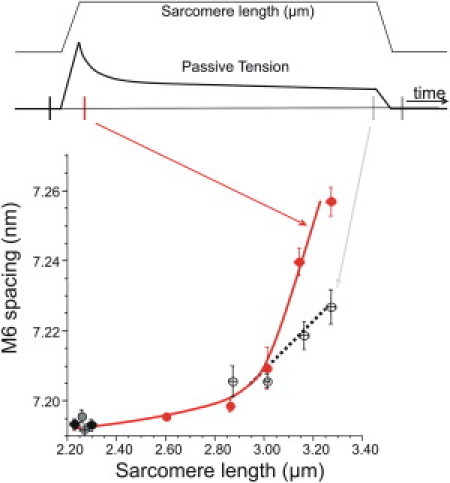
M6 spacing behavior during the stretch-hold-release protocol. (Top) The protocol with x-ray exposures taken at 1), prestretch; 2), immediately poststretch; 3), 20 min poststretch; and 4), postrelease. (Bottom) M6 spacing as a function of SL. Note the steep rise in M6 spacing at long SL at peak passive tension and the less steep relation after 20 min of stress relaxation.
Figure 5.
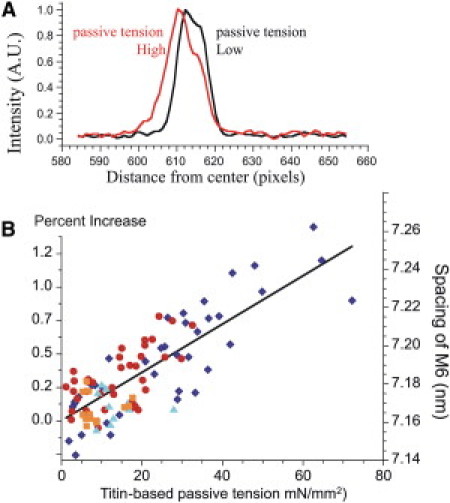
M6 spacing as a function of titin-based passive tension. (A) Examples of M6 intensity profiles from the same muscle at HPT and LPT (28 and 0 mN/mm2, respectively). Note that the profile at HPT is left-shifted (indicating an increase in M6 spacing). (B) Spacing data collected at peak passive tension (dark blue) and after 20 min of stress-relaxation (red) have the same relationship to passive tension. This relationship is not affected by the presence of 1.5% dextran (light blue, peak tension; orange, after 20 min of stress-relaxation). We conclude that thick filaments stretch elastically with increases in passive tension.
Fig. 5 B shows M6 spacing as a function of titin-based passive tension (left scale, M6 expressed relative to its value at slack length). Note that the spacing data collected at peak passive tension and after 20 min of stress-relaxation appear to obey the same linear relationship to passive tension. The slopes of these curves were not significantly different between data obtained at HPT versus LPT (1.4 × 10−3 nm/mN and 0.9 × 10−3 nm/mN, respectively). Fig. 5 B also shows the effect of adding 1.5% dextran on the relationship of M6 spacing to titin-based passive tension. The data obtained with and without dextran were indistinguishable (slope in dextran 1.2 × 10−3 nm/mN). Table 1 shows that the M6 spacing recovers completely after release in either the presence or absence of dextran. Thus, thick filaments stretch elastically with increases in passive tension (∼0.5% stretch for 40 mN/mm2) and their elasticity is unaffected by lattice compression. The compliance of the thick filament under passive conditions is unexpectedly large compared with the previously reported ∼0.25% stretch per ∼250 mN/mm2 (26,32,33) in activated muscle using slow stretches at the tetanic plateau (see Discussion).
Radial position of myosin heads and titin-based passive tension
To evaluate whether the radial disposition of the myosin heads is sensitive to passive tension, we measured the I1,1/I1,0 equatorial intensity ratio. Table 2 shows the I1,1/I1,0 intensity ratio, at short SL, just after the stretch, after 20 min of stress relaxation, and after the release. There is the expected reduction in I1,1/I1,0 as the thin filaments are pulled out of the A-band during the stretch, but there is no difference in I1,1/I1,0 at long SL before and after stress relaxation, indicating no difference in the relative amounts of mass centered on the thin filament versus that centered on the thin filament (i.e., there is no detectable change in the disposition of the myosin heads).
Table 2.
I1,1/I1,0 ratio (mean ± SE)
Another, independent measure of the disposition of the myosin heads can be obtained by the separation of the first maxima on the unsampled M4 (34). This can be related to the average radial position of the center of mass of the myosin heads in their three-start helical array on the thick-filament backbone. Table 3 shows that there are no differences in this quantity during stress-relaxation at long SL.
Table 3.
Radial position of the M4 layer line maxima (nm−1), with no dextran
Discussion
We obtained 2D x-ray diffraction patterns from rabbit skinned psoas fibers that were subjected to a stretch-hold-release protocol while passive tension was measured. Various structural parameters were studied over a range of titin-based passive tensions. The interfilament spacing in the A-band and the Z-disk regions of the sarcomere varied with titin-based passive tension in a viscoelastic manner in the absence of dextran, and elastically in the presence of dextran. The thick-filament backbone strain varied with titin-based passive tension in an elastic manner and independently of stretch history or the presence of dextran. Below, we discuss these findings and their functional significance.
Lattice spacing in the A-band region
It is well known that interfilament spacing in the overlap region of the sarcomere is reduced when muscle is stretched (for review, see Millman (23)), and this relation is thought to contribute to the increased calcium sensitivity of active tension at long length (35–39). We previously obtained evidence in cardiac muscle for a titin-based tension that compresses the myofilament lattice, and proposed that this contributes to the increased calcium sensitivity at high titin-based passive tension (13,14,18,19,40). This titin-based compressive tension can be explained by titin's spring region, which is attached at one end to the thin filament (near the Z-disk) and at the other end to the thick filament (edge of the A-band). As a result, titin does not run parallel to the thin and thick filaments, and this gives rise to a titin-based lateral tension that compresses both the A-band lattice (13) and the Z-disk lattice (see below). We found that the interfilament spacing, d1,0, varied linearly with titin-based passive tension under all conditions studied here, and our results support the view that titin-based tension is a factor that sets the interfilament spacing. This conclusion is supported by the previous work of Higuchi (41), who measured the interfilament lattice in single skinned fibers of frog and showed that spacing was increased after degradation of titin (connectin) with a mild trypsin treatment. When we took measurements in the presence of dextran, the lattice behaved elastically, as suggested by the overlap between the curve measured immediately after stretch was completed and the curve after 20 min of stretch relaxation (Fig. 3 B). However, the two curves deviated substantially in the absence of dextran, and a given level of passive tension had a lesser effect on lattice spacing immediately after stretch was completed compared with that observed 20 min later (Fig. 3 A). This suggests that when the lattice is expanded (no dextran), it has a lateral viscoelasticity, i.e., it is initially stiff when tension is applied (a small lattice compression for a given tension) and becomes more compliant during stress relaxation (larger lattice compression for the same tension). The basis for this phenomenon is likely to reside in structural proteins, such as the antiparallel myomesin dimers that link the thick filaments in the M-band (42) and are thought to develop in a compressed lattice a tension that is directed toward lattice expansion. Myomesin has complex viscoelastic properties that can be modified by alternative splicing (42), and our work suggests that at physiological thick-filament spacing (with dextran), myomesin functions elastically. However, in an expanded lattice (no dextran), structural rearrangements must occur such that when a compressive tension is applied, the myomesin will initially be stiff and then soften over time. This phenomenon is reversible, as is shown by the d1,0 measurement when the tension is removed, but several minutes are required for full recovery (Table 1).
The relation between passive tension and interfilament lattice spacing in the A-band region in rabbit psoas fibers is consistent with previous studies on cardiac muscle. In two such studies (13,15), the A-band interfilament spacing was expanded after abolishment of titin-based passive tension (due to titin proteolysis). In another study (14), myocardial tissues that expressed different titin isoforms were compared, and it was observed that the tissue with the lowest titin-based passive tension had the largest spacing. Thus, the compressive effect of titin-based tension on A-band interfilament lattice spacing may be a universal phenomenon in striated muscle. We previously proposed that the reduction in lattice spacing at HPT contributes to the length dependence of activation in cardiac muscle (13–15), and the results presented here indicate that this mechanism may also operate in skeletal muscle.
Lattice spacing in the Z-disk region
Reflections from the lattice formed by thin filaments in and near the Z-disk were clearly visible in the equatorial x-ray diffraction patterns as the z reflection located between the 1,0 and 1,1 A-band reflections. This z reflection arises from the square lattice of thin filaments in the Z-disk and its shift to a hexagonal packing in the overlap region of the sarcomere (30). Analogously to d1,0, dz also varies with passive tension, consistent with the notion that titin develops a lateral force that compresses the myofilament lattice in the A-band as well as in the Z-disk. Of interest, the behavior of dz was elastic in the presence of dextran (Fig. 3 D) and viscoelastic when dextran was absent (Fig. 3 C), which again is similar to what was found for d1,0. The main structural protein that maintains the Z-disk filament spacing is α-actinin, and our findings suggest that in an expanded lattice (no dextran), α-actinin has viscoelastic properties that result in softening when a tension is applied for a long time (Fig. 3 C) and a slow recovery of the prestretch spacing when the tension is removed (Table 1). At physiological lattice spacings (with dextran), this phenomenon is absent and the Z-disk structural proteins that are responsible for lattice expansion behave elastically. Thus, both the A-band and Z-disk lattices are optimized for elastic behavior at physiological lattice spacing, which is energetically beneficial because it prevents energy loss in repeated loading cycles.
Thick-filament compliance
Our work also reveals that the spacing of the meridional M6 (∼7.2 nm) scales with titin-based passive tension, indicating that titin strains the thick filament. The findings that during stress relaxation the M6 spacing decreases in proportion to passive tension (Fig. 5 B), and the spacing observed immediately after release is the same as that measured before stretch (Table 1) suggest that, within the force range studied, the thick filament stretches elastically. (Small levels of viscosity cannot be excluded, due to the noisy nature of the data.) Titin is well positioned to exert tension on the thick filament, with (most likely) six titin molecules attaching the end of each thick filament to the nearest Z-disk (5,43). We found that the M6 spacing increased ∼0.5% at a titin-based passive tension level of ∼40 mN/mm2 (Fig. 5 B). An increase in thick-filament axial repeats has also been reported for intact frog semitendinosus muscle stretched in the passive state to beyond overlap, with M6 increasing ∼0.85% (32). Thus, passive tension-induced stretching of the thick filament is likely be a universal property of passive muscle. The data we obtained in passive rabbit muscle fibers (∼0.5% stretch at 40 mN/mm2 passive tension) allows us to estimate the thick-filament compliance under relaxing conditions. The 40 mN/mm2 titin-based passive tension corresponds to ∼95 pN/thick filament (unit cell area: d1,02 × 2/√3; assumptions: d1,0 = 40 nm at slack length, and ∼75% of the cross-sectional area of the muscle is myofibril, or 407 × 106 thick filaments per mm2) and 0.5% strain corresponds to ∼8 nm stretch (assuming the thick filament is 1.6 μm long). Thus, the thick filaments stretch 8 nm under ∼95 pN of force, which corresponds to a compliance of ∼85 m/N.
Several groups have studied the extensibility of thick filaments during tetanic contraction of intact frog muscle (26,32,33) and assessed spacing changes while slowly stretching or releasing muscle during the plateau of isometric tetani. When results were scaled to 100% tetanic tension, the change in M6 spacing was ∼0.25%. The compliance of the thick filament during the tetanic force plateau has been estimated at 11–16 m/N (scaling up the values reported by Reconditi (20) to the length of the thick filament). Thus, the thick filament is ∼5–8 times more compliant (85/11 (16)) during passive stretch than during the tetanic force plateau.
Of interest, a study in which nanofabricated cantilevers were used to mechanically characterize single synthetic rabbit thick filaments (44) revealed that thick filaments have a nonlinear compliance, with a ∼10-fold larger compliance at low strains (<0.5%) than at high strains (>1.5%). This result supports our proposal regarding nonlinear thick-filament compliance in muscle fibers. Because synthetic thick filaments do not contain accessory proteins (e.g., MyBP-C), the single-filament study was also able to show that the nonlinear compliance of the thick filament required only myosin and was most likely due to some unique myosin packing characteristic.
In addition to measurements obtained during the plateau of the tetanus, investigators have also measured M6 spacings during the tetanic tension rise (20,26,32,33). Thick-filament axial spacings increase during the tension rise nearly 1.5% from the level measured at rest. This large change upon activation has been interpreted as being caused by structural changes that precede tension development (e.g., cross-bridge binding to actin) and not by thick-filament strain (26,32,33). It seems unlikely that this interpretation is valid for the increase in M6 spacing we observed, considering that our measurements were obtained in relaxing solution, with no evidence for a detectable change in the disposition of the myosin heads, as reflected by the constant I1,1/I1,0 ratio during stretch relaxation (Table 2) and the constant separation of the first maxima on M4 (Table 3). We conclude that the large increase in M6 spacing in passive muscle is likely due to stretch of the thick-filament backbone, and hence that the thick filament has a high compliance in passive muscle. Could this high thick-filament compliance also be present in active muscle and contribute to the large M6 spacing increase observed during the tetanic force rise? It is well known that upon muscle activation the M6 spacing increases faster versus time than the tension does (i.e., the M6 spacing leads tension) and this observation has been considered an important argument for the view that the M6 increase upon activation is not due to thick filament strain per se, but rather to some sort of global structural change due to the activation process itself (20,23,33,45). This lead, however, is expected if thick filaments have a larger compliance at low tension than at high tension (for example, when tension has only reached 1/3 of maximal, thick-filament stretch has already reached 2/3 of maximal (33)). We propose, therefore, that analogously to its behavior during passive stretch, the M6 increase during tetanic activation includes high thick-filament backbone compliance during early parts of the tetanus when force is low.
Filament compliance greatly affects the interpretation of many mechanical experiments that before the mid-1990s were based on the assumption that rigid filaments transmit applied length changes to the cross-bridges. Subsequently, investigators used experiments (46) and mathematical modeling of muscle contraction (47) to evaluate the effect of myofilament compliance and concluded that this compliance alters the kinetics of tension development, Ca2+ sensitivity, and cooperativity of activation. The thick-filament compliance that was used in the modeling studies was based on the low compliance measured during the tetanic tension plateau. Our work suggests that a more complex thick-filament compliance, characterized by a high compliance at low tension and a much-reduced compliance at high tension, may be required. Of interest, Bagni et al. (48) showed that stretching of activated muscle gives rise to a static stiffness that leads to tension development (as does M6), and whether this phenomenon is related to a nonlinear thick-filament compliance is worth examination in future studies. Furthermore, we also need to determine how increased thick-filament strain in stretched passive muscle affects subsequent activation characteristics. Unlike in activated muscle, where a strain gradient is expected along the thick filament (with minimal strain at the edge of the thick filament and maximal strain at the edge of the H-zone), titin-based strain in passive muscle is expected to be relatively uniform along the thick filament. The degree to which thick-filament strain in passive muscle influences subsequent activation, and whether this is a contributing factor to the relation between passive tension and calcium sensitivity are important topics for future research.
Conclusions
Using 2D x-ray diffraction, we performed a comprehensive study of the effect of titin on the sarcomeric structure of rabbit skinned muscle fibers that were stretched while in relaxing solution. We found that titin-based passive tension reduced the interfilament spacing in both the A-band and Z-disk regions of the sarcomere, and increased thick-filament strain by a surprisingly large amount. These effects of titin on sarcomeric structure may play functional roles in active tension development. Additional roles are possible as well. For example, the Z-disk and M-band regions of the sarcomere are highly populated with signaling molecules that are involved in the trophic and pathological responses of muscle to biomechanical stresses and strains (49–52), and it is not well known how mechanical signals are communicated to Z-disk and M-band based signaling proteins. Our findings suggest novel pathways. The reduced lattice spacing in both the A-band and Z-disk regions of the sarcomere when passive tension is high will increase steric hindrance and molecular crowding, and this is likely to affect the functionality of signaling networks and the ease with which members interact. Additionally, changes in thick-filament strain could affect the interaction between signaling molecules and either the thick filament or thick-filament-associated proteins. Such effects might include changes in the activity of the titin kinase domain, which is localized near the edge of the bare zone of the thick filament, and in vitro evidence suggests that this activity is strain-dependent (for review, see Granzier and Labeit (12)). Thus, the effect of titin on sarcomeric structure could be important not only for acute adaptations in contractility but also for more long-term muscle plasticity.
Acknowledgments
We thank S. R. Taylor, Krystyna Malinowska, and Joshua Nedrud for help with the x-ray data analysis.
This work was supported by the National Institutes of Health (grant HL67274 to H.G.). Use of the Advanced Photon Source was supported by the Office of Basic Energy Sciences, U.S. Department of Energy, under contract No. W-31-109-ENG-38. BioCAT is a National Institutes of Health-supported research center (RR-08630). The content is solely the responsibility of the authors and does not necessarily reflect the official views of the National Center for Research Resources or the National Institutes of Health.
Footnotes
Yiming Wu's present address is Department of Internal Medicine, University of Iowa, Iowa City, Iowa.
Gerrie P. Farman's present address is Richard Lewar Center of Excellence, Toronto, Ontario, Canada.
Norio Fukuda's present address is Department of Cell Physiology, Jikei University School of Medicine, Tokyo, Japan.
Supporting Material
References
- 1.Huxley H.E. Sliding filaments and molecular motile systems. J. Biol. Chem. 1990;265:8347–8350. [PubMed] [Google Scholar]
- 2.Maruyama K., Matsubara S., Kimura S. Connectin, an elastic protein of muscle. Characterization and function. J. Biochem. 1977;82:317–337. [PubMed] [Google Scholar]
- 3.Wang K., McClure J., Tu A. Titin: major myofibrillar components of striated muscle. Proc. Natl. Acad. Sci. USA. 1979;76:3698–3702. doi: 10.1073/pnas.76.8.3698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Fürst D.O., Osborn M., Weber K. The organization of titin filaments in the half-sarcomere revealed by monoclonal antibodies in immunoelectron microscopy: a map of ten nonrepetitive epitopes starting at the Z line extends close to the M line. J. Cell Biol. 1988;106:1563–1572. doi: 10.1083/jcb.106.5.1563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Granzier H.L., Irving T.C. Passive tension in cardiac muscle: contribution of collagen, titin, microtubules, and intermediate filaments. Biophys. J. 1995;68:1027–1044. doi: 10.1016/S0006-3495(95)80278-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Linke W.A., Ivemeyer M., Labeit S. Towards a molecular understanding of the elasticity of titin. J. Mol. Biol. 1996;261:62–71. doi: 10.1006/jmbi.1996.0441. [DOI] [PubMed] [Google Scholar]
- 7.Labeit S., Kolmerer B. Titins: giant proteins in charge of muscle ultrastructure and elasticity. Science. 1995;270:293–296. doi: 10.1126/science.270.5234.293. [DOI] [PubMed] [Google Scholar]
- 8.Freiburg A., Trombitas K., Labeit S. Series of exon-skipping events in the elastic spring region of titin as the structural basis for myofibrillar elastic diversity. Circ. Res. 2000;86:1114–1121. doi: 10.1161/01.res.86.11.1114. [DOI] [PubMed] [Google Scholar]
- 9.Trombitás K., Redkar A., Granzier H. Extensibility of isoforms of cardiac titin: variation in contour length of molecular subsegments provides a basis for cellular passive stiffness diversity. Biophys. J. 2000;79:3226–3234. doi: 10.1016/S0006-3495(00)76555-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Trombitás K., Wu Y., Granzier H. Cardiac titin isoforms are coexpressed in the half-sarcomere and extend independently. Am. J. Physiol. Heart Circ. Physiol. 2001;281:H1793–H1799. doi: 10.1152/ajpheart.2001.281.4.H1793. [DOI] [PubMed] [Google Scholar]
- 11.Prado L.G., Makarenko I., Linke W.A. Isoform diversity of giant proteins in relation to passive and active contractile properties of rabbit skeletal muscles. J. Gen. Physiol. 2005;126:461–480. doi: 10.1085/jgp.200509364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Granzier H., Labeit S. Structure-function relations of the giant elastic protein titin in striated and smooth muscle cells. Muscle Nerve. 2007;36:740–755. doi: 10.1002/mus.20886. [DOI] [PubMed] [Google Scholar]
- 13.Cazorla O., Wu Y., Granzier H. Titin-based modulation of calcium sensitivity of active tension in mouse skinned cardiac myocytes. Circ. Res. 2001;88:1028–1035. doi: 10.1161/hh1001.090876. [DOI] [PubMed] [Google Scholar]
- 14.Fukuda N., Wu Y., Granzier H. Titin isoform variance and length dependence of activation in skinned bovine cardiac muscle. J. Physiol. 2003;553:147–154. doi: 10.1113/jphysiol.2003.049759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fukuda N., Wu Y., Granzier H. Titin-based modulation of active tension and interfilament lattice spacing in skinned rat cardiac muscle. Pflugers Arch. 2005;449:449–457. doi: 10.1007/s00424-004-1354-6. [DOI] [PubMed] [Google Scholar]
- 16.Cazorla O., Szilagyi S., Lacampagne A. Transmural stretch-dependent regulation of contractile properties in rat heart and its alteration after myocardial infarction. FASEB J. 2005;19:88–90. doi: 10.1096/fj.04-2066fje. [DOI] [PubMed] [Google Scholar]
- 17.Cazorla O., Vassort G., Le Guennec J.Y. Length modulation of active force in rat cardiac myocytes: is titin the sensor? J. Mol. Cell. Cardiol. 1999;31:1215–1227. doi: 10.1006/jmcc.1999.0954. [DOI] [PubMed] [Google Scholar]
- 18.Fukuda N., Sasaki D., Kurihara S. Length dependence of tension generation in rat skinned cardiac muscle: role of titin in the Frank-Starling mechanism of the heart. Circulation. 2001;104:1639–1645. doi: 10.1161/hc3901.095898. [DOI] [PubMed] [Google Scholar]
- 19.Lee E.J., Peng J., Granzier H.L. Calcium sensitivity and the Frank-Starling mechanism of the heart are increased in titin N2B region-deficient mice. J. Mol. Cell. Cardiol. 2010;49:449–458. doi: 10.1016/j.yjmcc.2010.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reconditi M. Recent improvements in small angle x-ray diffraction for the study of muscle physiology. Rep. Prog. Phys. 2006;69:2709–2759. doi: 10.1088/0034-4885/69/10/R01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Huxley H.E. Recent X-ray diffraction studies of muscle contraction and their implications. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004;359:1879–1882. doi: 10.1098/rstb.2004.1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Irving T.C., Konhilas J., de Tombe P.P. Myofilament lattice spacing as a function of sarcomere length in isolated rat myocardium. Am. J. Physiol. Heart Circ. Physiol. 2000;279:H2568–H2573. doi: 10.1152/ajpheart.2000.279.5.H2568. [DOI] [PubMed] [Google Scholar]
- 23.Millman B.M. The filament lattice of striated muscle. Physiol. Rev. 1998;78:359–391. doi: 10.1152/physrev.1998.78.2.359. [DOI] [PubMed] [Google Scholar]
- 24.Irving T.C., Millman B.M. Changes in thick filament structure during compression of the filament lattice in relaxed frog sartorius muscle. J. Muscle Res. Cell Motil. 1989;10:385–394. doi: 10.1007/BF01758435. [DOI] [PubMed] [Google Scholar]
- 25.Haselgrove J.C., Stewart M., Huxley H.E. Cross-bridge movement during muscle contraction. Nature. 1976;261:606–608. doi: 10.1038/261606a0. [DOI] [PubMed] [Google Scholar]
- 26.Huxley H.E., Stewart A., Irving T. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 1994;67:2411–2421. doi: 10.1016/S0006-3495(94)80728-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang K., McCarter R., Ramirez-Mitchell R. Regulation of skeletal muscle stiffness and elasticity by titin isoforms: a test of the segmental extension model of resting tension. Proc. Natl. Acad. Sci. USA. 1991;88:7101–7105. doi: 10.1073/pnas.88.16.7101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wu Y., Cazorla O., Granzier H. Changes in titin and collagen underlie diastolic stiffness diversity of cardiac muscle. J. Mol. Cell. Cardiol. 2000;32:2151–2162. doi: 10.1006/jmcc.2000.1281. [DOI] [PubMed] [Google Scholar]
- 29.Granzier H.L., Wang K. Passive tension and stiffness of vertebrate skeletal and insect flight muscles: the contribution of weak cross-bridges and elastic filaments. Biophys. J. 1993;65:2141–2159. doi: 10.1016/S0006-3495(93)81262-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Irving T.C., Millman B.M. Z-line/I-band and A-band lattices of intact frog sartorius muscle at altered interfilament spacing. J. Muscle Res. Cell Motil. 1992;13:100–105. doi: 10.1007/BF01738433. [DOI] [PubMed] [Google Scholar]
- 31.Linari M., Piazzesi G., Lombardi V. Interference fine structure and sarcomere length dependence of the axial x-ray pattern from active single muscle fibers. Proc. Natl. Acad. Sci. USA. 2000;97:7226–7231. doi: 10.1073/pnas.97.13.7226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wakabayashi K., Sugimoto Y., Amemiya Y. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 1994;67:2422–2435. doi: 10.1016/S0006-3495(94)80729-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Brunello E., Bianco P., Lombardi V. Structural changes in the myosin filament and cross-bridges during active force development in single intact frog muscle fibres: stiffness and X-ray diffraction measurements. J. Physiol. 2006;577:971–984. doi: 10.1113/jphysiol.2006.115394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Malinchik S., Xu S., Yu L.C. Temperature-induced structural changes in the myosin thick filament of skinned rabbit psoas muscle. Biophys. J. 1997;73:2304–2312. doi: 10.1016/S0006-3495(97)78262-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.McDonald K.S., Moss R.L. Osmotic compression of single cardiac myocytes eliminates the reduction in Ca2+ sensitivity of tension at short sarcomere length. Circ. Res. 1995;77:199–205. doi: 10.1161/01.res.77.1.199. [DOI] [PubMed] [Google Scholar]
- 36.Wang Y., Fuchs F. Interfilament spacing, Ca2+ sensitivity, and Ca2+ binding in skinned bovine cardiac muscle. J. Muscle Res. Cell Motil. 2001;22:251–257. doi: 10.1023/a:1012298921684. [DOI] [PubMed] [Google Scholar]
- 37.Konhilas J.P., Irving T.C., de Tombe P.P. Myofilament calcium sensitivity in skinned rat cardiac trabeculae: role of interfilament spacing. Circ. Res. 2002;90:59–65. doi: 10.1161/hh0102.102269. [DOI] [PubMed] [Google Scholar]
- 38.Fuchs F., Martyn D.A. Length-dependent Ca(2+) activation in cardiac muscle: some remaining questions. J. Muscle Res. Cell Motil. 2005;26:199–212. doi: 10.1007/s10974-005-9011-z. [DOI] [PubMed] [Google Scholar]
- 39.de Tombe P.P., Mateja R.D., Irving T.C. Myofilament length dependent activation. J. Mol. Cell. Cardiol. 2010;48:851–858. doi: 10.1016/j.yjmcc.2009.12.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Fukuda N., Granzier H. Role of the giant elastic protein titin in the Frank-Starling mechanism of the heart. Curr. Vasc. Pharmacol. 2004;2:135–139. doi: 10.2174/1570161043476357. [DOI] [PubMed] [Google Scholar]
- 41.Higuchi H. Lattice swelling with the selective digestion of elastic components in single-skinned fibers of frog muscle. Biophys. J. 1987;52:29–32. doi: 10.1016/S0006-3495(87)83185-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schoenauer R., Bertoncini P., Agarkova I. Myomesin is a molecular spring with adaptable elasticity. J. Mol. Biol. 2005;349:367–379. doi: 10.1016/j.jmb.2005.03.055. [DOI] [PubMed] [Google Scholar]
- 43.Houmeida A., Baron A., Trinick J. Evidence for the oligomeric state of ‘elastic’ titin in muscle sarcomeres. J. Mol. Biol. 2008;384:299–312. doi: 10.1016/j.jmb.2008.09.030. [DOI] [PubMed] [Google Scholar]
- 44.Dunaway D., Fauver M., Pollack G. Direct measurement of single synthetic vertebrate thick filament elasticity using nanofabricated cantilevers. Biophys. J. 2002;82:3128–3133. doi: 10.1016/S0006-3495(02)75654-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kress M., Huxley H.E., Hendrix J. Structural changes during activation of frog muscle studied by time-resolved X-ray diffraction. J. Mol. Biol. 1986;188:325–342. doi: 10.1016/0022-2836(86)90158-0. [DOI] [PubMed] [Google Scholar]
- 46.Higuchi H., Yanagida T., Goldman Y.E. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys. J. 1995;69:1000–1010. doi: 10.1016/S0006-3495(95)79975-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chase P.B., Macpherson J.M., Daniel T.L. A spatially explicit nanomechanical model of the half-sarcomere: myofilament compliance affects Ca(2+)-activation. Ann. Biomed. Eng. 2004;32:1559–1568. doi: 10.1114/b:abme.0000049039.89173.08. [DOI] [PubMed] [Google Scholar]
- 48.Bagni M.A., Cecchi G., Colomo F. A non-cross-bridge stiffness in activated frog muscle fibers. Biophys. J. 2002;82:3118–3127. doi: 10.1016/S0006-3495(02)75653-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Linke W.A. Sense and stretchability: the role of titin and titin-associated proteins in myocardial stress-sensing and mechanical dysfunction. Cardiovasc. Res. 2008;77:637–648. doi: 10.1016/j.cardiores.2007.03.029. [DOI] [PubMed] [Google Scholar]
- 50.LeWinter M.M., Granzier H. Cardiac titin: a multifunctional giant. Circulation. 2010;121:2137–2145. doi: 10.1161/CIRCULATIONAHA.109.860171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hoshijima M. Mechanical stress-strain sensors embedded in cardiac cytoskeleton: Z disk, titin, and associated structures. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H1313–H1325. doi: 10.1152/ajpheart.00816.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pyle W.G., Solaro R.J. At the crossroads of myocardial signaling: the role of Z-discs in intracellular signaling and cardiac function. Circ. Res. 2004;94:296–305. doi: 10.1161/01.RES.0000116143.74830.A9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


