Secondary Flow as a Mechanism for the Formation of Biofilm Streamers

Abstract

In most environments, such as natural aquatic systems, bacteria are found predominantly in self-organized sessile communities known as biofilms. In the presence of a significant flow, mature multispecies biofilms often develop into long filamentous structures called streamers, which can greatly influence ecosystem processes by increasing transient storage and cycling of nutrients. However, the interplay between hydrodynamic stresses and streamer formation is still unclear. Here, we show that suspended thread-like biofilms steadily develop in zigzag microchannels with different radii of curvature. Numerical simulations of a low-Reynolds-number flow around these corners indicate the presence of a secondary vortical motion whose intensity is related to the bending angle of the turn. We demonstrate that the formation of streamers is directly proportional to the intensity of the secondary flow around the corners. In addition, we show that a model of an elastic filament in a two-dimensional corner flow is able to explain how the streamers can cross fluid streamlines and connect corners located at the opposite sides of the channel.

Introduction

Biofilms are colonies of microorganisms that are encased in a self-excreted matrix of extracellular polymeric substances. Over the last few decades, investigators have paid increasing attention to biofilms, motivated in large part by the fact that this form of microbial life is widespread in both natural environments and industrial systems (1,2). Biofilms are generally associated with an interface or, more commonly, a solid substrate, and are typically viewed as growing in thin-film configurations all over the surface. Biofilms can be very difficult to eradicate, which can cause costly problems for the shipping industry (e.g., because of biofouling) (3) and water purification systems (4). Of most importance, the presence of biofilms very often poses a serious risk of infection in clinical environments and indwelling medical devices (5,6). Several studies have shown that bacteria within biofilms can be significantly more resistant to antibiotics and antimicrobial agents (up to 1000 times in some cases) than planktonic cells of the same species (7,8).

Although biofilms play a critical role in medicine and industry, many of the biophysical aspects of formation and development of these fascinating multicellular systems are still unclear or only partially understood. In particular, the different steps in the life cycle of a biofilm (i.e., initial attachment, formation of microcolonies, production of extracellular matrix, and biofilm maturation and dispersal) offer many opportunities for scientific investigations, especially because they require different fields of expertise ranging from microbiology to physics and engineering.

A clear example of this multidisciplinary approach is the investigation of the effects of hydrodynamics (e.g., flow and shear stress) on bacterial adhesion and biofilm formation. Although there have been some studies in this direction (9–12), many questions remain unresolved, which is particularly relevant considering that most industrial and natural systems form biofilms in the presence of flow. For instance, the role played by a moving fluid environment in shaping the complex architectures and morphologies of biofilms is not fully understood. In this context, we previously showed (13) that suspended filamentous biofilms develop during laminar flow in channels with corners. In our initial study, solutions of Pseudomonas aeruginosa were flushed into microfluidic channels with round and sharp turns at a constant flow rate (Fig. 1 a). We observed typical thread-like biofilm structures, as shown in the confocal images taken exactly in the middle horizontal plane of the channel (Fig. 1 b). The filamentous structures that formed in our microfluidic experiments were made of cells held together by extracellular matrix and were freely suspended in the middle of the flow, connected only to the lateral walls of the channel in the proximity of the corners.

Figure 1.

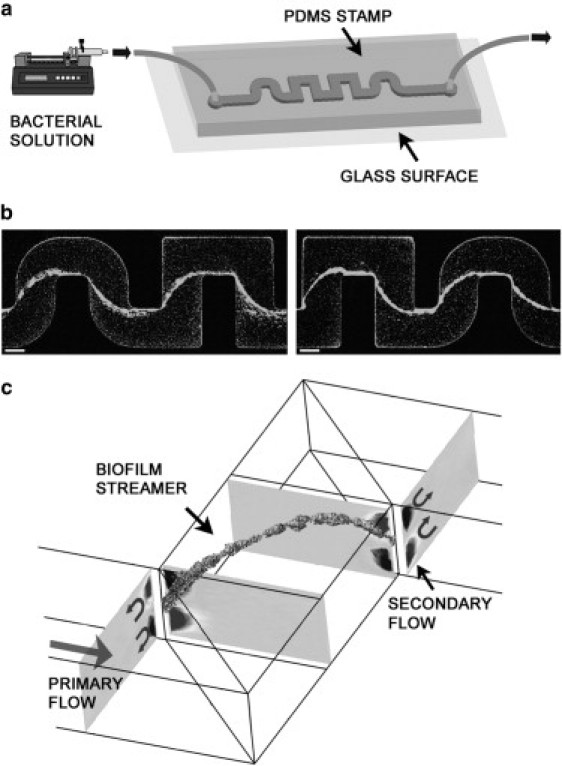
(a) Microfluidic experimental setup used to study biofilm formation under continuous flow and constant nutrient conditions. The channels are made in PDMS and sealed over a glass surface, which allows for a direct optical investigation (not to scale). (b) Confocal microscopy images taken in the middle-horizontal plane of the channel after 12 h of constant flow rate (from left to right) at 0.75 μl min⁻¹ for two different experiments. The bacteria are green fluorescent protein-labeled P. aeruginosa strain PA14. Scale bars: 100 μm. (c) Pictorial visualization of the suggested mechanism of streamer formation. The streamer is a 3D rendering from confocal image stacks, and the secondary flow contour plots were obtained from 3D numerical simulations of the flow.

Filamentous biofilms are generally found in natural environments, such as rivers, in which a strong stream flow is able to mold the morphology of surface-attached bacterial colonies. For this reason, these structures are usually referred to as streamers (14,15). Biofilm streamers are also typical of extreme environments ranging from arctic cold saline springs (16) to hydrothermal hot springs (17,18) and metal-rich acidic waters (19). These filamentous aggregates can reach macroscopic dimensions (20) and strongly influence stream ecosystems (21,22) because their oscillations can enhance particle trapping and transport of nutrients. Moreover, the presence of streamers has been observed in artificial systems under turbulent flow conditions. Besemer and co-workers (23,24) analyzed the formation of streamers in streamside flumes with mixed bacterial and eukaryotic populations, and showed that cells within the filamentous tail can be genetically different from those in the canopy or base. Stoodley and colleagues (25,26) reported the formation of biofilm streamers with mixed and monospecies cultures of P. aeruginosa in laboratory flow cells. Finally, filamentous biofilms found in filtration systems (e.g., membranes) have been reported to cause serious problems such as clogging and increased pressure drops (27,28).

In our previous work (13), we suggested a hydrodynamic mechanism for the formation of bacterial streamers under laminar flow in curved microfluidic channels. Numerical simulations of the three-dimensional (3D) flow field for these geometries showed the presence of a weak but significant secondary flow characterized by two counterrotating vortices localized in the proximity of the corners (Fig. 1 c). The good agreement between the numerical results and the experimental occurrence of these bacterial structures provides strong evidence for a causative hydrodynamic mechanism: biomass accumulates on the lateral walls of the channel and a precursor thread forms at half the channel height because of the stresses associated with the secondary flow, and the thread is then stretched by the mainstream flow until it reaches the next corner. Real-time experiments indicate that this process takes place at the same time at different corners (and precisely in the downstream part of every turn) all along the curved sections of the channel, and all of the initial filaments will eventually stick together if the corners are sufficiently close. In addition, streamers also develop on lateral hemicylindrical bumps, reinforcing the link with the hydrodynamic model and supporting the notion that streamers may be widespread (e.g., filters, membranes, and prosthetic devices).

The first phase of the formation of streamers is characterized by very thin filaments of almost pure extracellular matrix, and thus it is very difficult to visualize the early dynamics of this process. However, we can extrapolate from the experiments most of the parameters necessary to formulate a simple model of formation and growth of these biofilm structures. Moreover, some questions remain to be addressed, such as, how does the radius of curvature of the turns influence the streamer occurrence, and how does the growing filament cross the streamlines to reach the opposite corner? Therefore, our goal in this study was to elucidate the mechanisms that underlie the formation of biofilm streamers, using specifically designed experiments and numerical simulations.

Materials and Methods

Microfluidic experiments

We prepared microfluidic channels made from polydimethylsiloxane (PDMS, Sylgard 184; Dow Corning, Midland, MI) using conventional soft-lithography techniques (29). After replica molding of a photoresist master (SU-8; Microchem, Newton, MA) was completed, each PDMS channel was sealed against a thin microscope slide by 1 min exposure in a plasma chamber (Harrick Scientific, Pleasantville, NY).

This technique offers several advantages for the study of biofilms. First, the microfluidic framework allowed us to work for long periods of time under well-controlled conditions of flow of nutrients and bacteria. Second, because all of the devices were single-use and disposable, we were able to avoid contamination between successive tests. Last but not least, we could easily prepare channels with various patterns and dimensions. In addition to the channels shown above (Fig. 1 b) (13), we designed curved sections with different radii of curvature (Fig. 2) ranging from 30° to 150° (or, equivalently, from 210° to 330° if we consider the angle spanned by the flow, defined as α_fl). Each curved section had three consecutive full turns and two half turns at the beginning and end of the section, and presented a sharp inner and a round outer curve. All of these sections were repeated two times along the whole length of the channel and were connected by ∼6-mm-long straight sections. It is therefore reasonable to consider the sections as being independent of each other.

Figure 2.

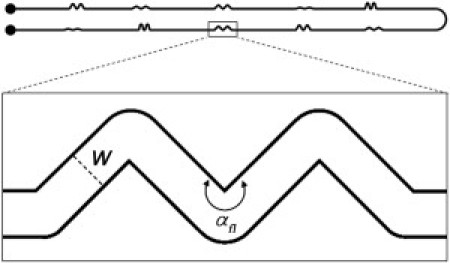
Experimental design used to investigate the influence of the secondary vortical motion associated with different curvatures of the channel on the process of biofilm streamer formation. The overall length of the microfluidic channel is ∼88.5 mm, including 10 curved sections (such as the one highlighted in the box) of different internal angles spanned by the fluid, i.e., ${\alpha }_{fl}=210°,240°,270°,300°,330°$. The channel has a typical width (W) and height (H) of 200 μm and 85 μm, respectively.

In all of the experiments we used the same protocol: colonies of P. aeruginosa (strain PA14) were grown overnight on Luria-Bertani agar plates, inoculated in tryptone broth medium, and incubated for 3 h on a rotary shaker (220 rpm) at 37°C. We measured the bacterial concentration of the solution for every experiment as the optical density at 600 nm (OD₆₀₀) using a spectrophotometer. We then adjusted the initial solution (usually in the range of OD₆₀₀ = 0.4–0.6) to the desired concentration (generally OD₆₀₀ = 0.1, equivalent to ∼10⁸ cfu ml⁻¹) by diluting it with pure tryptone broth, and injected it into the channel by means of a syringe pump (Harvard Apparatus, Holliston, MA). Typical flow rates were equal to 0.5–1.5 μl min⁻¹, which corresponds to a range of average velocities of ∼0.5–1.5 mm s⁻¹. We measured the optical density of the solution left in the syringe after each experiment, and typically observed an increase of at most 30% in the bacterial concentration after 18 h. The bacteria used in the experiments constitutively expressed the green fluorescent protein, which allowed us to track them in space and time using a confocal microscope (Leica TCS IRB). Vertical 1 μm scans of the entire height of the channel were performed every 15 min in all of the curved sections for a total acquisition time of ∼18 h.

Numerical simulations

We performed finite-element numerical simulations (COMSOL, Burlington, MA) of the flow in the channel shown in Fig. 2 with the same geometrical and physical parameters used in the experiments. The simulations employed the incompressible form of the Navier-Stokes and continuity equations. Pressure boundary conditions were imposed at the inlet and outlet of the channel, and no-slip conditions were imposed at the four bounding surfaces. The numerical solutions were validated via successive grid refinements (a typical mesh had at least 300,000 elements).

Although we were looking for solutions for an incompressible laminar flow problem, we had to consider a 3D geometry in the numerical simulations to capture flow features that would help us explain the appearance of streamers in the middle of the channel. We recently demonstrated (30), as previously suggested by Balsa (31), that even under conditions of very low Reynolds number (which is always less than unity in our experimental conditions), the flow field around a corner shows 3D features. More specifically, the change in the curvature of the side wall generates a secondary flow, identified by a nonzero velocity component in the plane transverse to the flow direction. This secondary vortical flow is then characterized by the presence of a pair of counterrotating vortices localized right before and after the corner. This motion is directed from the top and bottom planes toward the middle horizontal plane of the channel right after a turn, whereas the flow is reversed in the upstream part of the corner (as depicted in Fig. 1 c).

Because the strength of the secondary flow is related to the change in the curvature of the channel, we investigated the influence of the bending angle on the vortical features around a corner. Fig. 3, a–c, display contour plots of the component of the flow velocity, u_z, perpendicular to the plane of the channel (plane $x-y$) in a plane at a quarter of the channel thickness from the bottom surface. The numerical results clearly show that the tighter the bend of the channel, the larger is the secondary flow near the corner. In particular, u_z (normalized with respect to the average velocity in the channel, U), though small compared with the primary flow, is proportional to the angle of curvature of the corner (Fig. 3 d).

Figure 3.

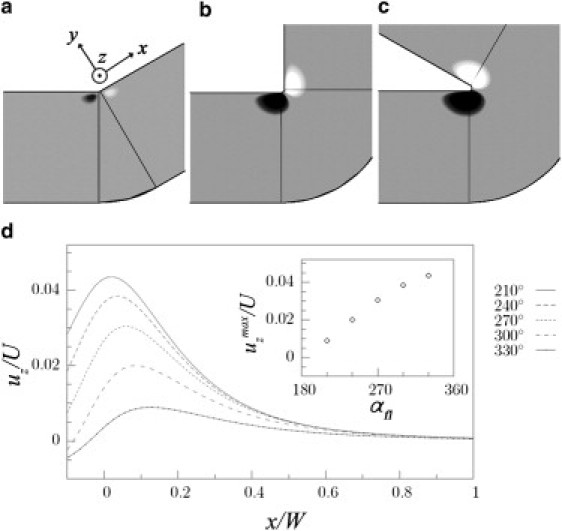
Contour plots from numerical simulations of the velocity component u_z in a plane at 1/4 of the channel height from the bottom surface, for the angles ${\alpha }_{fl}=210°\left(a\right);270°\left(b\right);330°\left(c\right)$. White and dark gray contours indicate positive and negative values of u_z, respectively, and gray contours represent vanishing values of u_z. (d) Distribution of u_z (normalized with respect to the mean speed in the channel, U) along the x axis (normalized with respect to W) for different curvatures of the corner. The distances $\overline{y}$ and $\overline{z}$ from the side wall and the bottom of the channel, respectively, were chosen such that $u_z/U$ has the maximum value (shown in the inset as a function of α_fl). The direction of the flow is from left to right.

Results

Biofilm streamer formation around corners with different angles

We performed experiments in which solutions of P. aeruginosa were injected into the channels for several hours. Confocal images taken after ∼18 h of flow showed the presence of thread-like biofilm streamers in the middle horizontal plane of the channel and only where there were curved sections (Fig. 4). Of most significance, the sharper the angle of the corner, the longer and thicker were the streamers observed. Consistent with our previous observations (13), although the bacterial cells progressively and uniformly covered the inner walls, such as the bottom surface of the channel (Fig. 4, left panel), the streamers developed only and precisely in the middle horizontal plane (Fig. 4, right panel).

Figure 4.

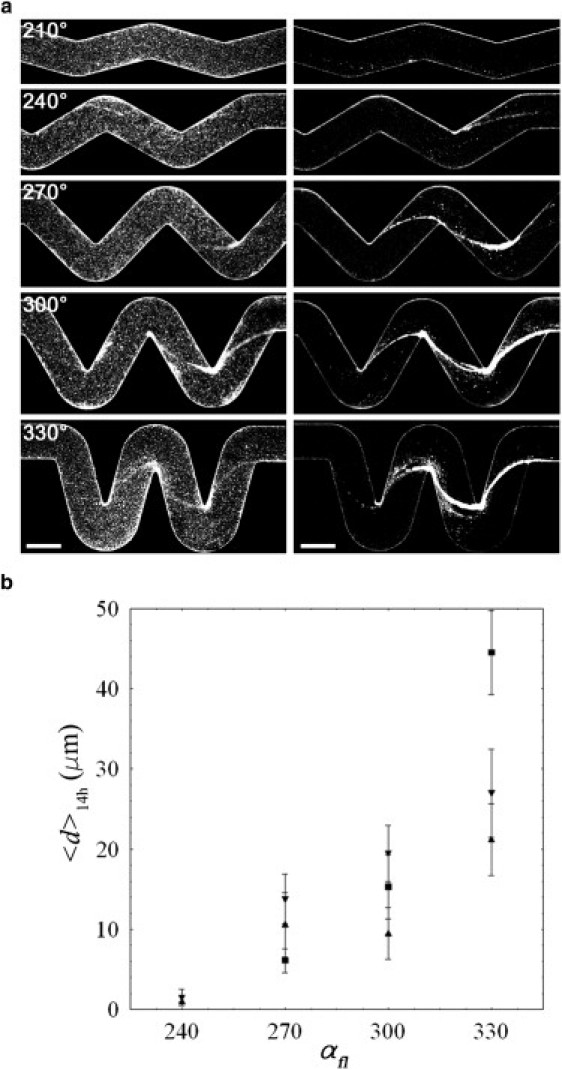
(a) Biofilm streamers that developed after 18 h of continuous flow, from left to right, at 0.5 μl min⁻¹ (OD₆₀₀$=0.25$). The confocal image sequences on the left and right sides were obtained from the bottom and mid-horizontal planes of the channel, respectively, for all of the curved sections shown in Fig. 2. Scale bars: 200 μm. (b) Average diameter of the streamers after ∼14 h of continuous flow versus α_fl for different flow rates, i.e., 0.5 μl min⁻¹$\left(\mathrm{▾}\right)$, 1 μl min⁻¹$\left(\mathrm{■}\right)$, and 1.5 μl min⁻¹$\left(\mathrm{▴}\right)$.

As shown by these confocal images, the tightness of the curves, or rate of change in the boundary shape, clearly influences the formation of these filamentous biofilm structures. Indeed, in the case of turns with the lowest angle (${\alpha }_{fl}={210}^{\circ }$), streamers were never observed to develop during the whole duration of the experiments, whereas at slightly sharper corners (${\alpha }_{fl}={240}^{\circ }$) very thin filaments were occasionally found (such as the one shown in the second image of the right-hand sequence of Fig. 4 a). Instead, for ${\alpha }_{fl}\ge {270}^{\circ }$, clearly visible streamers, which repeatedly formed at half the channel height, were suspended in the flow and connected only to the side walls of the channel in the proximity of the corners. Moreover, the thread-like biofilms grew directly from the downstream part of the turn (in Fig. 4 a the flow is from left to right), i.e., where the secondary vortical motion is directed from the bottom or top of the channel toward the middle plane. In addition, in qualitative agreement with the numerical simulations, we found that the streamers developed almost exclusively starting from the second turn (or the first full turn) of the section. This result follows since the first upstream half turn presents a lower curvature than the three subsequent half turns, and thus the secondary vortical motion right after this corner is much weaker. Therefore, a turn with an angle > 30° of deviation from the rectilinear path (which corresponds to a secondary velocity of >1% of the average velocity in the channel) seems to be a lower limit for the formation of the streamers, at least over the time course of our experiments. Finally, we also quantified the dependence of the formation of the streamers on the secondary flow in terms of the average diameter (denoted as $\langle d\rangle$) of the filaments after ∼14 h of flow (Fig. 4 b). We obtained the average diameter by measuring the area covered by the streamers (where the confocal scan shows the highest fluorescence intensity), divided by their length.

Onset time and temporal evolution

A further step is to consider the influence of the vortical flow at the corner on the timing of the initial appearance of the streamers and the subsequent temporal evolution. As shown by confocal images taken at different times (i.e., after 5, 10, and 15 h from the beginning of the experiment; Fig. 5 a), the sharper the angle of the turns, the faster is the formation of the streamers. For a more quantitative analysis, we defined the onset time, t₀, as the temporal occurrence of the first visible thread-like biofilm structure. We note that this time always corresponds to the appearance of a very thin filament of extracellular matrix that is detectable by the presence of a few bacteria attached to it, and is already crossing the channel to connect two consecutive corners (as shown, for instance, by the first image in the sequence of ${\alpha }_{fl}=330°$ in Fig. 5 a). A plot of the onset time as a function of the angle of curvature α_fl for three different flow rates (0.5, 1, and 1.5 μl min⁻¹), holding all the other experimental parameters constant (OD₆₀₀$=0.1$), is shown in Fig. 5 b. It is clear that t₀ is inversely proportional to the bending angle of the channel boundary for all the flow rates considered. In our numerical characterization of the flow in these geometries, we showed that the strength of the secondary vortical motion is proportional to α_fl (inset of Fig. 3 d). Thus, the same data, when multiplied by the maximum value of the secondary velocity u_z (normalized by the average flow speed U) obtained from the simulations, seem to collapse within a constant range (Fig. 5 b, inset).

Figure 5.

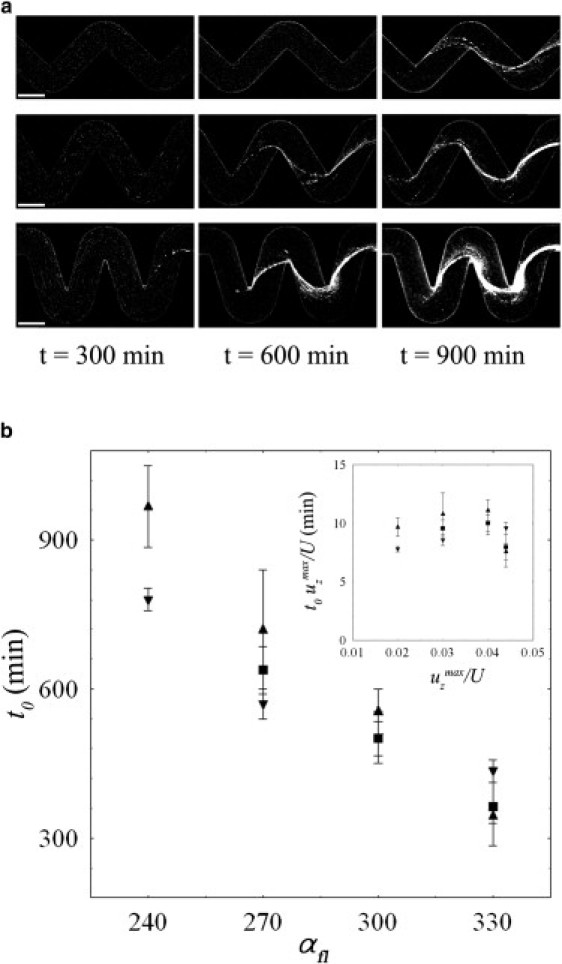
(a) Time-lapse confocal images of the formation of streamers for three bending angles: ${\alpha }_{fl}=270°,300°,330°$(from top to bottom). Each image was acquired in the middle horizontal plane of the channel at a flow rate of 1 μl min⁻¹. The initial concentration of bacteria was equal to OD₆₀₀$=0.1$. Scale bars: 200 μm. (b) Onset time (t₀) for the formation of streamers as a function of α_fl. The data shown represent different sets of experiments performed at flow rates of 0.5 μl min⁻¹ (▾), 1 μl min⁻¹ (■), and 1.5 μl min⁻¹ (▴), with the same initial concentration of bacteria in solution (OD₆₀₀$=0.1$). The inset shows the same data plotted as $t_0{u}_z^{max}/U$ versus the normalized maximum velocity perpendicular to the main flow direction, $u_z^{max}/U$, where $u_z^{max}$ is the velocity component obtained with the numerical simulations.

One should be careful in comparing different flow rates. A higher average flow speed means a higher secondary flow at the corner and a greater hydrodynamic force exerted on the forming filaments. On the other hand, shear stress can drastically affect the bacterial attachment and detachment kinetics on the boundaries of the channel (32,33). In the case of P. aeruginosa, for instance, it has been shown that the rate of accumulation of cells on a glass surface decreases as the shear increases (34), despite a higher rate of transfer from the bulk to the walls (as we observed in our experiments); thus, a higher flow speed would likely yield a slower-growing biofilm on the boundaries and consequently a lower rate of extracellular matrix production. Therefore, because of these two competing effects, the link between the time required for the streamers to build up and the average flow velocity in the channel is far from being a simple, direct relationship. Instead, by changing the geometry of the channel, we were able to keep all of these factors (on average) constant, and to unambiguously show the dependence of the streamer formation on the strength of the secondary flow.

As noted above, when the streamers are first recognizable in the experiments, they are already connecting the corners at opposite sides of the channel. From this time on, we quantified the growth rate of the filaments by measuring the mean diameter $\langle d\rangle$ with time. The temporal evolution of $\langle d\rangle$, relative to the three image sequences of Fig. 5 a, is shown by the log-linear plot of Fig. 6 a, given a flow rate of 1 μl min⁻¹ and 0.5 μl min⁻¹ (inset). Although the angle of curvature of the turns clearly influences the onset time of streamer formation, the growth rate seems to be roughly independent of the strength of the secondary flow around the corner. This observation may be consistent with the hypothesis that once the streamers are formed, they develop mainly as a result of advective transport by the mainstream flow, which is the same for all the three curves in Fig. 6 a. Moreover, because filaments with a larger section have a higher probability of catching bacteria and dispersed polymeric substances in the flow, the growth rate of the streamer, per unit length, would reasonably be proportional to its average diameter, which can be written as $\partial \langle d\rangle /\partial t\propto \langle d\rangle$, leading to $\langle d\rangle \propto \exp \left[const\cdot \left(t-t_0\right)\right]$. This exponential trend is approximately shown by the log-linear plot of Fig. 6 a. However, this is a highly simplified model, and other contributions, such as cell division (although, under our experimental conditions, the replication time is very slow) and spatial variations of the flow, might be taken into account. Moreover, given the heterogeneity and variability in the formation of the biofilm (e.g., in the morphology of the streamers), any attempt to extrapolate additional information or correlate the growth rate with the flow speed would be speculative at this time.

Figure 6.

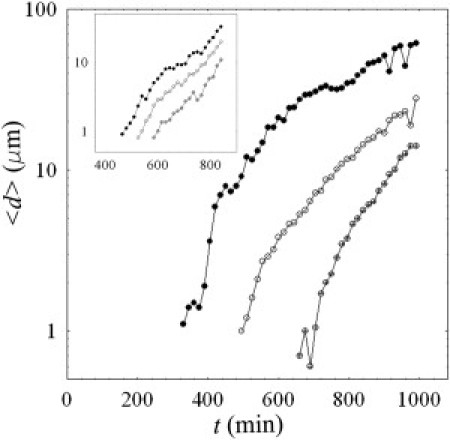
Log-linear plots of the average streamer diameter $\langle d\rangle$ as a function of time for different bending angles: ${\alpha }_{fl}=330°(●)$, $300°(○)$, and $270°(\oplus )$. The flow rates were equal to 1 μl min⁻¹ and 0.5 μl min⁻¹ (inset), given the same bacterial concentration (OD₆₀₀$=0.1$).

Mechanics of a flexible filament in a viscous flow

It is known that biofilms essentially behave as viscoelastic materials, with relaxation times on the order of seconds or minutes (35,36). However, a wide range of values for the material properties of intact biofilms are reported in the literature. Moreover, the properties obtained for a specific system will most likely not be accurate for a different strain or growth conditions. A further advantage of our experimental system is that it enables one to directly test the viscoelastic properties of the streamers by measuring the response under different flow rates, as previously proposed for surface-attached biofilm streamers (25,37). By using confocal microscopy, we were able to precisely identify the position and 3D morphology of the filaments. We then determined the elastic modulus by measuring the sudden variation in the length of the filaments while applying small increments in the flow rate (as shown in Fig. 7 a), and estimated the effective viscosity by considering the temporal variation of the strain at much longer timescales for a given applied stress (Fig. 7 b).

Figure 7.

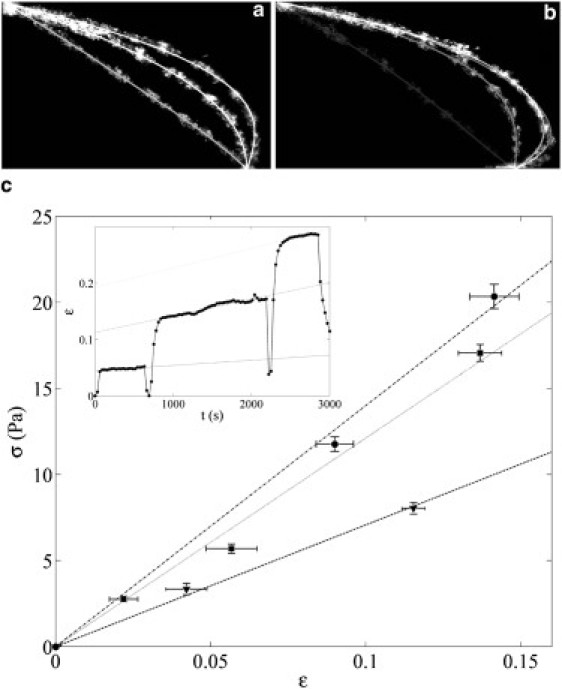
Viscoelastic properties of the streamers. Solid lines represent 4th-order polynomial interpolations of the shape of the filaments. (a) Image superimposition of a streamer at different flow rates (without flow, 0.25 μl min⁻¹, and 0.5 μl min⁻¹). (b) Image superimposition of the streamer without flow and with flow rate at 1 μl min⁻¹ after 30, 150, and 300 s, respectively, from the condition at rest. (c) Main graph: Stress-strain relationship for different streamers, with average diameters of ∼9.7 μm $\left(\mathrm{▾}\right)$, 21.3 μm $\left(\mathrm{■}\right)$, and 5.4 μm $(●)$. The filaments were all located in the middle horizontal plane of the channel while two consecutive corners were connected. Horizontal and vertical error bars represent variation in the strain and stress for the same flow rate over different tests. The effective elastic modulus, obtained from a linear fit of the data (dashed lines), varies in a range between 70 and 140 Pa. Inset: Streamer deformation as a function of time at viscous stresses of 5.7, 17, and 41 Pa applied for ∼600, 1500, and 600 s, respectively (interspersed with 30 s without flow). Dashed lines represent linear fits of the data during the flow conditions.

Specifically, in this study the streamers were left at rest for a few hours, and filaments with different thicknesses and lengths were tested. For flexible filaments like these streamers, the resistance to bending can be neglected in comparison with the resistance to stretching (38), and therefore the viscous force exerted by the flow in the channel will essentially cause an extension of the length of the streamers. The axial applied stress can be calculated from the friction coefficient on a long slender body (39) as $\sigma \approx 8\mu /d^2\ln \left(2L/d\right){\int }_0^L\left(2\cos \left(\theta \right)+\sin \left(\theta \right)\right)u\left(s\right)ds,$ where L is the length of the streamer, θ is the angle formed between the streamer and the direction of the flow (the factor of 2 in the equation is a consequence of the drag anisotropy for a slender object in a viscous flow), s is the curvilinear coordinate along the filament, and $u\left(s\right)$ is the velocity field. In the expression of $u\left(s\right)$, we considered the analytical velocity profile for a pressure-driven flow in a rectangular channel in the middle horizontal plane, averaged in the vertical direction over the diameter of the streamer. This way, we estimated values of the apparent or effective elastic modulus for the streamers (Fig. 7 c, main graph) in the range of 70–140 Pa, which is on the same order as previous results for P. aeruginosa biofilm streamers (40,41). In addition, we were able to perform the equivalent of a creep test, in which the flow was progressively increased, and to measure the variation of the strain as a function of time (Fig. 7 c, inset). From the slope of a linear fit of the rate of deformation for a constant applied stress, we estimated an effective extensional viscosity for the streamers on the order of $5\cdot {10}^5$ Pa s.

The final aspect we want to discuss here is the steady-state shape of the streamer while it grows until two consecutive corners are connected. With the value of elasticity obtained from the mechanical tests on the streamers, we considered the problem of an elastic filament in a fluid flow characterized by curved streamlines. We assumed that the streamer was fixed at one end (the nucleation site in the downstream part of the corner) and free at the other end. We computed the flow field by finite-element numerical simulations and determined the filament shape by solving an evolution equation that expresses the balance between viscous forces and filament forces (i.e., bending and tensile forces). Thus, the filament behavior was characterized by an effective compliance, which compares viscous forces with elastic forces (N. Autrusson, L. Guglielmini, S. Lecuyer, R. Rusconi, and H. A. Stone, unpublished). We assumed that the length of the filament was much larger than its radius, and that gravity and Brownian forces, as well as inertial effects, were negligible with respect to elastic and viscous forces. Because the timescale over which the filament elongates, which is set by the extensional viscosity, is much longer than the timescale that characterizes the dynamics of the filament, we treated the latter as inextensible. Thus, using the same values for flow speed, streamer elasticity, and thickness employed in the experiment, we were able to evaluate the position assumed by the filament with respect to the channel geometry for different increasing lengths of the streamer in a channel characterized by 300° turns (Fig. 8).

Figure 8.

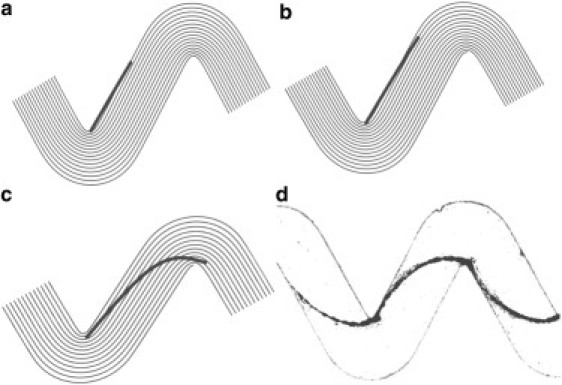
(a–c) Numerical results for a flexible filament in a viscous 2D flow around a corner. Steady-state positions for different lengths of the filament are shown. The values of elasticity, thickness of the filament, and Reynolds number used in the numerical model were 100 Pa, 1 μm, and 0.001, respectively. (d) Experimental biofilm streamer after 18 h of continuous flow at 0.5 μl min⁻¹.

In the straight portion of the channel, the flow is mainly rectilinear, and therefore as long as the filament length is smaller than the distance between corners, the filament will align with the streamlines and remain in proximity to the sidewall (as shown in Fig. 8, a and b). When the filament grows further, it reaches a region where streamlines are curved and tends to bend toward the corner, thus crossing flow streamlines (the filament tension decreases and bending energy is stored in the streamer). When the elastic filament is connected to the second corner, its computed final shape is then in good agreement with the shape of the streamer observed in the experiments (Fig. 8, c and d).

Conclusions

Understanding how fluid flow affects biological processes such as the formation and development of biofilms is of primary importance for many fields, either when these slimy microbial communities can be beneficial or detrimental to a given system. Despite the complexity and sophistication of biofilms, some distinguishing features in the dynamics or morphology of these multicellular organisms can be described in terms of purely physical phenomena. In the work presented here, we were able to trigger the formation of thread-like biofilm structures simply by changing the angle of curvature in channels with a zigzag pattern, which exclusively affected the characteristics of the flow field (i.e., the magnitude of the secondary flow around the corners). Because nonstraight conduits are very common in both natural environments and industrial systems, one can expect such structures to be widespread. Our findings may also be relevant for studies of permeability and fluid transport in porous media.