Abstract
High neighborhood density reduces the speed and accuracy of spoken word recognition. The two studies reported here investigated whether Clustering Coefficient (CC) — a graph theoretic variable measuring the degree to which a word’s neighbors are neighbors of one another, has similar effects on spoken word recognition. In Experiment 1, we found that high CC words were identified less accurately when spectrally degraded than low CC words. In Experiment 2, using a word repetition procedure, we observed longer response latencies for high CC words compared to low CC words. Taken together, the results of both studies indicate that higher CC leads to slower and less accurate spoken word recognition. The results are discussed in terms of activation-plus-competition models of spoken word recognition.
Keywords: clustering coefficient, complex networks, mental lexicon, and graph theory
A number of recent studies have modeled complex systems as a network or graph (see Albert & Barabási, 2002, for a review). In a graph, entities are represented as nodes and relations of interest between nodes are represented as links or edges between the nodes. For example, in a model of scientific collaboration, individual scientists may be represented as nodes. If two of those scientists have published together, then a link is placed between the two nodes representing those individual scientists (see Watts, 2003). Among other findings, knowing the structure of a graph may provide information on how that graph evolved over time (Albert & Barabási, 2002; Barabási & Albert, 1999). Understanding the properties of the network of scientific collaboration might provide new insights into the underlying processes that determine who collaborates with whom.
Several recent papers have used graph theory to address questions about how various forms of linguistic knowledge are represented in the mind (Dorogovtsev & Mendes, 2001; Ferrer i Cancho & Solé, 2001; Motter, de Moura, Lai, & Dasgupta, 2002; Soares, Corso, & Lucena, 2005; Steyvers & Tenenbaum, 2005; Vitevitch, 2008). Motter et al. (2002), for example, built a network of words, linking any two words that expressed similar concepts. Extending this approach, Steyvers and Tenenbaum (2005) modeled semantic memory — people’s mental representation of word meaning — as a graph. They constructed three separate graphs from three different sources of data. In each graph, words were represented as nodes. In the graph based on the word association norms originally collected by Nelson, McEvoy, and Schreiber (1999), two words were linked if one word was produced as an associate of the other in a free association task. A second graph was based on a version of Roget’s Thesaurus (Roget, 1911) which consisted of a large number of words classified into a smaller number of semantic categories. Each word and category was represented as a node and a link was placed between a word node and a category node if the word was a member of that category. Their third network was based on Word-Net (Fellbaum, 1998; Miller, 1995), a corpus of words and word meanings. Each word and word meaning was represented by a node. A word node was linked to a word-meaning if the word has that meaning. Word nodes were connected to one another if two words share a relation, such as antonymy (e.g., the words “black” and “white”) or hypernymy (e.g., “maple” and “tree”). Steyvers and Tenenbaum found that all three of these networks had properties that were similar to other complex networks, including the “small world” property described by Albert and Barabási (2002). The authors explained those properties with several hypotheses about the developmental processes children go through when learning word meanings.
Ferrer i Cancho and Solé (2001) modeled the English language by representing each word as a node and linking two nodes if the two words co-occurred with a frequency greater than chance (see also Dorogovtsev & Mendes, 2001). They appealed to the evolution of the language to explain the properties of the resulting graph. Finally, Vitevitch (2008) used graph theory to model the mental lexicon for spoken word recognition. Words were again represented as nodes and a link was placed between two nodes if one word could be transformed into the other by the deletion, addition, or substitution of a single phoneme (see Greenberg & Jenkins, 1964; Landauer & Streeter, 1973; Luce & Pisoni, 1998). This rule is referred to here as the DAS rule for Deletion, Addition, or Substitution. Like the other authors cited above, Vitevitch explained his results in terms of several hypotheses about processes involved in language acquisition and language evolution (see also Gruenenfelder & Pisoni, 2009; Vitevitch, 2008).
Following the work of Barabási and his colleagues (Albert & Barabási, 2002; Barabási & Albert, 1999), the focus of all of the studies described above was on how language acquisition and/or language evolution processes could account for the observed structure of the graph. An equally valid question concerns whether the observed structure and graph theoretic variables have any behavioral consequences for the human listeners when asked to perceive and process spoken words. Can a graph theoretic model of semantic memory, for example, make predictions about what word meanings will be particularly easy or hard to comprehend in a sentence? Is a graph theoretic model of the mental lexicon for spoken word recognition able to predict the relative ease and difficulty of recognizing different words? Although some authors (Motter et al., 2002; Vitevitch, 2008) have speculated on possible behavioral consequences of their observed network structures, very little empirical work investigating the relation between formal graph theoretic properties and behavioral data has been reported to date in the literature (although see Steyvers & Tenenbaum, 2005 for discussion on semantic networks).
The two experiments reported here explored the effects of a spoken word’s Clustering Coefficient (CC) on the ease with which a word is identified in spoken word recognition tasks. In a graph, nodes joined by a link are typically referred to as neighbors. A node’s CC is a measure of the probability that two of its neighbors are themselves neighbors of each other. Specifically, a node’s CC is the ratio , where n denotes the number of neighbors formed by (i.e., links between) that node’s neighbors, and p is the number of possible neighbor pairs that could exist among the node’s neighbors. Consider a node with 5 neighbors. The number of possible neighbor pairs is 5-choose-2 or 10. Suppose that those 5 neighbors in fact form 3 neighbor pairs. Then, the node’s CC is 3/10 = .30. CC represents a probability and ranges from 0 to 1.
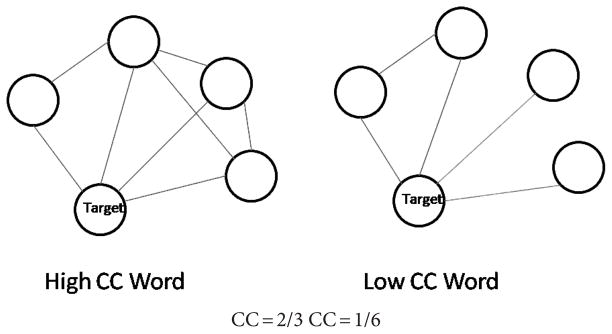
Following Vitevitch (2008), we created a network modeling the mental lexicon for spoken word recognition by using the DAS rule — two words were linked if one could be transformed into the other by a single phoneme deletion, addition, or substitution. Under the DAS rule, some of the neighbors of the word /sɪt/ are /lɪt/, /ɪt/, /rɪt/, and /sɪn/. Note that /lɪt/ and /ɪt/, /lɪt/ and /rɪt/, and /ɪt/ and /fɪt/ are all themselves neighbor pairs because they differ by one phoneme, and therefore add to the CC of the word /sɪt/. On the other hand, none of the following pairs: /lɪt/ and /sɪn/, /ɪt/ and /sɪn/, and /fɪt/ and /sɪn/ are neighbor pairs. The fact that these neighbors of /sɪt/ are not neighbors of each other subtracts from the CC of /sɪt/ (In this example, /sɪt/ has four neighbors. Hence, the number of possible neighbor pairs is 6. The number of actual neighbor pairs is 3. There the CC of /sɪt/ in the example is 3/6 = .50). Figure 1 below shows a graphical representation of high versus low CC words. Each target word in the figure has four neighbors, but the degree of clustering between the word’s neighbors differs.
Figure 1.
The target word on the left has a high CC while the target word on the right has a low CC. Each target word has four neighbors and therefore has the same neighborhood density.
Our interest in the behavioral consequences of the CC was motivated by three findings in the literature on spoken word recognition. First, in a post-hoc analysis of word repetition latencies collected in an earlier study by Luce and Pisoni (1998), Gruenenfelder and Pisoni (2005) found some evidence that words with a higher CC were repeated more slowly than words with a lower CC. Their findings led us to hypothesize that in general, words with a higher CC would be recognized more slowly and less accurately than words with a lower CC. Second, one of the motivations for applying graph theory to the study of complex systems is that some graph theoretic properties measure non-local or global properties of a node (of a word, in the case of the present study) than more traditional measures do. The CC is one such measure. The CC is a measure that can be made on a single node, although it takes into account characteristics of the graph that are not strictly local to just that node. The CC looks at how tightly inter-connected a word’s neighbors are in the entire graph structure rather than simply the number of neighbors a word has as a measure such as neighborhood density does (see Luce & Pisoni, 1998). Thus, the CC not only looks at the size of a word’s neighborhood but also the connectivity of the neighborhood of a word as a whole. Our hope was that our understanding of the process of spoken word recognition and the structure of the mental lexicon could be advanced by examining the effects of such non-local global variables on spoken word recognition processes. Third, as discussed in more detail below, variables similar to the CC have already been shown to have effects in visual word recognition tasks and we felt it would be worthwhile to determine if these indices had similar effects in spoken word recognition tasks.
The experiments reported below examined the effects of the CC on spoken word recognition in two different experimental tasks. We created a set of stimuli that controlled for neighborhood density, word frequency, neighborhood frequency (i.e., frequency weighted neighborhood density; Luce & Pisoni, 1998), phonotactic probability, word length, word familiarity, and syllable structure (CVC) while at the same time manipulating CC. As used here, a word’s neighborhood density, or more simply, just density, is the number of neighbors that word has according to the DAS rule. Experiment 1 examined the effects of the CC on listener’s accuracy in identifying spoken words under degraded listening conditions. Experiment 2 investigated the effects of the CC on response latency in a word repetition task.1
Experiment 1
Experiment 1 used a word identification task in which the stimuli were degraded by processing them with a noise-excited vocoder routinely used to simulate speech signals generated by a cochlear implant (CI) (see Shannon, Fan-Gang, Kamath, Wygonsky, & Ekelid, 1995). CIs are surgically implanted electronic devices that act as prosthetic aids for individuals with profound hearing loss. Interest in hearing impaired populations with CIs has increased in recent years affording researchers with an opportunity to study the effects of auditory deprivation on cognitive mechanisms underlying spoken word recognition (see Bergeson & Pisoni, 2004; and Pisoni, Cleary, Geers, & Tobey, 2000 for further discussion of this topic).
Our first experiment examined how CC affects word identification accuracy scores across two levels of spectral degradation using a cochlear implant simulator. Vocoded speech consists of speech filtered into a specific number of frequency bands or channels (Shannon et al., 1995). The amplitude envelope for each band is extracted with a low pass filter. Frequency information is then replaced in each band with white noise modulated by that amplitude. The intelligibility of the speech can be increased or decreased by varying the number of frequency channels (see Shannon et al., 1995). Two levels of stimulus degradation (10 and 12 channels) were chosen for this experiment based on Shannon et al.’s previous work investigating spoken word recognition under degraded conditions. These two levels were also selected in part because they elicit moderate to high levels of accuracy in spoken word recognition (70–80 % correct).
Method
Participants
The participants in Experiment 1 were 40 native speakers of American English who reported no prior history of speech or hearing disorders at the time of testing. Twenty participants were recruited for each of the two between-subject conditions from the undergraduate psychology pool at Indiana University in Bloomington. Listeners either received course credit or were paid seven dollars for their participation.
Design
A 2 × 2 design was used in Experiment 1. The between subject variable was the level of speech degradation (either 10 channels — high degradation — or 12 channels — low degradation).
The within subject variable was CC. The dependent variable was the percentage of words correctly identified.
Stimulus materials
The critical experimental stimuli consisted of 94 familiar (familiarity rating ≥ 6.25 for both high and low CC words; t(92) = .25, p = .80) mono-syllabic CVC words (three phonemes each: Consonant-Vowel-Consonant). Word familiarity measurements consisted of subjective measures obtained from a group of subjects using an ordinal scale, 1 through 7, with 7 being highly familiar and 1 being unfamiliar (see Nusbaum, Pisoni, & Davis, 1984). The 94 lexical stimuli were drawn from a larger set of 160 words (originally created for another study). The stimuli were divided into 47 low CC words and 47 high CC words based on a median split of CC for all words in the Hoosier Mental Lexicon, a corpus of approximately 20,000 American English words (Nusbaum et al., 1984). The average CC for high CC stimuli was .426, while the average CC for low stimuli was .257.
Each low CC word was matched with a high CC word that had approximately the same log frequency (Kucera & Francis, 1967). The mean log frequency was 2.21 for the low CC words, and was 2.17 for the high CC words, t(92) = .32, p = .75 (all t-tests are two-tailed). In addition, each low CC word’s corresponding high CC word had a neighborhood density within two of the low CC word’s density. For each case where the high CC word had a higher density than its low CC partner, there was another case where the high CC word had the lower density (In 41 of the 47 combinations, the low and high CC words had the same density). The average neighborhood density measure for low CC words was 19.55, and for high CC words it was 19.62, t(92) = −.05, p = .96. High and Low CC words also did not differ from one another in terms of frequency weighted neighborhood density (see Luce & Pisoni, 1998). The mean neighborhood frequency for low CC words was 146, and the mean neighborhood frequency for high CC words was 172, t(92) = .72, p = .47.
Phonotactic probability was also controlled across low and high CC pairs. Phonotactic probability was computed using Vitevitch’s online calculator (see Vitevitch & Luce, 2004). The average phone probability for low CC words was .145, and for high CC words it was .140, t(92) = 1.04, p = .30. The average bi-phone probability for low CC words was .0050, and for high CC words it was .0059, t(92) = .58, p = .56. The low and high CC words are shown in Appendix A.
Appendix A.
| Low CC Words | High CC Words | ||
|---|---|---|---|
| beach | noose | bail | pool |
| bead | peck | bath | rear |
| boom | pit | beige | shag |
| burn | pup | chain | shear |
| calm | purse | chat | sheep |
| chef | rood | chill | shin |
| cool | rough | dies | shine |
| coop | rush | dive | ship |
| cup | sang | dud | shore |
| dawn | shove | fad | shun |
| dog | shut | foul | siege |
| fed | sing | gag | thief |
| gas | sod | gap | third |
| hide | soup | gear | toad |
| hop | sour | gin | tongue |
| hurl | suck | goal | tour |
| known | sung | got | vain |
| lake | tape | hear | veal |
| lead | tough | hen | vile |
| learn | wash | jail | wage |
| loss | weed | knock | watt |
| mass | wig | league | wire |
| mike | witch | mug | youth |
| mood | nap | ||
Each of the stimulus tokens were recorded by a male talker (who was naïve to the purpose of the experiment) in a sound attenuated booth using a high-quality microphone. A randomized list of the stimulus words was presented to the talker on a CRT display and the words were recorded one at a time on a PC using the SAP program in the Speech Research Laboratory in Indiana University. The words were then digitized and edited into individual files using the Praat version 4.1.5 waveform editor (http://www.praat.org). The Level-16 v2.0 program was used to normalize the signal level’s amplitude of all the words at 65 dB (Tice & Carrell, 1998). Clustering Coefficient was computed using the Pajek program for Windows (Batagelj & Mrvar, 1998) (http://vlado.fmf.uni-lj.si/pub/networks/pajek/).2
Each listener heard and responded to each of the 94 stimuli. The stimuli in Experiment 1 were degraded using the Tiger Speech Cochlear Implant Simulator developed by Tiger Speech Technology, Inc., Version 1.01.07 (obtained from www.tigerspeech.com/tst_tigercis.html).
Procedure
Experiment 1 used an open-set word identification task. Words were played at a comfortable listening level over Beyer Dynamic DT 100 headphones connected to a Macintosh computer. Subjects were instructed to listen to the words and use the keyboard to type in whatever English word they thought they heard as accurately as possible.
Each trial began with the presentation of a plus sign (+) on the center of the computer screen displayed for 500 milliseconds. After the plus sign disappeared from the screen, a degraded word was played over the headphones. After the word finished playing, a dialogue box was displayed on the screen requesting the listener to type in what they heard. After the listener finished typing their response and hit “Return”, there was a 1,500 ms pause before the next trial began. The stimulus words were played in a different random order to each listener.
Results and Discussion
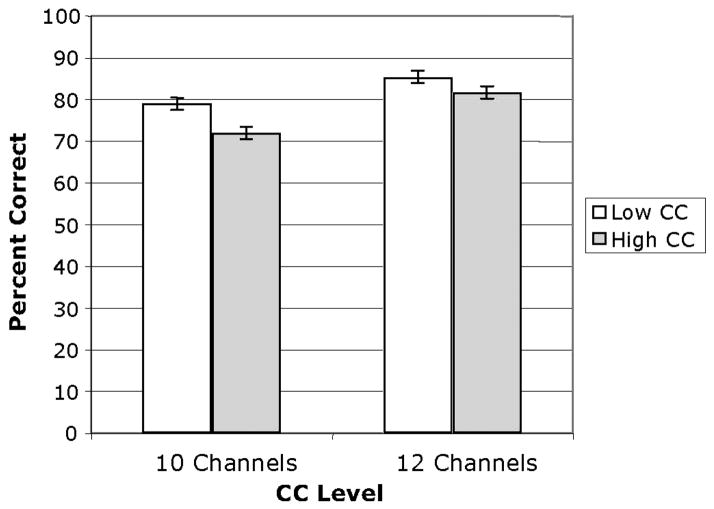
In the data analysis, both the target word and response were automatically transcribed using the phonemic alphabet from the CMU dictionary (Obtained from www.speech.cs.cmu.edu/cgi-bin/cmudict). If the transcription of the target and response matched in the onset, nucleus, and coda positions, the response was scored as correct. If listeners typed in a homonym of a target word, for example, by typing in the word sea instead of see, the response was also scored as correct since the phonetic transcriptions are identical. The overall percentage of words correctly identified as a function of number of channels and CC is shown below in Figure 2.
Figure 2.
Percent correct word identification as a function of CC and number of channels. Error bars represent one standard error of the mean.
For the data analysis, we implemented a generalized linear model (see Baayen, Davidson, & Bates, 2008; and Baayen, Feldman & Schreuder, 2006, for discussion on implementing linear models) with a logistic link function since responses across subjects and items were treated as either correct or incorrect (i.e., the proportion of correct responses was treated as a binomial random variable). The linear modeling approach has the advantage of adding statistical power to data analysis, in particular, because it allows variables such as CC to be treated as continuous rather than dichotomous.
The best fitting model was obtained by maximizing the log-likelihood ratio and including channels (10 vs. 12) and CC as main effects. As the level of degradation decreased by increasing the number of channels from 10 to 12, listeners identified words more accurately. The main effect of channel was statistically significant. Words were recognized correctly 75.5 percent of the time in the 10-channel condition (SD = .22) and 84.0 percent of the time in the 12-channel condition (SD = .182) (likelihood-ratio χ2(1) = 48.32, p < .0001). The main effect for CC was also highly significant as well. The mean percent correct words identified for low CC words was 82.2 percent (SD = .198), and for high CC words was 76.8 percent (SD = .218) (likelihood-ratio χ2(46) = 406.90, p < .0001).
Additionally, ANOVAs were carried out on the accuracy scores and were done separately treating subjects (F1 or t1) and items (F2 or t2) as random effects (Clark, 1973). Some researchers have questioned whether the use of F2 or t2 is well founded particularly when item variability is well controlled as it was in this study (e.g., Raaijmakers, Schrijnemakers, & Gremmen, 1999), although we still included the items in our analysis. In the F2 analysis, items falling 2.5 standard deviations above or below the mean accuracy score in each condition were eliminated. Three words were dropped from the items analysis in the ANOVA (two low CC words and one high CC word) as well as the subject analysis using this criterion.3
The results of Experiment 1 provided support for the hypothesis that a word’s CC affects spoken word recognition. Words with a higher CC were identified less accurately under degraded listening conditions than words with low CC.
Experiment 2
Experiment 2 was designed to obtain converging evidence for the hypothesis that a higher CC leads to poorer spoken word recognition performance than a lower CC. In this experiment we used a speeded word repetition task, a procedure that strongly encourages lexical access. On each trial listeners heard a spoken word under clear listening conditions and were simply required to repeat the word as quickly as possible back into the microphone. The dependent variable of interest was the listener’s reaction times.
Method
Participants
The participants in Experiment 2 were 21 native speakers of American English who reported no prior history of speech or hearing disorders at the time of testing. The participants were recruited for this experiment from the undergraduate psychology pool at Indiana University in Bloomington. Participants received course credit for their participation. None of the participants were used in Experiment 1.
Design
Experiment 2 measured response latencies in a word repetition task to low and high CC words. CC was a within subjects variable.
Stimulus materials
The same set of 47 high CC words and 47 low CC words used in Experiment 1 was used in Experiment 2.4 The words used in this experiment were not degraded and were presented under quiet listening conditions.
Procedure and Apparatus
The entire set of stimulus words were presented in a different random order for each subject in a sound attenuated booth. Words were played at a comfortable listening level over Beyer Dynamic DT 109 headphones connected to a Macintosh computer. Subjects were instructed to listen to the words and simply repeat the word they heard back into the microphone as quickly and as accurately as possible in an audible voice. The microphone in turn was interfaced to a voice key. Subjects were also instructed to listen carefully and not make any adjustments to the microphone that was connected to their headphones.
Each trial began with the presentation of a plus sign for 500 milliseconds in the center of a computer monitor screen. After the plus sign disappeared from the monitor, a word randomly selected from the stimulus set was played over the headphones. After the stimulus word was played, the timer began recording until the voice key was triggered by the listener’s response. There was a 2,000 ms pause before the next trial began. This inter-stimulus interval did not begin until the listener triggered the voice key with his/her response.
Both the spoken stimulus word and the listener’s verbal response were recorded through a mixer to a Tuscam DA-P1 digital audio tape recorder for later analysis.
Results and Discussion
The mean reaction times, standard deviations, and standard errors were computed for each listener. Any reaction time falling 2.5 standard deviations above or below the listener’s mean reaction time, reaction times to incorrect responses, and any reaction time falling below 100 ms were eliminated from the final data analysis (see Winer, 1971). The mean reaction time for low CC words was 452 ms (SD = 75.70; SE = 16.52) while the mean reaction time for high CC words was 472 ms (SD = 74.50; SE = 16.26). The results for mean reaction time across conditions are shown below in Figure 3. Fifteen of the 21 listeners responded more quickly to low CC words than to high CC words, a proportion significantly different from chance according to a binomial test, p = .05. Word repetition accuracy scores were nearly 100 percent. No participant made more than 2 percent errors in either condition.
Figure 3.
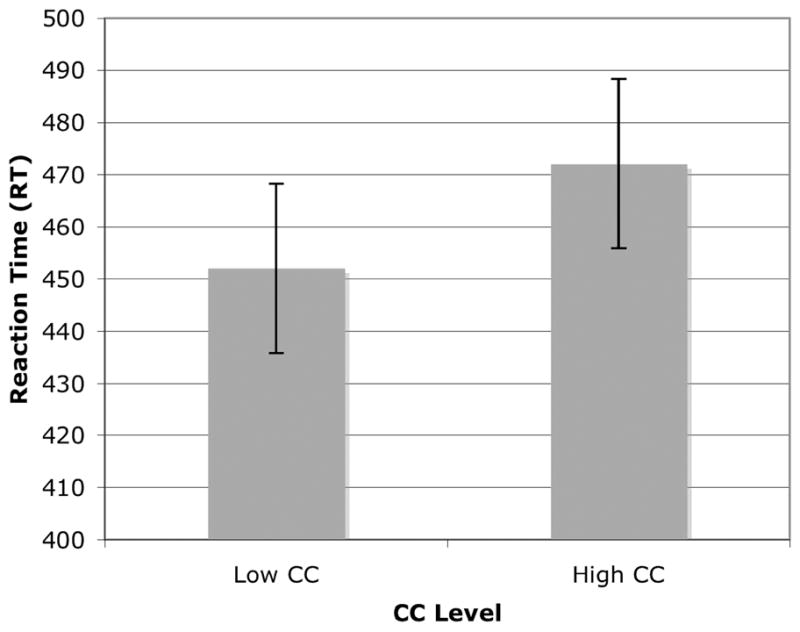
Mean reaction times for the high CC and low CC conditions in Experiment 2. Error bars represent one standard error of the mean.
We applied linear mixed effects models to the data set treating subjects and items as random effects and CC as a fixed effect (see Baayen et al., 2008). Since reaction time data is typically skewed to the right, we applied a logarithmic transformation on the data prior to the analysis. Two tests using linear mixed effects models were applied to the data set: one treating both subjects and items as random effects (since they are randomly sampled from their respective populations) and CC as a fixed effect, and a second reduced model with just subjects as a random effect and CC as a fixed effect. In each analysis, the effect of CC reached statistical significance. For the full model with both random effects F(1, 1632) = 3.77 p = .05 with the log-likelihood ratio = 597 (AIC = −964.70). For the reduced model with only subjects as a random effect, F(83, 1642) = 2.63, p = .0001 with the log-likelihood ratio = 584.50 (AIC = −959). The model selection criteria of the log-likelihood ratio and AIC were close for each model fit. We therefore selected the reduced model without items as the model that best characterized the data.5
Experiment 2 provided additional evidence supporting the hypothesis that CC, or the connectivity between the lexical neighbors of a word, affects spoken word recognition. The results from Experiment 2 showing faster latencies when repeating low CC words than when repeating high CC words are consistent with the results obtained in Experiment 1, where listeners identified low CC words more accurately than high CC words. It is possible that idiosyncratic perceptual strategies could be used in either paradigm to allow for lexical access to be bypassed. Still, evidence for the effects of CC in spoken word recognition was obtained by using two paradigms that encourage lexical access. Taken together, these findings suggest that the CC of a word affects both the speed and accuracy of spoken word recognition during the retrieval of words from the mental lexicon.
General Discussion
Experiment 1 provided evidence that a higher CC leads to poorer performance when recognizing spoken words under degraded listening conditions. Experiment 2 provided additional evidence that a higher CC leads to longer word repetition latencies. Taken together, the results of both experiments are consistent with the hypothesis that a higher CC has a deleterious effect on a listener’s ability to recognize isolated spoken words. The effects of CC demonstrate the importance of the global network structure and lexical connectivity, rather than simply the local structure, in spoken word recognition. What mechanisms might be responsible for producing the observed effects? Is the CC effect found here consistent with current models of spoken word recognition?
Most contemporary models of spoken word recognition are what could be called “activation-plus-competition models” (see Luce & Pisoni, 1998; McClelland & Elman, 1986; Norris, 1994; Norris, McQueen, & Cutler, 2000; although see Norris & McQueen, 2008, for a probability-based model). In such models, words are activated to the degree that their lexical representations are consistent with the acoustic-phonetic input in the speech signal. The activated words then compete with one another until one exceeds some threshold. In neural network models such as TRACE (e.g., McClelland & Elman, 1986) and MERGE/Shortlist (Norris et al., 2000), this competition is typically implemented as lateral inhibition between processing units or nodes. Competition occurs at both the phonological segment level where activated segments inhibit other segments and the lexical level where activated words inhibit other words (see Vitevitch & Luce, 1998).
Why would a higher CC result in more difficult spoken word recognition in the context of an activation-plus-competition model? Conceivably, feedback could drive the effects of CC. In an important contribution to the field of visual word recognition Mathey and Zagar (2000; see also Mathey, Robert, & Zagar, 2004) examined the effects of neighborhood distribution or what they called spread, and discussed the variable in the context of “activation-plus-competition” models. Spread denotes the number of different letter positions (phonological segment positions, in the case of spoken words) where a letter substitution (or phoneme) can result in a new word. For example, suppose that the only two neighbors of the word “sit” were “lit” and “kit”. Then, the spread of “sit” is 1 since both neighbors differ from “sit” in the same letter position. Now suppose that the only two neighbors of “sit” were “lit” and “sin”. Now its spread would be 2 since neighbors can be formed by a letter change at either the first or third letter position. Although it is theoretically possible to construct cases where a low spread is associated with a low CC and a high spread is associated with a high CC, a low spread typically means a high CC and a high spread means a low CC (i.e., spread and CC are negatively correlated).
Consider a 4-letter target word with 4 neighbors and a spread of 1. Since all 4 neighbors differ from one another at the same letter position, they themselves are all neighbors of one another and the CC of the target word is 1. Consider a 4-letter word target word with 4 neighbors and a spread of 4. Each neighbor differs from the target word at a different letter position. Hence, none of the neighbors are themselves neighbors of one another and the target word’s CC is 0. We analyzed our stimuli in terms of spread and found that the average spread for low CC words was 3, and the average spread for high CC was 2.77. While the mean value for the spread variable was numerically very close for both stimulus sets, a t-test revealed that the low CC set had a larger spread value (all words had spread 3) than the high CC stimulus set t(92) = 3.61, p < .001.
Mathey and Zagar (2000) reported slower lexical decision times to words with low spread (high CC) than to words with high spread (low CC), a finding that is consistent with our results for spoken word identification. They also simulated the effects of spread in McClelland and Rumelhart’s (1981) Interactive Activation Model (IAM), a visual word analogue of McClelland and Elman’s (1986) TRACE model for spoken word identification. They found that the IAM model correctly predicted the results of lexical spread. Although they did not directly test this hypothesis in their simulation, they did argue that, in the context of the IAM model, the effect of spread was due to feedback from the word level to the letter level.
Although similar to IAM, TRACE includes top-down feedback from the word level to the phonological segment level. One explanation for the observed effect of CC in our results is that feedback from lexical units somehow provides more facilitation to sub-lexical units (i.e., phonemes) in low CC words. When a word becomes active, it sends activation back down to the segment level, activating those segments contained in the word. The neighbors of low CC target words are typically inhibited by fewer words compared to high CC words. Intuitively, the lexical competitors of high CC words should be suppressed more than the competitors of low CC words, due to the fact that they are inhibited by more neighbors, thereby causing high CC words to reach their threshold sooner in the detection process. This effect though, may be offset by the effects of lexical feedback from low CC neighbors (which are, on average, more active than high CC neighbors due to fewer neighbors inhibiting them) providing greater facilitation to the phonemes that overlap with the target word. This process would essentially allow the effects of feedback to overcome inhibition. As a result of interactive activation, low CC words can, on average, reach threshold sooner than high CC words. Presumably in a behavioral experiment, this result would be reflected in faster response times and higher percent correct to low CC words than to high CC words, a finding that would be consistent with the results observed in Experiments 1 and 2. Thus, the effects of CC observed in our two experiments are generally consistent with the interactive framework in the TRACE model of McClelland and Elman (1986) as well as other potential activation-plus-competition models of spoken word recognition.
One major difference between TRACE and Norris’s (1994) Shortlist model and Norris et al.’s (2000) MERGE model is the presence of feedback from the word level to the phonological level in TRACE and the lack of feedback in Shortlist and MERGE. In fact, the need to incorporate such feedback has been a major source of controversy between the adherents of the two models (see e.g., Norris et al., 2000, for a thoughtful discussion of this point, as well as McClelland, Mirman, & Holt, 2006; McQueen, Norris, & Cutler, 2006; and Mirman, McClelland, & Holt, 2006). Strictly feed-forward mechanisms can theoretically produce faster/more accurate recognition for low CC words due to the fact that high CC words typically share a segment among many neighbors (i.e. because of lower spread). Thus, the neighbors of high CC words might remain active longer and inhibit the target for a greater duration. Future research designed to disentangle these two possible explanations of the effects of CC could also help discriminate between models of spoken word recognition that include feedback from the word to the phonological level, such as TRACE, from those that include no such feedback, such as MERGE.
Norris and McQueen (2008) recently developed a Bayesian probabilistic version of Shortlist, known as Shortlist B, as an alternative to activation based models. Unlike activation based connectionist models of word recognition, including the interactive activation model TRACE, or strictly feed forward models such as MERGE, Shortlist B performs computations on paths — a lattice of words in a sentence or a string of phonemes in a word. Some paths, naturally, have higher probabilities than others. Shortlist B computes the posterior probability (i.e., the probability of recognizing a word given the available perceptual evidence) on a string of words or phonemes by considering the available perceptual evidence conditioned on the overall probability of the string.
While the lattice structure inherent in Shortlist B differs from the structure of connected networks with inhibitory connections, both conceptualizations can account for the effects of neighborhood density. For words, Norris and McQueen (2008) pointed out that statistical dependencies are built into the lexicon in such a way that words with common sequences will also tend to have many lexical neighbors. These dependencies “modulate” word recognition rates as a function of the effect of similar sounding words. The more similar sounding words there are to a target word, the greater the impact on the available evidence. Note though that Mathey et al. (2004) explained the results for spread (CC) by arguing that lexical feedback counteracts the effects of lateral inhibition at the word level. Inhibition creates an advantage for high CC, but downward feedback apparently offsets this effect. It is therefore possible that the effects of CC might be predicted to go in the direction opposite to what we observed by models with inhibition but without feedback. Shortlist B does away with inhibition as well as feedback, and consequently, it might predict null effects for CC. However, the model is complex and simulations will be necessary to verify this reasoning.
Mathey and Zagar’s (2000) finding that lower spread has similar effects in visual word recognition as high CC has in spoken word recognition also raises the issue of how orthographic variables might be related to phonological variables in the mental lexicon. While the focus of our research was on the phonological mental lexicon, it is vital to recognize that lexical representations and information in those lexical networks carry information above and beyond the phonological. In fact, the focus on the phonological lexicon, and phonology in general is a simplification arrived at by dimensional reduction. True lexical representations in memory include multiple sources of information specific to the episode of the utterance, including talker specific information (Palmeri, Goldinger, & Pisoni, 1993). Phonological information stored in memory is, almost certainly, tightly coupled with other stimulus attributes such as orthographic, as well as information related to the role typically played by the word in a sentence (i.e., noun or verb?).6 One potential theory advocated recently by Port (2006) is that our knowledge of orthography, the alphabet, and even grammatical structure of the language provides the basis for our phonological representations and intuitions about phonology.
Finally, the effects of CC on spoken word recognition are not entirely unequivocal. Vitevitch (2007) recently examined the influence of phonemic spread (either 2 or 3) on spoken word processing of CVCs using three experimental paradigms: lexical decision, word repetition, and same-different discrimination. When neighborhood density is held constant, it is mathematically conceivable for two CVCs of different spread to have the same CC. In reality, though, as explained above for printed words, CVCs of spread 2 tend to have a higher CC than CVCs of spread 3. An analysis of the stimuli used by Vitevitch using a two-tailed t test confirmed that in fact the spread 2 words used in his study on average had a higher CC than the spread 3 words (p < .01). Nevertheless, Vitevitch found that words with a spread of 2 (high CC) were responded to more quickly in each of his three experimental paradigms than words with a spread of 3 (low CC), a result that is opposite of the findings of the present experiments. It is worth noting in this regard that we also used the same set of stimuli used in both Experiments 1 and 2 in a same-different task and found no difference in response times to high and low CC words.
One potential explanation for the discrepancy in the two studies may be due to task differences. Of the various tasks used, the same-different task seems to be the one least likely to require lexical access, since discrimination responses could at least theoretically be based on the degree of acoustic-phonetic similarity between the two stimuli on any given trial. If lexical access were not occurring, then there is little reason to expect CC to have any effect. Such an analysis is consistent with our finding of no effect of clustering in a same-different task. It does not, however, explain Vitevitch’s (2007) finding of faster responding to high CC words in lexical decision or in word repetition. Currently, there is no satisfactory explanation regarding the discrepancy across studies, and additional research will be needed in order to determine the reason for the discrepancy.
A similar state of affairs exists in the printed word recognition literature. Mathey and Zagar (2000) and Mathey et al. (2004) found faster and more accurate response times in a visual lexical decision task to what were in effect low CC words than to what were in effect high CC words. Other researchers (e.g., Johnson & Pugh, 1994; Pugh, Rexer, Peter, & Katz, 1994), also using a visual lexical decision task, found faster responding to what were in effect high CC than to low CC words. (Note that all these authors talked in terms of spread rather than CC). Mathey and Zagar argued that the discrepancy between their results and Johnson and Pugh’s (1994) results showing inhibitory effects for high spread (low CC) could be due to the distribution of the number of neighbors formed by changes at each letter position. For example, consider a word with a spread of 2 with six neighbors. Five of those neighbors could be formed by a change in the first letter position and one formed by a change in the second letter position (a distribution of 5-1-0). Or, three neighbors could be formed by a change in the first position and three by a change in the second position (a distribution of 3-3-0). Mathey and Zagar (2000) demonstrated in a series of simulations that the effects of spread did, in fact, vary as a function of neighborhood distribution. However, the variable of neighborhood distribution is completely confounded with CC. For example, consider a CVC with a spread of 2 and eight neighbors, four formed by changing the first phoneme and four by changing the second (4-4-0). The CC equals 12/28. Now consider another word also of spread 2 and with eight neighbors, but an unbalanced distribution of 7-1-0. Its CC is equal to 21/28. In the above example, the spread is identical across words (i.e., spread = 2), and the neighborhood density is held constant. CC though also differed considerably across words and covaried with spread.
Interestingly, when spread was held constant at 2, Mathey and Zagar observed higher activation levels when the neighbors were equally spread out over two letter positions compared to when they were unbalanced. Similar logic holds for words with spread equal to 3. Though likely to be difficult in practice, it is at least mathematically possible to hold spread and number of neighbors constant while varying CC. The balance of the neighborhood distribution would also vary with CC. It is also mathematically possible to hold CC constant while spread (and hence also the balance of the distribution) vary. Performing experiments like these (if possible) might help sort out which of these three seemingly inextricable intertwined variables has an effect.
In summary, our finding that a higher CC slows spoken word recognition and leads to less accurate word recognition under noise should lead to future studies exploring the effects of network and graph related variables in spoken word recognition. These findings, furthermore, have potential implications for model selection issues in spoken word recognition, such as whether it is necessary to incorporate feedback mechanisms in models.
Acknowledgments
This study was supported by the National Institute of Health Grant No. DC-00111, and the National Institute of Health T32 Training Grant No. DC-00012. We would like to thank Vsevolod Kapatsinski for discussion and insightful comments.
Footnotes
A same-different discrimination experiment was also carried out using the stimuli employed in Experiments 1 and 2. The hypothesis was that response latencies would be greater for high CC same pairs than low CC same pairs. Null results were observed in this experiment perhaps because the same-different paradigm might not encourage lexical access as much as word repetition or perceptual identification paradigms.
Pajek computes two measures of CC: One that is normalized by the relative number of neighbors, and one that is not. We used the measure of CC that is not normalized because we were interested in measuring CC as a lexical variable independent of neighborhood density.
More traditional ANOVAs were also carried out on the accuracy scores and were done separately treating subjects (F1 or t1) and items (F2 or t2) as random effects (Clark, 1973). Items falling 2.5 standard deviations above or below the mean accuracy score in each condition were eliminated. Three words were dropped from the items analysis in the ANOVA (two low CC words and one high CC word) as well as from the subject analysis using this criterion. The results for the One-Way ANOVA were as follows: For the main effect of Channel, both F1 and F2 analyses were significant (F1(1,38) = 23.73, d(effect size) = .41, p < .0001; F2(1, 89) = 19.56, p < .0001). The main effect of CC was highly significant in a subjects analysis, (F1(1,38) = 22.37, d = .26, p < .0001), and significant in an items analysis, (F2(1, 89) = 4.39, p < .05). The CC x channel interaction was not significant, (F1(1,38) = 1.61, p = .211; F2(1, 89) < 1).
Research has shown that phonetic biases can affect voice key response measurements. In particular, voiceless obstruent consonants (/s/, /ʃ/, /f/, /h/, and /θ/) have been shown to be detected later than stop consonants (/p/, /b/, /g/, /k/, /t/, and /d/) (see Kessler, Treiman, & Mullennix, 2002) since they typically produce less energy. The number of stop consonants (Low CC = 17 and High CC = 15) and voiceless and obstruent consonants (Low CC = 14 and High CC = 15) in the onset position were controlled across conditions.
We also carried out a traditional paired sample t-test (two-tailed) on the reaction times across subjects, and an independent samples t-test (two-tailed) on items. The effect of CC was significant in the subjects analysis (t1(20) = 2.09, d = .28, p = .05), but not in the items analysis where only a non-significant trend was observed, (t2(92) = 1.43, p = .16). Overall, the effect size was moderate.
A reviewer used a logistic regression model and a database (containing 75 out of 94 of our stimuli) to determine whether two principle components (PCs) (derived from 10 measures of orthographic consistency; Baayen, Feldman, & Schreuder, 2006) as well as the noun-verb ratio (the extent to which high vs. low CC words were used as nouns or verbs) differ across levels of CC. The results indicated the noun-verb ratio and both PCs serve as significant predictors for the level of CC. The analysis revealed that high CC words tend to be used as nouns more than verbs, and were associated with larger values of PC1 as well as higher values of the second PC related to “type and token counts” (PC4 in Baayen et al., 2006). PC1 contrasts the number of words with different pronunciations (for the same sequence of letters) with the number of orthographic neighbors. A large value of PC1 characterizes words with many neighbors, while a low value of PC1 is associated with words that are more likely to have multiple pronunciations for the same letter sequence. The reviewer suggested that one reason why nouns might contribute to more neighborhood connectivity than verbs might be due to the fact that verbs typically have a more complex argument structure. Finally, a post-hoc regression analysis was carried out on data collected by Balota and colleagues (Balota, Cortese, & Pilotti, 1999). The results from the linear model analysis revealed that reaction times (RTs) from a printed word lexical decision task were lower for low CC stimuli, with CC being a greater predictor than either the first principle component or the noun-verb ratio. Interestingly, these results are in line with the data obtained by Mathey and Zagar (2000) as well as with our own data using spoken words.
References
- Albert R, Barabási AL. Statistical mechanics of complex networks. Reviews of Modern Physics. 2002;74:47–97. [Google Scholar]
- Baayen RH, Davidson DJ, Bates D. Mixed-effects modeling with crossed random effects for subjects and items. Journal of Memory and Language. 2008;59:390–412. [Google Scholar]
- Baayen RH, Feldman L, Schreuder R. Morphological influences on the recognition of monosyllabic monomorphemic words. Journal of Memory and Language. 2006;53:496–512. [Google Scholar]
- Balota D, Cortese M, Pilotti M. Visual lexical decision latencies for 2096 words. 1999 [On-line], Available: http://www.artsci.wustl.edu/~dbalota/lexical_decision.html/
- Barabási AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- Batagelj V, Mrvar A. Pajek — A program for large network analysis. Connections. 1998;21:47–57. [Google Scholar]
- Bergeson TR, Pisoni DB. Audiovisual speech perception in deaf adults and children following cochlear implantation. In: Calvert GA, Spence C, Stein BE, editors. The Handbook of Multisensory Processes. Cambridge, MA: The MIT Press; 2004. pp. 153–176. [Google Scholar]
- Clark HH. The language-as-fixed-effect fallacy: A critique of language statistics in psychological research. Journal of Verbal Learning and Verbal Behavior. 1973;12:335–359. [Google Scholar]
- Dorogovtsev SN, Mendes JFF. Language as an evolving word web. Proceedings of the Royal Society of London B. 2001;268:2603–2606. doi: 10.1098/rspb.2001.1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fellbaum C, editor. WordNet, an electronic lexical database. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Ferrer i Cancho R, Solé RV. The small world of human language. Proceedings of the Royal Society of London B. 2001;268:2261–2265. doi: 10.1098/rspb.2001.1800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenberg JH, Jenkins JJ. Studies in the psychological correlates of the sound system of American English. Word. 1964;20:157–177. [Google Scholar]
- Gruenenfelder TM, Pisoni DB. Research on Spoken Language Processing Progress Report No. Vol. 27. Bloomington, IN: Speech Research Laboratory, Indiana University; 2005. Modeling the mental lexicon as a complex system: Some preliminary results using graph theoretic measures; pp. 27–47. [Google Scholar]
- Gruenenfelder TM, Pisoni DB. The lexical restructuring hypothesis and graph theoretic analyses of networks based on random lexicons. Journal of Speech, Language, and Hearing Research. 2009;52:596–609. doi: 10.1044/1092-4388(2009/08-0004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson NF, Pugh KR. A cohort model of visual word recognition. Cognitive Psychology. 1994;26:240–346. doi: 10.1006/cogp.1994.1008. [DOI] [PubMed] [Google Scholar]
- Kessler B, Treiman R, Mullenix J. Phonetic biases in voice key response time measurements. Journal of Memory and Language. 2002;47:145–171. [Google Scholar]
- Kucera F, Francis W. Computational Analysis of Present Day American English. Providence, RI: Brown University Press; 1967. [Google Scholar]
- Landauer TK, Streeter LA. Structural differences between common and rare words: Failure of equivalence assumptions for theories of word recognition. Journal of Verbal Learning and Verbal Behavior. 1973;12:119–131. [Google Scholar]
- Luce PA, Pisoni DB. Recognizing spoken words: The neighborhood activation model. Ear & Hearing. 1998;19:1–36. doi: 10.1097/00003446-199802000-00001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathey S, Robert C, Zagar D. Neighbourhood distribution interacts with orthographic priming in the lexical decision task. Language & Cognitive Processes. 2004;19:533–559. [Google Scholar]
- Mathey S, Zagar D. The neighborhood distribution effect in visual word recognition: Words with single and twin neighbors. Journal of Experimental Psychology: Human Perception & Performance. 2000;26:184–205. doi: 10.1037//0096-1523.26.1.184. [DOI] [PubMed] [Google Scholar]
- McClelland JL, Elman JL. The TRACE model of speech perception. Cognitive Psychology. 1986;18:1–86. doi: 10.1016/0010-0285(86)90015-0. [DOI] [PubMed] [Google Scholar]
- McClelland JL, Mirman D, Holt LL. Are there interactive processes in speech perception? Trends in Cognitive Sciences. 2006;10:364–369. doi: 10.1016/j.tics.2006.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL, Rumelhart DE. An interactive activation model of context effects in letter perception: Part I. An account of basic findings. Psychological Review. 1981;88:375–407. [PubMed] [Google Scholar]
- McQueen JM, Norris D, Cutler A. Are there really interactive processes in speech perception? Trends in Cognitive Sciences. 2006;12:533. doi: 10.1016/j.tics.2006.10.004. [DOI] [PubMed] [Google Scholar]
- Miller GA, Beckwith R, Fellbaum C, Gross D, Miller KJ. Introduction to Word-Net: An on-line lexical database. International Journal of Lexicography. 1990;3:235–244. [Google Scholar]
- Mirman D, McClelland JL, Holt LL. Response to McQueen et al.: Theoretical and empirical arguments support interactive processing. Trends in Cognitive Sciences. 2006;10:534. doi: 10.1016/j.tics.2006.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Motter AE, de Moura APS, Lai YC, Dasgupta P. Topology of the conceptual network of language. Physical Review E. 2002;65:065102. doi: 10.1103/PhysRevE.65.065102. [DOI] [PubMed] [Google Scholar]
- Nelson DL, McEvoy CL, Schreiber TA. The University of South Florida word association norms. 1999 doi: 10.3758/bf03195588. Retrieved from http://w3.usf.edu/FreeAssociation. [DOI] [PubMed]
- Norris D. Shortlist: A connectionist model of continuous speech recognition. Cognition. 1994;52:189–234. [Google Scholar]
- Norris D, McQueen JM. Shortlist B: A Bayesian model of continuous speech recognition. Psychological Review. 2008;115:357–395. doi: 10.1037/0033-295X.115.2.357. [DOI] [PubMed] [Google Scholar]
- Norris D, McQueen JM, Cutler A. Merging information in speech recognition: Feedback is never necessary. Behavioral and Brain Sciences. 2000;23:299–370. doi: 10.1017/s0140525x00003241. [DOI] [PubMed] [Google Scholar]
- Nusbaum HC, Pisoni DB, Davis CK. Research on Speech Perception Progress Report No. Vol. 10. Bloomington, IN: Speech Research Laboratory, Psychology Department, Indiana University; 1984. Sizing up the Hoosier mental lexicon: Measuring the familiarity of 20,000 words. [Google Scholar]
- Palmeri TJ, Goldinger SD, Pisoni DB. Episodic encoding of speaker’s voice and recognition memory for spoken words. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1993;19:309–328. doi: 10.1037//0278-7393.19.2.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pisoni DB, Cleary M, Geers AE, Tobey EA. Individual differences in effectiveness of cochlear implants in children who are prelingually deaf: New process measures of performance. Volta Review. 2000;101:111–164. [PMC free article] [PubMed] [Google Scholar]
- Port R. The graphical basis of phones and phonemes. In: Munro M, Bohn O-S, editors. Second Language Speech Learning: The Role of Language Experience in Speech Perception and Production. Amstardam: John Benjamins; 2006. pp. 349–367. [Google Scholar]
- Pugh KR, Rexer K, Peter M, Katz L. Neighborhood effects in visual word recognition: Effects of letter delay and nonword context difficulty. Journal of Experimental Psychology: Learning, Memory, & Cognition. 1994;20:639–648. doi: 10.1037//0278-7393.20.3.639. [DOI] [PubMed] [Google Scholar]
- Raaijmakers JGW, Schrijnemakers JMC, Gremmen F. How to deal with “the language-as-fixed-effect fallacy”: Common misconceptions and alternative solutions. Journal of Memory and Language. 1999;41:416–426. [Google Scholar]
- Roget PM. Roget’s thesaurus of English words and phrases. (1911) 1911 Retrieved from http://www.gutenberg.org/etext/10681.
- Shannon RV, Fan-Gang Z, Kamath V, Wygonski J, Ekelid M. Speech recognition with primarily temporal cues. Science. 1995;270:303–304. doi: 10.1126/science.270.5234.303. [DOI] [PubMed] [Google Scholar]
- Soares MM, Corso G, Lucena LS. The network of syllables in Portuguese. Physica A: Statistical Mechanics and its Applications. 2005;355:678–684. [Google Scholar]
- Steyvers M, Tenenbaum JB. The large-scale structure of semantic networks: Statistical analysis and a model of semantic growth. Cognitive Science. 2005;29:41–78. doi: 10.1207/s15516709cog2901_3. [DOI] [PubMed] [Google Scholar]
- Tice B, Carrell T. Level16. 2.0. University of Nebraska; 1998. [Google Scholar]
- Vitevitch MS. The spread of the phonological neighborhood influences spoken word recognition. Memory & Cognition. 2007;35:166–175. doi: 10.3758/bf03195952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitevitch MS. What can graph theory tell us about word learning and lexical retrieval? Journal of Speech, Language, & Hearing Research. 2008;51:408–422. doi: 10.1044/1092-4388(2008/030). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vitevitch MS, Luce PA. When words compete: Levels of processing in spoken word perception. Psychological Science. 1998;9:325–329. [Google Scholar]
- Vitevitch MS, Luce PA. A Web-based interface to calculate phonotactic probability for words and nonwords in English. Behavior Research Methods, Instruments, & Computers. 2004;36:481–487. doi: 10.3758/bf03195594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ. Six degrees: the science of a connected age. New York: W.W Norton Company, Inc; 2003. [Google Scholar]
- Winer BJ. Statistical principles in experimental design. New York: McGraw-Hill; 1971. [Google Scholar]