Markov Decision Processes: A Tool for Sequential Decision Making under Uncertainty

Abstract

We provide a tutorial on the construction and evaluation of Markov decision processes (MDPs), which are powerful analytical tools used for sequential decision making under uncertainty that have been widely used in many industrial and manufacturing applications but are underutilized in medical decision making (MDM). We demonstrate the use of an MDP to solve a sequential clinical treatment problem under uncertainty. Markov decision processes generalize standard Markov models in that a decision process is embedded in the model and multiple decisions are made over time. Furthermore, they have significant advantages over standard decision analysis. We compare MDPs to standard Markov-based simulation models by solving the problem of the optimal timing of living-donor liver transplantation using both methods. Both models result in the same optimal transplantation policy and the same total life expectancies for the same patient and living donor. The computation time for solving the MDP model is significantly smaller than that for solving the Markov model. We briefly describe the growing literature of MDPs applied to medical decisions.

Formal decision analysis has been increasingly used to address complex problems in health care. This complexity requires the use of more advanced modeling techniques. Initially, the most common methodology used to evaluate decision analysis problems was the standard decision tree. Standard decision trees have serious limitations in their ability to model complex situations, especially when outcomes or events occur (or may reoccur) over time.¹ As a result, standard decision trees are often replaced with the use of Markov process–based methods to model recurrent health states and future events. Since the description of Markov methods by Beck and Pauker,² their use has grown substantially in medical decision making (MDM).

However, standard decision trees based on a Markov model cannot be used to represent problems in which there is a large number of embedded decision nodes in the branches of the decision tree,³ which often occurs in situations that require sequential decision making. Because each iteration of a standard Markov process can evaluate only one set of decision rules at a time, simulation models based on standard Markov processes can be computationally impractical if there are a large number of possible embedded decisions, or decisions that occur repetitively over time. For instance, consider the optimal cadaveric organ acceptance/rejection problem faced by patients with end-stage liver disease (ESLD), who are placed on a waiting list, and offered various qualities of livers based on location and waiting time as well as current health.⁴ For this particular problem, a patient needs to make a decision whether to accept/reject a particular type of liver offer (14 types) for each possible health state (18 health states) at each possible ranking (30 possible ranks), which requires the use of 18*14*30 = 7560 nodes in a decision tree. A standard Markov-based simulation model needs to evaluate millions of possible accept/reject policy combinations to find the optimal solution for such a decision problem, which would be computationally intractable.

The purpose of this article is to provide an introduction to the construction and evaluation of Markov decision processes (MDPs) and to demonstrate the use of an MDP to solve a decision problem with sequential decisions that must be made under uncertainty. Markov decision processes are powerful analytical tools that have been widely used in many industrial and manufacturing applications such as logistics, finance, and inventory control⁵ but are not very common in MDM.⁶ Markov decision processes generalize standard Markov models by embedding the sequential decision process in the model and allowing multiple decisions in multiple time periods. Information about the mathematical theory of MDPs may be found in standard texts.^5,7–9

We will motivate MDPs within the context of the timing of liver transplantation in a patient who has a living donor available. Furthermore, we describe the problem in a sufficiently simple level of detail that a standard Markov process describing the sequential decisions can be evaluated for all plausible timing strategies, providing a direct homology between the MDP and a standard Markov process evaluated under all possible decision strategies.

PREVIOUS MDP APPLICATIONS IN MDM

The MDP applications in MDM prior to 2004 are best summarized by Schaefer et al.⁶ Among these, Lefevre¹⁰ uses a continuous-time MDP formulation to model the problem of controlling an epidemic in a closed population; Hu et al.¹¹ address the problem of choosing a drug infusion plan to administer to a patient using a partially observable MDP (POMDP) model; Hauskrecht and Fraser¹² use a POMDP framework to model and solve the problem of treating patients with ischemic heart disease (IHD); Ahn and Hornberger¹³ provide an MDP model that considers the accept/reject decision of a patient when there is a kidney offer.

Recently, MDPs have been applied to more MDM problems. Alagoz et al.^14–16 and Sandikci et al.⁴ consider the optimal liver acceptance problem; Shechter et al.¹⁷ apply MDPs to find the optimal time to initiate HIV therapy Alterovitz et al.¹⁸ use an MDP model to optimize motion planning in image-guided medical needle steering; Maillart et al.¹⁹ use a POMDP model to evaluate various breast cancer screening policies; Faissol et al.²⁰ apply an MDP framework to improve the timing of testing and treatment of hepatitis C; Chhatwal et al.²¹ develop and solve a finite-horizon MDP to optimize breast biopsy decisions based on mammographic findings and demographic risk factors; Denton et el.²² develop an MDP to determine the optimal time to start statin therapy for patients with diabetes; Kreke et al.²³ and Kreke²⁴ use MDPs for optimizing disease management decisions for patients with pneumonia-related sepsis; Kurt et al.²⁵ develop an MDP to solve the problem of initiating the statin treatment for cholesterol reduction. While there have been few MDP applications to MDM, such recent successful applications suggest that MDPs might provide useful tools for clinical decision making and will be more popular in the near future.

DEFINITION OF A DISCRETE-TIME MDP

The basic definition of a discrete-time MDP contains 5 components, described using a standard notation.⁴ For comparison, Table 1 lists the components of an MDP and provides the corresponding structure in a standard Markov process model. T = 1,..., N are the decision epochs, the set of points in time at which decisions are made (such as days or hours); S is the state space, the set of all possible values of dynamic information relevant to the decision process; for any state s ∈ S, A_s is the action space, the set of possible actions that the decision maker can take at state s; p_t(.|s,a) are the transition probabilities, the probabilities that determine the state of the system in the next decision epoch, which are conditional on the state and action at the current decision epoch; and r_t(s,a) is the reward function, the immediate result of taking action a at state s. (T, S, A_s, p_t(.|s,a), r_t(s,a)) collectively define an MDP.

Table 1.

Components of a Markov Decision Process (MDP) and the Comparable Structure in a Markov Process

MDP Component		Analogous Markov Model Component
Decision epoch	Time at which decisions are made	Cycle time
State space	Set of mutually exclusive, collectively exhaustive conditions that describe the state of the model	States
Action space	Set of possible decisions that can be made	Decision nodes
Transition probabilities	Probability of each possible state of the system in the next time period	Transition probabilities
Reward function	Immediate value of taking an action at each state	Incremental utility and tail utility
Decision rule	A specified action given each possible state	No specific analogy; for a single decision node, it is a specific action
Policy	A sequence of decision rules at each time period	No specific analogy

A decision rule is a procedure for action selection from A_s for each state at a particular decision epoch, namely, d_t(s) ∈ A_s. We can drop the index s from this expression and use d_t ∈ A, which represents a decision rule specifying the actions to be taken at all states, where A is the set of all actions. A policy δ is a sequence of the decision rules to be used at each decision epoch and defined as δ = (d₁,..., d_N-1). A policy is called stationary if d_t = d for all t ∈ T. For any specific policy, an MDP reduces to a standard Markov process.

The objective of solving an MDP is to find the policy that maximizes a measure of long-run expected rewards. Future rewards are often discounted over time.⁴ In the absence of a discounting factor, if we let u_t*(s_t) be the optimal value of the total expected reward when the state at time t is s and there are N-t periods to the end of the time horizon, then the optimal value functions and the optimal policy giving these can be obtained by iteratively solving the following recursive equations, which are also called Bellman equations:

$$u_N^{\ast }\left(s_N\right)=r_N\left(s_N\right)\text{for all}{s}_N\in S,$$ (1)

and

$$u_t^{\ast }\left(s_t\right)=\underset{a\in A_s}{\text{max}}\left\{r_t(s_t,a)+(1-\alpha )\sum _{j\in S}{p}_t(j\mid s_t,a)u_{t+1}^{\ast }\left(j\right)\right\}fort=1,\dots ,N-1,\text{and}{s}_t\in S,$$ (2)

where r_N(s_N) denotes the terminal reward that occurs at the end of the process when the state of the system at time N is s_N, and α represents the discounting factor (0 < α ≤ 1). Note that the MDP literature flips the interpretation of the discounting factor (1 – α) (0 < α ≤ 1); that is, 1 unit of reward at time 1 is equivalent to (1 – α) units of rewards at time 0. At each decision epoch t, the optimality equations given by equation 2 choose the action that maximizes the total expected reward that can be obtained for periods t, t +1,..., N for each state s_t. For a given state s_t and action a, the total expected reward is calculated by summing the immediate reward, r_t(s,a), and future reward, obtained by multiplying the probability of moving from state s_t to j at time t + 1 with the maximum total expected reward u_t+1*(j) for state j at time t + 1 and summing over all possible states at time t + 1.

A finite-horizon model is appropriate for systems that terminate at some specific point in time (e.g., production planning over a fixed period of time such as over the next year at a manufacturing system). At each stage, we choose the following:

$$a_{s_t,t}^{\ast }\in \underset{a\in A_s}{\text{arg}\text{max}}\left\{r_t(s_t,a)+(1-\alpha )\sum _{j\in S}{p}_t(j\mid s_t,a)u_{t+1}^{\ast }\left(j\right)\right\}fort=1,\dots ,N-1,$$ (3)

where $a_{s_t,t}^{\ast }$ is an action maximizing the total expected reward at time t for state s.⁵

In some situations, an infinite-horizon MDP (i.e., N = ∞) is more appropriate, in which case the use of a discount factor is sufficient to ensure the existence of an optimal policy. The most commonly used optimality criterion for infinite-horizon problems is the total expected discounted reward. In an infinite-horizon MDP, the following very reasonable assumptions guarantee the existence of optimal stationary policies: stationary (time-invariant) rewards and transition probabilities, discounting²⁶ with α, where 0 < α ≤ 1, and discrete state and action spaces. Optimal stationary policies still exist in the absence of a discounting factor when there is an absorbing state with immediate reward 0 (such as death in clinical decision models). In a stationary infinite-horizon MDP, the time indices can be dropped for the reward function and transition probabilities, and Bellman equations take the following form:

$$V\left(s\right)=\underset{a\in A_s}{\text{max}}\left\{r(s,a)+(1-\alpha )\sum _{j\in S}p(j\mid s,a)V\left(j\right)\right\}fors\in S,$$ (4)

where V(s) is the optimal value of the MDP for state s, that is, the expected value of future rewards discounted over an infinite horizon. The optimal policy consists of the actions maximizing this set of equations.

CLASSES OF MDPs

Markov decision processes may be classified according to the time horizon in which the decisions are made: finite- and infinite-horizon MDPs. Finite-horizon and infinite-horizon MDPs have different analytical properties and solution algorithms. Because the optimal solution of a finite-horizon MDP with stationary rewards and transition probabilities converges to that of an equivalent infinite-horizon MDP as the planning horizon increases and infinite-horizon MDPs are easier to solve and to calibrate than finite-horizon MDPs, infinite-horizon models are typically preferred when the transition probabilities and reward functions are stationary. However, in many situations, the stationary assumption is not reasonable, such as when the transition probability represents the probability of a disease outcome that is increasing over time or when age-dependent mortality is involved.

Markov decision processes can be also classified with respect to the timing of the decisions. In a discrete-time MDP, decisions can be made only at discrete-time intervals, whereas in a continuous-time MDP, the decisions can occur anytime. Continuous-time MDPs generalize discrete-time MDPs by allowing the decision maker to choose actions whenever the system state changes and/or by allowing the time spent in a particular state to follow an arbitrary probability distribution.

In MDPs, we assume that the state the system occupies at each decision epoch is completely observable. However, in some real-world problems, the actual system state is not entirely known by the decision maker, rendering the states only partially observable. Such MDPs are known as POMDPs, which have different mathematical properties than completely observable MDPs and are beyond the scope of this article. Technical details and other extensions for MDPs can be found elsewhere.⁵

SOLVING MDPs

There are different solution techniques for finiteand infinite-horizon problems. The most common method used for solving finite-horizon problems is backward induction. This method solves the Bellman equations given in equations 1 and 2 backwards in time and retains the optimal actions given in equation 3 to obtain the optimal policies.²⁷ The initial condition is defined by equation 1, and the value function is successfully calculated one epoch at a time.

There are 2 fundamental algorithms to solve infinite-horizon discounted MDPs: value iteration and policy iteration methods. The value iteration starts with an arbitrary value for each state and, at each iteration, solves equation 4 using the value from the previous iteration until the difference between successive values becomes sufficiently small. The value corresponding to the decision maximizing equation 4 is guaranteed to be within a desired distance from the optimal solution.

We use the policy iteration algorithm in solving the illustrative MDP model in this article.^8,9 It starts with an arbitrary decision rule and finds its value; if an improvement in the current decision rule is possible, using the current value function estimate, then the algorithm will find it; otherwise, the algorithm will stop, yielding the optimal decision rule. Let P_d and d* represent the transition probability matrix with components p_d(j|s) (j corresponds to the column index, and s corresponds to the row index) and optimal decision rules, respectively. Let also r_d represent the reward vector with components r_d(s). Then the policy iteration algorithm can be summarized as follows⁵:

• Step 1. Set n = 0, and select an arbitrary decision rule d⁰ ∈ D.

• Step 2. (Policy Evaluation): Obtain vⁿ by solving vⁿ = r_dⁿ + (1 – α)P_dⁿ vⁿ.

• Step 3. (Policy Improvement): Choose dⁿ⁺¹ ∈ arg max{r_d + (1 – α)P_dvⁿ}, setting dⁿ⁺¹ = dⁿ if possible. ^{d ∈ D}

• Step 4. If dⁿ⁺¹ = dⁿ, stop and set d* = dⁿ. Otherwise, increment n by 1, and return to step 2.

Policy iteration algorithm finds the value of a policy by applying the backward induction algorithm while ensuring that the value functions for any 2 subsequent steps are identical.

ILLUSTRATIVE EXAMPLE: MDPs V. MARKOV MODELS IN LIVER TRANSPLANTATION

Problem of Optimal Timing of Living-Donor Liver Transplantation

We use the organ transplantation decision problem faced by patients with ESLD as an application of MDPs. There are currently more than 18,000 ESLD patients waiting for a cadaveric liver in the United States. Most livers offered for transplantation are from cadaveric donors; however, livers from living donors are often used due to a shortage in cadaveric livers. In this section, we compare the MDP model of Alagoz et al.¹⁴ and a Markov model to determine the optimal timing of liver transplantation when an organ from a living donor is available to the decision maker. We seek a policy describing the patient health states in which transplantation is the optimal strategy and those where waiting is the optimal strategy. For the purpose of this example, we will assume that the health condition of the patient is sufficiently described by his or her Model for End-stage Liver Disease (MELD) score.¹³ The MELD score is an integer result of a survival equation that predicts the probability of survival at 3 months for patients with chronic ESLD. The score ranges from 6 to 40, with higher scores indicating sicker patients.¹³

Markov Process Model

The standard Markov model is illustrated in Figure 1. Due to sparsity in the data available, the states that describe the patient's health have been aggregated into 18 states defined by their MELD score, the healthiest state being those patients with a MELD score of 6 or 7, the sickest patients with a MELD score of 40. From any state, the patient may die (with a probability dependent upon the level of illness) or may transition to any other of the ordered health states. Although most common transitions are between nearly adjacent states (e.g., MELD 6–7 to MELD 8–9), all transitions are possible and are bidirectional: at any given state, there is some likelihood that the patient will remain the same, become sicker, or improve. Transition probabilities were estimated using the ESLD natural history model of Alagoz et al.²⁸ The posttransplant expected life days of a patient was found by using the post-transplant survival model developed by Roberts et al.²⁹ We choose the cycle time for the Markov model as 1 day; that is, the patient makes the decision to accept or wait on a daily basis. Our model discounted future rewards with a 3% annual discounting factor, a commonly used discount rate in MDM literature.²⁶

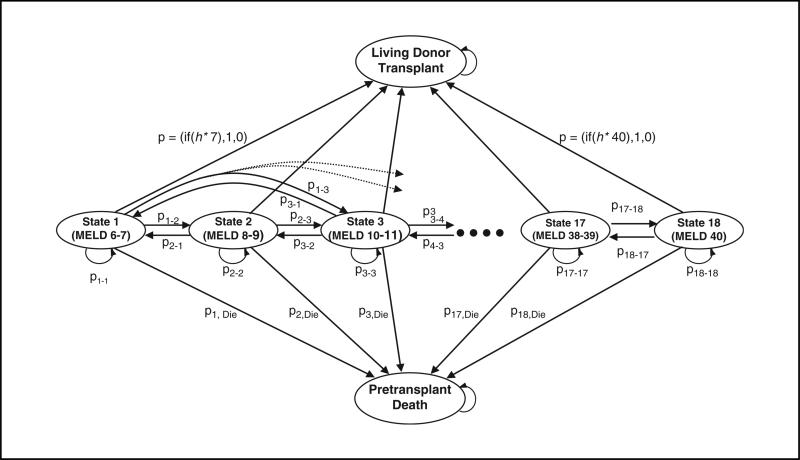
Figure 1.

State transition diagram for a Markov model. The circles labeled state 1 (Model for End-stage Liver Disease [MELD] 6–7) through state 18 (MELD 40) represent possible health states for the patient (i.e., the patient can be at one of the 18 states at any time period). Note that each state actually represents 2 adjacent MELD scores; for instance, 1 represents MELD scores 6 and 7, 2 represents MELD scores 8 and 9, and so on. Each time period, the patient may transit to one of the other MELD states or die. At each state, there is a Boolean node that will direct the patient to accept the living donor organ if the MELD score is greater than some value (h*): the optimal transplant MELD is found by solving the model over all possible values of h*. Note that the transition probabilities between pretrans-plant states in the figure depend on the policy; however, this dependency is suppressed for the clarity of presentation. As a result, the transition probabilities between pretransplant states in the figure represent only the transition probabilities when h* = 41.

To select the state at which transplantation is chosen, a flexible Boolean expression is placed in the transitions out of each state that would be of the following form: If MELD ≥ h*, transplant; otherwise, wait.

The execution of the Markov model calculates the total expected life years when a decision rule specifying h* is used. Because a Markov model is able to evaluate only one set of decision rules at a time, we evaluated all possible decision rules by executing the Markov model 19 times. At each iteration, we changed the threshold MELD scores (h*) to consider transplant options; that is, if the patient is in MELD score h < h*, then “Wait”; otherwise, “Transplant” the patient. We computed the total life expectancy for each Markov process run (h* = 6,8, . . . ,38,40,41). We then found the optimal policy by selecting the threshold patient health (h*) that results in the largest total life expectancy.

MDP Model

An MDP model provides a framework that is different from a standard Markov model in this problem, as the repetitive “Transplant” versus “Wait” decisions are directly incorporated into the model, with these decisions affecting the outcomes of one another. For example, the total expected life days of the patient at the current time period depend on his or her decision at the next time period. The severity of illness at the time of transplant affects the expected posttransplant life years of the patient; therefore, the dynamic behavior of patient health complicates the decisions further.

We developed an infinite-horizon, discounted stationary MDP model with total expected discounted reward criterion to solve this problem. Using an infinite horizon lets the model determine patient death. We could also use a finite-horizon model in which patients are not allowed to live after a certain age (e.g., 100). For stationary probabilities and reward functions, a sufficiently long finite horizon will give the same optimal solution as an infinite horizon.^5,7–9 Figure 2 shows a schematic representation of the MDP model that is used to solve the problem under consideration. Note that the state structure is identical to Figure 1. In the MDP model, the decision epochs are days. The states describe the clinical condition of the patient, which are represented by the MELD scores described above. Another necessary component of the MDP model is the transition probabilities that determine the progression of the liver disease, which in model terms is the probability of transitioning between pretransplant model states.

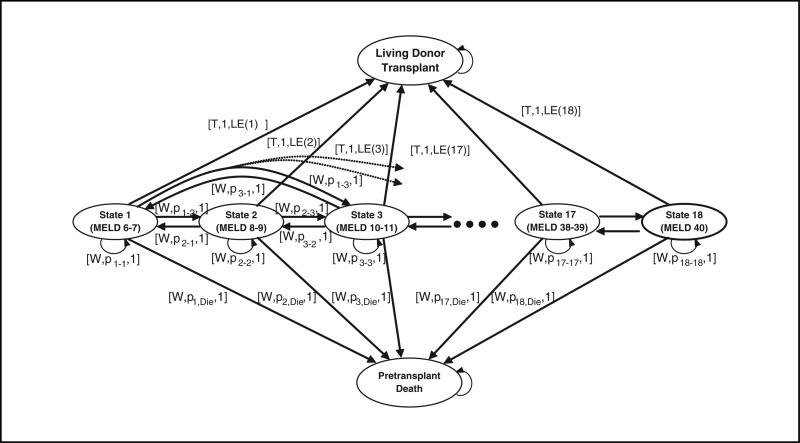
Figure 2.

State transition diagram of the Markov decision process model. The state space is identical to Figure 1. At each health state, the patient can take 2 actions: he or she can either choose to have the transplant at the current time period, which is represented by “T”, or wait for one more time period, which is represented by “W”. When the patient chooses the transplant option, he or she moves to the “Transplant” state, which is an absorbing state with probability 1 and gets a reward of r(h) that represents the expected posttransplant life days of the patient when his or her current health state is h. If the patient chooses to wait for one more decision period, he or she can stay at his or her current health state with probability p(h|h), he or she can move to some other health state h’ with probability p(h’|h), or he or she can die at the beginning of the next decision epoch with probability p(D|h). In all cases, the patient will receive a reward of 1 that corresponds to the additional day the patient will live without transplantation. The transitions occur randomly once the patient takes the action “Wait”. These “Transplant”/“Wait” decisions exist for each health state of the patient.

Slightly different in form from the Markov model are 2 types of actions that the decision maker can take at each time period for each health state. If the patient chooses the “Transplant” option in the current decision epoch, he or she obtains the posttransplant reward, which is equal to the expected discounted posttransplant life days of the patient given his or her health status and donated liver quality. On the other hand, if he or she postpones the decision until the next time period by taking the action “Wait”, he or she receives the pretransplant reward, which is equal to 1 day, and retains the option to select the transplant decision in the following period provided they are not in the dead state. Because posttransplant life expectancy depends on the pretransplant MELD score, the reward is not assigned to the transplanted state but to the action of transplantation from each particular MELD score. After transplantation and after dying, no more rewards are accumulated; therefore, the transition probabilities from the transplanted state do not influence the total reward, and this state can be modeled as an absorbing state (like death).

Let V(h) be the total expected life days of the patient using the optimal policy when his or her health is h, h=1, ...,18, where 18 is the sickest health state. Let LE(h) be the posttransplant expected discounted life days of the patient when his or her health is h at the time of transplantation, and let p(h’|h) be the stationary probability that the patient health will be h’ at time t + 1 given that it is h as time t given that the action is to wait (the action is removed from the notation due to clarity of the presentation; similarly, although LE(h) is a function of donor quality, we suppress this dependency for notational convenience). Under the above definitions, the optimal value of the total expected life years of the patient was found by solving the following recursive equation:

$$V\left(h\right)=Max\left\{LE\left(h\right),1+(1-\alpha ){\sum }_{h^{\prime }=1}^{18}p(h^{\prime }\mid h)V\left(h^{\prime }\right)\right\},h=1,\dots ,18.$$

Note that V(h) equals either LE(h), which corresponds to taking action “Transplant”, or 1 plus future discounted expected life days, which corresponds to taking action “Wait”. The optimality equations do not include the transitions to the “dead” and “transplanted” states because the value of staying in these states is equal to 0. The set of actions resulting in the maximum value gives a set of optimal policies.

Data Sources for Both Models

The data came from 2 sources. Posttransplant survival data were derived from a nationwide data set from UNOS that included 28,717 patients from 1990 to 1996.¹⁷ Natural history was calibrated using data from the Thomas E. Starzl Transplantation Institute at the University of Pittsburgh Medical Center (UPMC), one of the largest liver transplant centers in the world, consisting of clinical data of 3009 ESLD patients. One issue in estimating the natural history of the ESLD is related to the difficulty of taking periodic measurements and turning them into a daily measurement. We used the model by Alagoz et al.²⁸ to quantify the natural history of ESLD. Namely, we utilized cubic splines to interpolate daily laboratory values between actual laboratory determinations.²⁸ Daily interpolated MELD scores could be calculated from these laboratory values, and the day-to-day transitions from each MELD score were calculated over the entire sample. Different transition matrices were calculated for each major disease group: we only use data from the chronic hepatitis group in this example. Because we aggregated MELD scores in groups of 2, this produced an 18 × 18 matrix, although the probabilities of transitioning very far from the diagonal are small.

A Numerical Example

We consider a 65-year-old female hepatitis C patient who has a 30-year-old male living donor. We find the optimal transplantation policy using both a Markov-based simulation model and an MDP. Both models result in the same optimal policy, which is to wait until the MELD score rises to 30 and to receive the living-donor transplant when her MELD score exceeds 30. Furthermore, both models obtain the same total life expectancies given initial MELD scores. The computation time for solving the MDP model is less than 1 second, whereas it is approximately 1 minute for solving the Markov model. Although the computational time is not a major issue for this application, MDPs may be preferred over standard Markov models for more complex problems where the solution times might be longer. Because we could solve MDPs very fast, performing additional experiments is trivial. Extended computational experiments using the MDP model are reported elsewhere.^14,30

DISCUSSION

This study describes the use of MDPs for MDM problems. We compare MDPs to standard Markov-based simulation models by solving the problem of optimal timing of the living-donor liver transplantation problem using both methods. We show that both methods give the same optimal policies and optimal life expectancy values under the same parameter values, thus establishing their equivalence for a specific MDM problem.

A Markov-based simulation model can be used to evaluate only one set of decision rules at a time, and for the problem we consider, there are, in fact, an exponential number of possible decision rules. For example, if there are 18 states that represent patient health and 2 possible actions that can be taken at each health state, there are 2¹⁸ possible distinct decision rules. In this case, many of these possible policies do not seem credible: it seems impossible that a policy of wait at MELD 6–7, transplant at MELD 8–9, wait at MELD 10–11, transplant at MELD 12–13, and so on could possibly be optimal. However, in less straightforward or more clinically complex problems, the ability to intuitively restrict the possible set of policies may be more difficult, and evaluating each alternative by using a Markov-based simulation model is computationally impractical. In the standard Markov model described above, we assumed that the optimal policy has a threshold-type form; that is, there exists a MELD score such that the patient will wait until he or she reaches that MELD score and then transplant. As a result, the standard Markov model considered only 19 possible solutions for the optimal policy, and hence, we obtained the solution in just 19 runs of the simulation. However, because threshold policies are only a subset of all possible policies, the optimality of a threshold-type policy needed to be proven mathematically^14,30 before we could use the approach taken in the standard Markov model.

A solution method based on clinical intuition without searching all possible solutions may not lead to optimal results. For instance, Alagoz et al.¹⁵ consider the acceptance of cadaveric liver problem, an extension of the living-donor liver transplantation problem, in which the acceptance/rejection decisions are made for various cadaveric liver offers and MELD scores. One would expect to have a threshold-type policy in patient MELD score to be optimal as in the living-donor liver transplantation. However, as demonstrated in Alagoz et al.,¹⁵ the optimal policies may not have a threshold in the MELD score; that is, there are some cases where it is optimal to decline a particular liver type at a higher MELD score, whereas it is optimal to accept the same liver offer at a lower MELD score. This is because patients on the waiting list receive higher quality organ offers as their MELD scores rise and therefore may be more selective in accepting lower quality organ offers when they are at higher MELD scores.

Markov decision processes are able to model sequential decision problems in which there is an embedded decision node at each stage. There are some other advantages of using MDPs over standard Markov methodology. The computational time required for solving MDP models is much smaller than that for solving Markov models by simulation. This is critical particularly when the problem under consideration is very complex, that is, has large state and action spaces. For instance, Sandikci et al.⁴ consider an extension of the living-donor liver transplantation problem, in which the state space consists of over 7500 states. The solution of such a problem would be computationally impractical using standard Markov processes, whereas the optimal solution can be found in a very short time using the MDP framework.

Markov decision processes can also be used to obtain insights about a particular decision problem through structural analysis. Examples for how the structural analysis of MDPs provides insights can be found elsewhere.^14–16,30 In addition, MDPs are able to solve problems without making any assumptions about the form of the optimal policy such as the existence of threshold-type optimal policies in the living-donor liver transplant problem, whereas Markov models often need to make such assumptions for computational tractability. Furthermore, MDPs can model problems with complex horizon structures. For instance, MDPs can handle infinite horizons when parameters are stationary from a certain point T in time, a weak restriction. Then, infinite-horizon MDP methodology could be used to analyze the stationary part, followed by finite-horizon MDP methodology to analyze the preceding nonstationary part.

Markov decision processes also have some limitations. First, they have extensive data requirements because data are needed to estimate a transition probability function and a reward function for each possible action. Unlike Markov-based simulation methods, infinite-horizon MDPs assume that the rewards and the transition probabilities are stationary. In cases where rewards and transition probabilities are not stationary, we recommend the use of finite-horizon MDPs in solving problems. Furthermore, because there is no available easy-to-use software for solving MDPs, some extra programming effort (i.e., the use of general programming language such as C/C++ for coding MDP solution algorithms) is needed. On the other hand, there are many easy-to-use software programs that can be used to solve Markov models such as TreeAge Pro,³¹ which also makes the development of a standard Markov model easier than that of an MDP model. As the problem size increases, it becomes computationally difficult to optimally solve MDPs, which is often referred to as the “curse of dimensionality.” There is a growing area of research in approximate dynamic programming, which develops algorithms to solve MDPs faster and hence overcomes these limitations to some extent.³²