Attractive emulsion droplets probe the phase diagram of jammed granular matter

Abstract

It remains an open question whether statistical mechanics approaches apply to random packings of athermal particles. Although a jamming phase diagram has recently been proposed for hard spheres with varying friction, here we use a frictionless emulsion system in the presence of depletion forces to sample the available phase space of packing configurations. Using confocal microscopy, we access their packing microstructure and test the theoretical assumptions. As a function of attraction, our packing protocol under gravity leads to well-defined jammed structures in which global density initially increases above random close packing and subsequently decreases monotonically. Microscopically, the fluctuations in parameters describing each particle, such as the coordination number, number of neighbors, and local packing fraction, are for all attractions in excellent agreement with a local stochastic model, indicating that long-range correlations are not important. Furthermore, the distributions of local cell volumes can be collapsed onto a universal curve using the predicted k-gamma distribution, in which the shape parameter k is fixed by the polydispersity while the effect of attraction is captured by rescaling the average cell volume. Within the Edwards statistical mechanics framework, this result measures the decrease in compactivity with global density, which represents a direct experimental test of a jamming phase diagram in athermal systems. The success of these theoretical tools in describing yet another class of materials gives support to the much-debated statistical physics of jammed granular matter.

The random packing of particles is a problem of great practical and theoretical importance with applications to systems as diverse as granular materials, emulsions, and colloids. How athermal particles pack is affected by many parameters, including the packing protocol, the shape and roughness of the particles, as well as their polydispersity. Nevertheless, experiments and numerical simulations have suggested the existence of reproducible disordered packing structures, which can be achieved by sedimenting and shaking monodisperse (1, 2) and polydisperse (3) spheres, ellipsoids (4), and tetrahedra (5). For frictional particles, there emerges a reversible packing density curve from random loose packing (RLP) to random close packing (RCP) as a function of the applied tapping protocol (6). The dependence of density of jammed states on the friction coefficient has led to an equation of state and a prediction of a jamming phase diagram to describe the behavior of these systems in numerical simulations (7). Moreover, experiments on compressible two-dimensional packings of photoelastic beads (8) and foams (9) have probed configurations at different packing densities by applying an external load. The reproducibility of all these jammed states for a given set of experimental conditions suggests that a statistical mechanics framework may apply to these inherently out-of-equilibrium systems (10–12). Other studies have argued that the history dependence and heterogeneities in the packing preclude a general theory of jammed granular matter (13, 14).

In this paper, we introduce a route to jamming by packing athermal, frictionless spheres under gravity in the presence of a short-range attractive force. By examining the packing geometry in 3D, we find that the strength of the attractive interaction controls the packing density and the microstructure of jammed states. Whereas friction in granular systems introduces tangential forces into the locally jammed configurations to stabilize loose structures with fewer contacts (15), attractive forces play an analogous role via a different mechanism. When two particles almost touch under the force of gravity, the presence of short-range attraction introduces normal forces between the centers of neighboring spheres, which serve to mechanically stabilize otherwise inaccessible local configurations. The experimental distributions of local packing properties are in very good agreement with the theoretical predictions of recent models originally developed for repulsive particle aggregates: the “granocentric” model (3) and the “k-gamma distribution” of the local packing fraction (16). This result extends the range of applicability of geometrical modeling and statistical mechanics approaches to capture the effects of both attraction and polydispersity. Furthermore, the dependence of packing properties on the level of attraction provides a way to measure compactivity from the microstructure and thus explore the jamming phase diagram as a function of global parameters.

Jamming attractive athermal particles under gravity should not be confused with the widely studied gel transition in thermal systems, where classical thermodynamics applies (17–19). The absence of thermal fluctuations localizes the effect of attraction to the first shell of neighbors where the forces due to gravity and attraction balance to form a mechanically stable pack. Despite the fundamental differences between thermal and athermal systems, this study reveals one important similarity. We observe a reentrant behavior of packing density with attraction, analogous to that observed in thermal glassy systems (19, 20), thus questioning its postulated dynamical origin. Indeed, at the onset of attraction, the static packings reach densities higher than random close packing of the repulsive frictionless system. The existence of such states has been proposed numerically (13), but they have never been observed experimentally. The microscopic characterization of attractive packings therefore opens the way to new analogies between granular materials and glasses.

Results and Discussion

Characterization of Jammed Packings.

To create a jammed packing, we use athermal oil-in-water emulsions as described in refs. 21 and 22. Because the oil droplets are less dense than the continuous phase, they pack at the top surface by the buoyancy force—a process known as creaming. In addition, we introduce an attractive interparticle force by varying the concentration of the depletant SDS micelles (23), as explained in Materials and Methods. To image the static attractive packings, we use confocal microscopy (see Materials and Methods) and a typical 3D representation is shown in Fig. 1A. The two-dimensional slices of repulsive and attractive jammed packings, shown in Fig. 1 B and D, respectively, reveal that the presence of high enough attraction gives rise to voids within the packing. We reconstruct the packing structures and their navigation maps (3, 24) in Fig. 1 C and E (see Materials and Methods) to measure the number of contacts per particle, i.e., the coordination number, z (25), and the number of neighbors, n, a particle shares an interface with and the local packing fraction, ϕ_loc, which is the ratio between the particle volume, V_p, and the volume of the corresponding cell, V. The global density, ϕ, is determined by the total volume of the particles divided by the system volume.

Fig. 1.

(A) Three-dimensional representation of confocal images of an attractive emulsion packing in which the force of attraction 〈F_d〉 = 19 pN. Droplets are fluorescently labeled with Nile red dye and refractive index matched with the aqueous phase for transparency. Images are taken using a 63× oil immersion lens with a field of view of 65 μm in the xy plane. The 2D confocal slices and their reconstructed images are shown for repulsive (B and C) and attractive (D and E) packings. Ticks indicate two examples of the original spheres in the images and those found by the Fourier transform particle tracking algorithm. Navigation maps (white lines) are superimposed with the reconstructed packing (C and E) to identify cells belonging to particles. This mapping attributes each voxel of void space to the particle whose surface is closest to it. It unambiguously identifies neighbors, contacts, and cell volumes. As a function of attraction, the packings become looser and exhibit voids shown in D. These voids appear to occupy cells in the navigation map because particles above and below the confocal plane share void space in the third dimension.

Trends in Packing Properties with Attraction.

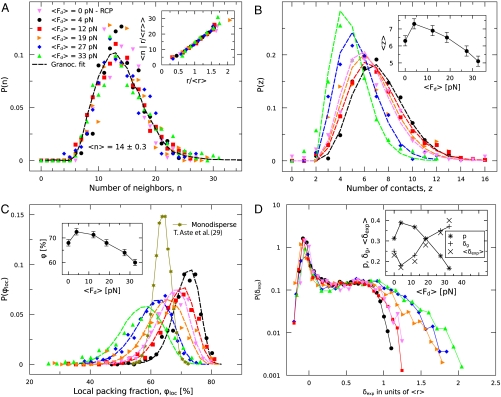
In Fig. 2 we present the probability density distributions of the local parameters z, n, and ϕ_loc as a function of attraction. Even though the packings exhibit more void space as the attraction is increased, the neighbor number distribution P(n), shown in Fig. 2A, is independent of attraction. Just as in the repulsive packings, the 〈n〉 is 14 ± 0.3 with a standard deviation of 30%, which makes sense because the navigation map partitions the extra void space between the neighbors, but the number of common interfaces remains the same. The inset shows that the particle size dependence on the number of neighbors also remains the same for all attractions, rendering the number of neighbors an insensitive measure of the packing structure.

Fig. 2.

Probability density distributions of the local quantities P(n) (A), P(z) (B), P(ϕ_loc) (C), and P(δ_exp) (D) are shown as a function of 〈F_d〉, whereas the insets present the dependency of the corresponding average values. The legend in A defines the colors and symbols for all datasets, which are used throughout the manuscript. (A) Shows that P(n) and the increase in 〈n〉 with the central particle radius are independent of attraction. By contrast, P(z) (B) and P(ϕ_loc) (C) shift to lower values as a function of attraction because looser packings are formed. This observation is corroborated by the broadening in the distribution of surface-to-surface distances between neighboring particles P(δ_exp) (D). Interestingly, repulsive emulsion packings at F_d = 0 indicate a turnover in the observed trends. All distributions are fitted very well by the granocentric model (dashed lines), whose parameters are shown in the inset in D and explained in the text.

The coordination number z reports on the number of force-bearing particles in the mechanically stable packing, which is greatly affected by the attractive forces in addition to gravity. The measured distributions P(z) in Fig. 2B peak at decreasing values from seven to four and become narrower as a function of attraction (26). The isostatic condition predicts a value of 〈z〉 = 6 for repulsive frictionless spheres in 3D (15), yet the inset in Fig. 2B shows that 〈z〉 decays as a function of 〈F_d〉 to below the isostatic limit. This decrease in 〈z〉 is possible because attractive forces allow one to locally stabilize structures with fewer than four contacts by creating loops and arches (27). With increasing attraction, the probability of such local configurations also increases, as shown in the P(z), thus shifting 〈z〉. Analogously, the distribution of local packing fraction P(ϕ), shown in Fig. 2C, shifts toward lower packing densities with wider distributions as a function of increasing attraction. The decrease in global density ϕ is also apparent in the inset. Although the trends with attraction are clear, the dataset obtained for repulsive packings at RCP reveals interesting anomalies in the local and global quantities.

An initial increase in 〈z〉 above isostaticity and ϕ above RCP at the onset of attraction is shown in the insets of Fig. 2 B and C to be significantly larger than the error bars on the measurements. It is difficult to obtain more points in the turnover region because the critical micelle concentration (cmc) occurs at 13 mM SDS (28), the weakest attraction of F_d = 4 pN is measured at 15 mM SDS, and the precision of the measurements is ± 2 mM. Nevertheless, the point at RCP is based on three different samples imaged in five different regions of 1,500 droplets each, such that the error bar quoted in the figure suggests that the reentrant transition is real. Because the deformation at such low forces has a negligible effect on the density, the answer must lie in the accessible configurations. Although jammed random states above RCP have been proposed theoretically (13), here we present an athermal experimental system that explores compact configurations while avoiding crystallization. Interestingly, a similar turnover in ϕ versus F_d has been observed in attractive thermal gels undergoing structural arrest and interpreted as the signature of a reentrant glass transition (19, 20). In our case, this turnover implies that isostatic packings with a density at RCP can also be achieved with a nonzero attractive potential, as shown by the F_d = 0 points and those at 19 pN in both insets in Fig. 2 B and C. Even though their global quantities 〈z〉 and ϕ are the same to within experimental error, we next explore the packing microstructure in search of deviations in their local configurations.

In order to characterize the local configurations of each particle, we measure the surface-to-surface distances δ_exp between a central particle and its neighbors. Those neighbors that are in contact with the central particle have a δ_exp ≤ 0, whereas the noncontacting neighbors exhibit a distribution of δ_exp that depends on the positions of the particles. In Fig. 2D, we show the distribution P(δ_exp) for all levels of attraction. They exhibit a peak in the distribution below δ_exp = 0 (signifying contacts) and a broad shoulder for the noncontacting neighbors situated at least 0.8〈r〉 away from the surface. As a function of the applied range of attraction between 4 and 33 pN, this tail broadens to reach values of interparticle distances as large as 2〈r〉, which explains the general decrease in global density. This trend is also reflected in the increasing average values of 〈δ_exp〉, shown in the inset. Interestingly, the two datasets at RCP and F_d = 19 pN with the same global quantities 〈z〉 and ϕ show significant differences in the P(δ_exp). The distribution for the 19-pN dataset displays a shift in the peak toward shorter distances and a much broader tail than that of the RCP packing. In other words, the probability of finding both tighter and looser structures is higher in the attractive than the repulsive case, which is a surprising structural distinction between packings with the same global properties. Whether these denser states become accessible due to polydispersity remains an open question.

Modeling of Local Fluctuations.

To understand the observed statistical trends quantitatively, we interpret the data using the granocentric local model introduced earlier to fit P(n), P(z), and P(ϕ_loc) (3). This model assumes two independent random processes: the filling of space around each particle with neighbors and the subsequent choice of contacts among them to ensure mechanical stability. The inputs of the model are the experimental values of 〈n〉, 〈z〉 (excluding particles with z ≤ 3), and global density ϕ, and the outputs are the distance δ_g between two neighboring sphere surfaces, as well as the distributions P(n), P(z), and P(ϕ_loc), shown in Fig. 2 A–C. In the inset in Fig. 2D , the ratio of contacts to neighbors, given by p = (〈z〉-3)/(〈n〉-3) is shown to decrease as a function of the attractive force due to the decrease in 〈z〉, whereas the predicted distance δ_g naturally increases as the packings become looser and agrees very well with the average experimental values 〈δ_exp〉.

Further confidence in the model is shown in Fig. 2 A–C by the agreement between the measured distributions and the theoretical predictions in which all parameters are fixed by experimentally determined values. Note that we do not include rattlers—particles that would move under infinitesimal shear—when fitting the granocentric model to P(z). The proportion of rattlers in the system changes the average coordination number to within the error in the image analysis and is therefore negligible in terms of the trend induced by attraction. It is surprising that this stochastic grain-centered model captures all the probability distributions because it assumes that there are no local correlations between neighboring particles nor long-range correlations beyond the first shell of neighbors. This result is in contrast to the structure of attractive colloidal gels, where the fractal dimension indicates correlations between thermal particles that persist throughout the system (17; 18).

Statistical Mechanics of Attractive Polydisperse Packings.

Given the success of the local granocentric description of the packing structure, we next consider the fluctuations in the volume V of each cell in the navigation map in terms of a statistical mechanics framework (10). Because the total volume of the packing V_tot is fixed, the navigation map partitions V_tot into N volumes V each one belonging to a particle. Independently picking volumes V from a uniform distribution between a minimum volume V_min, fixed by the smallest particle, and V_max = V_tot - NV_min results in an exponential probability distribution of volumes P(V) in the thermodynamic limit. This Boltzmann-type distribution maximizes the entropy given the constraints. Assuming that each cell V is made of k elementary cells (16, 29), this distribution becomes a shifted k-gamma distribution with a shape parameter k and a scale parameter 〈V〉-V_min:

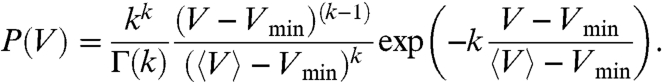[1]

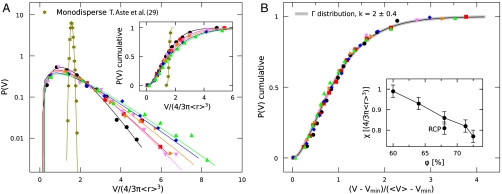
Indeed, a wide range of packings with different packing protocols and global densities have been successfully fit by this type of distribution (9, 16, 29–31). Here we investigate the effect of polydispersity and subsequent attraction on P(V). Fig. 3A shows that polydispersity of 25% alone significantly broadens the distribution compared to the previously measured monodisperse case (star symbols) (29) and shifts the global packing fraction to a higher value. If this effect were simply the result of a convolution of the monodisperse P(V) with the distribution of particle volumes, rescaling each V by the volume of the particle itself would lead to exactly the same distributions P(ϕ_loc) for the mono- and polydisperse cases, shown in Fig. 2C. However, even the rescaled polydisperse distribution remains broader, indicative of an additional source of randomness to the size distribution. Within the statistical mechanics framework, the volume V replaces the energy E and the compactivity χ is the analogue of temperature T. Because k is the derivative d〈V〉/dχ (16), it is equivalent to the specific heat in thermal systems. Fitting the mono and polydisperse cases with k ≈ 14 and k ≈ 2, respectively, captures the observed changes in shape and width of P(V) in Fig. 3A. This decrease in k means that polydispersity lowers the specific heat as fewer random variables are needed to define the volumes, thus approaching the Boltzmann distribution with maximum entropy.

Fig. 3.

(A) Evolution of P(V) and its cumulative distribution for different levels of attraction. Notice that V is rescaled by the volume of the average particle for each distribution. The distributions shift to larger volumes as a function of attraction. The data are fit with the shifted Γ distribution in Eq. 1 and compared to the monodisperse case. (B) Data collapse is observed when V is rescaled by the shifted average volume of the cell 〈V〉-V_min. This rescaling implies that the shape parameter k remains constant with attraction. The inset shows that the compactivity χ decreases with increasing density ϕ, which is consistent with the observed decrease in 〈V〉. The RCP point curiously does not have the lowest compactivity.

As a function of attraction, Fig. 3A shows an increase in both 〈V〉 and the standard deviation σ of the distributions, as expected from the looser packing structures. Because Eq. 1 gives 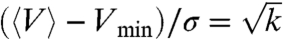, this dependence leads to a constant value of k = 2.0 ± 0.4 for all levels of attraction. This result is shown in Fig. 3B by the data collapse that results from rescaling the volumes as (V - V_min)/(〈V〉-V_min).

Within the thermodynamic framework, a simple counting argument of volumes leads to a definition of the entropy S and consequently an expression for the inverse compactivity χ^-1 = ∂S/∂V_tot in granular statistical mechanics. The resulting expression for χ = (〈V〉-V_min)/k is shown to be linearly decreasing with density in the inset in Fig. 3B. By comparison, compressed packings of 2D foams exhibit an increase in k with density, which leads to a sharper decrease in χ (9). Because χ is a measure of the ability to compact the system further, it makes sense that looser packings result in higher values of χ and have a higher entropy.

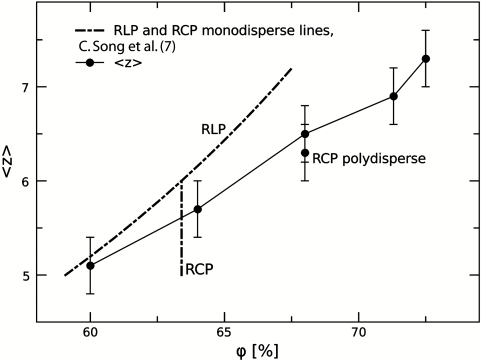
Recently, a phase diagram for jammed matter has been proposed in terms of the dependence of χ and 〈z〉 on density for monodisperse frictional hard spheres (7). Because polydisperse packings pack more efficiently than monodisperse ones, the RLP–RCP lines are shifted to higher densities (3, 32). Moreover, the theoretical RLP line is determined for infinite χ. Because the measured χ in our packings is decreasing with density, the values of 〈z〉 we obtain at different densities cannot be directly compared with those at infinite χ. For these reasons, our data shown in Fig. 4 lie below the predicted RLP line at infinite χ (dash-point line), which we have extended beyond the monodisperse RCP density of 64% for comparison with the polydisperse packings in the figure. These measurements therefore map out the predicted phase diagram for our particular experimental protocol and system, in which packings denser than RLP are achieved over the same range of 〈z〉, consistent with the fact that we explore states with decreasing values of χ. Surprisingly, we extend the limits of the phase diagram to hyperstatic packings up to 〈z〉 = 7.5 and densities up to 74%, which is above the RCP density (68% in the polydisperse case). The microscopic mechanism for jamming with attraction and the origin of these states provide interesting questions for further study.

Fig. 4.

The global trend in the average coordination number versus density maps out an equation of state for polydisperse packings at different levels of attraction. The resulting curve lies below the theoretical RLP line for monodisperse frictional spheres at infinite χ (7), which is to be expected because polydisperse packings occur at higher densities (as indicated by the shift in the polydisperse RCP point). Moreover, our packings exhibit a decrease in χ with density, such that they necessarily probe the phase diagram below the limit of infinite χ.

Materials and Methods

Depletion Attraction Forces.

The depletion energy has an entropic origin and its dependence on the surfactant concentration is derived in ref. 33 and validated for our emulsion system in refs. 23 and 34. Therefore the depletion attraction force between two spheres of radii r₁ and r₂ whose centers are a distance L apart is given by

[2]

if (L - r₁ - r₂) < d and F_d = 0 otherwise. Here d is the micelle diameter and P_m = k_BTn_m is the depletant pressure, where n_m is the depletant concentration, k_B is the Boltzmann constant, and T is the temperature. Given that the linear size of the micelles is approximately 500 times smaller than the size of the smallest emulsion droplet, and that the micelle volume fraction is always below 2%, it is adequate to model the depletant pressure as that of an ideal gas (35, 36).

We calculate F_d at an equilibrium distance L of around 10 nm (23) and using a cmc of 13 mM (28). The average depletion force 〈F_d〉 for each packing is defined as the force between two droplets of average radius 〈r〉 = 3.5 μm. Because the particle size distribution has a 25% standard deviation in radius, the depletion force between particle pairs picked at random and calculated using Eq. 2 has a distribution with a standard deviation of ± 20%. Note that the average attraction force increases significantly more than the spread of each distribution. The maximum force of 〈F_d〉 = 33 pN is set by the saturation point of SDS (i.e., 50 mM). This range is 10–100 times stronger than the weight of a single particle and corresponds to small deformations of 1–10 Å, such that the spherical approximation holds.

Confocal Imaging and Analysis.

The protocol to prepare the jammed packing sample involves creaming a very dilute emulsion (22) at a density ϕ ≈ 5% to avoid clustering and aggregation of the particles. Refractive index matching between the droplets and the aqueous phase allows us to image the dynamics of the packing process in real time and investigate the resulting structure in 3D using a fast scanning confocal microscope (Leica TCS SP5 II). The droplets deposit onto the surface one by one and subsequently slide, roll, and stick until they are locally jammed. Once the packing of approximately 1,500 droplets is formed, a box of volume 65 × 65 × 100 μm several particles away from the boundaries of a 1-mL container is imaged in the confocal microscope. The voxel size is 130 nm in the horizontal xy plane and 300 nm in the vertical z direction.

We analyze the structures in terms of the particle positions and radii with subvoxel accuracy using a Fourier transform algorithm (22). We then use the geometrical overlaps in the reconstructed spheres to identify particles that are in contact, which allows us to measure the number of contacts a particle has, i.e., its coordination number, z. The error in estimating particle positions and radii translates to an error of ± 0.3 in the 〈z〉 estimation. To characterize the local neighborhood of each particle we tessellate space using the navigation map (3, 24) shown in Fig. 1 C and E. This mapping defines the number of neighbors, n, the local packing fraction, ϕ_loc, and the volume of every cell, V.