Predicting clonal self-renewal and extinction of hematopoietic stem cells

Abstract

A single hematopoietic stem cell (HSC) can generate a clone, consisting of daughter HSCs and differentiated progeny, which can sustain the hematopoietic system of multiple hosts for a long time. At the same time, this massive expansion potential must be restrained to prevent abnormal, leukemic proliferation. We used an interdisciplinary approach, combining transplantation assays with mathematical and computational methods, to systematically analyze the proliferative potential of individual HSCs. We show that all HSC clones examined have an intrinsically limited life span. Daughter HSCs within a clone behaved synchronously in transplantation assays and eventually exhausted at the same time. These results indicate that each HSC is programmed to have a finite life span. This program and the memory of the life span of the mother HSC are inherited by all daughter HSCs. In contrast, there was extensive heterogeneity in life spans between individual HSC clones, ranging from 10 to almost 60 mo. We used model-based machine learning to develop a mathematical model that efficiently predicts the life spans of individual HSC clones on the basis of a few initial measurements of donor type cells in blood. Computer simulations predict that the probability of self-renewal decays with a logistic kinetic over the life span of a normal HSC clone. Other decay functions lead to either graft failure or leukemic proliferation. We propose that dynamical fate probabilities are a crucial condition that leads to self-limiting clonal proliferation.

As in all adult stem cells, hematopoietic stem cells (HSCs) are defined by multipotent differentiation ability and extensive self-renewal capacity. When a HSC commits to differentiate, it exits the stem cell pool and generates mature cells through a cascade of differentiation steps. HSCs also self-renew to give rise to daughter HSCs that again can self-renew and differentiate. Together these mechanisms can expand a single HSC into a large clone that can provide mature cells for the life span of the organisms and even can outlive the original donor (1–7). These findings have led to the idea that HSCs can live forever. However, not all HSCs form large clones and many HSCs are short-lived (1–3, 8–10). These data, in turn, prompted the hypothesis that individual HSCs have a short life span and sequential activation of dormant HSC is necessary to maintain the HSC compartment (11). However, it is now firmly established that many different HSCs are active at the same time and that these HSCs differ in their self-renewal capacity (2, 8, 10).

Numerous mechanisms, both HSC intrinsic and extrinsic, have been implicated in regulating HSC proliferation. For example, overexpression of many of the Hox genes can dramatically increase HSC self-renewal (12, 13). Modulation of the niche can change the number and location of HSCs (14–16). It is clear that the self-renewal capacity of HSCs must be tightly controlled. HSCs need extensive self-renewal capacity to prevent hematopoietic failure. However, uncontrolled proliferation leads to leukemia. In this context it is surprising that individual HSCs with the same genetic makeup differ in self-renewal capacity. The mechanisms that control these differences remain incompletely understood.

To investigate this, several groups have focused on two subpopulations of HSCs, called short-term and long-term repopulating HSCs. Both types of HSCs can generate all mature cells in transplantation settings, but only long-term repopulating HSCs have self-renewal capacity (7–9, 17). These HSC types can be separated phenotypically and they differ in expression of HoxB4 and Bmi1 (9, 12). These data suggest that differences in self-renewal capacity are deterministic (9).

The apparent dichotomy of HSCs that either lack or posses self-renewal capacity is misleading. Even long-term repopulating HSCs can differ noticeably in clone size and self-renewal capacity (1–7). To analyze the cellular and molecular mechanisms that differentially regulate the life span of long-term HSCs, it will be necessary to prospectively identify HSCs that differ in self-renewal.

Predicting HSC function has long been of interest in transplant settings (18, 19). Initially, the focus of these efforts was to ensure rapid engraftment because it determines short-term survival. A strong correlation of the number of CD34 cells injected with early onset of engraftment has been demonstrated by many transplant centers. So far, only few predictors for sustained engraftment have been identified. Telomere length in donor cells has been proposed to predict graft failure (20–22). The number of marrow cells transplanted (18, 23), early neutrophil engraftment (24), and T-lymphocyte chimerism (25) are positively correlated with sustained engraftment. Accurate predictions of long-term engraftment will be most important when the number of infused HSCs is limiting. Pauciclonal engraftment and eventual HSC extinction have been documented when HSCs expressing a corrected gene were transplanted for gene therapy (26).

We have developed an algorithm that predicts the long-term performance of individual HSC clones on the basis of a few initial measurements of the percentage of donor-type cells (%DT) in blood. In vitro and in silico analyses indicate that preprogrammed changes in the self-renewal program cause clonal extinction of HSCs. Together, these findings provide a new model of the dynamics of the clonal life and death of HSCs.

Results

Predicting HSC Self-Renewal.

We wished to identify more precise predictors for self-renewal capacity. Because self-renewal decisions are made by individual HSCs, we analyzed HSCs on the clonal level. Clonally derived HSCs were obtained by injecting limiting numbers of HSCs into ablated hosts as previously described (10, 27, 28). Serial transplants were performed to assess whether HSCs had self-renewed in the primary host to generate HSCs that could repopulate multiple secondary hosts (Figs. 1 and 2). At the time of the secondary transplant, the %DT in blood, bone marrow (BM), and spleen of the primary host were recorded. We also measured the frequency of donor-derived colony-forming units, common lymphoid progenitor (detected by its ability to initiate Whitlock–Witte cultures) (29), and long-term culture-initiating cells (30, 31) (a surrogate assay for HSCs) (Table S1). Principal component analysis of the data from 13 independent HSC clones identified two dimensions in the data set (Fig. S1A) represented by the “%DT in blood” and “%DT in BM.” These dimensions were used in best subset regression analysis. We found that %DT in blood in the primary hosts is the major predictor of self-renewal capacity (Fig. S1B) with a Bayesian information criterion of –22. Subsequent testing of individual linear regression models confirmed these findings (R² = 0.79; P = 2E-08). Most of the predictive power for self-renewal capacity derived from the myeloid cells in the %DT (R² = 0.74; P = 2E-08).

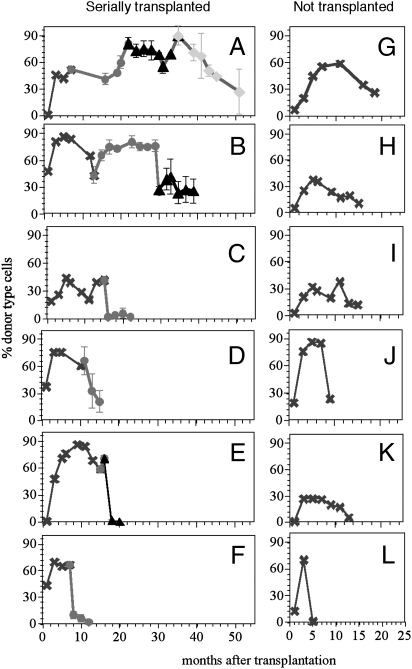
Fig. 1.

Individual HSCs have distinct clonal life spans. (A–L) The %DT at different times after transplant of a single HSC. (A–F) Serial transplants were performed. At the indicated time points HSCs from the primary host (x) were transplanted into the secondary (○), and then the tertiary (△), and finally the quaternary (◆). Because secondary and higher transplants used several hosts per HSC clone, mean repopulation (±SD) is shown. In some instances the errors are too small to be discernible. The small errors reflect the similarities in repopulation kinetics of HSCs within a clone. Extrapolation of the curves to the right intersection with the time axis was used to estimate ”actual” life spans. Early data points for the HSC clones in A and B were published previously (10). (G–L) Clonal HSC life spans without serial transplants. These HSCs aged in the primary host.

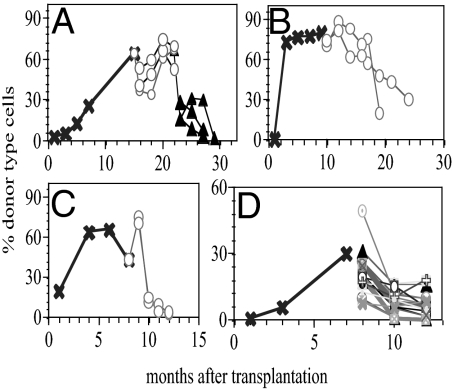
Fig. 2.

Concerted repopulation kinetics of daughter HSCs within a clone. (A–D) The %DT for individual hosts at different times (horizontal axis) after transplant of single HSCs. (A–C) At the indicated time points, 5 × 10⁶ BM cells from the primary host (x) were transplanted into 2–3 secondary (○) hosts, and then into 4 different tertiary (△) hosts. Occasionally, the symmetry of repopulation levels is broken. For example, one mouse in B rapidly lost DT cells in blood at 18 mo after injection. This mouse died shortly thereafter, suggesting that the abrupt shift in %DT was pathological. (D) A total of 4 × 10⁴ BM cells from the primary host were transferred into 15 secondary mice.

Programmed Life Spans of HSC Clones.

The life span of a HSC clone is a function of the self-renewal capacity of all HSCs in that clone. We define the life span of a HSC clone as the total time for which this clone generates both myeloid and lymphoid cells detected in blood. The results in the previous paragraph predict whether a HSC can self-renew but this approach does not provide a quantitative measure of self-renewal and, consequently, does not predict the life span of a HSC clone. From previous studies (10), we knew that a subset of HSCs repopulates late after transplant but then generates increasing levels of mature donor-type cells. HSCs with self-renewal capacity are found only in this group, but not all HSCs in this group can self-renew (10). To develop more precise predictions for self-renewal capacity, we focused on that HSC subset. HSCs with other kinetics of repopulation predictably have a short life span (10) reflecting their lack of self-renewal capacity.

While following 44 individual HSCs in vivo, we noted that all showed similar repopulation kinetics resembling a ballistic curve (Figs. 1 and 2). Every HSC clone examined ceased to generate mature cells at some time point. Once the %DT in blood had declined to ~20%, BM cells from these mice could not repopulate subsequent hosts. These results suggest that the decline in mature cells in the periphery marked the end of the life span of the HSC clone. To test if the serial transplants caused the ballistic shape, we followed 6 individual HSC clones in the primary hosts without attempting second transfers (Fig. 1 G–L). The same ballistic curves were seen, indicating that these kinetics reflect HSC-intrinsic properties.

Remarkably, HSCs within a clone proceeded synchronously through the life span kinetics. Daughter HSCs, derived from a single mother HSC, showed very similar kinetics of repopulation when transplanted into multiple secondary and/or tertiary hosts (Fig. 2). These data extend previous observations made on only two HSC clones (5). Are the similarities in the repopulation kinetics derived from the average behaviors of the daughter HSCs or are all daughter HSCs similar to each other? To test this, we performed a secondary transplant using close to clonal levels of HSCs isolated from the primary hosts (Fig. 3D). Thirty-one percent of the secondary hosts were negative with a corresponding probability of 88% that each mouse received a single or at most two HSCs. Again, the repopulation kinetics in the secondary hosts were very similar, suggesting that the life span is programmed into each daughter HSC within a clone. The programmed extinction of daughter HSCs within a clone allowed us to define a clear endpoint to the life span of each HSC clone. Moreover, it suggested that the life span of a HSC clone is programmed and therefore predictable.

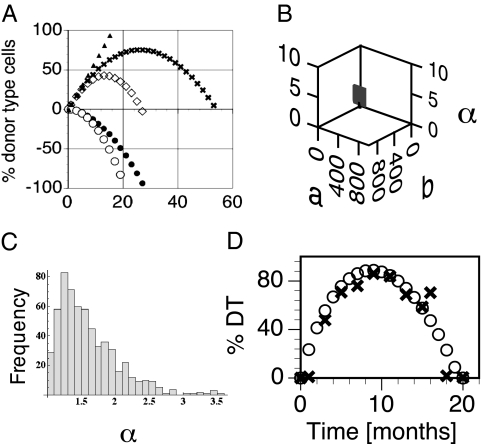
Fig. 3.

Ballistic model of clonal aging. (A) Examples of how the function D(t) is derived from the interplay between the growth function D⁺(t) = bt and the decline function D⁻(t) = −at^α. Here, b was fixed and a was normalized to 1. Different values for α yield distinct life-span curves; e.g., for α = 1.6, the decline function (●) interacted with the growth function (▲) to generate a long life span (x). For α = 2.0 (decline function ○), we obtained a short life span (◇). (B) Parameter space of the prediction model. We tested 10⁷ variations of the parameters (b, a, α) by Monte Carlo simulation. For a and b we used a range of 1–10⁵ and 1 < α < 10 [α > 1 excludes linear D(t); α < 10, because large α quickly yields very short life spans (<1 mo)]. Shown are (b, a, α) that generate permissible configurations (1 < T < 1,000). (C) Frequency distribution of α: No permissible values were found for α > 3.52. (D) The shapes of the predicted (○) and the experimental data (x) match well.

Predicting the Life Span of HSC Clones.

We found extensive heterogeneity in the life span of different HSC clones, ranging from 5 to 58 mo (Fig. 1). Next, we tested whether this measure could be used to predict the overall life span of a HSC clone. Each life-span curve (Figs. 1 and 2) is anchored on the time axis at the origin (t = 0) and the point of extinction (lifespan t = T) and generally follows a ballistic path. We used this shape as a guide for developing a predictive model of clonal life span of HSCs based on three parameters, denoted b, a, and α,

where t is time, D(t) is %DT as a function of time, b is the average rate of growth of all cells in a clone, a is the average rate of cell loss, and α is the degree of slowing down (32) of the life-span curve (decline of HSC self-renewal). Eq. 1 is an additive effects model with linear expansion D⁺(t) = bt and a Weibull failure process D⁻(t) = –at^α that models deceleration and extinction (Fig. 3A). The parameter α > 1 quantifies the degree of the phase transition (33) from growth to extinction. Together, the parameters (b, a, α) provide a quantitative model T = (b/a)^1/(α−1) for the life span of single HSC clones because the life span T can be calculated directly from Eq. 1 using the boundary condition D(T) = 0. We tested 10⁷ combinations of the parameters (b, a, α) to identify permissible configurations where 0 < T < ∞ (1,000 mo was used as a stand-in for infinity). The resulting parameter space is surprisingly small (15% permissible configurations) and clustered in a tight region in the lower end of the ranges (Fig. 3 B and C).

Any configuration in the permissible range can be used to calculate a complete life-span curve. The calculated curves can be compared with experimental repopulation data using a χ²-distance. A match (Tables S2 and S3) was scored only if two criteria were fulfilled: The configuration minimized (i) χ² for a few initial measurements and (ii) the fuzzy distance (34) between the life spans of in vivo and predicted kinetics (Fig. 3D). To optimize prediction, we used preexisting data (27) of the repopulation kinetics of 17 HSC clones (Table S2) as a training set. We applied reinforcement learning (35) to train the search for high-quality configurations in a large Monte Carlo database of permissible configurations. The rewards for correctly identified configurations consisted of local expansions of the database near χ² minima. Hence, training increased the efficiency of finding good predictors for new kinetics. At the end of the learning process, the rate of correct predictions had increased from 65 to 83% (Table S2). To validate this, we applied the trained algorithm to a priori predict the life span of 27 new HSC clones (Fig. 4 and Table S3). We correctly predicted the life span of 85% of the HSC clones in this set.

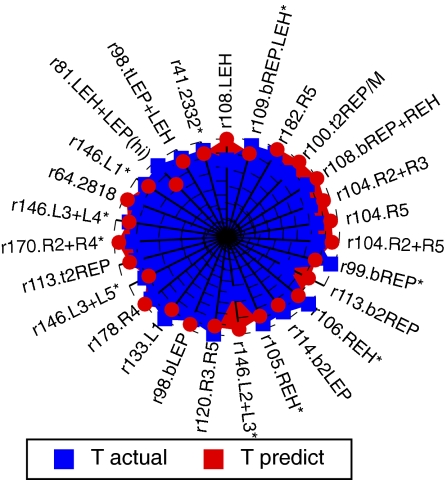
Fig. 4.

A priori prediction of the life span of 27 HSC clones. The predicted (red) and actual (blue) life spans are shown (from Table S3). Axis units are months.

Multiple rounds of cross-validation were performed to demonstrate the independence of outcomes from the training set selection. Training the algorithm using stochastic data (Brownian bridges) led to poor matches (17.3%; P = 3E-24). This result confirmed that the learning algorithm was trained to detect features of HSCs rather than random behaviors. The rate of correct predictions declined, when fewer data points were used. It was a respectable 76% when using the first three data points, but declined to 57% for two data points. Collectively, the data suggest that we have developed a powerful tool for predicting the life span of HSC clones on the basis of the first four experimental data points (%DT).

To determine the accuracy with which individual points in the curve are predicted, we calculated the logarithmic error function log(|X(t) − D(t)|) between the experimental data X(t) and the corresponding predicted values D(t). The curves were significantly different (P = 0.002), mostly due to dips in the experimental data caused by the serial transplants. However, on average, the data points of the curves deviated by only 11%DT. The small error attests to the strength of the simple deterministic model of HSC life spans.

Computer Simulation of Clonal Aging.

Previous models aimed at understanding the proliferation of HSCs focused on the dichotomy of self-renewal and differentiation (33, 36–38). Our results that programmed extinction is a key feature of all HSCs provide a new criterion to refine predictive models of HSC behavior. To identify parameters that affect the life span of HSC clones we used a cellular automaton simulation method that we had previously developed (39).

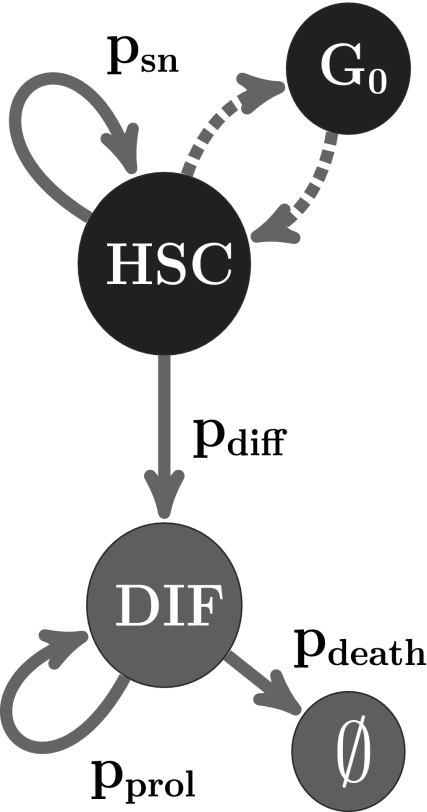
We started each simulation by transplanting a single HSC. A simulated cell (Fig. 5) is defined by a vector (c, ω, τ, θ) whose components are c, cell type; ω, proliferative capacity; τ, resistance to differentiation; and θ, division history. We consider two groups of cell types: HSC (c = 1) that can self-renew and differentiate and DIF (c = 2) that comprises all cell types derived from HSC and that can proliferate or die. DIF is any hematopoietic cell that is not a HSC. The parameters ω and τ are constant, cell-type specific, and the same for all daughter HSCs. Thus, the fundamental characteristics of a HSC are assumed to be conserved from generation to generation. A switch to different settings for ω and τ occurs only as the result of differentiation (or death). The local cellular automaton rules are:

Which rule is applied to an individual cell depends on a global, uniformly random, variable ρ. For example, an HSC self-renews if the self-renewal probability p_sn ≤ ρ. The probabilities of self-renewal, differentiation, proliferation, and death (p_sn, p_diff, p_prol, p_death) are generated by the system as functions of ω, τ, and θ. Thus, the transition probabilities are not necessarily constant. We systematically used different functions to represent four different decay models for making fate decisions. These were (i) constant, (ii) linear, (iii) nonlinear elliptic, and (iv) nonlinear logistic decay functions of θ. The single and unique constraint used here was that the life span of HSCs is finite.

Fig. 5.

Simulating clonal HSC life spans. Two cell types are considered. HSCs can self-renew, be in a quiescent state (G₀), or differentiate into precursors and mature cells (DIF). In the simulator, the resting state is a by-product of asynchronous updating (39). The likelihood that a HSC divides into two daughter HSCs or into two DIF cells is determined by transition probabilities. Asymmetrical division scenarios were also considered and gave comparable results.

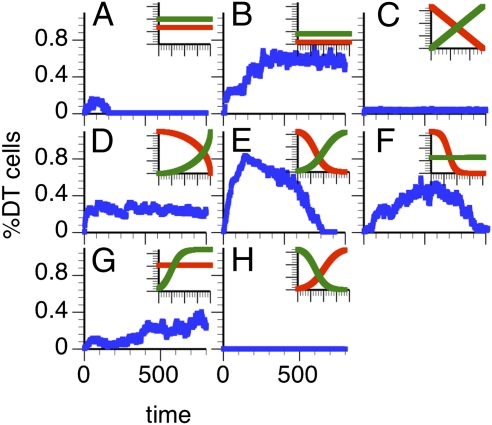
We conducted 5,000 computer experiments for each model. The lifespan T and the proportion of HSC clones with finite life spans were recorded. For the constant model, we systematically varied the constant probabilities p_sn and p_diff between 0 and 1 in steps of 0.05. We found that 97% of HSCs lived either an extremely short (T ≤ 1) (Fig. 6A) or an unlimited (T > 1,000) time (Fig. 6B). Thus, the constant model is not a good fit to the experimental data. Differences between the models (ii–iv) lie in the rate with which self-renewal/proliferation capacity is lost as a function of the division history and the resistance to differentiation. Most (61%) of the outcomes of the linear decay model yielded curves of extremely low clone size (Fig. 6C). The nonlinear elliptic (Fig. 6D) improved predictive value; only 29% of the curves show unlimited life spans. The best results (0% failure) were obtained with the logistic decay function (Fig. 6E). Only this model produced the characteristic ballistic shape and finite, nontrivial life span that we see in our experimental data. Interestingly, the type of differentiation function was not important for generating meaningful outcomes (Fig. 6 F–H). Constant p_sn and logistically increasing p_diff yielded slowly growing, immortal clones of moderate sizes (Fig. 6G). Collectively, the data show that nonlinear decline of the self-renewal capacity was the one parameter that was important to obtain good matches of simulations and experimental data. This model predicts that the self-renewal capacity is the essential parameter that determines the life span of HSC clones. Finally, to facilitate a direct comparison of the in silico and in vivo data, we calculated their scaling factor σ ~ 10. Thus, one simulation step represents 3–4 d in real time.

Fig. 6.

Simulations predict a logistic decline of self-renewal during the life span of HSC clones. (A–H) The simulated %DT (blue) after transplantation of a single HSC. All simulations were extended to 1,600 time points. (Insets) At the level of individual cells, the intrinsic fate probabilities as functions of division history (θ, horizontal axis) that yielded the blue curves. Red, probability of self-renewal (p_sn); green, probability of differentiation (p_diff). (A and B) Constant p_sn and p_diff; (C) p_sn and p_diff decline/increase linearly; (D) p_sn and p_diff decline/increase elliptically; (E) logistic change of p_sn and p_diff; (F) logistic p_sn with constant p_diff; (G) constant p_sn and increasing p_diff; (H) HSCs with high initial p_diff and low p_sn.

Discussion

The safety of applying ES cells (and related stem cells) for tissue regeneration depends on harnessing and precisely controlling the proliferative capacity of these cells. Therefore, a better understanding is needed of how adult tissue stem cells maintain extensive self-renewal capacity but guard against unregulated proliferation. We performed a systematical analysis of the long-term repopulation capacity of a large cohort of individual HSCs. Despite their extensive self-renewal capacity, each HSC clone ceased to produce mature progeny at some point. Our results predict that self-renewal declines nonlinearly, with a logistic kinetic, over the life span of the HSC clone. This prediction presents a new, testable model of HSC self-renewal.

The end of the clonal life span reflected a synchronized decline of all HSCs in the clone. Synchronous progression of all members of a clone through life is a hallmark of programmed aging (40, 41). Remarkably, HSCs within a clone proceeded synchronously even when the HSCs were located in different hosts, unable to communicate with each other. The data imply that the basis for this synchronicity is HSC intrinsic and, perhaps even more intriguing, that all daughter HSCs have a memory of their mother's and grandmother's lives. This result excludes random mechanisms such as mutations as major contributors to HSC aging. Programmed life span was previously documented in a colonial protochordate (41). Perhaps, programmed lifespan is a mechanism that has evolved in colony-forming, niche-invading systems. It is tempting to speculate that programmed aging governs the behavior of other types of stem cells.

The finding that all HSCs had a limited life span was the basis for our simulation approach. Interestingly, the simulations autonomously generated a model where self-renewal declines nonlinearly. This finding is a fundamental shift from the classical view of HSC self-renewal, which assumed a constant probability of self-renewal of ~0.5 (reviewed in ref. 42). A death rate that increases over time is characteristic of aging, whereas a constant (linear) death rate describes mortality through accidents and disease, mechanisms that are not related to aging (43). Thus, the logistic decline of self-renewal predicted by our model supports the interpretation that each HSC clone ages (although HSC aging occurs continuously throughout the life of the organism) (28).

Surprisingly, we found that the declining portions of the clonal repopulation curves fit a Weibull mortality function, but not a Gompertz or other model. In aging research, a Gompertz fit is a good estimator of general mortality (so-called “all causes” category). In contrast, a Weibull function is considered a fit for death caused by a single cause or disease (43, 44). The latter is consistent with the interpretation that the clonal HSC life span is limited by few, rather than many, factors. The mathematical model agrees well with the emerging concept that only a few factors are needed to determine the fate of stem cells (45).

Our logistic model was to some extent presaged by the generation-age hypothesis. This hypothesis postulated that HSCs lose some quality, termed stemness, at each division (46). Variations of this model have been explored by others (38). Our model now provides quantitative predictions of the life span and behavior of HSCs over time. Perhaps the logistic kinetic of the HSC life reflects dynamic changes in the HSC intrinsic molecular regulators of self-renewal. If so, positive regulators of self-renewal would decline, but would not be absent in HSCs at the end of the clonal life span. Inhibitors of self-renewal would be expected to have an opposite kinetic. On the basis of the fit with the Weilbull function, we predict that only a few regulators are necessary to determine the life span of HSCs. Such a simple model would readily explain the marked differences in life span of individual HSCs through differences in the gene dose of such regulators. Our model can make accurate and scalable predictions about the life span of HSC clones. This capability should facilitate the isolation of HSCs at distinct time points in their life span and, in turn, facilitate testing these predictions.

There is ample evidence that the environment can affect the proliferation of HSCs although our studies were not designed to detect extrinsic effects. Here, all HSC clones were followed in young hosts, supplemented with an excess of radioprotecting HSCs. Therefore, all HSC clones were exposed to a comparable environment known to be supportive of HSC expansion. All HSC clones encountered similar proliferative pressures. In this standardized environment, HSC clones showed remarkably different life spans, supporting the interpretation that HSC-intrinsic programs play a major role in the control of the life spans.

Several of the HSCs examined here had long lives, exceeding the life span of a single host. Therefore, serial transplants were necessary to determine the end of their life span. Several studies have shown that serial transplants do not damage HSCs (47, 48). Whereas primitive HSCs are activated, they return quickly to quiescence after transplantation. This process preserves their self-renewal capacity and counteracts potential transplantation-related effects (17, 47). Our observations further support the interpretation that the serial transplants did not distort the behavior of the HSCs: (i) HSCs follow the same ballistic life-span curve regardless of whether they experienced serial or only one transplant; (ii) Our algorithm provided accurate predictions on the basis of the repopulation data obtained in the primary host, regardless of whether the end of the clonal life span was seen after zero or up to three additional transplants. Thus, the life span of the HSC clone is already predictable during the first 5–7 mo after transplant and subsequent transplants do not change the life span. We cannot exclude that the primary transplant changed the behavior of HSCs. However, a predictive model of HSC behavior is most useful in a transplant setting—which our approach models. Collectively, the results show that our algorithm is an accurate tool for predicting clonal expansion and extinction of HSCs.

Materials and Methods

Clonal Analysis.

Freshly explanted BM cells were transplanted in limiting dilution into lethally irradiated CD45 congenic hosts exactly as described (5, 10, 27, 28). Each host received on average 0.2–0.5 HSCs together with 2×-tranplanted BM as a source of radioprotecting cells. Mice were bled in regular intervals and the percentages of myeloid and lymphoid cells among the DT cells were measured by flow cytometry. All experiments were approved by the Institutional Animal Care and Use Committee. For more details see SI Materials and Methods.

Software.

We used the R statistical programming environment for all computations. The Mann–Whitney test was used to calculate significances.

Determination of Life Spans from the in Vivo Database.

To determine the end of life for the experimental repopulation kinetics, we used the last four data points (%DT) to derive a regression line. We then used the intersection of the time axis with the 95% confidence interval around the regression line to derive an interval that contained the end of life of the HSC clone.

Computer Simulation of Life Spans.

This work was done as described in ref. 39. For more details see SI Materials and Methods.