Analysis of natural allelic variation in Arabidopsis using a multiparent recombinant inbred line population

Abstract

To exploit the diversity in Arabidopsis thaliana, eight founder accessions were crossed to produce six recombinant inbred line (RIL) subpopulations, together called an Arabidopsis multiparent RIL (AMPRIL) population. Founders were crossed pairwise to produce four F1 hybrids. These F1s were crossed according to a diallel scheme. The resulting offspring was then selfed for three generations. The F4 generation was genotyped with SNP and microsatellite markers. Data for flowering time and leaf morphology traits were determined in the F5 generation. Quantitative trait locus (QTL) analysis for these traits was performed using especially developed mixed-model methodology, allowing tests for QTL main effects, QTL by background interactions, and QTL by QTL interactions. Because RILs were genotyped in the F4 generation and phenotyped in the F5 generation, residual heterozygosity could be used to confirm and fine-map a number of the QTLs in the selfed progeny of lines containing such heterozygosity. The AMPRIL population is an attractive resource for the study of complex traits.

Most traits in cultivated and natural populations are quantitatively inherited and have a complex genetic basis (1, 2). The identification of quantitative trait loci (QTLs) represents a first step toward dissecting the molecular basis of such complex traits (3). Analyzing specifically created artificial populations has clearly been successful in detecting QTLs in plants, and some QTLs have been cloned not only in the model plant Arabidopsis (2) but also in crop plants.

A prerequisite for QTL mapping studies is the construction of mapping populations. Many population types have been derived from crossing two inbred parents. Among these populations, recombinant inbred lines (RILs) have the special advantage that they are “immortal” and can be used in multiple experiments. QTLs can only be detected in genomic regions for which the parents of a cross differ. Biparental populations represent a very limited sample of genetic variation and have a large probability for parents to carry the same alleles at a locus. In contrast, wide genetic variation can be included in association panels. Such panels promise high resolution because of strong accumulation of recombination events (4). A disadvantage of association panels is the variation in pairwise relationships between included genotypes, making it harder to distinguish true-positive from false-positive QTLs. An alternative to biparental populations that does allow inclusion of wide genetic diversity but does not suffer from the above inferential problem hindering association studies is provided by multiparent populations (5). Multiparent populations have increased probability of QTLs being polymorphic across the multiple parents (5). The properties of a multiparent population are determined by the mating design (6), the relationships between the parents (7, 8), and the type of families being developed [e.g., doubled haploid (DH), RIL]. Two main types of multiparent populations can be distinguished: (i) single multiparent populations developed from intercrossing many parents, followed by one or a few rounds of intermating of offspring and a few final rounds of inbreeding and (ii) populations consisting of a connected set of crosses or families. Multicross populations allow easy and powerful tests for epistasis in the form of QTL by background interaction, where the background refers to the differences between the crosses that act like subpopulations.

A presently popular type of multicross population is the star design population used in nested association mapping (NAM) (9, 10), where a central parent is crossed with other parents. The star design maximizes genetic variation across contributing parental lines. This design can facilitate physiological compatibility for the whole of the multicross population when the central parent is well adapted to the local conditions. Another type of multicross population is the diallel cross (7, 11). Many other types of multicross populations are possible.

An example of a single multiparent population that combines high resolution with large genetic diversity is the multiparent RIL population proposed for mice by the Complex Trait Consortium (12), known as the collaborative cross. Simulation studies demonstrated the power properties of this population for QTL mapping (12, 13). In plants, similar populations were proposed by Cavanagh et al. (5), under the name of multiparent advanced generation intercross (MAGIC) populations. Recently, Kover et al. (14) described such a MAGIC population for Arabidopsis consisting of 527 RILs derived from intercrossing 19 founders.

In this paper, we propose an Arabidopsis multiparent RIL (AMPRIL) population consisting of a set of six connected four-way crosses obtained from eight founder lines, diverse accessions of Arabidopsis thaliana (Fig. 1). We describe the structure of the population and introduce mixed-model methodology for QTL analyses. These analyses, using phenotypic data for 13 often related developmental traits (SI Appendix, Table 2), are followed by elaborations and discussions of the genetic properties of the AMPRIL population, such as resolution and power as well as the advantage of residual heterozygosity for QTL fine-mapping.

Fig. 1.

Construction of the AMPRIL population. (Upper) Four founder accessions (P1, P2, P3, and P4) are crossed to produce two hybrids (A and B) and one four-way cross. The resulting population is selfed for three generations (F1 to F4). For the whole of the AMPRIL population, eight parents (P1 to P8) were chosen, which led to four hybrids: A, P1 × P2 = Col × Kyo-1; B, P3 × P4 = Cvi × Sha; C, P5 × P6 = Eri-1 × An-1; and D, P7 × P8 = Ler × C24. (Lower) Hybrids were crossed according to the diallel scheme.

Results

Development and Genotyping of the AMPRIL Population.

A set of eight Arabidopsis accessions (Col, Kyo-1, Cvi, Sha, Eri-1, An-1, Ler, and C24; SI Appendix, Table 1) with different geographic origins was pairwise crossed to produce four two-way hybrids (we called them A, Col × Kyo-1; B, Cvi × Sha; C, Eri-1 × An-1; and D, Ler × C24). These four two-way hybrids were intercrossed in a diallel fashion. In the absence of reciprocal effects, reciprocal crosses were pooled, leading to the six four-way crosses AB, AC, AD, BC, BD, and CD, to which we will refer as F1 crosses. The six F1 crosses, consisting of ~90 four-way hybrid individuals each, with a total of 532 lines, were self-fertilized and advanced to the F5 generation by single-seed descent (Fig. 1). Single F4 plants that resulted in the F5 lines on selfing were genotyped.

We used 321 polymorphic molecular markers consisting of 91 simple sequence repeat (SSR) and 230 SNP markers. These markers were evenly distributed throughout the genome, separated by an average distance of 0.3 Mb (SI Appendix, Fig. 1). When absence of SNP markers led to larger gaps, SSR markers were used to fill these gaps. The AMPRIL population still contained some larger intervals between 1 and 2 Mb, however. For the estimation of identity by descent (IBD) probabilities between founders and F4 offspring lines, which were required for our QTL mapping approach, we converted distances on the physical map into genetic distances: 1 Mb = 5 cM, based on the assumption of an approximate linear relationship between physical and genetic distance (9, 15, 16). We estimated the number of recombinations for each F4 individual by counting the changes in genotype along a 1-cM grid across the chromosomes. Assignment of genotypes occurred on the basis of conditional multipoint genotype probabilities, given marker information. Effectively, probabilities were calculated of F4 individuals having inherited their alleles from one of four possible founders (SI Appendix, Materials and Methods). These probabilities were contained in so-called “genetic predictors” that formed the basis for our mixed-model QTL mapping approach (Materials and Methods). The number of “observed” recombinations per individual varied between 3 and 45, with a mean of 16.5. Direct derivation of the map expansion factor (accumulated recombination rate), assuming an infinitely dense map, for our four-way crosses produced a value of 3.625 (SI Appendix, Fig. 2), which is higher than the 2.0 of two-way RIL populations [the building block of the NAM design (17)] and the 3.0 of standard four-way RIL populations. Using this factor, the expected number of recombinations per individual becomes 23, slightly higher than the estimate following from observed marker information. Recombination rates along the genome differed slightly between the six subpopulations (SI Appendix, Fig. 3), without there being genomic regions that were consistently far below or above the theoretical value of 3.625.

Phenotypic Variation.

The AMPRIL population displayed considerable variation among the F5 lines for all the studied traits. The histograms of flowering time (FLT), ratio of leaf length to width (RLW), and serrated leaf margin (SM) show sizeable transgression at the cross level (SI Appendix, Fig. S4). A phenotypic analysis was performed at the plot level to estimate cross-specific genetic and (micro)environmental variances for calculation of broad sense heritability on a line mean basis. Heritability was generally high (SI Appendix, Table 2). These high values were likely attributable to the strictly controlled environmental conditions used in this study. Strong correlations were detected among the 13 developmental traits across the whole of the AMPRIL population (SI Appendix, Table 3). Correlations among flowering time traits [FLT, total leaf number (TLN), rosette leaf number (RLN), and cauline leaf number (CLN)] were generally positive and high (around 0.93). Most of the leaf shape traits [leaf perimeter (LP), petiole length (PL), leaf length (LL), leaf area (LA), leaf width (LW), and petiole width (PW)] were highly correlated among each other (around 0.92), although LP, LL and PL also had high correlations with FLT. RLW, ratio of leaf perimeter to area (RPA), and SM, conversely, were moderately correlated with the FLT trait and the other leaf traits.

QTL Mapping.

QTL analyses were first carried out for each cross individually, and subsequently for the whole of the AMPRIL population (Materials and Methods). Table 1 summarizes the FLT QTLs found in the AMPRIL population by simple interval mapping (SIM), composite interval mapping (CIM), and backward selection as in the study by Boer et al. (18) (Materials and Methods). Fig. 2 shows QTL profiles for FLT using SIM and CIM, respectively. Some of the identified QTLs in Table 1 corresponded to known candidate genes. By SIM at point-wise test level α_p = 0.05, we identified 13 significant QTLs; by CIM, we obtained 6 significant QTLs at a subset of the loci found with SIM. (In mixed-model QTL mapping, CIM does not necessarily produce equal or larger numbers of QTLs). A final QTL model was obtained by backward selection from the CIM model using a genome-wise test level α_g = 0.05, with the most important QTLs for FLT at the beginning and midpoint of chromosome 1, at the beginning of chromosome 4 (FRI candidate gene), and at the beginning of chromosome 5 (FLC candidate gene). The locus on chromosome 4 had both a strong main effect and a smaller but significant QTL by cross-interaction effect (Table 2). The QTLs identified by joint analysis of the crosses coincided with those in the QTL analysis of the individual crosses (SI Appendix, Fig. 5), with the exception of a QTL at about the midpoint of chromosome 5, which occurred exclusively in the cross AB. This QTL went undetected in our default joint analysis because its effect, being particular to just one cross, was averaged out in the joint analysis, but it could be picked up by modifying our joint QTL models to allow QTL effects to have cross-specific variances. SIM for RLW and SM (Fig. 2) identified 15 and 14 significant QTLs, respectively (SI Appendix, Tables 4 and 5), and CIM reduced the number of significant QTLs to 9 and 8, respectively. The final QTL model for RLW obtained by backward selection included 2 QTLs on chromosome 1 and another 2 QTLs on chromosome 5. A final QTL model for SM contained 7 main-effect QTLs: Chromosomes 2, 3, and 5 had 1 QTL each, and chromosomes 1 and 4 had 2 QTLs each. Only 1 QTL, identified on the top of chromosome 4, colocated with an FLT QTL at the FRI locus. Interestingly, the largest QTL (explaining 16.7% of the genetic variation) for SM was found on chromosome 2 (56 cM or ~11.2 Mb) and very likely corresponded to the ERECTA gene. ERECTA is a well-known pleiotropic gene (29), for which the Ler allele could be scored unambiguously based on its short petiole and bud position. QTL mapping for the remaining 10 traits led to trait-specific QTLs as well as QTLs that colocated with FLT QTLs. The QTLs for FLT on the top of chromosome 4 colocated with a QTL for most of the other traits. Similarly, the QTLs for FLT-related traits on the top of both chromosome 1 and chromosome 5 colocated with the QTL for leaf morphology-related traits (SI Appendix, Fig. 6). SI Appendix, Table 6 gives summary statistics for the 13 traits in this study, with heritability, the number of QTLs in the final QTL model, and the amount of genetic variance explained by the QTLs.

Table 1.

Results of QTL analyses for FLT: Chromosome; position; and -log10(P) values for SIM, CIM, and the final subset of QTLs after backward selection

Chr	Pos, cM	Pos, Mb	SIM	CIM	Final subset	Possible candidate gene	Gene no.	Position of candidate gene (TAIR9), Mb
1	20	4	4	2.2	—	CRY2 (19)	AT1G04400	1.2
1	39	7.8	5.6	2.3	4.9*	GI (20)	AT1G22770	8.1
1	91	18.2	1.5	—	—
1	112	22.4	3.4	2.6	6.0*	FT (21)	AT1G65480	24.3
1	147	29.4	1.8	—	—	FLM (22)	AT1G77080	28.9
2	10	2	3.6	—	—	SVP (23)	AT2G22540	9.6
4	2	0.4	37	42.9	50.1†	FRI (24)	AT4G00650	0.3
4	29	5.8	4.8	—	—
5	0	0	6.5	—	—
5	12	2.4	19	13.3	26.6*	FLC (25)	AT5G10140	3.2
5	24	4.8	16	—	—	FRL1 (26)	AT5G16320	5.3
5	39	7.8	9.1	2.2	—	HUA2 (27)	AT5G23150	7.8
5	47	9.4	2.6	—	—	FPF1 (28)	AT5G24860	8.5

Some of the QTLs were close to candidate genes. Chr, chromosome; Pos, position.

*QTL main effects were significant.

^†QTL main effects and QTLs by cross-interaction effects were significant.

Fig. 2.

QTL profiles obtained from SIM and CIM for three traits (FLT, RLW, and SM).

Table 2.

Final FLT QTL: Chromosome, position, explained genetic variance (h²_QTL), cross-identifier for QTLs by cross-interactions, and QTL effects (in days) for the eight founder alleles (expressed as twice the effect of an allele substitution relative to the average allele composition of the AMPRIL population), and minimum and maximum SEs for the range of QTL effects

Chr	Pos, cM	h2QTL, %	Cross	Cvi	Sha	Ler	C24	Col	Kyo	Eri	An	SE (min, max)
1	39	1.6		0.43	−0.24	0.3	−1.73	−0.65	0.34	−0.5	1.99	(0.56, 0.65)
1	112	3.5		−1.31	1.78	0.11	−1.38	−0.59	2.73	0.09	−0.88	(0.62, 0.79)
4	2	28.4		−3.35	3.4	−2.58	4.3	−2.63	7.26	−1.6	−3.25	(1.38, 1.49)
			AB	−0.98	−0.55	—	—	−0.63	−1.93	—	—	(1.45, 2.01)
			AC	—	—	—	—	−0.69	3.47	0.25	−0.94
4*	2	2.8	AD	—	—	−1.49	0.84	0.7	0.18	—	—
			BC	0.27	1.53	—	—	—	—	0.86	1.75
			BD	−0.09	−0.17	1.8	−1.54	—	—	—	—
			CD	—	—	−0.92	1.71	—	—	−1.49	−1.58
5	12	17.5		6.79	−3.98	−3.66	−1.3	5.47	−0.42	2.75	−1.23	(0.79, 1.05)

Three QTLs showed main effects only. For the QTLs on chromosome 4, both main effect and QTLs by cross-interaction were found. Chr, chromosome; max, maximum; min, minimum; Pos, position.

*QTLs by cross-interaction.

Analysis of QTL Epistatic Effects.

For identified QTLs with main effects in the final QTL model (after backward selection), pairwise epistatic interactions were tested. We detected one significant epistatic interaction for four traits (CLN, LA, LW, and RPA); two for FLT, TLN, PW, and SM; and three for RLN at α_p = 0.05 (SI Appendix, Table 7). Significant epistasis in FLT was detected between the locus on chromosome 4 and two other loci, respectively, at the lower half of chromosome 1 (at 112 cM) and at the top of chromosome 5 (at 12 cM). These two epistatic effects explained 1.7% and 2.6%, respectively, of the total genetic variation. For trait SM, epistatic effects were present between the locus on chromosome 2 at 56 cM and two other loci, namely, at 92 cM on chromosome 3 and 2 cM on chromosome 4 (FRI). These two epistatic effects explained 2.0% and 1.6%, respectively, of the total genetic variation.

Power and Resolution of the AMPRIL Population.

For the four FLT QTLs of the final model, Table 3 shows the comparison of the SIM analysis performed for the AMPRIL population as a whole compared with the QTL analyses of the individual four-way crosses. As expected, -log10(P) value was higher for the joint analysis of the whole AMPRIL population than the maximum observed for the analysis of the individual four-way crosses, indicating that the joint analysis is more powerful. The QTL at 112 cM on chromosome 1 was detected in only one (BD) of the six crosses, whereas the QTL at 39 cM on chromosome 1 was detected in two (BD and CD) of the six crosses. Both QTLs were detected in the joint analysis of the six crosses with a lower P value. With our mixed-model QTL analysis strategy, we detected QTLs as small as explaining 1.6% of the genotypic variation (Table 3). The default QTL model failed to detect a small QTL on chromosome 5 that was particular to the cross AB (SI Appendix, Fig. 5), and that was confirmed using residual heterozygosity (see below). This QTL does show up under a slight modification of the default model (see above).

Table 3.

Comparison of tests on FLT QTLs in overall AMPRIL population vs. those in individual crosses: Chromosome, position, 95% CI for QTL position, -log10(P) values for test on QTLs in AMPRIL population and individual crosses, number of individual crosses showing the QTLs, and genetic variation (h²_QTL) explained by the QTLs

Chr	Pos, cM	95% CI, cM	AMPRIL	AB	AC	AD	BC	BD	CD	Crosses with QTLs	h2QTL, %
1	39	(8, 70)	5.56	n.s.	n.s.	n.s.	n.s.	2.30	4.31	2	1.60
1	112	(98, 126)	3.41	n.s.	n.s.	n.s.	n.s.	2.72	n.s.	1	3.50
4	2	(0, 4)	36.98	2.58	16.47	5.24	3.17	5.34	8.93	6	31.20
5	12	(9, 15)	19.00	1.95	n.s.	5.34	2.75	7.29	3.19	5	17.50

Chr, chromosome; n.s., not significant; Pos, position.

QTL detection requires segregation in the subpopulations. We investigated to what extent the individual crosses could be considered polymorphic along the genome. To quantify polymorphism at a locus within a cross, we looked at the genotype probabilities, given marker information where genotypes consist of founder alleles (i.e., we looked at IBD probabilities). At each position, four homozygous genotypes are possible, corresponding to the founder genotypes as well as four heterozygotes. Because probabilities for heterozygotes were very low, heterozygotes were ignored in the QTL analyses. At any position, for a cross, a good indicator for segregation is the average, over all F4 individuals of that cross, of the maximum probability for one of the four founder genotypes. This statistic proved to reach high values along the genome in each of the six crosses (SI Appendix, Fig. 7). Therefore, the AMPRIL population could potentially have picked up QTLs everywhere. The fact that we detected rather few QTLs may be attributable to QTLs of different founder alleles having similar effects. Another indication of the power and reliability of QTL mapping in the AMPRIL population is the size of the 95% confidence intervals (CIs) for QTL location. For the FLT QTLs retained in the final model, the intervals are shown in Table 3 and were obtained as described by Darvasi and Soller (30). The QTLs on chromosome 1 had small effects (1.6% and 3.5% of the genotypic variation), with intervals between 30 and 60 cM. Large-effect QTLs, found on chromosomes 4 and 5, explained 31.2% and 17.5%, respectively, of the genotypic variation and had intervals between 4 and 6 cM.

Validation of QTLs for FLT.

A considerable number of the F4 plants still contained heterozygous regions. These regions can be used for validation of QTLs employing a heterozygous inbred family strategy (31). RILs were selected because they were homozygous for major-effect QTLs but segregating for the QTLs to be confirmed. For example, an F4 line from cross AB (line BA24) was homozygous at FRI, FLC, and HUA2 and contained two heterozygous regions as shown in SI Appendix, Fig. 8. Marker analysis of the F5 progeny of BA24 confirmed a QTL at chromosome 5 (85.5 cM) that was identified in the QTL analysis of the AB cross (SI Appendix, Fig. 5). The quantitative train locus for FLT located on chromosome 1 at 39 cM by SIM and CIM of the AMPRIL population was confirmed in a similar way in the progeny of line CD21 (SI Appendix, Fig. 9). The QTL at 24.0 cM on chromosome 5 by SIM in the AMPRIL population was confirmed by analyzing lines BD14 and DA16 (SI Appendix, Figs. 10 and 11).

Discussion

Recently, an interest in multiparent populations arose that would allow more complete exploitation of available germplasm, comparable to what can be obtained with association panels representing large germplasm pools. Among the QTLs detected in the AMPRIL population, several are likely to correspond to QTLs identified before in biparental populations for which candidate genes are known or suggested (Table 1). In general, the QTL effects for FLT found in our analysis agree with those found in other studies (15, 32–34), especially for the large effect of QTLs around FRI and FLC. We also missed a number of QTLs that were detected in biparental RIL populations involving parents of the AMPRIL population, however. An example is the QTLs at the bottom of chromosome 5 in the Ler/Sha population (35). An explanation for not detecting such QTLs may be the complexity of the genetic interactions, which may reduce the power of QTL detection. Just like us, Kover et al. (14) detected four QTLs (including FRI and FLC) for FLT, which is relatively low considering the large number of founders and the amount of QTLs detected in biparental populations. Based on our analyses, we hypothesize, first, that because of allelic effects of founders being comparable, relatively few QTLs may have been found in our multipopulation study and, second, that when QTLs with different effects segregate in only one or few of the subpopulations, the QTL model should be adapted to allow for separate QTL effect variances per subpopulation. The latter adaptation to the QTL model can be interpreted as a measure to counteract dilution of the QTLs across the whole of the AMPRIL population. A comparable lack of power attributable to dilution may have occurred in the study of Kover et al. (14) when a deviating QTL allele occurred in just a single founder. The MAGIC population mixes the germplasm from 19 founders in a balanced way (14). With regard to “balancedness” of founder contributions, the AMPRIL population is closer to the MAGIC population than to the star design population. Nevertheless, in the AMPRIL population, not all possible pairs of F1* hybrids (Fig. 1) were used to generate the next generation; therefore, not all possible allelic pairs segregate in the same number of populations. To improve the power of the current analyses, we produced an additional AMPRIL population of the same size using other combinations of founders to generate F1* hybrids, which will be characterized in a future study. Another important aspect in the comparison between different populations is the number of informative crossovers (i.e., the number of crossovers that has accumulated in the offspring population). The expected number of informative crossovers per morgan for one single offspring individual will be denoted by γ. For example, for a backcross population or a doubled haploid population, γ = 1. For fully inbred two-way RILs, γ = 2, and for fully inbred four-way RILs, γ = 3 (36). For a population with n generations of random mating, γ = n. In the MAGIC population, there are four generations of random mating, followed by selfing, which results in γ = 6(14). In the AMPRIL population, we derived that γ = 3.625 (SI Appendix, Materials and Methods). For a comparison of the resolution for QTLs, say the precision of QTL location (30), the expected total number of informative crossovers per centimorgan in the population is important. For the AMPRIL population, the expected number of recombinations is 19 cM⁻¹; for the MAGIC population, the expected number of recombinations is 32 cM⁻¹; and for the NAM population, the expected number of recombinations is 100 cM⁻¹. Including other combinations to generate F1* hybrids will further improve the resolution for QTL detection.

We detected 13 FLT QTLs by SIM and 6 QTLs by CIM, of which 4 QTLs remained after backward selection. In contrast to maize results, where QTL effects are relatively small and similar (37), we found that 2 major QTLs affect FLT in Arabidopsis, of which 1 QTL interacted epistatically with 2 other QTLs. Most of the FLT QTLs have been described before (2), but an additional QTL was found by SIM on chromosome 2. An indication for the power to find an additional QTL in QTL-rich regions is shown by the detection of a QTL by SIM on the top of chromosome 5, which probably represents FRL1 (26). The QTL was found to be a different locus than the FLC and HUA2 loci suggested to be major QTLs by many FLT QTL studies (2). Populations made up of multiple connected crosses are expected to increase the power to detect QTLs and to improve the precision of QTL location for QTLs that segregate in several crosses (38) compared with biparental populations. In Table 3, we show that the AMPRIL population was able to detect QTLs explaining 2% or more of a trait's genotypic variation. This is comparable to the QTL sizes reported for a population of 527 MAGIC lines in Arabidopsis by Kover et al. (14) and for five RIL populations of 350 lines each in a star design (33).

With regard to 95% CIs for QTL location, we calculated intervals of around 5 cM for QTLs explaining 18% and more of the genetic variation and between 30 and 60 cM for small QTLs that explained only 2% of the variation. Important for QTL detection is that we opted to correct for the genetic background by including a cross-effect in the QTL models. Effectively, this means that we concentrate on within-subpopulation segregation and we do not use the between-subpopulation differences to detect QTLs. The between-subpopulation differences will contain both main-effect QTL effects and epistatic effects as well as nongenetic effects. Because we restricted ourselves to within-subpopulation information, we used a rather liberal significance level in the SIM and CIM analyses, without correcting for multiple testing. Relatively small differences of around half a day to a day could be detected for FLT QTLs (Table 2). Smaller effect QTLs will require more lines, which will also allow the detection of more QTLs. One might also invest in the involvement of more parents to cover a wider genetic spectrum.

It is expected that the AMPRIL populations will provide an important additional resource for dissecting the genetics of natural variation, including those depending on interactions of specific alleles present in different natural accessions.

Materials and Methods

QTL Mapping.

To explore the QTLs for the different traits, we used linear mixed models in GenStat (39) to run a series of three models of increasing complexity. In a preliminary search for QTLs, we fitted single-QTL models every 1 cM along the genome. In a second step, we tested for QTLs at particular positions after correcting for QTLs elsewhere in the genome, as were identified in the preliminary analysis. In the third step, we first included in the model all significant QTLs obtained from the previous step as a candidate set of QTLs and then performed backward selection. Analyses were performed for the whole of the AMPRIL population, consisting of six crosses. Unless specified otherwise, we used a point-wise threshold of α_p = 0.05 [-log10(0.05) = 1.3]. As mentioned, in the first step, we tested the association of individual loci with a trait using a genome scan, a procedure commonly known as SIM (40). To compare results of single-cross QTL analyses with QTL analyses on the whole of the AMPRIL population, SIM was performed for single crosses as well as for the whole of the AMPRIL population. For the latter population, we fitted the following model to , the trait value for genotype i from cross k:

In Model 1, we include both random main-effect QTLs and random cross-specific QTL effects, each corresponding to a variance component. We follow the convention to underline random effects. Testing for QTLs is done by testing for variance components being larger than zero via deviance tests (41). Constant μ_k is the mean of cross k. Vector contains the genetic predictors [i.e., x_iklf is the probability that for F4-line i in cross k at locus l, the genotype is equal to that of founder f (with f = 1…8, although, effectively, for each individual, f can take only one of four values)], conditional on the totality of the marker information for that individual. The genetic predictors were calculated using a hidden Markov model (SI Appendix, Materials and Methods). Vector is an 8-dimensional vector of random founder effects corresponding to locus l. The term allows for QTL by cross-interactions. Vector is a 48-dimensional design vector for genotype i in cross k, containing the genetic predictors pertinent to cross k at the appropriate four positions and zeroes elsewhere. Vector is the corresponding vector of QTL by cross-interactions for locus l. Finally is the residual error for F4-line i in cross k, with cross-specific variance .

In the second step, we ran a genome scan using a multi-QTL model adjusting for background QTLs. The QTLs identified in step 1 were included as background (i.e., cofactors). The genome was scanned by CIM, whereas cofactors within 10 cM of the putative QTLs were excluded (36, 37):

Model 2 is Model 1 to which we have added a set C of cofactors to correct for QTLs elsewhere in the genome. At the end of this step, many of the QTLs found in the previous step shifted their positions slightly, by 1 or 2 cM.

At the last step, we included in the model all the significant genetic predictors found with Model 2 and then selected, by backward selection, a subset, S, of QTLs using a genome-wide threshold of 0.05. In this step, we imposed the restriction that QTL by cross-interaction terms could only be in the model when the corresponding main-effect QTL term was also in the model:

with (q ∈ S) the QTL main effect, (q* ∈ S*) the QTL by cross-interaction, and . For QTLs, the amount of genetic variance explained by a particular QTL was calculated by comparing the sum of the residual variances of the crosses in Model 3 (i.e., a model including all QTLs) with a model containing all QTLs except the one under test. The difference between those two models with all and all but one QTL was expressed in relation to the total genetic variance across the six crosses.

Analysis of QTL Epistatic Effects.

We tested epistatic effects between pairs of QTLs retained in model (3) after backward selection. These epistatic interactions were defined for a pair of QTLs, l₁ and l₂, by adding a term , with being a 64-dimensional vector containing the products of the genetic predictors for QTLs l₁ and l₂ and being a 64-dimensional vector containing random allele interaction effects between QTLs l₁ and l₂. The test for epistasis consisted of a deviance test for the variance component proper to the effects, .

95% CIs for QTL Location in the AMPRIL Population.

We calculated 95% CIs for the QTL location based on expressions for resolution (i.e., the 95% CI for QTL location when scoring an infinite number of markers, as given by Darvasi and Soller (30), for various populations, such as F2’s). The expression for an approximate 95% CI for QTL location in centimorgans for the AMPRIL population was:

Expression 4 is based on expression 4 in the study by Darvasi and Soller (30), with N being the population size and d being the proportion of genetic variance explained by the QTLs, such that 0 < d < 1. For the AMPRIL population, N depends on the number of crosses in which the QTLs segregate, which, theoretically, is between one and six. Based on our study of the segregation along the genome for the six four-way crosses (see above), we chose to make N equal to the number of lines for the whole of the AMPRIL population.

Correction for Multiple Testing.

To find a threshold that corrected for multiple testing, we ran 1,000 genome-wide simulations, doing full-genome scans, under the null hypothesis of no QTLs, on the responses as drawn from a normal distribution, y_i,0 , where 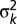is the error variance in population k. For each simulated response vector, y_i,0, we ran Model 2 to associate y_i,0 with the genetic predictors defined on the basis of map and marker scores and we kept the minimum P value. Based on the estimated distribution of these minima, we defined a threshold for a genome-wide significance level of α_g = 0.05. The simulations yielded an estimate of a point-wise threshold of α_p = 0.0006, or -log10(P) value = 3.2.