Chain stiffness of elastin-like polypeptides

Abstract

The hydrodynamic radii of a series of genetically engineered monodisperse elastin like polypeptides (ELP) was determined by dynamic light scattering in aqueous solution as function of molar mass. Utilizing the known theoretical expression for the hydrodynamic radius of wormlike chains, the Kuhn statistical segment length was determined to be l_k = 2.1 nm, assuming that the length of the peptide repeat unit was b = 0.365 nm, a value derived for a coiled conformation of ELP. The resulting chain stiffness is significantly larger than previously reported by force-distance curve analysis (l_k < 0.4 nm). The possible occurrence of superstructures, such as hairpins or helices, would reduce the contour length of the ELP, further increasing l_k. Accordingly, the value l_k = 2.1 nm reported here represents a lower limit of the chain stiffness for ELP.

Introduction

Elastin is a structural protein that is largely responsible for the elastic properties of tissues in vertebrates. It consists of alternating hydrophobic and crosslinking domains. The hydrophobic domains are dominated by hydrophobic amino acids, such as proline, valine, alanine and leucine. The crosslinking domains contain lysyl residues combined with proline-rich regions or polyalanine domains. Elastogenesis¹, the biological synthesis of elastin, involves the synthesis of a soluble precursor protein, tropoelastin, that binds to galactolectin after its translation to prevent its intracellular aggregation. After secretion of the tropoelastin-galactolectin complex into the extracellular space, tropoelastin is released locally and aligned at the microfibrillar scaffold.

Elastin-like Polypeptides (ELP), are a class of artificial repetitive polypeptides of the pentameric repeat Val-Pro-Gly-Xaa-Gly (where Xaa is a guest residue that is any amino acid except Pro), and are so named because this motif recurs in the tropoelastin gene of most vertebrates. ELPs exhibit a lower critical solution temperature (LCST) phase transition in aqueous solution. The LCST behavior² of ELPs can be precisely specified through the control of two orthogonal variables that can be completely controlled by genetically encoded synthesis of these amino acid-based biopolymers: ELP composition, notably by the type and mole fraction of the different guest residues (X), and by the chain length. ELPs are increasingly utilized for many biomedical applications, as they are non toxic, biodegradable and show good pharmacokinetics^3-8.

Despite extensive studies on the biophysics of ELPs^9-12, there is still some controversy regarding the origins of the LCST behavior of ELPs and their elastomeric properties. Two structural models for the remarkable elasticity of elastin have been proposed; the first “β-spiral model”, proposed by Urry⁹, is based on extensive studies on synthetic poly(ValProGlyValGly), and proposes that ELPs consist of a helical arrangement of type II β-spirals per pentameric peptide unit. The ProGly unit is positioned at the corner of the bend and a hydrogen bond connects the carbonyl group of the first valine with the amino residue of the fourth valine. The dipeptide segments of VG, suspended between the β-turns, exhibit large amplitude librations. The decrease of these librations upon extension results in a large decrease in entropy of the segments explaining the rubber elasticity of elastin. At variance with the classical theory of rubber elasticity, this model assumes fixed end-to-end chain lengths. Contradicting this model, molecular dynamics simulations assuming freely fluctuating ends resulted in a loss of the helical β-spiral structure¹³. A second model, proposed by Tamburro et al.¹⁴, involves the formation of non-recurring isolated type II β-turns for the (GlyXGlyGlyX) repeat units of the elastin sequence. The XGly or GlyGly segments build up the corners. The first and fourth glycine or the second and fifth X residue are connected via hydrogen bonds. Due to the absence of proline residues, the resulting β-turns can dynamically slide along the chain. The polypeptide can therefore freely fluctuate leading to high intrinsic entropy, which decreases upon extension. Both models have in common the presence of type II β-turns, but their dynamic interpretations are different. Molecular simulations^11-13 performed by Daggett and coworkers have indicated that the hydration of the hydrophobic residues largely contributes to the gain in entropy. Upon the collapse of the polypeptide the hydration water is released thus leading to a significant increase of solvent entropy.

The single molecule elasticity of ELP has been experimentally investigated by force microscopy as function of temperature and ionic strength¹⁵. The force distance curves were analyzed by standard expressions for a wormlike chain model which yields the persistence length, l_p, which is connected to the Kuhn statistical segment length, l_k, by l_p = l_k/2. At T = 25 °C a very small Kuhn length was determined to l_k = 0.3 nm (ELP4-120). Since it is well established that analysis of force distance curves of flexible polymers often yields values of the persistence length that are anomalously small,¹⁶ a reliable determination of the chain stiffness of ELP is still missing.

Results and Discussion

Herein, the Kuhn length of ELP was determined in dilute solution by analysis of the hydrodynamic radii (R_h) measured by dynamic light scattering (DLS) on a series of ELPs with different molecular weights. Five ELPs Gly(Val-Pro-Gly-Val-Gly)_n Phe-Cys with the guest residue Valine and a single Cysteine residue at the C-terminus were investigated. Their length varied from n=20 up to n=120 (notation ELP4-n), where n is the number of pentapeptide repeats. The recombinant synthesis of each ELP construct utilized plasmid reconstruction recursive directional ligation⁶, and is summarized along with their purification in the Supporting Information. The samples utilized are listed in Table 1.

Table 1.

Calculated molecular weight and hydrodynamic radii determined by DLS for ELP samples.

	MW/kDa	Rh/nm
ELP4-120	49.4	6.0
ELP4-60	24.9	4.2
ELP4-40	16.7	3.7
ELP4-30	12.6	3.4
ELP4-20	8.5	2.7

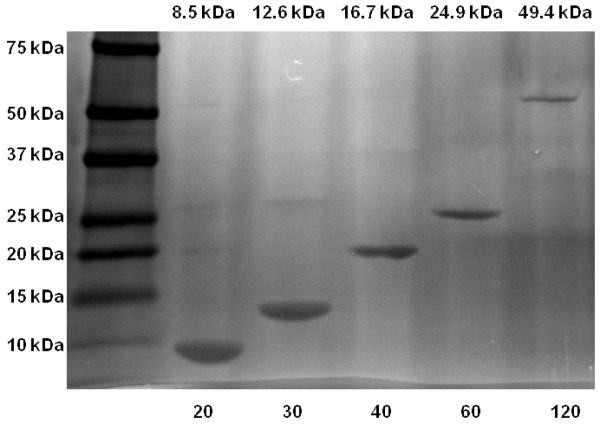
SDS-PAGE (see Figure 1) of the ELPs was carried out to verify the purity of the ELP samples utilized in this study and DLS was utilized in order to determine the R_h from the measured diffusion coefficient D by application of Stokes’ law

$${\mathrm{R}}_h=\mathrm{kT}∕\left(6\pi {\eta }_0\mathrm{D}\right)$$ (1)

where kT is the thermal energy and η₀ is the solvent viscosity. Experimental details of the DLS measurements are in the Supporting Information (SI). Briefly, the ELPs were dissolved in 20 mM NaCl, pH = 6.5, for the LS measurements at a concentration of 5 mg/mL. This small concentration effectively represents the infinite dilution limit, since R_h of sample ELP4-40 did not change when diluted to c = 0.5 g/L. All measurements were performed at a scattering angle of 30°. Due to the terminal cysteine group of the ELPs used in the present work, dimerization by formation of disulfide bridges is possible. Therefore all samples were measured directly after dissolution. Control measurements revealed that dimerization noticeably starts after 24h, only.

Figure 1.

SDS-PAGE (4-20% Tris-HCl, gradient) of purified ELPs visualized by copper staining. The left lane contains a molecular weight standard, labeled in kilodaltons (kDa). The expected molecular weight is indicated on the top of each lane. The length in pentapeptides of each ELP is labeled below each lane.

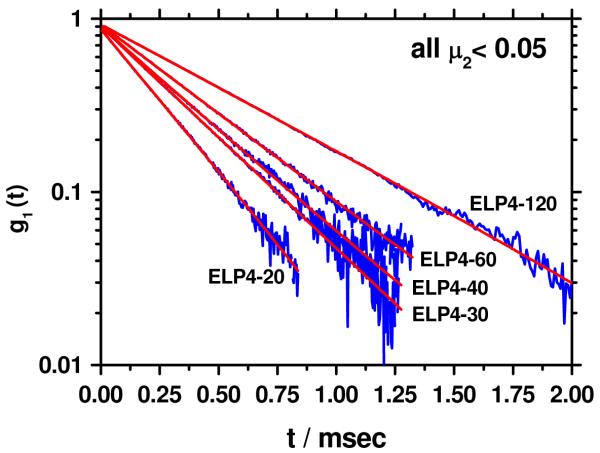
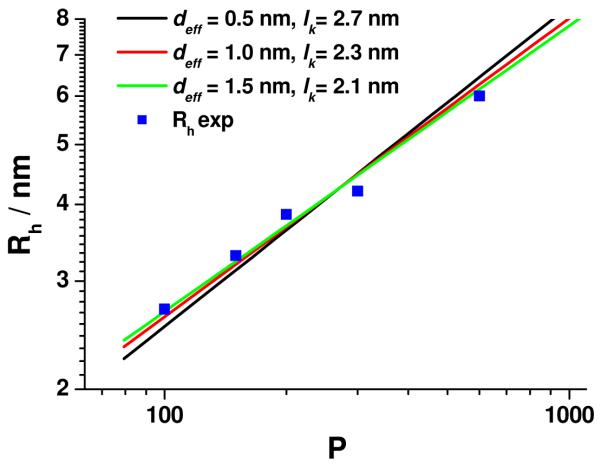
The correlation functions for all ELP samples decayed single exponentially for g₁(t) > 0.2 (Figure 2). If a cumulant fit is applied, the normalized 2^nd cumulant μ₂, a measure for the polydispersity of the sample, is negligible, i.e. μ₂< 0.05, which is within experimental error the expected range for monodisperse samples. In Figure 3 the double logarithmic plot of the hydrodynamic radius, R_h, of the ELPs versus the number of repeat units, P, is shown. A quantitative analysis of the data was performed by application of the Kratky-Porod wormlike chain model for the calculation of the hydrodynamic radius, as described in detail elsewhere.¹⁷ Briefly, the segment distribution function derived by Koyama¹⁸ was applied to numerically calculate R_h. The results are in perfect agreement with the Yamakawa-Fujii theory^19,20 for wormlike cylinders.

Figure 2.

Correlation function g₁ (t) of ELP4-20, ELP4-30, ELP4-40, ELP4-60 and ELP4-120 plotted vs. the correlation time t in a semi logarithmic scale. The red curves represent a single exponential fit to the data in a time regime where g₁(t) > 0.2.

Figure 3.

Double logarithmic plot of the hydrodynamic radius R_h vs. the number of peptide repeat units P. The lines represent the best fits to the data assuming a repeat unit length b = 0.365 nm. Black line: d_eff = 0.5 nm, l_k = 2.7 nm, red line: d_eff = 1.0 nm, l_k = 2.3 nm, green line: d_eff = 1.5 nm, l_k = 2.1 nm.

The Kuhn statistical length l_k is obtained by fitting the calculated R_h to the measured R_h values. The parameters needed for the fit are the length per repeat unit b and the effective chain cross-section d_eff. The calculated fits were obtained by assuming b = 0.365 nm, which was estimated from the well-known peptide bond lengths and angles²¹ and by assuming different values for the effective chain cross-section d_eff of 0.5 nm, 1.0 nm and 1.5 nm, which are impossible to exactly calculate for non rigid particles. Given the different side chain size of the amino acids in ELPs, the chosen d values include the extremes of a very small hydrodynamic effect of the side chain (d_eff = 0.5 nm) and a maximum effect reflecting the maximum extension of the largest amino acid side chain (Valine). The data are fitted best by d_eff = 1.5 nm and l_k = 2.1 nm, although the experimental data would also be compatible with d_eff = 1 nm and l_k = 2.3 nm (see separate plots and linear presentation of the data in the Supporting Information). This somewhat large value of d_eff could be either due to an additional hydration shell or could be caused by thicker chain regions originating from intramolecular superstructures like hair pins. The latter is unlikely as revealed by a recent simulation study combined with NMR investigations which have highlighted the role of proline for the conformational change of ELP with temperature.²² At T = 283 °K no evidence for intramolecular interactions are found whereas at T = 303 °K β_II-type turns may emerge. The data in the present work were recorded at T = 293 °K, where ELP most probably exhibits an “unstructured” conformation.

It should be noted that l_k = 2.1 nm is much larger than the previously reported l_k ≤ 0.4 nm derived from force-distance curve analysis in AFM measurements of single ELP molecules¹⁵. This discrepancy is not entirely unexpected, as AFM has been reported to yield extremely small Kuhn lengths that are physically anomalous.¹⁶

Conclusion

The present work has investigated the chain stiffness of ELP at temperatures well below the UCST based on the interpretation of the hydrodynamic radii by the Yamakawa-Fujii theory of wormlike chains. The value for the Kuhn statistical segment length, l_k = 2.1 nm, compares well with those reported for other water soluble flexible polymers such as PEO²³ (l_k = 2 nm), single stranded RNA²⁴ (l_k = 2 nm) or other coiled polypeptides like poly-sodium-L-glutamat²⁵ (l_k = 1.2 nm) or denatured bovine A1 basic protein²⁶ (l_k = 3.1 nm). As discussed above the contour length utilized in the present analysis ignores possible secondary structures of ELP such as helices, hair pins etc. Since such effects would shorten the contour length, leading to an increase of the Kuhn length, and accordingly, the value reported herein constitutes a minimum value of the Kuhn length of ELPs.

Unfortunately, the present results do not provide a better understanding of the LCST behavior of ELP as function of temperature or pH nor is the presented wormlike chain analysis applicable to folded or even compact rigid ELP conformations which are expected to form close to the LCST transition. Although hydrodynamic theories are well developed for instance for rigid and flexible rods^27,28 it would be difficult to consistently derive meaningful values for the contour length and the thickness, given the huge number of possible rigid conformations.