Exploring by Pulsed EPR the Electronic Structure of Ubisemiquinone Bound at the Q_H Site of Cytochrome bo₃ from Escherichia coli with in Vivo ¹³C-Labeled Methyl and Methoxy Substituents

Abstract

The cytochrome bo₃ ubiquinol oxidase from Escherichia coli resides in the bacterial cytoplasmic membrane and catalyzes the two-electron oxidation of ubiquinol-8 and four-electron reduction of O₂ to water. The one-electron reduced semiquinone forms transiently during the reaction, and the enzyme has been demonstrated to stabilize the semiquinone. The semiquinone is also formed in the D75E mutant, where the mutation has little influence on the catalytic activity, and in the D75H mutant, which is virtually inactive. In this work, wild-type cytochrome bo₃ as well as the D75E and D75H mutant proteins were prepared with ubiquinone-8 ¹³C-labeled selectively at the methyl and two methoxy groups. This was accomplished by expressing the proteins in a methionine auxotroph in the presence of l-methionine with the side chain methyl group ¹³C-labeled. The ¹³C-labeled quinone isolated from cytochrome bo₃ was also used for the generation of model anion radicals in alcohol. Two-dimensional pulsed EPR and ENDOR were used for the study of the ¹³C methyl and methoxy hyperfine couplings in the semiquinone generated in the three proteins indicated above and in the model system. The data were used to characterize the transferred unpaired spin densities on the methyl and methoxy substituents and the conformations of the methoxy groups. In the wild type and D75E mutant, the constraints on the configurations of the methoxy side chains are similar, but the D75H mutant appears to have altered methoxy configurations, which could be related to the perturbed electron distribution in the semiquinone and the loss of enzymatic activity.

Introduction

Ubiquinone (UQ)³ functions as a membrane-soluble two-electron carrier. It is often found as a cofactor in many respiratory and photosynthetic complexes and plays an important role in biological oxidation-reduction reactions. Many of these reactions consist of one-electron transfer steps and involve the one-electron reduced ubisemiquinone species as the intermediates. Knowledge of how the semiquinone (SQ) radicals are stabilized in these complexes is critical to understand their reaction mechanisms. The quinone binding sites located in the respiratory and photosynthetic enzymes are significantly different (1), and each protein fine tunes the properties of the bound quinone cofactor by providing a unique environment in order to accomplish its own electron transfer process (2). The well characterized quinone binding sites include those from bacterial photosynthetic reaction centers (3), cytochrome bo₃ ubiquinol oxidase (cyt bo₃) from Escherichia coli (4), cytochrome bc₁ complexes (5), photosystems I and II, and some others (6–9).

A SQ can bind within a protein site in a manner that favors either the neutral () or anionic () form or intermediate states with partial charge remaining on the SQ. The proton locations along the hydrogen bonds to the quinone carbonyls determine the net charge on the SQ. The formation of hydrogen bonds of different strengths to the quinone oxygens usually leads to an asymmetry of the unpaired spin density (or charge) distribution in the SQ. Existing evidence indicates a connection between this spin/charge asymmetry and enzyme function.

In addition to hydrogen bonds, the conformation of substituents on the quinone ring, especially the methoxy groups, is also believed to be crucial for the function of the UQ cofactors during electron transfer reactions (10, 11). In vitro electrochemical measurements indicate that a methoxy group attached to the quinone ring can lower the reduction potential through delocalization of the lone pair electrons from the methoxy oxygen to the π system of the ring, and the effect is largest for a methoxy group in a conformation coplanar to the ring (12). Based on molecular orbital calculations, the influence of the methoxy torsional angle on the reduction potentials of the UQ can be as significant as 0.4 eV, and it has been proposed that electron transfer reactions can be controlled allosterically through specific orientations of the methoxy groups of the UQ imposed by the protein environments (10). Indeed, it has been suggested that the differences in the infrared absorption by the carbonyl groups of the UQs at the Q_A and Q_B sites of bacterial photosynthetic reaction centers are due to differences in the conformations of the methoxy groups of the UQs, also resulting in a 70-mV difference in the reduction potentials of the cofactors at the two sites (11, 13). Although the hyperfine couplings for the methoxy protons of SQ anion radicals in isopropyl alcohol have been measured by ENDOR spectroscopy, it is difficult to analyze the conformation of the methoxy groups because the methoxy protons are far from the quinone ring and possess only small hyperfine couplings (14). There has been no report of the hyperfine couplings related to the SQ methoxy groups in biological complexes up to the present.

Cyt bo₃ from E. coli is a member of the heme-copper oxidase superfamily, which includes mitochondrial cyt c oxidase. Cyt bo₃ catalyzes the reduction of molecular oxygen to water using ubiquinol-8 as the electron donor. Similar to other heme-copper oxidases, cyt bo₃ couples the energy available from the electron transfer reaction to the translocation of protons across the cytoplasmic membrane (15). The enzyme contains two quinone binding sites known as the low affinity site (Q_L) and the high affinity site (Q_H) (16). The Q_L site functions as the substrate binding site, whereas a UQ cofactor is tightly bound at the Q_H site and is stabilized as an SQ intermediate during the reaction that can be detected by EPR (17, 18). The ability to stabilize the SQ radical indicates that the UQ at the Q_H site can function as a converter during the electron transfer from the two-electron carrier, ubiquinol, at the Q_L site, to the one-electron acceptor, heme b. In fact, comparison of the kinetics between the cyt bo₃ preparations with and without the tightly bound UQ cofactor or with the Q_H site's inhibitors demonstrated that the UQ at the Q_H site facilitates the fast electron transfer process from the substrate ubiquinol to the low spin heme b (19–22).

Although the only crystal structure of cyt bo₃ does not include a bound UQ-8, the residues at the Q_H site were identified from sequence alignments and confirmed by mutagenesis and biochemical studies (4, 23). In addition, previous EPR experiments have offered insights into the nature of interactions between the Q_H site residues and the SQ carbonyl groups (supplemental Fig. S1) (24–26). The EPR studies of the semiquinone at the Q_H site have also found hyperfine couplings with methyl and exchangeable, hydrogen-bonded protons consistent with a neutral radical species, indicating significant asymmetry in the distribution of the unpaired spin density (24–26). The D75E mutant of cyt bo₃ has been shown to be fully functional and possess similar interactions with the SQ at the Q_H site as in the WT cyt bo₃ (27). On the other hand, the D75H mutant of cyt bo₃ is unable to catalyze the reduction of molecular oxygen, and the anionic SQ radical at its Q_H site is stabilized by hydrogen bonds different from the ones identified with the WT enzyme (27). Relating the structural information of the D75H mutant Q_H site with the functional properties of the enzyme is critical to understand why this mutant enzyme is unable to reduce molecular oxygen. Thus, further studies of the electronic structure of the Q_H SQ and the conformations of the ring substituents are desirable. These studies are substantially aided by measurements of the ¹³C couplings of the carbon atoms of the ring and substituents. In proteins, such measurements have been limited to the ¹³C couplings of carbonyl groups (3, 24). In this work, we report the selective ¹³C labeling of the methyl and methoxy substituents of the UQ-8 cofactor in cyt bo₃. This has allowed electron spin echo envelope modulation (ESEEM) and electron-nuclear double resonance (ENDOR) measurements of the methyl and methoxy ¹³C hyperfine couplings of the SQ radical at the Q_H site of WT and D75E and D75H mutant cyt bo₃ and the UQ-8 anion radical in isopropyl alcohol glassy solution and their analysis for characterization of spin density distribution and conformation of methoxy groups.

EXPERIMENTAL PROCEDURES

E. coli Strain Construction

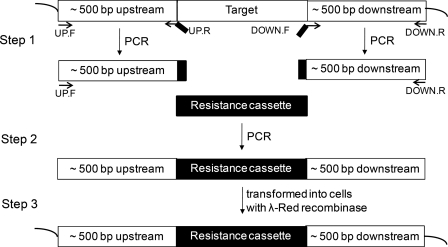
All E. coli C43(DE3) strains used in this study had cyoBCD deleted (21). A methionine (Met) auxotroph version of C43(DE3) was created by deleting the metA gene from the chromosome with the λ-Red recombination system (28). First, a three-step PCR technique was used to generate a linear double-stranded DNA that had the chloramphenicol resistance cassette flanked by ∼500-bp regions homologous to the upstream and downstream regions of metA (Fig. 1) (29). The linear DNA was then transformed into a C43(DE3) strain that expresses the λ-Red recombinase from the pKD46 vector (28). The ΔmetA C43(DE3) strains were selected by their newly acquired antibiotic resistance, and the deletion of metA in these strains was verified by PCR amplification of the metA locus on the chromosome as well as the Met auxotrophic phenotype.

FIGURE 1.

The three-step PCR technique used to generate linear double-stranded DNA with 500-bp-long homology extensions. In the first step, the upstream 500 bp and the downstream 500 bp of the target chromosomal gene were amplified independently. Each of the UP.R and DOWN.F primers had a short segment homologous to the respective region of the resistance marker. The second step generated the linear DNA from the two homologous 500-bp segments and the resistance marker. In the third step, the linear DNA was transformed into the expression strain and incorporated into the chromosome by homologous recombination.

Enzyme Preparation

The newly created Met auxotrophic C43(DE3) strain was used to achieve selective ¹³C labeling at the methyl and methoxy groups of UQ. [methyl-¹³C]Met was purchased from Cambridge Isotope Laboratories, Inc. and was added to modified M63 minimal growth medium to a concentration of 45 mg/liter. Preparation of the growth medium, overexpression of the His₆-tagged cyt bo₃, extraction of the enzyme complexes from the E. coli cytoplasmic membrane with n-dodecyl-β-d-maltoside, and purification of the enzymes by Ni²⁺-NTA affinity chromatography were carried out as described previously (27). The enzymes prepared in n-dodecyl-β-d-maltoside have one UQ-8 bound at the Q_H site. The purified enzymes were dialyzed against 0.5 liters of 50 mm potassium phosphate, 0.05% n-dodecyl-β-d-maltoside, 10 mm EDTA, 5% glycerol at pH 8.3 and were concentrated with a Microcon YM-100 to a final volume and concentration of ∼100–150 μl and 200–400 μm, respectively. Each sample was then reduced anaerobically by a 500-fold excess of sodium ascorbate using a vacuum line to remove most of the oxygen. This sample was incubated at 4 °C for 3 h in order to generate the semiquinone radical at the Q_H site. The mixture was then transferred to an argon-flushed EPR tube and rapidly frozen in liquid nitrogen.

UQ-8 Preparation

The procedure to extract UQ-8 from E. coli was based on a protocol described previously (30). The E. coli cell pellet from a 0.5–1-liter culture grown in modified M63 minimal medium with glucose as the sole carbon source was resuspended in 6.6 ml of water in a 50-ml conical glass centrifuge tube and then mixed with 20 ml of methanol and 13.4 ml of petroleum ether. The tube was then vortexed and incubated at 4 °C overnight while being slowly shaken on an orbitron. The tube was centrifuged at 2000 rpm for 10 min, and the upper petroleum ether layer was transferred to another tube. About 10 ml of petroleum ether was added to the first tube, and the contents were mixed by vortexing. The petroleum ether phase was isolated again by centrifuging, combined with the first extract, and dried under N₂ gas. The remaining yellow residue was further purified on a TLC silica gel 60 glass plate, without indicator, using a 70:30 chloroform/petroleum ether mixture as the mobile phase. The UQ-8 band observed at an R_f value of about 0.4–0.6 was extracted from the gel with ethanol. The concentration of air-oxidized UQ-8 was determined by its extinction coefficient value of 14.9 mm⁻¹ cm⁻¹ at 275 nm.

The semiquinone radicals in isopropyl alcohol were generated as follows. A few particles of potassium tert-butoxide (KO(CH₃)₃) were added to an EPR tube with ∼200 μl of 1–3 mm UQ-8, which was then immediately frozen in liquid nitrogen. The tube was attached to a vacuum line, and the mixture was melted at room temperature for a few seconds and then rapidly frozen in liquid nitrogen again. This melting and freezing cycle was repeated a few times until the solution turned green, indicating the formation of the semiquinone anion radical.

¹³C NMR Spectroscopy

Approximately 0.5 mg of UQ-8 extracted from E. coli was dissolved in ∼0.7 ml deuterated chloroform (CDCl₃) and transferred into a Wilmad 528 NMR tube. The ¹³C one-dimensional NMR spectrum was collected at the NMR Laboratory from the School of Chemical Sciences at the University of Illinois at Urbana-Champaign with a 500-MHz spectrometer (¹H frequency) in ¹H decoupling mode.

Mass Spectrometry of UQ-8

Approximately 100 ng each of unlabeled UQ-8 and the methoxy and methyl ¹³C-labeled UQ-8 extracted from E. coli were each dissolved in ∼20 μl of methanol. The mass spectrometry was performed at the Mass Spectrometry Laboratory of the School of Chemical Sciences at the University of Illinois at Urbana-Champaign with electrospray ionization in positive ion mode using a Micromass Q-Tof Ultima mass spectrometer.

ESEEM and ENDOR Measurements

The CW EPR measurements were performed on an X-band Varian EPR-E122 spectrometer. The pulsed EPR experiments were carried out using an X-band Bruker ELEXSYS E580 spectrometer equipped with Oxford CF 935 cryostats. Unless otherwise indicated, all measurements were made at 70 K. The two-dimensional, four-pulse experiment (π/2-τ-π/2-t₁-π-t₂-π/2-τ-echo, also called HYSCORE (31)), was employed with appropriate phase cycling schemes to eliminate unwanted features from the experimental echo envelopes. The intensity of the echo after the fourth pulse was measured with t₂ and t₁ varied and constant τ. The length of a π/2 pulse was nominally 16 ns, and a π pulse was 32 ns. HYSCORE data were collected in the form of two-dimensional time domain patterns containing 256 × 256 points with steps of 20 or 32 ns. Spectral processing of ESEEM patterns, including subtraction of the relaxation decay (fitting by polynomials of 3–6 degrees), apodization (Hamming window), zero filling, and fast Fourier transformation, were performed using Bruker WIN-EPR software. Pulsed ENDOR spectra of the radicals were obtained using the Mims sequence. The specifics of this experiment are described in detail elsewhere (32).

Density Functional Theory Calculations

Density functional theory calculations of hyperfine tensors were performed with the Amsterdam density functional theory (ADF) quantum chemistry software package (33). All of the electrons were considered explicitly (no frozen core approximation was used). Relativistic valence triple ζ (two polarization functions) ZORA/TZ2P bases were used in the zero order regular approximation approach (34–36). The calculation was carried out in spin-unrestricted mode for hyperfine interaction tensor. The Vosko et al. (37) local density approximation functional was used, whereas functionals for generalized gradient approximations were of the form Becke (gradient correction) (38) and Perdew (correlation term) (39). For comparison and test purposes for some selected optimized structures, single point calculations of isotropic hyperfine constants were also performed with the GAUSSIAN 98 quantum chemistry software package (40) within B3LYP approximation using a special EPR-optimized EPR-III basis set.

Powder ¹³C ESEEM and ENDOR Spectra

The high resolution pulsed EPR techniques, such as ESEEM and ENDOR, make use of the paramagnetic properties of the SQ intermediate and its interactions with nearby magnetic nuclei of the protein, the aqueous solvent, and the quinone molecule itself. One- and two-dimensional ESEEM and ENDOR can be used to explore the fine tuning of environment and geometry of substituents and electronic structure of the SQ via the isotropic and anisotropic hyperfine interactions with magnetic nuclei (¹³C in this work). ENDOR and ESEEM measure frequencies of nuclear transitions from nuclei interacting with an S = ½ electron spin of the SQ. There are only two transitions with frequencies ν_α and ν_β for ¹³C with nuclear spin I = ½, corresponding to two different states m_s = ±½ of the SQ electron spin in the applied constant magnetic field, respectively. The value of the frequencies depends on the vector sum of the applied magnetic field and local magnetic field induced on the nucleus by the isotropic and anisotropic hyperfine interactions with electron spin. In this work, we used X-band EPR with microwave frequency ∼9.5 GHz and magnetic field ∼350 mT. The X-band EPR spectrum of the SQ in frozen solutions is a single line with the width ∼0.8–1.0 mT with unresolved hyperfine structure. This width is comparable with the excitation width of the EPR spectrum by microwave pulses. In this case, the pulses can be considered as giving a complete excitation of the powder EPR spectrum, and thus the ESEEM and ENDOR spectra obtained are the powder-type spectra of nuclear frequencies with all different orientations of applied magnetic field relative to the principal axes of ¹³C hyperfine tensor(s). The frequencies of ν_α and ν_β transitions vary between Equations 1 and 2.

These correspond to the perpendicular and parallel orientations of the magnetic field and unique axis of axial hyperfine tensor (ν_c represents the Zeeman frequency of ¹³C in the applied magnetic field, A_⊥ = |a − T| and A_‖ = |a + 2T|, a is the isotropic hyperfine constant, and T is the component of anisotropic hyperfine tensor (−T, −T, 2T). The powder line shapes of the ν_α and ν_β transitions are, however, different in ENDOR and ESEEM spectra (see “Results”).

In this work, we used the two-dimensional ESEEM (HYSCORE) technique because it provides better resolution of extended lines of low intensity. The HYSCORE experiment creates off-diagonal cross-peaks (ν_α, ν_β) and (ν_β, ν_α) from each I = ½ nucleus in two-dimensional spectrum. Powder HYSCORE spectra of I = ½ nuclei reveal, in the form of cross-ridges, the interdependence between ν_α and ν_β in the same orientations. The two coordinates of the arbitrary point at the cross-ridge, described in the first order by Equation 3,

can be used for the first-order estimate of the corresponding hyperfine coupling constant A.

Analysis of the ridges in (ν_α)² versus (ν_β)² coordinates allows for direct, simultaneous determination of the isotropic a and anisotropic T components of the hyperfine tensor (41). Equations 1–4 can also be used for the determination of the hyperfine couplings from ENDOR spectra (see “Results”).

RESULTS

Selective ¹³C Labeling of the Methyl Substituents in UQ-8

In order to determine the ¹³C labeling pattern in the UQ-8 extracted from the Met auxotrophic E. coli strains, we collected a ¹³C one-dimensional NMR spectrum of the extracted compound (supplemental Fig. S2). The chemical shifts at 61.139, 61.126, and 11.933 ppm can be assigned to the two methoxy groups and the ring methyl group of UQ-8, respectively, based on the results previously reported for ¹³C uniformly labeled UQ-10 (42). In addition to these signals, another peak at 10.921 ppm with an intensity of about 40% of the peak at 11.933 ppm was also observed. The 10.921 ppm signal most likely originates from the ring methyl carbon of menaquinone-8, which was probably co-purified with the UQ-8 during extraction from E. coli.

Mass spectrometry of the unlabeled and ¹³C-labeled UQ-8 was performed to assess the level of ¹³C enrichment. The mass comparison of the protonated species as well as the Na⁺ and K⁺ species indicates that the mass of the ¹³C-labeled sample is 3 Da higher than that of the unlabeled UQ-8 (supplemental Fig. S3). The measured monoisotopic m/z of the protonated species from the unlabeled sample is 727.5672, which is within 1 ppm of the calculated value for ¹²C₄₉¹H₇₅¹⁶O₄ (727.5665), whereas the corresponding value from the ¹³C-labeled sample is 730.5734, which represents a −4.4 ppm difference compared to the calculated m/z of ¹²C₄₆¹³C₃¹H₇₅¹⁶O₄ (730.5766). In addition, the isotope distributions of the labeled compound are almost identical to the expected pattern calculated from the molecular formula. Based on these mass spectrometric data and the ¹³C NMR spectrum of the labeled sample, it can be concluded that ¹³C isotope was incorporated only into the methoxy and methyl groups in UQ-8, and using a Met auxotroph led to almost complete ¹³C enrichment at those target positions of UQ-8.

¹³C HYSCORE and ENDOR Spectra

The ¹³C hyperfine couplings in the SQs were probed by two-dimensional ESEEM (HYSCORE) experiments with the Q_H site SQ in WT and mutant cyt bo₃ as well as with the model anion radical of UQ-8 in an isopropyl alcohol glass. In our studies, we used uniformly ¹⁵N-labeled cyt bo₃ and mutant proteins. This is because the ¹⁴N nuclei of atoms hydrogen-bonded to the carbonyl oxygens of the SQs produce intense lines, which overlap partially with the lines of lower intensity from the ¹³C nuclei and interfere with the analysis. The lines from the ¹⁵N nuclei are located at lower frequencies, permitting observation of the ¹³C peaks. In addition, because the ¹⁵N nuclei produce an ESEEM that is shallower than that from ¹⁴N nuclei, this decreases the cross-suppression effect (43) of ¹⁴N nuclei on the intensity of the ¹³C lines.

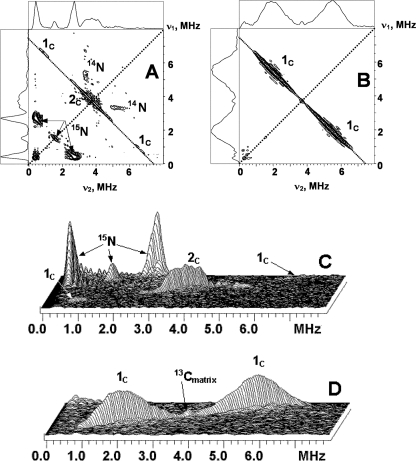
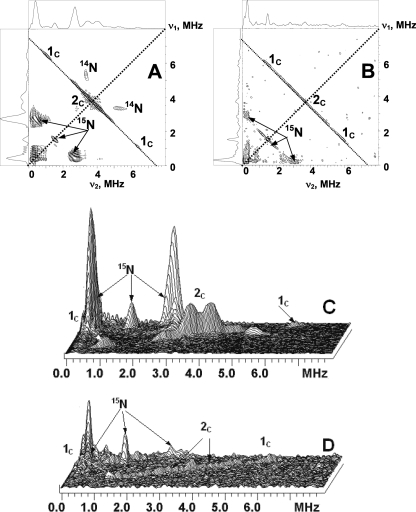
¹³C labeling of the methyls does not influence the SQ line width, indicating that the line width is still dominated by the g-tensor anisotropy. Fig. 2 shows representative HYSCORE spectra, measured with the time, τ, between the first and second pulses of 136 ns, for the WT cyt bo₃ and the anion radical in isopropyl alcohol in the frequency interval from 0 to 8 MHz for both axes. The spectra of the SQ in the proteins show the lines from both ¹⁵N and ¹³C. In this work, we will focus on the analysis of the ¹³C lines. The ¹³C lines are located along the antidiagonal, symmetrically around the diagonal point (ν_C, ν_C) where ν_C is the ¹³C Zeeman frequency, ∼3.7 MHz, in the applied magnetic field. The shape and location of the line maxima are significantly different for the two samples.

FIGURE 2.

Contour (A and B) and stacked (C and D) presentations of the HYSCORE spectra of the UQ-8 with ¹³C-labeled methyl and methoxy groups in the Q_H site of uniformly ¹⁵N-labeled wild-type cyt bo₃ (A and C) and in frozen isopropyl alcohol solution (B and D) (magnetic field 346.3 mT (bo₃) and 345.1 mT (isopropyl alcohol), time between first and second pulses τ = 136 ns, microwave frequency 9.711 GHz (bo₃) and 9.682 GHz (isopropyl alcohol)).

The spectrum of the SQ in WT cyt bo₃ consists of the pair of cross-peaks 1_C and feature 2_C located around the diagonal point (ν_C, ν_C). The central, most intensive part of the cross-peaks 1_C varies along antidiagonal between the points with coordinates (6.5, 0.9) and H(6.7, 0.7) MHz. This corresponds to a hyperfine coupling of 5.6–6.0 MHz as follows from Equation 1. Feature 2_C may be due to the presence of two poorly resolved splittings of ∼0.3 and 0.6 MHz in its central part, accompanied by shoulders of lower intensity up to 2.5 MHz of total length around the diagonal point (see also Fig. 5). The intensity of the peaks 1_C is enhanced, and 2_C is suppressed in the spectrum measured with τ = 200 ns (supplemental Fig. S4) so that only the most intense central part is resolved. This spectrum (supplemental Fig. S4), however, better resolves the two splittings indicated above (see also supplemental Fig. S7). The relative intensities of lines 1_C and 2_C are changed because the time, τ, which is kept constant in each individual experiment, influences the HYSCORE spectrum by modulating the intensity of the cross-peaks, producing attenuation and suppression of different sets of peaks as τ is varied.

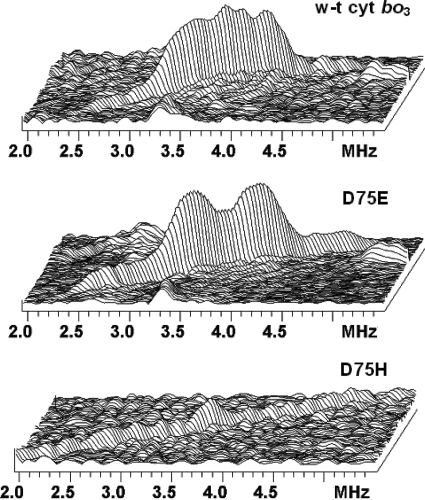
FIGURE 5.

Comparative view of the lines from methoxy groups in the stacked presentation of the ¹³C HYSCORE spectra of wild-type cyt bo₃ (top) and the D75E (middle) and D75H (bottom) mutants. Corresponding full ¹³C spectra are shown in Figs. 2C and 4 (C and D).

In contrast, the HYSCORE spectra for the ¹³C-labeled anion radical in isopropyl alcohol show an intense, broad cross-doublet, 1_C, also extended along the antidiagonal (Fig. 2). We were not able to resolve the separate contributions to these lines by varying the time τ, although the shape of the cross-peaks and locations of maxima were affected by this time change. The spectrum also contains a sharp peak of low intensity at the diagonal point (ν_C, ν_C), which is completely suppressed in the spectra measured with other times τ. We assign this line to weakly coupled ¹³C nuclei natural abundance, 1.1% present in the surrounding alcohol molecules in the glass.

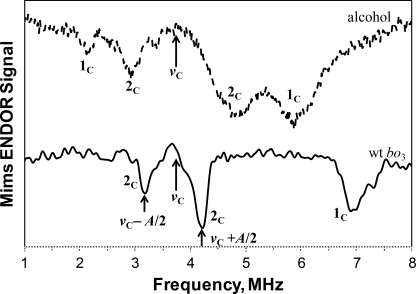
In addition, pulsed ENDOR experiments utilizing the Mims sequence were performed with these samples. The ENDOR spectrum resolves two sets of signals, 1_C and 2_C, for the anion radical in isopropyl alcohol. They are centered approximately at the ¹³C Zeeman frequency ν_C (Fig. 3), satisfying Equation 3. The ¹³C hyperfine couplings estimated using Equation 4 are ∼3.7 and 1.9 MHz for 1_C and 2_C, respectively. In contrast, the ENDOR spectrum for the SQ in cyt bo₃ shows the doublet 2_C centered at the ν_C with the coupling ∼1 MHz. In addition, the spectrum contains line 1_C at ∼7.0 MHz. The location of this line relative to the ν_C indicates hyperfine coupling of ∼6.6 MHz (if Equation 3 is used for ν_α) for the corresponding ¹³C. It means that the second line of the 1_C doublet has a frequency of ∼0.4 MHz and is not resolved in the ENDOR spectrum.

FIGURE 3.

Pulsed ENDOR spectra obtained using Mims ENDOR sequence for the ¹³C-labeled UQ-8 in the Q_H site of cyt bo₃ and UQ-8 anion radical in isopropyl alcohol. Length of the π/2 microwave pulse is 48 ns, and the length of the radiofrequency π pulse is 10 μs. The spectra shown represent a sum of seven individual spectra recorded at different τ values varied from initial time τ = 200 ns with the step 24 ns (magnetic field 344.3 mT (bo₃) and 344.5 mT (isopropyl alcohol), microwave frequency 9.668 GHz (bo₃) and 9.663 GHz (isopropyl alcohol)).

The positions of the line maxima in powder ENDOR and HYSCORE spectra and, consequently, the derived couplings are different. This is because ENDOR singularities correspond to orientations of the magnetic field along principal directions of the hyperfine tensor, but the maxima of the cross-peaks in HYSCORE spectra correspond to some generally unknown, intermediate orientations. Hence, it appears that the couplings determined from ENDOR spectra correspond to A_⊥ = |a − T| with numerous orientations of the magnetic field in the perpendicular plane of the hyperfine tensor.

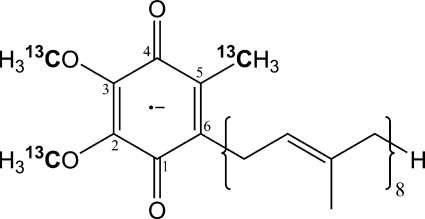
The HYSCORE spectra of the D75E and D75H mutants measured at times τ = 136 ns and 200 ns are shown in Figs. 4 and 5 and supplemental Figs. S5 and S6. The spectra of D75E are similar to the spectra of WT cyt bo₃ with ¹³C features 1_C and 2_C. The central part of the feature 2_C in D75E is, however, more smooth and consists of a better resolved doublet with the splitting of 0.6 MHz accompanied by shoulders of lower intensity up to 2.5 MHz of the same length as in WT cyt bo₃ (Fig. 5). It appears that the mutation removes some nonequivalence between the two methoxy groups seen in the spectra of cyt bo₃. In contrast, the spectrum of the D75H mutant shows a ridge of low intensity with the total length about 5.5 MHz extended along the antidiagonal without any well pronounced maxima (Figs. 4 and 5). In the spectrum recorded with τ = 200 ns (supplemental Fig. S5), the central part of the ridge is completely suppressed, and only the weak cross-peaks 1_C, with a splitting of about 5 MHz, are seen. This is consistent with the spectra of WT cyt bo₃ and D75E, in which the intensity of cross-peaks 1_C is significantly enhanced at τ = 200 ns.

FIGURE 4.

Contour (A and B) and stacked (C and D) presentations of the HYSCORE spectra of the Q_H SQ with ¹³C-labeled methyl and methoxy groups in uniformly ¹⁵N-labeled D75E and D75H enzymes (magnetic field 346.2 mT (D75E) and 345.7 mT (D75H), time between first and second pulses τ = 136 ns, microwave frequency 9.706 GHz (D75E) and 9.697 GHz (D75H)).

DISCUSSION

The conformations of substituents, such as the methoxy groups in UQ, are important in defining the properties of the cofactor. In E. coli, it is known that the methyltransferases responsible for the attachment of the ring methyl group and the two O-methyl groups of UQ-8 use S-adenosylmethionine as the methyl donor (44–46). In this study, we created an E. coli C43(DE3) Met auxotroph by knocking out the metA gene from the chromosome. The Met auxotroph (47) allowed us to achieve the site-specific ¹³C isotope labeling of the ring methyl and the two methoxy groups of UQ-8 (Scheme 1) and, subsequently, to visualize the ¹³C hyperfine interactions in the SQ radicals through pulsed EPR and ENDOR experiments.

SCHEME 1.

¹³C Couplings in the UQ Anion Radical

The ¹³C isotropic constants previously measured for UQ-10 anion radical in methanol solution is |a| = 4 MHz for the methyl and |a| < 0.3 MHz for the methoxy groups (48). The reported Car-Parrinello molecular dynamics simulations for the aqueous anion radical of UQ with an ethyl tail yielded a = −3 MHz, and T = 0.4 MHz for the ¹³C in the methyl group (49). A similar value for the ¹³C methyl isotropic coupling, |a| = 3.8 MHz, was reported for the duroquinone anion radical (50, 51). The calculated hyperfine tensor for this radical is a = −3.5 MHz, and T = 0.4 MHz (52). Based on these results, the coupling A_⊥ = |a − T| ∼ 3.9 MHz observed in the ¹³C ENDOR spectrum of the UQ-8 anion radical (Fig. 3) can be assigned to the methyl group.

Molecular dynamics simulations (49) show that two methoxy groups in the UQ anion radical are significantly nonequivalent, possessing different orientations (up and down) relative to the quinone plane and different dihedral angles. Despite this behavior, only one ¹³C hyperfine tensor for the methoxy groups has been reported, suggesting an average equivalence of these groups at long time intervals. The ¹³C hyperfine tensor components calculated in (49) for the methoxy groups are a = 1.2 MHz and T = 0.4 MHz, consistent with about half of the splitting A_⊥ = |a − T| = 0.8 MHz compared with the ∼2-MHz splitting observed in ENDOR spectrum.

Tensors with isotropic and anisotropic components similar with those reported previously (49) were obtained in our model density functional theory calculations for the 2,3-dimethoxy-5,6-dimethyl-1,4-benzoquinone anion radical in the conformation possessing minimum energy when the O-CH₃ bonds form dihedral angles of −123° and +124° with respect to the quinone plane (see Table 1). This table also shows that the isotropic hyperfine coupling can be substantially larger for conformations corresponding to the larger energies (in solution), in which the methoxy groups form dihedral angles of ∼−70°. In contrast, calculations show that the anisotropic tensor is not significantly influenced by conformational changes of methoxy group orientation. However, the location of the resonances assigned to the ¹³C methoxy groups in the spectra of the UQ-8 anion radical obtained in our experiments are not consistent with the available computational results, suggesting the need for further computational work.

TABLE 1.

Computed ¹³C hyperfine tensors for different conformations of isolated 2,3-dimethoxy-5,6-dimethyl-1,4-benzoquinone radical anion

Relative stabilitya	Dihedral angle τ2b (Group 2)	Dihedral angle τ3b (Group 3)	Isotropic hfic constant and three principal values of hfi tensor
			13C-O-CH3		C-O-13CH3
			Group 2	Group 3	Group 2	Group 3
cm−1	degrees	degrees	MHz
0a	−123	124	−2.2	−2.2	1.2	1.2
			9.5, −7.8, −8.3	9.5, −7.8, −8.3	2.0, 1.2, 0.6	1.9, 1.1, 0.6
727	−78	142	−1.4	−3.0	6.4	0.8
			10.9, −7.3, −7.7	8.7, −8.7, −9.2	7.4, 5.9, 5.9	1.4, 0.6, 0.2
830	−49	−119	−0.3	−3.5	5.2	0.7
			14.6, −7.4, −8.0	5.4, −7.8, −8.2	6.2, 4.7, 4.6	1.3, 0.7, 0.1
975	−121	−120	−2.4	−2.4	1.6	1.6
			9.5, −8.1, −8.6	9.5, −8.1, −8.6	2.3, 1.5, 0.9	2.4, 1.6, 1.0
1451	−67	−74	−0.7	−1.1	8.9	8.5
			13.6, −7.6, −8.1	12.6, −7.7, −8.2	9.9, 8.4, 8.3	9.5, 8.0, 8.0
1498	−120	143	−3.0	−2.4	1.2	0.8
			6.7, −7.6, −8.1	9.7, −8.2, −8.8	1.9, 1.2, 0.6	1.5, 0.7, 0.2
1505	180	180	−4.8	−4.8	−0.9	−0.9
			2.4, −8.1, −8.7	2.6, −8.1, −8.9	−0.4, −1.1, −1.2	−0.4, −1.1, −1.2
3824d	180	0	−5.8	−2.2	−0.7	−1.0
			0.5, −8.7, −9.2	8.6, −7.3, −7.9	−0.2, −0.9, −1.1	−0.6, −1.1, −1.3

^a Corresponds to the most stable conformation.

^b Dihedral angles are defined in the same manner, D(X_b-X_a-C_ortho-C_ortho), as in Ref. 49.

^c hfi, hyperfine interaction.

^d Saddle point.

¹³C Methyl Couplings in the SQ at the Q_H Site

The isolated location of the cross-peaks 1_C in the HYSCORE spectra of cyt bo₃ (Fig. 2 and supplemental Fig. S4) allows one to estimate the isotropic and anisotropic components for the ¹³C tensor from the linear fitting of the cross-peak 1_C frequencies in the coordinates (ν₁)² versus (ν₂)² (41). This analysis gives two possible solutions: T = 0.54 MHz, a = −6.1 MHz; and T = −0.54 MHz, a = −5.6 MHz. The computational results cited above allow one to select the solution with opposite signs of a and T as preferred, so that A_⊥ = |a − T| = 6.6 MHz. This is consistent with the location of the peak near 6.9 MHz in the ENDOR spectrum.

The cross-peaks 1_C in the spectra of D75E (Fig. 4 and supplemental Fig. S5) and in the spectrum of D75H (supplemental Fig. S5) similarly define the hyperfine tensor with a = −5.9 MHz and T = 0.6 MHz, and a = −4.7 MHz and T = 0.4 MHz, respectively, for these two mutants. Comparison of the ¹³C isotropic couplings obtained for the three proteins with the corresponding ¹H methyl couplings determined previously (27) yields a ratio of |a(¹H)/a(¹³C)| = 1.63 ± 0.07 for three proteins. This is only slightly different from the values calculated for UQ-10 and UQ-0 anion radicals using published data for ¹H and ¹³C couplings (Table 2). This comparison allows us to assign the features 1_C in the spectra to the methyl carbon.

TABLE 2.

Comparison of ¹H and ¹³C isotropic couplings in SQs

Protein	a(13C)	a(1H)a	|a(1H)/a(13C)|
	MHz	MHz
WT cyt bo3	−6.1	10a	1.64
D75E	−5.9	9.2a	1.56
D75H	−4.7	8.0a	1.70
(UQ-0)−	|4.76|b	6.7 c	1.41
(UQ-10)−	|4.0|c	6.0d	1.50

^a From Ref. 27.

^b From Ref. 53.

^c From Ref. 48.

^d From Ref. 14.

The ¹³C methyl isotropic hyperfine coupling determined from this analysis for WT cyt bo₃ is about 1.5 times larger than the values reported for the ¹³C methyl isotropic constant in anion radicals (48, 50, 51). It has previously been shown that the ¹H methyl coupling for the Q_H site SQ is about 2 times larger than the corresponding coupling in anion radicals (25, 27). These data indicate the substantial shift of the unpaired spin density toward the O1 side of the Q_H SQ. Unfortunately, very recent calculations devoted to the comparison of the unpaired spin density distributions in neutral and anionic SQ species of UQ (54, 55) do not report the values of the ¹³C methyl couplings, precluding any comparison of the values shown in Table 2 with theoretical values.

The hyperfine tensors obtained from ¹³C HYSCORE allow an estimation of the unpaired spin populations in the s and p orbitals of the methyl carbon. The hyperfine couplings calculated for the unit spin on the carbon 2s and 2p orbitals are 3777 MHz and 107.4 MHz, respectively (56). These values yield s and p populations of −(1.24–1.61) × 10⁻³ and (3.7–5.6) × 10⁻³, respectively, for the range of isotropic a = −(4.7–6.1) MHz and anisotropic T = 0.4–0.6 MHz couplings, determined for the ¹³C methyl in WT cyt bo₃ and the D75E and D75H mutants. On the other hand, the methyl proton couplings a = 8–10 MHz (Table 2) would correspond to a substantially larger s spin density of (5.6–7.0) × 10⁻³ with the ¹H hyperfine coupling of 1420 MHz for the unit spin on the 1s orbital. Taking into account that such spin density resides on each of three hydrogens of the methyl group, one can conclude that the total spin density on the methyl protons in the cyt bo₃ enzymes is close to 0.02.

¹³C Methoxy Couplings in the SQ at the Q_H Site

Two factors influence the ¹³C methoxy hyperfine couplings in cyt bo₃. First is the redistribution of the unpaired spin density toward the O1 side, which is indicated by the 1.5–2-fold increase of the ¹³C and ¹H methyl couplings. This could lead to the substantial differences in the spin densities on the C2 and C3 ring atoms and, consequently, on the methoxy substituents. Second is a possible difference in conformation of the methoxy groups enforced by the protein environment. An additional factor that can be considered is the well pronounced correlation between the conformation of the methoxy group and the ¹³C isotropic hyperfine coupling, as seen in Table 1. This correlation suggests that even a small difference (or spread) of dihedral angles for the two groups would cause a substantial broadening of the spectroscopic lines or their relative shifts in the ENDOR and HYSCORE spectra.

The ENDOR spectrum of cyt bo₃ resolves a pair of lines with a splitting of ∼1.0 MHz, which can be tentatively assigned to A_⊥ of the ¹³C in the methoxy group(s). This spectrum does not show any other intensity around the ¹³C Zeeman frequency. In contrast, the shape of the cross-peaks 2_C located in the same frequency region in the HYSCORE spectra is more complex. There is an increased intensity in the area about ∼1 MHz around the diagonal point, with extended shoulders of the lower intensity with total width of ∼2.5 MHz around the diagonal point. Using the combined information from the ENDOR and HYSCORE spectra, one can perform a separate estimate of the a and T values, assuming |A_⊥ = a − T| ∼ 1 MHz and |A_‖ = a + 2T| ∼ 2.5 MHz. There are two possible solutions: a = 1.5 MHz, T = 0.5 MHz; and a = 0.2 MHz, T = 1.2 MHz (or opposite signs for a and T simultaneously). However, neither of the two simulated spectra (supplemental Fig. S7) can reproduce the line shape and distribution of the intensity in the feature 2_C. The anisotropy of the order T > 1 MHz in the simulations suggests a deviation of the cross-features from the antidiagonal. This deviation is observed in the calculated spectrum with T = 1.2 MHz, but it is not seen in the experimental spectra where cross-ridges are straight along the antidiagonal. Thus, an alternative explanation is required for the line shapes from the methoxy groups in the HYSCORE spectra.

Considering the shape of 2_C in the spectra of the D75E mutant, one can suggest that it consists of two ¹³C signals. One of them possesses an isotropic hyperfine coupling a ∼ 0.6–1 MHz, and the second one has a larger isotropic hyperfine coupling. The anisotropic hyperfine coupling for these nuclei cannot exceed a value about T ∼0.5 MHz to avoid an observable deviation of the cross-peaks from the antidiagonal. Our attempts to simulate the line shape of the HYSCORE spectra of D75E with this assumption failed when using axial hyperfine tensors because the spectra show similar intensities of the lines with the splittings of ∼0.6 and 2 MHz. We were able to suppress the relative intensity of the line with the larger splitting by introducing substantial rhombicity to the hyperfine tensor. However, the spectrum of the D75H mutant, with a cross-ridge and total length of ∼5.5 MHz cannot be modeled in a similar way. In addition, the presence of the two small couplings resolved in the cyt bo₃ enzyme cannot be explained in this model.

An alternative model is to assume that the methoxy groups in cyt bo₃ and D75E have preferred conformations with limited angle distributions. The splittings corresponding to preferred conformations are ∼0.3 and 0.6 MHz in HYSCORE spectra of cyt bo₃ and ∼0.6 MHz for the D75E mutant. Any deviation from the most populated conformations is accompanied by a substantial increase of the isotropic constant, but the anisotropic interaction remains stable and does not exceed T ∼0.5 MHz. Such a distribution would produce cross-ridge elements shifted from the (ν_C, ν_C) along the antidiagonal but without the deviation from this line, as would be in the case if the cross-ridge resulted from one tensor producing a ridge of the same length. An approximately 2.0-fold increase of the isotropic coupling is sufficient for this explanation of the observed line shapes. Taking into account the results of the calculations in Table 1, this corresponds to an ∼10° change of the dihedral angle. In order to explain the spectrum in D75H, a broader random distribution of conformations for the methoxy groups would be required.

The current work is unable to provide the definitive conformations for the SQ methoxy groups. However, the results indicate that the Q_H site of the WT cyt bo₃, as well as the D75E mutant, stabilizes the SQ radical such that the methoxy groups have preferred orientations and that the constrained orientations contribute to the specific electronic configuration of the bound cofactor required for the subsequent electron transfer step. The failure to trap the methoxy groups in the necessary angles at the Q_H site of the D75H mutant cyt bo₃ could at least partially explain why this particular mutant enzyme is inactive.

CONCLUSION

In summary, two-dimensional ¹³C ESEEM spectra, obtained in this work, reflect fine differences in the ¹³C methyl and methoxy couplings between cyt bo₃, its mutants, and the model anion radical. Using these spectra, we determined the ¹³C methyl hyperfine tensors and showed that the isotropic couplings vary proportionally to ¹H methyl couplings previously reported (27). These are the first measured ¹³C tensors from the ring substituents in the quinone cofactor, and these data can be used in further calculations of the electronic structure of the SQ in the Q_H site in WT cyt bo₃ and mutants. It is noteworthy that the ¹³C lines from the two methoxy groups in WT cyt bo₃ and mutants have complex shapes. Simulations performed for models with fixed isotropic constants failed to explain the observed shapes. The two-dimensional ESEEM line shapes from the methoxy groups can be qualitatively explained by constraints on the dihedral angles characterizing the conformations of the methoxy groups and by the sharp dependence of the isotropic constant on this angle. A small change of this dihedral angle produces a substantial change of the isotropic coupling. It is not known if the observed spectral features can be completely explained by a static distribution of allowed dihedral angles or if other physical models are required. Unfortunately, we were not able to obtain the conclusive data about the ¹³C line shape from the methoxy groups in the model anion radical due to the overlap of the methyl and methoxy lines.

Further experimental and theoretical work is needed in order to characterize the spin density distribution over the methyl and methoxy substituents and the dependence between the conformation of the methoxy group and the ¹³C hyperfine couplings in enzymes and in model systems. Experimental progress will come from separating the spectroscopic contributions of methyl and individual methoxy groups by orientation-selected ENDOR at higher microwave frequencies (Q- or W-band) and by selective chemical labeling of each of the individual ring substituents.