Systems biology and integrative physiological modelling

Abstract

Over the last 10 years, ‘Systems Biology’ has focused on the integration of biology and medicine with information technology and computation. The current challenge is to use the discoveries of the last 20 years, such as genomics and proteomics, to develop targeted therapeutical strategies. These strategies are the result of understanding the aetiologies of complex diseases. Scientists predict the data will make personalized medicine rapidly available. However, the data need to be considered as a highly complex system comprising multiple inputs and feedback mechanisms. Translational medicine requires the functional and conceptual linkage of genetics to proteins, proteins to cells, cells to organs, organs to systems and systems to the organism. To help understand the complex integration of these systems, a mathematical model of the entire human body, which accurately links the functioning of all organs and systems together, could provide a framework for the development and testing of new hypotheses that will be important in clinical outcomes. There are several efforts to develop a ‘Human Physiome’, with the strengths and weaknesses of each being presented here. The development of a ‘Human Model’, with verification, documentation and validation of the underlying and integrative responses, is essential to provide a usable environment. Future development of a ‘Human Model’ requires integrative physiologists working in collaboration with other scientists, who have expertise in all areas of human biology, to develop the most accurate and usable human model.

Robert Hester, PhD (right) received his PhD in Biomedical Engineering from University of Mississippi Medical Center and Mississippi State University. He is a Professor in the Department of Physiology & Biophysics. Over the last 15 years he has been collaborating with Dr Tom Coleman in the development of integrative physiological models. Tom Coleman, PhD (left) has an undergraduate degree in electrical engineering, graduate degrees in electrical engineering and biomedical engineering and post-doctoral training in cardiovascular medicine. He has a long-standing interest in mathematical models of complex biomedical systems with an emphasis on human physiology. He is the principal author of the integrative physiological model HumMod.

Introduction

Over the last 10 years, there has been significant interest in ‘Systems Biology’. ‘Systems biology … is about putting together rather than taking apart, integration rather than reduction. It requires that we develop ways of thinking about integration that are as rigorous as our reductionist programmes, but different. … It means changing our philosophy, in the full sense of the term.’ (Noble, 2006.)

This issue of The Journal of Physiology provides a variety of papers addressing Systems Biology and how Systems Biology can provide insights into the physiological workings of the human body. These papers focus on single-level computational studies ranging from gene analysis to cellular metabolism to localized blood flow responses. However, most current ‘Systems Biology’ studies are not multilevel; they do not integrate the physiological responses from molecular to cellular to organ to the whole organism. The development of an integrated model of human physiology is essential for the understanding of how molecular, cellular, organs and systems levels interact for a total physiological response.

Biomedical systems are highly complex. This complexity results from the following.

• Non-linearities: many responses have upper and lower boundaries with different levels of physiological sensitivity in between.

• Redundancy: many physiological states are the result of multiple mechanisms pushing and pulling on the observable response. Redundancy makes it difficult for a researcher or clinician to identify important causal mechanisms.

• Disparate time constants: the importance of an observation often depends on the timing of the protocol. For instance, the control of arterial blood pressure is a mix of fast-acting neural mechanisms, slow-acting hormonal mechanisms, and long-term effects of body fluid volume and compositions.

• Individual variation: physiological responses are a qualitative and quantitative function of sex, age, body composition and other individualities.

• Emergence: many high-level, integrative behaviours of the biological system cannot be described by the sum of the respective inputs from basic processes.

Biomedical researchers can use integrative physiological models to better understand the fundamental relationships hidden in the complexity.

Translational Research has made integrative analysis of human physiology more relevant. The explosion of data over the last 20 years provides novel opportunities to develop new clinical treatments. New technologies – DNA sequencing, imaging, proteomics, etc. – provide massive amounts of new information about the human body. The ability to extract useful information from these data will lead to custom treatments for disease, such as cancer and haematological and metabolic disorders. These data have brought about the necessity of new methods of analysis. Genetic analysis suggests which genes may be important for clinical outcomes; however, the physiological relevance of changes in genetic makeup is not clear. This ambiguity necessitates goals for the integrative analysis.

Beard et al. (2005) and Kohl et al. (2010) provide excellent reviews of the goals of computational modelling and the value of computational modelling to systems research. This article addresses the history, the current state, the strengths and limitations, and the necessary future directions of physiological modelling.

History of mathematical modelling of physiology

Computational methods have been used to study and describe physiological responses since William Harvey estimated cardiac output and ejection fraction in his original publication De Motu Cordis in 1628 (see Harvey, 1957). Other early examples include Krogh's (1919) computation of oxygen flux in skeletal muscle and Hodgkin & Huxley's (1952) exquisite computational analysis of membrane potential. These examples lead to numerous studies that provide the basis for several clinical treatments. Despite the usefulness of these ‘niche’ computational models, there are few examples of integrative models of human physiology.

In the early 1960's, Dr Arthur Guyton started developing mathematical analyses of integrative physiology (Millhorn & Guyton, 1965). Over the next 10 years, Guyton and colleagues (1972) developed a model of cardiovascular physiology with ∼150 distinct variables. Guyton used the 1972 model to test a variety of physiological hypotheses, mainly focusing on acute and chronic blood pressure control and the role of the kidney in the long term regulation of blood pressure.

In 1983, with the advent of the personal computer, Coleman and Randall developed a model of human physiology called Human (Coleman & Randall, 1983). Human was an extension of the 1972 Guyton, Coleman and Granger model. Human was expanded into a Windows software package called Quantitative Circulatory Physiology (QCP).

QCP contains ∼4000 distinct variables and several hundred mathematical functions. The end result is a model describing cardiovascular, renal, neural, respiratory, endocrine and metabolic relationships within and across multiple organ systems in the body. QCP's variables provide a time-dependent simulation of human physiology. It is freely downloadable at http://hummod.org/downloads/qcp-2005.

Current efforts in integrative physiological modelling

Currently there are several centres around the world that are developing environments for developing integrative models of human physiology or ‘physiomes’. Each of these centres is approaching the development of such software from different aspects. The Physiome Project is a worldwide effort to develop databases and models to understand physiological responses. The International Union of Physiological Sciences (IUPS) Physiome Project designates itself as a ‘worldwide public domain effort to provide a computational framework for understanding human and other eukaryotic physiology’ (https://www.physiome.org.nz/). The IUPS Physiome Project comprises databases, markup languages, software for computational models of cell function, and software for interacting with organ models. The models are based on Cell ML, an Extensible Markup Language (XML)-based description of mathematical models for cell or tissue functions. For example, there are extensive models of different aspects of cardiovascular physiology under the ‘cardiovascular’ heading, but these are not linked together (http://models.cellml.org/cardiovascular_circulation). Many of these models are based on the 1972 Guyton model of integrative physiology (Guyton et al. 1972). Currently the major limitation with the Physiome Project is that there is no integration of these narrow-focus models which would lead to a comprehensive integrative model of human physiology.

The NSR Physiome Project at the University of Washington (http://www.physiome.org/) is affiliated with the IUPS Physiome Project. The NSR Physiome Project's models are written using JSim, a Java based simulation system. There are 274 separate models listed that will run in JSim. Similar to their affiliate, the NSR Physiome Project fails to integrate their models.

The SimBios project aims for multi-scale modelling. Unfortunately, its aim is limited to projects focusing on RNA folding, protein folding, neuromuscular dynamics, drug target dynamics, and neural prosthetic interactions. This group does have a cardiovascular dynamics project, but this work focuses mainly on computational fluid dynamics simulation of aortic flow and function. But SimBios fails to integrate these models.

The SAPHIR Project is supported by the French National Research Agency with the goal of developing a comprehensive modelling environment that focuses on regulation of blood pressure and body fluids. This work is also based on the 1972 Guyton model.

A derivative of the 1972 Guyton model to successfully integrate multiple systems is HumMod. HumMod was developed by the Centre for Computational Medicine and the Department of Physiology at the University of Mississippi Medical Centre. It is a large, multi-scale model of human physiology. HumMod is an extension of QCP, which was an extension of the 1972 Guyton model. HumMod and QCP are due in large parts to the efforts of Dr Tom Coleman, a contributor to the 1972 Guyton model.

The original HumMod, called QCP, contained ∼4000 variables. QCP's compiled language limited the ability of users to change the underlying equations that simulate the physiological processes. HumMod solves this problem. HumMod is a comprehensive, multilevel modelling environment for the simulation of human physiology. Physiological relationships and equations are written in XML. The current version has ∼5000 variables. The many hundreds of equations that specify the relationships between ∼5000 variables are written in XML. As a result, HumMod simulates a wide-range of interconnected organs and systems with easily modifiable code. HumMod is integrated and can simulate time-dependent responses. The time-dependent responses can range from seconds to years. HumMod is useful when physiological complexity needs to be explored.

All of the mathematical equations and relationships describing physiological responses are described in XML files. The XML files are simple files that may be modified in any text editor. Figs 1, 2 and 3 provide examples of physiological responses that HumMod can predict. Here HumMod simulates a pneumothorax with the clinical presentation seen in Fig. 1, with Fig. 2 demonstrating the blood oxygen levels, and Fig. 3 demonstrating the cerebral blood flow responses.

Figure 1. The clinical responses for the 30 min following the creation of a right-side pneumothorax.

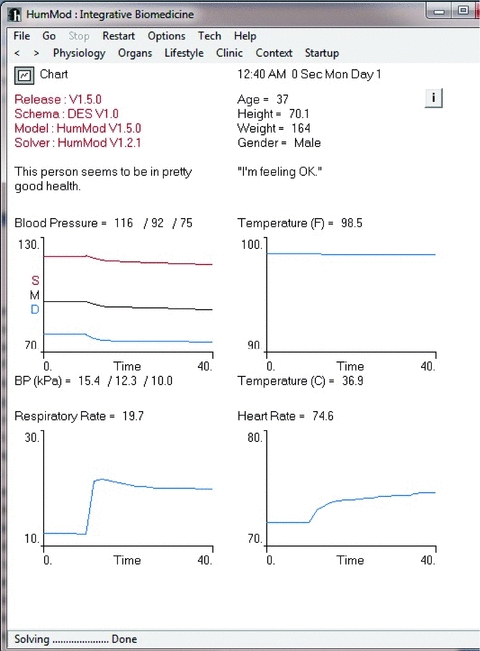
Note the reflex increase in respiratory rate, along with the increase in heart rate.

Figure 2. Details as to the arterial and venous oxygen responses following 30 min of a pneumothorax.

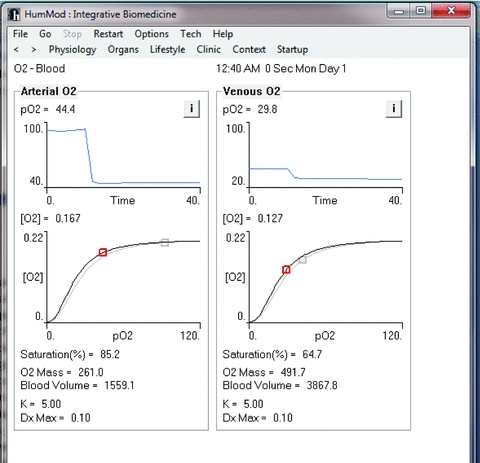
With a decrease in arterial oxygen levels there is a resultant decrease in venous oxygen levels.

Figure 3. The modelling responses of the brain circulation following the pneumothorax.

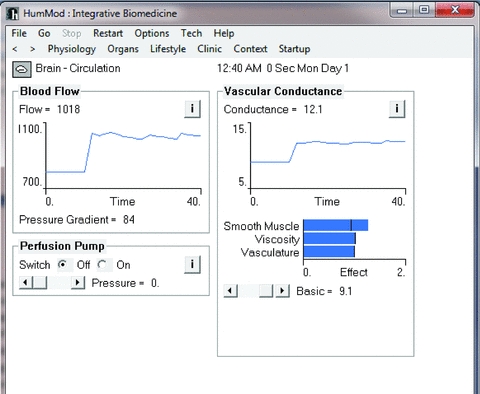
With the fall in arterial oxygen levels there is a reflex increase in vascular conductance and resultant increase in cerebral blood flow.

The executable file, HumMod.exe, directly parses and evaluates the mathematical expressions in its own math engine. HumMod parses the complete set of XML files, ∼2900 files, and creates the mathematical model in <10 s on a Dell desktop (2.8 GHz, 3 GB, Windows 7). Simulations are fast too; a 24 h simulation takes ∼30 s while a 7 day simulation takes ∼2 min. Long simulations, months to years, are produced with minimal time. HumMod is freely available at http://hummod.org/downloads.

Model development

Kohl et al. (2010) provide an analysis of the starting point for the development of multi-level systemic biological analysis, combining reduction and integration. They outline three ways to study systems biology: bottom-up, middle-out, or top-down.

The bottom-up approach is considered the molecular biology approach, starting with the description of genes and the genetic relationships. The wealth of genetic data and the multiple cellular processes require the bottom-up approach to be complemented by other approaches. The top-down approach is the classical physiological approach, performing an integrative analysis of the organ systems and then adding greater and greater detail to individual organs and systems. A potential complementary approach is the middle-out approach.

Kohl et al. propose that the middle-out approach would be the best approach. The middle-out approach combines bottom-up and top-down methods. Modelling with the middle-out approach begins at the level of the organism where suitable mathematical relationships are known and can be used to create a model. Future additions can move upward or downward in adding detail. The middle-out approach provided results in the modelling of the heart by combining genetic changes with electrical, mechanical and metabolic properties of the heart. The Physiome Project is cited as a success of the middle-out method.

The bottom-up and middle-out approaches yielded some mathematical analyses for successful simulations. Unfortunately, these methods have not led to a comprehensive model of human physiology or an environment of integrated models with time-dependent simulations incorporating appropriate feedback mechanisms. The middle-out modelling of the heart provided sound simulations; however, it will not simulate cardiac function during exercise and allow interfacing with the changing physiological variables (i.e. blood pressure, neural and hormonal changes). The bottom up and middle out approaches would be equivalent to the futile efforts of understanding human consciousness based solely on the description of individual neural processes and ignoring its emergent nature (Penrose, 2002).

The top-down approach, if done properly, leads to the appropriate environment for a comprehensive model of human physiology. The top-down approach requires sufficient detail of the underlying physiology to explain physiological responses. It does not require that all of the underlying physiology be rigorously described with mathematics. The 1972 Guyton model is an example of the top-down approach. The published model of cardiovascular regulation includes cardiac function, blood pressure regulation, neural activation, and local tissue responses. The block diagram in the original text describes some relationships by empirical curvilinear functions (Guyton et al. 1972). These functions describe physiological relationships where the underlying physiology was not completely known. The relationships were determined from either animal or clinical experiments. With the top-down approach these curvilinear functions can be described in more mathematical detail as the underlying physiology becomes known.

Further, the top-down approach allows the development of the model to be directly related to experimental and clinical data. Due to the many interactions and feedback pathways that are present in the human body, a top-down model allows users and developers to test the model with clinical data. Further, users and developers can determine if their understanding of physiology matches the clinical and experimental data. These points are addressed in the following sections on ‘Hypothesis testing’ and ‘Validation and verifications’.

Hypothesis testing

Mathematical simulation is used to understand the quantitative relationships between multiple physiological systems. The goal of mathematical simulation is to develop an understanding of integrated physiological systems. With the development of mathematical models, the investigator should compare the simulation results with experimental data. If experimental results are accurately simulated by the developed model, then the model developer may have an accurate understanding of physiological relationships. The model developer needs to ensure that the simulation results support multiple scenarios. QCP and HumMod have been used to understand many physiological responses, including the long-term control of blood pressure following baroreceptor stimulation (Iliescu & Lohmeier, 2010) and physiological responses to zero gravity (Summers et al. 2010). These studies are examples of the use of integrative modelling to identify and describe the underlying mechanisms responsible for these physiological responses.

Validation and verification

Mathematical models must provide a correct description of physiology and should lead to insights into the physiological processes. A major concern is whether a model will accurately simulate normal physiological responses and pathophysiological processes, which must be addressed by the systems biologist. The systems biologist should make every effort to verify the accuracy of the mathematical simulation.

Confidence in the predictions provided by any mathematical simulation can only be established if the model is properly validated and verified against both clinical and experimental data. The validation and verification must be performed on three levels.

• Specific functional interactions or physiological relations.

• Component systems or sub-models.

• Integrated, overall model performance.

If the model is validated only on the individual sub-model or component level, then there is no guarantee that it will accurately predict the integrated physiological response. If the model is validated only on the integrated, overall model performance, then there is the possibility that adjustments of several system parameters may mask error in the functioning of a specific sub-model or physiological relation.

Verification

Verification is defined as the physiological, mathematical and physical representation of the processes described within the model.

Verification criteria include the following.

• Physiological and mathematical fidelity of the interconnecting structures.

• Proper functionality of feedback mechanisms.

• Accurate representation of state parameters used in the physiological functional relations.

• Accurate predictions of key physiological determined variables that are globally affected by the system.

With verification the model needs to provide documentation of the variables and mathematics used to represent the physiology. Documentation should be included as part of the model structure, not an enumeration of publications. Universal acceptance of a model requires that users be able to view all aspects of the underlying structure. Developers should provide documentation in the code or associated files. The use of an XML structure, as with the IUPS Physiome Project and HumMod, for the model allows easy implementation of embedded documentation.

Validation

Validation means that a simulation produces results within the physiological and statistical bounds of comparative experimental data. All models and their components should be validated by benchmark testing. Benchmark testing requires simulation results be compared with well documented data from peer-reviewed literature or specified data sets. Model and software validation ensures the quality of physiological and numerical solution performance is established.

The quality of numerical solution performance requires overall simulations to provide stable outputs, with limited errors of physiological importance, within the context of the integration scheme.

• Qualitatively– It is important that the model behaves in the directionally appropriate manner that was observed experimentally. This type of analysis is of high value, especially in determining the clinical significance of a model.

• Quantitatively by steady state– Models must show stability and demonstrate steady state values that approach experimental data. The use of statistical techniques for estimating precision, bias and significance of state parameters should be employed.

• Quantitatively in dynamics– Models must demonstrate responses that are within reasonable accuracy during dynamic transitions. Quantitative evaluation of dynamic transition accuracy is more difficult; there are no standard methods.

For integrative models, validation of the breadth of the simulation can be a significant challenge, especially time-dependent simulations. It is valuable to compare simulation results with either animal or human studies. The wealth of clinical studies makes validation of integrative physiological models relatively easy. Validation of integrated simulations should be stronger than cellular models because of the integrative aspects of the clinical studies. However, there are several issues that can affect the process of verifying the accuracy of integrative modelling. For instance, the subjects of clinical studies may be of different ages and sexes, along with varying underlying alterations in physiology. There is no ‘ideal’ clinical subject. The model developer must develop sex and age specific models to accurately simulate the specific responses. We are not aware of sex and age specific models, though the HumMod model has the underpinning for the development of sex specific models (Hester et al. 2010). It is easier to find relevant data for larger models. The data cannot validate the total state of the model because all physiological variables in the model may not have associated animal or human studies. In most studies, the investigators focus on a specific hypothesis and measure a small set of physiological variables. Additionally, data collection may not be of high fidelity (i.e. clinical studies). Validating the total state of the model is possible only in trivial models.

Medical and clinical education

The major uses of mathematical simulations are for hypothesis testing and experimental design. However, an additional use of mathematical simulations and integrative models is education. Students, clinicians and researchers need to understand basic mechanisms that maintain a homeostatic balance in the human body and alterations that result in pathological states. A more comprehensive, validated model will have great use in education. QCP has been successfully used for medical education to help users understand the underlying mechanisms, feedback and interaction of physiological responses (Abram et al. 2007; Rodríguez-Barbero & López-Novoa 2008; Brands & Schumacher, 2009).

Future directions

Several issues must be addressed to ensure the continual development of useful integrative models. The modeller must understand all aspects of physiology. There are fewer and fewer physiologists that are being trained as integrative physiologists, which is important because reductionists are limited in their understanding of the magnitude of physiological changes that can occur in normal life. The numerous feedback systems create ranges of physiological responses that might be considered abnormal, yet to the integrative physiologists the values are feasible. For example, during exercise there are large increases in metabolic rate. The increases are so large that CO₂ production can increase 10- to 20-fold. However, arterial 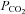does not increase and may decrease. The integrative physiologist understands that there are multiple mechanisms responsible for the regulation of ventilation and that it is entirely understandable that 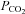will not increase during exercise. Integrative physiologists are able to understand the mechanisms involved in the range of physiological responses that occur.

Science has taken a reductionist approach in response to new techniques that allow scientists to understand gene responses, protein responses, and intracellular signalling. However, a clear, defined understanding of how cellular pathways fit into the overall picture is needed. This integration requires close interactions between integrated physiologists and other scientists.

Multi-scale integrative modelling needs a database of physiological variables. There are numerous ontological databases that address anatomical, genome and proteome data. However there appears to be no database of high level physiological parameters. These databases should include normal and pathological values for physiological variables from humans (male and female) and animals. There are numerous physiological values for humans that may not be experimentally available, which requires the use of experimental animal data.

Summary

In summary we have presented an overview of the current state of computational simulation of integrative physiology. There are numerous efforts directed at developing a human physiome, an extensive integrative model of human physiology that can be used for both hypothesis testing and medical education. For such a system to work there has to be a comprehensive development of multiple systems, and importantly a linkage with these cellular and organ systems that will provide implementation of the appropriate feedback systems.