Abstract
Several electrical methods have been introduced as non-invasive techniques to overcome the limited accessibility to root systems. Among them, the earth impedance method (EIM) represents the most recent development. Applying an electrical field between a cormus and the rooted soil, the EIM measures the absorptive root surface area (ARSA) from grounding resistance patterns. Allometric relationships suggested that this method was a valuable tool. Crucial assumptions for the applicability of the EIM, however, have not been tested experimentally. Focusing on tree root systems, the present study assesses the applicability of the EIM. Six hypotheses, deduced from the EIM approach, were tested in several experiments and the results were compared with conventional methods. None of the hypotheses could be verified and the results allow two major conclusions. First, in terms of an analogue electrical circuit, a tree-root–soil continuum appears as a serial circuit with xylem and soil resistance being the dominant components. Allometric variation in contact resistance, with the latter being the proxy for root surface area, are thus overruled by the spatial and seasonal variation of soil and xylem resistances. Second, in a tree-root–soil continuum, distal roots conduct only a negligible portion of the electric charge. Most of charge carriers leave the root system in the proximal parts of the root–soil interface.
Keywords: Absorbing root surface area, conductance, electrical resistance, tree capacitance
Introduction
The adaptation of the root surface to site-specific factors plays a key role in plant and ecosystem functioning (Jackson et al., 1997; Reich, 2002; Hodge, 2004). The large variety of edaphic and climatic factors results in a great interspecific and intraspecific variation in root systems (Köstler et al., 1968; Kutschera and Lichtenegger, 1982, 2002). While the adaptability of root systems is increasingly acknowledged, methodological constraints limit the access to and our knowledge of below-ground structural parameters. Root systems of small plants can be assessed by excavation or computer tomographical techniques (Asseng et al., 2000), but this is not feasible for large trees. For the latter, different methods are applied, focusing either on the coarse root system (e.g. manual excavation, air spade, ground-penetrating radar; Stokes et al., 2002; Nadezhdina and Čermák, 2003) or the fine root system (soil coring, root windows, minirhizotrons; Samson and Sinclair, 1994; Smit et al., 2000a; Ostonen et al., 2005; Hendricks et al., 2006). Most of these approaches, however, are invasive, time-consuming or represent only a subsample of the total root system. Moreover, differentiation between individual plants is rarely possible.
Root distribution patterns could successfully be visualized and root biomass be calculated by injecting an electrical current in soil segments and measuring the corresponding resistance (multi electrode resistivity imaging; Amato et al., 2008, 2009). This approach of resistivity tomography does not differentiate between individuals and therefore works on the stand level. Methods operating on the basis of individual trees using electrical characteristics (capacitance; Chloupek, 1972; Kendall et al., 1982; Dalton, 1995; van Beem et al., 1998; Preston et al., 2004; McBride et al., 2008, impedance; Ozier-Lafontaine and Bajazet, 2005; Aubrecht et al., 2006) were introduced to derive root system properties in situ and non-destructively on tree level. These methods that measure electrical parameters (resistance, capacitance, impedance) between the cormus and the rooting medium provide information on root properties of individual plants. Chloupek (1972) and Ozier-Lafontaine and Bajazet, (2005), for instance, found good correlations between root mass and root system capacitance and impedance suggesting the use of electrical root properties as a promising tool.
One of the most recent developments is the so-called earth impedance method (EIM; Aubrecht et al., 2006). The most innovative aspect was the possibility of calculating the absorbing root surface area (ARSA) of individual mature trees, even though ARSA was anatomically not defined. Based on mathematically derived equations, the method was verified on allometric relationships (Čermák et al., 2006) and recently applied by Butler et al. (2010). Basic assumptions, tacitly assumed to apply for the EIM, however, were not tested experimentally even though similar approaches clearly indicated extensive methodological limitations (Chloupek, 1972; Dvořák et al., 1981; Kendall et al., 1982; Dalton, 1995; Ozier-Lafontaine and Bajazet, 2005; Cao et al., 2010).
The aim of the present work was to test six assumptions intrinsically assumed for the EIM and to apply this method with the conclusions being critically compared with established methods and knowledge on root systems, respectively.
Experimental and theoretical considerations
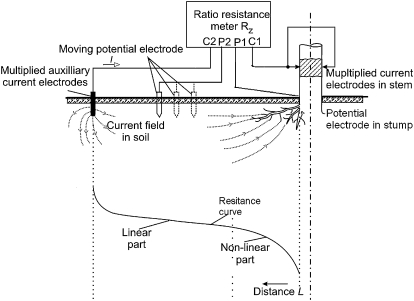
The EIM is based on a four-point electrode configuration (Jinx and Dawalibi, 2002; Aubrecht et al., 2006). While two electrodes are used to load an electrical current between the root system and the soil (current electrodes, C1 and C2), another pair is used to measure the resulting potential difference (potential electrodes, P1 and P2; Fig. 1). In the present study, all measurements were done following the suggestions of Aubrecht et al. (2006) and Čermák et al. (2006). The current electrode C1, made from knife blades, was hammered into the stem. The second (C2) was put in the soil at a distance from the stem ranging between 10–20 m depending on tree size. Both current electrodes were multiplied to avoid high transition resistances. While the potential electrode P1 remained fixed in the root collar, P2 was repeatedly inserted into the soil along the line connecting C1 and C2. Each time the grounding resistance (Rg) for different distances from the stem was computed given the current and the potential difference between P1 and P2. The resulting Rg-curve, i.e. Rg plotted against the distance from the stem, typically consisted of two parts, one non-linear and one linear part (Fig. 1). The distance to the stem corresponding to the transition between the two parts is referred to as Leff and is assumed to correspond to the length of the main coarse roots in the measured segment (Aubrecht et al., 2006).
Fig. 1.
Arrangement of the electrodes and an example of a resistance curve when potential electrode P2 is moved in a radial direction from the stem. The drawings have been modified after Aubrecht et al. (2006) and are reproduced by kind permission of Oxford University Press. Acronyms: C1, C2, electric current electrodes inserted, respectively, in the tree and soil; P1, P2, potential electrodes inserted, respectively, in the tree and soil.
The absorbing root surface area (ARSA) within the section between tree stem and electrode C2 was calculated according to the equation given by Aubrecht et al. (2006) and Čermák et al. (2006) where ρ is the wood resistivity (Ωm).
| (1) |
Values being calculated with Equation (1) are later referred to as ARSA. As recommended (Aubrecht et al., 2006), wood resistivity (ρ) was measured using the four-point Wenner method for large trees (diameter at breast height, DBH >15 cm, 2 cm electrode spacing) and the ‘long cylinder method’ for smaller trees (distance C1/2/P1/2=20 cm, distance P1/P2=5 cm), respectively (Samouëlian et al., 2005; Čermák et al., 2006). For the calculation of the whole tree ARSA, six root segments were used (Čermák et al., 2006). Correction factors to compensate for mutual electrical shielding, root mechanical damage, and outer current pathways, respectively, as suggested by Nadezhdina and Čermák (2003) and Aubrecht et al. (2006) were not available at the time of study.
Unlike previous methods that applied alternanting current (AC) with high frequency (c. 1000 Hz), low frequency AC is used in the EIM approach (c. 100 Hz). Hence, the contribution of imaginary resistances arising from capacitor like cell structures (e.g. membranes) is considered as negligible (Dvořák et al., 1981; Ozier-Lafontaine and Bajazet, 2005). In the present study, all measurements were performed using an earth tester (Fluke 1625, John Fluke, Everett, Washington, USA) operating at a peak voltage of 50 V AC and a low frequency of 111 Hz. If not transferred to ARSA values, results therefore are given as resistance or conductance, respectively. All electrodes used in the present work were made from stainless steel.
Hypotheses
The EIM was developed as an adaptation of the so-called ‘fall of potential’ method known from geophysics. Originally, this method was used for testing Rg of non-living objects, for example, lightning rods (Dwight, 1936; Tagg, 1970; Jinx and Dawalibi, 2002). In the case of the EIM, the lighting rod is replaced by a tree root system. Several assumptions drawn for the ‘fall of potential’ method were assumed to be applicable for the EIM (Aubrecht et al., 2006; Čermák et al., 2006). They are explained below and were used as hypotheses for the experiments of this study. In both approaches Rg is constituted by three resistors building a serial circuit but only one is assumed to dominate the two others.
Electrical resistance of the material of the lightning rod or the root xylem, respectively
Hypothesis I. Xylem resistance is a negligible part of a tree's Rg.
Grounding spikes used in geophysics are made from highly conductive materials. This makes the electrical resistance of a metal spike a negligible part of Rg (Tagg, 1970). Similarly, the EIM assumes the xylem resistance is negligible and is therefore not considered in the calculation of ARSA.
Hypothesis II. Radial electrical conductivity of the xylem is negligible. The bark of woody and/or suberized roots acts as an isolator.
A central assumption of the EIM is that there is no radial conduction in woody or suberized roots (Čermák et al., 2006; Aubrecht et al., 2006). The electrical current is assumed to flow through the entire root system, finally leaving exclusively via micro-sites for solute uptake (Marschner et al., 1986, 1991; Häussling et al., 1988; Van Praag et al., 1993).
Hypothesis III. Every absorptive part of a root branch equally contributes to the overall electrical conductance.
It follows from Hypothesis II that assessing the total ARSA requires the root system to be completely saturated with electrical current. The electrical current per unit of root absorbing surface area has to be the same in all parts of the root system (i.e. the same in the proximal and in the distal parts of the root system).
Hypothesis IV. A tree's conductance is the sum of the root branches’ conductance. A root branch's conductance, in turn, is the sum of suborder root branches’ conductance. Root branches are electrically discrete resistors and tree root segments can be measured separately.
The EIM assumes electrically discrete root segments, i.e. root branches are isolated from each other and the corresponding conductivity (or ARSA values), respectively, are additive. Stem xylem branches in first order roots thus building a parallel circuit. Likewise, first order roots equal a parallel circuit of suborder roots (cf. Dalton, 1995). According to Ohm's law the respective suborder units’ conductance must be additive:
Contact resistance between the lightning rod or roots, respectively, and the soil
Hypothesis V. ARSA is predominantly determined by the contact resistance.
Contact resistance between a metal rod and the soil is also assumed as very low provided the soil is firmly packed around the electrode (Tagg, 1970). In the case of the EIM, however, the contact resistance is crucial as it is the only resistance being directly related to ARSA (Nadezhdina and Čermák, 2003).
Soil resistance
Hypothesis VI. Soil resistance is a negligible part of a tree's Rg.
The resistance of the surrounding earth in ground testing of metal electrodes will be the largest of the three components of Rg (Dwight, 1936; Tagg, 1970; Jinx and Dawalibi, 2002). In contrast, it is assumed to play a minor role in the EIM.
Experiments
The six hypotheses were tested in seven experiments. An eighth experiment was performed as an application example of the EIM with its results being related to the prior findings. Table 1 summarizes the hypotheses and the corresponding experiments.
Table 1.
Overview of the experiments with the corresponding hypotheses, sites, and species observed
| Experiment | Hypothesis | Site | Species observed |
| 1 | 1, 3, 5 | Sobesice | Scots pine, wild cherry, Pedunculate oak, maple |
| 2 | 2 | Laboratory | Scots pine, Norway spruce, Pedunculate oak |
| 3 | 1, 3, 4, 5 | Laboratory | Scots pine, Norway spruce, Pedunculate oak |
| 3 | Sobesice, Wilrijk | Norway spruce, maple, Pedunculate oak | |
| 3 | Allschwil | European beech | |
| 4 | 4 | Vranov | Norway spruce |
| 5 | 5, 6 | Wilrijk | Pedunculate oak |
| 6 | 1, 5, 6 | Sobesice | Pedunculate oak, European ash, Scots pine |
| 6 | Brislach, Allschwil | European beech, Norway spruce | |
| 7 | 5, 6 | Chriby | European beech |
| 8 | 6 | Zürich | Norway spruce |
Experiment 1. Rg and ARSA values influenced by xylem resistance
The impact of xylem resistance on Rg and ARSA values was studied by experimentally increasing the xylem resistance. Tests were performed on mature trees of Scots pine (Pinus sylvestris), wild cherry (Prunus avium), Pedunculate oak (Quercus robur), and maple (Acer pseudoplatanus). Electrode P2 was put at Leff and P1 was progressively moved upwards along the stem, thus increasing the amount of xylem resistance of the stem tissue in measured Rgn. Grounding resistance Rgn and stem circumference were measured at every new position n with n =1, 2, 3…
Rgn was modelled according to the equation:
| (2) |
where ρ is the measured xylem resistivity, Ln the height of P1 above ground, Sn the corresponding cross-sectional area of the stem, and Rg0 the measured tree's grounding resistance when electrode P1 was at the lowest position. Given Hypotheses I and V, it was expected that the position of P1 does not affect Rg.
Experiment 2. Radial electrical conductance of suberized roots
The radial electrical conductance of suberized roots was assessed on saplings of Scots pine, Norway spruce (Picea abies) and Pedunculate oak. The plants were field-grown in sandy soil and manually excavated. The plant height was c. 1 m and diameter of the root collar was 5–8 mm. C2 and P2 electrodes were combined (C2/P2) and connected to the main root at different vertical positions. All root surfaces were dry except for the moistened contact area between the bark and the electrode. Given Hypothesis II, it was assumed that getting into contact with the main root would result in an infinite electrical resistance independent of the position on the root.
Experiment 3. Root immersion and severing experiments
Four experiments were performed in order to study the response of Rg as a result of experimentally reduced root surface area. While the first two experiments were performed with saplings under laboratory conditions, the latter two were done with old trees under field conditions.
The first two experiments were performed with the same saplings as described in experiment 2. The C1 electrode was inserted in the stem at 10 cm above the root collar and P1 into the root collar. First, the respective root system was immersed in tap water until the first order root branches submerged. The combined C2/P2 electrode was put into the water. The saplings were then gradually raised out of the water thus decreasing the amount of submersed and conductive root surface (‘gradual rising’ experiment). The vertical positions were the same as in experiment 1. At each step, Rg and the vertical distance between P1 and the water level was measured.
The same plant individuals were finally used in a ‘root severing’ experiment with their root systems being always immersed. The conductive ARSA was reduced by cutting the roots progressively at the positions corresponding to those of the former experiments. Each cut surface was insulated with a layer of wax. Rg was recorded at each step.
The other two root severing experiments are referred to as ‘one root cutting’ and ‘all roots cutting’, respectively. For the ‘one root cutting’ experiment each one tree (DBH c. 20 cm each) of maple (Acer platanoides) and Norway spruce growing close to Soběšice, Czech Republic (49°14' N, 16°36' E, 380 m a.s.l.) and Pedunculate oak growing close to Wilrijk, Belgium (51°9' N, 4°24' E, 14 m a.s.l.) were selected for root severing. No excavation was performed and all the roots and the stem base stayed in contact with the soil. The main root facing to the C2 electrode was cut at a distance of 30 cm from the stem. Rg was compared prior and after cutting.
The ‘all roots cutting’ experiment was performed with three spruce trees and one European beech tree (Fagus sylvatica, age 19 years, DBH=13–16 cm). Trees were growing close to Allschwil, Switzerland (47°32' N, 7°30' E, 380 m a.s.l.). Unlike in the ‘one root cutting’ experiment, all roots within a circle of c. 30 cm radius around the stem were completely excavated. Small injured roots were cut prior to measurements. Care was taken to withdraw any conductible contact between the stem base and the soil except for coarse roots. Twelve C2 and P2 electrodes, arranged in a circle around the stem, were used in order to establish a symmetrical electrical field around the tree. After measuring the whole tree's conductance, i.e. the inverse of Rg, coarse roots were successively cut close to the root collar. After cutting, the root's conductance was determined and the tree's conductance was remeasured. Root conductance was measured putting P1 and C1 electrodes at the proximal part close to the cut. The trees were fixed with ribbons to avoid accidental fall and injury to the root system. Given Hypotheses III and IV, a root's conductance was expected to equal the loss in overall tree conductance. Root conductance was thus used as a predictor for losses in tree conductance. The same procedure was applied for large secondary root branches.
Experiment 4. Spatial reproduction of the root system by the EIM
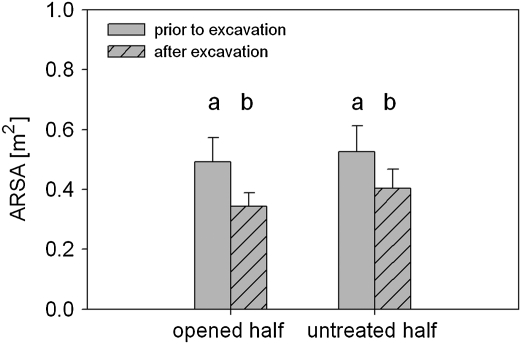
This experiment was done on 12 Norway spruce trees (age 25 years), growing close to Vranov, Czech Republic (49°20' N, 16°40' E, 420 m a.s.l.). Trees in the forest stand were originally planted in rows. Soil from the space between two neighbouring rows was removed using the air-spade technique, thus one half of the root system was excavated (Neruda et al., 2009). The other half was untreated. Excavated halves were left open for several weeks and were then covered with soil again. ARSA was determined for both halves prior to the opening and one week after recovering the root system with soil. It was expected that the treatment caused extensive root death. Accordingly, given Hypotheses III and IV, the treatment should cause ARSA to decrease for the opened half whereas the untreated half would not show any significant change.
Experiment 5. Rg values as influenced by the mean coarse root length
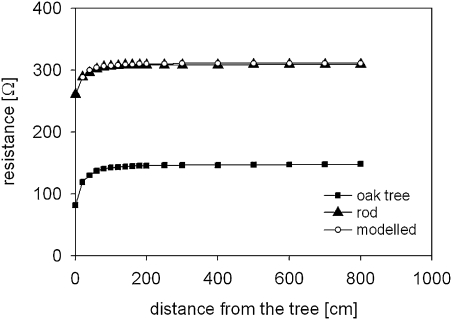
The Rg-curve was determined for a Pedunculate oak tree growing at the Wilrijk site with soil resistivity of 30 Ωm. The same was performed for Rg of a stainless steel rod (surface 25 cm2) inserted c. 1 m from the tree, therefore mirroring the course of soil resistance. In addition to the measurements, the increase of the resistance with distance from the rod was modelled as the cumulative resistance increase [Rg(l); cf. Equation (3)] assuming the electric current passing through a given amount of soil with resistivity ρ. To model the soil resistance, Equation (2) was modified for a hemispherical conductor. The spatial dimension of the soil segment was defined by the length of the individual hemisphere layer l (i.e. 1 cm) and the mean cross-sectional area of the hemisphere layer S. Rg(0.03) was set as the measured value of Rg(l) in the first step of measurement (i.e. 0.03 m from the rod).
| (3) |
Aubrecht et al. (2006) assumed that the shape of a tree's Rg-curve is determined solely by the mean length of the coarse roots, but not by soil properties (Hypotheses V and VI). Therefore, while the Rg-curve of the metal rod should closely match modelled values, a large discrepancy was assumed between the curves for the metal rod and the tree.
Experiment 6. Seasonal variation of ARSA and influence of soil moisture and xylem resistivity
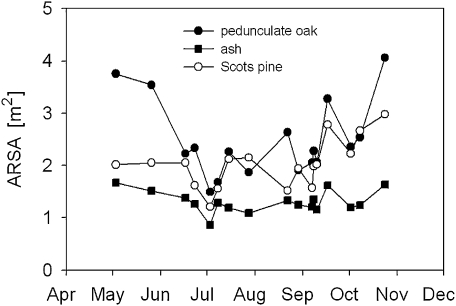
Potential seasonal variation of ARSA was measured in three mature trees of contrasting root structure, Pedunculate oak, European ash (Fraxinus excelsior), and Scots pine. The experiment was carried out at Sobesice, Czech Republic (49°14' N, 16°36' E, 380 m a.s.l.) during the growing season of 2008 (May to October). All electrodes were permanently installed in the trunk and soil, respectively.
The temporal course of ARSA was also determined in five mature and five young (age 19 years) trees of European beech and Norway spruce. Mature trees were growing close to Brislach, Switzerland (47°26' N, 7°3' E, 450 m a.s.l.) and the young trees were located at the Allschwil site, Switzerland. Volumetric soil water content, as an important determinant for short-term changes in soil resistivity (Samouëlian et al., 2005; al Hagrey, 2007), was measured at each sampling date using a TDR-probe (Delta T, Burwell, UK). Organic litter was removed carefully until the first roots appeared. The probe was inserted vertically, thus integrating soil water content down to 8 cm rooted soil depth. Measurements were made along the line connecting the C1 and C2 electrodes in distances from the tree of 1, 2, 4, and 7 m. For mature trees, an additional value was sampled at a distance of 10 m. Measurements at Brislach and Allschwil started in June 2008 and continued until the end of November 2008 with a targeted time interval of 14 d. ARSA data were normalized by the respective starting value in order to remove the variation caused by the different tree sizes (Čermák et al., 2006). Thus, Experiment 6 tested the validity of Hypotheses V, VI, and I.
Experiment 7. Allometric relationships related to soil conductivity
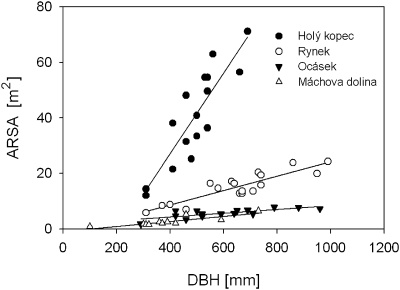
A total of 60 European beech trees were measured at four sites in the Chřiby hills (Czech Republic): Holy kopec (49°6' N, 17°17' E, 480 m a.s.l.), Rynek (49°6' N, 17°16' E, 490 m a.s.l.), Ocasek (49°5' N, 17°14' E, 550 m a.sl.), and Machova dolina (49°9' N, 17°18' E, 430 m a.s.l.). These sites had different soil electrical resistivities. The respective soil resistivity measured by the four-point Wenner method (Samouëlian et al., 2005; electrode distance = 0.5 m) accounted for 182, 780, 1875, and 2460 Ωm. Distinct differences were found for the soil fertility parameters that showed a similar site ranking as found for soil resistivity (Table 2). Using tree DBH as an independent variable, regression equations were calculated, respectively, for ARSA and ARSA values divided by the corresponding soil resistivity, i.e. normalized ARSA. Testing the validity of Hypothesis VI, it was expected that normalizing the data by soil resistivity does not affect the regression slopes, with the latter mirroring the allometric relationship between ARSA and DBH.
Table 2.
Soil fertility parameters for the sites Holy kopec, Rynek, Ocasek, and Machova dolina (Czech Republic)
| N (%) | C/N ratio | K (cmol kg−1) | Ca (cmol kg−1) | Mg (cmol kg−1) | Sum base cations(cmol kg−1) | |
| Rynek | 0.14 | 6.4 | 0.2 | 2.3 | 0.3 | 2.8 |
| Ocasek | 0.20 | 8.8 | 0.2 | 1.1 | 0.1 | 1.3 |
| Holy kopec | 0.20 | 8.1 | 0.1 | 0.5 | 0.1 | 0.7 |
| Machova Dolina | 0.15 | 19.0 | 0.1 | 0.2 | 0.1 | 0.3 |
Data refer to the A-horizon were most of beech fine root surface was found.
Experiment 8. Application example of fertilization
Mature spruce trees with pronounced potassium deficiency were fertilized with K2SO4 in a randomized experimental design. The study area was close to Zürich, Switzerland (47°25' N, 8°38' E, 514 m a.s.l.). The fertilizer was applied for three years (2006–2008) in the early spring being dispersed manually as a square around the stem (8×8 m, 250 kg K ha−1 year−1). In summer 2008, the EIM was applied on each of five fertilized and control trees in order to test if ARSA responded to the fertilization. In addition, one soil core per tree was taken (8 cm diameter, 20 cm soil depth). Soil cores were taken along the line connecting the C1 and C2 electrodes at a distance from the stem of approximately 1.5 m. Roots were separated from the soil by washing on a 1 mm sieve. Considering only live spruce fine roots, samples were scanned and analysed for fine root surface using the software package WinRHIZO (Regent Instruments Inc, Quebec, Canada). Fine roots were classified for diameters ≤1 mm and ≤2 mm, respectively. Due to the confined fertilizer application it was assumed that any change in ARSA corresponded to an altered fine root surface density (mm2 cm−3).
Statistical analysis
Differences between the root system halves’ ARSA (Experiment 4) were compared using a paired sampled t test. Data prior to and after excavation were compared pair-wise for treated and untreated halves. In Experiment 6, the correlation between ARSA, soil water content, and xylem resistivity, respectively, were tested using a multiple linear regression model. Soil water content was calculated as the mean of single measurements (Allschwil: n=4, Brislach: n=5). Parameters were assessed in the model only for α <0.05. Normal distribution of the residuals was controlled visually using the software package Statistica Rel. 6.1 (StatSoft Inc., Tulsa, Okla.). ARSA and root biomass between fertilized and control-trees (Experiment 8) were compared using a t test.
Results from linear regressions presented in all experiments are given only for significant results (α <0.05). Calculations were done using the software packages Statistica Rel. 6.1 (StatSoft Inc., Tulsa, Okla.) or Sigma Stat Rel. 3.1 (SysStat Software Inc.).
Results and discussion
Rg and ARSA values influenced by xylem
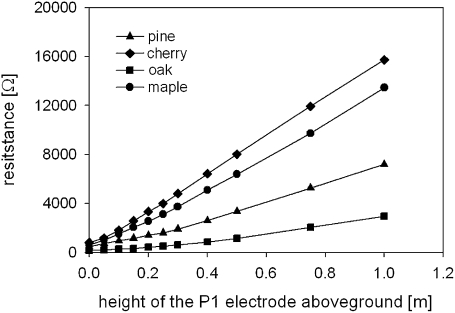
Rgn increased linearly in all the trees studied when the P1 electrode was moved upwards (Fig. 2; P <0.001). As a result, it was concluded that ARSA decreased in an inversely proportional way with the height of P1 above ground (data not shown). There was a strong correlation between measured and modelled Rgn values corroborating that the increment of Rgn was on account of the added xylem resistance (all P <0.001, r2 ≥0.97). The results clearly indicate that xylem resistance is an important component of Rg and thus contradicts Hypotheses I and V. Similarly, a strong impact of the height of the stem potential electrode on root system capacitance was reported by Dalton (1995) and van Beem et al. (1998).
Fig. 2.
Relationship between the vertical position of the potential electrode P1 and the tree's grounding resistance for four different tree species.
According to the linear regression, Rgn doubled compared with Rg0 when P1 was set to 0.12 m (pine), 0.08 m (cherry), 0.15 m (oak), and 0.09 m (maple) above the root collar. Xylem resistance of a stem segment with corresponding length thus equalled Rg0, i.e. the resistance of conducting roots and soil compartments. Assuming the resistivity ρ to be similar for roots and the stem xylem and the sum of cross-sectional areas of the coarse roots similar as in the stem (cf. the pipe theory; Shinozaki et al., 1964), the average length of the conducting roots can be deduced from the measured resistances and lengths (Appendix 1). Accordingly, the average conducting root length did not exceed the stem segment length corresponding to doubled Rg0 (0.08–0.15 m in this experiment). The results therefore indicate that, in a naturally grown tree-root–soil continuum, most of the charge carriers leave the root system in very proximal parts of the root system. This conclusion contradicts Hypothesis III.
Radial electrical conductance of suberized roots
Bringing the combined C2/P2 electrode into contact with suberized roots at different vertical positions caused a significant Rg-response (P <0.01; Table 3). This result contradicts Hypothesis II and clearly indicates that the bark of suberized roots is electrically conductive.
Table 3.
Slopes of the linear regression between the grounding resistance and the vertical distance to the C2/P2 electrode (experiment 2), the vertical distance between the P1 electrode and the water level (experiment 3 ‘gradual rising’), and the vertical distance to the root cut plane (experiment 3 ‘root severing’), respectively
| Experiment 2 ‘bark conductance’ | Experiment 3 ‘gradual rising’ | Experiment 3 ‘root severing’ | |
| Scots pine | 24.1±4.1 | 22.9±2.8 | 0.25±0.11 |
| Norway spruce | 19.5±2.8 | 16.5±0.9 | 0.09±0.02 |
| Pedunculate oak | 17.1±1.8 | 14.1±0.8 | 0.05±0.01 |
Regressions were in the form y=ax+b where a and b are constants, y is the grounding resistance, and x is the respective distance. Data are given as slope estimates [MΩ cm−1] ±confidence interval.
Electrical conduction in the root–soil continuum largely occurs in the liquid phase with ions being the charge carriers (Dvořák et al., 1981; Samouëlian et al., 2005) thus involving micro-sites for solute uptake in roots. Indeed, non-suberized parts of fine roots showed the highest permeability for solute uptake (Marschner et al., 1986, 1991; Häussling et al., 1988). There is, however, evidence that woody roots are water permeable and, because of their large surface, contribute significantly to the overall solute uptake (Chung and Kramer, 1975; Macfall et al., 1990, 1991; Van Rees and Comerford, 1990; Leuschner et al., 2003). These studies suggest that woody roots are capable of radial charge transport.
Root immersion and severing
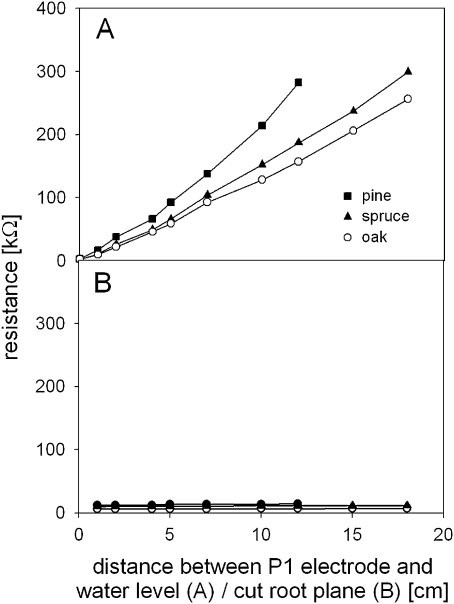
In the ‘gradual rising’ experiment, the measured resistance increased significantly when the root systems were raised out of the water (Fig. 3A; P <0.001). Rg-response curves were very similar to those found in Experiment 2 (Table 3). The respective slopes did not differ significantly between the experiments, except for the oak saplings.
Fig. 3.
Relationship between the vertical distance of the P1 electrode to the water level (A, ‘gradual rising’ experiment) and between P1 electrode and the cut root plane (B, ‘root severing’ experiment).
By contrast, there was a negligible resistance increase in the ‘root severing’ experiment where the root system size was successively cut (Fig. 3B; Table 3; P <0.001).
The results clearly indicate that changes in the saplings’ Rg were primarily determined by the xylem resistance through the altered pathway length, whereas the contact resistance was negligible (Cao et al., 2010).
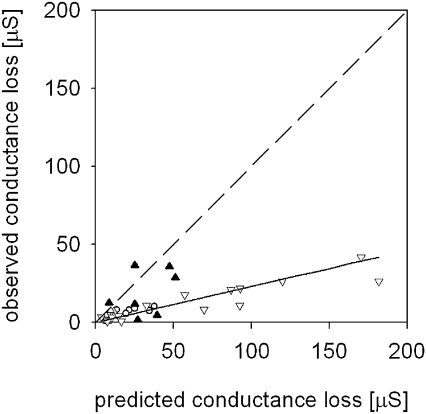
Similarly, in the ‘one root cutting’ experiment, cutting the main root facing the C2 electrode (at a distance of more than 30 cm from the stem) did not cause any response in Rg (data not shown). By contrast, a significant response was found in the ‘all roots cutting’ experiment where roots and the stem base were excavated prior to the cutting (Fig. 4). In the ‘all roots cutting’ experiment a significant but weak correlation was found between the predicted and observed conductance loss values (P <0.001, r2=0. 39). Moreover, contrary to Hypothesis IV, the regression slope differed significantly from unity (0.23±0.05, estimate ±confidence interval; Fig. 4).
Fig. 4.
Relationship between observed and predicted values of conductance loss in the ‘all roots cutting’ experiment performed close to Allschwil, Switzerland. Predicted values were derived from the cut root's conductance. Observed values were derived from the corresponding loss in total tree conductance after cutting the root. Data are shown for spruce (triangles) and beech (circles). The solid line indicates the regression across all trees. The dashed line indicates the 1:1 relationship.
The discrepancy between the experiments ‘gradual rising’ and ‘root severing’ and between the experiments ‘one root cutting’ and ‘all roots cutting’ strongly suggest that distal roots had negligible impact on Rg. Confirming the results of the Experiments 1 and 2, it appears that most of the electrical charge leaves the tree root system close to the stump, although most of the tree root surface area is located in more distal parts (Tatarinov et al., 2008).
In their immersion experiment with willow cuttings, Cao et al. (2010) came to very similar findings. The authors found that the root system's electrical resistance was halved when the stem base was in contact with the solution and complete removal of the root system did not affect the measured resistance (Cao et al., 2010). Similarly, working with red clover, Kendall et al. (1982) found no significant response after cutting off most of the roots. Only in the study of Čermák et al. (2006), was a significant decrease of ARSA observed with root severing. The authors, however, used an excavator to remove half of the root–soil continuum (Čermák et al., 2006). ARSA reasonably decreased because conducting elements (roots and soil) were totally removed.
In summary, the results from the immersion and root severing experiments severely conflicted with Hypotheses I, III, and V. Moreover, the ‘all roots cutting’ experiment showed that roots did not constitute electrically discrete segments hence conflicting with Hypothesis IV.
Spatial reproduction of the root system by the EIM
Prior to the excavation ARSA did not differ significantly between the root system halves (Fig. 5). Excavation and recovery caused ARSA of the opened half to decrease significantly by 24.5%. In contrast to expectations, ARSA also decreased significantly in the untreated half. The mean percentage loss was very similar for the opened half (23.1%) and again ARSA did not differ between the halves (Fig. 5).
Fig. 5.
Absorptive root surface areas (ARSA) for spruce trees with half of the root system being excavated. Data are shown for each half prior to excavation (grey bars) and one week after recovering (hatched bars). All data are means ±SE.
The similar decrease in ARSA for both sides contradicts Hypothesis IV. Supporting the findings of experiment 3 (‘all roots cutting’), the results indicate the absence of electrically discrete root segments.
Rg values as influenced by the mean coarse root length
The modelled resistance values and the values obtained with a metal rod correlated significantly (P <0.001, r2=0.97; Fig. 6) suggesting that the shape of the metal rod's curve was determined by the soil resistance. In contrast with this assumption, there was a significant correlation between values for the tree and the metal rod (P <0.001, r2 >0.99; Fig. 6) indicating that the shape of a tree's Rg-curve is largely determined by the soil resistance. This finding is in agreement with the general principles of Rg-measurements as studies on the ‘fall of potential’ method attributed the shape of the Rg-curve for an electrode solely to soil properties (Dwight, 1936; Tagg, 1970; Jinx and Dawalibi, 2002). The results thus conflict with Hypotheses V and VI suggesting that the EIM cannot conclude on the mean coarse root length. The validity of Equation (1) to conclude on ARSA therefore seems questionable, not only because of biased Rg values but also because of Leff values.
Fig. 6.
Grounding resistance-curves (Rg) determined empirically for a Pedunculate oak (rectangles), a metal rod set close to the tree (closed triangles) and modelled values (open circles). Measurements were done close to Wilrijk, Belgium.
Seasonal variation of ARSA and influence of soil moisture and xylem resistivity
Repeated measurements revealed, in all trees, a substantial seasonal variation of ARSA (Fig. 7). Coefficients of variation accounted for 28.8%, 22.3%, and 15.6%, respectively, for oak, pine, and ash. In all cases, ARSA was highest in the spring and decreased during the growing season, suggesting that there was high net fine root mortality at this time. On the other hand, autumn appeared to be the period of the most intensive net root surface formation (Fig. 7).
Fig. 7.
Seasonal dynamics of the absorptive root surface area (ARSA) for three individuals of different tree species measured at Sobesice, Czech Republic. Data were measured between May and October 2008.
Beech trees in Brislach and Allschwil showed a similar seasonal course of ARSA with coefficients of variation, respectively, ranging from 30.6–58.1% and from 16.4–58.9% for individual trees (data not shown). Spruce trees also showed substantial seasonal variation of ARSA with coefficients of variation, respectively for mature and young trees ranging from 28.5–42.9% and from 17.6–23.6%. Consistently, xylem resistivity and soil water content correlated significantly with normalized ARSA and explained up to 97% of its variation (Table 4). Xylem resistivity appeared to be more influential than soil moisture.
Table 4.
Results of the multiple linear regression in the form y=aWR+bW+c with WR, W, and c being wood resistivity (Ωm), soil water content (%), and intercept, respectively
| Site/species | Model significance | R2 | Normalized correlation coefficient |
Semi-partial correlation |
||
| Wood resistivity | Soil water content | Wood resistivity | Soil water content | |||
| Brislach/mature beech | P <0.001 | 0.97 | 0.93 | 0.23 | 0.92 | 0.23 |
| Brislach/mature spruce | P <0.001 | 0.81 | 0.81 | 0.24 | 0.78 | 0.23 |
| Allschwil/young beech | P <0.001 | 0.94 | 0.92 | 0.25 | 0.92 | 0.25 |
| Allschwil/young spruce | P <0.001 | 0.53 | 0.55 | 0.30 | 0.50 | 0.28 |
All parameter estimates were significant at P <0.001. Calculated absorptive root surface area (ARSA) values were normalized by the starting value.
Studies on temperate tree species, using established methods such as mini-rhizotrons, revealed a seasonal variation in the appearance of new and highly permeable fine roots and root hydraulic conductance (Lyr and Hoffmann, 1967; Smit et al., 2000b; Nardini et al., 2002; Tierney et al., 2003; Gaul et al., 2008; Mainiero et al., 2009, 2010). Both parameters largely coincide with the intense growth period and high water demand, i.e. they reach a maximum in late spring and summer. The seasonal course of ARSA thus severely conflicts with previous studies as it suggests the lowest absorption capacity in the summer.
As changes in ARSA correlated with xylem and soil moisture, the latter being a determinant for soil resistivity (Samouëlian et al., 2005; Amato et al., 2009), the present results provide strong evidence that both, xylem and soil resistance, are two major parts of a tree's Rg. Supporting the findings of experiments 1 and 3, the conclusions contrast to Hypotheses I, V, and VI.
Allometric relationships related to soil conductivity
On all sites, ARSA increased significantly with DBH (all sites P <0.001; Fig. 8). The regression slopes differed significantly among sites and decreased with increasing soil resistivity. Regression slopes (±confidence interval) for Holy kopec, Rynek, Ocasek, and Machova dolina were 145.1±46.1, 25.8±6.9, 6.9±3.4, and 8.9±4.1 m2 m−1, respectively. Accordingly, the data suggest considerable site-specific differences in allometric relationships for beech trees resulting in differences of ARSA up to one order of magnitude for similar sized trees (Fig. 8). The results are in agreement with ARSA values reported by Čermák et al. (2006) who also found up to 10-fold differences for similar tree sizes of the same species but at different sites. In contrast to the expectation, the differences found disappeared when ARSA was normalized by the corresponding soil resistivity (data not shown).
Fig. 8.
Relationship between the absorptive root surface area (ARSA) and the diameter at breast height (DBH) of European beech trees growing at four localities in the Czech Republic contrasting in soil conductivity. Site names in the legend are arranged according to soil conductivity with the latter increasing from Holy kopec to Machova dolina.
Variation of ARSA should correspond to the variation of fine root biomass density (Dalton, 1995). In their meta-analysis on beech growing along a broad range of soil conditions (19 sites), Leuschner and Hertel (2002) found between-site variation in fine root biomass density was only about 4-fold. The results obtained by the EIM from only four sites, however, show a much larger variation compared with currently reported fine root density values. Moreover, the root-to-shoot biomass ratio increases with decreasing soil fertility (Reich, 2002; Farrar and Jones, 2003; Hutchings and John, 2003). The results of the ARSA measurements, however, are contradictory as they indicate that the lowest root–shoot ratio coincided with the lowest nutrient availability (Fig. 8; Table 2).
Two reasons might explain the contradictory results: (i) assuming a relationship between ARSA and fine root biomass is inappropriate or (ii) a tree's Rg is not only determined by its root system conductance but also by the soil resistivity. While Aubrecht et al. (2006) did not consider soil resistivity in their calculation, several authors using a similar approach emphasized the overwhelming influence of the rooting medium on the measured parameters (Chloupek, 1972; Dvořák et al., 1981; Dalton, 1995; van Beem et al., 1998; Ozier-Lafontaine and Bajazet, 2005). As site-specific differences for ARSA relations disappeared when the data were normalized by soil resistivity the present results strongly suggest, in accordance to the previously cited studies and Experiment 6, that soil resistance largely influences a trees’ Rg and ARSA. The results therefore contradict Hypotheses V and VI.
Application example: fertilization experiment
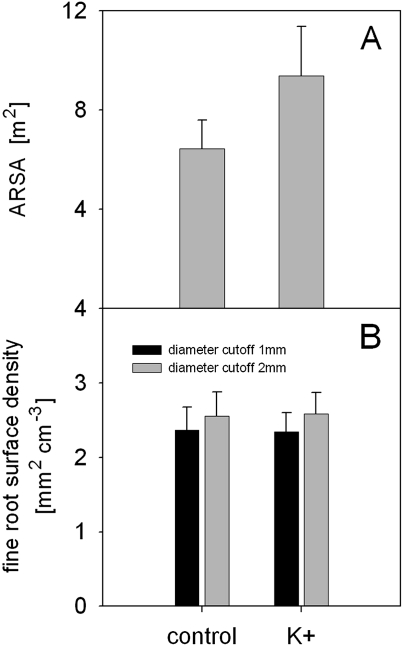
According to the EIM it was concluded that spruce trees responded to the fertilizer application by increasing ARSA by 45%, albeit a result that was not statistically significant (Fig. 9A). By contrast, results of the soil coring approach did not show any response in terms of fine root surface density for both fine root diameter classes (Fig. 9B). Soil resistivity, as determined in late autumn 2008, decreased by more than 20% as a result of the fertilization (control=1137.7±43.6 Ωm; fertilized=946.5±47.8 Ωm; means ±SE).
Fig. 9.
(A) Absorptive root surface area (ARSA) for untreated spruce trees (control) and trees fertilized with potassium (K+) growing close to Zürich, Switzerland. (B) Fine root surface density for living fine roots of the corresponding spruce trees classified for diameter cut-offs 1 mm (black columns) and 2 mm (grey columns). Data were obtained by the earth impedance method (A) and by soil coring (B), respectively and are given as means ±SE.
Soil coring studies on Norway spruce could detect structural root system responses one year after experimental treatments (Clemensson-Lindell and Persson, 1995; Genenger et al., 2003; Majdi et al., 2008; Helmisaari et al., 2009) suggesting that the soil coring technique is a sensitive tool. The present soil coring data agree with those of Clemensson-Lindell and Persson (1995) who studied the root responses of Norway spruce to mineral fertilizer application, and with the review by Hodge (2004). Accordingly, no response in terms of root surface was observed for plants treated locally with potassium fertilizer.
The results obtained by the EIM disagreed with the standard methods and the current knowledge, and must be interpreted as an artefact. Given the results of the former experiments, the lower soil resistivity resulted in lower Rg-values for fertilized trees. Accordingly, it appears from Equation (1) that ARSA was higher in fertilized trees, despite unaltered fine root surface density.
Conclusions
The present study could not confirm any of the hypotheses assumed to be applicable for the EIM (Nadezhdina and Čermák, 2003; Aubrecht et al., 2006; Čermák et al., 2006). In terms of an analogue electrical circuit, the present results clearly indicate a tree-root–soil continuum is a serial circuit with xylem and soil resistance over ruling the role of the contact resistance. In natural systems, a large array of interfering determinants for soil and xylem resistivity exists, such as soil texture and soil porosity (Chloupek, 1972; Samouëlian et al., 2005), root density (Amato et al., 2008, 2009; Zenone et al., 2008), soil and xylem temperature and solute concentration (Samouëlian et al., 2005), soil and xylem moisture (van Beem et al., 1998; Hagrey, 2007; Nadler and Tyree, 2008; Zenone et al., 2008), and cell anatomy and tissue integrity (Dvořák et al., 1981; Zhang and Willison, 1991, 1992; Zhang et al., 1993; van Beem et al., 1998; McBride et al., 2008). These factors vary considerably both in space and time. While those determinants’ variation causes Rg and Leff to vary independently of ARSA, the current approach of the EIM would result in altered ARSA values. Moreover, the present data strongly suggest that the EIM cannot provide reliable data on the absorptive area of the distal fine roots because most of the charge carriers leave the root system in very proximal parts of the root system. Applying the EIM in its current form on naturally grown plants inevitably results in misleading conclusions.
However, similar approaches using electrical properties (capacitance, resistance) showed that empirical calibrations between root electrical and root structural properties enabled root biomass to be determined non-destructively (Chloupek, 1972; Dalton, 1995; van Beem et al., 1998; Psarras and Merwin, 2000; Ozier-Lafontaine and Bajazet, 2005; McBride et al., 2008). Such empirical calibrations, however, require highly standardized rooting media and genotypes in order to minimize the variation in soil and root conductivity between individual plants.
Acknowledgments
The authors wish to thank Ing. Jiří Hruška (Kolejservis), Associate Professor Tapani Repo (Forest Research Institute, Joensuu), Professor Jan Čermák (Mendel University, Brno), Dr Sabine Braun (IAP) and Professor Reinhart Ceulemans (University of Antwerp), Dr Richard Volz (BAFU), and Dr Sabine Augustin (BAFU) for their valuable comments and support. We are grateful to Moise Groelly (IAP) and Dieter Bader (IAP) for technical support in the field.
This work was partly supported by the Flanders-Czech bilateral scientific cooperation (BWS BOF 2006), the foundation of the Mendel University Brno (IGA 9/2008 and IGA 12/2010), the EEA Grant (A/CZ0046/2/0009), Czech Science Foundation (GA526/08/1050), and the Federal Environment Agency of Switzerland (BAFU).
Glossary
Abbreviations
- AC
alternating current
- ARSA
calculated absorbing root surface area
- DBH
diameter at breast height
- EIM
earth impedance method
- Rg
grounding resistance
- TDR
time domain reflectrometry
- C
current electrode
- P
potential electrode
- ρ
electric resistivity
Appendix 1.
Let Rs be the electrical resistance of the stem segment corresponding to doubled grounding resistance at the lowermost position (Rg0). Assuming no diameter change along its length, ls, it follows from Ohm's law:
| (4) |
with Cs being the corresponding electrical conductance, ρs the stem electrical resistivity, and Ss the stem's cross-sectional area.
Assuming that the stem branches in n (first order) root laterals building a parallel circuit, a single root branch's resistance is given as
| (5) |
with Cni being the root branch's conductance, lni the conducting root length (with i=1, 2…n), ρr the root xylem resistivity and Sni the root branch's cross sectional area. Given that the sum of conducting root cross-sectional area Sni equals Ss (Shinozaki et al., 1964) it follows from Equations (4) and (5)
| (6) |
or, assuming that ρr equals ρs:
| (7) |
For the sake of simplicity, it is assumed that the stem branches in roots, each of equal conductance:
| (8) |
From Equations (7) and (8) it follows
| (9) |
or:
| (10) |
According to Equation (10), the average conducting root branch length does not exceed the stem segment length corresponding to double Rg0. According to Equation (7), however, ln of single roots can exceed ls if Cni is not equal among (first order) root branches. If soil resistance would be considered as a part of Rg0, lni would decrease further.
References
- al Hagrey SA. Geophysical imaging of root-zone, trunk, and moisture heterogeneity. Journal of Experimental Botany. 2007;58:839–854. doi: 10.1093/jxb/erl237. [DOI] [PubMed] [Google Scholar]
- Amato M, Basso B, Celano G, Bitella G, Morelli G, Rossi R. In situ detection of tree root distribution and biomass by multi-electrode resistivity imaging. Tree Physiology. 2008;28:1441–1448. doi: 10.1093/treephys/28.10.1441. [DOI] [PubMed] [Google Scholar]
- Amato M, Bitella G, Rossi R, Gomez JA, Lovelli S, Ferreira Gomes JJ. Multi-electrode 3D resistivity imaging of alfalfa root zone. European Journal of Agronomy. 2009;31:213–222. [Google Scholar]
- Asseng S, Aylmore LAG, Macfall JS, Hopmans JW, Gregory PJ. Computer-assisted tomography and magnetic resonance imaging. In: Smit AL, Bengough AG, Engels C, Van Noordwijk S, Pellerin S, Van de Geijn SC, editors. Root methods. Berlin: Springer-Verlag; 2000. pp. 343–364. [Google Scholar]
- Aubrecht L, Stanek Z, Koller J. Electrical measurement of the absorption surfaces of tree roots by the earth impedance method. 1. Theory. Tree Physiology. 2006;26:1105–1112. doi: 10.1093/treephys/26.9.1105. [DOI] [PubMed] [Google Scholar]
- Butler AJ, Barbier N, Čermák J, Koller J, Thornily C, McEvoy C Nicoll B, Perks M, Grace J, Meir P. Estimates and relationships between aboveground and belowground resource exchange surface areas in Sitka spruce managed forest. Tree Physiology. 2010;30:705–714. doi: 10.1093/treephys/tpq022. [DOI] [PubMed] [Google Scholar]
- Cao Y, Repo T, Silvennoinen R, Lehto T, Pelkonen P. An appraisal of the electrical resistance method for assessing root surface area. Journal of Experimental Botany. 2010;61:2491–2497. doi: 10.1093/jxb/erq078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Čermák J, Ulrich R, Staněk Z, Koller J, Aubrecht L. Electrical measurement of tree root absorbing surfaces by the earth impedance method. 2. Verification based on allometric relationships and root severing experiments. Tree Physiology. 2006;26:1113–1121. doi: 10.1093/treephys/26.9.1113. [DOI] [PubMed] [Google Scholar]
- Chloupek O. The relationship between electric capacitance and some other parameters of plant roots. Biologia Plantarum. 1972;14:227–230. [Google Scholar]
- Chung HH, Kramer PJ. Absorption of water and 32P through suberized and unsuberized roots of loblolly pine. Canadian Journal of Forest Research. 1975;5:229–235. [Google Scholar]
- Clemensson-Lindell A, Persson H. Fine-root vitality in a Norway spruce stand subjected to various nutrient supplies. Plant and Soil. 1995;168–169:167–172. [Google Scholar]
- Dalton F. In situ root extent measurements by electrical capacitance methods. Plant and Soil. 1995;173:157–165. [Google Scholar]
- Dvořák M, Černohorská J, Janáček K. Characteristics of current passage through plant tissue. Biologia Plantarum. 1981;23:306–310. [Google Scholar]
- Dwight HB. Calculation of resistance to ground. AIEE Transactions. 1936;55:1319–1328. [Google Scholar]
- Farrar JF, Jones DL. The control of carbon acquisition by and growth of roots. In: de Kroon H, Visser EJW, editors. Root ecology. Berlin: Springer Verlag; 2003. pp. 91–119. [Google Scholar]
- Gaul D, Hertel D, Borken W, Matzner E, Leuschner C. Effects of experimental drought on the fine root system of mature Norway spruce. Forest Ecology and Management. 2008;256:1151–1159. [Google Scholar]
- Genenger M, Zimmermann S, Hallenbarter D, Landolt W, Frossard E, Brunner I. Fine root growth and element concentrations of Norway spruce as affected by wood ash and liquid fertilisation. Plant and Soil. 2003;255:253–264. [Google Scholar]
- Häussling M, Jorns CA, Lehmbecker G, Hecht-Buchholz C, Marschner H. Ion and water uptake in relation to root developments in Norway spruce (Picea abies (L.) Karst.) Journal of Plant Physiology. 1988;133:486–491. [Google Scholar]
- Helmisaari HS, Saarsalmi A, Kukkola M. Effects of wood ash and nitrogen fertilization on fine root biomass and soil and foliage nutrients in a Norway spruce stand in Finland. Plant and Soil. 2009;314:121–132. [Google Scholar]
- Hendricks JJ, Hendrick RL, Wilson CA, Mitchell RJ, Pecot SD, Guo D. Assessing the patterns and control of fine root dynamics: an empirical test and methodological review. Journal of Ecology. 2006;94:40–57. [Google Scholar]
- Hodge A. The plastic plant: root responses to heterogenous supplies of nutrients. New Phytologist. 2004;162:9–24. [Google Scholar]
- Hutchings MJ, John EA. Distribution of roots in soil, and root foraging activity. In: de Kroon H, Visser EJW, editors. Root ecology. Berlin: Springer-Verlag; 2003. pp. 33–60. [Google Scholar]
- Jackson RB, Mooney HA, Schulze E-D. A global budget for fine root biomass, surface area, and nutrient contents. Proceedings of the National Academy of Sciences, USA. 1997;94:7362–7366. doi: 10.1073/pnas.94.14.7362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jinx M, Dawalibi FP. Extended analyis of ground impedance measurement using the fall-of-potential method. IEEE Transactions on Power Delivery. 2002;4:881–885. [Google Scholar]
- Kendall WA, Pederson GA, Hill RR., Jr. Root size estimates of red clover (Trifolium pratense) and alfalfa (Medicago sativa) based on electrical capacitance and root diameter measurements. Grass and Forage Science. 1982;37:253–256. [Google Scholar]
- Köstler JN, Brückner E, Bibelriether H. Die Wurzeln der Waldbäume. Hamburg: Verlag; 1968. Paul Parey. [Google Scholar]
- Kutschera L, Lichtenegger E. Wurzelatlas mitteleuropäischer Grünlandpflanzen. Stuttgart: Gustav Fischer Verlag; 1982. [Google Scholar]
- Kutschera L, Lichtenegger E. Wurzelatlas mitteleuropäischer Waldbäume und Sträucher. Graz: Leopold Stocker Verlag; 2002. [Google Scholar]
- Leuschner C, Coners H, Icke R, Hartmann K, Effinger N, Schreiber L. Chemical composition of the periderm in relation to in situ water absorption rates of oak, beech and spruce fine roots. Annals of Forest Science. 2003;60:763–772. [Google Scholar]
- Leuschner C, Hertel D. Fine root biomass of temperate forests in relation to soil acidity and fertility, climate, age and species. Progess in Botany. 2002;64:405–438. [Google Scholar]
- Lyr H, Hoffmann G. Growth rates and periodicity of tree roots. International Review of Forestry Research. 1967;2:131–236. [Google Scholar]
- Macfall JS, Johnson GA, Kramer PJ. Observation of a water-depletion region surrounding loblolly pine roots by magnetic resonance imaging. Proceedings of the National Academy of Sciences, USA. 1990;87:1203–1207. doi: 10.1073/pnas.87.3.1203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macfall JS, Johnson GA, Kramer PJ. Comparative water uptake by roots of different ages in seedlings of loblolly pine (Pinus taeda) New Phytologist. 1991;119:551–560. [Google Scholar]
- Mainiero R, Kazda M, Häberle K-H, Nikolova PS, Matyssek R. Fine root dynamics of mature European beech (Fagus sylvatica L.) as influenced by elevated ozone concentrations. Environmental Pollution. 2009;157:2638–2644. doi: 10.1016/j.envpol.2009.05.006. [DOI] [PubMed] [Google Scholar]
- Mainiero R, Kazda M, Schmid I. Fine root dynamics in 60-year-old stands of Fagus sylvatica and Picea abies growing on haplic luvisol soil. European Journal of Forest Research. 2010;129:1001–1009. [Google Scholar]
- Majdi H, Truus L, Johansson U, Nylund J-E, Wallander H. Effects of slash retention and wood ash addition on fine root biomass and production and fungal mycelium in a Norway spruce stand in SW Sweden. Forest Ecology and Management. 2008;255:2109–2117. [Google Scholar]
- Marschner H, Häussling M, George E. Ammonium and nitrate uptake rates and rhizosphere pH in non-mycrorhizal roots of Norway spruce [ Picea abies (L.) Karst.] Trees. 1991;5:14–21. [Google Scholar]
- Marschner H, Roemheld V, Horst WJ, Martin P. Root-induced changes in the rhizosphere importance for the mineral nutrition of plants. Zeitschrift für Pflanzenernaehrung und Bodenkunde. 1986;149:441–456. [Google Scholar]
- McBride R, Candido M, Ferguson J. Estimating root mass in maize genotypes using the electrical capacitance method. Archives of Agronomy and Soil Science. 2008;54:215–226. [Google Scholar]
- Nadezhdina N, Čermák J. Instrumental methods for studies of structure and function of root systems of large trees. Journal of Experimental Botany. 2003;54:1511–1521. doi: 10.1093/jxb/erg154. [DOI] [PubMed] [Google Scholar]
- Nadler A, Tyree MT. Substituting stem's water content by electrical conductivity for monitoring water status changes. Soil Science Society of America Journal. 2008;72:1006–1013. [Google Scholar]
- Nardini A, Salleo S, Tyree MT. Ecological aspects of water permeability of roots. In: Waisel Y, Eshel A, Kafkafi U, editors. Plant roots: the hidden half. New York: Marcel Dekker Inc.; 2002. pp. 683–698. [Google Scholar]
- Neruda J, Ulrich R, Nadezhdina N, Čermák J. 2009. Unfavorable impacts of forwarder technology on tree root systems along skidding trails and possibilites of their prevention. Proceedings of FORMEC, 21–24 June, 2009, Prague and Kostelec nad Cernymi lesy. [Google Scholar]
- Ostonen I, Löhmus K, Pajuste K. Fine root biomass, production and its proportion of NPP in a fertile middle-aged Norway spruce forest: comparison of soil core and in growth core methods. Forest Ecology and Management. 2005;212:264–277. [Google Scholar]
- Ozier-Lafontaine H, Bajazet T. Analysis of root growth by impedance spectroscopy (EIS) Plant and Soil. 2005;277:299–313. [Google Scholar]
- Preston M, McBride R, Bryan J, Candido M. Estimating root mass in young hybrid poplar trees using the electrical capacitance method. Agroforestry Systems. 2004;60:305–309. [Google Scholar]
- Psarras G, Merwin IA. Water stress affects rhizosphere respiration rates and root morphology of young ‘Mutsu’ apple trees on M.9 and MM.111 rootstocks. Journal of the American Society for Horticultural Science. 2000;125:588–595. [Google Scholar]
- Reich PB. Root–shoot relations: optimality in acclimation and adaptation or the ‘Emperor's new clothes’? In: Waisel Y, Eshel A, Kafkafi U, editors. Plant roots the hidden half. New York: Marcel Dekker; 2002. Inc., 205–220. [Google Scholar]
- Samouëlian A, Cousin I, Tabbagh A, Bruand A, Richard G. Electrical resistivity survey in soil science: a review. Soil and Tillage Research. 2005;83:173–193. [Google Scholar]
- Samson BK, Sinclair TR. Soil core and minirhizotron comparison for the determination of root length density. Plant and Soil. 1994;161:225–232. [Google Scholar]
- Shinozaki K, Yoda K, Hozumi K, Kira T. A quantitative analysis of plant form: the pipe model theory. I. Basic analyses. Japanese Journal of Ecology. 1964;14:97–103. [Google Scholar]
- Smit AL, Bengough AG, Engels C, Van Noordwijk M, Pellerin S, Van de Geijn SC. Root methods. Berlin: Springer Verlag; 2000a. [Google Scholar]
- Smit AL, George E, Groenwold J. Root observations and measurements at (transparent) interfaces with soil. In: Smit AL, Bengough AG, Engels C, Van Noordwijk S, Pellerin S, Van de Geijn SC, editors. Root methods. Berlin: Springer-Verlag; 2000b. pp. 235–256. [Google Scholar]
- Stokes A, Fourcaud T, Hruska J, Čermák J, Nadyezdhina N, Nadyezhdin V, Praus L. An evaluation of different methods to investigate root system architecture of urban trees in situ. I. Ground-penetrating radar. Journal of Arboriculture. 2002;28:2–10. [Google Scholar]
- Tagg GF. Measurement of the resistance of physically large earth-electrode systems. Proceedings of the IEEE. 1970;117:2185–2190. [Google Scholar]
- Tatarinov F, Urban J, Čermák J. Application of ‘clump technique’ for root system studies of Quercus robur and Fraxinus excelsior. Forest Ecology and Management. 2008;255:495–505. [Google Scholar]
- Tierney LT, Fahey TJ, Groffman PM, Hardy JP, Fitzhugh RD, Driscoll CT, Yavitt JB. Environmental control of fine root dynamics in a northern hardwood forest. Global Change Biology. 2003;9:670–679. [Google Scholar]
- van Beem J, Smith ME, Zobel RW. Estimating root mass in maize using a portable capacitance meter. Agronomy Journal. 1998;90:566–570. [Google Scholar]
- Van Praag HJ, Sougnez-Remy S, Waterkeyn L. L'absorption-translocation spécifique d’éléments nutritifs en relation avec la structure anatomique des radicelles de hêtre (Fagus sylvatica) et d’épicéa (Picea abies). I. Mesures de l'absorption-translocation spécifique. Belgian Journal of Botany. 1993;126:175–183. [Google Scholar]
- Van Rees KCJ, Comerford NB. The role of woody roots of slash pine seedlings in water and potassium absorption. Canadian Journal of Forest Research. 1990;20:1183–1191. [Google Scholar]
- Zenone T, Morelli G, Teobaldelli M, Fischanger F, Matteucci M, Sordini M, Armani A, Ferre C, Chiti T, Seufert G. Preliminary use of ground-penetrating radar and electrical resistivity tomography to study tree roots in pine forests and poplar plantations. Functional Plant Biology. 2008;35:1047–1058. doi: 10.1071/FP08062. [DOI] [PubMed] [Google Scholar]
- Zhang MI, Willison JHM. Electrical impedance analysis in plant tissues a double shell model. Journal of Experimental Botany. 1991;42:1465–1476. [Google Scholar]
- Zhang MI, Willison J. Electrical impedance analysis in plant tissues: in vivo detection of freezing injury. Canadian Journal of Botany. 1992;70:2254–2258. [Google Scholar]
- Zhang MI, Willison J, Cox M, Hall S. Measurement of heat injury in plant tissue by using electrical impedance analysis. Canadian Journal of Botany. 1993;71:1605–1611. [Google Scholar]