A comprehensive Plasmodium falciparum protein interaction map reveals a distinct architecture of a core interactome

Abstract

We derive a map of protein interactions in the parasite P. falciparum from conserved interactions in S. cerevisiae, C. elegans, D. melanogaster and E. coli and pool them with experimental interaction data. The application of a clique-percolation algorithm allows us to find overlapping clusters, strongly correlated with yeast specific conserved protein complexes. Such clusters contain core activities that govern gene expression, largely dominated by components of protein production and degradation processes as well as RNA metabolism. A critical role of protein hubs in the interactome of P. falciparum is supported by their appearance in multiple clusters and the tendencies of their interactions to reach into many distinct protein clusters. Parasite proteins with a human ortholog tend to appear in single complexes. Annotating each protein with the stage where it is maximally expressed we observe a high level of cluster integrity in the ring stage. While we find no signal in the trophozoite phase, expression patterns are reversed in the schizont phase, implying a preponderance of parasite specific functions in this late, invasive schizont stage. As such, the inference of potential protein interactions and their analysis contributes to our understanding of the parasite, indicating basic pathways and processes as unique targets for therapeutic intervention.

1 Introduction

An important challenge confronting modern biology is whether the wealth of information accruing from the study of model organisms can be transferred to pervasive, intractable microbial diseases that plague human kind. In particular, the global burden of malaria continues to worsen in many developing countries with a devastating impact on human health and corresponding impediment to economic improvement [1]. Recent sequencing efforts yielded extensive annotations of the Plasmodium falciparum genome as well as several other malaria parasites [2, 3, 4, 5]. Despite this abundance of primary genomic and proteomic information, surprisingly little is known about the web of protein interactions that governs the unique biology of malaria parasites. Recently, the first experimentally determined map of physical interactions between proteins of P.falciparum was released [6]. While impressive from an experimental point of view, this set is relatively small, roughly covering 25 % of all parasite proteins. Although a considerable number of conserved proteins exist, this map not surprisingly overlaps to only a small extent with a few existing interactomes of model organisms [7, 8, 9]. In a different approach, functional links between proteins in the parasite have been determined by investigating phylogenetic profiles and domain fusion events [10]. Although this map allows a large-scale glimpse into the intricate web of different relationships between proteins, this approach potentially points to but does not explicitly identify physical protein interactions. In the work presented here, we utilize information that has been retained by evolutionarily divergent model organisms to augment the existing map of experimentally determined protein interactions of the malaria parasite P.falciparum.

2 Materials and methods

Organism Specific Protein Interaction Data

As sources of reliable protein interaction information of diverse organisms, we utilized curated protein interactions obtained from large-scale approaches for S. cerevisiae [11], D. melanogaster [12], C. elegans [13], E. coli [13] and P. falciparum [6].

Orthologous Protein Data

Utilizing all-versus-all BLASTP searches determined by the InParanoid script [14] in protein sets of two species, sequence pairs with mutually best scores were selected as central orthologous pairs. Proteins of both species showing an elevated degree of homology were clustered around these central pairs, a procedure that forms orthologous groups. The quality of the clustering was then assessed by a standard bootstrap procedure. The central orthologous sequence pair that provides a confidence level of 100% was considered as the real orthologous relationship while proteins with a lower level of confidence were considered as their in-paralogs. Specifically, we obtained orthologs of Plasmodium proteins in S. cerevisiae, C. elegans, D. melanogaster, E.coli and H. sapiens.

Gene Expression

Utilizing data from [15] we calculated Pearson's correlation coefficient for every protein interaction over m time points defined as

$$r_P=\frac{m^{-1}\underset{i=1}{\overset{m}{\Sigma }}{x}_i{y}_i-\langle x\rangle \langle y\rangle }{{\sigma }_i{\sigma }_j}$$

where <x> and <y> are the sample means of expression values x_i and x_j , and σ_i and σ_j are their standard deviations. As for cell-cycle specific expression data, we utilized a data set of gene transcription data [16] which captures ring, trophozoite, and schizont phase of the erythrocytic stages and assigned each protein to one of the stages according to its maximum expression.

Functional Similarity

We apply hypergeometric distribution to determine the probability of obtaining a number of shared GO annotations [17] of proteins v and w at or above the observed number by chance. As such, this value reflects the functional similarity of two proteins. Since the function of a considerable amount of proteins in Plasmodium is still unknown, we only account for known GO terms in categories including biological processes, molecular function and cellular component. Considering T different GO terms thus obtained, we define the functional similarity of interacting proteins v, w as

$${\mathit{GO}}_{v,w}=-\log \underset{i=|\mathit{GO}\left(v\right)\cap \mathit{GO}\left(w\right)|}{\overset{\min (\left|\mathrm{GO}\left(v\right)\right|,\left|\mathit{GO}\left(w\right)\right|)}{\Sigma }}\frac{\left(\begin{array}{c}\hfill \left|\mathit{GO}\left(v\right)\right|\hfill \\ \hfill i\hfill \end{array}\right)\left(\begin{array}{c}\hfill T-\left|\mathit{GO}\left(v\right)\right|\hfill \\ \hfill \left|\mathit{GO}\left(w\right)\right|-i\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill T\hfill \\ \hfill \left|\mathit{GO}\left(w\right)\right|\hfill \end{array}\right)}$$

where Tx represents the list GO terms of a protein x and T is the total number of GO terms.

Yeast Protein Complexes

As a compilation of experimentally obtained protein complexes in Yeast we utilized data sets of genome-wide screens using affinity purification and mass spectrometry [18, 19].

Cluster Participation Coefficient

For each protein that is part of at least one cluster or complex, we calculate the cluster participation coefficient P_i of a protein i [20]. In particular, we define this value as

$$P_i=\underset{s=1}{\overset{N}{\Sigma }}{\left(\frac{n_{\mathit{is}}}{\underset{s=1}{\overset{N}{\Sigma }}{n}_{\mathit{is}}}\right)}^2,$$

where n_is is the number of links protein i has to proteins in complex s out of N total complexes. If a protein predominantly interacts with partners that are members of the same complex, we find that P tends to 1, while the opposite holds if the interaction partners are distributed among many different complexes.

Kernel Density Function

A simple way to analyze a series of values x = x₁ , …, x_n would be a histogram. However, if the number of observations is low the significance of a histogram is rather limited. Therefore, we define the kernel density approximation, a smoothing operation that allows the estimation of a putative probability density function of data points around a certain point x as

$$f\left(x\right)=n^{-1}\underset{i=1}{\overset{n}{\Sigma }}K\left(\frac{x-x_i}{h}\right)$$

where K(y) is the kernel function, satisfying

$${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}K\left(y\right)\mathit{dy}=1$$

and h is a smoothing parameter. In particular, we chose the Gaussian as kernel function

$$K\left(y\right)=\frac{1}{\sqrt{2\pi }}{e}^{-\frac{y^2}{2}}$$

and set the smoothing parameter h = 0.1.

Enrichment

In order to obtain an estimate if a certain function A is overrepresented in a sample of a larger sample space S, we calculate the corresponding fraction in the underlying sample. As a null hypothesis, we assume that feature A has been randomly distributed among the whole sample space S, calculate the corresponding randomized fraction f_r(A, s) and define ER(A,s) = f(A,s)/ f_r (A,s) as the enrichment of feature A in space s. We average ER over 10,000 randomization, allowing us to conclude that the distribution of A was a random process if ER = 1. In the same way, we find that feature A is enriched if ER > 1 and vice versa.

K-Clique Clustering Algorithm

In order to obtain overlapping clusters we apply the clique-percolation algorithm introduced in [21], designed to locate the k-clique communities of unweighted, undirected networks. This community definition is based on the observation that a typical member in a community is linked to many other members, but not necessarily to each other node in the community. Therefore, a community can be interpreted as a union of smaller, fully connected subgraphs that share nodes. Such complete subgraphs in a network are called k-cliques, where k refers to the number of nodes in the subgraph, and a k-clique-community is defined as the union of all k cliques that can be reached from each other through a series of adjacent k-cliques. Two k-cliques are considered adjacent if they share k - 1 nodes.

Secretome

To establish infection in the host, malaria parasites export remodeling and virulence proteins into the erythrocyte. Recent studies independently uncovered a host cell targeting (HCT) signal that allows proteins to cross into the human erythrocyte cell by passing several membranes [22, 23, 24]. Combining these data sets, we compile a list of 525 secreted proteins in P. falciparum.

Rich-Club Coefficient

The so-called rich-club phenomenon is quantitatively defined by the rich-club coefficient Φ(k) [25]. Denoting by E_≥kthe number of edges among the N_≥k nodes which have at least k interaction partners, the rich-club coefficient is expressed as

$$\mathrm{\Phi }\left(k\right)=\frac{2E_{\ge k}}{N_{\ge k}(N_{\ge k}-1)},$$

where N_≥K(N_≥k)/2 represents the maximally possible number of edges among the N_≥k nodes. An appropriate choice for normalizing the rich-club coefficient is provided by the ratio

$$\rho \left(k\right)=\frac{\mathrm{\Phi }\left(k\right)}{{\mathrm{\Phi }}_r\left(k\right)}$$

where Φ_r(k) is the rich-club coefficient of a random network with the same degree distribution P(k). The choice of pairs of links, whose end nodes are exchanged, allows us to obtain such a randomized network where the degree distribution is preserved [25, 26]. In order to have a reasonably large ensemble, we repeat the randomization process 10,000 times. Binning nodes according to their degrees k we obtain a degree dependent mean value of the rich-club coefficient by averaging over all ρ's. A ratio ρ(k) > 1, is the actual evidence for the presence of a rich-club phenomenon, an increase in the inter-connectivity of large degree nodes compared to the random case. This process is well displayed by the presence of an oligarchy of highly interacting nodes that are well connected among each other. A ratio ρ(k) < 1 points to a lack of inter-connectivity among large degree nodes which are separated in distinguishable modules.

3 Results

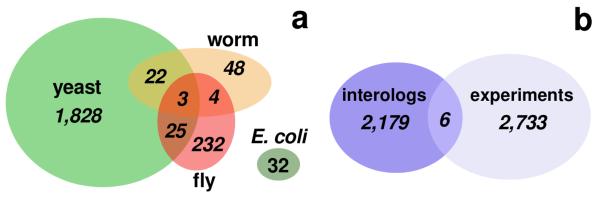
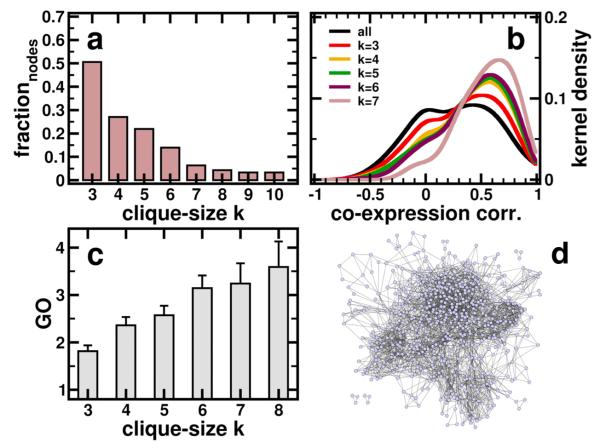
A significant proportion of the P. falciparum genome encodes a bundle of interactions that can be inferred despite significant phylogenetic divergences between P. falciparum and the model organisms for which comprehensive interaction data is available. To infer probable, yet experimentally undetermined physical protein interactions in P. falciparum we use interologs, protein interactions deemed evolutionarily conserved if participating proteins have interacting orthologs in at least one other organism [27]. Utilizing the InParanoid database [14], we find 1,872 interactions between 684 proteins in yeast that have orthologs in Plasmodium, 299 orthologous fly proteins embedded in 258 interactions, 71 interactions among 101 orthologous worm proteins and 32 interactions between 26 proteins in E. coli. While we do not find any interactions of E. coli that are shared with other organisms, we find relatively small fractions of yeast interologs significantly shared with worm and fly (Fig. 1a). In comparison, currently available sets of experimental protein interactions of P. falciparum [6] are small including 2,739 interactions among 1,301 proteins that overlap only minimally, but significantly with the interolog-based sets of interactions (Fig. 1b). Pooling all interaction sets we obtain a network consisting of 4,918 unique interactions among 1,872 proteins in Plasmodium. We determine the modular architecture of the underlying network, leading to a higher-order network view in which the presence of modules possibly indicate archetypical patterns of evolutionarily building blocks [28], a blueprint reinforced by the tendency of the genes to be coexpressed in modules [29]. The clique percolation algorithm, unlike other clustering approaches, [21] emphasizes overlapping clusters, thereby highlighting proteins that participate in more than one cluster, a characteristic that is well known from the analysis of experimentally obtained protein complexes [30]. To locate k-clique based communities of unweighted, undirected networks, the algorithm utilizes a community definition based on the observation that a typical member is linked to many other members, but not necessarily to all other nodes in a certain community. Therefore, a community can be interpreted as a union of smaller complete (fully connected) subgraphs that share multiple interacting nodes. Applying this algorithm to the underlying network of protein interactions in P. falciparum, we observe a steadily declining fraction of nodes that appear in clusters obtained with increasing clique sizes (Fig. 2a). Although we lose proteins as clique size increases, we improve the reliability of interactions in the underlying clusters. In fact, we find that coefficients of all interactions in the underlying interaction network follow a bimodal curve, when we calculate coexpression correlation coefficients and functional similarity of interacting proteins in clusters obtained with various clique sizes (Figure 2b). Accounting for interactions that appear in clusters of different clique sizes we find that the peak around r ~ 0.0 strongly decays. In contrast, the rise of the peak at r ~ 0.5 strongly indicate the presence of reliable interactions in clusters obtained with higher clique size. Another feature of protein interactions is their heightened tendency to share specific functions. Such observations are based on the fact that biological functions are frequently mediated by protein complexes. As such, highly clustered areas in protein interactions networks do not only mediate higher reliability [31], but also appear to be more functionally homogeneous [32]. Indeed, we find interactions that appear in clusters of larger cliques appear increasingly functionally homogeneous (Figure 2c), indicating a higher degree of reliability.

Figure 1.

(a) The diagram shows the sizes of the different sets of interactions in P.falciparum we inferred from well established other eukaryotic organisms. The overlaps between these sets of interactions are small but statistically significant (P < 10⁻³, assuming a hypergeometric distribution). (b) Similarly to (a), we find that the evolutionary derived set overlaps only to a small but significant extent with the experimental set of interactions (P < 10⁻³).

Figure 2.

(a) Since clique percolation algorithm does not partition the underlying network, we observe a steadily declining fraction of nodes that appear in clusters obtained with different clique sizes. (b) Calculating coexpression correlation coefficients r for all interactions in the underlying network we observe a bimodal distribution. Accounting for interactions that appear in clusters obtained with different clique sizes we find that the peak at r ~ 0.0 is strongly decaying, while we observe a pronunciation of the other peak at r ~ 0.5. (c) Similarly, interactions that appear in clusters of increasing clique sizes appear more functionally homogeneous. The combination of these observations allows us to conclude that interactions in clusters obtained with increasing clique size are more reliable. (d) Graphical representation of all interactions that appear in at least on cluster.

Concluding that interactions in clusters obtained with increasing clique size are increasingly reliable, we assume that the maximum clique size that places an interaction in a cluster is a reasonable measure of the interactions reliability. As such, we pooled all interactions that appear in at least one cluster presented in Figure 2d (a list of all interactions annotated with their maximum clique size can be found in the Supplementary Table 1).

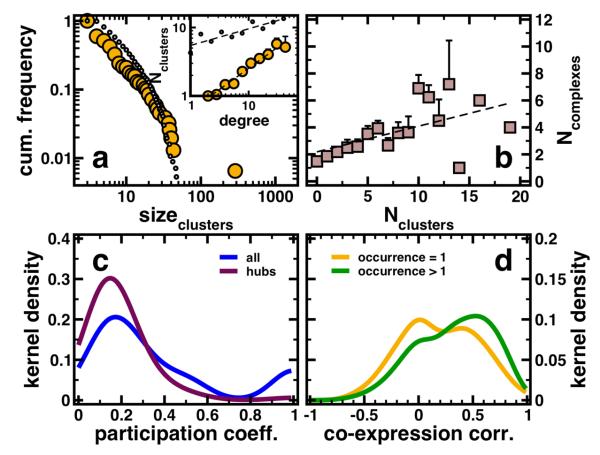
As a proxy to the real structure of protein complexes in P. falciparum we pooled all 154 clusters that have been obtained with different clique-sizes in the underlying protein interaction network (see Supplementary Table 2 for the complete annotated list of clusters). In order to assess the characteristics of the obtained clusters we compare them to protein complexes of yeast proteins that have orthologs in Plasmodium. In particular, we utilized an experimentally obtained large-scale data set of protein complexes [18, 19]. Determining all proteins in complexes that have an ortholog in Plasmodium we obtain 564 conserved protein complexes that have at least three proteins (see Supplementary Table 3 for the complete annotated list of conserved complexes). Comparing clusters obtained from the underlying interaction network with conserved protein complexes, we applied a hypergeometric distribution. We determined overlaps with P < 10⁻² and assigned a conserved protein complex to each cluster with the largest overlap. In the Supplementary Table 2, we labeled every protein that is shared by a cluster and its closest similar conserved complex. Determining similarities between protein complexes and clusters we obtain similar frequency distributions of corresponding sizes (Fig. 3a). In particular, both distributions decay as a power-law, indicating that most complexes are small while a small minority is large. Similarly, we observe that highly connected proteins participate in an increasing number of clusters (inset, Figure 3a).

Figure 3.

(a) Pooling all clusters that have been obtained with different clique-sizes, we observe a power-law in the frequency distribution of cluster sizes. As another benchmark of significance, we compared our clusters obtained with our clique percolation algorithm to protein complexes in Yeast that have orthologs in P. falciparum. We find a similar shape in the distribution of sizes in conserved protein complexes (dotted line). Since the clique percolation algorithm allows nodes to be affiliated with more than one cluster, we observe a strong correlation, indicating that hubs predominately are significantly present in an increasing numbers of clusters (inset, r = 0.57, P < 10⁻³). Similarly, we observe such a correlation for conserved protein complexes (dotted line, r = 0.23, P < 10⁻³). (b) Comparing the affiliation of proteins to clusters in our network and to conserved protein complexes, we observe a strong correlation (r = 0.64, P < 10⁻³). (c) A low value of the cluster participation coefficient represents the observation that the interactions of a protein are present in many different clusters and vice versa. Considering all proteins in clusters we obtain a maximum around low values. Focusing the analysis on hubs defined as proteins that have at least 5 interaction partners we find that the original signal is significantly reinforced at low values of the cluster participation coefficient. (d) Similarly to Fig. 2b, we obtain a bimodal distribution of coexpression correlation coefficients of interactions, where the proteins in question appear in only one cluster. Focusing on Proteins that appear in more than one cluster we find a pronunciation of the peak at higher values, suggesting that the majority of promiscuous proteins (as indicated by their occurrence in clusters) are coexpressed with their interaction partners.

As another quantitative measure of the similarity of clusters and complexes we determined the numbers of clusters and complexes each protein occurs in. Calculating Pearson's correlation coefficient we find a strong and significant correlation between clusters and complexes (Figure 3b, r = 0.64, P < 10⁻³). Although the conserved complexes of the parasite resemble the putative complex structure at best, our clusters can serve as a proxy to the real complex composition since they largely share similar characteristics. As such, we continue our analysis with the clusters we obtained from the underlying network topology. As a measure of cluster diversity, we define the cluster participation coefficient of a protein i, P_i[20]. If a protein predominantly interacts with partners that are members of the same cluster, P_i tends to 1, while the opposite holds if the interaction partners are distributed among many different clusters. Accounting for all proteins in the underlying interaction network we observe that interactions of a single protein occur in a variety of clusters, while relatively few interactions are confined to a small number of clusters (Figure 3c). Focusing on hubs, defined as proteins that have at least 5 interaction partners we find that the original signal is significantly reinforced at low values of the complex participation coefficient. As such, we conclude that hubs predominantly reach into many different clusters, securing a large degree of diversity. As observed in Fig. 2b, we obtain a bimodal distribution of coexpression correlation coefficients of interactions, where the hub protein in question appears in only one cluster. Focusing on hub proteins that appear in more than one cluster we find a pronunciation of the peak, suggesting that most promiscuous proteins (as indicated by their occurrence in clusters) are coexpressed with their interaction partners. As such, we conclude that hubs that are affiliated with one cluster largely share characteristics of date hubs where coexpression partners are unevenly expressed, whereas proteins occurring in many clusters tend to be expressed with their partners at the same time, indicative of party hubs (Fig. 3d) [33].

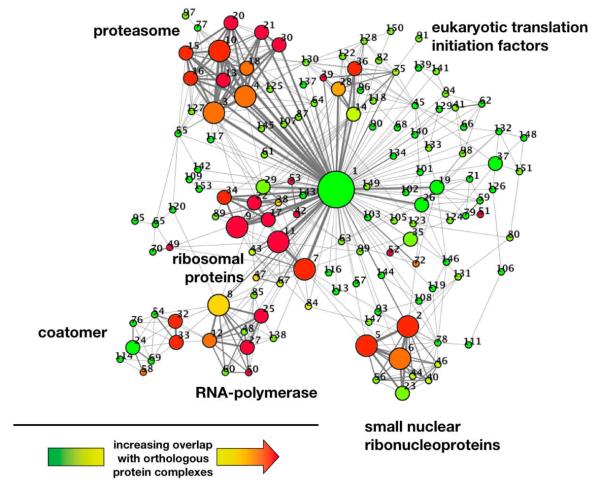
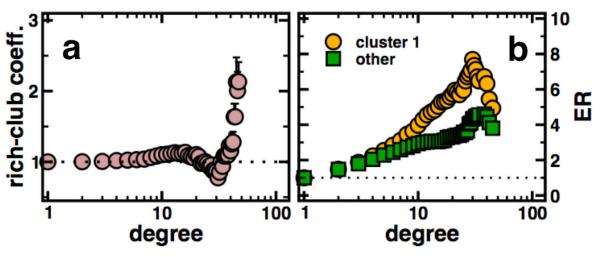
Representing the overlapping nature of clusters, we represent links between clusters if they share proteins (Figure 4). In particular, we find groups of modules that share many proteins and overlap with conserved protein complexes. The picture is dominated by protein degrading and producing components, polymerase, ribosome and coatomer functions as well as small nucleoproteins. Highly prominent in our clustering, we find a large complex (#1) that shares many proteins with other clusters. Numerous distinct functions appear in this cluster, suggesting the presence of a functional and central core in the interactome of P. falciparum. Previous reports found that the parasites interactome is composed of an oligarchy of highly interacting and intertwined nodes [8]. In general, this so-called rich-club phenomenon is defined by the rich-club coefficient ρ(k) (see Materials and Methods for details). ρ(k) > 1 points to the presence of a core of highly intertwined nodes with connectivity of at least k. In the absence of this phenomenon (i.e. ρ(k) < 1) networks are dominated by many well defined functional communities [25]. In our network, we confirm the presence of a strong rich-club signal (i.e. ρ(k) > 1) with higher degree of proteins (Fig. 5a).

Figure 4.

Representing the overlapping nature of clusters, we represent links between clusters if they share proteins. In particular, the size of nodes and width of edges reflects the size of the clusters and the number of shared proteins, respectively. The color of nodes indicates the degree of overlap with conserved protein complexes in yeast, where a gradient from green to red indicates increasing overlap. As for functional complexes, we find large groups of overlapping complexes providing protein degrading and producing, polymerase, ribosome and coatomer functions as well as small nucleoproteins. Numbers indicate clusters in the Supplementary Table 2, where each cluster is annotated with its proteins.

Figure 5.

(a) The distributions of the mean rich-club coefficient ρ(k) shows an increase with elevated connectivity in the parasites protein interaction network, suggesting the presence of an oligarchy of highly interacting and intertwined proteins. (b) Determining the enrichment of proteins that appear in the central cluster 1 and other clusters in Fig. 4, we largely find that especially proteins in rich clubs tend to appear in cluster 1.

Determining the composition of the central cluster (#1) in Fig. 4, we observe that especially such rich-club proteins are predominantly enriched (Fig. 5b), a result suggesting the presence of a functional and topological core that largely governs the parasites interactome.

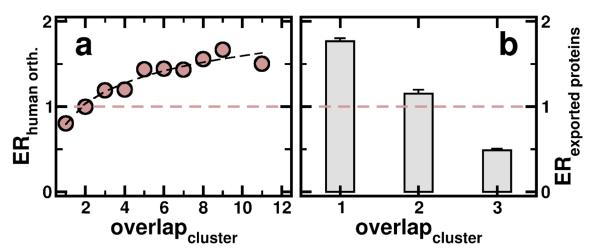
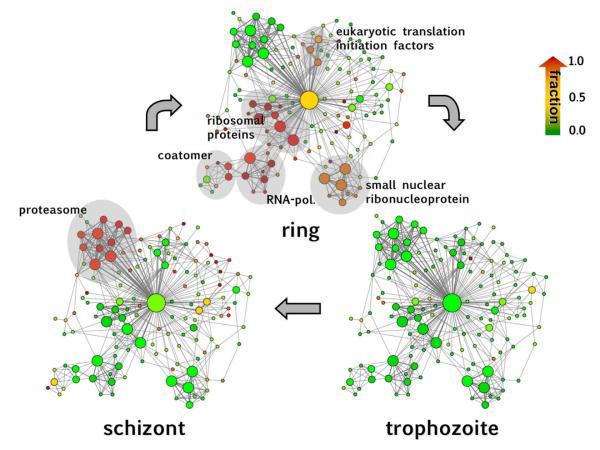
Determining the enrichment of human orthologs obtained from InParanoid [14] in bins of proteins that appear in a certain number of clusters, we find that protein predominately have orthologs in human (Figure 6a), corroborating an earlier observation that hubs in other organisms predominately are conserved in evolution [34]. However, for proteins that are important for the invasion process of the host, carrying a peptide export signal and being exported into the lumen of a red blood cell, we find that these proteins are increasingly diluted as involvement in multiple clusters increases (Figure 6b). In contrast to the enrichment of evolutionary relevant proteins this result suggests that proteins most important for the invasion process are more uniquely parasite features. Identification of this cohesion highlights fundamental, conserved modular units that are not necessarily readily observable from experimental studies of P. falciparum interactions, probably due to extreme AT-richness of the coding sequence and limited accessibility of mRNA of certain developmental stages in its complex life cycle. As a strength of our approach, the modularity of the inferred network can be used to identify prominent network features at various stages throughout the Plasmodium life cycle when overlaid with high-resolution Plasmodium-specific transcriptional profiles. In general, transcriptional activity of the parasite has the superficial appearance of a continuous cascade that masks the coordinated coexpression of functionally linked protein interactions. However, this picture is refined if each protein is assigned to the cell-cycle stage where its mRNA is expressed to its maximum level, indicating that the subnet modularity is development-dependent to a certain extent. Highlighting all modules where at least half of its proteins are expressed to their maximal extent in each stage, we observe that nearly all highest activity of the network coincides with ring (G1 phase) and schizont phases (M phase) while, remarkably, almost no maximum-level activity is observed in the trophozoite phase (S/G2 phase). Such changes in the expression of interacting proteins appear to reflect the changed course in the flow of metabolic activity expected to occur as the parasite progresses towards completion of its intraerythrocytic growth cycle. In ring stage parasites, the strongest expressed clusters are involved in gene expression and protein production, while in the late stage of the life cycle, the dominant protein interaction network highlights components of the proteasome, reflecting the requirement for total turnover as the parasite remodels itself for a shift to a new invasion stage (Fig. 7). Together, these results may suggest that genes (and their expression) in the trophozoite and schizont phase of the Plasmodium life cycle have undergone adaptations. Such results might occlude observations of an historical core, either due to extensive divergence or to unique gene origins. However, we have to stress that the outcome might differ, if we can extend the analysis to another parasite.

Figure 6.

(a) Determining the enrichment of human orthologs in bins of proteins that are involved in a certain number of clusters, we find that proteins that appear in an increasing number of clusters are predominately conserved in human. (b) In contrast, we find that proteins which carry a peptide export signal for being excreted to the lumen of a human red blood cell, are diluted with increasing involvement in multiple clusters.

Figure 7.

Assigning each protein to the cell-cycle stage where its mRNA is expressed to its maximum level, we highlight each cluster according to the fractions of maximally expressed proteins in the underlying stage, where the color gradient from green to red refers to increasing fractions. We observe that nearly all highest activity of the clusters coincides with ring and schizont phases while, remarkably, almost no maximum-level activity is observed in the trophozoite phase. In the ring stage the strongest expressed clusters are involved in gene expression and protein production. In the late stage of the life cycle, the dominant protein interaction network highlights components of the proteasome, reflecting the requirement for total turnover as the parasite remodels itself for a shift to a new invasion stage.

4 Discussion

Although the determination of potential interactions by evolutionary inference is currently an established technique, the gene/protein sequences of Plasmodium exhibit peculiarities that hamper the detection of orthologs in different organisms. In particular, large inserts obscure homology signals of true orthologs. However, by focusing on the most statistically significant ortholog pairs (the core pairs) we largely mitigate these effects.

Our approach recovers evolutionarily conserved cohesive topologies that can be observed as functional clusters in biological time by superimposing transcriptional profiles that partition the network with respect to the complex life cycle. In particular, the application of the k-clique clustering algorithm allows us to obtain a cluster structure that largely shares characteristics of experimentally obtained protein complexes. In lieu of such results or the parasite, we resorted to evolutionary portions of Yeast protein complexes, allowing us to conclude that the computational clustering reasonably reflects the large scale properties of a putative complex composition.

This method should provide an initial comprehensive interaction network for detailed experimental analysis, compliment experimental data and further bioinformatics approaches. Novelty in the parasite interactome, including absence of conserved clusters and their interactions, can provide insight into the parasites biology. Absent clusters may represent unique divergences that distinguish the Plasmodium network structure from other organisms. Assuming that all orthologous relationships can be detected, protein counterparts in other organisms with no orthologs in Plasmodium may represent either a loss of function or acquisition of novel malaria parasite-specific clusters. While this assumption certainly holds for the set of organisms considered, such specifics of Plasmodium might actually be common to other parasites, a hypothesis that can be tested once interactions in other parasites are available. In addition, such divergences may be especially interesting since it has been shown that increased rates of evolution may be focused at the connections between modules.

Therefore, even though the clusters themselves are highly conserved units, unique Plasmodium-specific proteins that appear in many complexes could highlight critical features of the parasite that can be exploited as therapeutic targets. Several extensions of our method can be envisioned to benefit from the proliferation of whole-genome databases that continuously enrich the power of network inference. Our initial elucidated network for malaria parasites can be strengthened by deeper searches for orthologs using all Plasmodium species. Similarly, a concatenated network comprising all known (and validated) interactions across the tree of life will be an important tool to recognize distant phylogenetic relationships with yeast and other organisms for which refined network data exist. More functional relationships can be elucidated within the dimensions of malaria genome expression by profiling transcription, at much higher resolution under a variety of conditions of cellular life (e.g. perturbations, and strain-specific variants). Eventually, we expect to construct a comprehensive phylogenetic scaffold of networks using the methods developed in this project onto which new protein-protein interaction data can be placed. Since there is still considerable noise in the protein interaction data available from current technologies, such as from yeast two-hybrid determinations, a universal scaffold will be a powerful tool for experimental investigation of proposed interactions. As such, our results further contribute to the understanding of the lethal biology of this parasite and possibly illuminate basic pathways and processes as unique targets for therapeutic intervention.