Substituent Effects on Electrophilic Catalysis by the Carbonyl Group: Anatomy of the Rate Acceleration for PLP-Catalyzed Deprotonation of Glycine

Abstract

First-order rate constants, determined by ¹H NMR, are reported for deuterium exchange between solvent D₂O and the α-amino carbon of glycine in the presence of increasing concentrations of carbonyl compounds (acetone, benzaldehyde and salicylaldehyde) and at different pD and buffer concentrations. These rate data were combined with ¹H NMR data that define the position of the equilibrium for formation of imines/iminium ions from addition of glycine to the respective carbonyl compounds, to give second-order rate constants k_DO for deprotonation of α-imino carbon by DO⁻. The assumption that these second-order rate constants lie on linear structure-reactivity correlations between log k_OL and pK_a was made in estimating the following pK_as for deprotonation of α-imino carbon: pK_a = 22, glycine–acetone iminium ion; pK_a = 27, glycine–benzaldehyde imine; pK_a ≈ 23, glycine–benzaldehyde iminium ion; and, pK_a = 25, glycine–salicylaldehyde iminium ion. The much lower pK_a of 17 [Toth, K.; Richard, J. P. J. Am. Chem. Soc. 2007, 129, 3013–3021] for carbon deprotonation of the adduct between 5′-deoxypyridoxal (DPL) and glycine shows that the strongly electron-withdrawing pyridinium ion is unique in driving the extended delocalization of negative charge from the α-iminium to the α-pyridinium carbon. This favors carbanion protonation at the α–pyridinium carbon, and catalysis of the 1,3-aza-allylic isomerization reaction that is a step in enzyme-catalyzed transamination reactions. An analysis of the effect of incremental changes in structure on the activity of benzaldehyde in catalysis of deprotonation of glycine shows the carbonyl group electrophile, the 2-O⁻ ring substituent and the cation pyridinium nitrogen of DPL each make a significant contribution to the catalytic activity of this cofactor analog. The extraordinary activity of DPL in catalysis of deprotonation of α–amino carbon results from the summation of these three smaller effects.

Introduction

We have worked over the last 15 years to characterize kinetic and thermodynamic barriers for deprotonation of the α-amino carbon of amino acids^1,2 (Chart 1) and peptides³ in water and to understand the mechanism by which enzymes lower these barriers in catalysis of deprotonation of amino acids.^2,4 Natural selection of small molecule catalysts has seen the evolution of pyridoxal 5′-phosphate as a cofactor for an enormous range of enzymes ^5–9 that catalyze deprotonation of α-amino acid carbon as the first step of more complex reactions. These enzymatic reactions include, racemization ^10–12 and decarboxylation ^13–18 of the amino acid, transamination to form an α–keto acid and pyridoxamine 5′-phosphate,^19–22 replacement of good nucleofuges at the β-amino position through elimination of the leaving group from a pyridoxal-stabilized carbanion to form an activated alkene, which undergoes addition of a second nucleophile,^23,24 and aldol type addition of the pyridoxal stabilized carbanion to formaldehyde ²⁵ or acetaldehyde.²⁶

Chart 1.

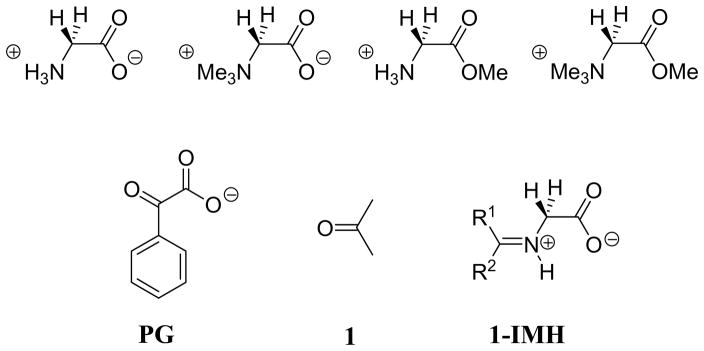
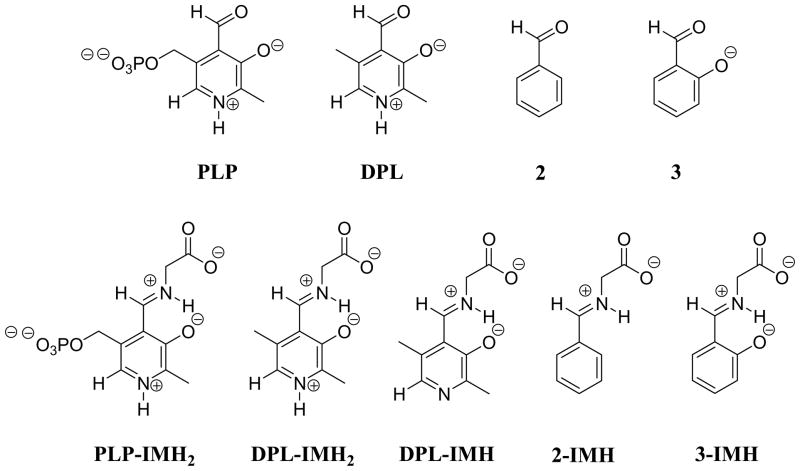
Our earliest studies on catalysis of deprotonation of amino acids focused on determining the effect of alkylation of the amino nitrogen and the carboxylate oxygen on the carbon acidity of glycine (Chart 1).^1,2 We next examined electrophilic catalysis of deprotonation of glycine methyl ester by the simple ketone acetone (1, Chart 1)^27,28 and of glycine by the pyruvoyl analog phenylglyoxylate (PG)²⁸ through the corresponding α-iminium ion reaction intermediates (e.g., 1-IMH). Finally, we have examined catalysis of deprotonation of glycine by 5′-deoxypyridoxal (DPL, Chart 2) over a broad range of pH.²⁹

Chart 2.

The effective catalysis of deprotonation of the α-amino carbon of glycine by acetone²⁸ shows that the carbonyl group of PLP is the underlying source of the catalytic power of PLP. This carbonyl group catalysis is assisted by other functionality at the cofactor. Most importantly, by the pyridinium nitrogen and the 2-O⁻ substituent at the pyridine ring. There has been speculation about the role of these substituents in catalysis of deprotonation of α-amino carbon,³⁰ but these roles have not been rigorously evaluated. An understanding of these substituent effects will provide assistance to the development of effective small molecule catalysts of these reactions,³¹ and insight into the mechanism of action of enzymes that utilize PLP as a cofactor.⁹

The 5′-phosphate of PLP should not strongly activate the cofactor for deprotonation of α-amino acids. The most likely role for this functional group is to provide binding energy for stabilization of the Michaelis complex and the transition states for reactions in which PLP serves as a cofactor.^32–34 The α-amino acid carbanion should be stabilized by delocalization of negative charge onto the pyridinium nitrogen of DPL-IMH₂, compared to delocalization onto the neutral pyridine nitrogen of DPL-IMH or onto the phenyl ring of 3-IMH. However, the amino acid carbanion is already highly delocalized at 3-IMH, and this should cause an attenuation of the effect of the cationic nitrogen at the 4-position of the pyridine ring on the stability of the carbanion.³⁵ We report here the results of experiments that allow a comparison of the activities of DPL and salicylaldehyde (3) as catalysts of deprotonation of glycine.

The 2-O⁻ substituent at DPL and salicylaldehyde activates aldehydes for catalysis by stabilization of the iminium ion glycine adducts DPL-IMH₂ and 3-IMH by an intramolecular hydrogen bond to the iminium nitrogen.³⁶ This effect is probably attenuated, because partial proton transfer from the cationic nitrogen to oxygen will cause the charge at this nitrogen and the resulting electrostatic stabilization of the α-amino acid carbanion to decrease. We report here the results of a study of deprotonation of glycine catalyzed by 2 and by 3 that defines the contribution of this 2-O⁻ substituent to catalysis of deprotonation of glycine by DPL.

2. Experimental Section

2.1 Materials

Glycine and salicylaldehyde were purchased from Fluka. Benzaldehyde, 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP), 2,2,2-trifluoroethanol (TFE), deuterium chloride (37 wt %, 99.5% D), potassium deuterioxide (40 wt %, 98 + % D), deuterium oxide (99.9% D), and acetone-d₆ (99.9 atom % D) were from Aldrich. All other organic and inorganic chemicals were reagent grade and were used without further purification.

2.2. General Methods

The acidic protons of glycine, K₂HPO₄ and KH₂PO₄, were exchanged for deuterium before preparation of solutions of these compounds in D₂O.² Salicylaldehyde, HFIP and TFE were dissolved directly in D₂O, which introduced < 1 atom % of protium into this solvent. Phosphate buffers were prepared by mixing stock solutions of K₂DPO₄ and KD₂PO₄ in D₂O at I = 1.0 (KCl) to give the desired acid/base ratio. Pyrophosphate and carbonate buffers were prepared by dissolving a measured amount of KCl and the basic form of the buffer in D₂O, and adding DCl to give the desired acid/base ratio at I = 1.0 (KCl). Buffers of HFIP and TFE were prepared by dissolving a measured amount of KCl and adding KOD to give the desired acid/base ratio at I = 1.0 (KCl).

Solution pD was determined at 25 °C using an Orion model 350 pH meter equipped with a Radiometer pHC4006-9 electrode. Values of pD were obtained by adding 0.4 to the observed reading of the pH meter.³⁷ The concentration of deuterioxide ion at any pD was calculated using eq 1, where K_w = 10^−14.87 is the ion product of deuterium oxide at 25 °C and γ_OL = 0.78 is the apparent activity coefficient of lyoxide ion under our experimental conditions.³⁸

$$[{\text{DO}}^{-}]=\frac{{10}^{\text{pD}-\text{p}{K}_w}}{{\gamma }_{\text{OL}}}$$ (1)

2.3. ¹H NMR Analyses

¹H NMR spectra at 500 MHz were recorded in D₂O at 25 °C on a Bruker AMX500 NMR spectrometer as described previously.^38,39 In all cases, the relaxation delay between pulses was at least 10-fold greater than the longest relaxation time of the protons of interest. Spectra were obtained with a sweep width of 2600 Hz, a 90° pulse angle and an acquisition time of 6 s. Baselines were corrected for drift before integration of the peaks. Chemical shifts are reported relative to (CH₃)₄N⁺ at 2.94 ppm.

2.4. Determination of Equilibrium Constants

The position of the equilibrium for addition of glycine to acetone to form the corresponding imine in D₂O at 25 °C and I = 1.0 (KCl) was determined by ¹H NMR spectroscopy as described in previous work.^28,36 Formation of the imine was monitored in solutions that contained 0.1 M glycine and 1.0 M acetone at I = 1.0 (KCl). The pD was maintained by use of 0.10 M of the following buffers: phosphate, pD 6.1 – 8.0; pyrophosphate, pD 8.6 – 9.5; carbonate, pD 10.0 – 11.1 and TFE, pD 12.0 – 13.0.

Values of the observed equilibrium constant (K_add)_obsd (M⁻¹) for imine formation were determined from the ratio of the integrated areas of the peaks for the methylene protons of the imine product ( $A_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}}$), and of the reactant glycine ( $A_{{\text{CH}}_2}^{\text{Gly}}$) according to eq 2, where [1-IM]_e and [Gly]_e are the total equilibrium concentrations of imine and glycine, respectively. The ratio of equilibrium concentrations of imine adduct and amino acid was determined 1–2 hours after mixing the reactants except at pD > 8, where it was determined after 24 hours in order to ensure that chemical equilibrium had been reached. Acetone-catalyzed deuterium incorporation into glycine also took place during this time period at pD 13. However, ¹H NMR analysis showed the same deuterium enrichment of the α–CH₂ groups of glycine and of the imine within experimental error. Therefore, the ratio of the equilibrium concentrations of imine adduct and glycine was determined as the ratio of the sum of peak areas for the -CH₂- and -CHD- groups.

$${(K_{\text{add}})}_{\text{obsd}}=\frac{{[\mathbf{1}-\mathbf{I}\text{M}]}_{\text{e}}}{{[\text{Gly}]}_{\text{e}}[\text{Acetone}]}=\frac{A_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}}}{A_{{\text{CH}}_2}^{\text{Gly}}[\text{Acetone}]}$$ (2)

2.5. Kinetic Measurements

All reactions were carried out in D₂O at 25 °C and I = 1.0 (KCl). The deuterium exchange reactions of glycine in the presence of acetone or 3 were initiated by mixing solutions of glycine, the catalyst and the buffer at the same pD and ionic strength (I = 1.0 (KCl)). The final concentration of the amino acid ranged from 5 to 15 mM. The deuterium exchange reactions of glycine in the presence of 2, in alkaline solutions of D₂O, were initiated by mixing solutions of glycine, 2 and KOD at the same ionic strength (I = 1.0 (KCl)) to give a final glycine concentration of 5 mM.

The exchange for deuterium of the first α-proton of glycine was followed by monitoring the disappearance of the singlet due to the α-CH₂ group of the substrate and the appearance of the upfield-shifted triplet due to the α-CHD group of the monodeuterated product by ¹H NMR spectroscopy at 500 MHz, as described in previous work.^2,27,28 Values of R, which is a measure of the progress of the deuterium exchange reaction, were calculated using eq 3, where A_CH2 and A_CHD are the integrated areas of the peaks for the α-CH₂ and the α-CHD groups, respectively. The reactions in the presence of acetone, 2 and 3 were followed during exchange for deuterium of 20–30%, 40–90%, and 60–90%, respectively, of the first proton of the α-CH₂ group of the substrate. In all cases an equilibrium mixture of glycine and the corresponding imine was observed before the formation of a significant amount of deuterium labelled glycine. Semilogarithmic plots of reaction progress, R, against time according to eq 4 were linear with negative slopes equal to k_obsd (s⁻¹), which is the rate constant for exchange of a single proton of the α-CH₂ group of the substrate. The values of the first-order rate constant for exchange of the first α-CH₂ proton to give the monodeuterated product, k_ex (s⁻¹), were determined as k_ex = 2 k_obsd.

$$R=\frac{A_{{\text{CH}}_2}}{A_{{\text{CH}}_2}+A_{\text{CHD}}}$$ (3)

$$lnR=-k_{\text{obsd}}t$$ (4)

3. Results

3.1. Equilibrium Constants for Imine Formation

Figure 1 shows the change with changing pD in the observed chemical shift ${({\delta }_{{\text{CH}}_2})}_{\text{obsd}}^{\mathbf{1}-\mathbf{IM}}(\text{ppm})$ of the signal for the α–CH₂ hydrogens of the mixture of 1-IM and 1-IM-D (Scheme 1) which forms in D₂O from the reaction of 0.1 M glycine and 1.0 M acetone at 25 °C and I = 1.0 (KCl). The change in the chemical shift of the α–methylene group is due to the change in the protonation state of the imine nitrogen. The solid line in Figure 1 shows the nonlinear least squares fit of the data to eq 5, derived for Scheme 1, where (a) ${\delta }_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}-\mathbf{D}}=4.05\text{ppm}$ and ${\delta }_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}}=3.69\text{ppm}$ are the chemical shifts for the α–CH₂ group observed at limiting low and high pD, and (b) the value of (K_a)_1-IM-D = 10^−9.64 is determined by treating this acidity constant as a variable parameter.

Figure 1.

The dependence on pD of (δ_CH2)_obsd (ppm) for the -CH₂- hydrogen of the imine formed in D₂O that contains 0.1 M glycine and 1 M acetone at 25 °C and I = 1.0 (KCl). The solid line shows the fit of the data to eq 5 derived for Scheme 1.

Scheme 1.

$${({\delta }_{{\text{CH}}_2})}_{\text{obsd}}^{\mathbf{1}-\mathbf{IM}}=\frac{{\delta }_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}}{(K_{\text{a}})}_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}+{\delta }_{{\text{CH}}_2}^{\mathbf{1}-\mathbf{IM}-\mathbf{D}}{a}_{\text{D}}}{({(K_{\text{a}})}_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}+a_{\text{D}})}$$ (5)

Values of the apparent equilibrium constants (K_add)_obsd (M⁻¹) for addition of glycine to acetone to form the corresponding imine in D₂O at 25 °C were determined by ¹H NMR analysis, as described in the Experimental Section. Figure 2 shows the change, with changing pD, in log (K_add)_obsd for addition of glycine to acetone. The line shows the fit of the data to eq 6, derived for Scheme 1, using (K_a)_GlyD = 3.5 × 10⁻¹¹ M, (K_a)_1-IM-D = 2.3 × 10⁻¹⁰ M (Table 1) and (K_add)_1-IM-D = 0.0056 M⁻¹ determined for the formation of the iminium ion at pD < 8.

Figure 2.

Logarithmic dependence of (K_add)_obsd (M⁻¹) on pD for conversion of glycine to the acetone imine in D₂O at 25 °C and I = 1.0 (KCl). The solid line was calculated using eq 6 and the equilibrium constants from Table 1.

Table 1.

Equilibrium Constants in D₂O for Addition of Glycine to Acetone.^a

Amino compound	Imine	p(Ka)Glyb	p(Ka)X-IM-Dc	Kaddd (M−1)
+D3 NCH2 COO−	1-IMD	10.44 ± 0.03	9.64 ± 0.03	(5.6 ± 0.1) × 10−3
D2 NCH2 COO−	1-IM			(3.5 ± 0.5) × 10−2

^aAt 25 °C and I = 1.0 (KCl).

^bThe acidity constant of the amino acid in D₂O at 25 °C and I = 1.0 (KCl) determined by ¹H NMR titration.

^cApparent acidity constant in D₂O at 25 °C and I = 1.0 (KCl), determined by NMR titration as described in the text.

^dEquilibrium constant for the addition of the amino acid to acetone to form the imine adduct.

$${(K_{\text{add}})}_{\text{obsd}}={(K_{\text{add}})}_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}\left(\frac{a_{\text{D}}+{(K_{\text{a}})}_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}}{a_{\text{D}}+{(K_{\text{a}})}_{\text{GlyD}}}\right)$$ (6)

3.2. Deuterium Exchange Reactions

3.2.1. Catalysis by Acetone

The exchange for deuterium of the first α-proton of glycine in D₂O at 25 °C and I = 1.0 (KCl) was monitored by ¹H NMR spectroscopy (500 MHz) as described previously.^2,28 Table S1 of the Supporting Information gives the observed first-order rate constants k_ex (s⁻¹) for deuterium exchange in the presence of various concentrations of acetone and HFIP buffer at pD 9.3, 9.9 and 10.5, determined as described in the Experimental Section. Figure 3 shows the effect of increasing concentrations of HFIP buffer (50% free base) on k_ex (s⁻¹) for reactions at different fixed concentrations of acetone. The intercepts of these linear correlations are the first-order rate constants k_o = k_w f_1-IM-D (s⁻¹, Table 2) for deuterium exchange catalyzed by the solvent at the given concentration of acetone, where f_1-IM-D is the fraction of glycine present as the iminium ion adduct 1-IM-D (eq 7, derived for Scheme 1)⁴⁰ and k_w is the apparent first-order rate constant for the solvent reaction. Table 2 reports values of k_w, calculated as k_w = k_o/f_1-IM-D, for reactions at different concentrations of acetone.

Figure 3.

Dependence of k_ex (s⁻¹) for exchange of the first α-proton of glycine in the presence of acetone on the total concentration of HFIP buffer at pD 9.98 ([RO⁻]/[ROH] = 1.0) in D₂O at 25 °C and I = 1.0 (KCl). Key: (●) 0.10 M acetone; (■) 0.25 M; (┤) 0.50 M.

Table 2.

Rate Constants for Exchange of the First α-Proton of Glycine in the Presence of Acetone and HFIP Buffers in D₂O^a

Base	fBc	pD	[acetone]/M	f1-IM-Dd	ko/s−1e	kw/s−1f	(kbuf)obsd/M−1s−1g	kB/M−1s−1h
HFIP	0.8	10.48	0.25	6.8 × 10−4	1.5 × 10−7	2.2 × 10−4	1.3 × 10−7	2.4 × 10−4
pKBD = 9.9b
	0.5	9.87	0.10	4.4 × 10−4	2.3 × 10−8	5.1 × 10−5	6.6 × 10−8	3.0 × 10−4
		9.94	0.25	1.1 × 10−3	7.0 × 10−8	6.5 × 10−5	1.2 × 10−7	2.3 × 10−4
		9.98	0.50	2.1 × 10−3	1.5 × 10−7	7.1 × 10−5	2.8 × 10−7	2.6 × 10−4
	0.2	9.27	0.25	1.3 × 10−3	2.1 × 10−8	1.6 × 10−5	5.8 × 10−8	2.2 × 10−4

^aAt 25 °C and I = 1.0 (KCl).

^bApparent pK_a of the conjugate acid in D₂O at 25 °C and I = 1.0 (KCl).

^cFraction of the buffer present in the basic form.

^dFraction of glycine present as the reactive iminium ion 1-IM-D, calculated from eq 7 using the values of the equilibrium constants reported in Table 1.

^eThe intercept of plots of k_ex against [buffer]_T (Figure 3).

^fApparent first-order rate constants for solvent-catalyzed deprotonation of 1-IM-D, calculated from the values of k_o as described in the text.

^gThe slope of plots of k_ex against [buffer]_T (Figure 3).

^hSecond-order rate constants for HFIP base-catalyzed deprotonation of 1-IM-D, calculated from the values of (k_buf)_obsd as described in the text.

$$f_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}=\frac{{(K_{\text{add}})}_{\mathbf{1}-\mathbf{IM}-\mathbf{D}}[\text{acetone}]}{\left(1+\frac{{(K_{\text{a}})}_{\text{GlyD}}}{a_{\text{D}}}\right)}$$ (7)

A similar analysis of data for reactions in 20 and 80% free base HFIP buffers (Table S1) gave k_w = 1.6 × 10⁻⁵ s⁻¹ and k_w = 2.2 × 10⁻⁴ s⁻¹ for deprotonation of the iminium ion at pD 9.27 and 10.48, respectively. Figure 4 (▼) shows the pD-rate profile of log k_w for deprotonation of 1-IM-D in D₂O. The solid line of unit slope shows the least-squares fit of the data to eq 8 using (k_DO)_1-IM-D = 4.2 M⁻¹s⁻¹ for deprotonation of 1-IM-D by DO⁻ (Scheme 1), where K_w = 10^−14.87 M² is the ion product of D₂O at 25 °C and γ_OL = 0.78 is the apparent activity coefficient of lyoxide ion under our experimental conditions.

Figure 4.

pD-rate profiles of k_w (s⁻¹) for exchange for deuterium of the first α–CH₂ hydrogen of: (▼), 1-IM-D; (┤), 2-IM; (●), 3-IM-D; (▽), N-protonated glycine;² (□) N-protonated glycine methyl ester;² (■), the acetone-glycine methyl ester iminium ion.²⁷,²⁸

$$log{k}_{\text{w}}=log\left(\frac{k_{\text{DO}}{K}_{\text{w}}}{{\gamma }_{\text{OL}}}\right)+\text{pD}$$ (8)

The slopes of the linear correlations in Figure 3 are equal to (k_buf)_obsd = (k_B)_1-IM-D f_B f_1-IM-D for the deuterium exchange reaction catalyzed by buffer at the given concentration of acetone, where (k_B)_1-IM-D (M⁻¹s⁻¹) is the second-order rate constant for deprotonation of 1-IM-D by the buffer base (Scheme 1) and f_B is the fraction of the catalyst in the basic form. The values of k_B reported in Table 2 were calculated from (k_buf)_obsd using the appropriate values of f_B and f_1-IM-D. A value of (k_B)_1-IM-D = 2.4 × 10⁻⁴ M⁻¹s⁻¹ for deprotonation of 1-IM-D by the HFIP base (Scheme 1) was calculated as the average of the values of k_B determined at different fractions of buffer base.

3.2.2. Catalysis by Benzaldehyde (2)

The exchange for deuterium of the first α-proton of glycine in the presence of 2 and various concentrations of deuterioxide ion in D₂O at 25 °C and I = 1.0 (KCl) was followed by ¹H NMR (500 MHz). Table S2 gives values of the first-order rate constant k_ex (s⁻¹) for the deuterium exchange reaction together with values of f_2-IM, the fraction of amino acid converted to the imine (Scheme 2) under the experimental reaction conditions, determined by ¹H NMR analysis of the mixture of glycine and 2 in D₂O, as described in previous work.³⁶ The rate constants for solvent-catalyzed deprotonation of the imine adduct, k_w = k_ex/f_2-IM, increase linearly with the concentration of deuterioxide ion (not shown). The slope of this correlation gives (k_DO)_2-IM = 2.90 × 10⁻⁴ M⁻¹s⁻¹ as the second-order rate constant for deprotonation of 2-IM catalyzed by deuterioxide ion. Figure 4 (┤) shows the pD-rate profile of log k_w for deprotonation of 2-IM in D₂O. The solid line of unit slope shows the fit of the data to eq 8 ((k_DO)_2-IM = 2.90 × 10⁻⁴ M⁻¹s⁻¹). It was not possible to determine a value of the second-order rate constant for deprotonation of 2-IM-D by DO⁻ because the deuterium exchange reaction is too slow to monitor at pD < 11, where the concentration of 2-IM-D would begin to become significant.

Scheme 2.

3.2.3. Catalysis by Salicylaldehyde (3)

The exchange for deuterium of the first α-proton of glycine was examined in D₂O at 25 °C and I = 1.0 (KCl) in solutions buffered with HFIP (pD 9.3–10.5). Table S3 of the Supporting Information gives the observed first-order rate constants k_ex (s⁻¹) for deuterium exchange in the presence of various concentrations of 3 and HFIP buffer at pD 9.3, 9.8 and 10.5, determined as described in the Experimental Section. Table S3 also reports values of f_3-IM-D, the fraction of total glycine that is converted to the reactive iminium ion adduct (Scheme 3) at each concentration of 3 at the given pD, determined by ¹H NMR analysis of the mixture of glycine and 3, as described in previous work.³⁶ Figure 5 shows the linear dependence of k_ex on the total concentration of HFIP buffer (pD 9.8) for reactions at two fixed concentrations of 3. The intercepts of these linear plots are the first-order rate constants k_o = k_w f_3-IM-D (s⁻¹, Table 3) for solvent-catalyzed exchange at the given pD, where k_w is the apparent first-order rate constant for the solvent reaction and f_3-IM-D is the fraction of glycine present as the iminium ion 3-IM-D (Table S3). Table 3 reports values of k_w, calculated as k_w = k_o/f_3-IM-D, for reactions at two different concentrations of 3. The same treatment of the data for reactions at pD 10.5 and 9.3 (Table 3) gives k_w = 1.1 × 10⁻⁵ s⁻¹ and k_w = 7.8 × 10⁻⁷ s⁻¹, respectively. The slope of a linear plot (not shown) of k_w against [DO⁻] gives the second-order rate constant (k_DO)_3-IM-D = 0.19 M⁻¹s⁻¹ for deprotonation of 3-IMD by deuterioxide ion. Figure 4 (●) shows the pD-rate profile of log k_w for deprotonation of 3-IMD in D₂O. The solid line of unit slope through the data was calculated from the value of k_DO using eq 8 and (k_DO)_3-IM-D = 0.19 M⁻¹s⁻¹.

Scheme 3.

Figure 5.

Dependence of k_ex (s⁻¹) for exchange for deuterium of the first α-proton of glycine in the presence of salicyaldehyde on the total concentration of HFIP buffer at pD 9.8 in D₂O at 25 °C and I = 1.0 (KCl). Key: (●) 10 mM 3; (○) 52 mM 3.

Table 3.

Rate Constants for Exchange of the First α-Proton of Glycine in the Presence of 3 and HFIP Buffers in D₂O^a

Base	fBc	pD	[aldehyde]/M	f3-IM-Dd	ko/s−1e	kw/s−1f	(kbuf)obsd/M−1s−1g	kB/M−1s−1h
HFIP	0.8	10.53	6.0 × 10−3	0.15	1.7 × 10−6	1.1 × 10−5	3.1 × 10−6	2.6 × 10−5
		10.52	2.0 × 10−2	0.39	4.4 × 10−6	1.1 × 10−5	8.8 × 10−6	2.8 × 10−5
pKBD = 9.9b
	0.5	9.80	1.0 × 10−2	0.32	6.9 × 10−7	2.2 × 10−6	4.2 × 10−6	2.6 × 10−5
		9.86	5.2 × 10−2	0.73	1.8 × 10−6	2.5 × 10−6	1.2 × 10−5	3.3 × 10−5
	0.2	9.35	2.0 × 10−2	0.45	3.5 × 10−7	7.8 × 10−7	2.9 × 10−6	3.2 × 10−5

^aAt 25 °C and I = 1.0 (KCl).

^bApparent pK_a of the conjugate acid in D₂O at 25 °C and I = 1.0 (KCl).

^cFraction of the buffer present in the basic form.

^dFraction of glycine present as the reactive iminium ion 3-IM-D at the given concentration of 3, determined by ¹H NMR analysis of an equilibrium mixture of glycine and the imine.

^eThe intercept of plots of k_ex against [buffer]_T (Figure 5).

^fApparent first-order rate constants for solvent-catalyzed deprotonation of 3-IM-D, calculated from the values of k_o as described in the text.

^gThe slope of plots of k_ex against [buffer]_T (Figure 5).

^hSecond-order rate constants for HFIP base-catalyzed deprotonation of 3-IM-D, calculated from the values of (k_buf)_obsd as described in the text.

The slopes of the linear correlations in Figure 5 are apparent second-order rate constants, (k_buf)_obsd = (k_B)_3-IM-D f_B f_3-IM-D for the buffer-catalyzed deuterium exchange reaction at the given concentration of 3, where (k_B)_3-IM-D (M⁻¹s⁻¹) is the second-order rate constant for deprotonation of 3-IM-D by the buffer base and f_B is the fraction of the catalyst in the basic form. Table 3 reports values of k_B that were calculated from (k_buf)_obsd using the appropriate values of f_B and f_3-IM-D. A value of (k_B)_3-IM-D = 2.9 × 10⁻⁵ M⁻¹s⁻¹ for deprotonation of 3-IM-D by the HFIP base was calculated as the average of the values of k_B determined at different fractions of buffer base.

4. DISCUSSION

Acetone (1), salicylaldehyde (3) and benzaldehyde (2) are effective catalysts of the deprotonation of the α–amino carbon of glycine in D₂O. This reaction leads to exchange of the α–hydrogen for deuterium from solvent, which is monitored by ¹H NMR. The observation that the deuterium exchange reactions are first-order in the concentration of the electrophilic catalyst and deuterioxide ion shows that they proceed by formation of imine or iminium ion adducts to glycine, which undergo deprotonation by deuterioxide ion to form enolates (Schemes 1, 2 and 3). Table 4 reports equilibrium constants K_add for formation of adducts between glycine and 1, 2 or 3; and, second-order rate constants k_DO for deprotonation of these adducts. Second-order rate constants k_HO = 2.9 M⁻¹s⁻¹, 0.13 M⁻¹s⁻¹ and 2.0 × 10⁻⁴ M⁻¹ s⁻¹ (Table 5) for deprotonation of 1-IMH, 3-IMH and 2-IM respectively, by hydroxide ion in H₂O were calculated from the experimental values of k_DO and an estimated secondary solvent deuterium isotope effect of k_DO/k_HO = 1.46.⁴¹ Table 5 summarizes the values of k_HO for deprotonation of glycine and derivatives of glycine reported here and in earlier work.^2,28,29

Table 4.

Equilibrium Constants in D₂O for Addition of Glycine to Carbonyl Compounds, and Second-Order Rate Constants k_DO for Carbon Deprotonation of the Imine or Iminium Ion Adduct.^a

Aldehyde	Carbon Acid	Kaddb (M−1)	(Kadd)+c (M−1)	kDOd (M−1 s−1)
		3.5 × 10−2	5.6 × 10−3	4.2
		44e	0.0033e	2.90 × 10−4
		1.76e	72e	0.19

^aAt 25 °C and I = 1.0 (KCl).

^bEquilibrium constant for addition of the basic amino form of glycine to the carbonyl compound.

^cEquilibrium constant for addition of glycine zwitterion to the carbonyl compound.

^dSecond-order rate constant for carbon deprotonation of the iminium ion adduct by deuterioxide ion in D₂O.

^eData from ref 36.

Table 5.

Rate and Equilibrium Constants for Carbon Deprotonation of Glycine and Glycine Derivatives in Water at 25 °C and I = 1.0 (KCl)

Carbon Acid	kHOa (M−1s−1)	pKab	Carbon Acid	kHOa (M−1s−1)	pKab
	4.5 × 10−5 c	28.9c		4.1c	21.0c
	3.3 × 10−4 c	27.3c		390c	18.0c
	2.9	21.9		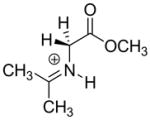9.0 × 103 d	14d
	2.0 × 10−4	27		ca. 1	ca. 23
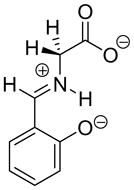	0.13	25		1.1 × 104 d	14d
	not determined	ca. 23 e		7.5 × 102 f	17f

^aSecond-order rate constant for deprotonation of the carbon acid by hydroxide ion calculated from data reported in this work, unless noted otherwise.

^bpK_a for ionization of the carbon acid in water calculated from data reported in this work, unless noted otherwise.

^cData from ref 2.

^dData from ref 28.

^eEstimated as described in the text.

^fData from ref 29.

4.1. Carbon Acid pK_a’s

Figure 6 (■) shows the linear relationship, with slope 0.44, between the statistically corrected values of log k_HO for deprotonation of cationic ketones and esters, and the pK_a of the carbon acid.² The carbon acid pK_as for 1-IMH and 3-IMH reported in Table 5 were estimated by assuming that the values of log k_OH for these carbon acids lie on the linear correlation for other cationic ketones and esters. Figure 6 (●) also shows the linear correlation between the statistically corrected values of log k_HO for deprotonation of neutral monocarbonyl carbon acids and the carbon acid pK_a.^{38,39,42–44} A pK_a of 27 (Table 5) for the ionization of 2-IM was calculated with the assumption that the value of log k_HO for this carbon acid lies on this linear correlation.

Figure 6.

Rate-equilibrium correlations of rate constants, k_HO (M⁻¹ s⁻¹), for deprotonation of α-carbonyl carbon acids by hydroxide ion with the pK_a of the carbon acid. The values of k_HO and pK_a were statistically corrected for the number of acidic protons p at the carbon acid. Correlation of log(k_HO/p) for deprotonation of neutral aldehydes, ketones, esters, and acetamide by hydroxide ion, constructed using data from earlier work (●). ³⁸,³⁹,⁴²–⁴⁴ Excluding the point for acetate anion (pK_a = 33.5), the data are correlated by log(k_HO/p) = 6.496 − 0.401(pK_a + log p). Correlation of log(k_HO/p) for deprotonation of cationic ketones and esters (■).² The data are correlated by log(k_HO/p) = 10.044 − 0.444(pK_a + log p). Data for deprotonation of the acetone-glycine methyl ester iminium ion (□).²⁷ Data for deprotonation of 1-IM-H and 3-IM-H (▵). Data for deprotonation of 2-IM (○).

The large equilibrium constant of K_add = 44 M⁻¹ for formation of the Schiff base 2-IM from 2 and glycine facilitates detection of the 2-catalyzed deuterium exchange reaction of glycine at high pD (Figure 4). It was not possible to detect the 2-catalyzed deuterium exchange reaction of glycine at low pD, where 2-IMD is the reacting carbon acid, because (K_add)⁺ = 0.0033 M⁻¹ for formation of 2-IMD is very small (Table 4) and the low solubility of benzaldehyde in water prevents experiments with concentrations of aldehyde larger than 0.02 M.

We have estimated k_HO for carbon-deprotonation of 2-IMH by making the assumption that N-protonation of glycine and of 2-IM will cause similar changes in the thermodynamic and kinetic acidity of the α–amino and α–imino carbon. The α-NH₃⁺ substituent causes a 4.6 unit decrease in carbon acid pK_a of acetate anion from 33.5 to 28.9 for glycine zwitterion ^2,42 and of ethyl acetate from 25.6 to 21.0 for glycine methyl ester.^2,38 By comparison the α-NH₂ substituent is expected to have a small effect on carbon acidity. For example, there is only a 0.5 unit difference between carbon acid pK_as of 26.5 for acetone and 26.0 for 2-dimethylaminoacetone in DMSO.⁴⁵ The weak acidifying effect of an α-dimethylamino group of acetone shows that the inductive effect of this electron-withdrawing group on pK_a is roughly canceled by the opposing enolate destabilization from repulsive interaction between the nonbonding electron lone pair at nitrogen and the delocalized electron pair at the enolate anion.⁴⁶ A similar cancellation of inductive and electronic substituent effects has been proposed to explain the small effects of α-hydroxy and α-alkoxy substituents on the kinetic acidity of α-carbonyl carbon.^46–49

Combining the 4.6 unit effect of the α-NH₃⁺ substituent on carbon acidity with the ca. 0.5 unit effect of the α-NH₂ substituent gives a ca. 4 unit effect for protonation of the α-amino nitrogen on the carbon acid pK_a of glycine zwitterion and glycine methyl ester (Scheme 4). We assume that protonation of the α-imino nitrogen of 2-IM will cause a similar 4 unit decrease in the pK_a of the carbon acid, from 27 to 23. The value of k_HO = 1 M⁻¹ s⁻¹ for carbon-acid deprotonation of 2-IMH reported in Table 5 was calculated from the estimated carbon acid pK_a of 23 using the linear correlation log(k_HO/p) = 10.044 − 0.444(pK_a + log p) established in earlier work (Figure 6).²

Scheme 4.

A comparison of kinetic data for deprotonation of DPL-IMH₂ and 3-IMH by HO⁻ shows that substitution of the ring 4–CH by –NH⁺ causes a 6,000-fold increase in k_HO for deprotonation of this carbon by hydroxide ion. The linear correlation between log k_HO and carbon acid pK_a shown in Figure 6 shows that this change in k_HO corresponds to a ca. 8-unit decrease in the pK_a of the α-imino carbon. We expect that a large fraction of this 8-unit effect is due to the unit increase in positive charge at the aromatic ring of DPL-IMH₂. For example, ca. 30% (2.1 pK_a units) of the similar 7.8-unit overall effect of the protonated pyridine nitrogen on the acidity constant for the ionization of the carbon acid benzyl phenyl ketone is observed for the charge-conservative nitrogen substitution, and the remaining 70% of this substituent effect (5.7 pK_a units) is expressed when nitrogen is protonated (Chart 3).^50,51 We estimate a pK_a of ca. 23 (Table 5) for ionization of DPL-IMH by making the assumption that 70% of the total 8-unit effect of the 4-CH for 4-NH⁺ substitution on carbon acidity is lost upon deprotonation of nitrogen.

Chart 3.

4.2. Substituent Effects on the Carbon Acidity of Glycine

4.2.1 Effect of the α-Iminium Nitrogen

The addition of acetone to glycine methyl ester to form the iminium ion results in a seven unit decrease in the carbon acid pK_a from 21 to 14 (Table 5),²⁷ while the addition of acetone to the glycine zwitterion results in a similar seven unit decrease in the carbon acid pK_a from 29 to 22 (Table 5). The overall effect of iminium ion formation on carbon acid pK_a is due to two contributing effects:

1. The enhancement of intramolecular electrostatic stabilization of the enolate anion by interaction with the cationic nitrogen when the hydrogen-bonded amino protons are replaced by nonpolar organic functionality.² This results in a 3 unit larger acidifying effect of the α-NMe₃⁺ group at betaine methyl ester (pK_CH = 18.0) than of the α-NH₃⁺ group at glycine methyl ester (pK_CH = 21.0).²

2. The stabilization of the enolate by direct delocalization of negative charge onto the α-imino carbon (Scheme 2). A similar delocalization of charge is a contributing factor in the ca. 3 unit lower pK_a of 15.2 for the C-2 proton of 3-cyclohexenone⁵² compared with the pK_a of 18.1 for cyclohexanone.⁴³

The following two experimental observations suggest that the effect of delocalization of negative charge onto the α-imino carbon on the pK_a of these acetone iminium ions is small.

1. Oxygen methylation of glycine and betaine zwitterion, which relieves destabilizing electrostatic interactions between neighboring negatively charged oxygen and carbon atoms, causes 8 and 9 unit decreases, respectively, in carbon acid pK_a (Table 5). The observation that oxygen methylation of 1-IMH causes a similar 8 unit decrease in carbon acid pK_a is consistent with similar destabilizing electrostatic interactions between neighboring negatively charged oxygen and carbon atoms at 1-IMH, so that there is no detectable relief of this interaction from delocalization of negative charge onto the α-imino carbon of 1-IMH.

2. The higher estimated pK_a of 23 for 2-IMH compared with 22 for 1-IMH shows that there is no significant stabilization of the glycine enolate of 1-IMH by the phenyl for methyl substitution. If there is little stabilization of 2-IMH by delocalization of negative charge from the α-imino carbon to the phenyl ring substituent, then the negative charge density at this carbon is almost certainly small.

4.2.2 Effect of Aromatic Substituents at the α-Iminium Nitrogen

Chart 4 summarizes the results of our studies of substituent effect of formation of iminium ions to simple aldehydes R-CHO on the pK_a for deprotonation of the α–amino carbon. The carbon acid pK_a of the iminium ion adduct of glycine to salicylaldehyde (25) is much higher than the pK_a of the iminium ion adduct of glycine to DPL (17). Apparently, a very strongly electron-withdrawing group such as the pyridinium ion is required to drive the extended delocalization of negative charge onto the α-iminium carbon and cause a further large increase in carbon acidity (Chart 5A). The low carbon acid pK_a of ca. 18 for the pyridoxamine analog 4-(aminomethyl)pyridine dication⁵³ provides supporting evidence that the α–pyridinium substituent provides powerful stabilization of negatively charged carbon.

Chart 4.

Chart 5.

Table 5 shows that the addition of the strongly resonance electron withdrawing –CO₂⁻ substituent to the α-imino carbon of 2-IMH also drives the extended delocalization of negative charge onto the α-iminium carbon and causes a large decrease in carbon acid pK_a from ca. 23 to 14²⁸ for the PG-glycine iminium ion (Chart 5B). We conclude that the second resonance electron-withdrawing group present in the pyruvoyl prosthetic group (-CO₂⁻) and PLP (pyridinium cation) provides a large kinetic push to electrophilic catalysis of deprotonation of glycine to catalysis of enzymatic reactions that proceed through α-amino carbanion intermediates.

4.3. Relevance to Enzymatic Catalysis

It has been suggested for PLP enzymes that protonation of the pyridine ring of the resonance delocalized α-imino carbanion causes a shift in negative charge density from the α-imino to the α–pyridyl carbon that favors protonation of the α–pyridyl carbon and the 1,3-aza-allylic isomerization reaction that is a step in enzyme-catalyzed transamination reactions.⁹ This proposal is consistent with the observation that the PLP cofactor bound to alanine racemase is stabilized by a hydrogen bond to the weakly acidic cation side chain of Arg-219,⁵⁴ while the cofactor bound to D-amino acid transaminase ^55,56 and alanine glyoxylate aminotransferase ⁵⁷ is almost certainly protonated by more strongly acidic carboxylic acid side-chains of Glu-177 and Asp-180, respectively. The 6 unit difference in the carbon acid pK_as for DPL-IMH and DPL-IMH₂ shows that protonation of the pyridine ring causes a substantial increase in the stability of negative charge at the distant α–amino carbon. This provides direct evidence for an increased delocalization of negative charge across the extended π-system that will favor the enyzme catalyzed 1,3-aza-allylic isomerization reaction. In summary, PLP-dependent racemases sacrifice part of the cofactor’s intrinsic catalytic power by using the cofactor in the neutral pyridine form. Apparently, the mechanistic imperative to direct the reaction towards proton transfer at the α–amino carbon, and avoid the wasteful dead-end transamination reaction overrides the competing imperative to utilize the cofactor in its most active form. This shows that the latent catalytic power of PLP-dependent racemases is so great that a portion may be sacrificed to ensure the proper reaction specificity.

4.4. Anatomy of the Rate Acceleration of PLP-Catalyzed Deprotonation of Glycine

Chart 6 compares the first-order rate constants k_o (s⁻¹) for solvent-catalyzed deprotonation of glycine at neutral pL in the absence and presence of 0.01 M carbonyl electrophiles.⁵⁸ These data allow a dissection of the contribution of component pieces of the PLP analog DPL to the enormous observed rate acceleration for deprotonation of glycine.

Chart 6.

1. The rate constant k_o = 2 × 10⁻¹¹ s⁻¹ for the reaction in the presence of 0.01 M acetone provides a metric for the intrinsic reactivity of the electrophilic carbonyl group as a catalyst of deprotonation of glycine.

2. The rate constant of k_o = 1 × 10⁻¹¹ s⁻¹ for the reaction in the presence of 0.01 M benzaldehyde shows that the phenyl for alkyl substitution does not greatly enhance the catalytic reactivity of the carbonyl group.

3. A comparison of k_o = 1 × 10⁻¹¹ and k_o = 5.4 × 10⁻⁹ s⁻¹ for catalysis by 0.01 M benzaldehyde and salicylaldehyde, respectively, shows that the ortho-phenoxy substituent stabilizes the transition state for deprotonation of glycine by 3.8 kcal/mol (Chart 6). This is due to the stabilizing intramolecular hydrogen bond between the ring oxygen anion and the iminum ion.³⁶ The strong intramolecular hydrogen bond causes the carbon acid pK_a to increase from 23 for 2-IMH to 25 for 3-IMH. This decrease in carbon acidity attenuates the transition state stabilization from hydrogen bonding, by causing a decrease in the reactivity of 3-IMH toward deprotonation by hydroxide ion.

4. The substitution of the strongly electron-withdrawing pyridinium cation for the phenyl ring at 3-IMH causes k_o to increase from 5.4 × 10⁻⁹ to ca 4.6 × 10⁻⁶ s⁻¹. Neglecting the small effect of the o-methyl group on the reactivity of DPL-IMH₂, there is an additional 4 kcal/mol stabilization of the transition state for deprotonation of glycine (Chart 6). This reflects the strong electron demand of the pyridinium cation, which drives the stabilization delocalization of charge across the extended π-system.

In conclusion, these results provide an impressive example of how the summation of several relatively small effects in the assembly of the complex molecules PLP and DPL has produced a type of catalyst of truly extraordinary power.³³ It is an open question of whether modern chemists will be able to match the brute-force success of the trial and error of evolution, and succeed in designing either small or large molecule catalysts with the power of those observed in nature.