Abstract
A set of techniques developed under the umbrella of the string method is used in combination with all-atom molecular dynamics simulations to analyze the conformation change between the prepowerstroke (PPS) and rigor (R) structures of the converter domain of myosin VI. The challenges specific to the application of these techniques to such a large and complex biomolecule are addressed in detail. These challenges include (i) identifying a proper set of collective variables to apply the string method, (ii) finding a suitable initial string, (iii) obtaining converged profiles of the free energy along the transition path, (iv) validating and interpreting the free energy profiles, and (v) computing the mean first passage time of the transition. A detailed description of the PPS↔R transition in the converter domain of myosin VI is obtained, including the transition path, the free energy along the path, and the rates of interconversion. The methodology developed here is expected to be useful more generally in studies of conformational transitions in complex biomolecules.
INTRODUCTION
The analysis of large-scale conformational changes in biomolecules is one of the most challenging problems in experimental and computational chemistry. Despite encouraging advances in computer speed, direct observation of such conformational changes in conventional molecular dynamics (MD) simulation is impossible in most cases, because it would require integration times that are orders of magnitude beyond the reach of most available computers. To confront this difficulty, several accelerated sampling techniques have been developed, such as transition path sampling (TPS),1, 2 the string method,3, 4, 5 metadynamics,6, 7 adaptive biasing force,8 and milestoning.9, 10 In each of these methods, the ultimate goal is to find a detailed and unbiased description of the transition without a priori assumptions. Unfortunately, such assumptions are often unavoidable [e.g., one must choose an initial path, collective variables (CVs), or the resolution of the transition path]. In the present paper, we address some of these assumptions in the context of the string method applied to a complex biomolecular system at atomic resolution.11, 12, 13
Specifically, we use the string method to find the most probable transition path between the prepowerstroke (PPS) and rigor (R) conformers of the converter domain of myosin VI (MVI),11, 12, 13 compute the free energy (FE) profile along the transition path, and estimate the rate of interconversion between the two conformers. The present example illustrates generic challenges that are likely to arise in the application of the string method to large biomolecular systems and provides solutions that can be implemented with present-day computers. We therefore expect that the methodology developed herein will extend the applicability of the string method to a wide class of biomolecules.
The string method provides a representative path for the transition, i.e., the minimum free energy path (MFEP). If certain conditions are met, as described in Sec. 2, the MFEP lies at the center of a tube in which the transition is most likely to occur.14, 15 The MFEP is much smoother than a trajectory (such as those found by TPS) and is likely to be more informative about the mechanism of the transition, because it averages out the motions that are unimportant in the transition. The elimination of the unimportant degrees of freedom is achieved because the MFEP is computed in a reduced space of the collective variables that are essential for describing the transition; such collective variables can be center-of-mass (COM) positions of groups of selected atoms, distances between such groups, bond or dihedral angles, etc. The introduction of a reduced collective variable space is necessary to justify the assumptions implicit in the string method and to make the calculation of MFEP affordable. In addition, unlike methods such as metadynamics that also use collective variables but require their number to be rather small, the string method can be used with large sets of collective variables (hundreds or more16). Although the string method has been applied to a number of problems,5, 16, 17, 18 the present study treats a more complex system, which requires the resolution of issues beyond those encountered in previous applications. For a detailed summary of the methods used in this study and the results obtained by their application to myosin VI, the reader is encouraged to read Secs. 4, 5, respectively, before the main body of the paper.
Sections 2, 3 describe the methodology and its implementation for the myosin VI converter in detail. In Sec. 2 we review the general techniques employed in this paper: collective variables are introduced in Sec. 2A, the MFEP is discussed in Sec. 2B, the string method in collective variables is summarized in Sec. 2C, and the calculation of the free energy and the rate of the transition is explained in Sec. 2D. Section 3 addresses the application of the methods to MVI. Section 3A discusses the preparation of MD simulation structures. Section 3B explains the use of targeted MD simulations to choose collective variables (two sets are chosen in order to ascertain that the free energy profiles and rates calculated are insensitive to the choice of collective variables). Section 3C describes the initial conditions used in the string simulations. In Sec. 3D we present the transition mechanism together with the corresponding free energy profiles and transition rates. Section 4 summarizes the accomplishments and the limitations of the present method, and in Sec. 5 we highlight key results from the myosin VI simulations.
Additional validation of the present methodology using the simple test case of the alanine dipeptide in vacuum is given in the supplementary materials.19
METHODOLOGY
The calculation by the string method of the free energy and the reaction rate associated with an optimized transition path proceed in several steps. First, a set of collective variables that are sufficient to describe the transition are selected. Initial values for the these collective variables (initial “string” of replicas) are determined from a minimum energy path (MEP) calculated between the endpoint structures using the zero-temperature string method in the full space of Cartesian atom positions.3, 20 With the string method in collective variables5 and starting from the initial string, the replicas are allowed to “relax” in the direction of the negative gradient of the free energy, with the arc-length between adjacent replicas kept approximately constant. The final converged string corresponds to an MFEP between the endpoint states in the collective variable space. Starting from the MFEP, the free energy profile and rate of the reaction can be calculated using the finite-temperature string method21 and milestoning,9, 18 respectively. Each step of the methodology is outlined below. Because the zero-temperature string method is conceptually similar to the string method in collective variables, it is summarized in the supplementary materials.19 Appendix A describes some technical calculations. Appendix B provides additional discussion of sources of errors in the finite-temperature string method, and in Appendix C we present a validation of the transition state obtained from one of the present simulations using an ensemble of unbiased trajectories.
Collective variables
An essential aspect of the present method is the selection of a set of collective variables that are appropriate for describing the transition of interest. Collective variables are scalar functions of the atomic coordinates of the system that characterize its state at a coarse-grained level. Examples are the Cartesian positions of representative atoms, the positions of the center of masses of groups of atoms, dihedral angles, and interatomic or atomic-group distances. The starting point for finding a suitable set of collective variables is the assumption that the transition path can be described by specifying the positions of a relatively small number of atoms. Restrained targeted molecular dynamics (RTMD) (Ref. 22) is used to find a small set of atoms, such that applying RTMD forces to the atoms in this set steers the converter structure from one conformation to the other. This set of atoms, denoted the “resolving set (RS),” is then used to define CVs. Letting x denote the Cartesian positions of all the atoms in the system, we identify a set of K CVs, which we denote by .
The identification of the resolving set and the construction of collective variables for the converter of MVI are described in detail in Sec. 3B. The specific CVs sets used are given in Tables 2, 3.
Table 2.
Atoms used to define the set of collective variables CVS1. For each atom, three CV are defined, which correspond to the Cartesian x, y, and z positions. Atoms are specified by their residue ID and the atom type. Atom positions on the converter structure are shown in Fig. 1. The total number of position CV is 177.
| CV description | Residue ID(s) | Atom type(s) | CV indices (number of CV) |
|---|---|---|---|
| Helix 1 position | 711–720 | CA | 1–30 (30) |
| Helix 4 position | 761–769 | CA | 31–57 (27) |
| Converter insert position | 774–788 | CA | 58–102 (45) |
| Loop 4 conformation | 770–773 | N, C, CA, O | 103–150 (48) |
| Sidechain position | R708 | CZ | 151–153 (3) |
| Sidechain position | E713 | CD | 154–156 (3) |
| Sidechain position | Y718 | CZ | 157–159 (3) |
| Sidechain position | F739 | CZ | 160–162 (3) |
| Sidechain position | Y749 | CZ | 163–165 (3) |
| Sidechain position | F751 | CZ | 166–168 (3) |
| Sidechain position | F758 | CZ | 169–171 (3) |
| Sidechain position | F766 | CZ | 172–174 (3) |
| Sidechain position | M770 | SD | 175–177 (3) |
Table 3.
CV in set 2. Each COM-position entry corresponds to three Cartesian positions. Residue numbers followed by an asterisk indicate that only the sidechain atoms were included in the CV definition (the backbone atoms C, N, CA, and O were excluded). CVs are indicated on the converter structure in Fig. 1b. The total number of CV is 51.
| CV description | CV type | Atoms involved | CV indices (No. of CV) | Equivalent CVs in CVS1 |
|---|---|---|---|---|
| H1 position | COM-position | Residue 711–715 | 1–3 (3) | 1–30 |
| COM-position | Residue 716–720 | 4–6 (3) | ||
| H2 position | COM-position | Residue 723–728 | 7–9 (3) | None |
| H4 position | COM-position | Residue 761–765 | 10–12 (3) | 31–57 |
| COM-position | Residue 766–770 | 13–15 (3) | ||
| CI position | COM-position | Residue 774–781 | 16–18 (3) | 58–102 |
| COM-position | Residue 782–788 | 19–21 (3) | ||
| Sidechain position | COM-position | Residue 718* | 22–24 (3) | 157–159 |
| Sidechain position | COM-position | Residue 722* | 25–27 (3) | None |
| Sidechain position | COM-position | Residue 739* | 28–30 (3) | 160–162 |
| Sidechain position | COM-position | Residue 749* | 31–33 (3) | 163–165 |
| Sidechain position | COM-position | Residue 751* | 34–36 (3) | 166–168 |
| Sidechain position | COM-position | Residue 758* | 37–39 (3) | 169–171 |
| Sidechain position | COM-position | Residue 766* | 40–42 (3) | 172–174 |
| Sidechain position | COM-position | Residue 770* | 43–45 (3) | 175–177 |
| L4 conformation | Dihedral (ϕ) | M770C∕K771N∕K771CA∕K771C | 46 (1) | 103–150 |
| Dihedral (ψ) | K771N∕K771CA∕K771C∕S772N | 47 (1) | ||
| Dihedral (ϕ) | K771C∕S772N∕S772CA∕S772C | 48 (1) | ||
| Dihedral (ψ) | S772N∕K772CA∕K772C∕D773N | 49 (1) | ||
| Dihedral (ϕ) | S772C∕D773N∕D773CA∕D773C | 50 (1) | ||
| Sidechain position | COM distance | Residues 708*, 713* | 51 (1) | 151–156 |
The minimum free energy path and its interpretation
An MFEP is a path of steepest descent on the free energy surface associated with the collective variables, scaled by a metric tensor that arises from the curvilinear nature of the collective variables, and guarantees that the location of the MFEP is invariant to nonlinear transformations of these variables.5 More precisely,
| (1) |
In Eq. 1, M(θ)∇G(θ) denotes the vector with Cartesian components,
| (2) |
G(θ) is the free energy associated with the collective variables,
| (3) |
and M(θ) is a tensor given by
| (4) |
In Eq. 3, β = 1∕kBT, where kB is Boltzmann’s constant and T is the temperature, and 〈 · 〉 denotes canonical average; in Eq. 4, mk are the masses of the atoms, the sum is taken over all the coordinates of all the atoms in the system, and denotes the conditional average . The estimation of G(θ) and M(θ) in the string method and the calculation of an MFEP are explained in Sec. 2C. The significance of the MFEP defined here is established in transition path theory (TPT).14, 15, 23 TPT analyzes the statistical mechanics properties of the reactive trajectories—those by which the transitions from one endpoint structure to the other actually happen—and gives expressions for the probability density and current of these trajectories.
Central in the expressions for both the probability density and the current is the committor function q(x, p) (pfold in protein folding studies24) which gives the probability that, if one initializes the system at position x with momentum p, the system will go to one end-point structure (the product) rather than the other (the reactant). In principle, the function q(x, p) is an ideal reaction coordinate for describing a transition. However, q(x, p), per se, gives limited insight into the transition mechanism because it does not provide direct information on the essential variables that govern the transition.24, 25, 26 Although q(x, p) satisfies a closed-form equation of Liouville or Fokker-Planck type, this equation cannot be solved directly in high dimensional systems. The equation for q(x, p) can, however, be used as the basis for meaningful approximations. Under the assumptions,
the committor function can be parametrized approximately as a function of the collective variables, i.e., for some function Q, and
projected in the space of collective variables, most of the probability flux of the reactive trajectories goes through one narrow channel (or a few channels separated by barriers much higher than kBT), referred to as transition tube(s),
it can be shown that, for the MFEPs defined by Eq. 1,5, 14, 15, 23
the MFEPs lie at the center of the transition tubes;
- locally around the MFEP, the isosurfaces of the committor function (isocommittor surfaces) can be approximated by the surfaces defined by
(5) - the value of the committor function along the MFEP is
(6)
In Eqs. 5, 6, θ(α) with α ∈ [0, 1] denotes a para- metrization of the MFEP [i.e., for every α ∈ [0, 1], θ(α) is a point along the MFEP]; the prime denotes derivative with respect to α; are the elements of the matrix M−1(θ); the scalar m(α) is defined as
| (7) |
and F(α) is the free energy defined as
| (8) |
where g(x, α) is a shorthand notation for the left hand side of Eq. 5,
| (9) |
The free energy F(α) [not to be confused with the free energy as a function of the collective variables G(θ) defined in Eq. 3] is the free energy as a function of the committor used as the reaction coordinate, since, by Eq. 5, g(x, α) = 0 approximates the isocommittor surface on which . As such, F(α) plotted vs Q(θ(α)) should be insensitive to the choice of collective variables, provided only that these variables are adequate; i.e., that is a good approximation of the actual committor function q(x, p). The free energy F is a one-dimensional function, whereas G(θ) of Eq. 3 is K-dimensional, with K equal to the number of collective variables. Profiles of G are evaluated only on the corresponding MFEP and have only local information about the free energy values for points not on the MFEP (see conditions 1 and 2 above). In contrast to G, the reaction free energy F maps the entire transition tube onto a single curve. For this reason, we define the function F(α) as the free energy profile of the reaction. In the special case that the transition tube is extremely narrow, or has uniform cross-sectional volume along the path, G ≃ F. We will show that this is not the case in the present study (see Sec. 3D5). Additional details on the calculation of free energy profiles and rates of transition can be found in the TPT papers14, 15, 23 and in Ref. 5. An alternative method to compute one-dimensional free energy profiles was proposed by Krivov and Karplus.27, 28 The method uses long MD trajectories during which multiple transition events are observed, in combination with the minimum-cut procedure (see Appendix D).
Assumptions (i) and (ii) above formalize the property that the collective variables are “good” variables to describe the transition. In principle, assumption (i) can be checked a posteriori by a committor test. This test amounts to launching trajectories from the isosurface on which and checking that these trajectories “commit” to the two endpoint structures with equal probability. The committor test can be computationally too costly for diffusive systems because (1) trajectories take a very long time to commit (e.g., micro- to milliseconds) and (2) a very large number of trajectories is needed to ensure a good statistical sample. For these reasons, we are unable to perform a full committor test for the present calculations. Instead, we perform a less stringent test: starting from configurations chosen randomly from a putative transition state ensemble, we launch a collection of relatively short unbiased MD trajectories and examine the distribution of the reaction coordinate values at the end of the simulations. We find that 41% and 59% of the trajectories terminate on the reactant and product sides along the reaction coordinate, respectively, although none of the trajectories reach the reactants or the products. The above “splitting” probability is considered sufficiently close to the optimal 50%∕50%, because the committor values are known to change rapidly in the vicinity of a transition state.29 Details of the calculations can be found in Appendix C.
In addition, we resort to an indirect qualitative strategy to validate assumption (i). We compute the reaction free energy, Eq. 8, using two different sets of collective variables. If the results are similar for the two sets, as we find for the present study (see Sec. 3D4), it is likely that either set is adequate to describe the transition. Note that, in contrast to F(α), the free energy G in Eq. 3 depends on the choice of collective variables and is more difficult to use for cross-validation.
Assumption (ii) can be tested a posteriori by examining the transition tubes corresponding to the MFEPs, as discussed in Sec. 3D.
String method in collective variables
The string method in collective variables was introduced in Ref. 5. It has been applied to an isomerization reaction in the alanine dipeptide in vacuum5 and in explicit solvent,17 the insertion of a coarse-grained model of a protein into a lipid bilayer,18 and to the collapse of a hydrophobic chain of beads, in which water molecules were represented explicitly and hundreds of thousands of collective variables were used.16 A number of closely related variants of the method were introduced recently.30, 31, 32, 33 Here we give a brief account of the method we use and refer the interested reader to Refs. 5 and 17 for more details.
The string method in collective variable space is a generalization of the string method in the Cartesian space.3, 20 The essence of the method is to evolve a curve—the string—using −M(θ)∇G(θ) as a force while maintaining a prescribed parametrization of the curve. If we parametrize the string as θ(α) with α ∈ [0, 1], this evolution can be written as
| (10) |
where γ is an adjustable friction coefficient (discussed below), the dot and the prime denote differentiation with the respect to tand α, respectively, and λθ′ is a Lagrange multiplier term added to enforce a specific parametrization of the string (in the present case, that the string have uniform arc-length increments; i.e., |θ′| = constant). Note that the steady-state solution of Eq. 10 satisfies λθ′ = −M(θ)∇G(θ), i.e., it is an MFEP according to the definition of Eq. 1.
To integrate Eq. 10, the string is discretized into N + 1 representative “images:”
| (11) |
At each iteration, these images are evolved in the following two steps:
- Evolution step. Each image is evolved independently of the others using
(12) - Reparametrization step. The images are reparametrized to enforce equal arc-length increments, which requires that
where | · | denotes the Euclidean norm.(13)
The evolution step Eq. 12 uses a forward Euler discretization of Eq. 10 with the Lagrange multiplier term neglected. [The computation of M(θn(t))∇G(θn(t)) is described below, and the numerical values for Δt and γ are specified in Sec. 3D1.]
The reparametrization step represents the action of the Lagrange multiplier term in Eq. 10. It is performed in two steps. First, we calculate the piecewise linear function ℓ(α), such that ℓ(0) = 0 and its values at α = n∕N with n = 1, …, N are
| (14) |
Second, we compute the images at new parameter values specified by
| (15) |
using linear interpolation. These new images satisfy Eq. 13 approximately. Although arbitrary accuracy can be achieved by applying the reparametrization step iteratively, we only used one iteration, after which the constraint was satisfied to greater than 1% accuracy.
For a string that is far from the MFEP (as would be observed in early stages of the string calculation), the reparametrization correction is small compared to the evolution step. On the other hand, after the string has converged to the MFEP, the reparametrization correction exactly cancels the evolution step, so that the string images remain stationary.
The evaluation of the terms M(θn) and ∇G(θn) is performed using MD sampling with restraints as follows. To each image θn, we assign an independent all-atom replica of the system, which we simulate by MD with the restraining potential
| (16) |
The force constants ki should be chosen such that the constraint is approximately satisfied during the MD simulation. In practice, however, it may be advantageous to use low force constants to accelerate equilibration of the replicas during MD. In particular, low force constants permit the use of Hamiltonian replica exchange (REX) (Refs. 34 and 35) to increase conformational sampling, as will be illustrated in Sec. 3D3. The use of low force constants, however, requires correcting the free energy gradients computed from the simulations, e.g., with the umbrella integration (UI) method.36
Denoting by xn(t) the MD trajectory of the replica assigned to image θn, the ith component of the free energy gradient ∇G(θn(t)) is estimated as
| (17) |
and the (i, j)th entry of the tensor M(θn(t)), as
| (18) |
Equations 12, 17, 18 suggest that γ−1Δt must be small enough so that the solution of Eq. 10 is stable and accurate; yet, Δt must be large enough so that the time averages in Eqs. 17, 18 are converged. This compromise can be achieved by choosing the friction coefficient γ sufficiently large. It was shown in Ref. 17 that for large values of γ, the integration step Δt can be made as low as that of a single MD evolution step (1-2fs) without compromising the accuracy of the MFEP. For γ large enough, the images θn evolve much more slowly than the corresponding MD replicas and effectively “feel,” via Eqs. 12, 17, 18, the average effect of the MD replica. The averages in Eqs. 17, 18 need not be converged to attain convergence of Eq. 12 to the MFEP. Furthermore, even for somewhat smaller values of γ (with Δtsufficiently small), the steady-state solution of Eq. 12 will oscillate around the MFEP, but will not diverge from it. The approximate values for γ and Δt used in the present simulations are 1500 ps−1 and 20 fs, respectively (see Sec. 3D1).
In the present simulations, the averages in Eqs. 17, 18 are computed using either 10 or 15 MD steps, depending on the simulation (see Sec. 3). The images are updated according to Eq. 10, and the string is reparametrized. Evolving and reparametrizing the string once in every several MD iterations only incurs a small additional cost compared to a regular MD simulation. Moreover, the MD replicas can be evolved in parallel using different sets of central processing units (CPUs) for each.
Convergence of the string to the MFEP is assessed by monitoring the quantity D(t) defined as
| (19) |
which measures the root-mean-square distance (RMSD) by which the images along the string have moved from their initial positions. Convergence is assumed after D(t) reaches a plateau (see Sec. 3).
Calculation of free energies and mean first passage times (MFPTs)
Free energy of the collective variables along the MFEP
Once the string has converged to the MFEP, the images θn are fixed, and we can compute the approximate gradient of the free energy, Eq. 3, at these images using
| (20) |
where xn(t) denotes the trajectory of the MD replica evolving in the potential with the restraint term of Eq. 16 and T is taken large enough for the average to converge. The free energy G(θ), relative to the endpoint value G(θ0) along the MFEP, can then be obtained by numerical integration. The trapezoidal rule yields
| (21) |
It is shown in Ref. 5 that the errors due to the use of a restraint instead of a constraint in the approximation, Eq. 20, are of the order (βki)−1 (see also Sec. 3D3). Thus, if the force constants ki are chosen sufficiently large, Eq. 21 will yield an accurate free energy profile. In the present application, we found that convergence was difficult to achieve using Eq. 20 as written, and Hamiltonian replica exchange was employed with the MD simulations to improve sampling.
The REX employed herein is based on the replica-exchange umbrella sampling (US) algorithm, in which umbrella potentials corresponding to adjacent “windows” of a progress coordinate are exchanged “on-the-fly” during the simulation.34 Unlike the implementations in Refs. 34, and 37, 38, 39, which implement one-dimensional US, we use the multidimensional biasing potential of Eq. 16. The number of windows equals the number of string replicas, and the windows are centered on the string images θn. To use REX, the restrained MD simulations must be performed concurrently for each image, so that exchange moves between adjacent images may be attempted. Specifically, after a prescribed number of iterations, we attempt to switch the atomic coordinates of the MD replicas xn and xn + 1 that correspond to the neighboring images θn and θn + 1, respectively,
| (22) |
where n is chosen randomly from 0, 1, …, N. The acceptance probability of the move in Eq. 22 is computed according to the Metropolis criterion,
| (23) |
In Eq. 23, U(x, θ) is the restraining potential defined in Eq. 16 and pacc is the probability of accepting the move in Eq. 22. To achieve high-enough acceptance rates in REX, the force constants had to be lowered so that the conformational ensembles corresponding to adjacent images have sufficient overlap. To correct the gradients obtained using lower force constants, we employ the umbrella integration method36 as follows. For each window centered on θn, we have40
| (24) |
where Gn is an estimate of G corresponding to the window, Pn(θ) is the probability density of θ, and Cn is an unknown constant. Differentiation of Eq. 24 with respect to θj gives
| (25) |
Approximating Pn(θ) by a Gaussian of the form36
| (26) |
in which and σn, i denote the mean and the standard deviation of the time series , respectively, and substituting into Eq. 25 leads to
| (27) |
The estimates ∂Gn(θ)∕∂θj from all windows are combined according to
| (28) |
in which Tn is the number of integration steps in the window corresponding to θn.
The values of θ at which gradients of G(θ) were computed were obtained by linearly interpolating the original string θn onto a finer string θm, m = 1, …, M = 500. The free energy profiles were calculated using the trapezoidal rule, as in Eq. 21. The results were insensitive to values of M in the range 200–1000, similar to the conclusions in Ref. 36. The choice of REX parameters is described in Sec. 3D3.
Free energy as a function of the reaction coordinate
As explained in Sec. 2B, the free energy expressed in terms of the collective variables, G(θ), is not the same as the free energy along the parametric reaction coordinate, F(α), defined in Eq. 8. To compute F(α), we use the procedure introduced in Ref. 21. Once the string has converged to the MFEP, we associate a cell Bn with each fixed image θn. The cell Bn is defined by
| (29) |
Thus, Bn contains all the points in configuration space that are closest to image θn, according to the distances,
| (30) |
where θa and θb are arbitrary K-dimensional vectors. The cells Bn form a tessellation of the entire configuration space. If the tensor M is proportional to the identity, the distances reduce to the standard Euclidean distance.
For two adjacent images on the string, θn and θn + 1, the boundary between the corresponding cells, Bn and Bn + 1, is defined by
| (31) |
Using Eq. 30 with m=n + 1 and that M−1 = M−T, the square of Eq. 31 can be written as
| (32) |
This equation is a second-order finite-difference approximation to Eq. 5 evaluated at α = (n + 1∕2)∕N. Consequently, the boundaries of successive cells along the string are local approximations of the isocommittor surfaces at the MFEP. Equations 8, 9 imply that, for n = 1, …, N − 1, up to discretization errors of order 1∕N,
| (33) |
where πn is the probability to find the system in cell Bn at equilibrium, V(x) denotes the MD potential, Z is the configurational partition function, and Fn = F(α = n∕N). Equation 33 gives the following estimate for Fn in terms of πn:
| (34) |
As shown in Ref. 21, there is a simple procedure to compute the probabilities πn. First, we run independent MD simulations in each of the cells Bn and impose a “reflection” rule at the cell boundaries, in which all particle momenta are reversed to maintain the MD replica in its cell. Specifically, if (xn(t), pn(t)) denotes the position and momentum at time t of the MD simulation assigned to the replica in cell Bn, we set
| (35) |
where denotes the time-evolved value of (xn(t), pn(t)) after one MD step of size δt. Up to time discretization errors, the trajectories generated in this way sample the canonical distribution for the cell Bn. The test involved in Eq. 35 is a distance check, in accord with Eq. 30.
Let Nn, m denote the number of collisions the MD replica in cell Bn makes with the boundary of cell Bm during the MD simulation interval Tn. For a sufficiently large Tn, the quantity
| (36) |
gives an estimate of the rate of escape from cell Bn to cell Bm. At a statistical steady state, the conservation of probability requires
| (37) |
which can be solved for πn using the normalization condition . The free energy Fn ≈ F(α = n∕N) can then be computed from Eq. 34.
Transition rate between the initial and final states
To compute the transition rate, the free energy calculation method described in Sec. 2D2 can be combined with the version of Markovian milestoning proposed in Ref. 18, which builds on the original works in Refs. 9, 10, 41, and 42.
In Markovian milestoning, one calculates from each MD trajectory the index of the “milestone” that the trajectory crossed most recently; in the string method, the milestones are defined as the boundaries between the cells Bn defined in Eq. 29. The time-evolution of the index is approximated by a continuous-time Markov chain. To calculate the rate of transition, one needs to estimate the rate matrix of this chain. Markovian milestoning is similar to Markov state modeling (MSM) (Refs. 43, 44, 45, 46, 47, 48, 49, 50) using master equations. The main difference is that in Markovian milestoning, the system states (milestones) are hypersurfaces, whereas in standard MSMs, the states form a partition of the configuration space. We denote by a, b, … the indices of the milestones (not to be confused with the index n of the cells). It was shown in Ref. 18 that the rate of instantaneous transition from milestone a to milestone b (ka, b) can be estimated as
| (38) |
In Eq. 38, πn is the equilibrium probability to find the system in cell Bn computed from Eq. 37, is the total number of transitions from milestone a to milestone b observed in the MD simulation confined to cell Bn, is the total time during this simulation during which a was the most recent milestone visited by the system, and Tn is the total duration of the simulation confined to cell Bn.
Given an arbitrary milestone denoted by b*, the instantaneous rate matrix and the MFPTs to the milestone b* from the other milestones in the system, denoted by Tb,b* with b≠b*, satisfy the relationship
| (39) |
This equation is a standard result in the theory of Markov chains51 and its derivation in the context of milestoning can be found in Ref. 18. If the milestones a* and b* are chosen as the isocommittor surfaces for the transition between two metastable states of a system (e.g., A and B) with qa*≈0 and qb*≈1, then (Ta*,b*)−1is an estimate of the rate of transition from A to B. Use of an unrealistic low friction with the implicit solvent model (Sec. 3D1), as was done for improved sampling, is expected to result in an overestimate of the transition rate (see Sec. 4).
It was shown in Ref. 52 that the MFPT estimate is exact if the milestones are isocommittor surfaces for the transition. This condition will be satisfied approximately, provided assumptions (i) and (ii) in Sec. 2B hold, because in that case the boundaries of the cells Bn, which we use as the milestones, are approximations of the isocommittor surfaces.
APPLICATION TO THE MYOSIN VI CONVERTER
Preparation of simulation structures
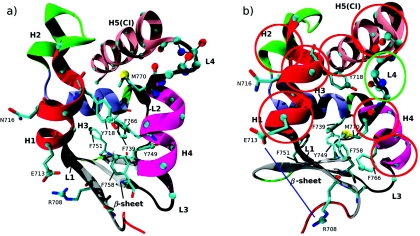
Crystal structures of MVI in the (R) and (PPS) conformations were obtained from the protein data bank (PDB entries 2BKH and 2V26, respectively). The resolution of the respective structures is 2.4 and 1.75 Å. Only residues 703–788, which correspond to the converter domain, were included. The R and PPS conformers are shown in panels (a) and (b), respectively, in Fig. 1. Atoms that form the basis for the collective variables defined in Sec. 3B2 and listed in Table 2 are shown as spheres. In the PPS structure, the atoms CD1 and ND2 in residue N716 were interchanged to optimize the local hydrogen bonding patterns. Assignment of histidine protonation states was based on a visual inspection of the local environment for each histidine residue. For both conformers, all histidines were singly protonated on the δ-nitrogen except for H776, which was singly protonated on the ε-hydrogen.
Figure 1.
VI converter in the R (a) and PPS (b) conformation. The secondary structure elements are helices 1–5 (H1–H5), loops 1–4 (L1–L4), and the β-sheet. We alternatively refer to H5 as the converter insert (CI) to emphasize that it is known to be present only in MVI (Ref. 53). The helices and loops are numbered in the order of increasing residue numbering. Atoms to which forces were applied in the RTMD or string simulations (see Tables 1, 2) are drawn as spheres. If forces were applied to a sidechain atom, the entire corresponding residue is shown. Atoms that are used to define the collective variables set CVS1 (Table 2) are shown as spheres. In (b), red circles are drawn approximately around subdomains that correspond to CV 1–21 in CVS2 (Table 3). The green oval is drawn around L4 and corresponds to the collective variables 46–50 in CVS2. The blue line corresponds to the distance CV 51 in CVS2.
The all-atom CHARMM22 topology and parameter files were used in the simulations. To approximate the effect of solvent, we employ the fast analytical continuum treatment of solvation (FACTS) model,54 which has been shown to yield accurate atomic solvation and pair interaction energies when compared with finite-difference Poisson–Boltzmann data. In applications, FACTS has been shown to maintain stable structures during long simulations (≈100 ns) of small proteins and has been implemented in CHARMM.55, 56
Prior to performing string calculations, each conformer was simulated for 60 ns by equilibrium MD in the canonical ensemble. The average backbone-atom RMSD of the simulation structures from the corresponding crystal structures is 1.6 and 1.25 Å for the R and PPS conformers, respectively, confirming that both converter domain structures are in metastable local minima. The RMSD between the backbone atoms in the x-ray structures is 4.2 Å, while that between the backbone atoms in the average MD structures is 3.9 Å.
Selection of collective variables
As explained in Sec. 2B, the quality of a given set of collective variables to describe a complex reaction can only be determined a posteriori, either by a committor test or by “cross-validating” the reaction free energy of the reaction rate computed using two or more sets of collective variables. In this section we propose a methodology to generate a priori candidate collective variables to describe conformational transitions in proteins.
Identification of a “resolving set” of atoms using RTMD
RTMD is closely related to the original TMD method.57, 58 The main difference is that targeting forces are applied in the form of a harmonic restraint, rather than a holonomic constraint.22 We apply RTMD forces only to the atoms in a putative RS starting with their positions in one structure to decrease the best-fit RMSD between this structure and the target structure. Let rrs∈R3N denote the vector containing the positions of the N atoms in the putative RS to which the RTMD forces are applied. The driving forces are derived from the potential
| (40) |
where k is the force constant and is the (fixed) value of the positions of the atom in the target structure. We start the simulation with rrs in the initial structure and set δ to the RMSD between rrs and . The value of δ is then decreased linearly to zero over ∼2 ns. After the zero value of δ is reached, the restraining potential U RTMD (rrs) is applied for ∼3 ns and then scaled linearly to zero over 1 ns, after which the system is allowed to relax for 1–3 ns. The RMSD between all heavy atoms in the relaxed structure and the target structure is taken as the indicator of the quality of our choice of the RS. The RTMD simulations performed in this study and the corresponding RSs are summarized in Table 1.
Table 1.
Summary of RTMD simulations. Residue numbers followed by an atom type indicate that only that atom was included. Residue numbers followed by “BB” indicate that the backbone atoms (N C O CA) were included. CHARMM atom nomenclature is used. “n∕a” indicates that the corresponding simulations were not performed. Important residues in the RS are shown in Figs. 1a, 1b. “RMSD (δ = 0)” is the minimum RMSD value observed after the target RMSD, δ, reaches 0, but before the forces are switched off. “RMSD (relaxed)” is the average RMSD value observed after the forces are switched off. RMSD values are computed using all heavy atoms. The force constant κ is given in units of kcal∕mol∕Å2. Simulation time is quoted in ns. For brevity, “P” denotes the “PPS” state. RMSD values are quoted in Angstroms.
| RMSD (δ = 0) | RMSD (relaxed) | Simulation time | |||
|---|---|---|---|---|---|
| RTMD | Resolving set (number of atoms) | κ | R→P∕P→R | R→P∕P→R | R→P∕P→R |
| 1 | 761–769 CA; 770–773 BB; | 0.5 | 4.2∕3.9 | (n∕a) | 2∕2 |
| 770 SD; 718 766 CG (28) | |||||
| 2 | 762–769 BB; 771–773 BB (44) | 0.5 | 3.8∕(n∕a) | (n∕a) | 2 |
| 3 | 761–769 711–720 774–788 CA; | 1.0 | 3.0∕3.4 | (n∕a) | 2 |
| 770–773 BB; 770 SD; 716 766 CG (38) | |||||
| 4 | 761–769 711–720 774–788 CA; | 1.0 | 1.75∕1.5 | 2.3∕1.65 | 6∕6 |
| 770–773 BB; 770 SD; | |||||
| 718 766 758 749 708 CZ (56) | |||||
| 5 | 761–769 711–720 774–788 CA; | 1.0 | 1.25∕1.26 | 1.60∕1.66 | 6∕10 |
| 770–773 BB; 770 SD; 713 CD; | |||||
| 718 766 758 749 708 739 751 CZ (59) | |||||
| 6 | 761–769 711–720 774–788 CA; | 1.0 | 1.26∕1.26 | 1.75∕1.45 | 6∕6 |
| 770–773 BB; 770 SD; 713 722 CD; | |||||
| 718 766 758 749 708 739 751 CZ (60) |
In the RTMD simulations, the was computed between the positions rrs and , after a best-fit orientation using the backbone atoms of helix 3 (H3) (see Fig. 1), which does not include any atoms from the RS. Because this orientation set and the RS are different, there is a net force and a net torque acting on the protein. To prevent the rigid-body motion of the simulation structures, the backbone atoms of H3 were restrained to their original positions with harmonic potentials of the form , where ri denotes the position of atom i, k equals 1 kcal∕mol∕Å2, and the superscript 0 refers to the initial position. These restraints are very unlikely to affect the path of the transition because (i) the restrained helix is relatively far away from the region in which the two endpoint structures differ appreciably and (ii) the RMSD between the helix backbone in the two conformations is only 0.24 Å. These two facts indicate that the helix is not involved in the conformational change and remains intact during the transition.
The first trial RS was chosen based on a visual inspection of the endpoint structures shown in Fig. 1. Two prominent qualitative differences between the structures are (i) the orientation of helix 4 (H4), which is vertical and approximately perpendicular to the β-sheet in the R structure, and inclined at ≃45o to the β-sheet in the PPS structure, and (ii) the conformation of loop 4 (L4), which is α-helical in the R structure, and unwound in the PPS conformation. In addition, going from the R structure to the PPS structure, H4 appears to rotate about its axis, moving the sidechains of M770 and F766 from the interior to the outside of the converter domain (Fig. 1). Based on these observations, we assumed that much of the conformational transition could be accounted for by the movement of H4, L4, M770, and F766. Therefore, the first RS includes the Cα atoms of H4 and L4, the Sδ atom of M770, and the Cγ atom of F766. Because we expect that the movement of M770 would involve significant motion of Y718 due to steric clashes between the two residues, we also included the Cγ atom of Y718 in the RS.
Starting from the first trial RS, which contained 28 atoms (listed as RTMD 1 in Table 1), additional atoms or domains were added until the heavy-atom RMSD between the final RTMD simulation structures and the corresponding the target structures was below 2.0 Å in both directions. The smallest tested RS that satisfies these criteria was used in RTMD simulation 5 in Table 1. It is composed of 59 atoms, which are drawn as spheres in Fig. 1 and listed in Table 1. This RS includes atoms from helices H1 and H5 as well as from several aromatic residues in the core of the converter domain.
We note that the RS found by the above procedure is unlikely to be unique. Furthermore, the composition of the RS will depend on the RMSD criterion above, such that a lower RMSD would probably require a larger RS. Therefore, although the search for the RS is systematic, the final choice of RS is somewhat subjective.
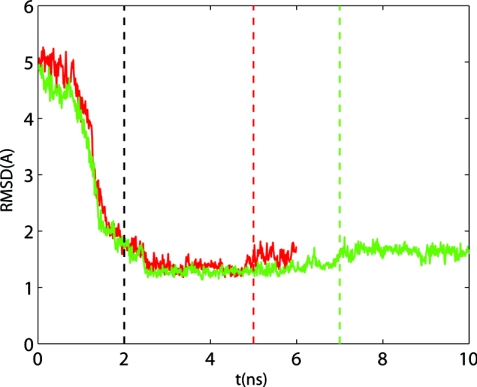
The evolution of the heavy-atom RMSD in RTMD 5 is shown in Fig. 2. The equilibration (with δ=0) and relaxation (forces turned off) phases were each 2 ns longer for the PPS→R transition to determine whether the final RMSD could dip below the R→PPS value (≃1.6 Å). A comparison of the final RMSD values from the PPS→R and R→PPS simulations shows that the extra 4 ns made no difference.
Figure 2.
Evolution of the RMSD of the heavy atoms between the RTMD simulation 5 structures and the corresponding target structures. Red solid line R structure (PPS target); green solid line PPS structure (R target); dashed vertical lines mark the times at which δ reaches 0.0 (black dashed line), the RTMD forces are switched off for the R→PPS simulation (red dashed line) and the PPS→R simulation (green dashed line).
The fact that the RMSD values (≃ 1.6 Å) between the final relaxed RTMD structures and the target structures are lower than the maximum RMSD values from the NVT simulations of the R and PPS structures (2.6 and 2.0 Å, respectively, see Fig. 2) strongly suggests that each simulation structure has reached a stable conformation near the corresponding target structure.
Because applying targeting forces only to the atoms in the RS used in the RTMD listed as number 5 in Table 1 is sufficient to enforce a complete conformational change, we assume that the mechanism of the transition can be understood by considering only the positions of these atoms. Two sets of collective variables used for the string simulations in this study were chosen on the basis of the RS used in RTMD 5.
First set of collective variables (CVS1)
A simple set of collective variables that can be constructed from the RS of RTMD 5 consists of just the positions of the atoms in the RS. Specifically, given the set of 59 atomic position triplets with i = 1, 2, …, 59, one can define a set of 3 × 59 = 177 CVs,
| (41) |
A serious drawback of this definition, however, is that the variables are not invariant under rigid-body translation or rotation of the simulation system. To guarantee rigid-body invariance of the CV defined above, the atomic positions in Eq. 41 were expressed in local coordinates as follows. A local frame of reference was constructed based on the positions of all atoms in H3 (this helix was restrained in the RTMD simulations). First, a mass-weighted 3 × 3 correlation tensor was computed as
| (42) |
In this equation, N is the number of atoms that comprise H3, rn, i is the ith coordinate of the atom indexed by n (i.e.,rn, 1 = xn, rn, 2 = yn, rn, 3 = zn, if [xn, yn, zn] are the x, y, and z positions of atom n), is the COM position vector of the N atoms, and mn is the mass of atom n. Ci, j is symmetric positive definite and therefore has three real eigenvalues, λi, i = 1, 2, 3, with three corresponding eigenvectors, vi, that are orthonormal (vi·vj=δij). These eigenvectors are taken to be the basis vectors of a moving coordinate frame in which the positions CV are computed. To ensure right-handedness of the coordinate frame, one of the eigenvectors occasionally needed to be inverted (vi→−vi) during the MD simulations. Additional constraints that guarantee the uniqueness of the computed coordinate frame and the details of computing the derivatives of the position CV expressed in a local frame of reference are given in Appendix A. The set of positions CV defined above is denoted as CVS1.
The positions CV expressed in the local reference frame are invariant with respect to rigid-body motion of the simulation system. Although such motions change the position vector relative to the absolute (simulation) frame, the position vector remains the same in the local frame, because both the frame and the rest of the molecule undergo the same rigid-body motion. We note that other methods of avoiding the change in CV due to rigid-body motion exist, such as those based on simple harmonic restraints,59 Eckart constraints,60, 61, 62 or moment of inertia tensor constraints.63 Each method, including ours, comes with disadvantages, such as additional complexity of implementation, or approximation in the force calculations. In the present simulations the eigenvectors of Ci, j were always unique, which ensured an unambiguous definition of the local frame. However, this will not be the case for some molecular geometries, such as those in which the atoms that define the coordinate frame have internal symmetry, such as backbones of α-helices. (In this case, one principal vector will be directed along the axis of the α-helix, but the two remaining vectors are unique only up to a rotation in the plane perpendicular to the first vector). In addition, coordinate frame vectors defined on the basis of very flexible bodies may fluctuate strongly during MD simulation, which could render any function of these vectors (such as positions) effectively ill-defined, and lead to instabilities if forces are applied based on these functions. Thus, the choice of local frame must be made with caution and may require experimentation.
We note that Ci, j can be related to the moment of inertia tensor,
| (43) |
by Ci, j = I*δi, j − Ii, j, where . Since the vectors vi are orthonormal, they also diagonalize I*δi, j and, consequently, Ii, j. Thus, the vectors vi are also eigenvectors of the moment of inertia tensor Ii, j (although the corresponding eigenvalues will be different).
The collective variables CVS1 defined in this subsection are listed in Table 2 and shown in Fig. 1.
Second set of collective variables (CVS2)
To cross-validate the results using the strategy explained in Sec. 2B, we constructed an additional set of collective variables, hereafter referred to as CVS2. In this set, the number of collective variables was reduced from 177 to 51 by first representing several groups of atomic positions used in CVS1 by the position of their COM expressed in local coordinates as explained above for CVS1 (see CV 1–21 in Table 3). In addition, the positions of several atoms in CV1 were replaced by five dihedral angles and one distance between the COMs of two sets of atoms (see CV 46–51 in Table 3).
Generation of initial conditions
The string method in collective variables described in Sec. 2C requires an initial string [i.e., a value for each θn(0)] and n all-atom configurations of the converter for the estimation of M(θn(t)) and ∇G(θn(t)) [see Eq. 12].
These initial conditions were obtained from MEPs generated using the zero-temperature string method in Cartesian coordinates (ZTS), which was implemented in CHARMM following Ref. 20. Because the ZTS method is conceptually and algorithmically very similar to the string method in collective variables described in Sec. 2C, with the mean force ∇G(θ) and the tensor M(θ) replaced by the atomic force, ∇V(x), and the inverse of the mass matrix, respectively, we refer the reader to the supplementary materials for full details.
ZTS was used to generate two MEP from which the initial conditions, described above, were computed. The purpose of generating two initial paths was twofold. First, it allowed us to investigate the extent to which the choice of the initial condition affects the computed free energy profile. We found a difference of several kilocalories per mole in the free energy barriers that correspond to the two initial paths, indicating a significant effect (see Sec. 3D1). Second, computing the free energy along two different paths provides a test of the accuracy of the calculation: since the endpoints of both paths correspond to the same metastable states, the free energy difference between the endpoints should be independent of the path. In practice, errors arising from the discretization of the string or insufficient sampling may lead to different free energy values. The magnitude of the difference is a measure of the accuracy of the computed free energy. The first MEP (referred to as MEP1), resolved using 256 replicas, was generated in seven cycles, starting from the two endpoint (R and PPS) structures. In each cycle, a linear interpolation in Cartesian space that doubles the number of replicas is performed, followed by 100 iterations of the ZTS method. Each iteration of the method consists of 20 steps of minimization using the steepest descent minimizer in CHARMM, followed by a reparametrization step, to enforce Eq. 13 with θ replaced by x (see supplementary materials).
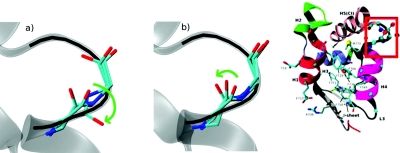
The second MEP (referred to as MEP2) was constructed by changing the direction of rotation of the dihedral angles in a flexible loop (see Fig. 3). In MEP1, the backbone oxygen of residue K771 (indicated by a green arrow) rotates to the “outside,” while in MEP2, it passes “under” the upper part of L4 (residue S772). A four-replica path was taken at the end of the first cycle in the generation of MEP1. The two intermediate structures were modified manually to change the direction of loop torsion. This path was then refined to 256 replicas, as described for MEP1.
Figure 3.
Conformational change in L4 in zero-temperature path MEP1 (a) and MEP2 (b). The converter in the R conformation is shown in transparent gray. For each case, the R, PPS, and one intermediate conformation of loop 4 are shown. The directions of loop torsion are shown by green arrows. The inset indicates the location of L4 in the converter domain.
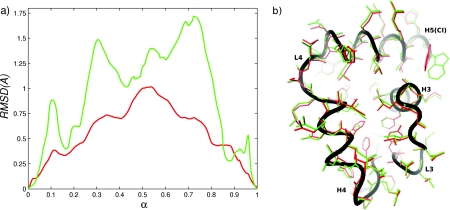
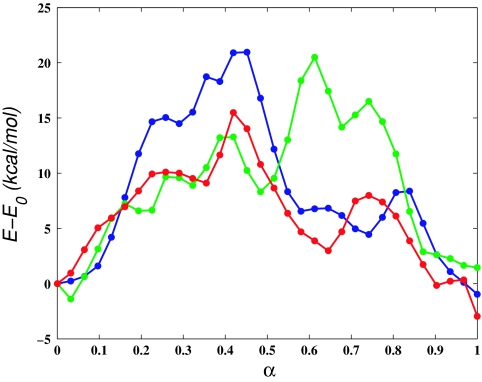
To quantify the difference between MEP1 and MEP2, we computed the RMSD between corresponding structures along the two paths, using all atoms and using only the atoms that belong to L4. The RMSD plots are shown in Fig. 4a. The difference in the configurations of L4 is more pronounced than the overall (all-atom) difference between the structures. This is expected because only the coordinates of L4 were modified directly in the construction of MEP2. However, the all-atom RMSD between MEP1 and MEP2 (maximum of 1 Å at α ≃ 0.5) suggests that the changes made to L4 propagate through the entire converter domain. In Fig. 4b we have superposed structures from MEP1 and MEP2 at α = 0.65 after a best-fit alignment.62 The figure makes clear that differences between the MEPs are not limited to L4, but are present throughout the entire converter structure. The potential energy along MEP1 and MEP2 is shown in Fig. 5. The figure indicates that at α ≃ 0.35 and α ≃ 0.65 MEP1 is higher in energy than MEP2 by ≃40 kcal∕mol. By examining the individual contributions to the total effective potential energy [i.e., bond, angle, linear and improper dihedral, electrostatic, van der Waals (vdW) and solvation energies], we found that most of the difference arises from differences in the dihedral and vdW energy terms. Figure 5 shows that if the dihedral and vdW energy terms are omitted, the profiles corresponding to MEP1 and MEP2 are very similar (the contributions of the two terms are approximately of the same magnitude). To see whether the differences in the energies arise primarily from differences in the conformations of L4, we computed the matrix of interaction energies between all pairs of residues at α = 0.65. We found the difference in the interaction energies between L4 and the rest of the converter to be ≃6 kcal∕mol (compared with the total energy difference of ≃40 kcal∕mol). Furthermore, the difference in the interaction energies was significant for many residue pairs throughout the converter domain. These findings indicate that MEP1 is a higher-energy path with the higher interaction energies not localized in a specific region of the converter (e.g., L4). Despite the ≃40 kcal∕mol differences in the potential energies between the MEPs at α = 0.65, Fig. 4b shows that most of the residue sidechains occupy similar positions and suggests that the origin of the differences in the energies between MEP1 and MEP2 is rather subtle (excluding L4).
Figure 4.
(a) RMSD between corresponding replicas from MEP1 and MEP2: red solid line computed using all atoms; green solid line computed using atoms of L4. (b) Superposition of structures from MEP1 and MEP2 at α = 0.66 (replica 170 of 256); red: MEP1; green: MEP2; black: backbone from MEP2.
Figure 5.
(a) Potential energy along the initial paths calculated using the zero-temperature string method (ZTS). MEP1: Red solid line iteration 400, 32 replicas; green solid line iteration 500, 64 replicas; blue solid line iteration 600, 128 replicas; magenta solid line iteration 700, 256 replicas; (magenta ○––) iteration 700, 256 replicas; energy from dihedral angles and van der Waals interactions excluded. MEP2: black solid line iteration 700, 256 replicas; (black ○––) iteration 700, 256 replicas; energy from dihedral angles and van der Waals interactions excluded.
Prior to running simulations using the string method in collective variables, the resolution of MEP1 and MEP2 was decreased from 256 to 32 replicas to reduce the computer cost of simulation. The resulting coordinate sets were used to calculate the initial values of the collective variables in CVS1 and CVS2 and to initialize the restrained MD simulations required for the estimation of M(θn(t)) and ∇G(θn(t)). The reduction in resolution is justified because the number of dimensions of the CV spaces (177 and 51 for CVS1 and CVS2, respectively), which contain the respective MFEPs, is much lower than the dimensionality of the full Cartesian space (4326). Consequently, the free energy landscape in the space of CV will be much smoother, requiring fewer discretization points. Furthermore, after the string has converged to the MFEP, the resolution can be increased by interpolation to improve the accuracy of discretization, as performed in Sec. 3D3. Animations of MEP1 and MEP2 can be found in the supplementary materials.19
Minimum free energy paths, free energies, and rates
Calculation of the MFEPs
To compute MFEPs, three simulations were performed using the string method in collective variables, as summarized in Table 4 (S1–S3). Each simulation was performed using a string discretized into 32 images, with one MD replica assigned to each image, using 1–4 processors per replica, so that the total CPU requirement was between 32 and 128 CPUs. Each replica was simulated in the NVT ensemble at 300 K using the Langevin dynamics thermostat coupled to heavy atoms using a friction constant of 1 ps−1. With this value of the friction constant, the temperature computed from the MD simulations fluctuated around 300K with a standard deviation of 6 K (computed over 20 ns of simulation). Covalent bonds to hydrogen atoms were constrained with SHAKE. The FACTS model was used to approximate the effects of solvent.54 The approximate time required to integrate 1 ns of MD was 15 CPU-core-hours per replica using a multiprocessor cluster equipped with quad-core Intel Xeon CPUs with the InfiniBand interconnect. Thus, simulation S1 (see Table 4) running on 32 quad-core processors of comparable speed (128 cores in total) would take 6 days.
Table 4.
Summary of string simulations performed in this study. Simulations G2fr and G3fr were performed with REX (see text). For simulations G2f10 and G3f10, all force constants in the restraining potential in Eq. 16 were increased by a factor of 10, as described in the text. Simulation durations correspond to the different procedures associated with the particular type of simulation (see text for details).
| Simulation index | CV set | Initial path | Number of images∕cells | Simulation duration (ns) |
|---|---|---|---|---|
| S1 | CVS1 | 1 | 32 | 36 |
| G1c | CVS1 | 1 | 32 | 20 |
| F1 | CVS1 | 1 | 32 | 30 |
| S2 | CVS2 | 1 | 32 | 40 |
| G2c | CVS2 | 1 | 32 | 20 |
| G2f | CVS2 | 1 | 128 | 15 |
| G2fr | CVS2 | 1 | 128 | 20 |
| G2f10 | CVS2 | 1 | 128 | 15 |
| F2 | CVS2 | 1 | 32 | 40 |
| S3 | CVS2 | 2 | 32 | 49 |
| G3c | CVS2 | 2 | 32 | 20 |
| G3f | CVS2 | 2 | 128 | 15 |
| G3fr | CVS2 | 2 | 128 | 20 |
| G3f10 | CVS2 | 2 | 128 | 15 |
| F3 | CVS2 | 2 | 32 | 30 |
For the string simulations using CVS1, the force constant in the restrained dynamics Eq. 16 was set to 1.0 kcal∕mol∕Å2 for all CVs. For each replica on the string, ten MD steps were performed to compute the average force and tensor M, which corresponds to Δt=20 fs in Sec. 2C. The CV values were updated using Eqs. 12, 13. The friction coefficient γ was set to 1673 ps-1. This value corresponds to five times the minimum value of γ for which γ−1Δt results in stable integration of Eq. 12 (determined by trial and error). In view of the Einstein relation for the Brownian motion (D = kBT∕mγ),64 in which m represents particle mass and D is the coefficient of diffusion of the particle, the need to use a large value for γ in the string simulation indicates a low rate of diffusion of the string on the landscape of the free energy G(θ) defined by Eq. 3, as would be expected for the evolution of a coarse-grained representation of the system.
For the string simulations with CVS2, the force constants in Eq. 16 were set to 1.0 kcal∕mol∕Å2 for position CVs and distance CVs and to 10.0 kcal∕mol∕rad2 for dihedral angle CVs. The average force on each CV was computed after every 15 MD steps, which corresponds to Δt = 30 fs. γ was set to 1255 ps-1, determined by trial and error as for simulations with CVS1.
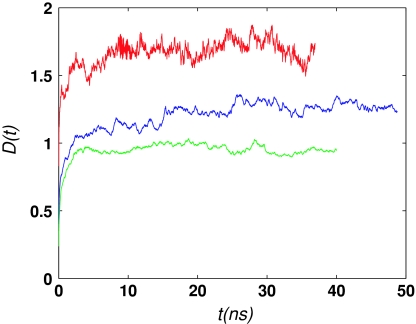
In each simulation, the string was evolved from the initial condition until convergence to the MFEP was obtained, according to Eq. 12. Figure 6 shows the evolution of D(t) in simulations S1–S3 (Table 4). Simulation S3 was run longer (49 ns) than either S1 (36 ns) or S2 (40 ns) to ascertain that D(t) was not continuing to increase. Since D(t) is a measure of the distance that a path has traveled from the initial path, the different plateau values in Fig. 6 corresponding to the simulations S1–S3 reflect the different distances between the MFEPs and the respective MEPs. Although simulations S1 and S2 were initialized from the same initial path, they employ different collective variables (different both in type and number), which is likely to be the reason for the difference in the respective plateau values. In addition, the different plateau distances between the MFEPs and the MEPs may be related to the different widths of the corresponding transition tubes (discussed in Sec. 3D4), with MFEP S1 having the widest transition tube and MFEP S2, the narrowest.
Figure 6.
Convergence of string simulations (see Table 4) monitored by the evolution of D(t) [Eq. 19]. Red solid line, S1; green solid line, S2; blue solid line, S3.
Description of the MFEP
In this section, we describe the mechanism of the transition corresponding to the MFEP from simulation S3. S3 is chosen in preference to S2 because the corresponding free energy profile associated with the committor is probably more accurate (discussed in Sec. 3D4). In addition, the profiles of the free energies G and F associated with simulation S3 exhibit lower barriers (see Sec. 3D3). This transition path, therefore, is more likely to be relevant for the ensemble of all transition paths. A brief discussion of the MFEP from S2 is available in the supplementary materials.19 S3 is chosen in preference to S1 because the calculated endpoint free energy difference is closer to that of MFEP S2 (discussed in Sec. 3D3).
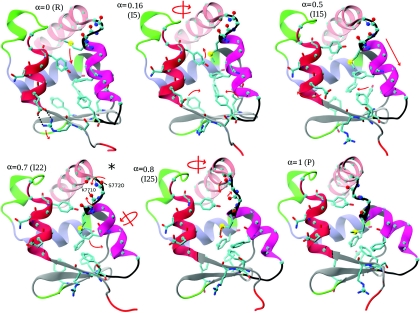
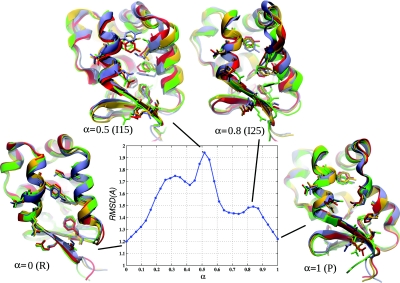
Six snapshots from the MFEP ordered in the R→PPS direction are shown in Fig. 7 to illustrate the transition mechanism; important residues and secondary structure elements are labeled in Fig. 1. The main differences between the R and PPS conformations of the converter were discussed in Sec. 3B1. Transition in the R→PPS direction begins with a downward motion of H4, which positions M770 in the middle of the converter interior and causes H5 to rotate (R to I5); (the numbers in parentheses correspond to image indices and R and P correspond to the rigor and prepowerstroke states); the hydrogen bonds between R708 and E713 break (I5); H4 continues its downward motion and M770 moves between the aromatic rings of Y718 and F766 (I15 to I22). Aromatic residues in the converter core (F739, Y749, F751, F758, F766) move into their PPS positions (I22 to I25). L4 begins to twist toward its PPS position (I22 to I25), and H4 begins to tilt and twist, accompanied by the motion of M771 and F766 to the outside of the converter interior (I22 to I25). H4 continues to tilt, and CI rotates into its PPS position (I25 to P). An animation of this MFEP can be found in the supplementary materials.19
Figure 7.
Snapshots from simulation S3 (Table 4) that illustrate the transition mechanism. The converter structures are shown, as in Fig. 1. Red arrows indicate the conformational change associated with the snapshot. The location of the snapshot on the transition path (α = Ix∕I31), and the corresponding image index (I0–I31) are shown for each snapshot. Images I0 and I31 correspond to the rigor (R) and pre-powerstroke (P) states, respectively. Hydrogen bonds between R708 and E713 are indicated by dotted black lines in the R snapshot. The metastable state is indicated by an asterisk. Residues and secondary structure elements are labeled in Fig. 1.
Structures I15 and I25 on the MFEP (Fig. 7) correspond to peaks in the free energies G(θ) and F(α) (not to be confused with the energy along the MEP shown in Fig. 5). Free energy profiles are discussed in Secs. 3D3, 3D4 below. In I15, M770 is involved in repulsive interactions with Y718 and F766 (while passing from the interior of the converter to the outside), and in I25, loop L4 is in a strained configuration (while twisting from the R into the PPS conformation). The global maximum of the committor free energy F corresponds to I15.
Structure I22 on the MFEP (located between I15 and I25) is at a local free energy minimum. In this case, M770 is in the PPS position, but L4 is still in the R position, i.e., M770 has completed crossing its barrier, but L4 has not yet begun. As a qualitative check of whether the snapshot I22 corresponds to a metastable state, a 40 ns equilibrium MD simulation was performed, starting from the structure I22. The heavy-atom RMSD from the initial configuration remained at ≃1.7 Å during the simulation, M770 and L4 both remained close to their starting positions, and no major structural changes in the conformation were observed, consistent with metastability.
Free energy as a function of the collective variables
In this subsection, we describe the calculation of G(θ), the free energy as a function of the collective variables defined in Eq. 3. We find that considerable care is required to compute accurate and converged profiles of G. The free energy of the committor (F) is discussed in Subsection 3D4.
After the simulations S1–S3 converged to the corresponding MFEPs, the images θn were held fixed, and restrained MD simulations were performed for approximately 20 ns in each case to compute the gradients ∇G(θn). These simulations are denoted G1c–G3c in Table 4. Free energies were then computed using the trapezoidal rule [Eq. 21], as described in Sec. 2D1 (not using umbrella integration).
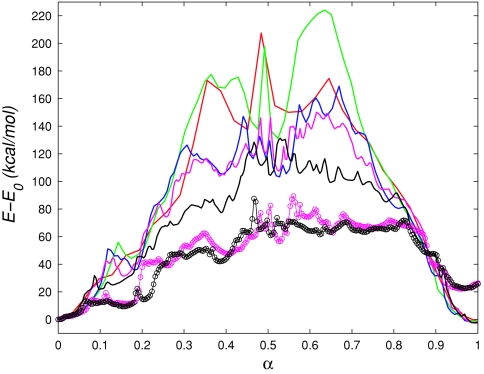
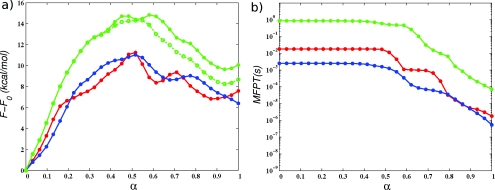
The resulting FE profiles are shown in Fig. 8a. The profiles corresponding to the 32-image calculations show that the PPS state has higher free energy than the R state. It was puzzling, however, that the FE difference between the two endstates was ∼12 kcal∕mol for G2c, but ∼5 kcal∕mol for G3c, because both the collective variables and the endpoint images along the initial string (computed from equilibrated x-ray structures) were the same for these simulations; only the initial paths connecting the two endpoints were different (see Table 4). The difference in paths, however, should have no impact on the FE difference between end states, since free energy is a function of state.
Figure 8.
(a) Free energy of the collective variables (G) along the MFEPs (red ×........), G1c; (green ×........), G2c; (blue ×........), G3c; (green - - -), G2f; (blue - - -), G3f; (green •—), G2fr; (blue •—), G3fr. (b) Comparison of the FE G for simulations G2f∕G2fr∕G2f10 and G3f∕G3fr∕G3f10 computed using different methods (see text). (Green ––), G2fr; (blue ––), G3fr. Umbrella integration (corrected gradients with low force constants). (Green - - -), G2f10; (blue - - -), G3f10. Simple trapezoidal integration (uncorrected gradients with high force constants). (Green − · −), G2fr; (Blue − · −), G3fr. Simple trapezoidal integration (uncorrected gradients with low force constants).
Three potential causes for the discrepancy were considered: (I) integration error of the trapezoidal rule, (II) movement of the endpoints during the string simulations that could position them in different locations on the FE landscape, and (III) inadequate sampling in the estimation of the FE gradient ∇G(θn).
To rule out (I), the MFEPs from S2 and S3 were interpolated onto 128-image strings using linear interpolation, and the FE was calculated from restrained MD simulations for ∼15 ns, followed by trapezoidal rule integration, as before. Fig. 8a shows that the resulting profiles did not change significantly. These simulations are denoted G2f and G3f in Table 4 and Figs. 8a, 8b.
To rule out (II), we constructed four-replica strings between the corresponding endpoints of the MFEPs in S2 and S3 using linear interpolation (the resulting path was acceptable because the endpoints were very close, e.g., within ∼1 Å RMSD of one another). Restrained simulations were performed for 20 ns, and the FE profiles was computed as before. The FE difference between the endpoint images was found to be ∼0.5 kcal∕mol for each pair, which cannot account for the 7 kcal∕mol difference in the FE change described above.
To test (III) efficiently, rather than running additional simulations beyond the original 20 ns (which could require much longer integration times), we combined restrained MD simulations with Hamiltonian replica exchange (see Sec. 2D1). The algorithm is a generalization of umbrella sampling replica exchange,34 in which restraining potentials are exchanged between neighboring windows, according to the Metropolis criterion.
Twenty-nanosecond simulations with REX were performed using 128-image strings, interpolated from the MFEPs. These simulations are denoted G2fr and G3fr in Table 4 and Figs. 8a and 8(b). Trial moves for all replicas were attempted simultaneously (i.e., 0 ↔ 1, 2 ↔ 3, …, or 1 ↔ 2, 3 ↔ 4, …, by a random decision) once in every 100 MD iterations. The average acceptance probability pacc was ∼70%, although the minimum pacc was ∼10%, corresponding to the replica from MFEP S3 located at α ≃ 0.5 [see Fig. 8a].
The results of the REX simulations shown in Fig. 8a demonstrate that 7 kcal∕mol discrepancy in the endpoint free energy difference between simulations G2c∕G2f and G3c∕G3f was caused by insufficient sampling in the evaluation of the gradient ∇G(θn). The enhanced sampling of REX is most significant for the replicas near α ≃ 0.5 of simulations G3. At this location on the path, the free energy gradients computed without REX are underestimated, lowering the free energy by several kilocalories per mole, relative to the simulations with REX. As noted above, α ≃ 0.5 is also the location of minimum pacc values, which means that the MD replicas that correspond to adjacent images near α ≃ 0.5 sample somewhat different regions of space and probably have to overcome greater energy barriers in order to exchange. This explanation is consistent with the fact that the free energy profile in the vicinity of α ≃ 0.5 has sharp variations. For simulation G2fr, the minimum of pacc (∼15%) occurs near α ≃ 0.8, which is also the location of a sharp free energy peak [Fig. 8a].
In addition to the 128-image REX simulations, 32-replica REX simulations were performed. However, the acceptance probabilities were very low in the vicinity of α ≃ 0.5 (MFEP from S3) (<1%), and therefore we did not see substantial improvement in the FE profile over that from G2c (results not shown).
As discussed in Sec. 2B, since the free energy G(θ) does not correspond to the free energy as a function of the committor reaction coordinate, it is less informative than F(α) and more difficult to interpret. While REX simulations G2fr∕G3fr were necessary to establish the accuracy of the thermodynamic integration Eq. 21 for computing G(θ), we decided that the additional computational cost of performing a 128-replica REX simulation for MFEP S1 was not justified, and this simulation was not performed. The corresponding free energy profile in Fig. 8a is therefore less accurate than that for the other simulations.
As described in Sec. 2D1, the errors in the estimation of the gradients ∇G(θn) due to the use of a restraint instead of a constraint in Eq. 20 are small if the force constants used in the restraint potential are sufficiently large. On the other hand, in order to use REX efficiently in the calculation of FE gradients, the force constants have to be sufficiently low to ensure high acceptance probabilities. To assess the accuracy of the FE profiles from simulations G2 and G3, shown in Fig. 8a, we corrected the gradients computed from the 128-image REX simulations using UI (Ref. 36) and repeated the integration, as discussed in Sec. 2D1. In addition, we increased all force constants by a factor of 10 and repeated the 128-image simulations (REX was not used because of the high constants), following by integration. These simulations are denoted G2f10 and G3f10 in Table 4.
The resulting FE profiles are compared in Fig. 8b. In the profiles obtained by integrating the gradients computed from the REX simulations directly (without using UI), the peaks are underestimated almost by a factor of 2, compared to the other two sets of profiles. This indicates that the force constants used in the REX simulations (1.0 kcal∕mol∕Å2 for position and distance CV to 10.0 kcal∕mol∕rad2 for dihedral angle CV) are too low to obtain an accurate free energy profile. On the other hand, if UI is used to correct the gradients obtained from REX simulations, the resulting FE profiles agree well with those computed directly from simulations that employ the larger force constants. The good overall agreement also suggests that the higher force constants are sufficiently large to estimate the magnitude of the FE barriers. Unfortunately, in this case, REX cannot be used efficiently, and the gradients are affected by sampling errors, as before (note e.g., the ∼7 kcal∕mol endpoint FE difference between the plots corresponding to the high force constants).
It is not surprising that the FE profiles computed directly from simulations that use low force constants underestimate the magnitude of the FE profiles. Equation 17, which is used to approximate gradients of G(θ), becomes exact (assuming no sampling errors) for a “smoothed” free energy defined by,
| (44) |
in which U(x, θ) is the potential defined in Eq. 16, N(0,(βk)−1) is the multivariate Gaussian distribution centered at zero with variances (βki)−1 for i = 1, …, K, (*) is the convolution operation, and C1 is a normalization constant. Equation 44 follows from the definition of G(θ) in Eq. 3 and the properties of the delta function. Thus, the use of the estimate in Eq. 17 is equivalent to applying a Gaussian filter to (the probability density of θ) and computing the gradients of the smoother FE G*(θ). Using low force constants implies that the variances of the Gaussian will be large, which will lead to greater smoothing of the peaks and valleys of the true FE G(θ). Note, also, that in the limit of zero ki, G*(θ) is identically zero.
The preceding discussion demonstrates that obtaining accurate profiles of the free energy as a function of the collective variables can be laborious. In the present simulations we used replica exchange to improve sampling, which required reinterpolation of the MFEP from 32 to 128 images to obtain high exchange probabilities, quadrupling the computational cost. Furthermore, because the use of REX requires lowering force constants in the restraining potentials, an additional postprocessing step is needed to compute corrected FE gradients by UI.
The definition of G(θ) given in Eq. 3 depends on the collective variables chosen to describe the transition. Not surprisingly, profiles of G(θ) obtained using different CV sets but the same initial paths (i.e., G1 vs G2) in Fig. 8a are quite different, although the corresponding MFEPs represent the same transition. We show in Subsection 3D4 that the differences between the different simulations can be accounted for if one considers instead the free energy of the reaction coordinate. We also discuss the correspondence between the structures along the MFEP shown in Fig. 7 and their free energy.
One-dimensional free energy profiles and rates of transition
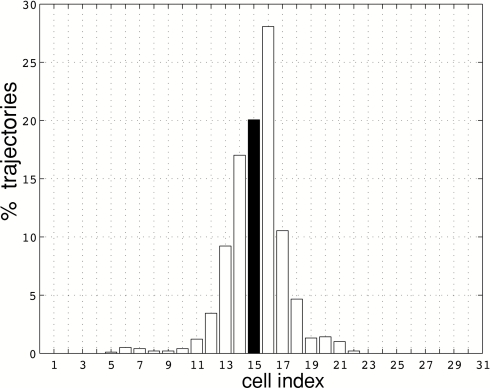
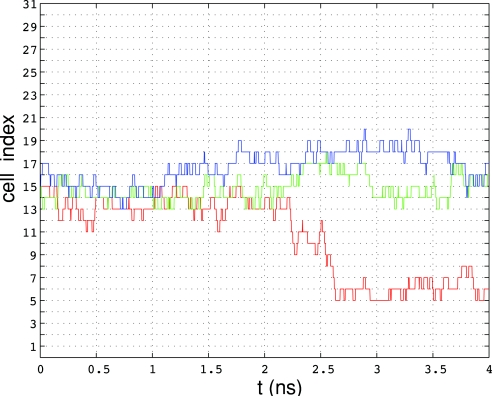
The free energy as a function of the committor reaction coordinate [Eq. 8 in Sec. 2B] was computed as described in Sec. 2D2. After the string had converged to the corresponding MFEP, the images θn were fixed, and unrestrained MD simulations were performed concurrently for each cell to estimate the rates of escape νm, n. Three simulations were carried out, denoted for brevity as free energy simulations F1, F2, and F3, in correspondence to the string simulations S1, S2, and S3. The computational requirements of the free energy simulations were approximately the same as those for the string calculations used to compute the MFEPs and considerably less than those required to compute accurate profiles of G using REX (see Table 4). Convergence of the free energy simulations was assessed by monitoring the total rate of escape from all cells. This quantity reached a plateau after 5–10 ns of MD simulation for simulations F1 and F3 and after ∼15 ns for simulation F2. The apparent reason for the longer time to convergence, required for F2, is a fairly large number of collisions between cells corresponding to nonadjacent images compared to simulations F1 and F3. This issue will be discussed further below because it affects the accuracy of the computed free energy profiles.
After the total rate of escape was stationary, MD integration was continued for 20 ns for simulations F1 and F3 and for 25 ns for simulation F2. Statistics obtained from these trajectory segments were used to compute the free energy and the rate. The FE profiles computed from the entire 20–25 ns trajectory segment were compared to those computed using only the first half of the corresponding segment. The maximum difference was ∼0.4 kcal∕mol.
Free energy profiles computed from simulations F1–F3 are shown in Fig. 9a, and the MFPTs from the milestones Bi∩Bi + 1 (the “main” milestones, since they approximate isocommittor surfaces, as described in Sec. 2D2) for i = 1, 2, …, N − 2 to the (last) milestone BN − 1∩BN, are shown in Fig. 9b. The FE profiles for simulations F1 and F3 are in good agreement, even though the corresponding collective variables sets have different type and size (see Tables 2, 3). In particular, the FE barriers and the FE difference between the end states are in agreement to within ∼1 kcal∕mol. The second FE peak appears to be in slightly different locations (α ≃ 0.71 for F1 and α ≃ 0.78 for F3). This shift is due to the different parametrizations of the respective MFEPs from S1 and S3. Both are parametrized by arc-length, but the definition of the arc-length involves the collective variables, which are different in type. The actual atomic configurations that correspond to this FE peak are similar for the two paths (compared in the supplementary materials19). The profiles of the MFPT for transitions from the main milestones to the last milestone along the paths computed in S1 and S3 are also in fair agreement. The profiles show that the MFPT to the last milestone is approximately constant for the milestones that correspond to α < 0.5, indicating that the main FE barrier that occurs near α = 0.5 for both paths is the transition “bottleneck.”
Figure 9.
(a) Free energy of reaction (F). (b) MFPT to the milestone nearest to the PPS state. The symbols are as follows: (red •—), F1; (green •—), F2; (green ○⋅⋅⋅), corrected F2 (only for a); (blue •—), F3; see text and Table 4 for a description of each simulation.
The FE profile from simulation F2, on the other hand, has consistently higher energies than the profiles from F1 and F3. Examining the rates of escape νn, m [from which the free energy is computed via Eqs. 37, 34], we observed that in simulation F2, a large fraction (13%) of the total rate of escape from all cells Bn involved pairs of cells that correspond to nonadjacent images (for simulations F1 and F3, this fraction was 0.3% and 0.7%, respectively). Most of the “flux” between nonadjacent cells involved a replica restricted to one of the cells Bi for i = 14, …, 21 (93% of the cases), which correspond approximately to α ∈ [0.45, 0.67] in Fig. 9, and no replicas restricted to an endpoint cell (i = 0 or i = 31). Although the presence of nonzero fluxes between nonadjacent cells poses no concerns for the estimation of the probabilities πn, it implies that the planar approximation to the isocommittor surface in Eq. 5 is not accurate at certain points away from the MFEP within the transition tube (see Appendix B). The inadequacy of the approximation suggests a problem with assumption (ii) in Sec. 2B for simulation S2 (i.e., that the transition tube through which most of the reactive trajectories proceed is narrow).
It should be stressed that this finding does not invalidate the use of CVS2 in general, because the quality of the approximation of isocommittor surfaces by hyperplanes depends not only on the collective variables but also on the curvature of the MFEP and the local free energy landscape (see Appendix B). The fact that the flux between nonadjacent cells in simulation F3 is only 0.3% of the total flux suggests that the present problem does not arise for simulation F3. An approximately corrected free energy profile can be computed by setting the fluxes between nonadjacent cells to zero. This (ad hoc) approach corresponds most closely to discarding a portion of the reactive trajectories that are sufficiently far from the MFEP that the hyperplane approximation of the isocommittor surfaces is inaccurate. While accounting for such trajectories properly would produce a more accurate free energy profile, it is impossible to do this without a higher-order approximation to the isocommittor surface.
The corresponding FE profile [included in Fig. 9a] shows a significant improvement in the free energy difference between the endpoint states relative to simulations F1 and F3. Since, as mentioned above, 93% of the flux between nonadjacent cells involves MD replicas in cells Bi for i = 14, …, 21, and no MD replicas in the endpoint cells, the discarding of the fluxes should affect to the greatest extent the values of the free energy near the barrier (“middle” of the path) and to a lesser extent the FE difference between the endpoints.
One possible reason for the higher FE barrier in simulation F2 relative to simulation F3 is that the FE profile computed in F2 is less accurate due to the spurious transitions between nonadjacent cells described above. In addition, the higher barrier in F2 may be caused by differences in the MFEPs. Recall that calculations S2 and S3 start from initial paths 1 and 2, respectively (see Sec. 3C), which specify opposite directions of rotation of the dihedral angles in the loop L4. These dihedrals are explicitly present in the CV set used in simulations S2∕G2∕F2 and S3∕G3∕F3 (CVS2), which means that the MFEPs and the transition tubes associated with simulations F2 and F3 cannot intersect. Therefore, paths from F3 may simply be higher in free energy than those from F2. It seems somewhat surprising that the free energy barriers computed from the simulations F1 and F2 differ by ≃3 kcal∕mol [Fig. 9a]. However, although the corresponding simulations S1 and S2 were both initialized from zero-temperature path 1, some instantaneous MD configurations observed in simulation F1 were found to be more consistent with path 2. This observation suggests that simulation F1 represents a broader ensemble of transition paths, since it contains configurations that are similar to those from both paths 1 and 2. A broader ensemble of paths is likely to result in a lower free energy barrier. As a check of this conjecture, we estimated the width of the transition tube from the free energy simulations (F1–F3) by computing the average,
| (45) |
for each cell Bn.
From the simulations F1, F2, and F3, respectively, we found the values of wn for cells at α = 0.5 ± 0.1 to be approximately 2wave, 1wave, and 1.5wave, where wave is the average width of the transition tube (wn < 1wave at the endpoint states). This is in accord with the suggestion that transition tube associated with MFEP S2 is narrower than those for MFEPs S1 and S3, explaining the higher free energy barrier obtained in simulation F2. The quantity wn, however, is only useful as a qualitative measure of the size of the ensemble of transition paths. It is contaminated by large statistical errors because of the high dimensionality of the CV space (177 and 51 for CVS1 and CVS2). In addition, if the shape of the transition tube is irregular, which is likely to be the case in many dimensions, wn will not provide an accurate estimate for the volume of the transition tube. We note, also, that that the low apparent width of the transition tube in F2 may be caused by spurious reflections of MD replicas due to collisions with nonadjacent cells (see above).
Having computed profiles of the one-dimensional free energy as a function of the committor, we briefly return to the free energy as a function of the collective variables (G). Although computing G accurately requires great care (see Sec. 3D3), the significance of this free energy for the present simulation system appears to be limited, because G cannot be related simply to the reaction free energy F. Indeed, although the MFEP lies approximately in the center of the corresponding transition tube, it does not, by itself, contain information on how the volume of this transition tube varies along the path (see Appendix B). From the above estimates of the width of the transition tubes for simulations F1–F3, we can conclude that the transition tube is generally larger at intermediate states along the path compared to the endpoint states. This indicates that the entropic contribution to the reaction FE neglected in G due to the “freezing” of the K collective variables is nonuniform along the MFEP. Consistent with this interpretation, a comparison of Figs. 8b, 9a shows a dramatic reduction in the free energy values at intermediate locations along the free energy profiles, going from G to F. Higher entropic contributions to the FE at intermediate values of the reaction would imply that, in Cartesian space, more configurations are required to characterize these intermediate states.
The curve in Fig. 10 shows the RMSD computed between the structures in each cell Bn and the initial structure (a corresponding replica on the MFEP) for simulation F3. The RMSD is generally higher for intermediate cells than for the endpoint cells, and the highest value occurs at the location of the FE barrier [α ≃ 0.5 in Fig. 9a]. Surrounding the RMSD curve, we show overlays of four configurations taken from simulation F3 that correspond to α = 0, 0.5, 0.8, and 1.0. The intermediate values of α correspond to the two FE peaks in Fig. 9a and also to the snapshots I15 and I25 on the MFEP shown in Fig. 7. The larger differences between the overlaid conformations are evident for α = 0.5 and 0.8, than for α = 0 and 1.0, consistent with the RMSD plot, and suggest that transitions occur via many paths.
Figure 10.
The curve corresponds to the RMSD computed between the structures in each cell Bn and the initial structure in each cell for simulation F3. The structures correspond to instantaneous MD configurations from simulation F2 in Table 4 constrained to cells B0, B15, B25, and B31.
Despite the differences in the magnitudes of G and F, a qualitative comparison of Figs. 8b, 9a suggests that profiles of G and F are correlated, so that based on G, one can identify correctly not only the relative stability of the endpoint states but also configurations along the MFEPs that correspond to high-energy and metastable states. However, if one aims to compute a one-dimensional free energy profile (versus a parametric curve on a multidimensional landscape) and rates of transition, in addition to the calculation of the MFEP(s), separate free energy simulations are required.
Estimates of energy and entropy of transition
To estimate the energetic and entropic contributions to the free energy profiles in Fig. 9a, we computed the average potential energy in each cell Bn from the trajectories in F1–F3. The corresponding energy profiles are shown in Fig. 11. The standard deviation of the energies in each cell was ∼27 kcal∕mol, and the standard deviation of the averages shown in the figure is about 9 kcal∕mol (based on computing nine block averages ∼2 ns in length). Because of the large error bars, the relative contributions of the energy and entropy discussed herein should be considered qualitative.
Figure 11.
Average potential energy of the tessellations Bn; (red •—), F1; (green •—), F2; (blue •—), F3.
We note that that the endpoints have approximately equal energies, which indicates that the FE difference between the R and PPS conformers of the converter (∼8 kcal∕mol) is of entropic origin. As a rough check of this conclusion, we estimated the configurational entropy of the R and PPS conformers from quasiharmonic analysis of 60 ns unbiased MD simulations of the two conformers. Using the harmonic oscillator formula in Ref. 65, the value for −TΔS for the PPS state was ∼17 kcal∕mol higher than that for the R state, qualitatively consistent with the main results.
A second observation from Figs. 119a is that for intermediate values of the progress variable α, the entropic contribution to the FE is similar in magnitude to the energetic contribution (∼10 kcal∕mol). This finding is qualitatively consistent with the larger widths of the transition tube in the vicinity of α ≃ 0.5 than at the endpoints, as discussed in Subsection 3D4, and the somewhat broader conformational ensembles found for MD trajectories restricted to intermediate cells Bn (Fig. 10). This result underscores the important point that a single path connecting two states separated by a barrier is unlikely to provide a full description of the transition. However, this does not impact the utility of the MFEP as an “average” path, i.e., located in the center of a transition tube that may itself be quite wide.
DISCUSSION OF METHODOLOGY
In the study of the prepowerstroke ↔ rigor transition of the converter domain of myosin VI, several challenges were addressed that are likely to arise in the application of the string method to other complex biomolecular systems. The choice of CVs to describe the transition under study is far from obvious. In the present approach, we first found a set of atoms, such that applying forces to just these atoms in a targeting simulation (RTMD) drives either conformation toward the other. To be confident that the final RTMD simulation structure was in a local minimum corresponding to the target, the structure was “relaxed” by gradually removing the restraints and allowing it to equilibrate without external forces; the relaxed structure was within 1.6 Å (heavy-atom RMSD) of the target. Using this atomic set, we constructed two sets of CV. The first CV set is comprised of just the positions of the atoms, expressed in an internal frame of reference. In the second set, the number of CV is reduced by a factor of 3 compared to the first set. Since any CV set that can be used to parametrize the committor function with reasonable accuracy should represent the behavior of the system equally well (and, in particular, lead to the same free energy profiles and rates), using the two different CV sets allows us to “cross-validate” the results. The fact that we have obtained similar paths and reaction free energies for the transition in the MVI converter indicates the robustness of the present approach.
To use the string method, one must have initial values for the CV as well as complete coordinates for the corresponding MD replicas. Starting with a linear interpolant in Cartesian coordinates between the two structures, a minimum energy path was obtained with the zero-temperature string method. Although linear interpolation produces distorted intermediate structures, subsequent energy minimizations restore equilibrium bond lengths and angles, and alleviate bad contacts. We note that other interpolation algorithms can be used for zero-temperature path generation, such as the chain-of-states method,66 the nudged elastic band method67 and conjugate peak refinement.68 The main advantage of the zero-temperature string over these methods is that it can be used “out-of-the-box” with many solvation models in CHARMM, including FACTS. Although initial conditions to the string methods can also be generated from targeted molecular dynamics simulations with constraints57, 58 or restraints22 (as well as TMD enhanced with Monte-Carlo sampling in trajectory space69), we did not employ such methods. Since TMD simulation structures in general are not in equilibrium (i.e., far from an MFEP), the direction in which TMD is performed can introduce directional bias into the transition path (this was also found for the symmetric TMD of Ref. 22). In contrast, in (symmetric) interpolation methods, endpoint structures contribute equally.
Two types of free energies were used in this study [see Eqs. 3, 8]. G is the free energy as a function of the collective variables along the MFEP, and F is the free energy of reaction as a function of the committor function q (plotted versus the parameter α). Thus, the free energy G is a K-dimensional function, with K equal to the number of collective variables, whereas F is one-dimensional. The profiles of G computed in this study are evaluated only along the corresponding MFEP and have no information about the free energy values for points not on the MFEP (other than that they are higher in free energy locally near the MFEP). In contrast to G, the reaction free energy F maps the entire transition tube onto a single curve. In the special case that the transition tube is extremely narrow or has uniform cross-sectional volume along the path, G ≃ F. If the volume of the tube cross section is variable (which is true for the present system), G does not provide an accurate measure of the free energy of the reaction. A qualitative comparison of the profiles of G and F [Figs. 8b, 9a] suggests that G can be used to identify high-energy states and metastable intermediates.
The function F can be calculated by taking a Boltzmann average of G along all reactive trajectories that pass through the transition tube with the same value of the committor function q(α). This approach is equivalent to the Boltzmann-weighted integration of G over the isocommittor surfaces. To perform this integration, we make use of assumption (ii) in Sec. 2B and approximate the isocommittor surfaces by hyperplanes of θ(x) that are perpendicular to the MFEP (scaled by M−1). The free energy F is computed by tessellating the configurational space into cells with boundaries that coincide locally with the hyperplanes. MD is then used to estimate the rate of escape from each cell by recording the number of collisions between the cell boundaries.
If assumption (ii) is satisfied, then the hyperplane approximation to the isocommittor surface is accurate, and only collisions between adjacent cells will be observed. Conversely, a significant number of collisions between nonadjacent cells indicates a failure of assumption (ii). In this case, F defined by Eq. 8 will not be an accurate approximation of the true free energy of the reaction coordinate (i.e., FE of the committor).
In one of the free energy simulations performed, 13% of all collisions were between nonadjacent cells (in the other two cases, this number was less than 1%), and the endpoint free energy difference computed from this simulation differed from the other two. In a corrected free energy profile, which was calculated by setting the fluxes between nonadjacent cells to zero, the free energy difference was in agreement with the other two profiles.
The preceding discussion suggests that optimal sets of CV for studying transitions are those which correspond to relatively narrow transition tubes. It is likely that the constructions of appropriate CV will require specific analysis of each transition.
Although the use of the FACTS model to represent the effects of solvation is unrelated to the string method per se, it was essential for the present calculations. A simulation with explicit water molecules would increase the size of the system to approximately 17 000 atoms, compared to 1442 atoms required with FACTS. The calculation of additional MD forces arising from FACTS was found to slow down the overall speed of the calculation by a factor of 2. Therefore, the computational cost of performing MD simulations with explicit solvation would be roughly six times greater.
Reaction rate calculations with implicit solvent models require inclusion of realistic solvent friction. To improve conformational sampling, in the present study we used a simple Langevin friction model with a very low value (1 ps−1) for the friction coefficient (see Sec. 3D1). This choice of friction kernel will most likely lead to an overestimation of the rate. An approximate magnitude of the error can be obtained by considering a friction model based on hydrodynamic interactions. Models in which atoms or atom groups are treated as point particles interacting via the Oseen or the Rotne–Prager tensors70, 71 have led to good agreement between the computed and experimentally determined translational and rotational diffusion tensors72 [provided that a hydration shell of thickness 1.1–1.5 Å (Refs. 72 and 73) is modeled around the protein]. Such a model could be incorporated into the present calculations via, e.g., the Langevin equation74 using a parametrization of the friction constants based on Stokes’ law and an accessible surface area model.75, 76 Venable and Pastor76 found that if the friction coefficient in their hydrodynamic model is reduced by a factor of 10, the computed diffusional and rotational tensors increase by factors of ≃6 and ≃15, respectively. Reference 76 recommends using mass-scaled friction constants of ≃50 ps−1 compared to 1 ps−1 used in the present study. These considerations suggest that with a realistic solvent friction model the rate of transition would be slowed by an order of magnitude. Another concern with solvation models is the long-time stability of the protein structure. In the present calculations, the two endpoint structures were stable for around 100 ns of simulation (including equilibration and string calculations). FACTS was thus an excellent choice for the myosin VI converter domain, but this may not be true for all systems.
CONCLUDING DISCUSSION
The present results demonstrate the utility of the string method in computing transition paths, free energy profiles and rates of transition in complex biomolecular systems. In particular, the prepowerstroke ↔ rigor transition of myosin VI considered here is complicated in that it involves rearrangements of residue side chains, large motions of alpha helices, and changes in the backbone structure of a flexible loop (see Sec. 3D1 and Fig. 7). The presence of diffusive motion along the transition path is evident in the behavior of unbiased trajectories launched from the transition state found in one of the simulations: the evolution of the system projected onto the reaction coordinate is slow, with frequent reversals of the direction of motion (see Appendix C). Such behavior makes it difficult to use transition path sampling,1, 2 because the trajectories would require very long integration times to reach the endpoint structures. Since the reaction coordinate for transitions in complex biomolecular systems is usually unknown, the ability of the string method to use a fairly large number of collective variables in the approximation of the reaction coordinate (defined here as the committor function) is an essential aspect of the method. In contrast, other methods based on collective variables, such as metadynamics6 or adaptive biasing force,8 require their number to be rather small. Thus, the string method, although not trivial to use (see Sec. 2), appears to be well-suited for obtaining transition paths and free energies in complex biomolecular systems.
The present study of the prepowerstroke ↔ rigor transition of the myosin VI converter is an important step toward the understanding of the powerstroke.11, 12, 13 The mean first passage times of the transition computed from the simulations [10−3–10−2 s; see Fig. 9b] are consistent with an experimental study that find the rate-limiting step of the powerstroke transition in myosin VI to be ≤90 s−1.77 (However, as mentioned at the end of Sec. 2D3, the rate calculation does not take into account the implicit solvent approximation, and probably overestimates the rate by an order of magnitude.) The computed free energy profiles reveal the structures that have the highest free energies along the transition paths and that correspond to the transition states, as shown by an analysis of unbiased trajectories (see Appendix C). The predicted structures can be tested by experimental mutagenesis studies, e.g., by mutating residues Y718, F766, or M770 (see Fig. 7). In addition, the simulations predict the existence of a metastable state along the transition path at α ≃ 0.65 [see Fig. 9a], which suggests that the lever arm of myosin VI may occupy a position that is intermediate between the rigor and prepowerstroke states, and could help to explain the variable step size observed for myosin VI dimers.78, 79 Finally, we find that the prepowerstroke converter conformation is higher in free energy than the rigor conformation by ≃8 kcal∕mol. This result should be viewed with caution, however, because only the converter domain was simulated in the present study; the rest of the myosin VI molecule that was excluded from the simulations to decrease computational cost may preferentially stabilize one conformation of the converter. Calculations that treat the entire myosin VI head are in progress to examine this question.
ACKNOWLEDGMENTS
The authors are grateful to Giovanni Ciccotti, Maddalena Venturoli, and Kwangho Nam for stimulating discussions. Supercomputer resources for the calculations performed in this study were provided by the National Energy Resource Supercomputing Center and the FAS Research Computing Group at Harvard. V.O. acknowledges financial support under the NRSA fellowship 1F32GM083422-01. The work done at Harvard was supported in part by a grant from the National Institutes of Health and by a grant from the Human Frontiers Grant Science Program. E.V.-E. was supported by a grant from the National Science Foundation (Grant No. DMS-0708140) and by a grant from the Office of Naval Research (Grant No. N00114-04-1-6046).
APPENDIX A: DERIVATIVES OF THE POSITION CV
Let A=[v1,v2,v3] and let o = [o1, o2, o3] denote the origin of the coordinate frame A (o is the COM of the atom group that defines the frame). Let p* denote the absolute coordinates of a point P. In the frame of A, the coordinates of P are p = AT(p* − o), and we have used the orthogonality of A. Differentiating this expression with respect to an absolute atomic coordinate, , we obtain
| (A1) |
The only nontrivial derivative in Eq. A1 is . Since A depends on through Ci, j, i.e., , we first compute the derivative of A with respect to the components of Ci, j. Let v be an eigenvector and λ the corresponding eigenvalue. Differentiating the eigenvalue relation (Ci, j − δijλ)vj = 0 with respect to Cp, q, we have
| (A2) |
where vi is the ith component of v. Multiplying Eq. A2 by vi and applying the eigenvalue relation yields
| (A3) |
| (A4) |
| (A5) |
where we have assumed that the eigenvectors vi have been normalized to unity and summed on i and j. Inserting Eq. A5 into Eq. A3 and rearranging, we obtain a following matrix equation that involves the eigenvector derivative:
| (A6) |
Equation A6 cannot be solved because Ci, j − δijλ is singular. The singularity can be removed by augmenting Eq. A6 with the relation
| (A7) |
which expresses the fact that the norm of the eigenvector v is constant (which we set to unity). Equations A6, A7 can now be inverted to yield ∂vj∕∂Cp, q. The procedure is carried out for each eigenvalue/eigenvector pair. The derivative (where is the k-component of the absolute position of atom q) is computed by differentiating Eq. 42 (with r replaced by r*),
| (A8) |
The derivative can now be computed as
| (A9) |
where vji is the ith component of vj.
We note that position CVs expressed in a local moving frame are somewhat more costly to calculate than those in an absolute frame, since the tensor Ci, j must be diagonalized at every MD iteration, and computing eigenvector derivatives requires that Eqs. A6, A7 to be solved six times for each eigenvector (only six inversions are necessary because of the symmetry in Ci, j). Furthermore, each derivative in Eq. A1 requires two matrix multiplications. To increase the speed of matrix diagonalization, a special-purpose routine for 3 × 3 symmetric positive semidefinite matrices was implemented in CHARMM, in which the cubic characteristic polynomial is solved using Cardano’s formula, and the eigenvectors are determined using Cramer∕s rule. In addition, the 3 × 3 matrix multiplications were programmed in-line to avoid function calls.
Since, for a right-handed coordinate frame, one can invert any two coordinate vectors simultaneously to generate another right-handed coordinate frame, an additional constraint on the eigenvectors is needed to guarantee a unique solution for the coordinate frame. (There are four ways to define a right-handed frame using three orthonormal vectors.) Given the coordinate frame computed at the previous timestep, , the new coordinate frame [v1,v2,v3] is chosen from the four possible right-handed frames such that the scalar product
| (A10) |
is maximal. This criterion ensures that the frame vectors evolve continuously during the simulation. The coordinate frame at the first step of the simulation is chosen randomly from the four possible definitions. To compute the coordinate frame vectors consistently for the images along the string, a similar criterion is used. Given two adjacent images, i and i+1, and a best-fit rotation matrix A that aligns the atoms (those used to define the frame) of image i+1 with those of image i in the sense of minimal RMSD, the coordinate frame chosen for the image i+1 is that which maximizes the product
| (A11) |
The constraint in Eq. A11 is enforced explicitly at the beginning of a string simulation, and is guaranteed to hold at each step of the simulation in view of the constraint in Eq. A10.
APPENDIX B: A DISCUSSION OF FLUXES BETWEEN NON-ADJACENT CELLS
A tessellation of a hypothetical two-dimensional space of collective variables shown in Fig. 12 can be used to understand the implication of fluxes between nonadjacent images. In the ideal case, trajectories initiated from the points the MFEP will stay within the transition tube bounded by the two thick black lines. Then, for any internal image point i, only the fluxes Bi↔Bi − 1 and Bi↔Bi + 1 are possible (these are fluxes between adjacent cells). If, on the other hand, the ensemble of trajectories is bounded by the dotted line, trajectories launched inside cells Bi for i=2,3,4,6,7,8,9,10 will collide with boundaries that correspond to nonadjacent cells. For example, trajectories in B9 and B10 will collide with the cell B1. In this case, some hyperplanes Bi∩Bi + 1 provide poor approximations to the corresponding isocommittor surfaces in regions through which reactive trajectories pass with a significant probability. Indeed, if all of the hyperplanes coincide precisely with isocommittor surfaces, then it will be impossible for any trajectory restricted to a cell Bi to cross into any cell other than Bi ± 1, since this would imply that two isosurfaces that correspond to different values of the committor function must intersect.
Figure 12.
A tessellation of a two-dimensional space of collective variables based on a hypothetical MFEP discretized into 20 images. The cells Bn are drawn in thin solid lines. Two putative transition tubes are shown with boundaries drawn in thick solid and dotted lines (the upper dotted line coincides with the solid line). The area inside the first transition tube (solid lines) is shaded in gray. The numbers correspond to the images and to the associated cells Bn.
The effect of the curvature of the MFEP on the occurrence of fluxes between nonadjacent cells can be understood by referring to Fig. 12. For replicas 10–16, the path is approximately straight, i.e., the curvature is low, and the boundaries of adjacent cells Bn are approximately parallel. The figure suggests that the widest transition tube that is located inside Bi for i = 10, …, 16 and that does not include boundaries between nonadjacent cells is much larger than the one shaded in gray. For replicas 2–7, however, the path is curved, and even a slightly larger transition tube contains boundaries between no-adjacent cells (e.g., B4 and B6).
The curvature of the MFEPs computed in this study was approximated using the formula
| (B1) |
which uses a second-order finite-difference approximation of second derivatives of the MFEPs and where explicit dependence on time t has been omitted.
For the values given below, C(n) was averaged over the duration of the simulations S2 and S3. In the vicinity of α = 0.5, (n ≃ 15), C ≃ 1.5 for MFEP S2, and C ≃ 1.1 for MFEP S3; at the endpoints (n = 1 and n = 30), C ≃ 1 for both MFEPs. This difference may explain why the flux between nonadjacent cells in simulation F2 is significantly larger than that in simulation F3. We also computed the curvature for the MFEP from simulation S1. We found that C(n) ≃ 1.1 at the endpoints of the path and C(n) ≃1.3 for intermediate values of n. However, the curvature from MFEP S1 should not be compared directly to that from MFEP S2 (or MFEP S3) because the CVs are different (see Tables 2, 3).
APPENDIX C: ANALYSIS OF THE TRANSITION STATE IN F3 USING UNBIASED TRAJECTORIES
Whether a given region (or surface) of configurational space corresponds to a transition state is typically tested by commitment analysis, which involves launching trajectories from configurations sampled from the region and checking whether the trajectories reach the endpoint structures with equal probability.
Because the full committor test was computationally infeasible for the present system due to the long integration times involved (see below), the following (less demanding) test was performed. Twenty-five instantaneous structures were chosen randomly from the MD trajectory from simulation F3 confined to cell B15 (α ≃ 0.5). For each structure, 40 sets of momenta were generated according to the Maxwell–Boltzmann distribution using different random seeds, and 25 × 40 = 1000 4-ns trajectories were generated by regular MD at 300 K (with the same thermostat parameters as used for the main calculations). For the final structure in each trajectory, the corresponding cell Bn was determined by using the criterion in Eq. 29. The set of final cell indices is shown in a histogram in Fig. 13. We find that none of the trajectories reach the reactants or the products in the allotted simulation time. In addition, most of the trajectories do not travel far, terminating in the cells B14, B15, and B16. In particular, 20% of the trajectories remain in the initial cell (B15), suggesting that long integration times would be needed for these trajectories to commit to an endstate. We also find that 41% and 59% of the trajectories that escape from B15 terminate on the reactant side (Bn for n < 15) and the product side (Bn for n > 15), respectively. Since the committor values are known to change rapidly in the vicinity of a transition state,29 the 41%/59% ratio should be considered satisfactory.
Figure 13.
Percent histogram of the indices of the cells Bn computed for the final structures of the unbiased trajectories launched from configurations in the cell B15 (filled in black color) of simulation F3.
In Fig. 14 we show the time series of the index of the cells Bn computed for three unbiased trajectories. The two series shown in blue and green were chosen randomly from the entire sample of the trajectories; as expected from Fig. 13, the corresponding trajectories terminate near the starting cell in cells B16 and B17. The time series drawn in red correspond to a rare trajectory chosen such that it terminates in cell B6 (see Fig. 13). The figure shows that the evolution of the trajectories is rather slow, with frequent reversals of the direction of motion, consistent with diffusive behavior.
Figure 14.
Time series of the cell index for three unbiased trajectories launched from configurations in the cell B15 (see text).
APPENDIX D: FREE ENERGY PROFILES COMPUTED BY KRIVOV AND KARPLUS
In this appendix, we describe the difference between the one-dimensional free energy profiles computed in the present study and those computed by Krivov and Karplus in Sec. 2.4 of Ref. 27. Krivov and Karplus construct an MSM from long MD simulation trajectories, with the system states characterized by trajectory clustering, and the rates of transitions between the states computed directly from the trajectory. The values of the committor function are evaluated directly from the MSM, and the partition function Z(q*−Δ<q(x,p)<q*+Δ) of a region that corresponds to a particular value q* of the committor function is proportional to the number of transitions across the q(x, p) = q* surface, computed using the minimum-cut80 and the balanced-cut algorithms.27 The difference from the present definition of the free energy profile is that the free energy is plotted as a function of the progress coordinate r(q*)=Z(q(x,p)<q*)∕Z(q(x,p)≤1). The use of r(q*) ensures that the computed free energy profile is invariant with respect to arbitrary invertible transformations of r(q*).27, 28 The two types of free energy profiles are related simply by a transformation of the abscissa; r(q*) can be computed from the present results using Eqs. 6, 7, 8.
References
- Dellago C., Bolhuis P., and Geissler P., Adv. Chem. Phys. 123, 1 (2002). 10.1002/0471231509 [DOI] [Google Scholar]
- Bolhuis P., Chandler D., Dellago C., and Geissler P., Annu. Rev. Phys. Chem. 53, 291 (2002). 10.1146/physchem.2002.53.issue-1 [DOI] [PubMed] [Google Scholar]
- E W., Ren W., and Vanden-Eijnden E., Phys. Rev. B 66, 052301 (2002). 10.1103/PhysRevB.66.052301 [DOI] [Google Scholar]
- E W., Ren W., and Vanden-Eijnden E., J. Phys. Chem. B 109, 6688 (2005). 10.1021/jp0455430 [DOI] [PubMed] [Google Scholar]
- Maragliano L., Fischer A., Vanden-Eijnden E., and Ciccotti G., J. Chem. Phys. 125, 024106 (2006). 10.1063/1.2212942 [DOI] [PubMed] [Google Scholar]
- Laio A. and Parrinello M., Proc. Natl. Acad. Sci. U.S.A. 99, 12562 (2002). 10.1073/pnas.202427399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iannuzzi M., Laio A., and Parrinello M., Phys. Rev. Lett. 90, 238302 (2003). 10.1103/PhysRevLett.90.238302 [DOI] [PubMed] [Google Scholar]
- Hénin J., Fiorin G., Chipot C., and Klein M. L., J. Chem. Theory Comput. 6, 35 (2010). 10.1021/ct9004432 [DOI] [PubMed] [Google Scholar]
- Faradjian A. and Elber R., J. Chem. Phys. 120, 10880 (2004). 10.1063/1.1738640 [DOI] [PubMed] [Google Scholar]
- Shalloway D. and Faradjian K., J. Chem. Phys. 124, 054112 (2006). 10.1063/1.2161211 [DOI] [PubMed] [Google Scholar]
- Ménétrey J., Bahloul A., Wells A., Yengo C., Morris C., Sweeney H. L., and Houdusse A., Nature (London) 435, 779 (2005). 10.1038/nature03592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ménétrey J., Llinas P., Mukherjea M., Sweeney H., and Houdusse A., Cell 131, 300 (2007). 10.1016/j.cell.2007.08.027 [DOI] [PubMed] [Google Scholar]
- Ménétrey J., Llinas P., Cicolari J., Squires G., Liu X., Li A., Sweeney H., and Houdusse A., EMBO J. 27, 244 (2008). 10.1038/sj.emboj.7601937 [DOI] [PMC free article] [PubMed] [Google Scholar]
- E W. and Vanden-Eijnden E., J. Stat. Phys. 123, 503 (2006). 10.1007/s10955-005-9003-9 [DOI] [Google Scholar]
- Vanden-Eijnden E., Computer Simulations in Condensed Matter: From Materials to Chemical Biology, edited by Ferrario M., Ciccotti G., and Binder K. (Springer, Berlin, 2006),Vol. 1, pp. 439–478. [Google Scholar]
- T. F.MillerIII, Vanden-Eijnden E., and Chandler D., Proc. Natl. Acad. Sci. U.S.A. 104, 14559 (2007). 10.1073/pnas.0705830104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maragliano L. and Vanden-Eijnden E., Chem. Phys. Lett. 446, 182 (2007). 10.1016/j.cplett.2007.08.017 [DOI] [Google Scholar]
- Vanden-Eijnden E. and Venturoli M., J. Chem. Phys. 130, 194101 (2009). 10.1063/1.3129843 [DOI] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3544209 for a summary of the zero-temperature string method, the alanine dipeptide test case, and for further discussion of MFEPs S2 and S3; for an animation of MEP1; for an animation of MEP2; for an animation of MFEP S3.
- E W., Ren W. and Vanden-Eijnden E., J. Chem. Phys. 126, 164103 (2007). 10.1063/1.2720838 [DOI] [PubMed] [Google Scholar]
- Vanden-Eijnden E. and Venturoli M., J. Chem. Phys. 130, 194103 (2009). 10.1063/1.3130083 [DOI] [PubMed] [Google Scholar]
- Apostolakis J., Ferrara P., and Caflisch A., J. Chem. Phys. 110, 2099 (1999). 10.1063/1.477819 [DOI] [Google Scholar]
- Metzner P., Schütte C., and Vanden-Eijnden E., J. Chem. Phys. 125, 084110 (2006). 10.1063/1.2335447 [DOI] [PubMed] [Google Scholar]
- Du R., Pande V., Grosberg A., Tanaka T., and Shakhnovich E., J. Chem. Phys. 109, 334 (1998). 10.1063/1.475393 [DOI] [Google Scholar]
- Ma A. and Dinner A., J. Phys. Chem. B 109, 6769 (2005). 10.1021/jp045546c [DOI] [PubMed] [Google Scholar]
- E W., Ren W., and Vanden-Eijnden E., Chem. Phys. Lett. 413, 242 (2005). 10.1016/j.cplett.2005.07.084 [DOI] [Google Scholar]
- Krivov S. and Karplus M., J. Phys. Chem. B 110, 12689 (2006). 10.1021/jp060039b [DOI] [PubMed] [Google Scholar]
- Krivov S. and Karplus M., Proc. Natl. Acad. Sci. U.S.A. 105, 13841 (2008). 10.1073/pnas.0800228105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. and Hummer G., Proc. Natl. Acad. Sci. U.S.A. 102, 6732 (2005). 10.1073/pnas.0408098102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khavrutskii I., Arora K., and C.BrooksIII, J. Phys. Chem. 125, 174108 (2006). 10.1063/1.2363379 [DOI] [PubMed] [Google Scholar]
- Khavrutskii I. and McCammon J., J. Chem. Phys. 127, 124901 (2007). 10.1063/1.2771172 [DOI] [PubMed] [Google Scholar]
- Branduardi D., Gervasio F., and Parrinello M., J. Chem. Phys. 126, 054103 (2007). 10.1063/1.2432340 [DOI] [PubMed] [Google Scholar]
- Pan A., Sezer D., and Roux B., J. Phys. Chem. B 112, 3432 (2008). 10.1021/jp0777059 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugita Y., Kitao A., and Okamoto Y., J. Chem. Phys. 113, 6042 (2000). 10.1063/1.1308516 [DOI] [Google Scholar]
- Fukunishi H., Watanabe O., and Takada S., J. Chem. Phys. 116, 9058 (2002). 10.1063/1.1472510 [DOI] [Google Scholar]
- Kästner J. and Thiel W., J. Chem. Phys. 123, 144104 (2005). 10.1063/1.2052648 [DOI] [PubMed] [Google Scholar]
- Murata K., Sugita Y., and Okomoto Y., Chem. Phys. Lett. 385, 1 (2004). 10.1016/j.cplett.2003.10.159 [DOI] [Google Scholar]
- Lou H. and Cuckier R., J. Phys. Chem. B 110, 24121 (2006). 10.1021/jp064303c [DOI] [PubMed] [Google Scholar]
- Wolf M., Jongejan J., Laman J., and de Leeuw S., J. Phys. Chem. B 112, 13493 (2008). 10.1021/jp804285e [DOI] [PubMed] [Google Scholar]
- Torrie G. and Valleau J., J. Comput. Phys. 23, 187 (1977). 10.1016/0021-9991(77)90121-8 [DOI] [Google Scholar]
- West A., Elber R., and Shalloway D., J. Chem. Phys. 126, 145104 (2007). 10.1063/1.2716389 [DOI] [PubMed] [Google Scholar]
- Elber R., Biophys. J. 92, L85 (2007). 10.1529/biophysj.106.101899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shalloway D., J. Chem. Phys. 105, 9986 (1996). 10.1063/1.472830 [DOI] [Google Scholar]
- Hummer G. and Kevrekidis I., J. Chem. Phys. 118, 10762 (2003). 10.1063/1.1574777 [DOI] [Google Scholar]
- Swope W., Pitera J., and Suits F., J. Phys. Chem. B 108, 6571 (2004). 10.1021/jp037421y [DOI] [Google Scholar]
- Swope W., Pitera J., Suits F., Pitman M., Eleftheriou M., Fitch B., Germain R., Rayshubski A., Ward T., Zhestkov Y., and Zhou R., J. Phys. Chem. B 108, 6582 (2004). 10.1021/jp037422q [DOI] [Google Scholar]
- Krivov S. and Karplus M., J. Chem. Phys. 117, 10894 (2002). 10.1063/1.1517606 [DOI] [Google Scholar]
- Chodera J., Singhal N., Pande V., Dill K., and Swope W., J. Chem. Phys. 126, 15501 (2007). 10.1063/1.2714538 [DOI] [PubMed] [Google Scholar]
- Noe F., Horenko I., Schütte C., and Smith J., J. Chem. Phys. 126, 155102 (2007). 10.1063/1.2714539 [DOI] [PubMed] [Google Scholar]
- Buchete N. and Hummer G., J. Phys. Chem. B 112, 6057 (2008). 10.1021/jp0761665 [DOI] [PubMed] [Google Scholar]
- Norris J., Markov Chains, Cambridge Series in Statistical and Probabilistic Mathematics (Cambridge University Press, Cambridge, 2004). [Google Scholar]
- Vanden-Eijnden E., Venturoli M., Ciccotti G., and Elber R., J. Chem. Phys. 129, 174102 (2008). 10.1063/1.2996509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells A., Lin A., Chen L., Safer D., Cain S., Hasson T., Carragher B., Milligan R., and Sweeney H., Nature (London) 401, 505 (1999). 10.1038/46835 [DOI] [PubMed] [Google Scholar]
- Haberthür U. and Caflisch A., J. Comput. Chem. 29, 701 (2008). 10.1002/jcc.20832 [DOI] [PubMed] [Google Scholar]
- Brooks B., Bruccoleri R., Olafson B., States D., Swaminathan S., and Karplus M., J. Comput. Chem. 4, 187 (1983). 10.1002/(ISSN)1096-987X [DOI] [Google Scholar]
- Brooks B. R., C. L.BrooksIII, A. D.MacKerellJr., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., Karplus M., J. Comput. Chem. 30, 1545 (2009). 10.1002/jcc.v30:10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engels M., Jacoby E., Krüger P., Schlitter J., and Wollmer A., Protein Eng. 5, 669 (1992). 10.1093/protein/5.7.669 [DOI] [PubMed] [Google Scholar]
- Schlitter J., Engels M., Krüger P., Jacoby E., and Wollmer A., Targeted molecular dynamics simulation of conformational change—application to the T → R transition in insulin Mol. Simul. 10, 291 (1993). 10.1080/08927029308022170 [DOI] [Google Scholar]
- Ren W., Vanden-Eijnden E., Maragakis P., and E W., J. Chem. Phys. 123, 134109 (2005). 10.1063/1.2013256 [DOI] [PubMed] [Google Scholar]
- Eckart C., Phys. Rev. 47, 552 (1935). 10.1103/PhysRev.47.552 [DOI] [Google Scholar]
- Czerminski R. and Elber R., J. Chem. Phys. 92, 5580 (1990). 10.1063/1.458491 [DOI] [Google Scholar]
- Kabsch W., Acta Cryst. A32, 922 (1976). 10.1107/S0567739476001873 [DOI] [Google Scholar]
- Maragliano L., Cottone G., Ciccotti G., and Vanden-Eijnden E., J. Am. Chem. Soc. 132, 1010 (2010). 10.1021/ja905671x [DOI] [PubMed] [Google Scholar]
- Risken H., The Fokker-Planck Equation. Methods of Solution and Applications, ed. (Springer-Verlag, Berlin, 1989). [Google Scholar]
- Andricioaei I. and Karplus M., J. Chem. Phys. 115, 6289 (2001). 10.1063/1.1401821 [DOI] [Google Scholar]
- Elber R. and Karplus M., Chem. Phys. Lett. 139, 375 (1987). 10.1016/0009-2614(87)80576-6 [DOI] [Google Scholar]
- Jónsson G. and Jacobsen K., “Nudged elastic band method for ending minimum energy paths,” in Classical and Quantum Dynamics in Condensed Phase Simulations, edited by Berne B., Ciccotti G., and Coker D. (World Scientific, Singapore, 1998) pp. 385–404. [Google Scholar]
- Fisher S. and Karplus M., Chem. Phys. Lett. 194, 252 (1992). 10.1016/0009-2614(92)85543-J [DOI] [Google Scholar]
- Hu J., Ma A., and Dinner A., J. Chem. Phys. 125, 114101 (2006). 10.1063/1.2335640 [DOI] [PubMed] [Google Scholar]
- Oseen C. W., Hydrodynamik (Akademisches, Leipzig, 1927). [Google Scholar]
- Rotne J. and Prager S., J. Chem. Phys. 50, 4831 (1969). 10.1063/1.1670977 [DOI] [Google Scholar]
- de la Torre J., Huertas M., and Carrasco B., Biophys. J. 78, 719 (2000). 10.1016/S0006-3495(00)76630-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aragon S. and Hahn D., Biophys. J. 91, 1591 (2006). 10.1529/biophysj.105.078188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwanzig R., Adv. Chem. Phys. 15, 325 (1969). 10.1002/SERIES2007 [DOI] [Google Scholar]
- Pastor R. and Karplus M., J. Phys. Chem 92, 2636 (1988). 10.1021/j100320a047 [DOI] [Google Scholar]
- Venable R. and Pastor R. W., Biopolymers 27, 1001 (1988). 10.1002/(ISSN)1097-0282 [DOI] [PubMed] [Google Scholar]
- Cruz E. D. L., Ostap E., and Sweeney H., J. Biol. Chem. 276, 32373 (2001). 10.1074/jbc.M104136200 [DOI] [PubMed] [Google Scholar]
- Rock R., Rice S., Wells A., Purcell T., Spudich J., and Sweeney H., Proc. Natl. Acad. Sci. U.S.A. 98, 13655 (2001). 10.1073/pnas.191512398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H., Li A., Chen L.-Q., Houdusse A., Selvin P., and Sweeney L., Proc. Natl. Acad. Sci. U.S.A., 104, 778 (2007). 10.1073/pnas.0610066104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gomory R. and Hu T., SIAM (Soc. Ind. Appl. Math.) J. Appl. Math. 9, 551 (1961). 10.1137/0109047 [DOI] [Google Scholar]