Measurement of regional compliance using 4DCT images for assessment of radiation treatment

Abstract

Purpose: Radiation-induced damage, such as inflammation and fibrosis, can compromise ventilation capability of local functional units (alveoli) of the lung. Ventilation function as measured with ventilation images, however, is often complicated by the underlying mechanical variations. The purpose of this study is to present a 4DCT-based method to measure the regional ventilation capability, namely, regional compliance, for the evaluation of radiation-induced lung damage.

Methods: Six 4DCT images were investigated in this study: One previously used in the generation of a POPI model and the other five acquired at Henry Ford Health System. A tetrahedral geometrical model was created and scaled to encompass each of the 4DCT image domains. Image registrations were performed on each of the 4DCT images using a multiresolution Demons algorithm. The images at the end of exhalation were selected as a reference. Images at other exhalation phases were registered to the reference phase. For the POPI-modeled patient, each of these registration instances was validated using 40 landmarks. The displacement vector fields (DVFs) were used first to calculate the volumetric variation of each tetrahedron, which represents the change in the air volume. The calculated results were interpolated to generate 3D ventilation images. With the computed DVF, a finite element method (FEM) framework was developed to compute the stress images of the lung tissue. The regional compliance was then defined as the ratio of the ventilation and stress values and was calculated for each phase. Based on iterative FEM simulations, the potential range of the mechanical parameters for the lung was determined by comparing the model-computed average stress to the clinical reference value of airway pressure. The effect of the parameter variations on the computed stress distributions was estimated using Pearson correlation coefficients.

Results: For the POPI-modeled patient, five exhalation phases from the start to the end of exhalation were denoted by P_i, i=1,…,5, respectively. The average lung volume variation relative to the reference phase (P₅) was reduced from 18% at P₁ to 4.8% at P₄. The average stress at phase P_i was 1.42, 1.34, 0.74, and 0.28 kPa, and the average regional compliance was 0.19, 0.20, 0.20, and 0.24 for i=1,…,4, respectively. For the other five patients, their average R_v value at the end-inhalation phase was 21.1%, 19.6%, 22.4%, 22.5%, and 18.8%, respectively, and the regional compliance averaged over all six patients is 0.2. For elasticity parameters chosen from the potential parameter range, the resultant stress distributions were found to be similar to each other with Pearson correlation coefficients greater than 0.81.

Conclusions: A 4DCT-based mechanical model has been developed to calculate the ventilation and stress images of the lung. The resultant regional compliance represents the lung’s elasticity property and is potentially useful in correlating regions of lung damage with radiation dose following a course of radiation therapy.

INTRODUCTION

Modern functional imaging techniques, such as single photon emission computed tomography (SPECT),^{1, 2, 3} hyperpolarized magnetic resonance imaging (MRI),^{4, 5} and xenon-enhanced computed tomography (Xe-CT),^{6, 7} have been used for diagnosis and treatment of pulmonary diseases. Ventilation images have also been combined with pulmonary mechanics to analyze regional physiology⁷ and compliance changes.⁸ Recently, from CT image sequences, Simon et al.^{9, 10} noted that the average lung density decreased when the lung volume increased along with the inflow of air. Based on a mass conservation principle, Simon et al. assumed that all the volume changes are due to the increase in air volume, i.e., V_EI−V_EE=V_AI−V_AE, where V_EI and V_EE are the lung volumes at the ends of inhalation (EI) and exhalation (EE), and V_AI and V_AE are their corresponding air volumes, respectively. Suppose that the Hounsfield unit (H) of air is approximately −1000 and the air fraction factor F is F=−H∕1000. The specific change in air volume can, consequently, be represented as

$${\text{sVol}}_{\text{air}}=\frac{V_{\text{AI}}-V_{\text{AE}}}{V_{\text{AE}}}=1000\frac{H_{\text{EI}}-H_{\text{EE}}}{H_{\text{EE}}\left(H_{\text{EI}}+1000\right)}.$$ (1)

On the other hand, Reinhardt et al.¹¹ demonstrated that the Jacobian determinant J_φ of the transformation, φ, between two deformed images is correlated with their corresponding Xe-CT measured ventilation. Actually, when the volume V_EI(p) of the image voxel p at the phase EI is changed to V_EE(p) at the phase EE, the two volumes satisfy the correlation V_EI(p)≈V_EE(p)J_φ(p). Consequently, the specific change in geometric volume can be calculated by

$${\text{sVol}}_{\text{geo}}\left(p\right)=\frac{V_{\text{EI}}\left(p\right)-V_{\text{EE}}\left(p\right)}{V_{\text{EE}}\left(p\right)}\approx J_{\phi }\left(p\right)-1.$$ (2)

These 4DCT-based methods [by Eq. 1 or Eq. 2] have the advantage of directly incorporating the ventilation function into radiation treatment planning without requiring additional image registration procedures.^{12, 13} It has been shown that functional planning can reduce the high-functional lung dose at the cost of the increased dose in low-functional lung volume¹ or the degraded PTV conformity and homogeneity.¹³ The ventilation function gained in these applications could be maximized if a quantitative relationship between radiation dose and radiation-induced ventilation reduction can be established.

Recently, Ding et al.¹⁴ demonstrated that there is a weak correlation between the radiation dose and the reduction in the ventilation function, and that this relationship varies at different locations. The weak correlation could be explained partly by the fact that the radiation-induced elasticity changes at one place could impact remote ventilation distributions. On the other hand, Reinhardt et al.¹¹ observed that the correlation between the Jacobian based ventilation and the Xe-CT ventilation was optimal when the Jacobian was calculated with the airway pressure changed from 1.0 to 1.5 kPa. Guerrero et al.⁸ investigated the effect of irradiation on the ventilation function under airway pressures of 0.2, 1.0, and 1.8 kPa and found that irradiation reduced ventilation up to 60% under low pressures; the change was found to be less pronounced at higher distending pressures. These results indicate that ventilation measurements are closely related to pulmonary mechanics. Further analysis of regional stress and elasticity changes may help assess radiation-induced tissue damage.

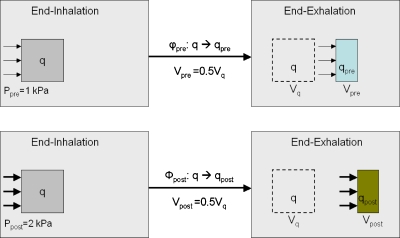
The impact of regional stress on ventilation measurement can be illustrated as in Fig. 1. Let the regional compliance (RC) of the lung at each image voxel be defined as ventilation per unit stress. Suppose that φ_pre and φ_post represent two deformation maps that are from the end-inhalation (EI) to the end-exhalation (EE) in the cases of the pre- and post-treatments, respectively. With the deformation maps φ_pre and φ_post, the voxel q was compressed to half of its initial volume, i.e., ${\text{sVol}}_{\text{geo}}^{{\phi }_{\text{pre}}}\left(q\right)={\text{sVol}}_{\text{geo}}^{{\phi }_{\text{post}}}\left(q\right)=0.5$. Due to radiation-induced elasticity changes, the required stresses P_pre and P_post at the voxel q could be different for the two maps φ_pre and φ_post. If P_post=2P_pre=2 kPa, then the regional compliance of the maps φ_pre and φ_post at q is equal to 0.5 and 0.25∕kPa, respectively. In this case, sVol_geo-ventilation images cannot show the radiation-induced change in regional compliance at the voxel q.

Figure 1.

The sVol_geo value calculated at the voxel q is 0.5 in both pre- and post-treatments, while the voxel has different regional compliances. The sVol_geo images cannot show the RC difference at the voxel q.

Regional compliance represents the ventilation capability of the alveoli in the lung and can be used for the evaluation of radiation-induced lung damage. The purpose of this study is to present a 4DCT-based method to measure changes in the regional compliance. Specifically, a finite element technique is combined with deformable image registration (DIR) to calculate the distribution of elastic stress at various respiration phases. Images quantifying lung ventilation and regional compliance are then computed. The accuracies of the DIR and mechanical modeling are evaluated and their impact on the computed stress and ventilation are analyzed statistically.

MATERIALS AND METHODS

Image preprocessing and deformable registration

Six 4DCT images acquired from lung cancer patients were used in this study. One of these images is named POPI image, which was used for creating the point-validated pixel-based (POPI) breathing thorax model (www.creatis.insa-lyon.fr/rio/popi-model).¹⁵ The POPI image consists of ten respiratory phase-correlated CT datasets with 40 landmarks identified for each phase. The other 4DCT images were acquired from five lung cancer patients treated in the Department of Radiation Oncology, Henry Ford Health System (HFHS). Under a protocol approved by the HFHS Institutional Review Board, free-breathing 4DCT acquisition was performed using multislice helical CT (Brilliance Big Bore; Philips Medical Systems, Cleveland, OH) coupled with Varian RPM^™ respiratory gating system. 4DCT scans were retrospectively sorted into four different phases: end-inhalation, midexhalation, end-exhalation, and midinhalation. The images of all the phases were imported into the PINNACLE treatment planning system (Philips Medical Systems) with the CT image intensities automatically converted into the range between 0 and 4096. Lung tissue was contoured using the automatic thresholding tool in PINNACLE, and manual corrections were applied where necessary.

The multiresolution Demons algorithm implemented in ITK (Ref. ¹⁶) was used for deformable image registration. The number of iterations in the algorithm was set to 200, and other parameters were set as described in the article by Zhong et al.¹⁷ Image registrations were performed from each of the expiration-correlated phases to the reference phase, which was chosen to be at the end of exhalation. The resultant displacement vector field (DVF) was compared to the standard displacements computed from the positions of the landmarks identified on the two images being registered.

Lung stress images

Based on the principle of conservation of elastic energy, tissue deformation can be quantified using a finite element method (FEM) that leads to the establishment of a set of linear equations,¹⁸

$$M{U}^T=F^T,$$ (3)

where U and F are the vectors of all displacements and external forces and M is the global stiffness matrix. Each entry in M is composed of multiple entries in a matrix D that describes the relation between stress σ and strain ε. For the linear isotropic relation, D is defined by

$$D=\frac{E}{\left(1+\rho \right)\left(1-2\rho \right)}\left[\begin{array}{cccccc}1-\rho & \rho & \rho & 0& 0& 0\\ \rho & 1-\rho & \rho & 0& 0& 0\\ \rho & \rho & 1-\rho ,& 0& 0& 0\\ & & & \frac{1-2\rho }{2}& 0& 0\\ & \text{Sym}& & & \frac{1-2\rho }{2}& 0\\ & & & & & \frac{1-2\rho }{2}\end{array}\right],$$ (4)

where E and ρ are Young’s modulus and Poisson ratio, respectively. M is a sparse matrix, and the mechanical stress in each element depends on the displacements of the vertices adjacent to this element. After the displacements of all the vertices are computed, the mechanical stress within each element in the lung is then uniquely determined by the lung’s elastic property.

Displacements of each node in the finite element model were interpolated from the DVF of deformable image registrations performed on a 4DCT image dataset. Specifically, two images at different phases were registered using the Demons algorithm, and the resultant displacements were saved in the image domain. The displacement vector $\left[u_x^k,u_y^k,u_z^k\right]$ of tetrahedral vertex k was assigned from the displacement vector of the image voxel occupied by the vertex k. The displacement vectors of all the vertices were substituted into Eq. 3 to calculate the component forces f^e_j at the vertices of element j. Suppose that the image voxel i is centered at c_i, which is located within element j. v is a vertex of the element j. N_v is the neighbor element set of the vertex v. The mechanical stress of the image voxel i is then defined by

$$p\left(i\right)=\sum _{\nu =1,2,3,4}\frac{w_{i,\nu }}{\pi r_{\nu }^2}\sum _{e_j∊N_{\nu }}\left|f_{\nu }^{e_j}\left(u\right)\right|,$$ (5)

where $f_{\nu }^{e_j}\left(u\right)$ is the force calculated by Eq. 3, r_v is the radius averaged over all the elements in N_v, and w_i,ν is the volume coordinate defined by¹⁸

$$w_{i,\nu }=\frac{V\left(S_{\nu },c_i\right)}{V\left(S_1,c_i\right)+V\left(S_2,c_i\right)+V\left(S_3,c_i\right)+V\left(S_4,c_i\right)},\nu =1,\dots ,4,$$ (6)

where S_ν represents the triangle face opposite to ν and V(S_ν,c_i) is the volume of the tetrahedron (S_ν,c_i). The calculated p(i) and the displacements have units of kPa and cm, respectively. In FEM modeling, the external forces at any internal node should be zero; but inaccurate displacements may result in nonzero forces at these nodes.¹⁹ Consequently, the error of the calculated mechanical stress associated with inaccurate displacements and parameters can be quantified by

$$\delta \left(i\right)=\sum _{\nu =1,2,3,4}\frac{w_{i,\nu }}{\pi r_{\nu }^2}\sum _{e_j∊N_{\nu }}{f}_{\nu }^{e_j}\left(u\right),$$ (7)

where the variables are defined as in Eq. 5. The stress value calculated by Eq. 5 reflects the regional mechanical status of the deformed lung and may be compared to the results of experiments such as spirometry tests^{20, 21} or external chest stress measurements.²²

Regional compliance images

Previous registration-based ventilation imaging techniques used either the specific ratio of density variations⁹ or Jacobian determinants¹¹ to represent the ventilation function within each image voxel. The quality of the computed images is subject to the accuracy and smoothness of the displacements of the registration.

Since the change in lung volume is equivalent to the change in air volume,⁹ the ventilation value of each image voxel can be calculated from the volumetric variation of each tetrahedron. Specifically, when a CT image is modeled, a cubic prototype mesh that consists of 131 614 nodes and 747 384 tetrahedral elements is scaled to match the corresponding image domain. Consequently, the coordinate vector $\left(x_j^k,y_j^k,z_j^k\right)$ of vertex k (k=1,…,4) of element j in the mesh can be derived, and the volume of tetrahedron j is then calculated by

$$V\left(j\right)=\frac{1}{6}\left|\begin{array}{cccc}1& 1& 1& 1\\ x_j^1& x_j^2& x_j^3& x_j^4\\ y_j^1& y_j^2& y_j^3& y_j^4\\ z_j^1& z_j^2& z_j^3& z_j^4\end{array}\right|.$$ (8)

Displacements resulted from the deformation map φ of lung tissue (computed using deformable image registration) are used to update the coordinates of each vertex of the tetrahedral mesh and then to recalculate the volume of the deformed mesh. The relative volumetric variation R_V(j) of element j is then defined by

$$R_V\left(j\right)=\frac{\left|V_{\text{EI}}\left(j\right)-V_{\text{EE}}\left(j\right)\right|}{V_{\text{EE}}\left(j\right)},$$ (9)

where V_EI and V_EE are the lung volumes calculated by Eq. 8 at the ends of inhalation and exhalation. The computed values of R_V(j) are interpolated to generate a ventilation image for the deformation map φ.

With the stress p(i) and the volumetric variation R_V(i) defined in Eqs. 5, 9, the voxel-based regional compliance, RC(i), at voxel i can be defined by

$$\text{RC}\left(i\right)=\frac{R_V\left(i\right)}{p\left(i\right)}=\left|\frac{V_{\text{EI}}\left(i\right)-V_{\text{EE}}\left(i\right)}{p\left(i\right)V_{\text{EE}}\left(i\right)}\right|.$$ (10)

As the stress-corrected ventilation, the RC image represents the ventilation capability of the alveoli in the lung and reveals the elasticity property of the lung tissue.

Effect of elasticity parameters on computed stress images

With the displacements generated from the Demons registration, the stress computed is then determined by the elasticity parameters used. The elasticity parameters of the lung reported, however, vary largely due to different experimental conditions or calibration methods.²³ For example, the Poisson ratio is often assigned using values of ρ=0.3 or ρ=0.42 in modeling the lung deformation.^{23, 24} While the influence of the parameter variations on the accuracy of spatial deformation was reported to be negligible,²³ the elastic force calculated by Eq. 3 is linearly proportional to the Young’s modulus and increases along with the Poisson ratio. In this study, the potential range of the lung’s elasticity parameters was estimated based on the comparison between the computed stress values and the clinical reference value of airway pressure.

Previous studies show that the free-breathing airway pressures are in the range of 1 kPa.^{25, 26} The computed elastic stress is consequently assumed to have a similar range. The parameters with which the computed stress falls within this range will form a potential parameter domain. The similarity of stress distributions computed with the elasticity parameters chosen from this domain was investigated using the Pearson correlation coefficient. Specifically, suppose A and B represent two stress images. Let $\overline{A}$ and $\overline{B}$ be their means, and σ_A and σ_B are their standard deviations, respectively. The similarity of the two images can be measured by the Pearson correlation coefficient τ,

$$\tau \left(A,B\right)=\frac{\sum \left(A\left(i\right)-\overline{A}\right)\left(B\left(i\right)-\overline{B}\right)}{{\sigma }_A{\sigma }_B}.$$ (11)

With the similarity metric τ, the stress images calculated with different parameters can be compared to each other. When the τ approaches one, the two images are statistically identical in their intensity distributions.

RESULTS

Evaluation of deformable image registrations

For the POPI-modeled patient, five exhalation phases, from the start to the end of exhalation, corresponding to phases P₁ to P₅, respectively, were studied using the downloaded 4DCT dataset. The phase at the end of exhalation (P₅) was selected as the reference dataset. The other four phases were registered to the reference. Mean displacements of these registrations were found to be 5.8, 5.3, 3.6, and 1.5 mm, respectively. The standard displacements were derived from the comparison of the 40 landmark positions identified on each image. The registration-derived displacements were compared to the standard displacements with their mean errors shown in Table 1.

Table 1.

The mean errors of the Demons registrations related to the measured landmark displacements.

Mean error (mm)	P1→P5	P2→P5	P3→P5	P4→P5
X	0.73	0.80	0.68	0.55
Y	0.69	0.79	0.64	0.52
Z	0.80	0.92	1.14	0.91

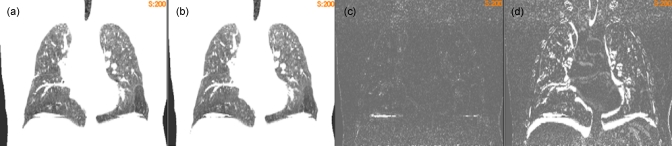
After 200 iterations, the registration errors in Table 1 are within the dimensions of a single voxel (0.98×0.98×2.0 mm). Figure 2 shows that for the registration from P₁ to P₅, there is a good agreement between the reference image [Fig. 2a] and the warped moving image [Fig. 2b]. The mean value of their difference image [Fig. 2c] is 7.3, which is reduced from the mean difference of 106.4 between the reference and the original moving images [Fig. 2d]. It can be observed that the motion-induced 4D sorting artifacts [Fig. 2a] caused the registration errors in the diaphragm region [Fig. 2c]. However, this region, like other soft-tissue areas, can be excluded from ventilation analysis at the beginning of this study because of the limited air volume contained in this region.

Figure 2.

(a) The reference image of the POPI-modeled patient. (b) The warped moving image of the POPI-modeled patient. (c) The difference image between the reference and the warped moving images. (d) The difference image between the reference and the original moving images. The images in (a) and (b) are displayed at the window and level of 500/180, and the images in (c) and (d) are at the window and level of 500/50.

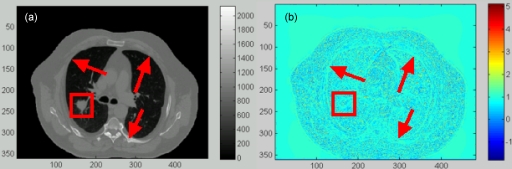
In general, the DIR errors in regions with low image contrasts (e.g., within the tumor) cannot be identified by the intensity difference of the two images being registered. In these regions, the registration errors can be evaluated based on the compressibility of the registered organs. Since the tumor is nearly incompressible, the Jacobian values calculated inside the tumor should be equal to 1. Figure 3b shows that there is a unitary annulus around the tumor boundary in the calculated Jacobian image. This indicates that the Demons registration can achieve a reasonable accuracy at the tumor boundary, but not in the interior of the tumor. The general accuracy of the DIR and the associated stress computation will be further evaluated in Sec. 3B.

Figure 3.

(a) A transversal slice of the reference image of the POPI-modeled patient with the tumor marked within the square box. (b) The Jacobian image of the Demons DVF.

Computation of elastic stress images

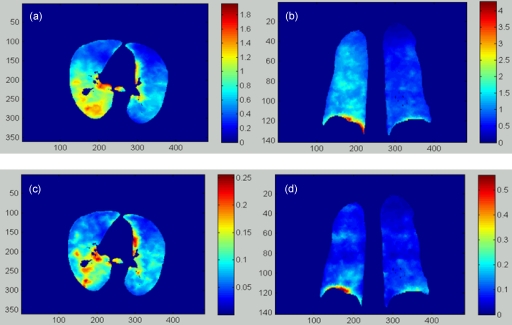
With the DVFs generated from the 4DCT image of the POPI-modeled patient, the elastic stress distribution was computed for each phase. The mechanical parameters of the lung were assigned using E=1.0 kPa and ρ=0.3, as recommended by Werner et al.²³ The stress value at each image voxel was calculated using Eq. 5. The resultant stress images were segmented with the lung contour in the reference phase. The computed results for the POPI-modeled patient are illustrated in Fig. 4.

Figure 4.

(a) and (b) are the transversal and coronal cuts of the stress image (kPa) of the POPI-modeled patient calculated from phase 1 to phase 5. (c) and (d) are the corresponding cuts of the stress image (kPa) calculated from phase 4 to phase 5.

The transversal and coronal slices of the elastic stress images for the deformation from phase 1 to phase 5 are shown in Figs. 4a, 4b, and those for the deformation from phase 4 to phase 5 are shown in Figs. 4c, 4d, respectively. As illustrated by the color bars, the stress magnitude decreases as the phase increases. For this patient, the right lung is more compressed than the left one [Figs. 4a, 4b]. Furthermore, the patterns of the unevenly distributed physical stress change from phase to phase, as illustrated in Fig. 4.

The average elastic stress decreased from 1.42 to 0.28 kPa when the expiration proceeded from phase 1 to phase 4 (see Table 2). The elastic stress at the reference phase (P₅) was assumed to be zero. The accuracy of the stress computation was verified using the δ image calculated by Eq. 7. As shown in Table 2, the impact of these registration errors on the computed stress is limited and the percentage of the stress error relative to the end-inhalation stress is less than 7.7%. The small δ values in Fig. 5 suggest that the registration-related uncertainty in stress computation is limited. The quantitative stress images in Fig. 4 reflect the region-specific pulmonary dynamics and provide more information than a single value of the airway pressure for analysis of ventilation function.

Table 2.

The elastic stress and the associated errors for the deformation map from phase i (i=1,…,4) to phase 5 were computed using the registration-based biomechanical model.

Mean	Phase 1	Phase 2	Phase 3	Phase 4
Stress p (kPa)	1.42	1.34	0.74	0.28
Error δ (kPa)	0.11	0.10	0.09	0.07

Figure 5.

The residue errors of the elastic stress computed at (a) phase 1 and (b) phase 4.

Computation of mesh-based ventilation images

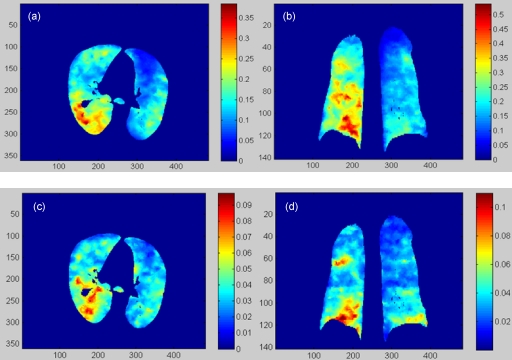
The R_V-ventilation images of the POPI-modeled patient, as shown in Fig. 6, were generated from Eq. 9 with the registrations performed from phase 1 and phase 4 to phase 5. The image intensity in these figures represents the percentage of the volume changes in each voxel, relative to the volume in the reference phase. From Fig. 6b, it can be observed that for this patient, the ventilation in the right lung is stronger than in the left.

Figure 6.

(a) and (b) are the transversal and coronal cuts of the R_V ventilation image of the POPI-modeled patient calculated from phase 1 to phase 5. (c) and (d) are the corresponding cuts of the R_V image calculated from phase 4 to phase 5.

Similarly, the R_V images of the lung deformation from phase i (i=2,3) to phase 5 were also calculated. The average R_V value decreased from 18.3% in phase 1 to 4.8% in phase 4, with high ventilation shown mainly in the dorsal and basal regions (Fig. 6). Note that while the DIR may have relatively large errors inside the tumor and the diaphragm, these regions do not have ventilation and have been excluded in the following statistics analysis.

Computation of regional compliance images

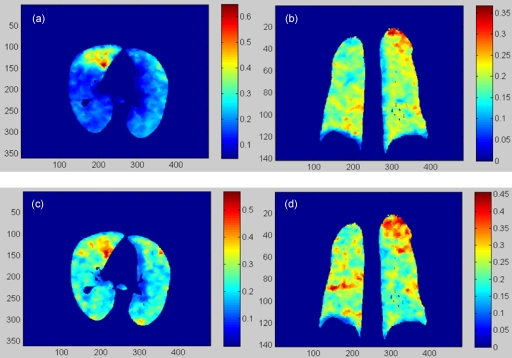
The regional compliance images were computed using Eqs. 7, 9, 10 based on the displacements of the registrations from phase i (i=1,…,4) to phase 5. The resultant regional compliance images for the POPI-modeled patient are shown in Fig. 7. The mean values of the regional compliance calculated for the registration from phase i to phase 5 are 0.186, 0.199, 0.201, and 0.239 for i=1,…,4, respectively. Recall that the average stress of the lung changes from 1.42 to 0.28 kPa when the phase changes from phase 1 to phase 4. Consequently, the above results show that the average regional compliance slightly increases as the average stress decreases.

Figure 7.

(a) and (b) are the transversal and coronal cuts of the RC image (1/kPa) calculated from phase 1 to phase 5 for the POPI-modeled patient. (c) and (d) are the corresponding cuts of the RC-image calculated from phase 4 to phase 5.

Note that the average computed ventilation at phase 1 is four times larger than that in phase 4, but the variation in the regional compliance computed between different phases is less than 28%. This may suggest that the regional compliance, which reveals the elastic property of the lung tissue, is less influenced by variation in the respiratory cycle.

Regional compliance images of different patients

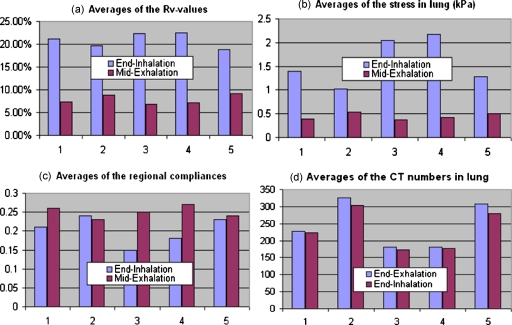
The 4DCT images for the rest five lung cancer patients were acquired at HFHS with the patients trained for smooth breathing. These images were sorted into four phases. Deformable image registrations were performed from the end-inhalation phase and the midexhalation phase to the end-exhalation phase, respectively. The resultant displacements were used to calculate the regional compliance images for the five patients. It has been observed that their average R_v values at the end-inhalation are 21.1%, 19.6%, 22.4%, 22.5%, and 18.8%, respectively [Fig. 8a]. The mechanical model developed for the POPI-modeled patient was applied to the five patients to calculate their stress and regional compliance images. The average stresses calculated at the end-inhalation for the five patients are 1.39, 1.03, 2.04, 2.18, and 1.29 (kPa), the average regional compliances are 0.21, 0.24, 0.15, 0.18, and 0.23, and the regional compliance averaged over all the six patients is 0.2. For the midexhalation phase, the R_v and compliance values have also been calculated and shown in Fig. 8. It is noted that average ventilation and stress values decreased for all the five patients [Figs. 8a, 8b] and average compliance values increased for patients 1 and 3–5 [Fig. 8c] as the phase was changed from the endinhalation to the midexhalation. Except for patient 2, the results from the other four patients are consistent with the observation that compliance is a decreasing function of the stress as the phase changes from end-inhalation to midexhalation.²⁷ Compared to other patients, patients 2 and 5 have higher lung CT numbers [Fig. 8d] and greater lung density differences between the endinhalation and the endexhalation phases. Also the two patients (especially patient 2) have smaller lung volumes [Fig. 9e] but larger density variations between the different deformation stages, so their mean computed stress values may be more sensitive to mechanical modeling inaccuracies. This may partly explain why the mean compliances of these two patients have limited variation between the midexhalation and end-inhalation phases, as shown in Fig. 8c.

Figure 8.

The ventilation and compliance measured from the 4DCT images of the five patients treated in HFHS: (a) The average R_v values, (b) the average stresses, (c) the average regional compliances, and (d) the average CT numbers in the lung.

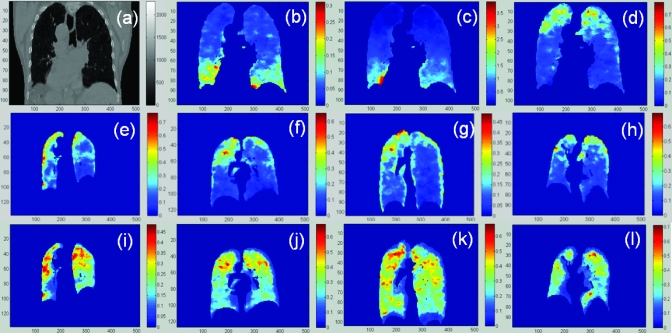
Figure 9.

(a) the CT image of the first patient treated in HFHS; [(b)–(d)] the R_v, stress, and regional compliance images; [(e)–(h)] the regional compliance images of the other four patients at the endinhalation phase and [(i)–(l)] the corresponding images at the midexhalation phase.

The CT image of the first patient treated in HFHS is illustrated in Fig. 9a and the corresponding ventilation, stress, and regional compliance images are shown in Figs. 9b, 9c, 9d. From Figs. 9b, 9c, it can be observed that both the ventilation and the stress values are high in the inferior part of the lung. This is consistent with the previous observation that alveolar ventilation is uneven, even in a healthy lung, and that conditions for air exchange are most favorable in the basal regions.²⁸

For the rest four patients treated in HFHS, the regional compliance images at the end-inhalation and midexhalation phases are shown in the middle and bottom lines of Fig. 9, respectively. It is observed that the regional compliance is relatively high in the superior regions where the stress is low. This phenomenon can be explained by the fact that less pressure is required to get the same amount of the volume expanded in a low stress region than in a high stress region. Consequently, relatively high compliance appears in the lowly stressed superior lung region [Fig. 9d, 9e, 9f, 9g, 9h, 9i, 9j, 9k, 9l].

Effects of elasticity parameters on computed stress distributions

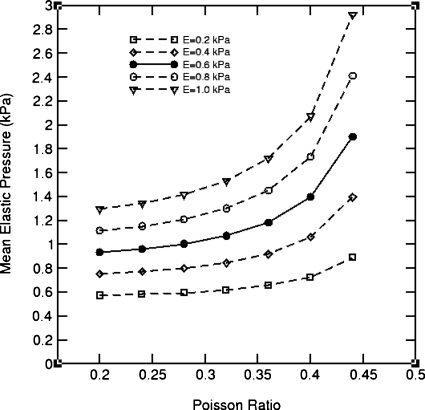
Displacements derived from the Demons-based deformable image registration for the POPI-modeled patient were substituted into Eq. 5 to calculate elastic stress, where the Young’s modulus E was assigned by E=0.2+0.2j (kPa), j=0,…,4, and the Poisson ratio ρ assigned by ρ=0.2+0.04j, j=0,…,6, respectively. For each pair of the parameters, the FEM computation was repeated. The computed stress values averaged in the lung are shown in Fig. 10.

Figure 10.

The average elastic stress of the lung deformation of the POPI-modeled patient simulated with different elasticity parameters and with the displacements derived from the Demons registration from phase 1 to phase 5.

It can be observed that the average stress increases monotonically with the Young’s modulus and Poisson ratio. The results in Fig. 10 may suggest that E should be located in the range of 0.4–0.8 kPa when the Poisson ratio is assigned to 0.3 by Werner et al.²³ In general, the magnitude of the computed average stress increases as these parameters increase in value.

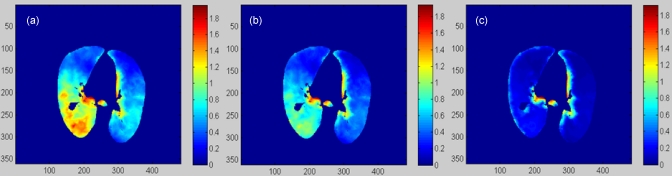
Unlike the magnitude, the spatial distribution of the computed elastic stress in the lung generally is insensitive to changes in the elasticity parameters. To verify this point, three pairs of parameters were used to construct the stress images: (A) E=1.0, ρ=0.40; (B) E=0.6, ρ=0.32; and (C) E=0.2, ρ=0.24. The transversal slices of these stress images are shown in Fig. 11.

Figure 11.

(a), (b), and (c) represent a transversal cut of the stress images calculated with the parameters (a), (b), and (c), respectively.

The Pearson correlation coefficients of these images are τ(A,B)=0.95 and τ(A,C)=0.81. These results indicate that the computed stress images in Fig. 11 differ from each other mainly in their intensity magnitude; however, the spatial distributions of the stress intensities are generally consistent with each other. The stress computed at the lung’s boundary in Fig. 11 was compromised by the constant parameters assigned to the adjacent soft tissue in the above three cases.

DISCUSSION

Changes in the ventilation function can be caused by chronic obstructive pulmonary disease (COPD)²⁹ or radiation injuries.¹⁴ Various imaging techniques, such as SPECT, helium-3 MRI, or 4DCT, have been used in quantifying region-specific ventilation activities. Due to the lack of mechanical information, the intensity values of these images in individual regions are not yet correlated with the general physiological functions,³⁰ and the relation between the changes in ventilation and radiation dose has not yet been established.¹⁴ Since ventilation function is largely determined by regional compliance,³¹ development of regional compliance images not only helps understand the status of COPD and ventilator-related lung injury²⁰ but may also provide real-time functional information for radiation treatment planning for achieving better treatment outcomes.¹³

Functional radiation treatment planning was implemented based on the assumption that the dose delivered to the lower-functioning regions of the lung will have less effects on the overall lung function than would dose delivered to the higher-functioning regions.¹ However, recent studies show that the effect of the radiation dose on ventilation reduction depends on both airway pressure⁸ and irradiated locations,¹⁴ and radiation damage cannot be quantified correctly without specifying these conditions. In fact, radiation-induced tissue damage may cause ventilation changes not only at the region of direct tissue damage but also in an extended surrounding region. Consequently, the ventilation change can be separated into two parts: A primary change and an associated change. The primary change is caused by the change in the local tissue’s elasticity (due to radiation damage to the local tissue). The associated change arises from tissue damage and mechanical changes outside this area. The primary change is directly related to radiation-induced tissue damage and can be derived from the change in regional compliance images. This separation may help establish the relationship between the delivered radiation dose and the change in the ventilation function.

The accuracy of the regional compliance computation relies on the accuracy of the DVF and the elasticity parameters used. In vivo calibration of the lung elasticity parameters is challenging. Previous studies have shown substantial differences in the calibrated mechanical parameters of the lung.^{23, 24} In this study, the displacements were derived from the Demons-based deformable registration and are independent of the parameters used in the FEM modeling. With these derived displacements, the average stress computed is then proportional to the elasticity parameters used (see Fig. 10), but the spatial distributions of the stresses computed with different parameters are similar. Figure 11 shows that the Pearson coefficients of the stress images computed with the elasticity parameters chosen from the two ends of the potential parameter domain were above 0.81. This manifests that the computed regional stress distribution is largely determined by the displacements of the deformable image registrations rather than the parameters used. The low volumetric change in the upper region [Fig. 9b] is consistent to the low stress computed in this region, as shown in Fig. 9c.

As demonstrated in Figs. 9d, 9e, 9f, 9g, 9h, 9i, 9j, 9k, 9l, the regional compliances computed for the five patients are relatively high in the superior lung regions where the elastic stresses are smaller than those in the inferior regions [Fig. 9c]. This suggests that regional compliance is inversely proportional to stress. Actually, regional compliance is inversely related to the bulk modulus, which is proportional to Young’s modulus.^{32, 33} It has been shown that the Young’s modulus of soft tissue is smaller at low stress but increases quickly at high stress.³⁴ So, it is reasonable to see that regional compliance is high in regions of low stress, like the upper regions in Fig. 9. The stress-compliance relation has also been verified in the case of the POPI-modeled patient where the average compliance increases but the average stress decreases as the phase is changed from phase 1 to phase 4. A similar trend can be observed among all the HFHS patients except patient 2, who has the smallest lung volume but the highest lung density among the five patients. With such “abnormal” density variations, due perhaps to conditions such as COPD, the use of uniformly assigned mechanical parameters in modeling this patient is likely not accurate. Consequently, patient-specific parameters and then explicit stress-compliance relations are worth investigating further in future studies.

Demons-based registrations, in general, are accurate in regions with high intensity gradients, e.g., in the lung.¹⁷ In this study, the registration instances were verified with the standard displacements, calculated as the difference of landmark positions in the two registered images. The mean errors of the registration displacements quantified with these landmarks were found to fall within the dimensions of a single voxel. Regions with low image gradients (e.g., within the tumor and the diaphragm) may have large DIR errors. These regions usually do not have air contributing to ventilation function and can be excluded from ventilation computation. This may limit the comprehensive analysis of radiation damage (e.g., studying radiation-induced elasticity changes in tumor) but can reduce the impact of the DIR errors on the computed ventilation function. It should be mentioned that ventilation values calculated from small image voxels are sensitive to uncertainties in the registration process³⁵ and a subvoxel displacement error can significantly impact the ventilation value computed at this voxel. In contrast, relatively large tetrahedral volumes may reduce the R_v’s sensitivity to the subvoxel uncertainty in the registration. In general, as our method relies on the accuracy of the DIR process and the associated DVF, errors in the DVF will result in uncertainties in the correlation of regional compliance and radiation-induced lung damage. Furthermore, interpatient variations in tissue elasticity present a requirement for further verification of the stress and regional compliance computed in this study before the method can be used clinically.

The stress computation in this study is different from the conventional mechanical modeling approach in that all the displacements were derived from deformable image registration before the FEM computation. The method developed may provide three-dimensional stress information, instead of a single value of airway pressure, for the calculation of the regional compliance that represents the ventilation capability of the alveoli in the lung. Since the air inhaled in the alveoli is not necessarily exchanged with that in the surrounding capillaries, the ventilation capability mainly reveals the elastic compressibility of the lung tissue rather than the air exchange capability between the alveoli and capillaries.

CONCLUSION

In this study, we have integrated deformable image registration and mechanical modeling techniques to calculate the three-dimensional images of elastic stress, ventilation, and regional compliance of the lung. Each of these images reveals part of the pulmonary function and their combination may prove to be of benefit in our understanding of radiation-induced lung injury.