Adaptations for economical bipedal running: the effect of limb structure on three-dimensional joint mechanics

Abstract

The purpose of this study was to examine the mechanical adaptations linked to economical locomotion in cursorial bipeds. We addressed this question by comparing mass-matched humans and avian bipeds (ostriches), which exhibit marked differences in limb structure and running economy. We hypothesized that the nearly 50 per cent lower energy cost of running in ostriches is a result of: (i) lower limb-swing mechanical power, (ii) greater stance-phase storage and release of elastic energy, and (iii) lower total muscle power output. To test these hypotheses, we used three-dimensional joint mechanical measurements and a simple model to estimate the elastic and muscle contributions to joint work and power. Contradictory to our first hypothesis, we found that ostriches and humans generate the same amounts of mechanical power to swing the limbs at a similar self-selected running speed, indicating that limb swing probably does not contribute to the difference in energy cost of running between these species. In contrast, we estimated that ostriches generate 120 per cent more stance-phase mechanical joint power via release of elastic energy compared with humans. This elastic mechanical power occurs nearly exclusively at the tarsometatarso-phalangeal joint, demonstrating a shift of mechanical power generation to distal joints compared with humans. We also estimated that positive muscle fibre power is 35 per cent lower in ostriches compared with humans, and is accounted for primarily by higher capacity for storage and release of elastic energy. Furthermore, our analysis revealed much larger frontal and internal/external rotation joint loads during ostrich running than in humans. Together, these findings support the hypothesis that a primary limb structure specialization linked to economical running in cursorial species is an elevated storage and release of elastic energy in tendon. In the ostrich, energy-saving specializations may also include passive frontal and internal/external rotation load-bearing mechanisms.

1. Introduction

Cursorial animal species are characterized by a limb morphology with lighter (and often reduced) skeletal elements, more proximally located muscle mass and elongated distal limb segments and tendons that are thought to allow faster and more economical running [1]. The ostrich, for example can achieve extraordinary speeds (greater than 50 km h⁻¹) and possess a remarkable economy of locomotion; for their size, their energy cost of running (J kg⁻¹ m⁻¹) is among the lowest recorded [2]. What are the specific relationships between cursorial musculoskeletal specializations and gait mechanics that allow these species to run with a low metabolic energy cost? This question has been of interest to biologists trying to understand structure–function relationships among both extant species [3–5] and extinct species such as dinosaurs [1,6] or early hominids [7–9]. The relationship between limb structure and locomotor economy is also pertinent to several bioengineering fields. For example, the emerging discipline of bioinspired robotics aims to exploit design principles found in nature in order to achieve agile, stable and economical robot locomotion [10–12]. Likewise, the design of energy-efficient prosthetic limbs and limb orthoses for assisting human locomotion depends on a sound understanding of the relationship between limb structure and locomotor mechanics and economy [13,14]. Engineered solutions for robotic and human locomotion can thus benefit from the insights and principles learnt in addressing biological questions such as the one posed above.

Our current understanding of the link between limb structure and locomotor mechanics and economy stems predominantly from anatomical studies (e.g. [15–17]) and scaling studies, where the effect of size is the key variable of interest [18–21]. Surprisingly, what remains much less studied are the mass-independent effects of limb structure on locomotor mechanics and economy, and thus the influence of limb structure per se remains unclear.

Two common explanations for economical running in cursorial animals are: (i) that a reduced number of bones in the distal limb and a more proximal limb-mass distribution reduce lower limb mass and moment of inertia, and subsequently the mechanical power required for limb swing (swing phase of running) [4,22,23] and (ii) that greater storage and release of elastic strain energy in tendons reduces the mechanical power required of muscle fibres during the stance phase of running [3,5,24,25]. Although there is anatomical evidence to support both these hypotheses [5,16,17,26], little quantitative data exist on the extent to which these musculoskeletal adaptations affect locomotor mechanics and energetics.

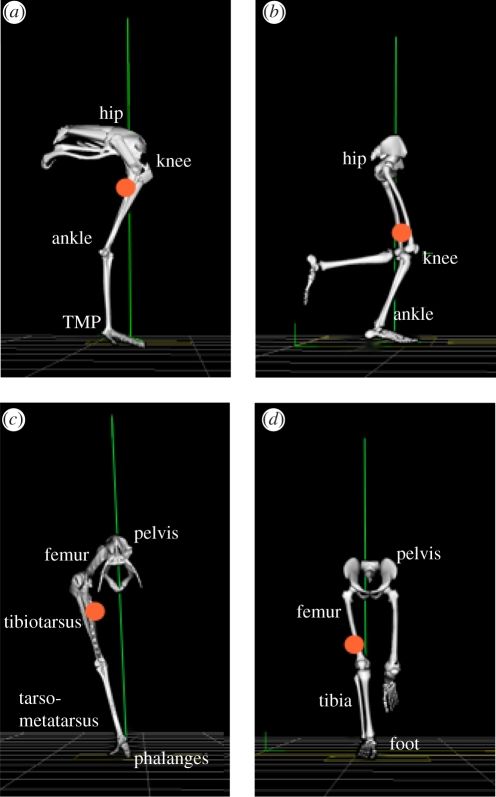
The purpose of this study was to compare the limb mechanics between a species with a cursorial limb structure and low energy cost of running to that with a non-cursorial limb structure and a higher energy cost of running, but which share a common body mass. We have chosen to study ostrich and human bipedalism among the many possible choices of species because such a comparison offers several advantages. Firstly, ostriches and humans have a similar mass and the contrast between their limb structures is more pronounced than those found between most other suitable animals, exemplifying the cursorial adaptations linked to economical locomotion (figure 1; also see electronic supplementary material, table S1 and motion files). These adaptations include: (i) a digitigrade stance in ostriches (standing on digits with raised metatarsal bones) versus a plantigrade stance in humans (standing with metatarsals flush to the ground), (ii) a longer limb length, reduced distal limb bones and a more proximal limb-mass distribution [26] (figure 1), and (iii) longer tendons with a greater capacity for elastic energy storage and release [26,27]. Secondly, ostriches and humans are compared because ostriches are able to reach maximal speeds two times those of humans (60 versus 30 km h⁻¹) [27] and, importantly, have a metabolic cost of running that is nearly 50 per cent lower [2,28]. Finally, by comparing ostrich with human bipedalism, the information gained may be more readily applied to human-based technologies (e.g. prosthetic limb design, rehabilitation robotics).

Figure 1.

Human and ostrich hind-limb postures during mid-stance of running: (a,b) sagittal plane; (c,d) frontal plane. Note: only the right limb is displayed for the ostrich. The vertical line represents the orientation of the ground reaction force vector. The circular mark represents the position of the combined centre of mass for all lower limb segments of the right limb (excluding pelvis). Differences between limb structures include: (i) a more distal limb-mass distribution in humans compared with ostriches, (ii) a plantigrade posture where the metatarsal bones of the foot are kept in contact with the ground in humans compared with a digitigrade posture in ostriches (walking/running on toes), resulting in a longer effective limb length and an additional joint for storing and releasing elastic energy (tarsometatarso-phalangeal (TMP) joint), and (iii) shorter tendons crossing the distal joints (ankle and TMP) in humans compared with ostriches; tendons crossing these joints originate from muscle–tendon junctions close to the knee joint (and mid-shank for the human soleus). Images developed from Vicon BodyBuilder software (Oxford Metrics, Oxford, UK) and bone images from OpenSim software at corresponding limb postures (SimTK; www.simtk.org). For motion files of ostrich and human running, see electronic supplementary material.

Our primary aims were to test the following three hypotheses: (i) the joint work and power required for limb swing is lower in ostriches compared with humans, (ii) the estimated joint work and power attributed to storage and release of elastic energy during stance is greater in ostriches compared with humans, and (iii) the estimated joint mechanical power attributed to muscle fibres during running is lower in ostriches compared with humans. These hypotheses were tested using three-dimensional inverse dynamic analysis techniques and a simple model of joint actuation. Furthermore, given that relatively little is known about bipedal joint mechanics in a comparative context despite the well-accepted merit of joint mechanics to understanding gait function [29,30], another aim of this study was to explore the magnitude and distribution of three-dimensional joint moments and mechanical work and power across the hind-limb joints between human and avian bipedal running. Measurements were made in three dimensions because considerable information regarding joint kinematics [31,32] and bone loading [33,34] is known for non-sagittal planes in both species and thus analyses restricted to the sagittal plane may obscure important structure–function relationships. These analyses allow for a detailed understanding of the relationship between limb structure and its influence on locomotor function.

2. Methods

2.1. Animals and human subjects

Five recreationally active male participants volunteered to participate (mean mass 70.5 ± 0.5 kg s.d.; mean hip height and total limb segment length 0.94 ± 0.03 and 1.14 ± 0.05 m s.d., respectively; mean age 25 ± 1.5 years s.d.). Five ostriches obtained from a local breeder were hand-reared and trained 3–4 days per week for a period of eight months prior to biomechanical analyses (mean mass at time of experiment 75.2 ± 0.5 kg s.d.; mean hip height and total limb segment length 1.15 ± 0.09 and 1.40 ± 0.05 m s.d., respectively; age 12–14 months). After training, two animals (mass 70.0 and 78.7 kg) were amenable to the procedures required for full three-dimensional gait analysis. A third animal (mass 75.9 kg) provided additional data on three-dimensional pelvic motion as well as overall three-dimensional limb displacement, and all five animals provided three-dimensional ground reaction force data. All ground reaction force and kinematic data matched closely those of the animals used for full three-dimensional gait measurements. Animals were kept in a large outdoor field (5000 m²) and provided with unlimited access to food and water. All experiments were performed in accordance with the Animal and Human Ethics Committees of the University of Western Australia.

2.2. Three-dimensional joint kinematics and kinetics

The procedures used for three-dimensional joint kinematic and kinetic measurements in humans and ostriches have been detailed in Besier et al. [31], and three-dimensional joint kinematic measurements in ostriches have been previously detailed in Rubenson et al. [32]. Briefly, motion analysis of the humans was performed using a six-camera Vicon motion analysis system (Oxford Metrics, Oxford, UK; 200 Hz) with a 1200 mm × 600 mm force plate (AMTI, Watertown, MA, USA; 2000 Hz). Retro-reflective markers were placed on each subject's lower body marker set and consisted of markers placed on anatomical landmarks (hip and foot), and clusters of three markers on the thigh and shank [31]. Prior to testing, subject calibration trials were performed [31] to locate anatomical landmarks and define joint coordinates systems. These functional hip and knee tasks were performed to locate hip joint centres by fitting a sphere to the motion of the thigh markers, with the knee joint flexion/extension axes defined using a mean helical axis-based method. The subject also stood on a foot calibration rig, which was used to establish the position of the foot markers and to measure foot abduction/adduction and rear foot inversion/eversion angles. These protocols have been shown to improve repeatability of joint kinematic and kinetic data [31]. Subjects were asked to run at a comfortable, freely chosen speed (recorded by timing gates). These speeds corresponded well to those observed for ostriches (3.0–3.5 m s⁻¹), and only those trials that matched the running speed of ostriches were selected for analysis.

Ostrich gait analyses were made on a custom-built 50 m long outdoor gait runway equipped with two 200 Hz video cameras (Peak Performance, Centenial, CO, USA) and a 600 × 400 mm force plate (Kistler Type 9865E; Winterthur, Switzerland), and constructed with similar surface materials to those of the human laboratory. An approximately 3 m³ calibrated volume was constructed at the centre of the runway using a direct linear transformation method with Peak Motus software [35]. The animals' self-selected running speeds were determined both from timing gates and from kinematic data. Motion capture trials were performed at night under artificial light in order to optimize marker tracking. Ground reaction force signals were sampled at 2000 Hz and synchronized with the video capture using a manually triggered +5 V square wave that generated a barcode on the corresponding video field. The marker motion and ground reaction force data were filtered using a fourth-order zero-lag Butterworth low-pass filter (MATLAB, The Mathworks, Natick, MA, USA) at the same cut-off frequency as marker filtering (15 Hz), following the recommendations of van den Bogert & de Koning [36]. The best cut-off frequency was selected using a residual analysis and visual inspection of the final kinematic and kinetic data from pilot trials in both species. The force data were down-sampled to 200 Hz to match the video data (MATLAB, The Mathworks). In order to integrate the force data and kinematic data, the force data were transformed into the global kinematic coordinate system by video recording retro-reflective markers secured to the mounting holes of the force plate. This permitted spatial transformations between the force plate and global coordinate systems.

Ostrich gait measurements were made using, as much as possible, the same methodologies as those for humans [31,32]. In the ostriches, joint kinematics and kinetics were calculated using a five-segment, 17-degree-of-freedom model of the ostrich hind limb based on anatomical landmarks and computed virtual landmarks (see [32] for a detailed description of the model and kinematic measurements), and included calculations for the hip, knee, ankle and tarsometatarso-phalangeal (TMP) joints. Three-dimensional limb segment motion was measured using clusters of retro-reflective markers attached to the pelvis, femur, tibiotarsus and tarsometatarsus and a marker placed on the distal phalanx of digit III. The individual x-, y- and z-marker coordinates were filtered using a fourth-order zero-lag Butterworth low-pass filter (MATLAB, The Mathworks) at a cut-off frequency between 5 and 15 Hz.

For both humans and ostriches, the three-dimensional joint kinematics and kinetics were computed using BodyBuilder modelling software (Oxford Metrics). Joint angles were calculated using the Euler/Cardan method [37,38]. Inverse dynamics employing a Newton–Euler formulation was used to estimate the joint reaction forces and net joint moments and powers. This engineering technique computes forces and moments from rigid-segment linear and rotational motion and their inertial properties [39]. For detailed limb segment parameters and inverse dynamic calculations, see the electronic supplementary material.

2.3. Mechanical joint work and average mechanical power during running

The positive and negative mechanical work of each joint was computed over both the stance and swing phase of running and multiplied by two to represent both limbs:

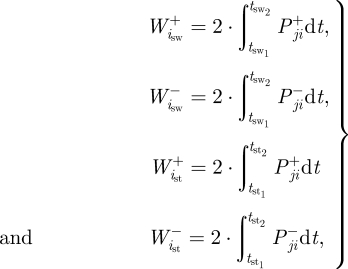2.1

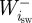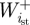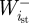where and are the positive and negative work (J) at the ith joint over the swing phase, and are the positive and negative work at the ith joint over the stance phase an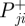d and 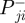are the positive and negative net joint powers at these joints, respectively. The total positive and negative work in the stance and swing phases was calculated as the sum of the positive and negative work at each of the N joints (N = 3 for humans; N = 4 for ostrich:

2.2

Total positive and negative mass-specific mechanical work terms for the complete stride (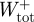, 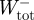) were subsequently calculated as the sum of 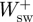and 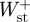, and the sum of 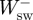and 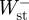, respectively. The positive and negative mass-specific work terms were subsequently divided by the stride time to give a mass-specific power term (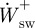, , 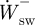, , 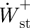, 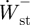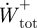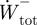; W kg⁻¹).

2.4. Elastic and muscle joint work and power estimates

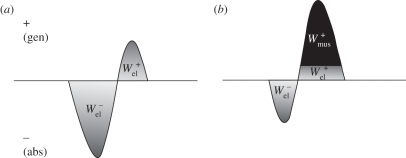
During steady-speed level running, the ankle joint, as well as the TMP joint in birds, is believed to function primarily as a spring, storing energy in the first half of stance (negative power) and releasing energy in the latter half (positive power) [3,5,25,29,40]. The structures responsible for this in ostriches are the tendons of the gastrocnemius and the digital flexors that cross both the ankle and TMP joints, and in humans it is the Achilles tendon crossing the ankle. Our model for ostrich and human running assumed that all of the energy absorbed at the ankle and TMP joints (in the ostrich) during stance occurred elastically and thus assessed the potential for elastic energy storage and release. This simplification was made on the basis that the tendon anatomy of the aforementioned muscles in ostriches and humans allows them to store the amount of energy absorbed at the joints during running [26,27,41,42] and from previous studies that have reported that these muscles function primarily elastically [25,27,43,44]. Subsequently, a series of simple calculations were used to estimate the maximum amount of positive mechanical work that could theoretically be provided during stance by the release of stored elastic energy, as well as the remaining mechanical work that would need to be provided by muscle fibres (referred to here as muscle work). First, in order for elastic energy storage and release to be considered, the joint power curve had to exhibit a pattern of negative power (energy absorption) followed by positive power (energy generation). Calculations were only made over these portions of the joint power curves (typically only one clear absorption–generation sequence was present). We assumed that the elastic energy storage equalled the negative work at the ankle and TMP joints (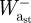 and 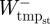, respectively). We subsequently estimated the positive mass-specific muscular work at the ankle and TMP joints that could not be provided by elastic recoil by integrating the joint power over its absorption–generation phase. If a negative value was computed, it was assumed that all the positive joint work was supplied through elastic recoil and no muscle work was required at the joint (i.e. net absorption of energy; figure 2):

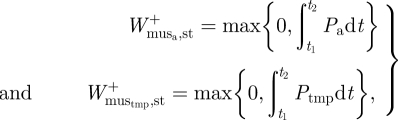2.3

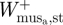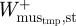where and are the positive mass-specific muscle work during stance at the ankle and TMP joints of a single limb, respectively. Finally, the positive elastic work during the stride was estimated as

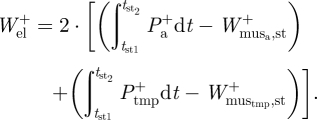2.4

Figure 2.

A graphical representation of the calculation of the negative and positive elastic work and the positive muscle fibre work estimated at the joints during running. The power traces represent scenarios where either (a) all of the positive joint work (area under joint power curve) is provided by the recoil of stored elastic strain energy or (b) where only a fraction of the positive joint work is provided passively by the recoil of stored elastic strain energy with the remainder attributed to muscle fibres.

The total muscle work over the stride was computed by subtracting the positive elastic work (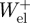) from the total positive mechanical work (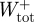). Finally, the mass-specific positive mechanical power attributed to elastic recoil (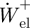) and muscle (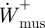) was computed by dividing the positive elastic work and positive muscle work by stride time, respectively.

2.5. Comparison of net joint moment, power and work distribution

In order to compare the pattern and distribution of the net joint moments and powers between ostriches and humans, we normalized the moment and power traces to 101 points over one stride using a cubic spline interpolation, allowing a mean ± s.d. of the kinetic curves to be determined for each group. The distribution of mechanical work among the hind-limb joints was compared between species by partitioning the joint work as follows: (i) positive and negative stance-phase joint mechanical work at each joint expressed as a percentage of the total positive and negative stance-phase work, respectively, and (ii) positive and negative swing-phase joint mechanical work at each joint expressed as a percentage of the total positive and negative swing-phase work, respectively.

2.6. Statistics

Joint moments, power and work were normalized to body mass in order to take into account any effect of small mass differences. We also performed joint moment comparisons normalized to body mass and total leg segment length (dimensionless) given that leg length can affect joint moment magnitudes. Although allometric normalizing can non-dimensionalize the data, this has a negligible effect on our comparison because of the small (approx. 5%) between-species difference in body mass. Running trials for analysis were restricted within a narrow range of self-selected speeds, ranging from 3.0 to 3.5 m s⁻¹ in order to minimize speed effects on our comparisons. Furthermore, at running speeds above 3 m s⁻¹, both humans and ostriches adopt a dynamic running gait (where the gravitational and kinetic energies of the centre of mass fluctuate in phase) that includes an aerial phase [28], indicating a dynamically similar gait in both species. A minimum of five trials per individual were used to calculate individual mean data, which were subsequently used for group mean comparisons. An unpaired, one-tailed Student's t-test was used to compare limb-swing mechanical work (predicted to be lower in ostriches compared with humans) and the estimated elastic and muscle fibre work (predicted to be higher and lower in ostriches compared with humans, respectively). Peak joint moments and joint work distribution were compared using a two-tailed Student's t-test. The variance in the data in each group was assessed and found not to be significantly different (equal variance) using an F-test. The alpha level was set to p < 0.05.

3. Results

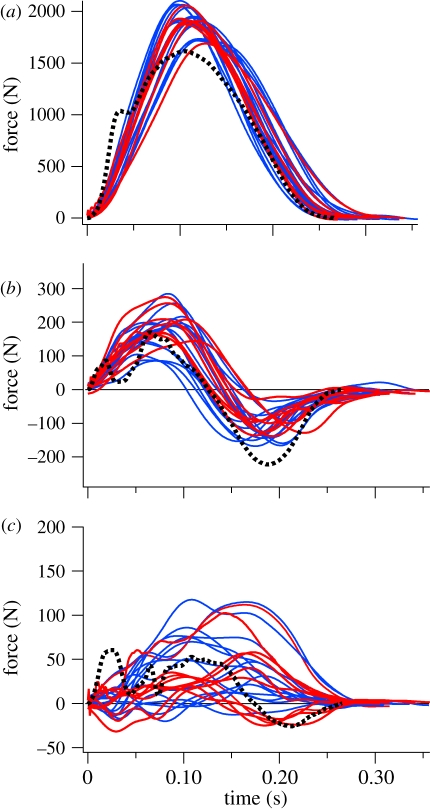
The running speeds of the ostrich and human trials were 3.24 ± 0.22 and 3.25 ± 0.37 m s⁻¹ (mean ± s.d.), respectively, and were not statistically different (p = 0.97; t = −0.03). Spatial–temporal parameters including stride time, stance time, swing time, stride length and frequency, and duty factor are listed in table 1. Both ostriches and humans had duty factors below 0.5 (0.42 ± 0.03 and 0.33 ± 0.03 (mean ± s.d.), respectively), indicating an aerial phase, and the Froude numbers (u²/gL, where u is speed, g is the acceleration due to gravity and L is leg length) were 0.93 and 1.14, respectively. The three-dimensional joint angles of ostrich running trials matched closely those from the larger dataset of Rubenson et al. [32], with peak angles and excursions differing by less than 5 per cent. The ground reaction forces of ostriches were similar to those of human running in magnitude and pattern, although the vertical component of the ground reaction force did not exhibit a transient at foot contact, which often occurs in humans [42] (figure 3). The lack of a ground reaction force transient in ostriches probably reflects the lack of a heel strike, and is consistent with recent analyses of human running in which fore-foot strikers similarly lacked a force transient [45]. The ground reaction force from the trials used for three-dimensional calculations represented those from the larger data from all five animals (figure 3).

Table 1.

Spatial–temporal gait parameters during running in humans and ostriches. Data are from running at 3.25 and 3.24 m s⁻¹ in humans and ostriches, respectively (mean ± s.d.).

	stride time (s)	stance time (s)	swing time (s)	stride frequency (Hz)	stride length (m)	duty factor
human	0.786 ± 0.032	0.255 ± 0.025	0.531 ± 0.032	1.28 ± 0.05	2.64 ± 0.28	0.327 ± 0. 025
ostrich	0.694 ± 0.006	0.291 ± 0.012	0.403 ± 0.018	1.44 ± 0.01	2.27±0.51	0.423 ± 0. 030

Figure 3.

Ground reaction force profiles for ostriches (solid lines) and a typical human trace (dotted line): (a) vertical, (b) fore–aft, and (c) medio-lateral directions. Red traces represent ostrich data from those trials used for full three-dimensional joint mechanical analyses (five traces per animal), and blue traces represent data from an additional three animals from which ground reaction forces were collected (five traces per animal).

3.1. Limb-swing mechanical work and power

The total positive mechanical joint work and mechanical power performed over the swing phase was not significantly different between ostriches and humans (figure 4a,b; p = 0.42; t = −0.21, p = 0.45; t = 0.18, respectively). The differences in limb-swing mechanical work and power were the same when normalized to limb mass, given that approximately 40 per cent of the body mass is attributed to the limbs in both humans [46] and ostriches (electronic supplementary material, table S1).

Figure 4.

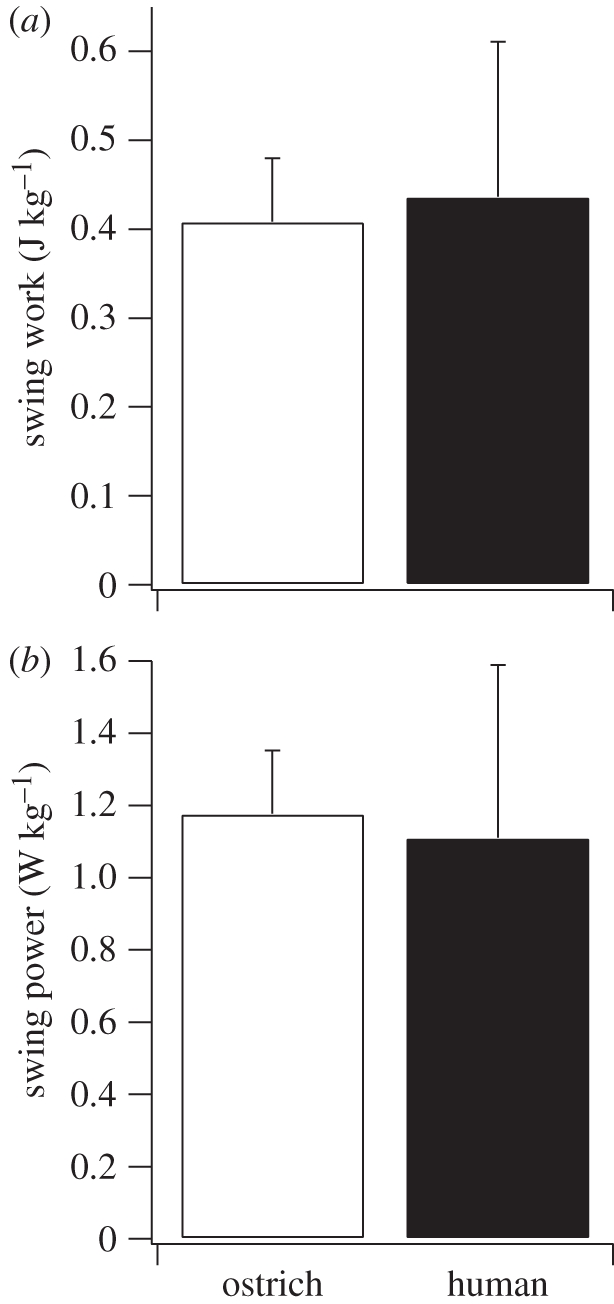
(a) Total positive body mass-specific joint mechanical work during limb swing and (b) the average positive body mass-specific mechanical power used to swing the limb during running in ostriches and humans.

3.2. Estimated elastic joint work and power

The amount of positive mechanical work per step (stance phase) estimated from the return of elastic energy was 83 per cent greater in ostriches compared with humans (p = 0.012; t = 3.22; figure 5a). The positive elastic work was calculated solely from ankle joint work in humans (the omission of an analysis of the human metatarsal–phalangeal joint is addressed below). In ostriches, the positive elastic work was estimated from both ankle and TMP joint work, although nearly all (98%) of the elastic work was attributed to the TMP joint (figure 8). After dividing the positive elastic mechanical work in both limbs by stride time, we estimated that the mechanical power generated from elastic recoil during running was 120 per cent greater in ostriches compared with humans (p = 0.005; t = 4.14; figure 5b). The percentage of the total positive mechanical work and power attributed to elastic recoil in the joints over the stance phase was 54.0 ± 0.1% in ostriches and 25 ± 6.3% in humans (mean ± s.d.; figure 5c).

Figure 5.

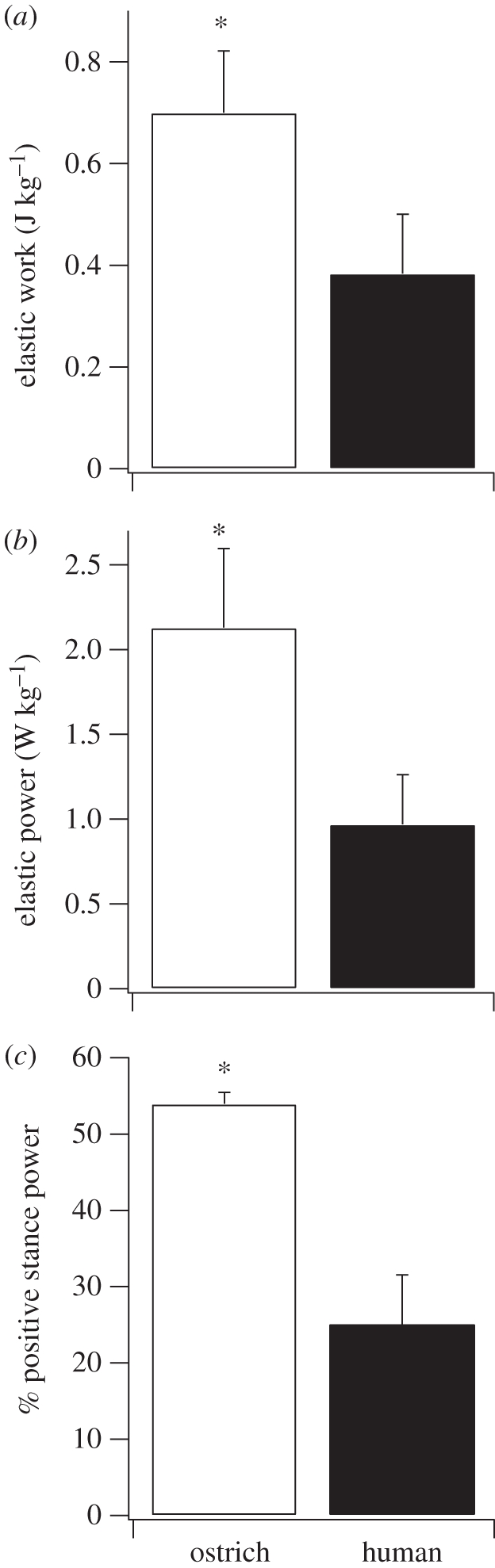
(a) Total positive body mass-specific joint mechanical work estimated to be generated via release of stored elastic energy during the stance phase (single limb), (b) the average positive body mass-specific mechanical power estimated to be generated by the release of elastic energy (both limbs), and (c) the percentage of the total positive mechanical power during the stance phase that is generated by the release of stored elastic energy in ostriches and humans. The asterisk denotes a significant difference between ostriches and humans (p < 0.05).

Figure 8.

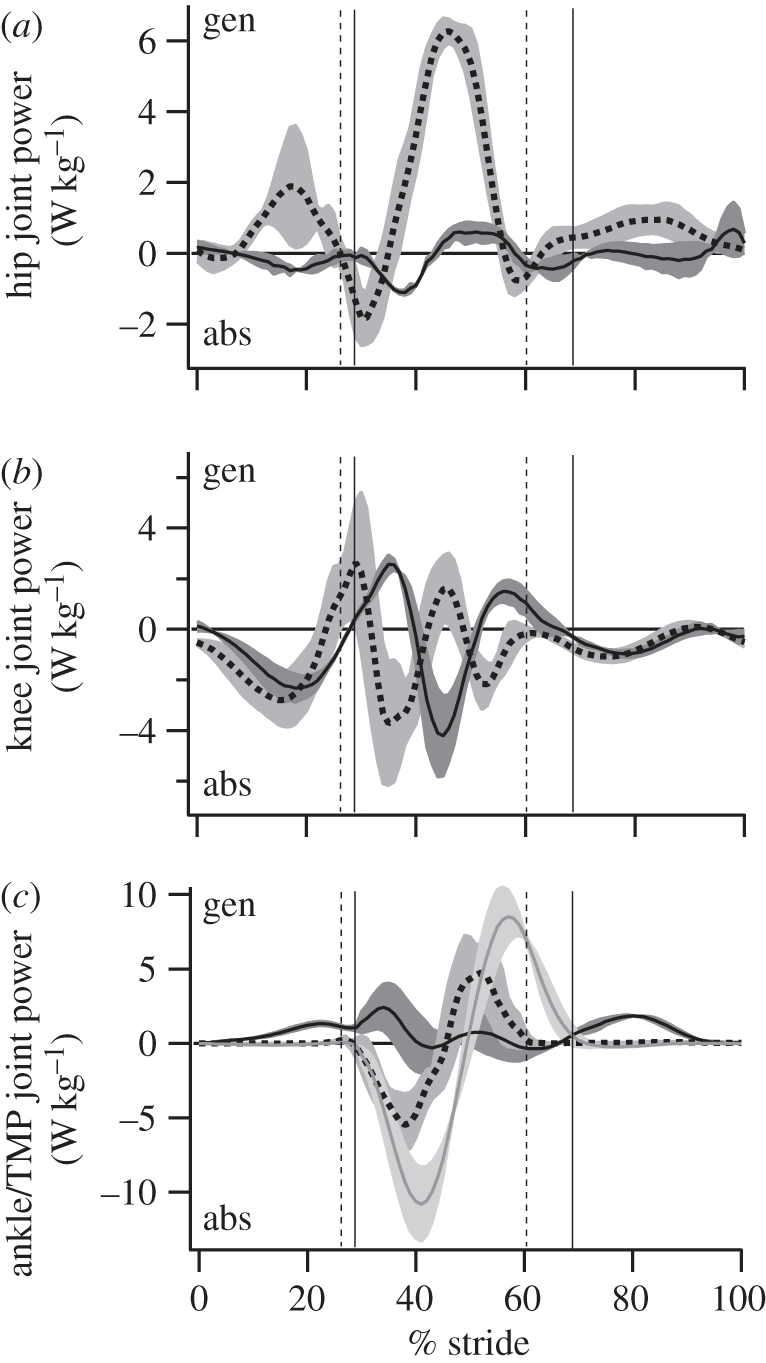
The average (±s.d.; grey shaded regions) mass-specific joint power in humans (dotted lines) and ostriches (solid lines) over the stride (mid-swing to mid-swing). Toe/foot-down and toe-off are designated by the vertical bars. (a,b) Dotted, humans; solid, ostriches. (c) Grey lines, ostrich (TMP).

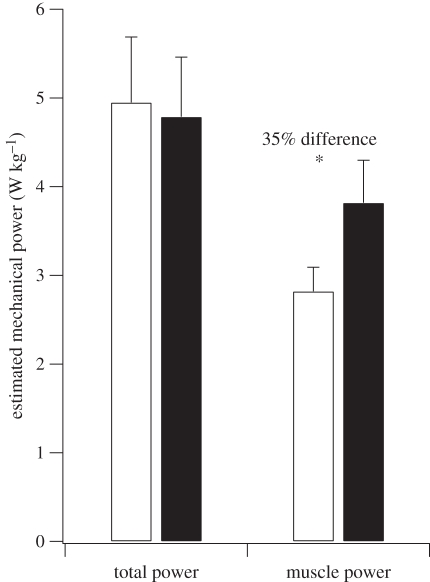
3.3. Total mechanical power and estimated muscle power

The estimated total positive mechanical power during running was similar between human and ostriches and not significantly different (figure 6). After the joint mechanical power attributed to elastic recoil was removed, the estimated positive mechanical power of the muscle fibres during running was 35 per cent lower in ostriches compared with humans (p = 0.02; t = −2.68; figure 6).

Figure 6.

The total average positive body mass-specific mechanical power during running in humans and ostriches and the average positive body mass-specific mechanical power estimated to be attributed to muscle fibres. The asterisk denotes a significant difference between ostriches and humans (p < 0.05). White bars, ostrich; black bars, human.

3.4. Joint moment and power profile

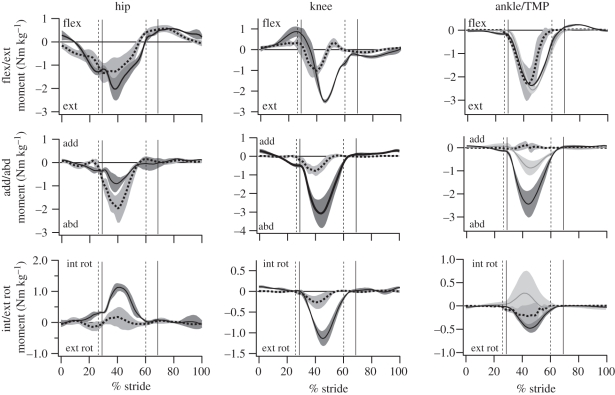
The magnitude and direction of the mass-normalized net flexion/extension joint moments were similar at the hip and ankle in ostriches and humans, although ostriches exhibit larger moments at the ankle during limb swing (table 2 and figure 7). Ostriches also have larger knee extension moments during stance compared with humans (table 2 and figure 7). Peak abduction moments were substantially higher at all joints in ostriches compared with humans (table 2 and figure 7). Internal/external rotation joint moments were also larger in the joints of ostriches compared with humans. In particular, a large internal rotation moment occurred in the ostrich hip, and a large external rotation moment occurred at the knee during mid-stance.

Table 2.

Peak joint moments and power in humans and ostriches. Data are from running at 3.25 and 3.24 m s⁻¹ in humans and ostriches, respectively (mean ± s.d.). Moments are expressed normalized to body mass (Nm kg⁻¹) and body mass and leg length (Nm kg⁻¹ m⁻¹; dimensionless). Positive net joint moments represent net internal (i.e. muscle) flexion moments (dorsi-flexion and digital extension at the ankle and TMP in humans and ostriches, respectively). Negative net joint moments represent net internal (i.e. muscle) extension moments (plantar flexion and digital flexion at the ankle and TMP in humans and ostriches, respectively). Positive (+) joint power represents energy generation; negative (−) joint power represents energy absorption. Bold denotes a significant difference between humans and ostriches (p < 0.05). Abbreviations: flex/ext, flexion/extension; add/abd, adduction/abduction; int/ext rot, internal/external rotation; TMP, tarsometatarso-phalangeal joint.

	flex/ext moment		add/abd moment		int/ext rot moment		power (W kg−1)
	Nm kg−1	Nm kg−1 m−1	Nm kg−1	Nm kg−1 m−1	Nm kg−1	Nm kg−1 m−1	+	–
hip
human	−1.47 ± 0.64	−1.24 ± 0.50	−2.03 ± 0.59	−1.77 ± 0.46	0.27 ± 0.14	0.24 ± 0.13	6.36 ± 0.22	−2.08±0.47
ostrich	−2.03 ± 0.46	−1.44 ± 0.28	−0.93 ± 0.31	−0.67 ± 0.25	1.14 ± 0.11	0.81 ± 0.10	1.01 ± 0.22	−1.11 ± 0.05
knee
human	−1.08 ± 0.23	−0.96 ± 0.25	−0.80 ± 0.25	−0.70 ± 0.20	0.28 ± 0.15	0.25 ± 0.14	3.66 ± 0.80	−4.64 ± 0.66
ostrich	−2.50 ± 0.07	−1.79±0.02	−3.08 ± 0.75	−2.19 ± 0.45	−1.14 ± 0.17	−0.81 ± 0.09	2.61 ± 0.22	−4.21 ± 0.05
ankle
human	−2.40 ± 0.74	−2.09 ± 0.55	−0.17 ± 0.13	−0.12 ± 0.11	−0.28 ± 0.21	−0.25 ± 0.20	6.24 ± 1.30	−6.14 ± 0.79
ostrich	−2.37 ± 0.01	−1.69 ± 0.05	−2.45 ± 0.56	−1.74 ± 0.33	−0.48 ± 0.08	−0.48 ± 0.05	2.70 ± 0.85	−1.17 ± 0.25
TMP
ostrich	−2.57 ± 0.13	−1.84 ± 0.03	−0.88 ± 0.30	−0.62 ± 0.19	0.30 ± 0.43	0.21 ± 0.30	8.68 ± 1.19	−10.8 ± 1.77

Figure 7.

The average (±s.d.; grey-shaded regions) net mass-specific joint moments in humans (dotted lines) and ostriches (solid lines) over the stride (mid-swing to mid-swing). Solid grey lines, ostrich (TMP). Toe/foot-down and toe-off are designated by the vertical bars (dotted, humans; solid, ostriches). Joint moments are the internal (i.e. muscle) net joint moment (negative values represent moments countering gravity).

The magnitude as well as pattern of joint powers differed between ostriches and humans (table 2 and figure 8). The hip joint generated power during limb swing in humans and exhibited a small burst of power absorption followed by a prominent burst of power generation in stance. In ostriches, the hip generated and absorbed little power, owing primarily to the small joint excursion. The knee joint in humans underwent a complex pattern of power absorption–generation–absorption in stance, and exclusively absorbed power during swing. During stance, the ostrich knee exhibited a complex pattern opposite to that of humans, where the joint underwent power generation–absorption–generation. Like humans, the ostrich knee absorbed power throughout limb swing. The ankle joint in humans is characterized by power absorption followed by generation over the stance phase. This pattern was not observed in the ostrich, where only modest power generation was present, again reflecting a minimal change in joint angle during stance [32]. Considerable generation of power was observed at the ankle during limb swing in ostriches. The joint power profile and magnitude of the TMP joint in ostriches were similar to those of the human ankle, characterized by a prominent burst of power absorption in the first half of stance, followed by power generation in the latter half.

3.5. Distribution of joint work

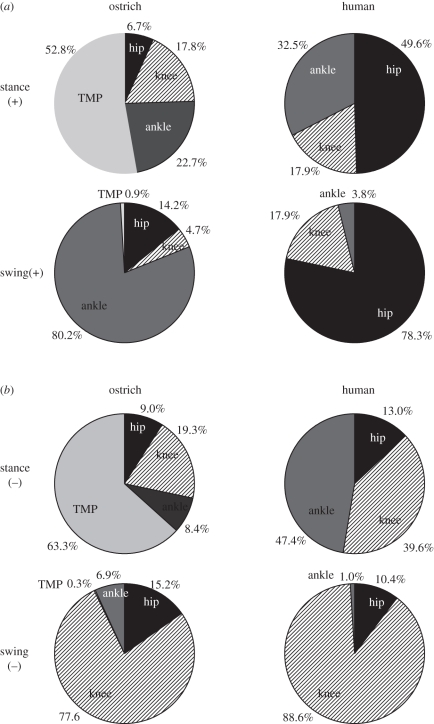
The hip joint produced most of the positive mechanical work in human running, accounting for 50.0 ± 10.1% (mean ± s.d.) of the positive mechanical work during stance and 78.3 ± 4.2% (mean ± s.d.) in limb swing (figure 9a). In humans, the ankle contributed substantially to positive stance-phase mechanical work (32.5 ± 9.0%; mean ± s.d.). In contrast, in the ostrich, the majority of the stance-phase mechanical work was performed in the TMP joint (52.8 ± 0.2%; mean ± s.d.), with the hip contributing a small amount of positive work (figure 9a). During limb swing in the ostrich, the positive mechanical work occurred predominantly at the ankle joint.

Figure 9.

The distribution of (a) positive mechanical work and (b) negative mechanical work among the hind-limb joints during stance and swing in ostriches and humans.

The ankle and knee joints accounted for the majority of the negative mechanical work during stance in humans (figure 9b), and during limb swing, the knee accounted for nearly all of the negative work. In ostriches, the majority (63.3 ± 1.0%; mean ± s.d.) of the negative stance-phase work was performed at the TMP joint, with the hip, knee and ankle contributing only moderate amounts. As in humans, the limb-swing negative mechanical work in ostriches was performed primarily (77.6 ± 5.4%; mean ± s.d.) at the knee.

4. Discussion

Cursorial species, such as the ostrich, are able to run both quickly and economically [2,5,27]. The aim of this study was to explore the features of bipedal joint mechanics that can help explain the low energy cost of running in these cursorial animals. To this end, we made a case comparison of running in mass- and speed-matched ostriches and humans. These species were compared because the specializations that have previously been hypothesized to reduce the energy cost of running are typified in the comparison between the avian and human lower limbs, and because humans are known to have a nearly 50 per cent higher cost of running compared with their avian bipedal counterpart.

4.1. Mechanical power of limb swing

Several recent experimental and modelling studies have found that the metabolic cost of limb swing is a substantial (approx. 20–30%) component of the total metabolic cost of running [47–50]. This large limb-swing cost corroborates the long-standing hypothesis that animals specialized for economical running benefit from having a comparatively low limb mass and moment of inertia, resulting in lower limb-swing mechanical power and thus metabolic energy use [4,16,22,23]. At the outset, this hypothesis seems to fit with our human–ostrich comparison. Ostriches have a similar limb mass, but a more proximal mass distribution compared with humans (figure 1), which has the effect of lowering their limb moment of inertia. The combined centre of mass of the lower limb segments (weighted average excluding the pelvis mass) is approximately 0.27 m from the hip joint in ostriches and 0.34 m in humans, representing a relative position of approximately 28 and approximately 40 per cent along the length of the limb in ostriches and humans, respectively (the position of the combined centre of mass of the lower limb segments is represented by the circular mark in figure 1). However, despite this anatomical difference, our results do not show strong support for the limb-swing-cost hypothesis. The mechanical power of swinging the limbs across strides is not substantially different between humans and ostriches, and is thus probably not a major factor contributing to their lower energy cost of running.

The finding that ostrich and human limb-swing mechanical power is not substantially different does not, however, imply that limb structure has no bearing on swing cost, as has been suggested previously [51,52], or that the ostrich limb structure does not reflect specialization for reducing limb-swing energy use. It is reasonable to assume that, were the limb moment of inertia to be higher in the ostrich, they would incur a larger limb-swing cost and would thus consume more energy when running with the same limb mechanics. In this regard, their lower limb moment of inertia may be viewed as an adaptation that permits them to use a high stride frequency, long contact time and a rapid limb swing, which may confer benefits such as stability, while maintaining a relatively low limb-swing energy expenditure.

It should also be stressed that the exact relationship between limb-swing mechanical power and energy use is not known for ostriches or humans. In guinea fowl, it has been found that the relationship between limb-swing mechanical power and the rate of limb-swing metabolic energy use (limb-swing efficiency) is variable across speed [48]. It is possible that different limb-swing mechanical efficiencies exist between ostriches and humans, and therefore it is unclear whether the difference in limb-swing cost is necessarily represented by limb-swing mechanical power. Nevertheless, our results do not offer support for the hypothesis that the energy cost of running in ostriches is lower compared with humans owing to lower limb-swing mechanical power.

4.2. Estimated elastic and muscle power

In agreement with our second hypothesis, we estimated that approximately 83 per cent more work is generated by the release of elastic energy in the ostrich joints during stance compared with humans. Our model of elastic work and power production at the origin of this finding was based on joint power measurements and a prediction of whether a joint's actuation could feasibly be accomplished using elastic storage and release based on muscle–tendon unit architecture (see below). When taking into account stride frequency, over two times (approx. 1.2 W kg⁻¹) more stance-phase positive mechanical power is estimated to be generated by the release of elastic energy in ostriches than in humans (figure 5a,b). It is important to stress that the overall mechanical power generated by the return of elastic energy is more directly associated with reducing the rate of metabolic energy use than elastic work per se, and that the large difference in elastically generated power may thus help explain the 50 per cent lower cost of running between these species. The discrepancy in the capacity for elastic power generation is further supported by the observation that ostriches are estimated to generate over twice as much relative stance-phase positive mechanical power by the release of elastic energy, compared with humans (figure 5c).

One surprising finding was the distribution of elastic energy storage and release in the ostrich. Practically all of the elastic energy storage and release was observed in the TMP joint, confirming that this joint is highly specialized for elastic power production [27] and a more effective spring than that of the human ankle. The lack of energy absorption and generation at the ankle in ostriches was unexpected. The ostrich gastrocnemius muscle–tendon unit is ideal for storing and releasing elastic energy at the ankle [26], but the pattern of joint power during stance indicated that the gastrocnemius does not function as a spring during running at the speeds studied (figure 8). Given that the speed examined is well below the maximum speed of ostriches, it is possible that the ankle and gastrocnemius muscle group function to store and release elastic energy only at faster speeds, where greater mechanical power is required. In this case, an even larger discrepancy between ostrich and human elastic joint function may exist at faster speeds. This scenario would fit with the ankle-based elastic energy storage and release that has been observed in other running ground birds, including turkeys [25] and guinea fowl [53]. Interestingly, these later studies examined faster relative speeds compared with the ostrich in the present study; Froude numbers were approximately 1.5 for the turkey and guinea fowl and 0.93 for the ostrich.

Our results also support our third hypothesis, that the estimated total muscle power is lower in ostriches than in humans. When an estimate of the storage and release of elastic energy at the joints is taken into account, the remaining mechanical power attributed to the muscle fibres was 35 per cent lower in ostriches compared with humans. It should be noted that because the total positive mechanical power is similar between humans and ostriches (figure 6), the factor contributing to the lower muscle power in ostriches, as estimated from our model, remains the greater joint power attributed to the return of stored elastic energy in ostriches, which acts to spare muscle fibre power. These results reinforce our interpretation that reduced muscle fibre power output may be linked to economical running in cursorial species such as the ostrich. Our findings indicate that muscle power may be a more important factor dictating energy use than often purported [54,55], and that it should not be overlooked when addressing links between locomotor mechanics and energetics. This may be partly because the present approach addresses several of the limitations in earlier studies linking muscle power to locomotor energy use (e.g. joint-level versus whole-body work measurements and estimates of elastic energy contributions).

Nevertheless, producing force isometrically, as would be required by the muscles crossing the ankle and TMP joints in our model, also exacts a metabolic cost. It remains possible that a lower energy cost of running in ostriches is also, in part, a result of more economical force production. This seems plausible given the importance of the distal joints to powering running, especially in the ostrich, where muscles with small volumes (that are inherently economical force producers) [56] are predicted to function isometrically and possibly with slower rates of force development. A simple estimate of the cost of ground force production can be made using foot contact times [20], where metabolic rates are predicted to be inversely related to the time the foot spends in contact with the ground in each step. The 14 per cent longer foot contact time in ostriches suggests that the cost of producing ground force may explain some of the 50 per cent difference in metabolic cost between species. However, this interpretation must be tempered by stressing that this very simple assessment of cost of force only takes into account differences in the time course for force production. Without estimating muscle forces and volumes [56], we are not able to accurately distinguish between costs of isometric force production and work production.

4.3. Limitations to elastic and muscle power estimates

Our estimate of elastic power generation and muscle power relies on a simple inverse dynamic model of joint work. It has been argued previously that joint work does not necessarily equate to muscle–tendon unit work owing to muscle co-contraction [29]. If co-contraction were to occur, our estimate of work and power would be underestimated, but there does not exist, to the best of our knowledge, data that indicate whether levels of co-contraction differ between human and avian bipedal running. Similarly, passive moments at the joints may alter the requirement of active muscle fibre work. A recent analysis of passive moments by Whittington et al. [57] revealed that a moderate amount of positive joint work in humans (approx. 22% of the total positive work) might be provided by passive muscle moments during walking, primarily at the hip. It remains unclear how passive moments affect active muscle work during running. Given that passive moments have been found to be independent of joint angular velocity [58], increases in passive moments between walking and running are probably smaller (and owing primarily to angular excursion) compared with the net joint moments, which increase substantially with speed. This relationship is evident between slow and fast walking speeds [57] and indicates that passive moments may, in general, play a relatively smaller role in running. However, the lack of data on passive moments during human running and in avian bipedalism makes assessing their contribution to our estimates of work production difficult.

Furthermore, inverse dynamic analysis does not in itself differentiate between tendon and muscle fibre work and power. We make the assumption that all of the work and power at the ankle and TMP joints during steady-speed running can theoretically be provided via storage and release of elastic energy in the tendons crossing these joints if the positive joint work produced is preceded by an equal or greater amount of absorbed (negative) joint work. As such, our analyses serve to assess the potential for elastic energy storage and release rather than a precise partition of elastic and muscle fibre power production.

Although it is possible that not all of the measured negative and positive joint work at the ankle and TMP joints occurs as storage and release of elastic energy in tendons, there are several factors which indicate that these joints do function primarily elastically. Firstly, the architecture of the ankle and TMP muscle–tendon units suggests that they are designed for elastic energy storage and return, as opposed to position control where the joint excursion is accomplished by muscle fibre lengthening/shortening [3]. In humans, the primary plantar-flexor muscle, the soleus, has an optimal fibre length and moment arm of approximately 4 cm [59,60]. Assuming no tendon stretch, the approximately 40° of movement at the ankle during stance would result in over 50 per cent muscle strain, a value that would result in a severely limited force-producing capacity of the muscle owing to the force–length relationship (a prediction using a musculoskeletal model indicates the muscle would be restricted to less than 50 per cent force capacity; OpenSim, simtk.org) [59]. For the muscle to function over a narrow, high-force, region on the force–length curve, the tendon must account for 75 per cent of the muscle–tendon unit strain. This amount of tendon strain, or more, is realistic considering that if all of the joint motion during the energy-absorbing phase (approx. 20° dorsi-flexion) is attributed to tendon stretch (free tendon + aponeurosis), the tendon would experience a strain of 4.6 per cent based on the muscle moment arm and tendon slack length parameters in Arnold et al. [59]. Tendon strain of this magnitude or greater has been reported for the medial gastrocnemius, which shares the common Achilles tendon with the soleus muscle (e.g. up to 5.5 per cent strain has been reported for the medial gastrocnemius free tendon and aponeurosis during the energy-absorption phase of running [44]). The relationship between muscle–tendon unit architecture and tendon strain is even more pronounced in ostriches. The digital flexor muscles that cross the TMP joint have muscle fibres that are between 1.5 and 4 cm long [26], with tendon slack lengths up to 80 cm. With a mean moment arm of approximately 3 cm [61], the muscle fibres can only account for a negligible component of the TMP joint excursion within a realistic range of muscle fibre strain, suggesting that the joint excursion occurs as a result of tendon stretch and recoil.

A second factor indicating that the ankle and TMP joints function primarily elastically is that the fibres of the gastrocnemius and soleus muscles in humans [44,62] and the gastrocnemius and digital flexor muscles in birds [25,53] undergo much smaller length changes than their tendons during stance. These findings indicate that tendon is primarily responsible for storage and release of elastic energy at the ankle and TMP joints. Finally, the estimated storage of elastic energy at the TMP and ankle joints in the present study matches closely previous elastic energy storage estimates in both the digital flexor tendons in the ostrich during running (67.8 J this study versus 60 J [27]) and the Achilles tendon in humans (37.5 J this study versus 35 J [41]; note moderately higher/lower estimates of elastic energy storage in the Achilles tendon have been reported with variation in the Achilles moment arm [63]). Furthermore, using the cross-section areas and moment arms of the digital flexor tendons (from [26,61]), the measured peak TMP joint moment from the present study (table 1) and a tendon modulus of elasticity of 1.2 GN m⁻² (following the calculations of Alexander et al. [27]), we computed 75.5 J of energy storage in the ostrich digital flexor tendons during running. The similarity of this second estimate of elastic energy storage in the tendons crossing the TMP joint compared with our estimate from joint work further substantiates our estimate of elastic energy storage and release based on our joint work model.

The present study did not include an analysis of joints distal to the ankle in humans and the TMP joint in ostriches, and assumed no elastic energy storage and return at proximal joints. Proximal joints (the hip and knee) may be capable of storing and returning some elastic energy (e.g. in the tendon of the quadriceps [64]). The joint power profile of the hip and knee in both ostriches and humans exhibits periods in the stance phase that would permit elastic energy storage and return according to our elastic model (equations (2.3) and (2.4); figures 2 and 8). However, the amount of power absorbed at these joints is much less than at the ankle and TMP joints (figure 8). Furthermore, in both humans and ostriches, the proportion of the energy absorbed elastically at the hip and knee is probably minimal given that the large majority of the muscle–tendon units at these joints are parallel fibred and possess little tendinous material compared with muscles at the distal joints [26,59,60]. It is also interesting to note that the amount of elastically generated positive work at the hip and knee, as defined by our joint model, is similar in ostriches and humans, further indicating that these joints probably do not influence the difference in elastic energy storage and release and total positive muscle fibre work during running between these species.

Mechanical work and power in the form of elastic energy storage and release may exist at more distal joints than those studied, including the metatarsal–phalangeal joint in humans and the interphalangeal joints in ostriches. In ostriches, any mechanical power at the interphalangeal joint is performed primarily by storage and release of elastic energy in the digital flexor tendons given that minimal muscle tissue exists in the distal phalanges. The interphalangeal joint excursion mirrors that of the TMP joint during stance (J. Rubenson 2006, unpublished results), indicating that our estimate of elastic energy storage and release may be underestimated. However, because the centre of pressure of the ground reaction force is close to the interphalangeal joint during stance, the joint moment and hence elastic power absorption/production at the interphalangeal joint are expected to be less than at the TMP joint. In humans, it has been shown that the metatarsal–phalangeal joint absorbs mechanical power nearly exclusively during running [65]. Therefore, this joint is not expected to contribute to either elastic- or muscle-generated positive mechanical power. The arch of the human foot has also been identified as a spring mechanism during running. Ker et al. [41] estimated that the ligaments in the arch of the foot can return approximately 17 J of energy when running at 4.5 m s⁻¹ (approx. 0.24 J kg⁻¹). Using the energy versus load plot and the load balance theory of Ker et al. [41], the average (mass-normalized) peak joint reaction force from our inverse dynamic analysis, and a predicted Achilles tendon moment arm of 4 cm [59], we estimated approximately 10 J (0.14 J kg⁻¹) of energy return from elastic recoil in the arch of the foot. If all else remains equal, this amount of elastic energy return would lower the difference in mass-specific positive elastic work between ostriches and humans to 34 per cent, and lower the difference in mass-specific elastic power between species to 61 per cent (the differences in estimated elastic work and power between species remained significant; p < 0.05). This scenario probably represents a lower limit in the difference in positive elastic power between humans and ostriches. The amount of elastic energy stored in the arch of the foot may be less than 10 J since the force required to balance a considerable metatarsal–phalangeal moment during running [65] will reduce the load in the foot ligaments. Furthermore, the elastic energy storage and return may be slightly higher in ostriches owing to the interphalangeal joint. Therefore, although this study has not provided a precise quantification of elastic power production, it is reasonable to conclude that a significantly higher potential for elastic power output exists in ostriches compared with humans. Furthermore, because the interphalangeal joint in ostriches and the arch of the human foot are expected to function purely elastically, the estimate of positive muscle fibre power would not be affected by their omission.

4.4. Pattern of joint moments, power and work

The pattern of the sagittal plane moments at all of the joints was surprisingly similar between ostriches and humans, both during stance and limb swing (figure 7). This finding extends the concept that legged animals share similar dynamics of running beyond overall centre of mass movement [66] to the level of the joint. However, frontal and long-axis moments exhibit clear differences in magnitude. The much larger frontal plane loads at the knee and ankle of the ostrich are due largely to the abducted posture of the hip joint and the resulting bow-legged (varus) posture required to return the phalanges under the body (figure 1; also see motion files of running humans and ostriches in the electronic supplementary material). The large internal rotation moment at the hip corroborates the prediction of Hutchinson & Gatesy [67] that, together, the horizontal femur posture and the varus lower limb posture of birds necessitate a hip internal rotation support moment. While Carrano [33] and Main & Biewener [34] provided bone strain data indicating long-axis loading, the present study is the first to quantify long-axis loading at the joint level.

It is intriguing that, despite the very large frontal and internal rotation moments, the energy cost of running in ostriches remains low. These findings suggest passive support mechanisms may function in vivo to relieve the requirement of energy-consuming muscle force. These mechanisms may be present in the form of ligaments or bony constraints at the joint. These mechanisms seem obvious at the ankle, which lacks muscles with abduction moment arms (with the exception of the fibularis longus), but less obvious at the knee and hip. Alternatively, economical joint stabilization may arise from active muscle force with favourable moment arms.

In humans, power production is shared nearly equally among the proximal and distal joints, whereas one of the striking features of ostrich running is a clear shift in the distribution of work and power production to the distal joints; the hip contributes a small amount of positive power during locomotion and the TMP joint contributes over 50 per cent (figures 8 and 9). The use of distal joints to power running reflects a limb structure with a greater reliance on elastic energy storage and release. The increased lower limb length in ostriches, in particular the tarsometatarsus, results in very long and slender tendons of the digital flexors that are ideal for elastic energy storage and release [26,27]. A more distal distribution of joint power is also observed during limb swing (figure 8), with humans and ostriches adopting a hip-driven and ankle-driven limb swing, respectively. The increased limb-swing ankle power production in ostriches compared with humans may reflect a trade-off between increasing the elastic energy storage capacity during stance arising from a longer lower limb in ostriches, and an increase in energy required to accelerate this longer limb during swing.

In summary, the present study demonstrates that a primary limb structure adaptation linked to economical locomotion in ostriches is probably an increased ability to store and return elastic energy, thereby reducing the amount of positive power required by muscle fibres. At the speeds analysed in this study, the estimated increased reliance on elastic energy and sparing of muscle fibre power is achieved by a shift of power production to distal joints that are ideally suited for elastic power production, although surprisingly not the ankle. Ostriches do not have a reduction in the amount of mechanical power required for limb swing compared with humans, despite having a typical cursorial limb structure with a low limb moment of inertia. When considering adaptations for economical locomotion in avian bipeds, attention should also be given to mechanisms that reduce the need for active muscle stabilization of frontal plane loads at the ankle and knee and internal rotation loads at the hip.