Chemotaxis can take plant-parasitic nematodes to the source of a chemo-attractant via the shortest possible routes

Abstract

It has long been recognized that chemotaxis is the primary means by which nematodes locate host plants. Nonetheless, chemotaxis has received scant attention. We show that chemotaxis is predicted to take nematodes to a source of a chemo-attractant via the shortest possible routes through the labyrinth of air-filled or water-filled channels within a soil through which the attractant diffuses. There are just two provisos: (i) all of the channels through which the attractant diffuses are accessible to the nematodes and (ii) nematodes can resolve all chemical gradients no matter how small. Previously, this remarkable consequence of chemotaxis had gone unnoticed. The predictions are supported by experimental studies of the movement patterns of the root-knot nematodes Meloidogyne incognita and Meloidogyne graminicola in modified Y-chamber olfactometers filled with Pluronic gel. By providing two routes to a source of the attractant, one long and one short, our experiments, the first to demonstrate the routes taken by nematodes to plant roots, serve to test our predictions. Our data show that nematodes take the most direct route to their preferred hosts (as predicted) but often take the longest route towards poor hosts. We hypothesize that a complex of repellent and attractant chemicals influences the interaction between nematodes and their hosts.

1. Introduction

Nematodes, thread-like worms, mostly about 1 mm in length, are among the most ubiquitous organisms on Earth. One hundred grams of soil typically houses about 3000 individuals [1]. Plant-parasitic nematodes attack plants and cause US$70 billion of crop losses annually. It has long been recognized that chemotaxis is the primary means by which nematodes locate host plants. Chemotaxis is a movement in the direction of higher concentrations of semiochemicals such as plant chemical signals. Nematodes are attracted to plant roots via soluble and gaseous attractants produced by the root itself or by attendant rhizosphere micro-organisms [2–6]. These attractants have been classified [7,8] as long-distance, short-distance and local attractants. Long-distance attractants are those that attract nematodes to the general root area, short-distance attractants are those that attract nematodes to the roots themselves and local attractants are those that enable endoparasitic nematodes, such as Meloidogyne, to orient to the preferred invasion site. Volatile molecules travel quickly by diffusion in air, whereas water-soluble molecules in the soil tend to diffuse more slowly. This suggests that water-soluble chemicals are used mainly for short-range chemotaxis to plant roots, and that volatile chemicals can be used for longer range chemotaxis to distant plant roots. Nematode responses to many known compounds and also to unknown compounds from insect hosts [9], plants [5,10–12], bacteria [4], fungi [13] and other nematodes [14,15] have been investigated. At least 50 different kinds of behavioural assays have been employed in these studies. Most studies have used 0.5–3% agar as a migration matrix, but others have used natural sand [16–20] and soil [16,21–24]. Although experiments using a soil substitute may indicate response to a gradient of a test compound, it cannot be assumed that the same gradient will exist in soil.

Research on the role of volatiles for plant-parasitic nematodes is scarce, but extensive study regarding host-searching behaviour of entomopathogenic nematodes has been made. Investigations have used a Y-chamber choice apparatus with air containing or not containing host volatiles being pumped through each half of the ‘Y’ [25]. Also, ‘T’ and ‘U’ choice apparatuses have been utilized [26].

Although the sources of the stimuli of interest in most cases are ecologically obvious, the connection between nematode ecology and the kinds of migration matrices used in behavioural studies is less obvious. The effectiveness of chemotaxis in structured media such as soils has, for example, received little attention but is of considerable importance when attempting to understand and to predict the important role that nematodes play in soil ecosystems by mediating nutrient turnover, inflicting damage on crops, benefiting plants by consuming pathogenic organisms, and by transporting otherwise relatively immobile micro-organisms through the soil that can transmit disease or provide essential nutrients [3,27–30]. Current knowledge relates to how pore (or aggregate) size with associated moisture regimes affects the movement and the diffusion of volatile organic compounds [31–34].

The classic experimental studies of Wallace [31,32] leave open the key challenge of understanding how plant nematodes use chemical cues to navigate through the labyrinth of air-filled channels within a soil to locate a distant host plant and invite a simulation modelling approach to help resolve the issue, along with further experimentation to support theory developed from the modelling. Furthermore, nematodes, especially the infective stages of cyst and root-knot nematodes, have limited resources of stored energy and must find their hosts efficiently; infected juveniles with depleted lipid reserves are unable to infect plant roots [35]. Here, through the employment of numerical simulations, we address the challenge of understanding how nematodes move economically through soil to locate host plants. The results of these numerical simulations are supported by experimental studies of the movement patterns of the root-knot nematodes Meloidogyne incognita and Meloidogyne graminicola in modified Y-chamber olfactometers filled with Pluronic gel. In these experiments, nematodes can take one of two possible routes, one long and one short, to the roots of living plants.

2. Methods

2.1. Simulating chemotaxis

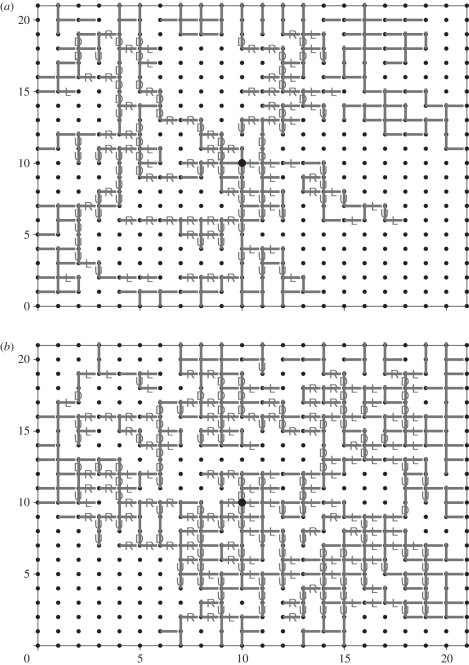
Soils can be regarded as porous media comprising pores that are connected together by ‘channels’. Volatiles produced by plant roots, and that can serve as attractants for nematodes, can diffuse along air-filled channels. Networks of air-filled channels are created as a soil begins to drain. Attention is here focused on drainage owing to the uptake of water by plant roots. It is assumed that the roots create a constant suction pressure and that this suction is sufficiently slow for the pressure of the drawn-in air, P, to be the same at each location within the soil. The interfacial tension at an air–water interface within a channel induces a pressure difference on either side of the interface. This pressure difference, called the capillary pressure, P_c, is inversely proportional to the diameter of the channel. At a given suction pressure, air can only penetrate channels with P_c < P. The drawing of air into soil can therefore be modelled with reference to a network of pores and channels; a practice common in numerical studies of transport in soil [36]. Channels for which P_c < P can be occupied by air, the rest are water-filled, but only those clusters of channels in contact with the face through which the air enters will be air-filled. The proportion of air-filled channels depends on the distribution of the capillary radii and the suction pressure. Clusters of inter-connected air-filled channels span the network when 1/2 or more of the channels are air-filled [37]. The proportion 1/2 corresponds to the suction pressure at which air can first pass through the soil. Here, soil structures are modelled on a regular square lattice, but this is without loss of generality to the structure of soil. Each node of the lattice represents a pore while the links between nodes represent channels. For our simulation, channel radii, r, are randomly and uniformly distributed between 0 and 1 arbitrary size units. All the channels are initially assumed to be water-filled. Larger channels with radii exceeding a threshold value are then drained (figure 1). Air enters the soil (lattice) at its top surface. The diffusion of the volatile chemo-attractant from a centrally located source through the air-filled channels was simulated using a random walk model (e.g. [38]). This model simulates the trajectories of individual packets of chemo-attractant through the labyrinth of air-filled channels. Random walks are sequences of individual random movements over time. Specifically here, starting from its source, at each time step a packet of chemo-attractant moves randomly to an adjacent node (pore) along one of the adjoining air-filled channels, e.g. if the packet is currently at a node with coordinates (i, j) and there are water-filled channels going leftwards and downwards and air-filled channels going rightwards and upwards, then at the next time step the packet can move either to node (i + 1, j) with probability 1/2, or to (i, j + 1) with probability 1/2. If there are three air-filled channels connected to the node at (i, j), then the packet can move in one of three possible directions, and each possibility would have probability 1/3, and so on. Random walks are equivalent to diffusion equations but are used here in preference to diffusion equations because they are easier to implement on the complex geometry of the proposed lattice structure for the soil. Concentrations of chemo-attractant at each node at time step n = 500, owing to the presence of a continuous source of chemo-attractant that became active at time step n = 0, were calculated as follows. First, 10⁴ packets were tracked from the source over one time step and their final positions were recorded. This procedure was then repeated for 2, 3, … , 500 time steps. Finally, for each location within the lattice, the concentration of chemo-attractant (i.e. the total number of packets present) was found by counting the number of packets having the final position (i, j). For most locations within the modelled soil structures considered here, the directions of maximum gradients in concentration did not change at time steps greater than 500. When far fewer packets were tracked and for much fewer time steps, gradients in chemo-attractant at some locations were found to be affected by stochastic fluctuations in concentration. Random walks of chemical packets were terminated if they reached the outer edges of the modelled soil structure.

Figure 1.

Example distributions of air-filled channels (horizontal and vertical lines) that connect some adjacent pores (small filled circles) together. The suction pressure can draw air through all channels with (a) radii r > 0.45 and (b) radii r > 0.35 arbitrary size units. Channel radii are randomly and uniformly distributed between 0 and 1 arbitrary size units, so that (a) 55% and (b) 65% of the channels are potentially air-filled. Some channels (shown in grey) in contact with the upper face of the soil (i.e. the atmosphere) have been invaded by air. The remaining channels are water-filled. The directions, (U)p, (D)own, (R)ight and (L)eft, in which chemotaxis will take a nematode in response to a chemo-attractant are indicated. The overall movement track of a nematode from an arbitrarily chosen starting location can be seen by moving through the network in the directions indicated. It is seen that, irrespective of their starting location, nematodes always take the shortest, most direct route to the source of the chemo-attractant which is located in the centre of the network (large filled circles). The nematodes never become trapped and never take a wrong turn.

Wallace [31] found that air-breakthrough initiates nematode movement but that with a modest further reduction in water content movement is impeded. These observations led Wallace [32] to suggest that nematodes move through thin water films that are aligned with air-filled channels. The thickness of these films reduces as soil drains. Wallace [32] attributed the eventual cessation of nematode movements to this reduction in water-film thickness and so to the increase in the surface tension that pulls nematodes against soil aggregates. Following Wallace [32], it is initially assumed that nematodes move through thin water films that are aligned with the air-filled channels. It is further assumed that nematodes can resolve and respond to all chemical gradients no matter how small. This latter condition is not overly restrictive. As a soil drains, successively narrower channels become air-filled so that eventually size-exclusion could impede chemotaxis. But before this happens, all movements could be impeded by the reduction in the thickness of the water films. Observations of the movements of Heterodera schachtii in water films indicate that these nematodes move at a speed of about 10 cm h^–1 when the thickness of the film is about one-fourth of the body diameter (5 µm), and that they stop moving when the film is about 1 µm thick [32]. Note also that volatiles, mainly small lipophilic molecules, solubilized in water can be perceived by plant-parasitic nematodes even though the sensory organs, the amphids, are wet (in water or soil solution).

Later on, model predictions are obtained under the assumption that nematode movements are confined to well-aerated water-filled channels, as this behaviour is also consistent with the observations of Wallace [24].

2.2. Observing the movement patterns of Meloidogyne incognita and Meloidogyne graminicola in modified Y-chamber olfactometers

2.2.1. Nematode species

Meloidogyne graminicola (from Bangladesh) normally infects rice, wheat and several other graminaceous plants [39,40] but have also been reported to infect certain dicotyledonous plants [40,41]. Meloidogyne incognita (race 1 NCSU) is a serious pest of dicotyledonous crops and occasionally infects cereals. Preliminary studies in our laboratory have shown that M. graminicola prefers rice to tomato roots while M. incognita prefers tomato to rice roots.

2.2.2. Culturing of nematodes

Meloidogyne incognita and M. graminicola were maintained, respectively, on tomato (Solanum lycopersicum cv. Tiny Tim) and rice (Oryza sativa cv. Ballila) in 15 cm diameter pots containing equal mix of sterilized sand : peat : top soil at 27°C, 30–65% relative humidity and 16 L : 8 D photoperiod in a glasshouse. Egg masses were handpicked, using sterilized forceps, from carefully washed roots of eight-week-old plants and kept in a piece of 10 µm porous cloth supported on mira cloth held by two plastic rings in a flat-bottomed evaporating dish containing distilled water [42,43] and incubated at 27°C. Freshly hatched second-stage juveniles (J2s) were used for the attraction bioassay experiment.

2.2.3. Germination of seeds

Seeds of tomato (S. lycopersicum cv. Tiny Tim), rice (O. sativa cv. Ballila) and mustard (Brassica napus cv. Oscar) were surface sterilized in 0.1 per cent sodium hypochlorite for 2 min and then washed three times with glass-distilled water. They were then placed on wet filter paper in Petri dishes, wrapped in aluminium foil and incubated at 27°C. For the attraction bioassay experiments, 4–5-day-old germinated seedlings were used.

2.2.4. Attraction assays

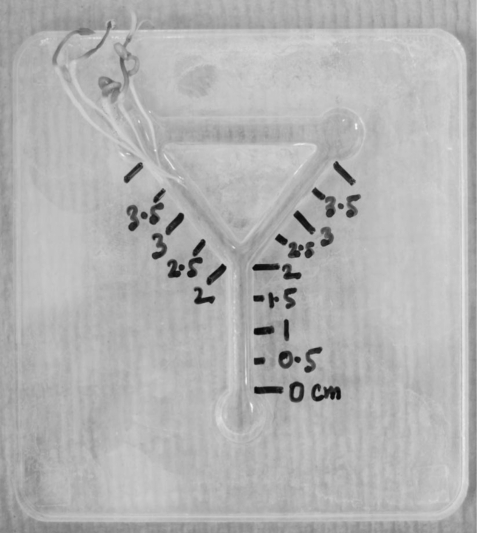
Nematode behaviour is studied in the simplest kind of maze (lattice) consisting of a modified Y-chamber olfactometer in which there are just two routes to a plant root, one long and one short. Modified Y-chambers were made up of acrylic sheets having Y-shaped 5 mm deep and 4 mm wide channels. The basal arm of a Y-chamber, i.e. the common channel, was 2 cm. This was joined by 2 cm left and right channels. Left and right channels were joined together by another 2 cm channel across the top of the Y-chamber (figure 2). Distances of 0.5, 1, 1.5 and 2 cm were marked beside the common channel, whereas 2.5, 3, 3.5 and 4 cm were marked beside both left and right channels. Five seedlings of tomato, or rice, or mustard were put together at the terminal position of the left channel where root tips reached the 3.5 cm marked distance (figure 2). One millilitre of 23 per cent Pluronic gel was pipetted into the Y-chamber, which was then placed in an incubator at 27°C for 10 min, to set the gel, followed by scooping out gel from the terminal position of the common channel. This was replaced by 50 µl suspension of approximately 100 J2s of M. incognita or M. graminicola and then this end of the Y-chamber was sealed with a few drops of gel. The chambers were placed in a humid tray and kept at 27°C. The number of J2s at each distance was counted after 1, 2, 3 and 4 h. Tomato and rice were known to be the good and poor host for M. incognita, respectively, and vice versa in the case of M. graminicola [40], whereas mustard was the non-host for both species, which served as the negative control. A control (without any plant to account for nematode random movement) was also used. There were three replicates for each combination of nematode species with plant species, and of the control. The common, left and right channels were designated as ‘basal arm’, ‘short route’ and ‘long route’, respectively. The photograph of a Y-chamber (figure 2) was taken using a Nikon D40X digital camera (Nikon Corp., Japan).

Figure 2.

Photograph of a modified Y-chamber.

2.2.5. Preparation of Pluronic gel

Pluronic gel was used to investigate the attraction of plant-parasitic nematodes to host roots and their accumulation around certain sites. Nematodes move on their sides in a two-dimensional system (such as the surface of an agar plate), which is quite unlike their movement in the soil environment. The agar plate assay is generally limited to evaluating horizontal migration. By contrast, assays using Pluronic gel, which resembles the three-dimensional natural soil environment, have proved particularly useful in investigating the short-distance attraction of plant-parasitic nematodes to host roots and their accumulation around certain sites in the roots. The transparency of this gel makes monitoring of nematode movement easy. A gel of 23 per cent solution is semisolid at room temperature but is liquid at temperature of 15°C and below [44,45]. To make 23 per cent solution gel, 23 g of Pluronic F-127 powder (SIGMA life science, BASF, USA) was added to 80 ml of distilled water and allowed to dissolve by stirring for 24 h at 4°C. The dissolved gel was refrigerated at 4°C and aliquots were dispensed for the attraction bioassay experiments.

2.2.6. Statistical analysis

For each nematode species separately, data from the attraction bioassay, i.e. counts of nematodes over distance and time, were (natural) log-transformed for regression analysis to fit a generalized linear model [46] assuming a Poisson distribution for the counts. Change in deviance (similar to sums of squares in analysis of variance), which is distributed as χ², was used to assess the significance of the effects of time, distance, plant species and region (basal arm, short route and long route) and the interactions between these variates (time and distance) and factors in the model. Hence, with similarity to previous modelling of ecological count data [47], the log-linear model fitted was

where α is a constant; B_i is the effect of replicate i, i = 1,… ,3; P_j is the effect of plant type j, j = 1,… ,4 (tomato, rice, mustard, control); β is the coefficient of time (T); γ is the coefficient of distance (D); δ is the coefficient of the distance by time interaction; (DR)_k is the interaction between distance and region (region being nested within distance), k = 1,… ,3 (basal arm, short route and long route); and followed by all other possible interactions with coefficients denoted by the appropriate subscripts j and k. Given the most complex significant (p < 0.05) terms in the model, predicted means (counts) of interest were compared using approximate least significant difference (LSD) values, as provided with the predictions, at the 5 per cent level (p < 0.05) of significance. The [48] statistical system was used for this analysis.

3. Results

3.1. Predicted movement patterns of nematodes

Irrespective of the starting location, nematodes are always predicted to take the shortest, most direct route to the source of a chemo-attractant (figure 1), following the simulated chemical gradient. The overall movement track of a nematode from an arbitrarily chosen starting location can be seen by moving through the network in the directions indicated: (U)p, (D)own, (R)ight and (L)eft (figure 1). The nematodes never become trapped and never take a ‘wrong’ turn. This remarkable consequence of chemotaxis is not dependent on the geometrical make-up of the network, and holds for both two- and three-dimensional networks. It is, for instance, predicted to arise when fissures criss-cross the soil and when some channels are blocked by the presence of small aggregates. It is also predicted to arise when soils are partially drained quasi-statically at a constant flow rate. Drainage then causes the curvatures of all of the meniscuses (of water in soil pores) to gradually increase. The pressure grows until the widest channel faced by the set of these meniscuses is crossed. Air then invades the corresponding pore. This invasion momentarily fixes the pressure of all the meniscuses at the capillary pressure of this channel. The process then repeats. The mechanism is known as ‘invasion percolation’ [37]. Our simulations also reveal that the shortest route is taken to line (rather than point) sources of attractant, and when the attractant can occasionally degrade or become immobilized by soil aggregates. There are just two provisos: (i) all of the air-filled channels are accessible to the nematodes and (ii) nematodes can resolve all chemical gradients no matter how small. When these conditions hold, the simulations predict that nematodes will never take a wrong turn and that they will never become trapped in dead ends. In other words, the gradient in a chemo-attractant is predicted to be steepest along the shortest route through the air-filled channels. This is no surprise when the geometrical make-up of the air-filled channels is relatively simple. But when air first breaks through a soil, the air-filled channels have a tortuous fractal geometry [37] creating multiple pathways from a source to each and every air-filled channel, each of which contributes to the gradient in a chemo-attractant.

Results of further simulations (not shown) indicate that chemotaxis will take nematodes to the source of short-ranged water-soluble attractants by the shortest route through well-aerated water-filled channels that exist around the threshold of percolation.

3.2. Observed movement patterns of Meloidogyne incognita and Meloidogyne graminicola in modified Y-chambers using Pluronic gel

3.2.1. Attraction of Meloidogyne incognita towards different hosts in modified Y-chambers

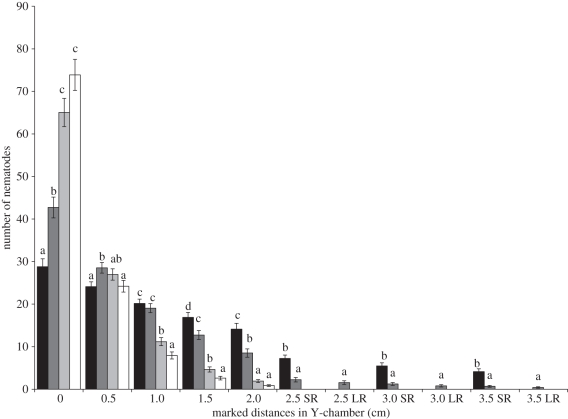
At 2 h, none of the nematodes had moved further than 1 cm along the basal arm of the Y-chamber (data not shown). By this time, equilibrium gradients of attractant would have been established throughout the Y-chamber [44,49,50]. Analysis of deviance revealed a significant three-way interaction between time, distance travelled and region (p < 0.001), indicating differential movement in the regions. More importantly, there was also an interaction between distance travelled, plant species and region (p < 0.001). The predicted mean counts for combinations of these three terms at 4 h (figure 3) revealed that significantly (p < 0.05) greater numbers of J2s remained at 0 cm in the case of mustard and control, while greater numbers of J2s migrated towards tomato than towards rice. No significant difference (p > 0.05) was observed among the number of J2s at 0.5 cm for tomato, mustard and control. Greater numbers of J2s moved to 1 cm in both tomato and rice compared with mustard or control, while among tomato and rice there was no significant difference (p > 0.05). Greater numbers of J2s migrated to 1.5 and 2 cm in the case of tomato compared with rice, mustard and control. No J2s travelled further than 2 cm for Y-chambers using mustard and control. Significantly (p < 0.05) greater numbers of J2s reached 2.5, 3 and 3.5 cm on the short route towards tomato compared with rice. A few J2s took the long route in the case of rice (figure 3). There is no evidence up to the 4 h observation that M. incognita arrive at the poor host by taking the long route.

Figure 3.

Attraction of M. incognita towards different hosts in modified Y-chambers at 4 h (SR, short route; LR, long route). Predicted means are presented, given a generalized linear model fitted to observed counts. Significant difference between plant species within each distance and region combination are marked with a different letter (LSD, p < 0.05). (Error bars indicate prediction standard error.) Black bars, tomato; dark grey bars, rice; light grey bars, mustard; white bars, control.

3.2.2. Attraction of Meloidogyne graminicola towards different hosts in modified Y-chambers

At 2 h, none of the nematodes had moved further than 1 cm along the basal arm of the Y-chamber (data not shown). By this time, equilibrium gradients of attractant would have been established in the long and short arm of the chamber [44,49,50]. For this nematode species, there was also a significant interaction between time, distance travelled and region (p < 0.001), indicating differential movement in the regions. An interaction between distance travelled, plant species and region was also significant (p < 0.001). Predicted means at 4 h (figure 4) revealed that significantly (p < 0.05) greater numbers of J2s remained at 0 cm in the case of mustard and control, while the number of J2s that migrated towards rice was greater than for tomato. No significant difference (p > 0.05) was found between the number of J2s at 0.5 cm in the case of tomato, rice and mustard. For both tomato and rice, greater numbers of J2s moved to 1, 1.5 and 2 cm compared with mustard and control, while among tomato and rice, no significant difference (p > 0.05) was observed at 1 and 1.5 cm distance, although the number of J2s was greater in rice than in tomato at 2 cm (p < 0.05). No J2s travelled further than 2 cm for Y-chambers using mustard or control. Significantly greater (p < 0.05) numbers of J2s reached 2.5, 3 and 3.5 cm on the short route towards rice compared with tomato. A few J2s took the long route in the case of tomato (figure 4). There is no evidence up to the 4 h observation that M. graminicola arrive at the poor host by taking the long route.

Figure 4.

Attraction of M. graminicola towards different hosts in modified Y-chambers at 4 h (SR, short route; LR, long route). Predicted means are presented, given a generalized linear model fitted to observed counts. Significant difference between plant species within each distance and region combination are marked with a different letter (LSD, p < 0.05). (Error bars indicate prediction standard error.) Black bars, tomato; dark grey bars, rice; light grey bars, mustard; white bars, control.

4. Discussion

Anderson et al. [51,52] reported that the presence of localized bacterial food source (Escherichia coli) acting as a chemo-attractant caused the movements of the nematode Caenorhabditis elegans on a homogeneous layer of nutrient agar in a Petri dish to become straighter and more directed. These movements approximate to a straight line, which is, of course, the shortest possible route to the source of the chemo-attractant. The results of our numerical simulations build upon the study of Anderson et al. [51,52] and provide a provocative answer to the question of how plant-parasitic nematodes locate distant sources of chemo-attractant. They indicate that chemotaxis can take a nematode to the source of a pure chemo-attractant by the shortest, most direct route through the labyrinth of air-filled or water-filled channels within a soil through which the attractant diffuses. Previously, this remarkable consequence of chemotaxis had gone unnoticed. Searching strategies and maze-solving algorithms are not required. Chemotaxis does, in fact, outperform maze-solving algorithms, the best known of which are the ‘wall follower’, the ‘pledge’ and Tremaux's algorithm [53]. Of these, only Tremaux's algorithm (a depth-first search) will find a solution for all mazes, but not necessarily the shortest path when there are multiple paths. Shortest paths can be identified using a breadth-first search. A breadth-first search begins with an exploration of all locations in the neighbourhood of an initial starting location. Then for each of these locations, all unexplored neighbouring locations are explored, and so on, until the goal is located. This algorithm may be implemented by the plasmodium of the slime mould Physarum polycephalum, a large amoeba-like cell consisting of a dendritic network of chamber-like structures (pseudopodia) [54]. However, these algorithms do not assume that the searcher can react to a chemical gradient: chemotactic maze-solving is dependent upon nematodes being able to resolve all gradients in a chemo-attractant, no matter how small, and their being able to travel through any of the air-filled channels through which the attractant diffuses.

Model predictions could not be tested directly because nematode movement patterns cannot be observed in soil. Nonetheless, our in vitro studies, using Pluronic gel as a substitute for a natural soil environment, are the first to examine the routes taken by plant-parasitic nematodes to the roots of host plants. In these studies, nematodes respond to water-soluble plant compounds produced by a living plant and present in concentrations comparable with that found in the rhizosphere. The nematodes can take one of possible routes to the plant root. Previous studies with choice chambers have provided only one route to an attractant. By 4 h, no nematodes travelled further than 2 cm for Y-chambers using mustard or control, possibly reflecting their random movement, or attraction to non-specific compounds in the case of mustard. However, within the same time period, many J2s entered the short or long route on their journey to a preferred host, possibly indicating that these nematodes were under the influence of more specific attractants. Our experiments show that M. incognita and M. graminicola are attracted to their preferred hosts in greater numbers and show only limited attraction towards poor hosts and no attraction to mustard. More importantly, our data show that nematodes take the most direct route to their preferred hosts (as predicted), but often take the longer of two possible routes towards their poor hosts. This behaviour can be reproduced in our simulations if nematodes resort to random searching when gradients in chemo-attractants become sufficiently weak. This is consistent with the expectation that poor hosts are only weakly attractive or highly repellent.

Other studies have suggested that host location and non-host avoidance by insects involve olfactory recognition of specific blends of host-derived semiochemicals (see [55] and references therein). Our data with nematodes suggest that host location behaviour may be modified in a similar manner. It can be anticipated that a complex of attractant and repellent semiochemicals influences the interaction between host and parasite, as hosts have been selected to defend themselves against parasites, while parasites have been selected for more efficient ways to locate hosts. This interaction is likely to be host- and parasite-specific, as the ability to orient towards plant roots enhances nematode survival. No nematode attraction to the non-host plant was observed, which indicates that more specific short- and local-distance attractants might be operating during the host recognition process for Meloidogyne spp. We hypothesize that M. incognita and other ‘generalists’ with a very broad host range may rely almost exclusively on general plant cues with the right blend and concentration of semiochemicals. On the other hand, nematodes with a narrower host range, such as the root-knot nematode M. gramincola and cyst nematodes, may utilize semiochemicals that elicit more specific responses. Only when repellents are insufficiently present or active are nematodes predicted to take the shortest, most direct route to a root. Our experimental data suggest that either (i) the blend of semiochemicals is different in good and poor hosts or that (ii) relatively long-range attractants in combination with shorter range repellents might affect nematode movement patterns. This warrants further investigation. What is required now is a thorough experimental and theoretical examination of the complex influences that attractants and repellents have on nematode movements when present in concentrations and proportions typical of that found in the rhizosphere. A better understanding of the nature of semiochemicals present in root exudates affecting nematode behaviour will reveal targets for chemical or genetic intervention to control plant-parasitic nematodes. Prolonging the migratory phase of nematodes in soil will reduce their infectivity and increase their exposure to natural enemies.