Decomposing phylogenetic entropy into α, β and γ components

Abstract

Measuring the phylogenetic diversity of communities has become a key issue for biogeography and conservation. However, most diversity indices that rely on interspecies phylogenetic distances may increase with species loss and thus violate the principle of weak monotonicity. Moreover, most published phylogenetic diversity indices ignore the abundance distribution along phylogenetic trees, even though lineage abundances are crucial components of biodiversity. The recently introduced concept of phylogenetic entropy overcomes these limitations, but has not been decomposed across scales, i.e. into α, β and γ components. A full understanding of mechanisms sustaining biological diversity within and between communities needs such decomposition. Here, we propose an additive decomposition framework for estimating α, β and γ components of phylogenetic entropy. Based on simulated trees, we demonstrate its robustness to phylogenetic tree shape and species richness. Our decomposition fulfils the requirements of both independence between components and weak monotonicity. Finally, our decomposition can also be adapted to the partitioning of functional diversity across different scales with the same desirable properties.

1. Introduction

Within the context of the global extinction crisis, it has been argued that protecting the Tree of Life is a key component of conservation prioritization [1]. However, we cannot begin to map the distribution of phylogenetic diversity or to measure how fast it is disappearing unless we can appropriately measure it.

Many estimators are available for approximating the phylogenetic diversity of a species assemblage [2], with Faith's PD [3] being the most popular. However, some of these indices rely only on the phylogenetic links between species, neglecting relative abundances. Indices including abundances only consider the species level, whereas the abundance of lineages and the distribution of abundance along the entire phylogenetic tree deserve to be included. For instance, the potential loss of phylogenetic diversity is linked to lineage extinction probabilities [4], which depend on abundance distributions among tree branches. Other phylogenetic diversity indices, such as Rao's entropy, do not satisfy the principle of weak monotonicity [5], i.e. the addition of a species may decrease the diversity value if other species abundances change marginally. This principle is critical for conservation issues, as it ensures that promoting the highest phylogenetic distinctiveness among species and maintaining species richness do not conflict [6]. In a recent paper, Allen et al. [6] presented a new phylogenetic diversity index overcoming these limitations; this method and biogeographically weighted evolutionary distinctness [7] are the only indices based on both tree branches as biological units and abundances. Moreover, it satisfies the principle of weak monotonicity.

There is a growing consensus that biodiversity across different scales should be considered, e.g. [8]. Traditionally, ecologists have defined three levels of biodiversity: (i) local biodiversity, termed α-diversity, (ii) regional biodiversity, or γ-diversity, and (iii) the differentiation among local biodiversities, called β-diversity (or biological turnover). The turnover between local diversities has been recognized as a key determinant of biodiversity establishment and maintenance at regional [9] and global [10] scales.

To overcome the limitations of previous indices, we propose decomposing the phylogenetic entropy introduced by Allen et al. [6] into α, β and γ components. Using simulations, we show that this decomposition provides a measure of phylobetadiversity [8], robust to phylogenetic tree shape and species richness. We also indicate, through simulations, that the decomposition into α-, β- and γ-phylogenetic diversities yields independent components.

2. Material and methods

Allen et al. [6] proved that the phylogenetic entropy generalizes the Shannon index in the same way that two other widely used phylogenetic diversity indices—quadratic diversity [11] and phylogenetic diversity [3]—generalize Simpson's index and species richness, respectively (table 1). Thus, the properties previously demonstrated for the Shannon index are conserved [12,13].

Table 1.

Phylogenetic diversity estimators available to measure α, γ and β components.

	presence/absence	abundances included
		Simpson index	Shannon index
α- and γ-diversity	phylogenetic diversity [3]	phylogenetic quadratic entropy [19,20]	phylogenetic entropy [6]
β-diversity	PhyloSor [9,21]	phylogenetic quadratic entropy decomposition [19]	phylogenetic entropy decomposition (this work)

Jost [12] demonstrated that the decomposition of diversity indices into α, β and γ components has often produced β estimates with a hidden dependence on α, preventing comparisons and eventually leading to spurious results. As an alternative, Jost [12] proposed using ‘number equivalents’ permitting the decomposition of any diversity index into independent components. The obtained decomposition is not systematically additive or multiplicative, but must be analytically derived for each diversity index. The author showed that the decomposition of the Shannon entropy is additive, and is the only standard diversity measure partitionable into meaningful, independent α and β components when community weights are unequal. Furthermore, this concave function always satisfies the condition that α-diversity does not exceed γ-diversity [12,14]. We thus used this additive decomposition to propose α, β and γ components adapted from the phylogenetic entropy of Allen et al. [6].

Let A_ik be the abundance (number of individuals or biomass) of species i within site k, the regional pool having a total of S species and K sites. The weight f of each site k is proportional to its relative abundance over sites:

2.1

Local phylogenetic entropy (within site k), following Allen et al. [6], is given by:

2.2

where T is a phylogenetic tree for the species regional pool, l(b_t) is the length of a branch b_t and p_k(b_t) is the local proportion of abundance:

2.3

where S_t is the number of species or leaves descending from b_t.The regional phylogenetic entropy (γ) was defined as:

2.4

where the regional proportion of abundance belonging to branch b_t is:

2.5

Combining formulae (2.1), (2.3) and (2.5), we can express p_γ(b_t) as:

2.6

The regional proportion of abundance belonging to branch b_t is thus the weighted sum of local proportions of abundance of this branch b_t.

The average within-site (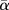) phylogenetic entropy, 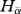, is presented as the expectation of H_k over all sites according to the weight w_k:

2.7

The weight is w_k = 1/K, if each site k is given the same weight regardless of its regional contribution, or w_k = f_k, if each site k weight corresponds to its regional contribution. In any case:

2.7

The aim of our study is not to discuss these alternative approaches to site weighting. Both methods have been proposed, and the final choice depends on the question investigated and the data available [15,16].

Following the additive partitioning of Shannon diversity, β phylogenetic entropy is estimated by: H_β = H_γ − .

Accordingly, H_β can be expressed as:

2.8

Thus, we obtain:

2.9

H_β = 0, when all local proportions of abundance belonging to branch b_t are equivalent to the corresponding regional proportions, i.e. for each site k, p_k(b_t) = p_γ(b_t). In this case, there is no phylogenetic turnover among sites, because all branches have similar abundances. By contrast, when species compositions or local relative abundances belonging to branch b_t vary among sites, then H_β increases. Pavoine et al. [17] demonstrated that partitioning any concave index into α, β and γ components, using an ultrametric phylogenetic tree and abundances at the γ scale including those of local communities (α scale), prevents negative H_β values. Since this approach corresponds to the weighted method in equation (2.7), we have:

2.10

and H_β ≥ 0.

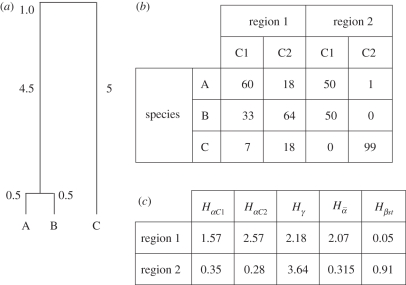
As an illustration, we propose two simple decompositions in figure 1 (see electronic supplementary material, S1 for details).

Figure 1.

A hypothetical case study illustrating the calculation of α-, β- and γ-phylogenetic diversities. (a) Phylogenetic relationships among three species in a regional pool. Phylogenetic distances (branch lengths) among pairs of species are indicated on the dendrogram. (b) Local abundances of species A, B and C in two hypothetical regions, each divided into two communities (C1 and C2). The total abundance per species and per site is indicated. (c) α, β and γ components estimated for each regional pool and each local community. H_αCx: local phylogenetic diversity; H_γ: regional phylogenetic diversity; : mean local phylogenetic diversity estimated on local communities; H_βst: phylogenetic turnover.

To investigate the potential influence of tree shape and community size on the phylogenetic entropy decomposition, we simulated artificial trees with different species richness values and tree structure. We produced 50-species and 100-species trees using two contrasted models, either the Yule model or the proportional-to-distinguishable arrangements (PDA) model (electronic supplementary material, S2). To explore the influence of species richness on our decomposition, we built communities by randomly sampling species along a gradient of richness (from 1 to 50 or 1 to 100 species), which were then compared with a given 20-species community. α-, β- and γ-diversity values were calculated for each pair of communities combining one 20-species community and one n-species community (n ranging from 1 to the regional pool size). Species abundances were allocated to each community using a lognormal distribution commonly observed in nature ([18]; see electronic supplementary material, S2 for details). We also investigated the independence between α, β and γ components using these simulated communities.

3. Results

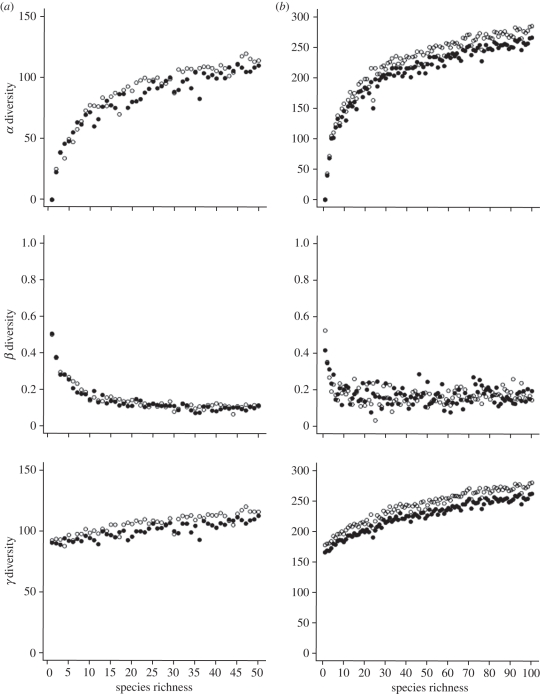
According to our results, tree shape (Yule or PDA) had no influence on β-diversity values (figure 2). However, β-diversity values were weakly influenced by species richness above a certain level. The probability of sharing species with the 20-species community decreased with the number of species composing the regional pool of species. Thus, β-diversity values might be overestimated at low species-richness levels.

Figure 2.

α-, β- and γ-diversity values estimated on communities sampled among (a) 50-species or (b) 100-species trees generated under the Yule (closed circles) or PDA (open circles) model. α- (based on average local diversity values (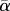)), β- and γ-diversity values were calculated on pairs of communities composed of one 20-species community and one n-community (n ranging from 1 to 50 or 1 to 100 species depending on the regional tree size). β-diversity is expressed as the proportion of biological turnover (i.e. H_βst = 1 − [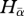/H_γ]).

α- and γ-diversity values were higher when using the PDA model than the Yule model, although the total branch length of trees simulated under Yule and PDA models was equal for a given number of tips (i.e. species). Tree imbalance induced by the PDA model led to asymmetric trees and older divergence, compared with trees generated under the Yule model, which induced a higher degree of phylogenetic similarity between species.

Our simulations also showed that the total species richness influenced α- and γ-diversity values (figure 2). Indeed, for a given level of species richness in the communities, there were more branches linking species on 100-species trees.

Finally, we found that β-diversity was weakly related to α- and γ-diversity values regardless of models, while α- and γ-diversity were highly correlated (table 2). Consequently, α- and γ-diversity levels do not influence β-diversity values.

Table 2.

Spearman correlation coefficients among α-, β- and γ-diversity components. (All coefficients were significantly different from 0 (p < 0.001). α- (based on average local diversity values (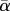)), β- and γ-diversity values were calculated on pairs of communities composed of one 20-species community and one n-community (n ranging from 1 to 100 species) sampled among 100-species trees generated under Yule or PDA (proportional-to-distinguishable arrangements) model.)

	Yule			PDA
	α	β	γ	α	β	γ
α	1			1
β	0.09	1		0.13	1
γ	0.97	0.12	1	0.98	0.17	1

4. Discussion

Here, we develop a new method to estimate how spatial scale influences the distribution of abundance along phylogenetic trees within and between communities. Our decomposition of phylogenetic entropy considers phylogenetic distances and relative abundances simultaneously. It fulfils the requirement of independence between diversity components and weak monotonicity, which may be necessary for an appropriate additive measure of α-, β- and γ-diversities within a conservation context. Furthermore, we show that the structure and size of the phylogenetic tree as well as the size of the sampled communities, influence α- and γ-diversity levels. Nevertheless, β-diversity exhibits consistent values across species richness levels (excepting low levels), total tree sizes and diversification models, allowing comparisons. Such a decomposition contributes to a better understanding of the phylogenetic diversity distribution across space and time, and thus to define appropriate conservation efforts towards the preservation of the Tree of Life. Our decomposition could be adapted to the partitioning of functional diversity when species are clustered along functional trees.