Continual reassessment method with multiple toxicity constraints

Abstract

This paper addresses the dose-finding problem in cancer trials in which we are concerned with the gradation of severe toxicities that are considered dose limiting. In order to differentiate the tolerance for different toxicity types and grades, we propose a novel extension of the continual reassessment method that explicitly accounts for multiple toxicity constraints. We apply the proposed methods to redesign a bortezomib trial in lymphoma patients and compare their performance with that of the existing methods. Based on simulations, our proposed methods achieve comparable accuracy in identifying the maximum tolerated dose but have better control of the erroneous allocation and recommendation of an overdose.

1. INTRODUCTION

Phase I trials of a new drug are typically small studies that evaluate its toxicity profile and identify a safe dose for further studies. This objective is usually achieved by the determination of the maximum tolerated dose (MTD), defined as the dose that causes a dose-limiting toxicity (DLT) with a prespecified probability. While the precise definition of DLT varies from trial to trial, a DLT is typically defined as a grade 3 or higher toxicity according to the National Cancer Institute Common Terminology Criteria for Adverse Events (National Cancer Institute, 2003), from 0 indicating no toxicity to 5 indicating toxic death. Many statistical designs have been proposed to address this dose-finding objective as a sequential quantile estimation problem. A few examples in the growing literature are the continual reassessment method (CRM; O'Quigley and others, 1990), the biased coin design (Durham and others, 1997), stepwise procedures (Cheung, 2007), and the interval-based method (Ji and others, 2007). These designs, utilizing the binary DLT data for estimation, provide clinicians with convenient options without reference to the nature of toxicity for the specific clinical situations. In many settings, however, it is important to differentiate grade 3 from the higher-grade toxicities and to distinguish between toxicities types of the same grade.

Consider, for example, a phase I trial in lymphoma patients treated with bortezomib plus the standard CHOP–Rituximab (CHOP-R) regimen (Leonard and others, 2005). The objective of the trial was to determine the MTD of bortezomib, a potent and reversible proteasome inhibitor that could cause neurologic toxicity. In the trial, a grade 3 or higher peripheral neuropathy with grade 3 neuropathic pain resulting in discontinuation of treatment and a very low platelet count were considered dose limiting. The MTD was defined as the dose associated with a 25% DLT probability. While grade 3 neuropathy is a symptomatic toxicity interfering with activities of daily life, it may be resolved by symptomatic treatment. In contrast, a grade 4 neuropathy is life threatening or disabling and hence irreversible. Thus, while 25% grade 3 neuropathy is acceptable in the bortezomib trial, the tolerance for grade 4 neuropathy is much lower. Another shortcoming of using only the DLT, in this example, is that it does not differentiate between a grade 4 neuropathy and very low platelet count. Both are considered DLT, however, the tolerance for grade 4 neuropathy is much lower.

Motivated by these concerns, Bekele and Thall (BT, 2004) introduce the concept of severity weights and define the MTD as a dose associated with a prespecified expected total toxicity burden (TTB). In brief, a TTB is the sum of severity weights for the grades of toxicities across different toxicity types, where the weights are elicited from the physicians for each toxicity type and grade. To describe the relationship between TTB and dose, the authors propose a model motivated by latent variables for the joint probability distribution of the severity weights. The model is highly complex as the dimension of the joint distribution equals the number of types of toxicity considered. As a result, the BT method is computational intensive, and it is time-consuming to perform a thorough investigation of the method's robustness via simulations. Yuan and others (2007) subsequently propose a simpler quasi-likelihood estimation approach based on equivalent toxicity scores and aim to identify a dose associated with a prespecified expected equivalent toxicity score. Since an equivalent toxicity score is essentially a TTB when only one toxicity type is considered, the dose-finding objective in Yuan and others (2007) is the same as the BT method. However, the authors do not consider the more realistic situations where there are multiple toxicity types. In practice, it is difficult to apply either method because the TTB objective does not correspond to the conventional percentile definition of MTD, and physicians may find it an abstract endeavor to specify a target TTB value. As an alternative to the TTB, Lee and others (2009) propose to summarize the toxicity profile by a single numerical index, called the toxicity burden score (TBS), which is calibrated through a regression model by fitting the TBS using historical data. Both the TTB and the TBS summarize toxicities using a weighted sum of grades and types of toxicities.

In this article, we propose a novel extension of the CRM that defines the MTD with respect to multiple toxicity constraints applied on a continuous or ordinal toxicity measure such as toxicity grades, TBS, or TTB. By applying the method on a toxicity summary measure and using multiple toxicity constraints, the method incorporates information on both grades and types of toxicity for the estimation of the MTD. Briefly, our proposed method is different from the BT method in 2 ways. First, the method can be used with any continuous or ordinal toxicity outcome, thus, the dimension of the probability model is much reduced, and a systematic design calibration process is feasible. Second, we expect that the proposed method has a better ability to control for the probability of recommending an overdose through the explicit constraints on higher-grade toxicities. Section 2 describes the probability model and the dose-finding algorithm. As in the CRM, it is important to calibrate the design to obtain good operating characteristics under a variety of real life scenarios. Ideally, the calibration process can be done solely based on clinician input. However, the necessary information is seldom available in the setting of phase I trials. Thus, a design calibration approach is proposed in Section 3. In Section 4, the proposed method and the calibration approach are illustrated in the context of the bortezomib trial. A numerical illustration of the method in the context of the bortezomib trial and a simulation study are presented in Section 5. A discussion of the method is given in Section 6.

2. CRM WITH MULTIPLE CONSTRAINTS

2.1. Problem formulation

Consider an ordinal or continuous toxicity outcome (T) such as toxicity grades in the one toxicity case, TTB as defined by Bekele and Thall (2004) or TBS as defined by Lee and others (2009) in the multiple toxicity case. We define the MTD, denoted by θ, as the maximum dose that satisfies L prespecified toxicity constraints in terms of T. Precisely, let Pr(T ≥ t|x) denote the tail probability of T under dose x. Then

(2.1)

where t₁ < ⋯ < t_L are prespecified toxicity thresholds and p₁ > ⋯ > p_L > 0 are their respective target probabilities.

To build the dose–toxicity model, let Z denote a normally distributed random variable with mean α + βx so that t_l ≤ T < t_{l + 1} if and only if γ_l ≤ Z < γ_{l + 1} for l = 0,…,L, with the convention that t₀≡ − ∞ and t_{L + 1}≡∞. In addition, to ensure that the model is identifiable, the variance of Z is set to be 1, γ₀≡ − ∞ and γ₁≡0. This model, motivated by a latent variable modeling approach as also used in Bekele and Thall (2004), is particularly useful because the trial objective (2.1) is invariant to the specific distribution of T within each interval [t_l,t_{l + 1}) once Pr(t_l ≤ T < t_{l + 1}|x) is fixed for any dose x. Under this model, the tail probability at t_l can be expressed as

(2.2)

where Φ is the distribution function of a standard normal. Under the special case when there is only L = 1 constraint (i.e. DLT only), the formulation reduces to the traditional phase I quantile estimation objective. In fact, the probit model (2.2) is very similar to the commonly used logit model in the CRM literature where the intercept term α is taken as fixed (Goodman and others, 1995). Postulating such a strong model assumption avoids the rigidity problem prescribed in Cheung (2002) who shows that using an over-flexible model in conjunction with sequential dose finding will confine a trial to a suboptimal dose with a nonnegligible probability. Therefore, we shall consider the intercept α as fixed, specifically α = 3, in line with the CRM convention. Since there are L free parameters (β,γ₂,…,γ_L), the model can adequately characterize the tail probabilities at t₁,…,t_L simultaneously at any given dose x.

In general, with L ≥ 2, the objective θ can be written as θ = min{θ₁,…,θ_L} = θ_λ, where θ_l satisfies the individual constraint Pr(T ≥ t_l|θ_l) = p_l and λ = argmin_lθ_l. Furthermore, under model (2.2), each constrained objective θ_l = {γ_l + Φ ^{− 1}(p_l) − 3}/β is an explicit function of the model parameters. In practice, the test doses are limited to a discrete set of K levels, denoted by {d₁,…,d_K}. Thus, the operating objective is argmin_dk|d_k − θ|. This is chosen in convention with the CRM (Cheung and Elkind, 2010). In practice, the highest dose less than or equal to θ can be assigned.

2.2. Dose-escalation algorithm

We adopt the same dose assignment strategy as the CRM by which the next patient is treated at an updated model-based MTD estimate, and whereby the estimation is done under a Bayesian framework. In particular, we assume that the prior distribution of β,γ₂, and γ_l − γ_{l − 1}, l = 3,…,L, are independent exponential variables with rate 1 in line with the CRM convention (O'Quigley and others, 1990, Yuan and others, 2007). This choice of prior distributions guarantees that the probability of DLT is strictly increasing in dose and that 0 < γ₂ < ⋯ < γ_L.

A natural estimate for θ at the start of the trial is its prior median, denoted by ₀, that is, the Bayes estimator with respect to the absolute error loss. Generally, with observations from the first n patients, we estimate θ by its posterior median, denoted by _n and defined such that 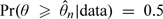. Computationally, let 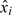_i and T_i be the dose and toxicity score of patient i, respectively, then the joint posterior distribution given the first n observations is proportional to

The joint posterior distribution of model parameters (β,γ₂,…,γ_L) can be obtained using Markov chain Monte Carlo (MCMC), and hence the joint posterior of (θ₁,…,θ_L). The next patient is treated at 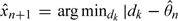, where _n is the posterior median of θ. This method is referred to as CRM-MC₁. We opt to use the posterior median instead of the posterior mean of θ in applications to sequential trials because the former will provide more stable estimation than the latter. It is known that the posterior distribution of a parameter whose definition involves ratios is likely to be heavy tailed, especially when the sample size is small, thus causing an effect on its mean.

Because the MTD, θ, is a minimum of several parameters, the posterior median _n may underestimate θ. Therefore, we also consider a second estimator that is hoped to attenuate the bias. Precisely, we define 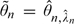, where _{n, l} denotes the marginal posterior median of θ_l given the first n observations, and 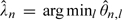. The next patient is given 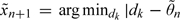. This method is referred to as CRM-MC₂.

There are various ways to start a trial. One can use a predetermined dose sequence to dictate dose escalation until the first appearance of toxicity. Specifically, set x_i = x_i,0 for the ith patient, where x_i,0∈{d₁,…,d_K} is a nondecreasing sequence of doses with x_i,0 ≤ x_{i + 1,0} and switch to 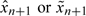once {T_i ≥ t_l} is observed for some i ≤ n and some l (Cheung, 2005). Alternatively, as done in the bortezomib trial, one may start the first patient at the prior MTD. Using the proposed method, we therefore set 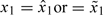depending on the choice of estimator. With either start-up rule, the reassessment process is to be continued until a prespecified sample size is reached. In addition, to avoid aggressive escalation, one can set rules to restrict the trial from skipping an untested dose or escalating after a DLT is observed.

3. DESIGN CALIBRATION

In any model-based design, it is important to calibrate the model so as to yield good operating characteristics under a realistic set of scenarios. We propose a design calibration that is similar to the approach suggested by Lee and Cheung (2009) for the CRM which has the same specification problem. As in the CRM, the doses d₁,…,d_K used in the proposed methods are not the actual doses administered, but are defined on a conceptual scale that represents an ordering of the risks of toxicity (Cheung and Elkind, 2010). These doses are obtained using backward substitution by matching the initial guess of DLT probability (denoted by p_0,k) associated with dose level k and the prior model–based DLT rate, that is, 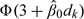according to the probit model (2.2), where γ₁≡0 by convention and 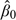is a prior guess of β. That is,

(3.1)

for k = 1,…,K. Naturally, in the current context, we take 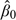as the prior median of β.

Ideally, the initial guesses p_0,ks are elicited from the clinicians as they reflect the prior belief about the DLT rates associated the test doses. In practice, such information is seldom available. Lee and Cheung (2009) propose eliciting the starting dose level and taking a pragmatic approach to calibrate p_0,ks with respect to the sensitivity of the working model; model sensitivity is in turn measured by the half-width of the indifference interval of the model. The indifference interval is an interval centered around the target DLT probability such that the CRM may select a neighboring dose level of the MTD whose toxicity probability falls in this interval (Cheung and Chappell, 2002). The narrower the indifference interval, the closer the CRM recommended dose converges to the MTD. Since indifference interval is an asymptotic concept, it is also necessary to examine its operating characteristics for finite-sample sizes. Specifically, under model (2.2), in order to achieve an indifference interval with a prespecified half-width, δ, we may rescale the doses by first setting 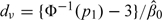and then iterating recursively:

(3.2)

for k = 2,…,ν; and

(3.3)

for k = ν,…,K − 1. The backward substitution process via (3.4) and (3.5) reduces the number of model parameters from K (for p_0,ks) to 1 (for δ) while providing a theoretical basis with respect to model sensitivity. As a result, the half-width (δ) is the only design parameter to be specified in each application. The design parameter δ is chosen via simulation over a grid of candidates to maximize the average percentage of correct selection (PCS) under a wide variety of calibration scenarios. This is illustrated in the context of the bortezomib trial in Section 4.2.

A starting dose should be set to be the lowest dose or, ideally, match the clinician's prior guess of the MTD. However, when L ≥ 2, specifying such a prior MTD requires a clinician to make prior guesses on multiple parameters θ₁,…,θ_l and λ = argmin_lθ_l, which in practice is infeasible. On the other hand, it is comparatively feasible for a clinician to make a prior guess on a single parameter θ₁ as d_ν, as is done in the current paper. Since θ = min{θ₁,…,θ_L} ≤ θ₁, it is reasonable to believe that a prior guess of MTD should be somewhere below d_ν. In light of this, we call a starting dose x₁ permissible if x₁ ≤ d_ν.

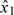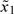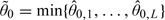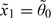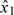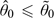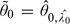When the scaled doses are obtained via backward substitution (3.3), both and are permissible starting doses. To see this, let , where _0,l is the prior median of θ_l, l = 1,…,L. Since d_ν is by construction one of the doses under study, is permissible. To prove is permissible, we need to show that . Suppose, we have . Let , then and 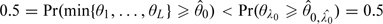, which is impossible. Therefore, ₀, and hence 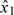, is also permissible.

We emphasize the DLT constraint (i.e. p₁) in defining a permissible starting dose since DLT is the primary toxicity and d_ν is easy to calculate via (3.3). For a higher toxicity constraint, say, p_l for some l ≥ 2, a permissible starting dose can be obtained as _0,l, the prior median of θ_l. There is no closed form for _0,l, but it can be determined numerically.

4. APPLICATION

4.1. The study design for the bortezomib trial

The original bortezomib trial was a dose-finding study in patients with previously untreated diffuse large B cell or mantle cell non-Hodgkin's lymphoma (Leonard and others, 2005). Its main objective was to determine the MTD of bortezomib when administered in combination with CHOP-R. The DLT was defined as life threatening or disabling neurologic toxicity, very low platelet count, or symptomatic nonneurologic or nonhematologic toxicity requiring intervention. The main neurologic toxicity of interest was neuropathy. The target probability of DLT was 0.25. Eighteen patients were treated for six 21-day cycles (126 days). The standard dose for CHOP-R was administered every 21 days. There were 5 dose levels of bortezomib, and the dose escalation for this trial was conducted according to the CRM. The dose–toxicity model was assumed to be empiric, that is, the probability of DLT at dose x was modeled as x^exp(β), with the prior distribution for β being normal with μ = 0 and σ² = 1.34. The initial guesses of the probabilities of DLT at the 5 doses were 0.05, 0.12, 0.25, 0.40, and 0.55, respectively. These were selected based on extensive simulations evaluating the operating characteristics of various initial guesses of the probabilities of DLT. The starting dose was therefore the dose at the third level. The CRM did not allow dose skipping during escalation nor dose escalation immediately after a DLT was observed (Cheung, 2005). In this section, we adopt the general setting of this bortezomib trial for our numerical studies and choose TBS as the ordinal toxicity outcome on which to apply the CRM in the context of multiple toxicities.

4.2. Redesign of the bortezomib trial

For patient i, let Y_i,j∈{0,1,…,5} be the toxicity grade experienced for treatment-related toxicity type j and W_i be an overall measure of toxicity unrelated to the treatment, where j = 1,…,J and J is the number of treatment-related toxicity types. Then, (Y_i,1,…,Y_i,J,W_i) summarizes the entire toxicity profile experienced by patient i. The method proposed by Lee and others (2009) to summarize the severity of multiple toxicities into a TBS is defined as

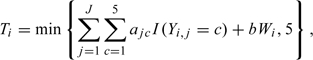(4.1)

where a_jcs and b are constants preestimated by fitting a linear mixed effects model to historical data for drugs of the same mechanism and a_j5≡5. By definition, T_i = 5 when there is a treatment-related death. Lee and others (2009) illustrate their method using the bortezomib trial data. Two main toxicities, neuropathy, and low platelet count, are identified as related to bortezomib, that is, J = 2. The number of grade 3 or higher-grade nonhematologic toxicities unrelated to bortezomib is included as variable W in (4.6) because it is believed that excessive toxicities, possibly due to the CHOP-R regimen, are concerning even though they may not be a direct result of bortezomib. To obtain the coefficients a_jcs and b, multiple clinicians are asked to assign a severity score based on the toxicity grades and types experienced by each patient in the bortezomib trial, with the guideline that a score of 1 should amount to a DLT, 0 to no toxicity, and 5 to treatment-related death. These assigned severity scores are used as the dependent variables in a linear mixed-effects model that gives the following significant fixed-effects coefficients: a₁₁ = 0.19,a₁₂ = 0.64,a₁₃ = 1.03, and a₁₄ = 2.53 for neuropathy, a₂₁ = a₂₂ = 0.17 and a₂₃ = 0.40,a₂₄ = 0.85 for low platelet count, and b = 0.17.

To implement and assess the proposed methods, we consider the bortezomib trial with 3 toxicity levels in term of TBS: T < 1, 1 ≤ T < 1.5, and T ≥ 1.5. Thus, L = 2, t₀ = 0,t₁ = 1, and t₂ = 1.5. We set t₁ = 1 as the DLT constraint in accordance with how the TBS is elicited in Lee and others (2009). The threshold toxicity probabilities are p₁ = 0.25 and p₂ = 0.10. We call the constraint Pr(T ≥ 1|x) ≤ p₁ = 0.25, the primary constraint and Pr(T ≥ 1.5|x) ≤ p₂ = 0.10, the secondary constraint. As in the original CRM design, we consider K = 5 test doses with a starting dose at level 3 and a sample size of 18 in our proposed design. In addition, we do not allow for dose skipping and dose escalation immediately after T ≥ 1 is observed. By backward substitution with ν = 3,p₁ = 0.25, and 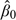= 0.69, the scaled d₃ = − 5.30. The remaining design parameters are the scaled doses (d₁,d₂,d₄,d₅) defined via the half-width, δ, using (3.4) and (3.5).

To calibrate the parameter δ, we take a similar approach to that in Lee and Cheung (2009) and consider a set of 10 calibration scenarios, where a scenario is a complete specification of the toxicity probabilities Pr(T ≥ 1|d_k) and Pr(T ≥ 1.5|d_k) for k = 1,⋯,5. Precisely, for any fixed k^*∈{1,2,3,4,5}, we first set the toxicity probability for T ≥ 1 as Pr(T ≥ 1|d_k^*) = 0.25, Pr(T ≥ 1|d_k) = 0.14 for k < k^*, and Pr(T ≥ 1|d_k) = 0.40 for k > k^*. This is the plateau configuration used in Lee and Cheung (2009). Then we determine the toxicity probability for T ≥ 1.5 by letting s = 0.30 or 0.70 in

(4.2)

for k = 1,…,K. By construction, k^* is the true MTD under the 2 calibration scenarios corresponding to s = 0.30 and s = 0.70, respectively. The positive parameter s determines the conditional probability of T ≥ 1.5 given T ≥ 1 at any dose level, and a bigger value of s corresponds to a more drastic increase of the probability Pr(T ≥ 1.5|d_k) as k increases. Equation (4.7) is equivalent to the conditional log-odds model used for ordinal categorical data (Fleiss and others, 2003).

The design parameter δ is chosen over the grid {0.02,0.04,0.06,0.08,0.10} such that the average PCS over the 10 calibration scenarios is maximized. The upper limit of δ is set to be 0.10 because an indifference interval beyond 0.25±0.10 is considered clinically unacceptable. The average PCS for any given δ is estimated by the CRM-MC₂ method based on 1000 simulations with 100 simulations performed under each of the 10 different calibration scenarios. The simulations are performed using WinBUGS (Lunn and others, 2000). For the MCMC, a burn-in of 1000 with 10 000 iterations keeping every fifth sample provides adequate convergence. The initial values for both β and γ₂ are set as 1 for the MCMC. Based on these simulations, the average PCS corresponding to δ = 0.02,0.04,0.06,0.08 and 0.10 are 0.43, 0.47, 0.49, 0.51, and 0.51, respectively. Thus, both δ values of 0.08 and 0.10 yield an average PCS of 0.51. A δ value of 0.08 is chosen as it yields a smaller indifference interval. Using (3.4) and (3.5), the corresponding scaled doses are d₁ = − 7.00,d₂ = − 6.09,d₃ = − 5.30,d₄ = − 4.61, and d₅ = − 4.01.

5. SIMULATION STUDY

To illustrate our proposed methods, we simulated a single trial using the design parameters specified in Section 4.2. The toxicities were generated using a latent uniform approach. Specifically, a random variable with a uniform distribution over interval (0,1) was sampled using the same seed for each patient and denoted as u. Supposing that this patient is assigned to dose d_k, then we set the toxicity outcome of this patient as T < 1 if u ≤ Pr(T < 1|d_k); 1 ≤ T < 1.5 if Pr(T < 1|d_k) < u ≤ Pr(T < 1.5|d_k); and T ≥ 1.5 if otherwise. This approach implied that given the same dose the toxicity outcome for a patient is the same, and therefore, ensured that the results obtained using the 2 proposed methods in Section 2.2 were comparable.

Table 1 displays the prior estimates, the dose levels assigned, and the outcomes for the 18 patients in the trial. Since ₀ = −5.51 and 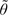₀ = −5.30, both methods recommended dose level 3 hence were permissible. The first patient was treated at dose level 3 with no toxicity, resulting in ₁ = −3.00 and 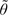₁ = −2.91. However, since we did not allow for dose skipping, dose level 4 was recommended for the second patient. This was the only occasion in this trial that the no dose-skipping restriction was in effect, indicating that the estimators stabilized quickly after very few observations. 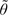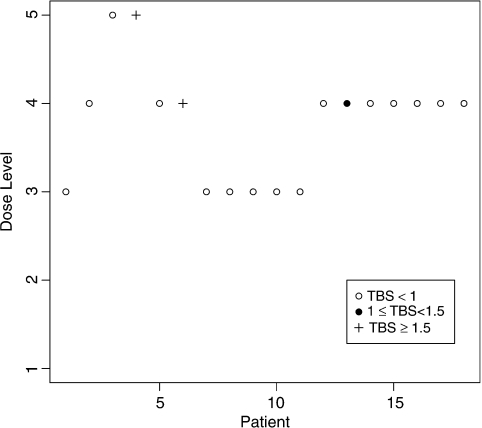In this simulated trial, the recommended MTD and the dose assigned based on both estimators were the same except for patients 12 and 14 who were assigned dose level 3 based on ₁₁ = −4.96 and ₁₃ = −4.99, respectively, but dose level 4 based on ₁₁ = −4.94 and 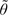₁₃ = −4.87, respectively. At the end of the trial, dose level 4 was recommended as the MTD by both methods. Figure 1 summarizes graphically the dose assignments and outcomes for the 18 patients using the CRM-MC₂ method. The dose was escalated after each of the first 2 patients with no toxicities being observed. The fourth patient experienced a severe toxicity at dose level 5 and the dose was deescalated. The dose was deescalated again after the sixth patient experienced another severe toxicity. As a result, the following 5 patients were treated at dose level 3. With no toxicities being observed, the dose was escalated after the eleventh patient and the method recommended dose level 4 for the remaining 7 patients. One toxicity was observed among these 7 patients. At the end of the trial, toxicities were reported in 3 out of the 18 patients (17%), with 2 (11%) patients having a severe toxicity.

Table 1.

Simulated trial using CRM-MC(_n) and CRM-MC(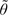_n = min{_n,1, _n,2}) methods with the 5-scaled doses being – 7.00, – 6.09, – 5.30, – 4.61, and – 4.01. T level = 1 if T < 1, T level = 2 if 1 ≤ T < 1.5, and T level = 3 if T ≥ 1.5

n	Dose level	T level	n	Dose level	T level	n,1	n,2	n
0			− 5.51			− 5.30	− 4.59	− 5.30
1	3	1	− 3.00	3	1	− 2.91	− 2.56	− 2.91
2	4	1	− 2.71	4	1	− 2.60	− 2.23	− 2.60
3	5	1	− 2.54	5	1	− 2.43	− 2.19	− 2.43
4	5	3	− 4.90	5	3	− 4.55	− 4.79	− 4.79
5	4	1	− 4.66	4	1	− 4.31	− 4.58	− 4.58
6	4	3	− 5.50	4	3	− 5.02	− 5.47	− 5.47
7	3	1	− 5.26	3	1	− 4.80	− 5.23	− 5.23
8	3	1	− 5.22	3	1	− 4.74	− 5.19	− 5.19
9	3	1	− 5.11	3	1	− 4.66	− 5.10	− 5.10
10	3	1	− 5.03	3	1	− 4.56	− 5.01	− 5.01
11	3	1	− 4.96	3	1	− 4.50	− 4.94	− 4.94
12	3	1	− 4.91	4	1	− 4.39	− 4.82	− 4.82
13	4	2	− 4.99	4	2	− 4.65	− 4.87	− 4.87
14	3	1	− 4.92	4	1	− 4.58	− 4.82	− 4.82
15	4	1	− 4.88	4	1	− 4.52	− 4.76	− 4.76
16	4	1	− 4.80	4	1	− 4.47	− 4.70	− 4.70
17	4	1	− 4.73	4	1	− 4.41	− 4.65	− 4.65
18	4	1	− 4.69	4	1	− 4.37	− 4.61	− 4.61

Fig. 1.

Simulated trial using CRM-MC₂ method.

The performance of the 2 proposed methods, CRM-MC₁ and CRM-MC₂, was assessed with further simulations under 6 scenarios that might be encountered in practice and compared with those of the CRM (i.e. ignoring the higher toxicity constraint Pr(T ≥ 1.5|x) ≤ p₂ = 0.10) and the BT method which is the only alternative in the literature for multiple toxicities. One thousand simulations were performed for each scenario with 18 subjects for each simulation using the 5 doses specified at the end of Section 4.2.

The complete configuration of the true toxicity probabilities for the 6 scenarios is depicted in Table 2. Unlike the 10 calibration scenarios used to select the optimal δ value in the calibration process, these 6 scenarios were selected in collaboration with clinicians. In the first 4 scenarios, the true probabilities of T ≥ 1 correspond to the probabilities of DLT that were originally used in the calibration of the CRM design for the bortezomib trial. In these scenarios, θ = θ₁ = θ₂. In Scenario 5, θ = θ₁ < θ₂. Thus, there is no risk of ignoring the secondary constraint since θ = θ₁. However, in Scenario 6, θ = θ₂ < θ₁. This means that if the secondary constraint is ignored and only the primary constraint is used, the wrongly believed MTD would be θ₁ = d₃, resulting in an inflated chance of severe toxicity since Pr(T ≥ 1.5|d₃) = 0.23 > 0.10 = p₂. This is a scenario in which the higher toxicity constraint should not be ignored.

Table 2.

True probabilities of the 2 types of toxicities under 6 scenarios used in the simulation study

Toxicity	Severity	Dose level					Dose level					Dose level
		1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
		Scenario 1					Scenario 2					Scenario 3
Neuropathy	Grade 0	0.47	0.37	0.36	0.36	0.34	0.47	0.47	0.37	0.35	0.30	0.47	0.47	0.39	0.37	0.35
	Grade 1	0.23	0.20	0.20	0.20	0.20	0.23	0.23	0.20	0.20	0.20	0.23	0.23	0.30	0.20	0.20
	Grade 2	0.27	0.25	0.12	0.11	0.02	0.27	0.27	0.25	0.12	0.11	0.27	0.27	0.27	0.25	0.12
	Grade 3	0.02	0.09	0.14	0.07	0.07	0.03	0.02	0.09	0.14	0.07	0.03	0.02	0.03	0.09	0.14
	Grade 4	0.01	0.10	0.18	0.27	0.37	0.01	0.01	0.10	0.19	0.32	0.01	0.01	0.02	0.10	0.19
Low platelets	Grade 0	0.56	0.31	0.30	0.25	0.20	0.66	0.56	0.31	0.25	0.15	0.66	0.56	0.41	0.31	0.25
	Grade 1 or 2	0.40	0.50	0.35	0.30	0.20	0.30	0.40	0.50	0.30	0.25	0.30	0.40	0.50	0.50	0.30
	Grade 3	0.02	0.12	0.15	0.10	0.10	0.03	0.02	0.12	0.10	0.15	0.03	0.02	0.05	0.12	0.10
	Grade 4	0.02	0.07	0.20	0.35	0.50	0.01	0.02	0.07	0.35	0.45	0.01	0.02	0.04	0.07	0.35
TBS	T < 1	0.95	0.75	0.60	0.55	0.45	0.95	0.95	0.75	0.55	0.45	0.95	0.95	0.92	0.75	0.55
	1 ≤ T < 1.5	0.04	0.15	0.19	0.16	0.14	0.04	0.04	0.15	0.21	0.20	0.04	0.04	0.06	0.15	0.21
	T ≥ 1.5	0.01	0.10	0.21	0.29	0.41	0.01	0.01	0.10	0.24	0.35	0.01	0.01	0.02	0.10	0.24
		Scenario 4					Scenario 5					Scenario 6
Neuropathy	Grade 0	0.47	0.47	0.39	0.38	0.37	0.47	0.47	0.40	0.23	0.17	0.64	0.61	0.59	0.36	0.29
	Grade 1	0.23	0.23	0.30	0.25	0.20	0.23	0.23	0.22	0.20	0.20	0.17	0.15	0.15	0.20	0.20
	Grade 2	0.27	0.27	0.27	0.32	0.25	0.27	0.27	0.18	0.27	0.28	0.15	0.10	0.03	0.05	0.05
	Grade 3	0.03	0.03	0.02	0.02	0.09	0.03	0.02	0.16	0.25	0.22	0.03	0.04	0.00	0.05	0.04
	Grade 4	0.00	0.01	0.02	0.03	0.10	0.01	0.01	0.04	0.05	0.13	0.01	0.10	0.23	0.34	0.42
Low platelets	Grade 0	0.81	0.66	0.41	0.32	0.31	0.66	0.56	0.40	0.30	0.20	0.73	0.60	0.50	0.30	0.20
	Grade 1 or 2	0.15	0.30	0.50	0.50	0.50	0.30	0.40	0.40	0.30	0.30	0.20	0.25	0.30	0.30	0.30
	Grade 3	0.02	0.03	0.05	0.13	0.12	0.03	0.02	0.15	0.20	0.20	0.06	0.10	0.10	0.20	0.20
	Grade 4	0.01	0.01	0.04	0.05	0.07	0.01	0.02	0.05	0.20	0.30	0.01	0.05	0.10	0.20	0.30
TBS	T < 1	0.95	0.95	0.92	0.88	0.75	0.95	0.95	0.75	0.55	0.45	0.95	0.84	0.75	0.55	0.45
	1 ≤ T < 1.5	0.05	0.04	0.06	0.08	0.15	0.05	0.04	0.20	0.35	0.35	0.04	0.06	0.02	0.10	0.12
	T ≥ 1.5	0.00	0.01	0.02	0.04	0.10	0.00	0.01	0.05	0.10	0.20	0.01	0.10	0.23	0.35	0.43

To compare our results with those of the BT method, we excluded the variable W from the definition of T in (4.6). Thus, in the context of the bortezomib trial, T = 0.19I(Y₁ = 1) + 0.64I(Y₁ = 2) + 1.03I(Y₁ = 3) + 2.53I(Y₁ = 4) + 0.17I(Y₂ = 1,2) + 0.40I(Y₂ = 3) + 0.85I(Y₂ = 4). This was equivalent to the definition of TTB used by Bekele and Thall (2004) with the coefficients being the toxicity weights. We obtained the joint probability distributions of the 2 toxicities from the 2 marginals under independence. The marginal probabilities for the grades of neuropathy and low platelets were chosen such that they corresponded to the prespecified Pr(T ≥ 1.5|d_k) and Pr(1 ≤ T < 1.5|d_k). For example, for dose level 1 under Scenario 1, Pr(T ≥ 1.5|d₁) = Pr(Y₁ = 4) + Pr(Y₁ = 3,Y₂ = 4) = 0.014 and Pr(1 ≤ T < 1.5|d₁) = Pr(Y₁ = 3,Y₂ < 4) + Pr(Y₁ = 2,Y₂ ≥ 3) + Pr(Y₁ = 1,Y₂ = 4) = 0.035.

For the BT method, the prior means of the intercept parameters for the 2 toxicity types were 0.5 and the prior means of the slope parameters were 1.0. The prior precision for all regression parameters was 1.0. The doses are 1, 2, 3, 4, and 5. The target TTB score was set at 0.72. The method did not allow for dose skipping.

Table 3 displays the percentage of recommending a particular dose (% Recommended) and the percentages of toxicities (% T ≥ 1 and % T ≥ 1.5) for each of the 4 methods. For the BT method, E(TTB) = 0.19π_1,1 + 0.64π_1,2 + 1.03π_1,3 + 2.53π_1,4 + 0.17π_2,1or2 + 0.40π_2,3 + 0.85π_2,4, where π_j,c is the marginal probability of toxicity for a grade c toxicity of type j. When θ₁ = θ₂ (Scenarios 1–4), the PCS using either CRM-MC₁ or CRM-MC₂ method is similar to the one using CRM. Compared to the BT method, CRM-MC₁ and CRM-MC₂ have similar accuracy and are occasionally superior (Scenario 3). CRM-MC₁, CRM-MC₂, and BT recommend dose levels above the MTD less frequently than the CRM. Compared with CRM-MC₂, the CRM-MC₁ method recommends a dose above the MTD less frequently and has lower percentages of toxicities across the 6 scenarios but yields a lower PCS when the true MTD is high.

Table 3.

Operating characteristics of the CRM, BT, CRM-MC₁, and CRM-MC₂ methods

	Dose level					% T ≥ 1	% T ≥ 1.5
	1	2	3	4	5
Scenario 1
Probability of T ≥ 1	0.05	0.25	0.40	0.45	0.55
Probability of T ≥ 1.5	0.01	0.10	0.21	0.29	0.41
E(TTB)	0.37	0.72	1.00	1.24	1.56
% recommended by CRM	12	55	27	6	1	30	15
% recommended by BT	18	61	20	2	0	26	12
% recommended by CRM-MC1	24	58	16	3	0	26	13
% recommended by CRM-MC2	20	57	19	4	0	27	14
Scenario 2
Probability of T ≥ 1	0.05	0.05	0.25	0.45	0.55
Probability of T ≥ 1.5	0.01	0.01	0.10	0.24	0.35
E(TTB)	0.33	0.37	0.72	1.13	1.48
% recommended by CRM	1	17	62	19	1	26	12
% recommended by BT	0	27	60	12	1	22	10
% recommended by CRM-MC1	2	25	62	11	0	24	11
% recommended by CRM-MC2	1	23	62	13	1	25	12
Scenario 3
Probability of T ≥ 1	0.05	0.05	0.08	0.25	0.45
Probability of T ≥ 1.5	0.01	0.01	0.02	0.10	0.24
E(TTB)	0.33	0.37	0.45	0.72	1.13
% recommended by CRM	0	1	22	60	17	23	10
% recommended by BT	0	3	36	46	14	20	9
% recommended by CRM-MC1	0	3	31	57	9	22	9
% recommended by CRM-MC2	0	2	26	59	13	23	10
Scenario 4
Probability of T ≥ 1	0.05	0.05	0.08	0.12	0.25
Probability of T ≥ 1.5	0.00	0.01	0.02	0.04	0.10
E(TTB)	0.30	0.33	0.45	0.54	0.72
% recommended by CRM	0	0	5	29	65	18	7
% recommended by BT	0	1	14	28	57	16	6
% recommended by CRM-MC1	0	2	6	36	57	18	7
% recommended by CRM-MC2	0	1	5	31	63	18	7
Scenario 5
Probability of T ≥ 1	0.05	0.05	0.25	0.45	0.55
Probability of T ≥ 1.5	0.00	0.01	0.05	0.10	0.20
E(TTB)	0.33	0.37	0.59	0.90	1.16
% recommended by CRM	1	17	62	19	1	26	6
% recommended by BT	0	8	48	39	6	30	7
% recommended by CRM-MC1	1	17	64	17	1	26	6
% recommended by CRM-MC2	1	15	64	18	2	27	6
Scenario 6
Probability of T ≥ 1	0.05	0.16	0.25	0.45	0.55
Probability of T ≥ 1.5	0.01	0.10	0.23	0.35	0.43
E(TTB)	0.25	0.51	0.81	1.28	1.56
% recommended by CRM	3	30	49	18	1	27	22
% recommended by BT	5	52	37	5	1	22	17
% recommended by CRM-MC1	16	52	27	4	0	22	16
% recommended by CRM-MC2	15	52	28	5	0	23	17

Note: Bold indicates the maximum tolerated dose (MTD).

When θ₁ < θ₂ (Scenario 5), CRM-MC₁ and CRM-MC₂ methods perform similar to the CRM in terms of percentage of dose recommended and percentage of toxicities. However, when θ₁ > θ₂ (Scenario 6), the CRM is more likely to recommend a toxic dose as it does not take into account the secondary constraint. Both CRM-MC₁ and CRM-MC₂ methods recommend the correct dose more than 50% of the time with much lower frequencies of recommending a toxic dose. Both CRM-MC₁ and CRM-MC₂ methods outperform the BT method in terms of the PCS, the frequency of recommending a dose above the MTD and the percentage of toxicities. However, the overdosing of the BT method is an artifact since the target is misspecified, and in both Scenarios 5 and 6, the target TTB of 0.72 falls in between dose levels. For example, under Scenario 5, the target TTB value of 0.72 lies somewhere between the expected TTB of dose level 3 (0.59) and dose level 4 (0.90). Therefore, it is not unexpected that the BT method recommends dose level 4 with a somewhat high probability. In this sense, the simulation comparison is unfair. On the other hand, it reveals the limitations of the target TTB both in terms of interpretation and elicitation. The objective of the BT method is to find the dose associated with a target TTB that is not directly related to a probability of toxicity.

6. DISCUSSION

Our work is primarily motivated by the concern with the gradation of severe toxicities that are considered dose limiting as well as the severity differences between toxicities types of the same grade. In this article, we achieve this goal by applying multiple toxicity constraints in conjunction with the use of the CRM. This is a natural extension of the regular CRM, with an explicit objective defined in terms of the probability of severe toxicity. The proposed method is intuitive and in line with current practice. By setting multiple constraints, it decreases the frequency of recommending doses above the MTD compared to the CRM. Since the high risk of overdosing is one of the main disadvantages of the CRM, the method can be used in the traditional maximal toxicity case to curb the erroneous allocation and recommendation of an overdose.

The objective of our work is to be distinguished from that of Bekele and Thall (2004), Yuan and others (2007), Ivanova and Kim (2009), and Bekele and others (2009), who define the MTD with respect to a target value that is essentially the mean of a continuous outcome. Not only does this target value require a labor intensive and potentially irreproducible elicitation process but also the elicited target may not correspond to a clinically sound definition of MTD (cf. Table 3, Scenarios 5 and 6). From a statistical viewpoint, in fact, matching the expected TTB with a target value is in discordance with the conventional dose-finding objective where the MTD is defined to control for the tail probability of toxicity since the expected TTB does not correspond to any explicit cutoff value of the tail probability of toxicity. This may partly explain the bimodal distribution of the estimated MTD under Scenarios 5 and 6. In addition, the BT method assumes parallel regressions of the ordinal probit model that may affect the performance of their method even when the target TTB coincides.

In this article, we apply the CRM with multiple constraints to the TBS introduced in Lee and others (2009). The TBS is a precalibrated outcome measure of toxicity with respect to the conventional definition of DLT. The proposed method can also be applied with other continuous or ordinal toxicity measure (e.g. TTB) as long as the outcome is well calibrated. From a modeling viewpoint, the proposed approach, which involves fewer parameters, has a clear practical advantage in design calibration as it avoids postulating a joint model for a number of toxicity types.

Two approaches for estimation, namely CRM-MC₁ and CRM-MC₂, are proposed in this paper with the latter being slightly less conservative. The choice between these 2 options depends on the specific clinical settings. For example, for oncology trials where patients are in urgent need of treatment, CRM-MC₂ would be the preferred choice to yield a dose high enough to benefit the patients.

In some clinical situations such as in cancer prevention trials, it may be desirable to control also for the rate of lower-grade toxicities; see, for example, Simon and others (1997). In our specific application, this is implicitly achieved via the use of the TBS formula (4.6). Additionally, the methods proposed here can be altered to explicitly accommodate these situations by including a threshold value, say t₀ that is less than t₁ in the objective (2.1).

FUNDING

National Institutes of Health (R01 NS055809).