A Comparison of Vestibular Spatiotemporal Tuning in Macaque Parietoinsular Vestibular Cortex, Ventral Intraparietal Area, and Medial Superior Temporal Area

Abstract

Vestibular responses have been reported in the parietoinsular vestibular cortex (PIVC), the ventral intraparietal area (VIP), and the dorsal medial superior temporal area (MSTd) of macaques. However, differences between areas remain largely unknown, and it is not clear whether there is a hierarchy in cortical vestibular processing. We examine the spatiotemporal characteristics of macaque vestibular responses to translational motion stimuli using both empirical and model-based analyses. Temporal dynamics of direction selectivity were similar across areas, although there was a gradual shift in the time of peak directional tuning, with responses in MSTd typically being delayed by 100–150 ms relative to responses in PIVC (VIP was intermediate). Responses as a function of both stimulus direction and time were fit with a spatiotemporal model consisting of separable spatial and temporal response profiles. Temporal responses were characterized by a Gaussian function of velocity, a weighted sum of velocity and acceleration, or a weighted sum of velocity, acceleration, and position. Velocity and acceleration components contributed most to response dynamics, with a gradual shift from acceleration dominance in PIVC to velocity dominance in MSTd. The position component contributed little to temporal responses overall, but was substantially larger in MSTd than PIVC or VIP. The overall temporal delay in model fits also increased substantially from PIVC to VIP to MSTd. This gradual transformation of temporal responses suggests a hierarchy in cortical vestibular processing, with PIVC being most proximal to the vestibular periphery and MSTd being most distal.

Introduction

Cortical processing of vestibular information is important for perception of self-motion and spatial orientation. Vestibular signals have been reported in several cortical areas, including area 2v at the anterior tip of the intraparietal sulcus (Schwarz and Fredrickson, 1971; Büttner and Buettner, 1978), the arm and/or neck-trunk representation of area 3a in the primary somatosensory cortex (Odkvist et al., 1974; Guldin et al., 1992), the parietoinsular vestibular cortex (PIVC) at the tip of the lateral sulcus (Grüsser et al., 1990; Chen et al., 2010), the pursuit area of the frontal eye fields (FEFp) (Fukushima et al., 2004), the dorsal medial superior temporal area (MSTd) (Duffy, 1998; Page and Duffy, 2003; Gu et al., 2006, 2007), and the ventral intraparietal area (VIP) in the fundus of the intraparietal sulcus (Bremmer et al., 2002).

Anatomical studies have shown that MSTd is bidirectionally connected with VIP and FEF (Huerta et al., 1987; Barbas, 1988; Boussaoud et al., 1990; Baizer et al., 1991; Bullier et al., 1996) and that PIVC projects to area VIP (Lewis and Van Essen, 2000). PIVC has also been shown to be reciprocally interconnected with areas 2v, 3a, and the FEF (Guldin et al., 1992). However, the hierarchy of these cortical areas in terms of processing vestibular signals remains unknown. In particular, areas 2v, 3a, PIVC, and FEFp are thought to receive short-latency vestibular information directly through the thalamus (Boisacq-Schepens and Hanus, 1972; Odkvist et al., 1974, 1975; Odkvist, 1975; Sans et al., 1976; Akbarian et al., 1992; Ebata et al., 2004). In contrast, the ventral posterior and intralaminar nuclei, vestibular relay stations in the macaque thalamus (Lang et al., 1979; Meng et al., 2007; Meng and Angelaki, 2010), are not known to send projections to VIP and MSTd. Thus, vestibular signals in VIP and MSTd may arise through projections from other cortical areas. Importantly, area MT, which is thought to provide areas VIP and MSTd with visual motion information, does not respond to vestibular stimulation (Chowdhury et al., 2009). This leaves PIVC and FEFp as the major candidates for routing vestibular information to extrastriate visual cortex.

Given the sparsity of neuroanatomical data, we reasoned that a direct comparison of response properties using identical experimental protocols and analyses might help to elucidate the hierarchical organization of vestibular cortical signals. In the present study, we compare the spatiotemporal properties of PIVC, MSTd, and VIP responses to identical three-dimensional (3D) translation (heading) stimuli. Although some of these data have been included in previous publications (Gu et al., 2006; Takahashi et al., 2007; Chen et al., 2010), spatiotemporal dynamics were not characterized in these previous studies, thus not allowing for quantitative comparisons among areas. Here we use both empirical and model-based approaches to quantitatively compare vestibular responses of neurons in PIVC, VIP, and MSTd. Differences in response timing and dynamics are revealed, suggesting a hierarchical processing of vestibular translation signals from PIVC to VIP to MSTd.

Materials and Methods

Extracellular recordings were made from 12 hemispheres in eight male rhesus monkeys (Macaca mulatta). The methods for surgical preparation, training, and electrophysiological recordings have been described in detail in previous publications (Gu et al., 2006; Fetsch et al., 2007; Takahashi et al., 2007; Chen et al., 2010). Each animal was chronically implanted with a circular molded, lightweight plastic ring for head restraint and a scleral search coil for monitoring eye movements inside a magnetic field (CNC Engineering). Behavioral training was accomplished using standard operant conditioning procedures. All animal care and experimental procedures conformed to guidelines established by the National Institutes of Health, and were approved by the Animal Studies Committee at Washington University.

Vestibular stimuli and experimental protocols.

During experiments, the monkey was seated comfortably in a primate chair, which was secured to a six-degree-of-freedom motion platform (MOOG 6DOF2000E). Three-dimensional movements along any arbitrary axis could be delivered by this platform. We examined each cell's 3D spatiotemporal tuning by recording neural responses while the animal was translated along each of 26 directions sampled evenly around a sphere (Fig. 1A) [see also Gu et al. (2006) and Takahashi et al. (2007)]. This included all combinations of movement vectors having eight different azimuth angles (0, 45, 90, 135, 180, 225, 270, and 315°) and three different elevation angles: 0° (the horizontal plane) and ±45° (for a subtotal of 8 × 3 = 24 directions). Two additional movement vectors, with elevation angles of −90° and 90°, corresponded to upward and downward directions, respectively. Each movement trajectory followed a 2 s Gaussian velocity profile with a corresponding biphasic acceleration profile (Fig. 1B). The total displacement was 13 cm, and the peak acceleration was 0.1 × g. All movements originated from the center of the movement range of the motion platform, and the platform returned to this starting position during the 2 s intertrial interval. The stimuli were presented in random order within blocks of trials. Neurons were included in the sample if each stimulus direction was successfully repeated at least three times; for 90% of neurons, at least five repetitions of each distinct stimulus were completed.

Figure 1.

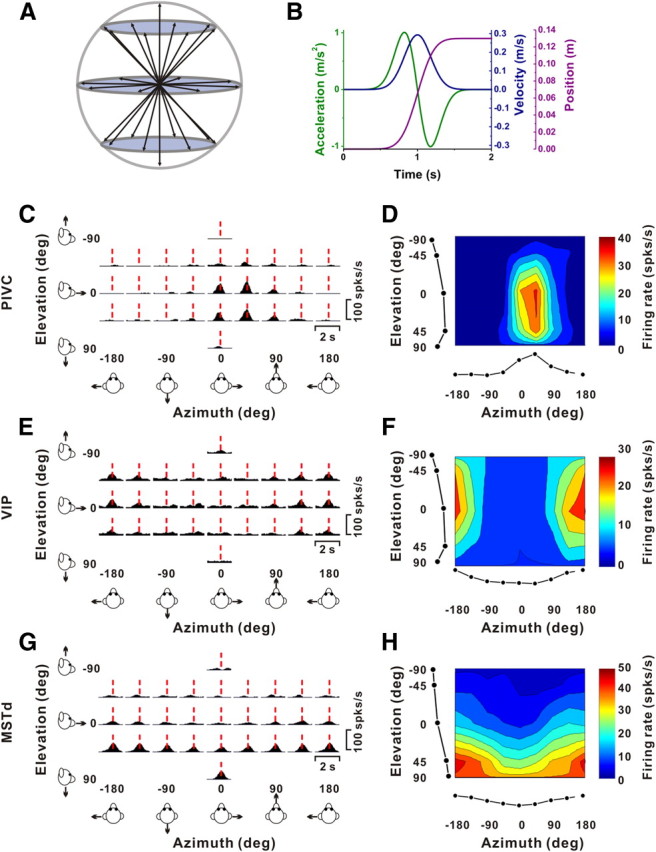
Stimulus parameters and example responses from single-peaked cells. A, Schematic illustration of the 26 3D movement trajectories spaced 45° apart in both azimuth and elevation. B, All movements had a 2 s duration, originated from the center position, and had a Gaussian velocity profile (peak of 30 cm/s, blue) with a corresponding biphasic linear acceleration profile (peak of ±1 m/s², green) and a sigmoidal displacement of 13 cm (magenta). C, E, G, Response PSTHs for three example neurons from PIVC (C), VIP (E), and MSTd (G). Vertical dashed red lines indicate the respective peak times, when the maximum response across directions occurred. PSTHs were computed with sequential 25 ms bins and then smoothed with a 400 ms sliding window (see Materials and Methods). D, F, H, Corresponding color contour maps showing 3D direction tuning profiles (Lambert cylindrical projection) at peak time (t) for the cells in C (t = 0.94 s, DDI = 0.77), E (t = 0.98 s, DDI = 0.70), and G (t = 1.08 s, DDI = 0.76). Tuning curves along the margins illustrate mean firing rates plotted versus elevation or azimuth (averaged across azimuth or elevation, respectively).

For all recordings in VIP and MSTd and most (115/128) recordings in PIVC, the animal was required to fixate a central target (0.2° in diameter) for 200 ms before motion onset (fixation windows spanned 2 × 2° of visual angle). The animals were rewarded at the end of each trial for maintaining fixation throughout the stimulus presentation. If fixation was broken at any time during the stimulus, the trial was aborted and the data were discarded. Some recordings in PIVC (n = 13) were obtained during vestibular stimulation in complete darkness. In these cases, there was no behavioral requirement to fixate, and rewards were delivered manually to keep the animal alert. Note that response properties in PIVC were not different for fixation versus darkness protocols (Chen et al., 2010); thus, all data are presented together without any further distinction here.

Electrophysiological recordings.

Tungsten microelectrodes (Frederick Haer Company; tip diameter 3 μm, impedance 1–2 MΩ at 1 kHz) were inserted into the cortex through a transdural guide tube, using a hydraulic microdrive (Frederick Haer Company). Behavioral control and data acquisition were coordinated by a commercially available software package (TEMPO, Reflective Computing). Neural voltage signals were amplified, filtered (400–5000 Hz), discriminated (Bak Electronics), and displayed on an oscilloscope. The times of occurrence of action potentials and behavioral events were stored with 1 ms resolution. At the same time, raw neural signals were digitized at a rate of 25 kHz using a CED Power 1401 data acquisition system (Cambridge Electronic Design) along with Spike2 software. These raw data were stored to disk for offline spike sorting.

Areas PIVC (two animals), VIP (five animals), and MSTd (three animals) were identified based on the patterns of gray and white matter transitions along electrode penetrations with respect to MRI scans, depth from the surface of the cortex, and physiological response properties [for details, see Gu et al. (2006), Takahashi et al. (2007), and Chen et al. (2010)]. For two animals, all three areas (PIVC, VIP, and MSTd) were physiologically identified and recording maps were reconstructed using MRI (Chen et al., 2010) (Fig. 1). For another two animals, data were recorded from both VIP and PIVC. In the present analysis, all PIVC neurons were located in the upper bank and tip of the lateral sulcus, whereas cells in the lower bank were excluded (Chen et al., 2010). Area VIP was identified based on a high percentage of neurons with direction-selective visual responses, and its position close to the fundus of the intraparietal sulcus, extending 10 mm anterior to posterior. The medial part of VIP is the tip of intraparietal sulcus. The lateral border of VIP was identified as the point at which we could no longer find cells with direction-selective visual responses.

Because the data analyzed here were recorded as part of different studies at different times, different criteria were used to search for and select neurons. In area PIVC, only cells with clear, audible response modulation to sinusoidal translation or rotation were studied further with the 3D translation protocol (see Chen et al., 2010). On the other hand, in areas MSTd and VIP, the 3D spatiotemporal tuning protocol was performed for each well isolated cell, without any selection criteria (e.g., Gu et al., 2006). Thus, to allow a fair comparison among areas, we have only included cells with significant temporal response modulation and significant 3D directional tuning in response to vestibular translation (see below for criteria used).

Data analysis.

Analysis of spike data and statistical tests were performed using MATLAB (MathWorks). Peristimulus time histograms (PSTHs) were constructed for each direction of translation using 25 ms time bins and smoothed with a 400 ms boxcar filter. The temporal modulation along each stimulus direction was considered significant when the spike count distribution from the time bin containing the maximum and/or minimum response differed significantly from the baseline response distribution (−100 to 300 ms poststimulus onset, Wilcoxon signed rank test, p < 0.01) (for details, see Chen et al., 2010). Only neurons with a minimum of two nearby (≤45°) stimulus directions having significantly modulated responses were further considered for analysis. Cells with significant positive modulation along at least two nearby directions were classified as excitatory, while cells with significant negative (and no positive) modulation along at least two nearby directions were classified as inhibitory.

Next, we calculated the maximum (for excitatory cells)/minimum (for inhibitory cells) response of the neuron across stimulus directions for each 25 ms time bin between 0.5 and 2 s after motion onset and performed ANOVA to assess the statistical significance of directional selectivity for each time bin. This analysis determined the statistical significance of direction tuning as a function of time and assessed whether there are multiple time periods in which a neuron shows distinct temporal peaks of directional tuning (see Chen et al., 2010). “Peak times” were then defined as the times of local maxima (for excitatory cells) or minima (for inhibitory cells) at which distinct epochs of directional tuning were observed. Cells with no peak times (i.e., no significant directional tuning at any time during the response window) were excluded from this analysis. Thus, cells included in the present study were required to have significant temporal response modulation and significant directional tuning. Our goal was then to compare the spatiotemporal tuning properties among neurons from PIVC, VIP, and MSTd. Note that the temporal relationship between response and stimulus has been adjusted for the time delay (115 ms) intrinsic to the dynamics of the motion platform, that is, the delay between the motion command signal and the actual movement of the platform (see Fetsch et al., 2007).

The strength of directional tuning at each peak time was quantified using a direction discrimination index (DDI), given by the following (Takahashi et al., 2007):

where R_max and R_min are the maximum and minimum responses from the 3D tuning function, respectively. SSE is the sum squared error around the mean response, N is the total number of observations (trials), and M is the number of stimulus directions (M = 26). The DDI ranges between 0 and 1 and compares the difference in firing rate between the preferred and null directions against response variability; it quantifies a neuron's reliability for distinguishing between preferred and null motion directions. DDI values close to 1 indicate neurons with large response modulations relative to the noise level, whereas DDI values close to 0 correspond to neurons with weak response modulation.

The precision of the population activity in each of the three areas for discriminating heading around different directions in the horizontal plane was evaluated using Fisher information. For a population of neurons with Poisson-like statistics, Fisher information (I_F) is computed as follows (Seung and Sompolinsky, 1993; Pouget et al., 1998):

In this equation, N denotes the number of neurons in the population, R_i^′(x_ref) denotes the derivative of the tuning curve for the ith neuron at x_ref, and σ_i²(x_ref) is the variance of the response of the ith neuron at x_ref. Based on Equation 2, I_F is computed from the slope of each neuron's tuning curve at x_ref and the standard deviation of its response at x_ref. To compute the slope, we used a spline function (0.1° resolution) to interpolate among the coarsely sampled data points (45° spacing). The tuning curve slope, R_i^′(x_ref), was then obtained as the spatial derivative of the spline fit. Under the assumption of Poisson spiking statistics, the variance of the neuron's response is equal to the mean firing rate at x_ref, i.e., σ_i²(x_ref)= μ_i(x_ref), which can be simply read off from the interpolated tuning curve. Using Equation 2, Fisher information was computed as a function of the azimuth angle for each neuron with significant spatial tuning.

Spatiotemporal curve fitting.

To provide a compact description of the spatiotemporal tuning properties of neurons in areas PIVC, VIP, and MSTd, we developed a model to fit the heading tuning functions of these neurons. Our goal was twofold: (1) to determine whether the temporal dynamics of neural responses were most consistent with coding of linear acceleration, velocity, and/or position; and (2) to distinguish between temporal delay and response dynamics. Because our goal was not to quantify the preferred stimulus direction in 3D [this information is available in previous publications (Gu et al., 2006, 2010; Chen et al., 2010)], we simplified the task by constructing models to fit spatiotemporal tuning in each one of the three cardinal planes (horizontal, frontal, and median), as long as the cell's spatiotemporal tuning in that plane met the following criteria: (1) at least two nearby directions (≤45°) had significant temporal response modulation (by the criteria described above), and (2) there was significant space–time structure in that plane (p < 0.001, two-way ANOVA, significant main effects of space and time and significant interaction). The space–time structure was visualized by plotting the data as a color-contour map of response amplitude, in which stimulus direction is plotted along the abscissa and time (during the 0–2 s stimulus profile) is plotted along the ordinate (e.g., see Figs. 6A, 7A).

Figure 6.

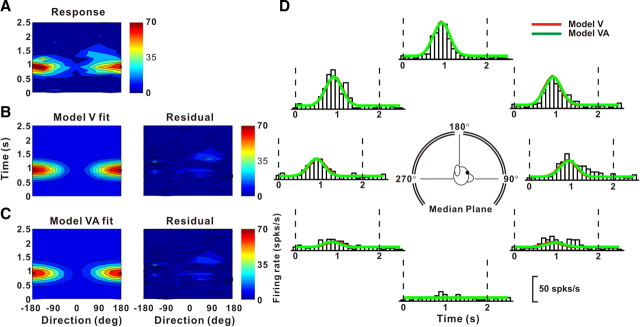
Example fits of the velocity (model V) and velocity + acceleration (model VA) models to the spatiotemporal response profile of a neuron dominated by stimulus velocity. A, Direction–time plot showing how direction tuning evolves over the time course of the response (resolution: 45° and 100 ms). B, C, Model fits (left) and response residuals (right). For model V (B): t₀ = 0.80 s, θ₀ = 181°, r² = 0.85. For model VA (C): t₀ = 0.90 s, θ₀ = 181°, w_v = 0.78, r² = 0.86. D, Response PSTHs (open bars) for the eight directions in the median plane (see inset), along with superimposed fits of model V (red) and model VA (green). Vertical dashed lines mark the 2 s duration of the stimulus.

Figure 7.

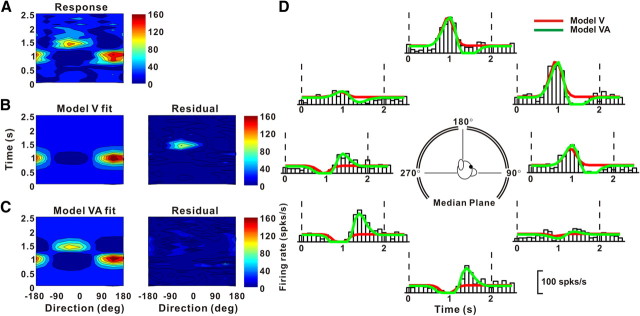
Example fits of model V and model VA to responses of a neuron with both velocity and acceleration response components. A, Direction–time plot showing how direction tuning evolves over time. B, C, Model fits (left) and response residuals (right). For model V (B): t₀ = 0.83 s, θ₀ = 146°, r² = 0.56. For model VA (C): t₀ = 1.11 s, θ₀ = 144°, w_v = 0.06, Δθ_va = 0°, r² = 0.84. D, Response PSTHs (open bars) for eight directions in the median plane, along with the superimposed fits of model V (red) and model VA (green). The format is as in Figure 6.

Three different models were used to fit the spatiotemporal response profile of each cell. The simplest “velocity” model (model V) consisted of the product of a modified cosine function of stimulus direction (space) and a Gaussian velocity profile in time, as given by the following:

where R(θ, t) represents the neuron's response (in spikes/s) as a function of space and time, A is the overall response amplitude, θ denotes the stimulus direction (range: 0 to 2π), θ₀ represents the cell's direction preference, DC indicates a baseline shift of the spatial tuning (range: 0 to 0.5), G(t) represents the temporal response profile of the neuron as defined below, and R₀ is a constant corresponding to the resting firing rate of the neuron.

The cosine spatial tuning in the model is modified by two nonlinearities. First, F(x, n) indicates a “squashing” nonlinearity as given by Nguyenkim and DeAngelis (2003):

When n approaches zero, F(x, n) ∼ x, and the nonlinearity has no effect. As n increases, F(x, n) causes the peak of the cosine function to become taller and narrower, while the trough becomes shallower and wider. This nonlinearity was useful to fit the heading tuning of many neurons, which is typically somewhat narrower than pure cosine tuning (see Gu et al., 2010). Second, the operation denoted by [ ] in Equation 3 indicates that the spatial tuning curve was normalized to be in the range [0 1] following application of F(x, n). This normalization substantially reduced correlations between the parameter of the squashing nonlinearity (n) and the overall amplitude (A) and baseline response (R₀) parameters, and thus improved convergence of the fits.

The temporal response profile in model V, G(t), is a temporal Gaussian function, given by the following:

where t₀ is the time at which the peak response occurs and σ_t indicates the standard deviation. In total, model V has seven free parameters: A, DC, θ₀, n, σ_t, t₀, and R₀.

For each cardinal plane, Equation 2 was fit to the data using a nonlinear least-squares optimization procedure (“lsqcurvefit” function in Matlab). The data to be fit were response PSTHs, having 100 ms bins, for each of the eight stimulus directions (45° apart) in one of the cardinal planes.

The second (“velocity + acceleration”) model (model VA) incorporates a second spatiotemporal response component to account for the possibility that both velocity and acceleration were encoded by the neurons. This additional component is the product of an offset spatial tuning curve and an acceleration profile in time (derivative of G(t)). Thus, model VA allows the temporal responses to be mixtures of velocity and acceleration, and also allows the directional tuning of the acceleration component to differ from that of the velocity component. The formulation is given by the following:

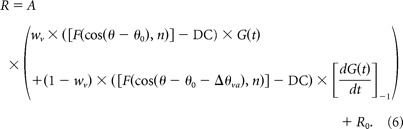Model VA contains two additional free parameters compared to model V, for a total of nine. The first additional parameter is the difference between direction preferences for the velocity and acceleration components, denoted by Δθ_va. The second additional parameter, w_v, specifies the relative weight of the velocity component, with the acceleration weight given by w_a = (1 − w_v). Thus, for a purely velocity response, w_v = 1; for a purely acceleration response, w_v = 0; and for a balanced mixture, w_v = 0.5. A ratio of acceleration to velocity components was computed as w_a/w_v = (1 − w_v)/w_v. The temporal derivative term in Equation 6 was normalized into the range [−1 1], as noted by [ ]₋₁.

Finally, the third (“velocity + acceleration + position”) model (model VAP) incorporated an additional spatiotemporal component to allow for a position contribution. The position component was represented as the product of an offset spatial tuning curve and a position profile in time (integral of G(t)), as follows:

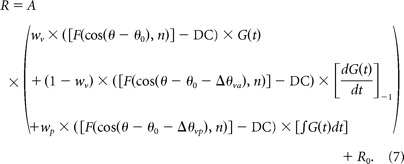Relative to model VA, model VAP again adds two additional free parameters (for a total of 11). One parameter is the difference in direction preference between the velocity and position components, Δθ_vp, and the second parameter is the weight of the position component, w_p, ranging from 0 to 1. Note that the temporal integral term in Equation 7 was normalized into the range [0 1], as done for the velocity component.

In all of these models, t₀ = 1 s corresponds to the peak of the Gaussian velocity profile of the stimulus. In the model fits presented, all parameters were free to take any value, except for DC, which was bounded in the range [0 0.5]. We repeated the fits after constraining the temporal delay parameter, t₀, to be >1. Although the results were generally similar, model V fit some cells better with the unbounded delay because acceleration components could make the response reach its peak before peak stimulus velocity. However, the fits of models VA and VAP were largely unaffected by bounding the delay parameter.

The relative quality of fits of the different models was evaluated using the Akaike information criterion (AIC) (Akaike, 1992):

where N is the number of data points, K is the number of model parameters, and SS is the sum squared error. The AIC is a statistical measure for comparing different models and is dependent on both the goodness of fit and the number of independent parameters included in the models. The best model based on this criterion is the one with the lowest AIC value. Thus, the difference in AIC between model B (more parameters) and model A (fewer parameters) was computed as follows:

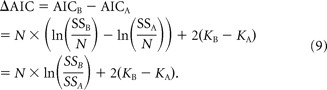Because model A has fewer parameters than model B, K_B > K_A and SS_A > SS_B. If ΔAIC is negative, the difference in sum squared error between models is greater than that expected based on the difference in the number of parameters, implying that model B (the model with more parameters) provides a better characterization of the data.

The three models were fitted to responses of each neuron for any (or all) of the three cardinal planes (horizontal, frontal, and median), as long as each plane exhibited significant spatiotemporal tuning by the criteria given above. Because there was no significant difference in ΔAIC values among the three cardinal planes for our population of neurons (p > 0.4, paired t test), we report results from the plane with the strongest response amplitude for each neuron.

Results

We recorded extracellularly from neurons in areas PIVC (upper bank and tip of the lateral sulcus), VIP (lower bank and tip of the intraparietal sulcus), and MSTd (upper bank of the superior-temporal sulcus) as animals were passively translated along one of 26 directions sampled uniformly around a sphere (Fig. 1A,B; see Materials and Methods). Our goal in this study was to compare the spatiotemporal responses of translation-responsive cells in these areas. Thus, we only analyzed data from neurons that showed significant temporal response modulation for a minimum of two nearby directions and were spatially tuned for heading during the motion stimulus. These criteria were satisfied by a total of 382 neurons (PIVC, n = 128; VIP, n = 84; MSTd, n = 170), which were analyzed further. For a more extensive characterization of all neurons isolated in PIVC and MSTd, see Chen et al. (2010) and Gu et al. (2006; 2010), respectively.

Spatiotemporal dynamics and direction tuning

Examples of typical PSTHs for the 26 directions of translation are shown for representative neurons from PIVC, VIP, and MSTd in Figure 1, C, E, and G, respectively. Each PSTH shows the mean responses to each stimulus direction defined in spherical coordinates by two angles, azimuth (varying along the abscissa) and elevation (varying along the ordinate). Red dashed lines show the peak response time for each neuron, which was defined as the time bin that produced the largest departure in firing rate from the baseline response. At this peak time for each neuron, we computed 3D directional tuning curves, where mean firing rate is plotted as a function of azimuth and elevation, as shown by the color contour maps in Figure 1, D, F, and H.

All three cells were significantly tuned for the direction of translation (ANOVA, p < 0.01) and exhibited broad tuning, with preferred directions (computed as the vector sum of responses) at azimuth = 38.9° and elevation = 22.6° for the PIVC cell of Figure 1, C and D (corresponding to a rightward and slightly downward movement), azimuth = 169.5° and elevation = −17.8° for the VIP cell of Figure 1, E and F (corresponding to a leftward and slightly upward movement), and azimuth = 178.1° and elevation = 75.7° for the MSTd neuron of Figure 1, G and H (corresponding to a leftward and downward trajectory). Note that the azimuth axis in the contour maps is circular, such that the tuning in Figure 1F is spatially unimodal; note also that negative elevations correspond to upward movement directions, by convention. We refer to neurons that show a single epoch of directional selectivity in which the heading preference remains constant over time (see Materials and Methods and Chen et al., 2010) as “single-peaked” cells. Because of the temporal profile of our stimuli (Fig. 1B), single-peaked responses would be expected from neurons that follow the velocity waveform of the motion trajectory.

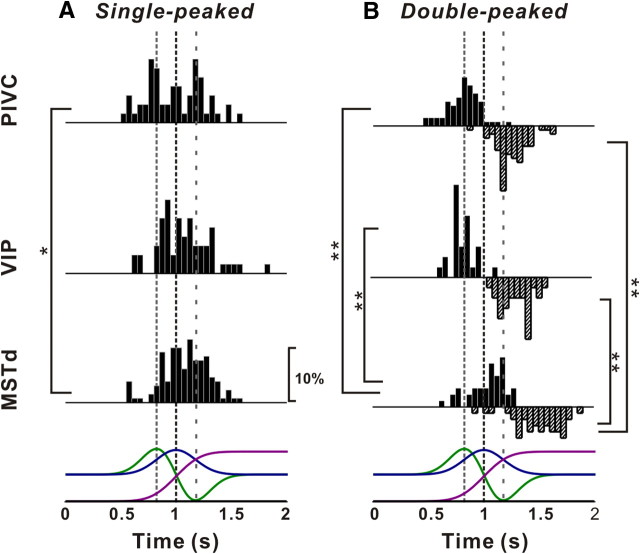
Neurons that follow the linear acceleration profile of the motion trajectory, on the other hand, would be expected to exhibit two peaks of directional selectivity. These two peaks should be separated in time and have opposite direction preferences, corresponding to the acceleration and deceleration phases of the stimulus (Chen et al., 2010). Indeed, such neurons, which we refer to as “double-peaked” cells, were encountered in all three areas, as illustrated in Figure 2. For these cells, there are two peak times, one corresponding to an early peak in some of the PSTHs (Fig. 2A,D,G, vertical dashed red lines) and the other corresponding to a late peak in some PSTHs (vertical dashed green lines).

Figure 2.

Example responses from double-peaked neurons. A, D, G, PSTHs for three example neurons from PIVC (A), VIP (D), and MSTd (G). Vertical dashed red and green lines illustrate the two peak times for each cell. B, C, E, F, H, I, Color contour maps showing 3D direction tuning profiles (Lambert cylindrical projection) at the two peak times (t) for the cells in A (t = 0.80 s, DDI = 0.92 and t = 1.34 s, DDI = 0.86), D (t = 0.91 s, DDI = 0.74 and t = 1.41 s, DDI = 0.70), and G (t = 0.96 s, DDI = 0.74 and t = 1.64 s, DDI = 0.75). The format is as in Figure 1.

For the example PIVC neuron, the direction tuning at the first peak time had a heading preference at [azimuth, elevation] = [−2.8°, 14.4°] (Fig. 2B), whereas the later peak of tuning was centered at [azimuth, elevation] = [−175.7°, −2.6°] (Fig. 2C), illustrating a clear direction reversal over time. The difference between the two direction preferences for this neuron was 166.3°. Similar reversals in tuning were also seen for the example cells from VIP (first peak at [38.6°, −16.3°], second peak at [−125.9°, 9.4°]) (Fig. 2E,F, respectively) and MSTd (first peak at [−165.5°, −14.2°], second peak at [18.7°, 5.9°]) (Fig. 2H,I, respectively). These changes in direction preference over time measured 163.4° and 170.7° for the VIP and MSTd cells, respectively.

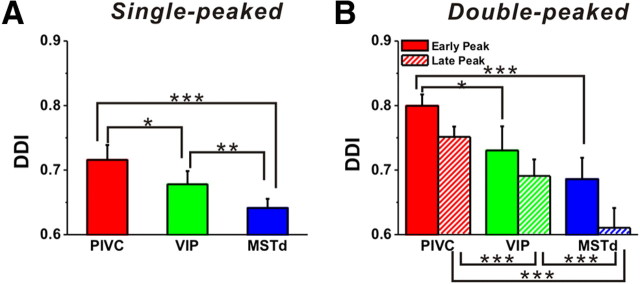
In PIVC, we found more double-peaked cells (66/128, 51.6%) than single-peaked cells (59/128, 46.1%) (see Table 1). The remaining three PIVC neurons (2.3%) had three distinct peaks of tuning (for details, see Chen et al., 2010); because of the small sample size, these triple-peaked cells have not been considered further here. In contrast, the percentage of double-peaked cells was much lower in VIP (26/84, 31%) and MSTd (43/170, 34%), where single-peaked neurons were much more common (Table 1). No triple-peaked cells were encountered in VIP and MSTd. Across all double-peaked cells, the absolute difference in direction preference between the two peaks of selectivity averaged (±SE) 159.5 ± 1.5° (PIVC, n = 66), 154.4 ± 2.9° (VIP, n = 26), and 140.5 ± 6.9° (MSTd, n = 43).

Table 1.

Cell classification

	PIVC	VIP	MSTd
Excitatory
Single-peaked	51	44	101
Double-peaked	66	22	40
Triple-peaked	3	0	0
Inhibitory
Single-peaked	8	14	26
Double-peaked	0	4	3
Triple-peaked	0	0	0
All	128	84	170

“Excitatory tuned” are cells with significant positive modulation along at least two nearby directions. “Inhibitory tuned” are cells with significant negative (and no positive) modulation along at least two nearby directions.

The strength of direction tuning was quantified using a DDI that ranges from 0 to 1 (poor to strong tuning, respectively). PIVC had the highest and MSTd the lowest average DDI, and this was true for both single-peaked (Fig. 3A) and double-peaked (Fig. 3B) cells. For single-peaked cells, the mean DDI for PIVC (0.72 ± 0.01) was significantly greater than the mean DDI for MSTd (0.64 ± 0.01) (Wilcoxon rank sum test, p < 0.001) (Fig. 3A). These differences were also significant for both peak times of double-peaked cells (p < 0.001) (Fig. 3B). Average DDI values for VIP neurons were intermediate between those of PIVC and MSTd, with the pairwise differences also being significant (p < 0.05) (Fig. 3A,B). Note that, for double-peaked cells, DDI values were consistently smaller for the second peak in all three areas (t test, p < 0.001 for each area). Peak firing rates also tended to be lower for the second peak than the first (p < 0.001 for each area, data not shown), and it is possible that this effect could be due to adaptation.

Figure 3.

Population summary of directional tuning strength in areas PIVC (red), VIP (green), and MSTd (blue). A, B, Mean (±SE) values of DDI for single-peaked and double-peaked cells (early peak: solid bars; late peak: hatched bars). Statistical significance (Wilcoxon rank test) of differences is denoted as follows: ***p < 0.001; **0.001 < p < 0.01; *0.01 < p < 0.05.

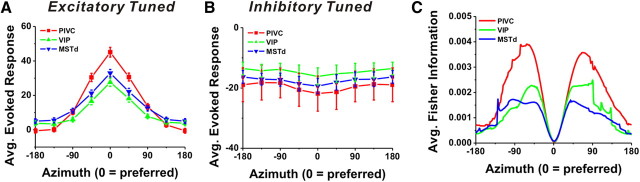
To provide a simple graphical summary of the heading tuning in these three brain areas, we computed population tuning curves from responses to the subset of eight stimulus directions in the horizontal plane (Fig. 4A for excitatory and 4B for inhibitory cells). Note that all tuning curves were shifted and centered at 0° (and spontaneous activity was subtracted) before the population average was computed. Thus, 0° in this plot represents the preferred direction. The average heading tuning curve of PIVC neurons (red) shows the largest peak-to-trough modulation, which is significantly greater than the average modulation in VIP (green) and MSTd (blue) (p < 0.001, Wilcoxon rank test). Note that the average tuning curves of the excitatory cells (Fig. 4A) for the three areas have similar widths, with standard deviations of 62.9°, 57.3°, and 69.5° for PIVC, VIP, and MSTd, respectively (based on wrapped Gaussian fits to the data). Similar results were observed for the inhibitory cells (Fig. 4B), with standard deviations of 89.9°, 98.8°, and 101.3° for PIVC, VIP, and MSTd, respectively.

Figure 4.

Population summary of directional discrimination in areas PIVC (red), VIP (green), and MSTd (blue). A, Population tuning curves of the excitatory cells in the horizontal plane (PIVC: n = 120, VIP: n = 66, and MSTd: n = 141). B, Population tuning curves of the inhibitory cells in the horizontal plane (PIVC: n = 8, VIP: n = 18, and MSTd: n = 29). Data have been aligned to the peak (for excitatory cells) or trough (for inhibitory cells) response direction of each cell (0°), and spontaneous activity was subtracted before averaging. C, Comparison of averaged Fisher information in the horizontal plane among three areas. Fisher information was aligned to the preferred azimuth direction of each neuron, which is illustrated here as 0°.

To compare the sensitivity of neurons in discriminating heading direction, we also computed the average Fisher information for each area, as shown in Figure 4C. Fisher information provides an upper limit on the precision with which any unbiased estimator can discriminate between small variations in direction around a reference. Assuming Poisson statistics and independent noise among neurons, Fisher information can be computed as the ratio of the square of the cell's tuning curve slope (at a particular reference heading) divided by the corresponding mean firing rate (Eq. 2; see Materials and Methods). As expected from this equation, maximum Fisher information, which corresponds to the minimum neuronal discrimination threshold, is encountered at approximately the steepest point along the tuning curve, not at its peak (0° in Fig. 4C). To provide a quantitative comparison, for each neuron we computed a mean Fisher information in a range of ±45° around the axis perpendicular to the cell's preferred direction (i.e., ±90° in Fig. 4C). PIVC neurons were more sensitive than either VIP or MSTd cells (p < 0.001, Wilcoxon rank test). There was no significant difference between VIP and MSTd (p > 0.4, Wilcoxon rank test).

Perhaps the most salient difference in spatiotemporal tuning between the three areas involved the timing of peaks of directional tuning relative to the motion stimulus profile, as illustrated in Figure 5 (see also Table 2). Although the distributions of peak times of directional tuning were broad, there was a progressive shift toward longer (i.e., later) peak times from PIVC to VIP to MSTd. Specifically, peak times for single-peaked cells (Fig. 5A) averaged (±SE) 0.98 ± 0.03 s for PIVC (n = 59), 1.07 ± 0.03 s for VIP (n = 58), and 1.08 ± 0.02 s for MSTd (n = 127), and this difference was significant between PIVC and MSTd (Fig. 5A, *p = 0.01, Wilcoxon rank test). For double-peaked cells (Fig. 5B, see also Table 2), both early and late peak times in MSTd were significantly longer than those in both PIVC and VIP (p < 0.001, Wilcoxon rank tests). No significant difference was seen between PIVC and VIP (p > 0.05).

Figure 5.

Distribution of peak times for single-peaked (A) and double-peaked (B) cells in areas PIVC, VIP, and MSTd. Solid and hatched bars in B indicate the early and late peak times, respectively, for double-peaked cells. Stimulus velocity (blue), acceleration (green), and position (magenta) profiles are overlaid for comparison (bottom row). Vertical dashed lines indicate the times of peak acceleration/deceleration and peak velocity. Note that the late peak time distributions for double-peaked cells were plotted as downward projecting histograms simply for illustrative purposes.

Table 2.

Summary of peak times (mean ± SE)

	PIVC	VIP	MSTd
Single-peaked	0.98 ± 0.03	1.07 ± 0.03	1.08 ± 0.02
Double-peaked
First peak	0.82 ± 0.02	0.83 ± 0.02	1.03 ± 0.03
Second peak	1.25 ± 0.02	1.32 ± 0.03	1.50 ± 0.03

Peak time values are expressed relative to stimulus onset (i.e., a peak time of 1 s occurs at the time of peak stimulus velocity).

The fact that peak times in MSTd occurred substantially later than in PIVC and VIP suggests that vestibular signals in PIVC might be of shorter latency than in MSTd. For example, the results of Figure 5 could be consistent with vestibular signals reaching PIVC and then being transmitted to VIP and MSTd; i.e., they might reflect a hierarchy in cortical vestibular processing. However, because of the smooth profile of velocity and acceleration in our motion trajectories, this difference in peak times might not necessarily reflect response latency. Instead, differences in peak time between areas could reflect a transition from coding acceleration in PIVC to coding velocity and position in MSTd. Next, we describe a curve-fitting analysis that allows us to quantify both the latency and the temporal components (velocity, acceleration, and position) of vestibular responses to translation in PIVC, VIP, and MSTd.

Curve-fitting analysis: velocity versus acceleration components

Three different models, reflecting coding of velocity (model V), velocity + acceleration (model VA), or velocity + acceleration + position (model VAP), were fit to the spatiotemporal responses of each neuron (see Materials and Methods for formulation of the models). For simplicity, each model was fit to two-dimensional data from the horizontal, frontal, and median planes of the stimulus space, provided that directional tuning in each plane met the following criteria: (1) at least two nearby directions with significant temporal modulation and (2) a significant space–time structure in that plane, as described in Materials and Methods. These criteria were met for at least one of the three planes in 106 PIVC, 52 VIP, and 96 MSTd neurons. We report results from the plane with the strongest response modulation for each neuron.

Figures 6 and 7 show example fits of models V and VA. The spatiotemporal responses of the neurons and the respective model fits are illustrated both as color contour maps (Fig. 6A–C) and as PSTHs along with fitted curves (Fig. 6D). Responses from the neuron in Figure 6 were equally well fit by model V (Fig. 6B) and model VA (Fig. 6C), as illustrated by the residuals in the right panels. Indeed, the fits of the two models (red and green traces in Fig. 6D) are highly overlapping, consistent with a velocity weight, w_v, of 0.78 for model VA. For this neuron, model VA is not justified given the increase in the number of parameters, as shown by AIC_VvsVA > 0 (see Materials and Methods). Model V accounts for 85% of the variance in the data (86% for model VA) and thus provides a good description of the spatiotemporal response profile of this neuron.

In contrast, responses of the example neuron in Figure 7 were significantly better fit by model VA than model V. The presence of a robust acceleration component is evident by the double peaks in the color contour plots (Fig. 7A), as well as by the clear biphasic responses in PSTHs for some stimulus directions (Fig. 7D). Only model VA reproduces the structure of these responses well, as shown by the residuals in Figure 7C (right). In contrast, the residuals for model V show substantial systematic errors (Fig. 7B, right). In this case, AIC_VvsVA < 0, indicating that the extra parameters of model VA were justified by the improvement in the fit. For this cell, the weights of the velocity and acceleration components of model VA were w_v = 0.06 and w_a = 1 − w_v = 0.94, respectively. The acceleration component had a direction preference that was approximately the same as the velocity component.

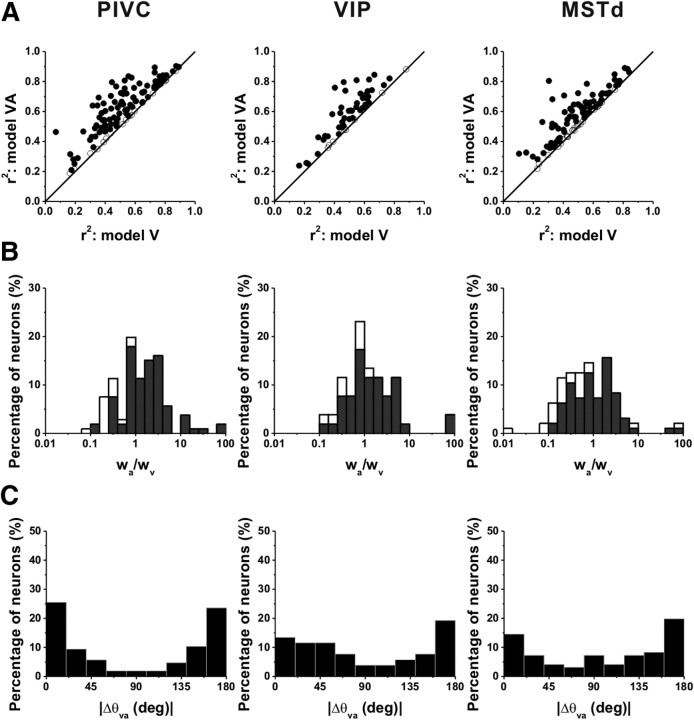
For many neurons in all three areas, model VA gave a substantially better fit than model V, as illustrated by the scatter plots in Figure 8A. The improvement in the fit was significant (AIC_VvsVA < 0, filled symbols) for the majority of neurons in PIVC (90/106), VIP (44/52), and MSTd (73/96). Thus, only 7% of PIVC, 8% of VIP, and 11% of MSTd neurons were better described by the velocity-only model (Table 3).

Figure 8.

Population comparison between fits of model V and model VA. A, Scatter plots showing the r² for model VA plotted against the r² for model V. Data are shown for populations of neurons from area PIVC (left, n = 106), VIP (middle, n = 52), and MSTd (right, n = 96). B, Distributions of the ratio of acceleration to velocity weights (w_a/w_v). Open symbols/bars represent cells with responses that were better fit by the velocity model (AIC_VvsVA > 0). Black symbols/bars represent cells with responses better fit by model VA (AIC_VvsVA < 0). C, Distributions of the absolute difference in direction preference of velocity and acceleration components (plotted only for cells that were fit significantly better by model VA).

Table 3.

Summary of best-fitting models

	PIVC	VIP	MSTd
Velocity only (model V)	7 (7%)	4 (8%)	11 (11%)
Velocity + acceleration (model VA)	52 (49%)	27 (52%)	32 (33%)
Velocity + acceleration + position (model VAP)	47 (44%)	21 (40%)	53 (55%)
All	106	52	96

Values shown represent the number (and percentage) of neurons in areas PIVC, VIP, and MSTd that were better fit by model V, model VA, or model VAP according to the AIC (see Materials and Methods).

To summarize the relative strengths of velocity and acceleration components in the neural responses, we computed the ratio of the acceleration and velocity weights, w_a/w_v. Distributions of the weight ratios for each area are shown in Figure 8B (filled bars: AIC_VvsVA < 0; open bars: AIC_VvsVA > 0). Considering all cells in each area (filled and open bars), the acceleration to velocity weight ratio was significantly larger in PIVC (geometric mean ± SE: 1.35 ± 0.36; geometric median: 1.29) than in MSTd (geometric mean: 0.76 ± 0.48; median: 0.75) (p < 0.001, Wilcoxon rank test). The weight ratio for VIP was intermediate between PIVC and MSTd (geometric mean: 1.25 ± 0.51; median: 1.03). Thus, vestibular responses in PIVC were most often dominated by the linear acceleration component, whereas responses in MSTd were most often dominated by the velocity component and VIP responses were typically balanced.

As summarized for cells from the three areas in Figure 8C, the distributions of the difference in direction preference between velocity and acceleration components were nonuniform (p < 0.01, uniformity test) and bimodal (p_uni < 0.05, p_bi > 0.05, modality test), with modes near 0° and 180°. This indicates that the direction preferences of velocity and acceleration components tended to be either aligned or opposite.

Curve-fitting analysis: position contribution

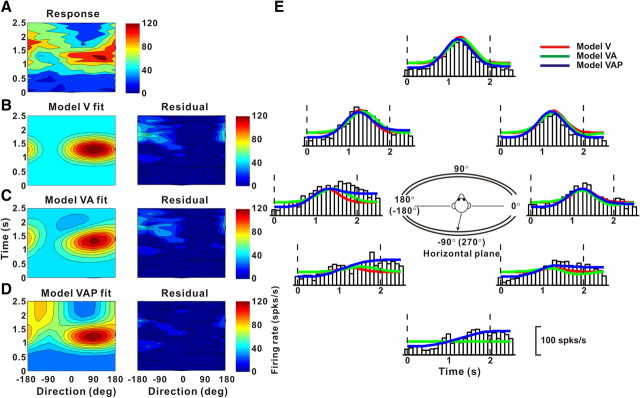
The presence of some very late peak times in responses of double-peaked neurons in area MSTd (Fig. 5) raises the possibility that some neurons might also carry information about linear displacement or position (the latter increases gradually throughout the motion profile) (Fig. 1B). Thus, we also fitted neural responses with a third model that included velocity, acceleration, and position components (Eq. 7 in Materials and Methods). Figure 9 shows the spatiotemporal tuning, in the horizontal plane, of another example neuron from MSTd. Its space–time response profile (Fig. 9A) was not satisfactorily reproduced by either model V (r² = 0.51) (Fig. 9B) or model VA (r² = 0.54) (Fig. 9C), as shown by substantial systematic errors in the space–time structure of the residuals (Fig. 9B,C, right). However, the spatiotemporal responses of this neuron were fit adequately with model VAP, which also incorporates a position component in the temporal response (r² = 0.82) (Fig. 9D). This improvement arises because the firing rate at the end of the stimulus was higher than the firing rate before stimulus onset for some directions of motion (e.g., Fig. 9E, PSTH for −90°). Only model VAP captures this gradual monotonic change in firing rate (Fig. 9E, compare blue with red and green fits). Indeed, model VAP was found to fit significantly better than model V or model VA for this neuron (AIC_VvsVAP, AIC_VAvsVAP < 0), indicating that increasing the number of parameters to 11 (from 7 and 9, respectively) was justified by the improvement in the fit. The best fit of model VAP gave a velocity weight of w_v = 0.94 (w_a = 0.06) and a position weight of w_p = 0.57 for this cell.

Figure 9.

Example fits of models V, VA, and VAP to responses of a neuron showing a position component. A, Direction–time plot. B–D, Model fits (left) and response residuals (right). For model V (B): t₀ = 1.16 s, θ₀ = 92°, r² = 0.51. For model VA (C): t₀ = 1.44 s, θ₀ = 106°, Δθ_va = 141°, w_v = 0.67, r² = 0.54. For model VAP (D): t₀ = 1.11 s, θ₀ = 78°, w_v = 0.95, Δθ_va = 169°, w_p = 0.58, Δθ_vp = 155,° r² = 0.82. E, Response PSTHs (open bars) for the horizontal plane (see inset), along with model fits. The format is as in Figure 6.

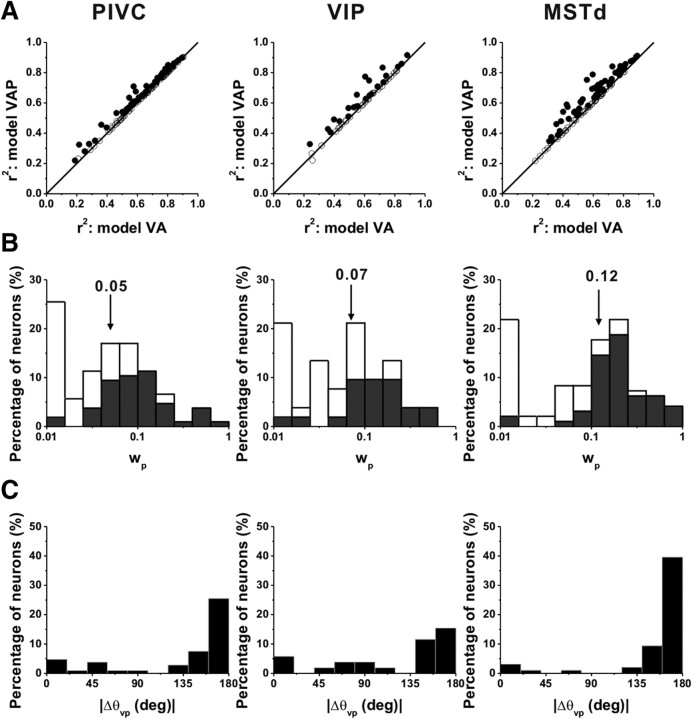
Scatter plots comparing correlation coefficients for models VA and VAP are shown in Figure 10A. For 47/106 (44%) cells in PIVC, 21/52 (40%) in VIP, and 53/96(55%) in MSTd, the model VAP fit significantly better than model VA such that AIC_VAvsVAP < 0 (see also Table 3). Thus, a majority of MSTd cells, but substantially fewer PIVC or VIP cells, carry some information about linear displacement. Comparing Figure 10A to Figure 8A, however, one can see that the incremental gain in r² achieved by adding the position component was substantially smaller than the gain in r² achieved by adding the acceleration component to the velocity model. To quantify the relative strength of the position component, we computed the ratio of position weight to the sum of the velocity and acceleration weights, w_p/(w_v + w_a) = w_p, since w_v + w_a = 1. In PIVC, ∼24% (25/106) of the cells had w_p > 0.1 (Fig. 10B, left). Similarly, 32% (17/52) of VIP cells had w_p > 0.1 (Fig. 10B, middle). By comparison, more than half (57%, 55/96) of MSTd cells had w_p > 0.1 (Fig. 10B, right). Across the population, the w_p in MSTd (geometric mean ± SE: 0.08 ± 0.38; geometric median: 0.12) was significantly greater than that in PIVC (geometric mean: 0.04 ± 0.29; median: 0.05) (p < 0.001, Wilcoxon rank test). Again, VIP values were intermediate (geometric mean: 0.06 ± 0.47; median: 0.07), differing significantly from MSTd (p = 0.05) but not from PIVC (p = 0.19). Among cells for which model VAP gave the best fit, direction preferences of the position component tended to be mostly opposite to those of the velocity component (Fig. 10C).

Figure 10.

Population comparison between fits of model VAP and model VA. A, Scatter plots of r² for model VAP against r² for model VA. Data from area PIVC (left, n = 106), VIP (middle, n = 52), and MSTd (right, n = 96). B, Distribution of position weight, w_p. Open symbols/bars represent cells whose responses were better fit by model VA (AIC_VAPvsVA > 0). Black symbols/bars represent cells with responses better fit by model VAP (AIC_VAPvsVA < 0). C, Distributions of the absolute difference in direction preference between velocity and position components (for cells better fit with model VAP). The format is as in Figure 8.

In addition to estimating the relative contributions of velocity, acceleration, and position signals to neural responses, the model-fitting analysis also allowed us to compute the overall latency of the response (parameter t₀ in Eq. 5), independent of the specific mixture of temporal response components needed to fit each neuron's response. Figure 11 shows distributions of response delays, from the best-fitting model, for areas PIVC (top), VIP (middle), and MSTd (bottom). In agreement with the peak time analysis of Figure 5, PIVC cells had the smallest average response latency (mean ± SE: 65 ± 20 ms), which was significantly smaller than the latencies for VIP (mean ± SE: 155 ± 31 ms) and MSTd (mean ± SE: 222 ± 35 ms) (p = 0.025 and p < 0.001, respectively, Wilcoxon rank test). The difference in latency between VIP and MSTd was not significant (p = 0.15, Wilcoxon rank test).

Figure 11.

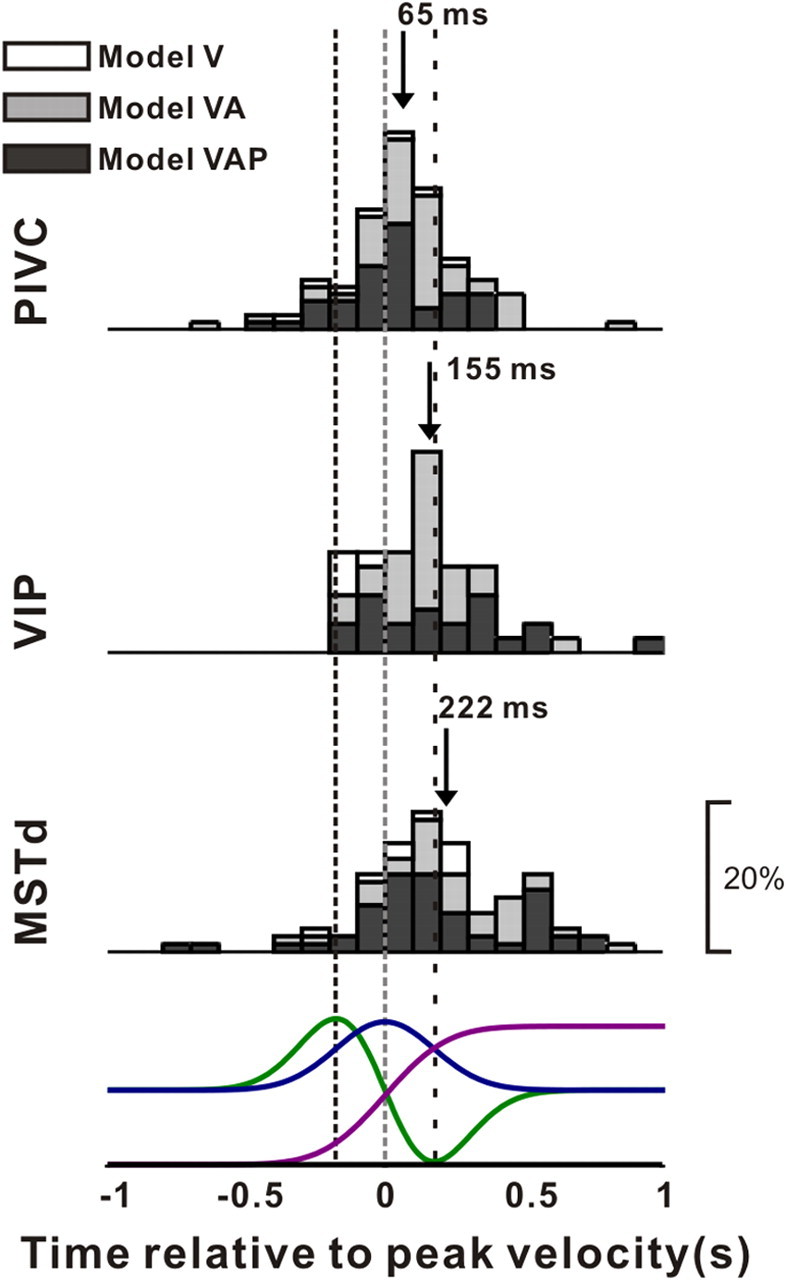
Distributions of response latency, derived from model fits, for neurons in area PIVC (top), VIP (middle), and MSTd (bottom). Data shown are from the best-fitting model. Open bars, Cells better fit with model V; gray bars, cells better fit with model VA; black bars, cells better fit with model VAP. Arrows indicate mean values. Stimulus velocity (blue), acceleration (green), and position (magenta) profiles are shown in the bottom row. Vertical dashed lines indicate the times of peak acceleration/deceleration and peak velocity.

Discussion

We have compared the spatiotemporal response properties of vestibular translation-sensitive neurons in three cortical areas: PIVC—an area traditionally considered to be “vestibular cortex”—and areas VIP and MSTd, which are best known mainly for their visual motion response properties. Using both empirical and model-based analyses, we have shown the following: (1) that the strongest direction tuning is seen in PIVC, as compared to VIP and MSTd; (2) that there is a gradual shift in response latency across areas, with PIVC neurons showing the fastest and MSTd neurons showing the most sluggish responses; and (3) that there is a gradual shift in response dynamics from PIVC to VIP to MSTd. The strongest acceleration responses are observed in PIVC, with weaker acceleration components observed in MSTd and VIP. Correspondingly, velocity response components are strongest in MSTd and weakest in PIVC. Although these results are derived, somewhat indirectly, from functional data instead of anatomical connections, they constitute strong evidence favoring the hypothesis that there is a hierarchy in cortical vestibular processing, with PIVC being closest to the vestibular periphery and MSTd being furthest away.

Velocity, acceleration, and position coding

The curve-fitting results indicate that responses of neurons in all three areas represent diverse mixtures of stimulus velocity and acceleration, both within and across motion directions. The observation that multiple stimulus parameters (velocity, acceleration, and position) are represented simultaneously in the activity of single neurons has been also made for VIP responses to yaw rotation (Klam and Graf, 2003). This broad range of spatiotemporal dynamics may reflect the need to use vestibular signals for diverse functions, from spatial perception to motor control. In the only study to characterize vestibular translation responses in VIP, some cells were reported to respond in phase with stimulus velocity and others in phase with position/acceleration (Schlack et al., 2002). In fact, response phase to sinusoidal linear acceleration was reported to be uniformly distributed (Schlack et al., 2002). Unfortunately, as sinusoidal translation at a single frequency and along a single direction (forward/backward) was the only stimulus condition used in that study, it was not possible to determine the dynamics of VIP responses to translation. This is particularly problematic because the phase of otolith-driven responses in central vestibular areas is variable from cell to cell and has no clear relationship to response dynamics (Angelaki and Dickman, 2000; Shaikh et al., 2005; Liu and Angelaki, 2009; Liu et al., 2010).

As concluded previously using different analyses, neural activity in MSTd is mostly related to stimulus velocity (Gu et al., 2006; Fetsch et al., 2010). This property may reflect the need to match the temporal dynamics of vestibular signals with those of visual signals (optic flow) related to self-motion perception, as visual responses to motion typically represent velocity instead of acceleration (Rodman and Albright, 1987; Lisberger and Movshon, 1999; Gu et al., 2006). However, the curve-fitting results indicate that MSTd neurons also encode other kinematic parameters of vestibular stimuli. In addition to acceleration, which is the signal encoded by neurons at the vestibular periphery (Fernández and Goldberg, 1976), MSTd neurons also carry information about linear displacement. These position-related signals, which represent a double integral of linear acceleration, might be functionally important for spatial navigation (Ono et al., 1993; O'Mara et al., 1994). For example, it is possible that the positional response components quantified here allow some degree of estimation of distance traveled during passive displacements (i.e., path integration) (Berthoz et al., 1995; Israël et al., 1997). In agreement with the present results, position-related signals in MSTd have also been reported by Froehler and Duffy (2002) and were proposed to reflect the need to combine positional information with information about heading or path.

Vestibular inputs to PIVC/VIP/MSTd and functional connectivity between cortical vestibular areas

Of the three cortical areas studied here, only PIVC has been shown to receive direct projections from regions of the thalamus known to exhibit vestibular responses (Akbarian et al., 1992). The present results, showing smaller response delays and stronger acceleration components in PIVC responses, as compared to MSTd and VIP, are in agreement with these previous neuroanatomical observations. By contrast, it is unlikely that there are direct vestibular projections from the thalamus to MSTd or VIP. The vestibular-responsive areas in the ventral posterior thalamic nuclei do not appear to project to visual cortex (Jones, 1987, 2000; Steriade, 1997). Instead, MSTd and VIP receive projections from the medial inferior pulvinar (Bender, 1982; Boussaoud et al., 1992; Adams et al., 2000; Kaas and Lyon, 2007), an area that is not known to receive brainstem and cerebellar vestibular signals (Meng et al., 2007; Meng and Angelaki, 2010).

It was previously suggested that vestibular inputs to VIP arise from one of three possible routes (Klam and Graf, 2006): first, via direct thalamic projections to PIVC and area 2v, areas known to project to VIP (Lewis and Van Essen, 2000); second, through a direct projection from deep cerebellar nuclei to VIP via the pulvinar (Graf et al., 2005); and third, via MSTd neurons, which are known to modulate during vestibular motion in darkness (Page and Duffy, 2003; Gu et al., 2006; Gu et al., 2007) and which send projections to VIP. The present results suggest strongly that the latter possibility is incorrect because vestibular responses in MSTd are slower and more strongly represent velocity and position than responses in VIP. This conclusion is further supported by the fact that area MT, which provides the major visual motion inputs to area MSTd, does not respond to vestibular stimulation (Chowdhury et al., 2009). Whereas there appears to be a hierarchical flow of visual information from MT to MSTd to VIP (Lewis and Van Essen, 2000), this is clearly not the case for vestibular signals. The second possibility described above, a vestibular pathway through the pulvinar, has also not been verified but cannot be firmly excluded at this time (Meng and Angelaki, 2010). Thus, it appears most likely that vestibular signals reach VIP through PIVC, and our results are consistent with this hypothesis.

An important missing piece to the puzzle involves the responses of neurons in the FEFp during optic flow and vestibular stimulation. This area is strongly and bidirectionally connected with both MST and VIP, and it receives smaller projections from PIVC and VPS (also often referred to as T3 or Tpt) in the retroinsular area (Lewis and Van Essen, 2000; Stanton et al., 2005). Indeed, FEFp neurons respond to vestibular stimulation (Fukushima et al., 2004). It remains to be seen how the temporal and spatial vestibular responses in FEFp compare to those in MSTd, VIP, and PIVC. For example, it is possible that the MSTd signal is coming from FEFp, independent of the signal to VIP, which could have its origin in PIVC. Continued studies of the timing of information processing in different cortical areas, layers, and functional cell types will be necessary to fully understand the neural circuits that underlie vestibular signal processing.