Abstract
Image phase from gradient echo MRI provides a unique contrast that reflects brain tissue composition variations, such as iron and myelin distribution. Phase imaging is emerging as a powerful tool for the investigation of functional brain anatomy and disease diagnosis. However, the quantitative value of phase is compromised by its nonlocal and orientation dependent properties. There is an increasing need for reliable quantification of magnetic susceptibility, the intrinsic property of tissue. In this study, we developed a novel and accurate susceptibility mapping method that is also phase-wrap insensitive. The proposed susceptibility mapping method utilized two complementary equations: (1) the Fourier relationship of phase and magnetic susceptibility; and (2) the first-order partial derivative of the first equation in the spatial frequency domain. In numerical simulation, this method reconstructed the susceptibility map almost free of streaking artifact. Further, the iterative implementation of this method allowed for high quality reconstruction of susceptibility maps of human brain in vivo. The reconstructed susceptibility map provided excellent contrast of iron-rich deep nuclei and white matter bundles from surrounding tissues. Further, it also revealed anisotropic magnetic susceptibility in brain white matter. Hence, the proposed susceptibility mapping method may provide a powerful tool for the study of brain physiology and pathophysiology. Further elucidation of anisotropic magnetic susceptibility in vivo may allow us to gain more insight into the white matter microarchitectures.
Keywords: Phase imaging, susceptibility mapping, iron, myelin, anisotropic magnetic susceptibility
Introduction
The phase information present in MRI images are typically discarded except in a limited number of cases such as the measuring of flow in angiography, enhancing image contrast in susceptibility weighted images and temperature mapping (Gatehouse et al., 2005; Haacke et al., 2009; Haacke et al., 2004; Mittal et al., 2009; Ishihara et al., 1995). Traditionally, in the vast majority of MRI acquisitions, phase images are typically noisy and lack of tissue contrast, hence have limited diagnostic utility. With improved phase processing, Rauscher et al demonstrated that phase images could show excellent contrast and reveal anatomic structures, such as the deep nuclei and white matter structures, which are not visible on the corresponding magnitude images at 1.5T (Rauscher et al., 2005). The emerging ultra-high field (7T and higher) MRI have started to reveal more interesting contrast in the phase images with improved signal-to-noise ratio (SNR). Using gradient-echo MRI at 7T, Duyn et al showed that phase contrast was associated with major fiber bundles within white matter, while the contrast within gray matter exhibited characteristic layered structure (Duyn et al., 2007). More recently, they demonstrated that the layered phase variations in cerebral cortex were highly correlated with ion distribution (Fukunaga et al., 2010). Despite these advances, one intrinsic limitation of signal phase is that phase contrast is non-local, orientation dependent, and thus not easily reproducible. Therefore, it is of great interest to determine the intrinsic property of the tissue, i.e. the magnetic susceptibility, from the measured signal phase.
The quantification of susceptibility from phase images is a well known ill-posed problem, since the Fourier transform of susceptibility, denoted as χ(k), cannot be accurately determined in regions near the conical surfaces defined by (de Rochefort et al., 2010). A variety of approaches have been proposed to address this issue. For example, threshold method has been used to avoid division by zero and approximate the χ(k) values at the two conical surfaces (Shmueli et al., 2009). This method is straightforward to implement; the accuracy, however, is rather limited. Residual artifacts and noise amplification in the reconstructed susceptibility maps may hamper the visualization of subtle tissue structures, especially at ultra-high resolution. A more effective but less efficient way to address the issue is to increase the number of sampling orientations by rotating the object in the scanner (Liu et al., 2009; Wharton et al., 2010). The multiplied scan time is unfortunately unfavorable, especially when the acquisition of high resolution 3D images is already lengthy. Further, recent studies showed that susceptibility of white matter is orientation dependent (Lee et al., 2010; Liu, 2010). Thus, the multiple orientation method may not be accurate for susceptibility mapping of white matter. In this regard, single-orientation susceptibility mapping method is desirable, especially for assessment of susceptibility anisotropy of white matter. Numerical optimization relying on nonlinear regularization has shown an excellent capability in suppressing the streaking artifacts (de Rochefort et al., 2010; Kressler et al., 2010). Typically, regularized optimization requires a careful choice of the regularization parameters. One common concern is the introduction of excessive external constraints that may cause degradation of intrinsic tissue susceptibility contrast. Although the aforementioned methods are different in many aspects, they share one common feature: additional data or constraints are introduced to compensate the uncertainty in χ(k) at the conical surfaces. In this regard, it would be more desirable if the true solution at conical surfaces of χ(k) can be determined from the same dataset and included in the process of susceptibility reconstruction.
In the current study, we developed a novel susceptibility mapping method insensitive to phase wrapping that, in principle, provides the exact solution of the underlying susceptibility distribution given a 3D volume of measured phase images. The objective of the proposed approach is to generate two equations that complement each other so that the zero-coefficient surface can be completely eliminated. The first equation is described through a Fourier transform (FT) relationship; the second equation is generated by taking a first-order partial differentiation of the first equation with respect to spatial frequency coordinates. In numerical simulations, the proposed method offers a direct inversion, which results in a near exact solution. We further demonstrate that combining the two equations allows high quality reconstruction of susceptibility maps of human brain in vivo. The resulting maps allowed quantitative assessment of the susceptibility contrast at various anatomical structures (e.g. the iron-rich deep brain nuclei and white matter bundles) and the dependence of susceptibility on the white matter microstructures.
Theory
Fourier Relationship between Phase and Magnetic Susceptibility
Given a susceptibility distribution, χ(r), and the applied magnetic field, H0, the resonance frequency offset, Δf (r), can be determined using the following equation (Koch et al., 2006; Marques and Bowtell, 2005; Salomir et al., 2003):
| [1] |
where k is the spatial frequency vector, , . Δf (r) can be determined from the phase offset divided by the time of echo (TE). The non-local property of phase data, and its orientation dependence is apparent from the term D2(k). At the center of k-space, D2(k = 0) = −2/3 (Appendix A).
Define ψ(r)=Δf (r) /γH0, and we can take a Fourier transform of both sides of Eq. [1] and rewrite the equation as
| [2] |
Here, ψ(k) and χ(k) is the Fourier transform of ψ(r) and χ(r), respectively. Given the frequency shift, the susceptibility can be calculated with a direct inversion as follows:
| [3] |
However, at the conical surface in the frequency domain defined by D2(k) = 0 (or ), the inversion for susceptibility calculation is invalid. On the other hand, the forward problem of Eq. [2], which is to determine the phase distribution from a given susceptibility distribution, seems to suggest that the resulting phase distribution would lack certain frequency components defined by .
Susceptibility Mapping Using Weighted k-Space Partial Derivatives
To calculate the χ(k) values on the conical surfaces, we utilize the first-order derivatives of Eq. [2] in the frequency domain. The rationale is that although D2(k) = 0 on the conical surfaces, its derivative is not. Utilizing the gradient field to compute χ(k) requires the spectrum of susceptibility distribution to be first-order differentiable. Such an assumption is reasonable due to the spatial continuity of brain tissues and is always compatible with digital evaluation using Fourier transform. The resulting derivative relationship at the conical surfaces provides an effective complement to Eq. [2] so that the zero-coefficient surface can be completely eliminated or significantly reduced.
The first-order differentiation of Eq. [2] with respect to kz is evaluated as follows
| [4] |
Here, the partial differentiations of ψ(k) and χ(k) are both carried out with respect to kz, which can be evaluated using Fourier transform (Appendix B).
Define , then Eq. [4] can be rewritten as
| [5] |
Near the conical surfaces, D2(k) is very small, such that the term D2(k)·FT [i · rzχ(r)]is negligible. Under this condition, Eq. [5] can be reduced to
| [6] |
Here, rz represents the z-axis of the image domain. Although Eq. [6] is derived directly from Eq. [2], the non-local property of differentiations eliminates the zero-coefficient scenario that exists in Eq. [2]. In addition, the magnitude of D3(k) is only large in proximity to the conical surface. Hence, the derivative relationship shown in Eq. [6] is restricted to regions on or close to the conical surface in k-space.
Combining Eq. [3] and Eq. [6], the complete solution for susceptibility mapping is given as follows:
| [7] |
| [8] |
Here, ε is a predetermined threshold level.
Once χ(k) is computed from Eqs. [7-8], the susceptibility map in the spatial domain can be calculated using an inverse Fourier transform. For simplicity, we refer this method as the “direct” method. As a comparison, χ(k) at conical surfaces is also calculated with the “threshold” method by replacing Eq. [8] with the following approximation:
| [9] |
It should be noted that the derivation of Eq. [7] and [8] is based on the assumption that the phase values within the entire field of view (FOV) are available. In the simulated data, phase values can be generated for the entire FOV. For in vivo brain imaging, however, the phase outside of the brain is not available. Therefore, the lack of phase information in parts of the FOV must be taken into consideration. Hence, Eqs. [2] and [5] are rewritten as:
| [10] |
| [11] |
Here, Mbrain is a binary mask with ones in the tissue and zeros in the background; MD3 is smooth weighting function (Appendix C), which is to emphasize the derivative relationship near the conical surfaces.
Eqs. [10] and [11] constitute the relationship between phase and susceptibility for in vivo brain susceptibility mapping. Due to the presence of the brain mask Mbrain, these two equations can no longer be solved through direct voxel-by-voxel inversion. Instead, we propose to solve them iteratively using the orthogonal and right triangular decomposition (LSQR) method (Paige and Saunders, 1982). Prior to solving the equations, both sides of Eq. [10] were multiplied by the conjugate transpose of the coefficient matrix, i.e. CTC ·χ(r)=CT ·ψ(r), to improve the numerical stability. Here C is the matrix representation of relationship between phase and susceptibility as defined in Eq. [10]. For simplicity, this method is referred to as the “weighted k-space derivative (WKD)” method. To evaluate the effect of including the derivative relationship shown in Eq. [11], we also calculated the susceptibility map only with Eq. [10] by using the same LSQR algorithm. As a comparison, the method of using LSQR to solve Eq. [10] alone is referred to as “LSQR” method.
Phase-Wrap Insensitive Background Phase Removal for Susceptibility Mapping
A complicating situation may arise during susceptibility quantification when the image phase is wrapped around 2π. Phase wrapping appears commonly in high field imaging especially when large off-resonance is present and when TE is relatively long. The presence of large background phase not only disguises local tissue contrast, but also worsens the undesirable phase wrapping issue. The uncertainty in wrapped phase, if uncorrected, results in large errors in the estimated susceptibility map. A common approach in calculating susceptibility is to perform a phase unwrapping procedure followed by a high-pass filtering operation prior to susceptibility mapping (Kressler et al., 2010; Shmueli et al., 2009). The challenge and limitation of this approach are two-folds. Firstly, accurate and reliable phase unwrapping is difficult to achieve especially when the data are noisy, despite the continuous advances in this field; secondly, high-pass filtering removes important local-frequency information that is specific and crucial for larger white matter fiber bundles.
To calculate the susceptibility, all we need is the Fourier transform of the phase image. Here, we propose a method to calculate the phase image and to remove the background phase in the k-space. This method involves two steps and is inherently insensitive to phase wrapping. In the first step, a Laplacian operator is applied to the phase image that only uses the trigonometric functions of the phase. The Laplacian operator is not only insensitive to phase wraps, but also automatically removes the phase components originating from outside of the FOV, since they satisfy the Laplacian equation (∇2θ = 0). At this step, the brain tissue phase still contains components originated from tissue outside the brain, such as the skin, skull and so on. In the second step, background phase from tissue outside the brain will be further cleaned with a sphere mean value filtering method. Specifically, the Laplacian of the phase is calculated using only cosine and sine functions of the phase as follows (Schofield and Zhu, 2003):
| [12] |
This operation is intrinsically indifferent to phase wrapping. From Eq. [12], the Fourier transform of phase can be derived as follows (Appendix D):
| [13] |
Here θ includes both background phase (i.e., the coil phase and phase generated by tissue outside of region of interest) and brain local phase. The θ(k) calculated from Eq. [13] can be directly used in the subsequent background phase removal following the spherical mean value (SMV) method proposed by Schweser et al (Schweser, 2010). Briefly, the background phase satisfied the Laplacian equation. In other words, the background phase is the harmonic phase inside the brain that is generated by susceptibility sources outside the brain. For solutions of Laplacian equation, the SMV property of Laplacian holds, i.e. the mean value of the harmonic phase on a spherical shell equals the harmonic phase at the sphere center. Therefore, the background harmonic phase can be removed using SMV filtering followed by a deconvolution operation to restore the low frequency local phase. All these operations can be performed in Fourier domain (Schweser, 2010).
Materials and Methods
Numerical Simulations
A 3D 128×128×128 Shepp-Logan phantom was generated to evaluate the accuracy of these susceptibility mapping methods. The phantom was composed of multiple ellipsoids placed in a homogenous background with zero susceptibility. The susceptibility values for the ellipsoids were 0, 0.2, 0.3 and 1 ppm, respectively. To minimize Gibbs ringing, the phantom was further zero padded to 256×256×256 for accurate simulation of the corresponding resonance frequency map. Both the direct method and the threshold method were used to compute the susceptibility distribution. The calculated χ1(k), χ1(r), error map calculated from the difference of the true χ0(r) and calculated χ1(r), and Fourier transform of the error map were compared.
Brain MR Imaging
In vivo brain imaging of healthy adult volunteers was conducted on a GE MR750 3.0T scanner (GE Healthcare, Waukesha, WI) equipped with an 8-channel head coil. High-resolution phase images with whole-brain coverage were acquired using a standard flow-compensated 3D spoiled-gradient-recalled (SPGR) sequence with the following parameters: TE = 42 ms, TR = 60 ms, flip angle = 20°, FOV = 256×256×180 mm3, matrix size = 256×256×180. This protocol resulted in an isotropic resolution with a voxel size of 1×1×1 mm3. To map out the white matter fiber orientations, diffusion tensor images were also acquired using a standard single-shot EPI sequence with ASSET parallel imaging and an acceleration factor of 2. The parameters were as follows: TE = 82 ms, TR = 8 s, FOV = 256×256 mm2, matrix size = 128×128, slice thickness = 2 mm without gap, b-value = 800 s/mm2, 5 non-diffusion weighted images and 32 diffusion encoding directions. 54 slices were acquired to cover the whole brain. To investigate the dependence of magnetic susceptibility on white matter fiber orientation, we also acquired several additional sets of SPGR images with reduced matrix size and thus reduced spatial resolution (2×2×2 mm3) using a larger single-channel head coil with various brain orientations with respect to the main magnetic field. All other imaging parameters were kept the same. All experiments were approved by the institutional review board of Duke University.
Image Analysis
The brain image was reconstructed with 3D Fast Fourier transform using the complex k-space data for each of the 8 receiver coils, and then separated into magnitude and phase. The magnitude image was obtained from the squared summation of the 8 magnitude images, and then used for the extraction of the brain tissue using ITK-SNAP (Yushkevich et al., 2006). The Fourier transform of phase image for each individual coil was calculated from the original wrapped phase data (Eq. [16]). The resultant phase Fourier transforms were then averaged to yield the Fourier transform of the final combined signal phase. An inverse Fourier transform was employed to visualize the unwrapped phase, though this step is not necessary for the calculation of susceptibility. The background phase were then removed using the spherical mean value method with a filter radius of 8 (Schweser, 2010). One requirement for SMV calculation is that all voxels contained in the sphere must be valid, which cannot be met at the brain boundary. Hence, the filter radius was gradually reduced to the largest size possible at brain boundaries. For example, the sphere with a radius of 8 will contain some voxels from the outside the brain at the location that is 5 voxel away from the boundary. Under this condition, the sphere mean value is calculated using the maximal sphere radius allowed, which is 5. Since the sphere size is finite, the phase generated by the brain tissue outside the sphere is harmonic in the sphere, and thus can also be removed along with the background phase. According to Schweser, this removed low frequency phase from the brain tissue can be restored with a deconvolution operation (Schweser, 2010). The resonance frequency map was then calculated from the resultant local phase image. Quantitative susceptibility map was calculated from the frequency map using the WKD method (Eqs. [10-11]) and the LSQR method (Eq. [10]). The iteration was terminated when the relative residual norm was less than 0.05. Following the same procedure, the susceptibility maps were reconstructed independently for each orientation of the multi-orientation SPGR datasets. The resulting susceptibility maps were linearly registered with FSL-FLIRT (Oxford University, UK). Diffusion tensor images were analyzed as described previously (Basser et al., 1994; Liu et al., 2004). All the programs were written using Matlab R2009b (Mathworks, Natick, MA). The calculations were performed on a desktop computer with an AMD Phenom™ II X4 965 processor and 8GB RAM.
Results
Susceptibility Mapping of the Numerical Phantom
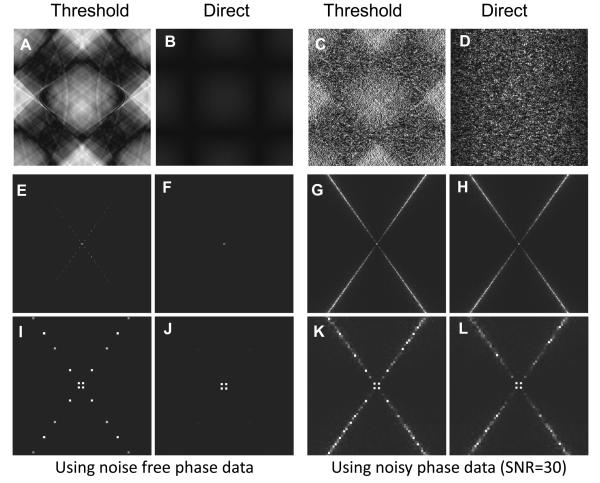
The phase image simulated using the Shepp-Logan Phantom shows the bipolar patterns around the phantom in the X-Z (and Y-Z, not shown) plane (Fig. 1A). Such bipolar pattern is not present in the X-Y plane, which is perpendicular to the main magnetic field that is along the Z-axis (Fig. 1B). The spectrum of the susceptibility, χ(k), was calculated from the simulated phase images using two methods: the threshold method and the direct method. The threshold method yielded discontinuous χ(k) at the conical surfaces (Fig. 1C), indicating inaccurate results. Such discontinuities were absent using the direct method (Fig. 1D). Accordingly, the streaking artifact was obvious using the threshold method (Fig. 1E&G), while it was not visible using the direct method (Fig. 1F&H).
Fig. 1.
Susceptibility mapping of the 3D Shepp-Logan phantom. A&B: phase map simulated with main magnetic field parallel to Z-axis in X-Z plane (A) and X-Y plane (B), respectively. C&D: χ(k) image calculated by the threshold (C) and the direct method (D) in the X-Z plane. χ(k) is displayed as log10(|χ(k)|). The arrow in panel C indicates the discontinuous χ(k) values. Such discontinuity is virtually absent in panel D. E&F: susceptibility map calculated by the threshold (E) and the direct method (F) in the X-Y plane. G&H: susceptibility map calculated by the threshold (G) and the direct method (H) in the X-Z plane. I&J: susceptibility map calculated by the threshold (I) and the direct method (J) in the presence of noise with the SNR of 30.
For more quantitative error assessment, the error map was obtained by calculating the difference of the reconstructed and the original susceptibility image. The threshold method yielded extensive streaking artifact (Fig. 2A), while the error map by the direct method was much more uniform (Fig. 2B). Fourier analysis indicated that all the error is caused by inaccuracies at the conical surfaces for both methods (Fig. 2C&D). The direct method shows less error comparing to the threshold method (Fig. 2C-F). The total energy of the error image by the direct method is 2.1% of that using the threshold method. The residual error map by the direct method is mainly a baseline drift and non-structural that is due to the residual error at the center of k-space. At the center of k-space, the value of χ′(k) in Eq. [5] is large, which renders the subsequent simplifications in Eq. [6] less accurate than at peripheral k-space. If the 8 most inaccurate voxels at the k-space center are excluded, the total energy of error map by the direct method is only 0.4% of that by the threshold method. These results demonstrated that the χ(k) at the conical surfaces calculated from the first-order derivatives indeed complements the original relationship between phase and susceptibility (Eq [1]).
Fig. 2.
Error analysis. A-D: error map calculated as the difference between original susceptibility map and susceptibility map calculated with the threshold (A&C) and direct (B&D) method, respectively. The images were displayed as |χ1(r)− χ0(r)|. E-H: Fourier transform of the error map using the threshold (E&G) and direct (F&H) method, respectively. The images were displayed as |χ1(k)− χ0(k)]. I-L: Fourier transform of the error map near the center of k-space using the threshold (I&K) and direct (J&L) method, respectively. In this figure, A, B, E, F, I and J are calculated using noise free phase data, while others are calculated with noisy phase data with SNR of 30.
Since the deconvolution of phase is critically dependent on noise (Grabner et al, 2010), the effect of noise on the susceptibility mapping was also evaluated using the Shepp-Logan phantom. Gaussian noise was added to the phase image to make an equivalent SNR of 30. Fig. 1 I&J showed the reconstructed susceptibility maps. Similar to that using noise free data, the error map of the threshold method showed obvious patterns (Fig. 2C), while such pattern was significantly reduced using the direct method (Fig. 2D). In addition, the noise amplitude by direct method was smaller than by the threshold method (Fig. 2C&D). These results indicated that the derivative relationship is still useful when the SNR is around 30.
Phase-Wrap Insensitive Background Phase Removal
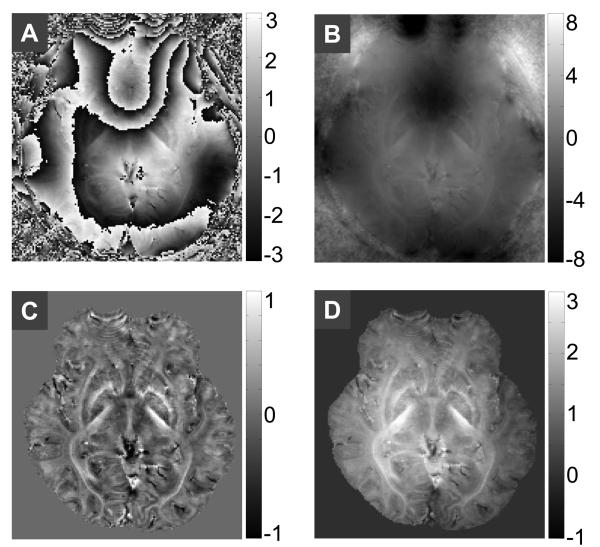
Figure 3A showed the original phase image, from which the Fourier transform of the phase image was calculated. A simple inverse Fourier transform allowed the visualization of the unwrapped phase (Fig. 3B). The resulting unwrapped phase is continuous, even at the tissue air boundary, demonstrating the excellent robustness. The background phase was then filtered with the spherical mean value (Fig. 3C). Note that some of the local phase is also removed along with the harmonic background phase. Hence, the SMV filtered image was further deconvolved to restore the local phase (Fig. 3D). The resultant local phase images were then converted to local frequency map for subsequent susceptibility reconstruction.
Fig. 3.
Phase wrap insensitive background removal. A: original phase. B. unwrapped phase calculated using Eq. [13] followed by an inverse Fourier transform. C: SMV filtered phase. D: local phase after deconvolution.
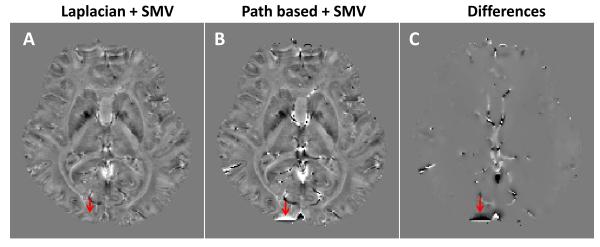
The accuracy of Laplacian-based phase unwrapping (Eq. 13) is evaluated by comparing it with a widely used path-based phase unwrapping method (Fig. 4). For better visualization, SMV filtering (without deconvolution) is performed to remove the background phase. Fig. 4A shows the unwrapped phase using the Laplacian based method followed by SMV filtering. Fig. 4B shows the phase unwrapped with traditional path-based method followed by SMV filtering. Their difference is shown in Fig. 4C. It can be seen that their phase contrast is the same except at locations with sharp phase variations. Under this condition, the Laplacian-based method yields continuous phase, which is beneficial for susceptibility mapping. In addition, the accuracy of the SMV filtering is verified using numerical simulations (supplementary material).
Fig. 4.
Comparison between Laplacian based phase unwrapping and the traditional path-based phase unwrapping. A: Phase unwrapped with the Laplacian based method, followed by SMV filtering. B: Phase unwrapped with path-based method, followed by SMV filtering. C: Difference between A and B.
Quantitative Susceptibility Mapping of Human Brain
The quantification of susceptibility involves D2(k), D3(k) and MD3. From Fig. 5A, the magnitude of D2(k) shows the zero-coefficient cone as defined by , while such zero-coefficient cone is not present in the magnitude of D3(k) (Fig. 5B). These results demonstrate that the original equation and its first order derivatives (Eqs. [10] and [11]) are complementary. The continuous mask for derivative operation (MD3) is shown in Fig. 5C. The detailed calculation of MD3 was listed in Appendix C.
Fig. 5.
Magnitude of D2(k) (A), D3(k) (B) and MD3 (C) used in the WKD method.
The WKD and the LSQR methods for susceptibility mapping were compared in Fig. 6. The LSQR method already yields good-quality susceptibility maps without noticeable streaking artifacts (Fig. 6A&E). The imperfection of LSQR method is visible in k-space as evidenced by the reduced amplitude along the conical surfaces (Fig. 6G), as pointed by the arrow. In contrast, the discontinuity in χ(k) is significantly reduced using the WKD method (Fig 6H). Similar to the LSQR method, the WKD method determined susceptibility is also almost streaking artifact free (Fig. 6B&F), while the corresponding local susceptibility seems to show more contrast than the LSQR method (Fig. 6F), as indicated by the arrows.
Fig. 6.
Comparison between the LSQR methods and the WKD method. A&B: susceptibility map in X-Y plane by LSQR and WKD method, respectively. C&D: χ1(k) corresponding to A and B, respectively. E&F: susceptibility map in X-Z plane by LSQR and WKD method, respectively. G&H: the Fourier transforms of E and F, respectively.
Distinct Contrast of Susceptibility Comparing to Magnitude and Phase
The susceptibility contrast is significantly different from its corresponding phase and magnitude contrast (Figs. 7 and 8). In the brain, the iron-enriched structures, including globus pallitus (Fig. 8H), red nucleus (Fig. 8I), substantia nigra (Fig. 8I), and dentate nucleus (Fig. 7C), showed strong paramagnetic shift comparing to the surrounding tissue. The susceptibility values of these structures relative to that of cerebrospinal fluid (CSF) (Fig. 8C) was summarized in Table 1. The susceptibility/phase images also allows excellent delineation of the thalamus, lateral ventricle, globus pallitus and internal capsule (Fig. 7C), while such differentiation is not as clear from the corresponding magnitude image. In addition, from these figures, non-local property of phase is apparent (Fig. 8 E&F, Fig 7B), which results in blurred tissue boundaries. On the other hand, the susceptibility of all the above mentioned brain structures are well localized, indicating the superiority of susceptibility for quantitative analysis.
Fig. 7.
Magnitude, phase and susceptibility contrast in the sagittal view of human brain. A: magnitude. B: phase. C: susceptibility map. Dn: dentate nucleus; LV: lateral ventricle; Cd: caudate nucleus; Th: thalamus; GP: globus pallitus; IC: internal capsule.
Fig. 8.
Magnitude, phase and susceptibility contrast in the axial view of the brain. A-C: magnitude images of the brain from different axial views. D-F: phase images at the same locations as those in A-C, respectively. G-I: susceptibility images at the same locations as those in A-C, respectively. GP: globus pallitus; Pu: putamen; CI: capsula interna; RN: red nucleus; SS: sagittal stratum; scc: splenium of the corpus collosum. SN: substantia nigra. The scale for susceptibility was the same as that in Fig. 6.
Table1.
Susceptibility of various anatomical structures relative to CSF
| Anatomical structure | Relative χ (ppm) |
|---|---|
| CSF (reference) | 0 ± 0.019 |
| Red nucleus | 0.032± 0.024 |
| Substantia nigra | 0.053±0.026 |
| Globus pallitus | 0.087±0.028 |
| Putamen | 0.043±0.020 |
| Caudate nucleus | 0.019±0.012 |
| Dentate nucleus | 0.064±0.034 |
| Internal capsule | −0.068±0.014 |
| Genu of corpus collosum | −0.033±0.013 |
| Splenium of corpus collosum | −0.038±0.013 |
| Sagittal stratum | −0.075±0.019 |
| Capsula interna | −0.002±0.012 |
In addition to the deep brain nuclei, the susceptibility image also shows excellent contrast between gray and white matter. From Fig. 8H, the white matter structures, such as splenium of the corpus collosum, capsula interna and sagittal stratum can be easily delineated. Another interesting observation is that sagittal stratum is brighter (more diamagnetic) than surrounding tissue, but it appears darker in the magnitude image. In contrast, the deep nuclei, such as red nucleus, substantia nigra, and globus pallidas were all darker in both susceptibility and magnitude image. In addition, capsula interna can be easily distinguished from the surrounding tissue in susceptibility map but not in the magnitude image (Fig. 7C and Fig. 8H). Table 1 also listed the susceptibility values of several white matter structures relative to that of CSF.
Dependence of Susceptibility on While Matter Microstructure
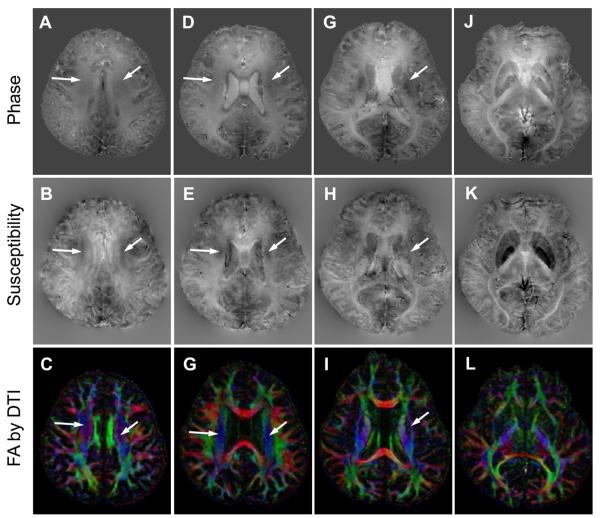
Fig. 8D shows that the magnetic susceptibility of the white matter is heterogeneous. It is possible that such inhomogeneity was due to the white matter fiber orientation. To explore the underlying reason, we compared the susceptibility map with the colored fractional anisotropy map obtained from diffusion tensor imaging (Fig. 9 bottom row). The blue color represents the fiber orientation in the superior-inferior direction. The arrows point to a number of selected white matter fiber bundles that run approximately in the superior-inferior direction, i.e., in parallel to the main magnetic field. The susceptibility of these particular fibers appears to be significantly more paramagnetic compared to that of the surrounding white matter fibers of different orientation. In contrast, such orientation dependence is not obvious in the corresponding signal phase.
Fig. 9.
Susceptibility heterogeneity of the white matter and its corresponding fiber orientation. The first row: phase maps. The second row: susceptibility maps. The third row: colored fractional anisotropy (FA) maps by diffusion tensor imaging (DTI). Blue color: superior-inferior direction.
To further verify this anisotropic magnetic susceptibility, we also performed susceptibility mapping of brain with various head orientations with respect to the main magnetic field (Fig. 10). As pointed by the arrows, the susceptibility contrast between white matter and gray matter indeed showed significant difference between different orientations. These results provide unambiguous evidences that white matter susceptibility is anisotropic in the human brain, which is consistent with two recent reports (Liu 2010; Lee et al 2010).
Fig. 10.
Alteration in susceptibility contrast of human brain with 3 different head orientations with respect to the main magnetic field.
Discussion
In this study, we have developed a novel method for susceptibility reconstruction from single-orientation 3D phase data. The proposed method is based on two complementary equations. The first equation is the well known Fourier relationship between phase and susceptibility; the second equation is constructed as the first-order derivative of the first equation evaluated on and near the conical surfaces defined by D2(k) < ε, where the inversion of the first equation fails. In principle, the combination of these two equations permits a direct calculation of the 3D magnetic susceptibility distribution. In practice, due to a limited data support in the FOV, the two equations are solved iteratively. The proposed method was first validated with simulation. The inclusion of the second relationship also allowed a high quality reconstruction of magnetic susceptibility map of human brain in vivo. The resulting susceptibility maps revealed contrast from molecular composition, i.e. ion and myelin distribution, and heterogeneous susceptibility values within white matter fibers and evidences of susceptibility anisotropy.
The validity of the current method is demonstrated in both numerical simulations and in vivo experiments. The main challenge of conventional susceptibility mapping methods relying on the Fourier relationship is that the coefficients become zero on an extended surface in the k-space, prohibiting the inversion of the equation (Fig. 5A). This difficulty is effectively overcome by including a relationship on the gradient field (Eq. [5]). The coefficients of the two equations are nearly orthogonal and thus complementing each other (Fig. 5A&B). The accuracy of Eq. [5] is clearly demonstrated using numerically simulated phase data as the direct method gives a near exact susceptibility map as the original one, which is as good as the multiple orientation method, the gold standard for mapping of isotropic susceptibility. Recent studies suggested that susceptibility of the brain white matter was anisotropic (Lee et al, 2010; Liu, 2010). Hence, the current single-orientation susceptibility mapping method will be particularly useful for evaluation of the orientation dependence of magnetic susceptibility.
From in vivo brain imaging, the LSQR method already yielded a susceptibility map with good image quality and without obvious streaking artifacts. The LSQR method is robust, easy to implement, thus provides a convenient tool for routine susceptibility mapping with moderate accuracy. One limitation of LSQR method is that the Fourier transform of the susceptibility map by LSQR method shows obvious discontinuity on and near the conical surfaces (Fig. 6G), which must be a reconstruction artifact instead of the intrinsic property of the brain tissue. This is because the LSQR method tends to penalize the k-space values near or at conical surfaces to improve its numerical stability. With the WKD method, the missing values at the conical surfaces are restored, which seems to be associated with improved susceptibility contrast (Fig. 6F). It can be noticed that the restoration of the conical surface values at low frequency is significantly better than that at higher frequencies. This is because we purposely reduced the magnitude of MD3 at high frequency due to the noise amplification nature by the derivative operation and the smaller magnitude of D3(k). The noise amplification property of derivative operation is obvious from Fig. 2B as some of the edges are visible on the error map. In the k-space, the majority of energy is located at the center, so the less accurate high-frequency k-space component will not influence of the overall quality of the reconstructed susceptibility maps. Complete elimination of this discontinuity at high frequency may require further optimization of MD3 and/or inclusion of additional equations, such as partial derivatives with respect to kx and/or ky directions. From the theory and simulation, the proposed susceptibility mapping method is accurate. However, in reality, there is no ground truth for the susceptibility of the brain tissue due to the lacking of phase data outside the brain. Hence, the accuracy of the susceptibility mapping of the human brain is ultimately limited by accuracy of the phase preprocessing rather than the susceptibility mapping method itself.
Accurate phase unwrapping and removal of background phase can also be a very important factor that determines the quality of the final susceptibility map. Previously, the Laplacian based method has been used to determine the integer multiple (n) of 2π needed to produce the true phase in the specific location for the interferometric applications (Schofield and Zhu, 2003). We found that it is unnecessary to determine the exact ‘n’, but the unwrapped 3D phase using the Laplacian operator (Eq. [13]) is directly useful for susceptibility mapping, since the background phase is not needed for susceptibility reconstruction. The Laplacian based method is very insensitive to phase wrapping due to the utilization of the sine and cosine functions. As a result, the resulting phase is always free of erroneous abrupt phase discontinuity (Fig4. A), which is very important for susceptibility mapping due to its nature of deconvolution. Furthermore, the application of the sphere mean value filtering can ensure a clean local phase map that is free of interfering phase from coils and from the tissue outside of the brain (Schweser et al., 2010). Due to the robustness of the phase preprocessing, the susceptibility maps obtained from both the LSQR and the WKD method shows fine anatomic details but without obvious streaking artifacts. In addition, the phase preprocessing is also very fast, which will only take <2 minutes to finish. Such robustness and efficiency will be particularly valuable for routine clinical use and scientific research. Despite these advantages, it should be noted that the impact of the imaging parameters, such as field strength, echo time, flip angle, spatial resolution and etc., on the accuracy of phase preprocessing and the resulting susceptibility mapping remains unknown, and needs to be further investigated.
Brain tissue contains a number of molecular compounds that can significantly affect the tissue susceptibility and the resultant resonance frequency shift, including nonheme iron, iron in deoxyhemoglobin, myelin, and proteins (Duyn, 2010). In basal ganglia, the iron content is relative high and myelin content is relative low. Hence, the nonheme iron, especially that in the iron storage protein ferritin, may present a major source of magnetic susceptibility in these regions (Haacke et al., 2005). Our results showed that the iron-enriched deep brain nuclei, including red nucleus, substantia nigra, globus pallitus, dentate nuclei, and etc, did exhibit strong paramagnetic shift comparing to CSF and the surrounding white matter. These results are in good agreement with previous studies (de Rochefort et al., 2010; Wharton et al., 2010). Table 1 listed the susceptibility of various anatomical structures of the brain tissue. It should be noted that the susceptibility reconstructed from the phase is not the absolute value, since the phase values outside the brain is not available and the background phase is removed. The susceptibility obtained in the current study is close to that reported by Shmueli et al and Wharton et al with < 40% differences in terms of susceptibility difference between putamen and globus pallidus or substantia nigra (Shmueli et al., 2009; Wharton and Bowtell, 2010). This difference is reasonable considering the large standard derivation and the possible inter-subject variability. In addition to ferritin, changes in magnetic susceptibility due to accumulation of hemosidersin, degradation product of ferritin, can also reflect iron overload and hemorrhage (Bizzi et al., 1990; Haacke et al., 2005). There has been great interest in mapping brain iron due to its value in the disease diagnosis and the understanding of disease pathogenesis. Alteration in iron content has been documented in many neurological diseases, such as Huntington's disease, Parkinson's disease, Alzheimer's disease, multiple sclerosis, chronic hemorrhage and etc (Haacke et al., 2005). Previous studies have utilized the R2 map to evaluate the iron distribution inside the brain (Yao et al., 2009). However, R2 is not only affected by iron distribution, but may also be affected by other factors, such as water content (Haacke et al., 2005). Alternatively, the susceptibility map may provide a more quantitative and physically meaningful index, thus warrants further application of susceptibility mapping for assessment of brain iron content in vivo.
The utilization of susceptibility in the study of gray matter has been well demonstrated in quite a few previous studies (de Rochefort et al., 2010; Shmueli et al., 2009; Wharton and Bowtell, 2010; Wharton et al., 2010). In addition to gray matter, the susceptibility mapping can also be very useful for the study of white matter. In contrast to deep nuclei, brain white matter has lower iron content, but high myelin content. As a result, myelin may present as a major factor that affects tissue susceptibility in white matter. Consistent with the diamagnetic property of myelin, white matter is more diamagnetic than gray matter. Evidently, the susceptibility map shows excellent contrast between gray and white matter (Fig. 7H). The importance of myelin in susceptibility contrast was supported by a recent finding in our laboratory that dysmyelination in genetically manipulated shiverer mice can lead to an almost complete loss of phase and susceptibility contrast (Liu et al, manuscript in review). Dysmyelination is one of the most prominent phenotype of many neurological diseases, such as acute disseminated encephalomyelitis, transverse myelitis, chronic inflammatory demyelinating polyneuropathy, Guillain-Barré Syndrome, and etc. The magnetic susceptibility contrast may provide a potentially powerful tool for early disease diagnosis and for monitoring of medical treatment of these diseases.
Unlike the homogenous magnetic property of gray matter, the white matter has highly organized microstructures. In basic NMR, magnetic susceptibility anisotropy of solids and liquid solution has been known for decades (Gayathri et al. 1982; Lohman and Maclean, 1978, 1979; Rochette et al., 1992; Uyeda et al., 1963). However, in vivo evidence of magnetic susceptibility anisotropy of the brain tissue with reasonable spatial resolution is essentially lacking. Previously, it is generally assumed that susceptibility of brain tissue, including both gray and white matter, is isotropic. Until recently, emerging evidences started to show that the phase/susceptibility contrast is actually dependent on fiber orientation. He et al reported that phase contrast is dependent on white matter fiber orientation (He and Yablonskiy, 2009). They interpreted this dependence using the Lorentz cylinder model. Duyn and colleagues also reported the orientation dependence of magnetic susceptibility using in vitro preparations of human corpus callosum stripes (Lee et al., 2010). However, their results seemed inconsistent with the nonspherical Lorentzian model, but rather supported the model of anisotropic magnetic susceptibility. At the same time, Liu observed the anisotropic magnetic susceptibility in mouse brain (Liu, 2010). He further characterized the anisotropic magnetic susceptibility comprehensively using a tensor model, which revealed interesting microarchitecture that resembled those from diffusion tensor imaging. In the current study, we showed direct evidences from in vivo brain that the susceptibility of human brain white matter is indeed anisotropic. Further susceptibility tensor imaging of human brain may allow us to get invaluable insight into the magnetic microarchitecture inside the human brain. Such information can be particularly useful in guiding us to better utilize the phase/susceptibility information in disease diagnosis and to further our understanding of human brain physiology.
Phase contrast and susceptibility contrast have different characteristics. Phase is non-local, therefore, the phase values with large susceptibility differences from surrounding tissue is really hard to quantify, especially the iron rich deep nuclei, such as globus pallidus, red nucleus, substantia nigra and etc. Susceptibility contrast is excellent for these structures, and yields much localized and uniform contrast in these tissues. At the cerebral cortex, the phase values outside the brain tissue is not available, this may lead to reduced accuracy in susceptibility mapping. Hence, at certain locations of the cerebral cortex, the contrast of the original phase map is better than the susceptibility contrast. However, the phase information is nonlocal, orientation dependent, thus not easily reproducible, so the susceptibility contrast is still valuable at these locations since it reflects the intrinsic property of the tissue. The accuracy of susceptibility mapping at cerebral cortex can be improved with higher spatial resolution. At other locations of the cerebral cortex, the susceptibility maps can show better contrast compared to the original phase map.
Conclusion
In conclusion, we developed a novel susceptibility mapping method with phase wrap insensitive background phase removal using single-orientation 3D phase images. The validity and accuracy of this method is demonstrated using the numerical phantom. This method allows high quality reconstruction of susceptibility map of human brain in vivo. The reconstructed susceptibility maps highlight regions rich in iron content, providing clear visualization and intrinsic quantification of, for example, the deep nuclei. More importantly, the reconstructed susceptibility map provides an excellent delineation of white matter fiber bundles. It also reveals the orientation dependence of magnetic susceptibility in the white matter that is otherwise disguised in the phase maps. We believe the proposed method could serve an accurate approach for quantifying tissue magnetic susceptibility and may allow us to further study the brain iron content and white matter micro-architecture.
Supplementary Material
Acknowledgement
We are grateful to Arnaud Guidon and Alexandru Avram for the help with brain analysis software. The study is supported by the National Institutes of Health (NIH) through grant R00EB007182 to C. L.
Appendix
A: Calculation of D2(k) at the center of k-space
Rearrange Eq. [2] and take the first-order partial derivative with respect to kz:
| [A.1] |
Eq. [A.1] evaluates to:
| [A.2] |
Since and , at the k-space center (k = 0), the Eq. [A.2] can be reduced to:
| [A.3] |
Hence, it is defined that D2(k = 0) = −2 / 3.
B: Calculation of ψ′(k), χ′(k) using Fourier transform
| [B.1] |
| [B.2] |
C: D3(k) is determined empirically as follows
| [C.1] |
where rz = −N/2, …, −1,0,1,…,N/2–1; α = 15, β = 1/(|D2(k)| + 0.1) and r0 = 48 for N = 256.
D: Evaluation of Laplacian of the trigonometric functions using Fourier transforms
| [D.1] |
| [D.2] |
| [D.3] |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Basser PJ, Mattiello J, Lebihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994;66:259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bizzi A, Brooks RA, Brunetti A, Hill JM, Alger JR, Miletich RS, Francavilla TL, Dichiro G. Role of iron and ferritin in MR imaging of the brain - a study in primates at different field strengths. Radiology. 1990;177:59–65. doi: 10.1148/radiology.177.1.2399339. [DOI] [PubMed] [Google Scholar]
- de Rochefort L, Liu T, Kressler B, Liu J, Spincemaille P, Lebon V, Wu JL, Wang Y. Quantitative susceptibility map reconstruction from MR phase data using Bayesian regularization: validation and application to brain imaging. Magn. Reson. Med. 2010;63:194–206. doi: 10.1002/mrm.22187. [DOI] [PubMed] [Google Scholar]
- Duyn JH. Study of brain anatomy with high-field MRI: recent progress. Magn. Reson. Imaging. 2010;28:1210–1215. doi: 10.1016/j.mri.2010.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duyn JH, van Gelderen P, Li TQ, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proc. Natl. Acad. Sci. USA. 2007;104:11796–11801. doi: 10.1073/pnas.0610821104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunaga M, Li TQ, van Gelderen P, de Zwart JA, Shmueli K, Yao B, Lee J, Maric D, Aronova MA, Zhang GF, Leapman RD, Schenck JF, Merkle H, Duyn JH. Layer-specific variation of iron content in cerebral cortex as a source of MRI contrast. Proc. Natl. Acad. Sci. USA. 2010;107:3834–3839. doi: 10.1073/pnas.0911177107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatehouse PD, Keegan J, Crowe LA, Masood S, Mohiaddin RH, Kreitner KF, Firmin DN. Applications of phase-contrast flow and velocity imaging in cardiovascular MRI. Eur. Radiol. 2005;15:2172–2184. doi: 10.1007/s00330-005-2829-3. [DOI] [PubMed] [Google Scholar]
- Grabner G, Trattnig S, Barth M. Filtered deconvolution of a simulated and an in vivo phase model of the human brain. J. Magn. Reson. Imaging. 2010;32:289–297. doi: 10.1002/jmri.22246. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Chengb NYC, House MJ, Liu Q, Neelavalli J, Ogg RJ, Khan A, Ayaz M, Kirsch W, Obenaus A. Imaging iron stores in the brain using magnetic resonance imaging. Magn. Reson. Imaging. 2005;23:1–25. doi: 10.1016/j.mri.2004.10.001. [DOI] [PubMed] [Google Scholar]
- Haacke EM, Mittal S, Wu Z, Neelavalli J, Cheng YCN. Susceptibility-weighted imaging: technical aspects and clinical applications, part 1. Am. J. Neuroradiol. 2009;30:19–30. doi: 10.3174/ajnr.A1400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haacke EM, Xu YB, Cheng YCN, Reichenbach JR. Susceptibility weighted imaging (SWI) Magn. Reson. Med. 2004;52:612–618. doi: 10.1002/mrm.20198. [DOI] [PubMed] [Google Scholar]
- He X, Yablonskiy DA. Biophysical mechanisms of phase contrast in gradient echo MRI. Proc. Natl. Acad. Sci. USA. 2009;106:13558–13563. doi: 10.1073/pnas.0904899106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K, Suzuki Y. A precise and fast temperature mapping using water proton chemical-shift. Magn. Reson. Med. 1995;34:814–823. doi: 10.1002/mrm.1910340606. [DOI] [PubMed] [Google Scholar]
- Koch KM, Papademetris X, Rothman DL, de Graaf RA. Rapid calculations of susceptibility-induced magnetostatic field perturbations for in vivo magnetic resonance. Phys. Med. Biol. 2006;51:6381–6402. doi: 10.1088/0031-9155/51/24/007. [DOI] [PubMed] [Google Scholar]
- Kressler B, de Rochefort L, Liu T, Spincemaille P, Jiang Q, Wang Y. Nonlinear regularization for per voxel estimation of magnetic susceptibility distributions from MRI field maps. IEEE Trans. Med. Imaging. 2010;29:273–281. doi: 10.1109/TMI.2009.2023787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Shmueli K, Fukunaga M, van Gelderen P, Merkle H, Silva AC, Duyn JH. Sensitivity of MRI resonance frequency to the orientation of brain tissue microstructure. Proc. Natl. Acad. Sci. USA. 2010;107:5130–5135. doi: 10.1073/pnas.0910222107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu CL. Susceptibility tensor imaging. Magn. Reson. Med. 2010;63:1471–1477. doi: 10.1002/mrm.22482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu CL, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): Application to high-resolution diffusion tensor imaging. Magn. Reson. Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magn. Reson. Med. 2009;61:196–204. doi: 10.1002/mrm.21828. [DOI] [PubMed] [Google Scholar]
- Gayathri C, Bothner-By AA, Van Zijl PCM, Maclean C. Dlpolar magnetic field effects in NMR spectra of liquids. Chem. Phys. Letters. 1982;87:192–196. [Google Scholar]
- Lohman JAB, Maclean C. Alignment effects on high-resolution NMR-spectra, induced by the magnetic-field. Chem. Phys. 1978;35:269–274. [Google Scholar]
- Lohman JAB, Maclean C. Magnetic-susceptibility anisotropies from quadrupolar magnetic-field effects in high-field H-2 NMR. Mol. Phys. 1979;38:1255–1261. [Google Scholar]
- Marques JP, Bowtell R. Application of a Fourier-based method for rapid calculation of field inhomogeneity due to spatial variation of magnetic susceptibility. Concept Magn. Reson. B. 2005;25B:65–78. [Google Scholar]
- Mittal S, Wu Z, Neelavalli J, Haacke EM. Susceptibility-weighted imaging: technical aspects and clinical applications, part 2. Am. J. Neuroradiol. 2009;30:232–252. doi: 10.3174/ajnr.A1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paige CC, Saunders MA. LSQR - an algorithm for sparse linear-equations and sparse least-squares. Acm. T. Math. Software. 1982;8:43–71. [Google Scholar]
- Rauscher A, Sedlacik J, Barth M, Mentzel HJ, Reichenbach JR. Magnetic susceptibility-weighted MR phase imaging of the human brain. Am. J. Neuroradiol. 2005;26:736–742. [PMC free article] [PubMed] [Google Scholar]
- Rochette P, Jackson M, Aubourg C. rock magnetism and the interpretation of anisotropy of magnetic-susceptibility. Rev Geophys. 1992;30:209–226. [Google Scholar]
- Salomir R, De Senneville BD, Moonen CTW. A fast calculation method for magnetic field inhomogeneity due to an arbitrary distribution of bulk susceptibility. Concept Magn. Reson. B. 2003;19B:26–34. [Google Scholar]
- Schofield MA, Zhu Y. Fast phase unwrapping algorithm for interferometric applications. Opt. Lett. 2003;28:1194–1196. doi: 10.1364/ol.28.001194. [DOI] [PubMed] [Google Scholar]
- Schweser F, Deistung A, Berengar WL, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: An approach to in vivo brain iron metabolism? NeuroImage. 2010 doi: 10.1016/j.neuroimage.2010.10.070. doi:10.1016/j.neuroimage.2010.10.070. [DOI] [PubMed] [Google Scholar]
- Shmueli K, de Zwart JA, van Gelderen P, Li TQ, Dodd SJ, Duyn JH. Magnetic susceptibility mapping of brain tissue in vivo using MRI phase data. Magn. Reson. Med. 2009;62:1510–1522. doi: 10.1002/mrm.22135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uyeda S, Fuller MD, Belshe JC, Girdler RW. Anisotropy of magnetic susceptibility of rocks and minerals. J Geophys Res. 1963;68:279–291. [Google Scholar]
- Wharton S, Schafer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magn. Reson. Med. 2010;63:1292–1304. doi: 10.1002/mrm.22334. [DOI] [PubMed] [Google Scholar]
- Wharton S, Bowtell R. Whole-brain susceptibility mapping at high field: A comparison of multiple- and single-orientation methods. Neuroimage. 2010;53:515–525. doi: 10.1016/j.neuroimage.2010.06.070. [DOI] [PubMed] [Google Scholar]
- Yao B, Li TQ, van Gelderen P, Shmueli K, de Zwart JA, Duyn JH. Susceptibility contrast in high field MRI of human brain as a function of tissue iron content. Neuroimage. 2009;44:1259–1266. doi: 10.1016/j.neuroimage.2008.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31:1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.