Abstract
In recent years, diffusion tensor imaging (DTI) has become the modality of choice to investigate white matter pathology in the developing brain. To study neonate Krabbe disease with DTI, we evaluate the performance of linear and non-linear DTI registration algorithms for atlas based fiber tract analysis. The DTI scans of 10 age-matched neonates with infantile Krabbe disease are mapped into an atlas for the analysis of major fiber tracts - the genu and splenium of the corpus callosum, the internal capsules tracts and the uncinate fasciculi. The neonate atlas is based on 377 healthy control subjects, generated using an unbiased diffeomorphic atlas building method. To evaluate the performance of one linear and seven nonlinear commonly used registration algorithms for DTI we propose the use of two novel evaluation metrics: a regional matching quality criterion incorporating the local tensor orientation similarity, and a fiber property profile based metric using normative correlation. Our experimental results indicate that the whole tensor based registration method within the DTI-ToolKit (DTI-TK) shows the best performance for our application.
Keywords: Diffusion tensor imaging, Registration, Krabbe disease, fiber tracts, MRI, Evaluation metrics
Introduction
Diffusion tensor imaging (DTI) is a magnetic resonance imaging (MRI) technique that enables the measurement of restricted diffusion of water molecules in tissue to produce neural tract images. This technique, although relatively new, has become increasingly important for studies of anatomical and functional connectivity of the brain regions. DTI is now extensively used to study the fiber architecture in the living human brain via DTI tractography. This technique has proven especially of value in clinical studies of white matter (WM) integrity in the developing brain for diseases (Basser et al., 1994), such as metachromatic leukodystrophy (MLD), cerebral palsy and Krabbe (Escolar et al., 2009).
Krabbe disease (also called globoid cell leukodystrophy) is a rare, autosomal recessive neurodegenerative disorder caused by a deficiency of an enzyme called galactocerebrosidase, which aids in the breakdown and removal of galactolipids found in myelin (Wenger et al., 2001). The buildup of these galactolipids affects the growth of the nerve’s protective myelin sheath and causes degeneration of myelin in both the central and peripheral nervous system. If left untreated, children with Krabbe’s disease generally experience severe neurologic deterioration and death. (Escolar et al., 2005). The major forms of the disease include an early onset (infantile) form and a late onset (juvenile or adult) form. The early onset form is more severe type and is characterized by rapidly progressing neurological deterioration resulting in vegetative state and typically death within the first few years of life. The infantile form is seen in 1 for every 70 000–100 000 (Wenger et al., 2001). Children with infantile Krabbe disease are seen to have hyperintense lesions within the white matter on T2-weighted MR images. Particularly the abnormal hyperintense signal is observed in the posterior limb of the internal capsule, the white matter adjacent to the lateral ventricles, the centrum semiovale, the corona radiate and the white matter and dentate nuclei of the cerebellum. Hematopoietic stem cell transplantation has shown promise as therapy for Krabbe disease based on the fact that donor leukocytes can provide the deficient enzymes to cells in the peripheral and central nervous system. Treatment at asymptomatic, neonate stage has shown to stop disease progression (Escolar et al., 2005).
Water motion in myelinated white matter is anisotropic and DTI MR signal is sensitized to microscopic movement of water molecules. Myelinated white matter is seen to have higher anisotropy values on DTI derived anisotropy maps (Provenzale et. al. 2005). Previous studies show that patients with infantile Krabbe disease have lower fractional anisotropy (FA) across the corpus callosum (Guo et al., 2001) and along the DTI fiber bundle of internal capsules (IC) when compared with healthy age-matched controls (Escolar et al., 2009). Escolar et al. (2009) also showed a correlation of pretreatment FA measurements with post treatment gross motor function.
Based on the above research findings (Escolar et al., 2009; Goodlett et al., 2009), we use atlas based fiber tract analysis for analyzing DTI images of Krabbe subjects. For an accurate analysis it is crucial to establish a registration based voxel-wise correspondence between a normal control neonate DTI atlas (with prior information of fiber tract locations) and the Krabbe subjects DTI images. The research presented in this paper highlights our work to determine the best state-of-the-art approach to individually register DTI images of Krabbe subjects into the atlas space.
Challenges in DTI Registration for Krabbe Neonates
The registration of diffusion tensor images is particularly challenging when compared to registering scalar images as DTI data is multi-dimensional and the tensor orientations after image transformations must remain consistent with the anatomy (Alexander et al., 2001; Gee and Alexander, 2005). The application of the registration methods on DTI of Krabbe neonates makes the problem even more challenging due to the following factors. Most of the registration methods discussed in this paper are based on the intensity of the fiber tracts in the fractional anisotropy maps and as discussed earlier, the Krabbe patients have lower FA values as compared to the control group. Lower FA values are due to the anisotropy caused by the demyelination of the nerves. Relatively rapid changes occur in white matter during the first year of life restricting the control provided age matched controls to a relatively narrow age range relative to the patient. Also regional variations between FA values in white matter sites could cause inaccurate comparisons and hence the analysis needs to be performed in specific well defined white matter structures (Provenzale et. al. 2005). In addition to these points, the analysis in this paper is restricted to neonates and this adds to the complexity as DTI MRI of neonates have low signal-to-noise (SNR) and poorly developed white matter tracts.
DTI Registration Algorithms
DTI registration algorithms can be broadly categorized into two groups (Zhang et al., 2006). The first kind uses scalar images derived from DTI images and performs deformable registration with traditional image registration algorithms (Schnabel et al., 2001; Joshi et al., 2004; Andersson et al., 2007). Although this group discards the orientation component of the data, it is the most commonly used method because of the simplicity and the ease of implementation. The second group of DTI registration algorithms directly use higher order information of diffusion tensor images like the corresponding principal eigenvectors (Yap et al., 2009), or the full tensor information (Zhang et al., 2006; Yeo et al., 2008). Due to the complexity involved and the difficulty in realizing such algorithms, this group has not been explored extensively.
In this paper, we investigate eight DTI registration approaches from both groups, available either in-house or publicly:
Affine registration by Studholme et al. (1999) using normalized mutual information as a registration metric within the Image Registration Toolkit1 (referred to as Affine in this paper).
B-spline based registration by Schnabel et al. (2001) using normalized mutual information as a registration metric within the Image Registration Toolkit (referred to as B-spline in this paper).
B-spline based registration by Andersson et al. (2007) using weighted sum of scaled sum-of-squared differences as a registration metric via the “fnirt” implementation within FSL2 (referred to as FSL in this paper).
Diffeomorphic demons3 by Vercauteren et al. (2009) using sum-of-squared differences as a registration metric3 (referred to as Demons in this paper).
Log demons3 by Vercauteren et al. (2008) using sum-of-squared differences as a registration metric (referred to as Demons-log in this paper).
Fluid registration by Joshi et al. (2004) using sum-of-squared differences as a registration metric (referred to as Fluid in this paper).
Tensor-based registration by Zhang et al. (2006) using explicit optimization of tensor reorientation in an analytic manner within DTI-ToolKit4 (referred to as DTI-TK in this paper).
Diffeomorphic tensor-based registration by Yeo et al. (2008) using the exact finite strain gradient within MedINRIA5 (referred to as MedINRIA in this paper).
The first six methods are based on normalized FA maps whereas the last two are whole tensor based registration methods. An evaluation of algorithms from both the groups will give an insight into the higher performance of one group over the other, particularly considering the complexities in registering Krabbe neonates. To evaluate the performance of the registration algorithms, we introduce two novel evaluation metrics. The first metric is based on the matching quality of the local tensor orientation and atlas anisotropy in each voxel. The voxel-wise metric values are averaged over predefined regions within the atlas (such as the genu, splenium, internal capsules and uncinates). The second evaluation metric employs a normative fiber tract profile based criterion, which computes the correlation of the FA profile along the major tracts in the registered dataset and the atlas.
Materials and methods
Subjects
The studies are approved by the institutional review board at the University of North Carolina. Due to the difficulty of Krabbe data acquisition, only ten neonates with Krabbe disease identified by family history or through the New York State screening program were used in this study. The ten Krabbe neonates are aged 8 to 67 days (mean: 22 days) at the time of scan. These subjects were referred to the Program for Neuro-developmental Function in Rare Disorders (NFRD) at the University of North Carolina at Chapel Hill for assessment of baseline neurologic function before receiving unrelated umbilical cord blood transplantation at Duke University Medical Center. The assessment included a detailed neurodevelopmental evaluation concurrent with a brain MR imaging within the first four weeks of life. 377 age-matched neonatal controls (aged 7 days to 92 days with a mean value of 23 days) were recruited in a separate, unrelated study of brain development in normal controls and high risk offspring as part of UNC’s Conte center (Knickmeyer et al., 2008).
Scans
All neonates (control and Krabbe subjects) were scanned without sedation on an Allegra 3T head-only MR scanner (Magnetom Allegra; Siemens, Erlangen, Germany). Two separate DTI protocols were employed due to change in DTI acquisition methodology. Protocol 1, the protocol employed in scans – before July 2008, acquired seven images, one without diffusion gradient (b = 0) and six diffusion weighted images along unique gradient directions with b = 1000 s/mm2 (TR = 4219 ms; TE = 92.2 ms; in-plane resolution = 2×2 mm2; slice thickness = 2 mm; five averages). Since July 2008, a newer protocol (protocol 2) was employed to improve SNR and the gradient direction acquisition scheme. Protocol 2, forty-nine images are acquired, seven without diffusion gradients (b = 0) and 42 diffusion weighted images along unique gradient directions with b = 1000 s/mm2 (TR = 7680 ms; TE = 82 ms; in-plane resolution = 2×2 mm2; slice thickness = 2 mm; one average). The first seven Krabbe neonates as well as all healthy control subjects were scanned with protocol 1 (K1 to K7). The three final Krabbe neonates were scanned with protocol 2 (K8 to K10). No sedation was used; all scans were performed with subjects fully asleep. Neonates were fed before scanning, then swaddled, put to sleep and were fitted with ear protection and had their heads were secured in a vacuum-fixation device. A physician or nurse was present during each scan; a pulse oximeter was used to monitor heart rate and oxygen saturation. More details of the image acquisition and processing can be found in Gilmore et al. (2004).
DTI atlas building
In order to build the normative DTI atlas, we used a scalar, unbiased diffeomorphic atlas building method based on a nonlinear high-dimensional fluid deformation method (Joshi et al., 2004). The DTI derived intensity-histogram normalized FA is selected as the feature for atlas building. Nonlinear transformations are applied on the feature image to produce a deformation field for each image. All the tensor images are then reoriented into the unbiased space using the finite strain approximation proposed by Alexander et al. (2001). The atlas is then developed by averaging all the reoriented tensor images in log-Euclidean space (Arsigny et al., 2006). The selection of normalized FA image as the feature is based on the studies of Liu et al. (2010), wherein the authors show that this feature is the best scalar feature for DTI atlas building among all the other scalar measurements and their combinations. We did not investigate the use of alternative atlas building methods as part of this paper.
Pre-processing of Krabbe datasets
All the Krabbe datasets were subjected to a quality control (QC) using the DTIPrep6 tool to identify any artifacts in the diffusion weighted images (DWI), as well as to correct for motion and eddy current artifacts. The datasets were also cropped or embedded into consistent image dimensions. Diffusion tensors were then estimated for each dataset from the QC ed DWIs using weighted least squares tensor estimation (Salvador et al., 2005). Skull stripping was performed semi-automatically for all Krabbe datasets by a trained expert.
Registration Methods
In this section, we briefly present the working principle of the registration algorithms evaluated in this paper. The first five methods are based on intensity-histogram normalized FA images, while the last two are based on the whole tensor information.
Affine registration is a linear transform method that is commonly used as an initialization step for most deformable registrations (Studholme et al., 1999). The Affine registration used in this paper optimizes fifteen linear parameters (three for rotation, translation and scaling and six for skewing – defining the skewing angles in different planes) by maximizing the normalized mutual information. This is accomplished in a multi-resolution framework using Gaussian smoothing to compute lower resolution steps.
B-spline is a parametric, non-rigid image registration method based on multi-resolution adaptable free-form deformations using B-splines (Schnabel et al., 2001). Similar to Affine, this method also maximizes normalized mutual information in a multi-resolution framework using Gaussian smoothing to compute lower resolution steps.
FSL (or rather “FSL-B-Spline”) is similar to the previous method in that it represents displacement fields as B-splines on a regular grid (Andersson et al. 2007). But in this method the regularization of the field is based on membrane energy and the registration criterion is based on the weighted sum-of-squared intensity differences and the membrane energy.
Demons is a non-parametric, diffeomorphic deformable image registration algorithm based on the Thirion Demons warp software in the Insight Toolkit (Vercauteren et al. 2007 and 2009). The deformation model is based on optical flow and the registration criterion is based on the sum-of-squared intensity differences.
Demons-log is similar to the above Demons but works completely in the log-domain, i.e. it uses a stationary velocity field to encode the spatial transformation as its exponential (Vercauteren et al. 2008).
Fluid is a non-parametric, diffeomorphic deformable image registration that employs a dilatational-viscous fluid flow formulation (Joshi et al., 2004) with sum-of-squared intensity differences as the registration criterion.
DTI-TK is a non-parametric, diffeomorphic deformable image registration (Zhang et al., 2007) that incrementally estimates its displacement field using a tensor-based registration formulation (Zhang et al., 2006). It is designed to take advantage of similarity measures comparing whole tensors via explicit optimization of tensor reorientation (Zhang et al., 2006).
MedINRIA is also a diffeomorphic deformable image registration (Yeo et al., 2008) that incorporates the exact finite strain gradient into a diffeomorphic DTI registration scheme.
In order to be consistent across methods, we adopted the deformation fields from each registration method and performed DTI reorientation and interpolation using the same software (ResampleDTILogEuclidean7) based on standard finite strain tensor realignment (Alexander et al., 2001).
For all the registration methods, the default parameters were used except in the case of Fluid, wherein the parameters were slightly modified for comparable performance.
Evaluation of Registration Accuracy
In central WM, FA values in DTI of neonates are considerably lower than those at older ages (Gilmore et al., 2003). The WM pathology causes FA values of Krabbe patients to be even lower than those of healthy age-matched controls. In addition, Krabbe subjects are likely to have regionally differing levels of white matter pathology. All of these observations indicate that the development of an evaluation criterion for the registration algorithms is a challenging task, but also that the results may not easily be generalized to other settings.
For our evaluation, we tested one linear and seven nonlinear algorithms to determine the most suitable method for our application. We mainly focused on the tracts of i) the genu of the corpus callosum ii) the splenium of the corpus callosum iii) the internal capsule of both the hemispheres (left and right) and iv) the uncinate tracts (left and right). The same tests can be further extended to a larger selection of tracts.
While there are several ongoing initiatives towards an unbiased evaluation of deformable registration algorithms, there is currently no widely accepted metric standard for the evaluation of nonlinear registration algorithms, even more so for DTI registration. The following sections discuss our evaluation strategy.
Visual assessment
The first step of our evaluation strategy consists of a qualitative, visual quality control. To achieve this, we visualize FA and color-oriented FA images of all the registered datasets using a multi-dataset overview with MRIWatcher8. While this kind of assessment is subjective, significant errors can be easily detected. The registration is judged to have failed on datasets that show large errors.
Regional matching quality criterion
For the second step in our evaluation framework, we propose a novel regional matching criterion that is tailored to atlas based analysis methods. In our specific setting, we have the following conditions: 1) the streamline fiber tractography employed in our fiber based analysis framework follows a concept developed by Mori et al. (1999) and Xu et al. (2002), which is based on the local principal eigenvectors eP (i.e. the vector associated with the largest of the three principal directions of the diffusion tensor: λ1 ≥ λ2 ≥ λ3); 2) fiber tracts of the genu and splenium of the corpus callosum as well as both hemispheric internal capsule and uncinate tracts have higher intensity in FA images as compared to their neighboring tracts.
The orientation agreement between the principal eigenvectors of the individual subject (source) and the atlas (target) is the basis of this criterion. In order to enhance the specific regions associated with the selected fiber tracts and to render the method stable against small changes in the regional definition, we use the FA value of the atlas as a weight on the local orientation criterion. Thus, the proposed similarity value sv is defined for each voxel as:
| (1) |
where ePI is the subject’s principal eigenvector, ePA is the atlas principal eigenvector, and FAA ∈ (0,1) is the atlas FA value. Notation | | in the above equation indicates the absolute value and ‘.’ indicates the dot product. In the particular case that the principal eigenvectors of the individual subject and the atlas are oriented in same or fully opposite direction, the term |ePI · ePA| becomes || ePA ||2, which is 1, and sv will be equal to FAA. Using this local criterion, we compute a scalar matching image representing the registration quality at each voxel.
Next, regions of interest (ROIs) on the atlas are defined representing WM sections the major fiber tracts. The average regional similarity value on these ROIs represents the regional matching quality criterion. Thus for region r, the average similarity value s̄r is:
| (2) |
where Nr is the number of voxels in region r, sv,i is the similarity value at voxel i. Larger values of s̄r represent better registration accuracy in our settings.
Fiber property profile based criterion
As a third step in our evaluation framework, we propose another novel matching criterion that evaluates the DTI property measurements along the fiber tracts, called tract profiles (Goodlett et al., 2009). The fiber tracts tracked in atlas space are resampled in each registered DTI dataset. Using a prior definition of a tract origin plane, which defines a curvilinear re-parameterization of the tracts, corresponding average tract property profiles (we focus on FA profiles) are extracted from each individual fiber tract. The average is thereby computed across the individual streamlines and the profile is plotted along the fiber tract.
For the evaluation, we calculated the normative correlation between each fiber tract profile in the registered subjects DTI datasets and the atlas. For this criterion also we expect larger values to represent better accuracy in registration. It is further noteworthy that high degrees of white matter pathology are likely to decrease this evaluation metric, though that does not lessen its comparative merit in the presented work here.
Results
Visualization results
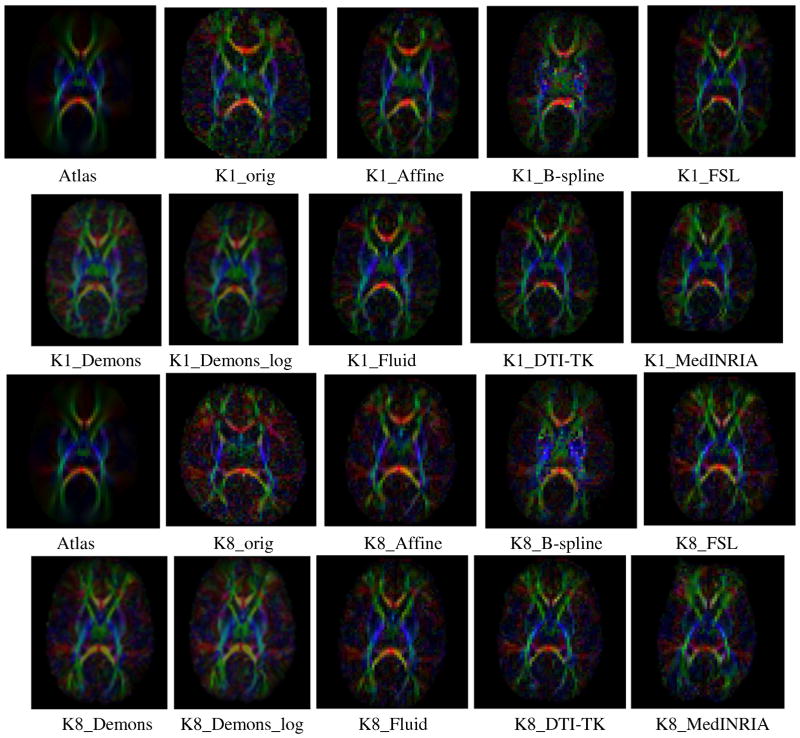
We present detailed results for two individual representative cases, K1 (with protocol 1) and K8 (with protocol 2), as well as the summary results across the whole Krabbe population of 10 subjects. As illustrated in Fig. 1, qualitative inspection of the registration results of K1 and K8 indicate that all deformable registration algorithms show satisfactory results. The linear Affine registration method fails to map the fiber tracts of the subjects into the atlas space, as clearly seen for the internal capsule tracts. Several qualitative differences can be seen between the registration results, like the result from B-spline algorithm captures the local anatomy and orientations poorly when compared to the other methods.
Figure 1.
Color-oriented FA images of the atlas, subjects (K1 and K8) and seven registration results.
Regional matching quality criterion results
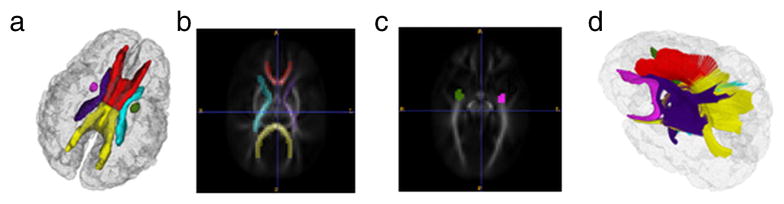
To test the regional matching quality criterion, we manually defined six regions on the atlas labeled 1 to 6 (Fig. 2). The regions defined represent the six tracts of interest – genu, splenium, internal capsules (left and right) and uncinate fasciculis (left and right). Fig. 2(a) shows the 3D visualization of ROIs position inside the brain with Slicer9. The relationship between the ROIs and the atlas FA image in 2D are shown in Fig. 2(b) and (c) using ITK-SNAP10 (Yushkevich et al., 2006). Fig. 2(d) shows the 3D color visualization of the target fiber tracts genu (red), splenium (yellow), right hemisphere internal capsule (purple), left hemisphere internal capsule (blue) and uncinate (green) with Slicer (Catani and Thiebaut de Schotten, 2008; Wakana et al, 2004).
Figure 2.
Regional definition in a) 3D brain, b) and c) on two axial FA slices.In d), 3D visualization of target fiber tracts (red for genu, yellow for splenium, celeste & smalt for left and right internal capsules and peachblow & green for left and right uncinate.)
The average similarity values for each registration method for genu, splenium, left hemisphere internal capsule and left hemisphere uncinate is shown in Table 1. The analysis on the right hemisphere internal capsule and uncinate show similar results to their corresponding left hemisphere tracts and hence their tables are not shown. The values in the tables indicate that the similarity values of subject K1 and subject K8 agree with the visualization results. This illustrates the effectiveness of our regional matching quality criterion as a potential for quality control of DTI registration, as well as a valid evaluation measure that highlights differences across methods.
Table 1.
Average similarity values for various fiber tracts. Results significantly different from the best performance algorithm are marked with * (p<5%) and ** (p<1%).
| Fiber Tracts | Affine | B-spline | FSL | Demon s | Demon s-log | Fluid | DTI-TK | MedINRI A | Best Performance | |
|---|---|---|---|---|---|---|---|---|---|---|
| GENU | MEAN | 0.1177 | 0.1098 | 0.1257 | 0.1247 | 0.1233 | 0.1237 | 0.1272 | 0.124 | DTI-TK |
| STDEV | 0.0055 | 0.0063 | 0.0031 | 0.0028 | 0.0033 | 0.0025 | 0.0032 | 0.0042 | ||
| p-value | 0.0007** | 0.0001** | 0.0174* | 0.0924 | 0.0184 | 0.0101* | 0.0538 | |||
| Rank | 7 | 8 | 2 | 3 | 6 | 5 | 1 | 4 | ||
| SPLENIUM | MEAN | 0.1414 | 0.132 | 0.1506 | 0.1494 | 0.1473 | 0.1475 | 0.1519 | 0.149 | DTI-TK |
| STDEV | 0.0062 | 0.0071 | 0.0029 | 0.0038 | 0.0025 | 0.0025 | 0.0037 | 0.0059 | ||
| p-value | 0.0008** | 0.0001** | 0.3114 | 0.1179 | 0.0043 | 0.0089** | 0.1711 | |||
| Rank | 7 | 8 | 2 | 3 | 6 | 5 | 1 | 4 | ||
| LEFT HEMISPHERE INTERNAL CAPSULE | MEAN | 0.1325 | 0.1501 | 0.1908 | 0.1882 | 0.187 | 0.1843 | 0.1925 | 0.1895 | DTI-TK |
| STDEV | 0.0091 | 0.0166 | 0.0026 | 0.0026 | 0.0045 | 0.0023 | 0.0032 | 0.0018 | ||
| p-value | 0.0001** | 0.0001** | 0.3014 | 0.0243 | 0.0186 | 0.0001** | 0.0295* | |||
| Rank | 8 | 7 | 2 | 4 | 5 | 6 | 1 | 3 | ||
| LEFT HEMISPHERE UNCINATE | MEAN | 0.0746 | 0.0883 | 0.1357 | 0.1181 | 0.1158 | 0.0926 | 0.135 | 0.1317 | FSL |
| STDEV | 0.0219 | 0.0156 | 0.0018 | 0.0215 | 0.0224 | 0.0203 | 0.0039 | 0.0027 | ||
| p-value | <0.0001** | 0.0001** | 0.0475 | 0.0314 | 0.0001** | 0.6117 | 0.0039** | |||
| Rank | 8 | 7 | 1 | 4 | 5 | 6 | 2 | 3 | ||
Results from Table 1 show that DTI-TK gives the best results. This algorithm shows the best performance for the tracts of genu, splenium and both hemispheric internal capsules. For the uncinate fasciculi, the performance is second best to the FSL method. None of these seven registration methods can be said to give optimal results on each ROI for every subject.
We repeated the full evaluation with slightly modified regional definitions (the six regions were independently and manually redefined). The ranking of the methods was preserved in all regions, thus indicating that the computed regional matching criterion is stable and reliable.
Fiber property profile based criterion results
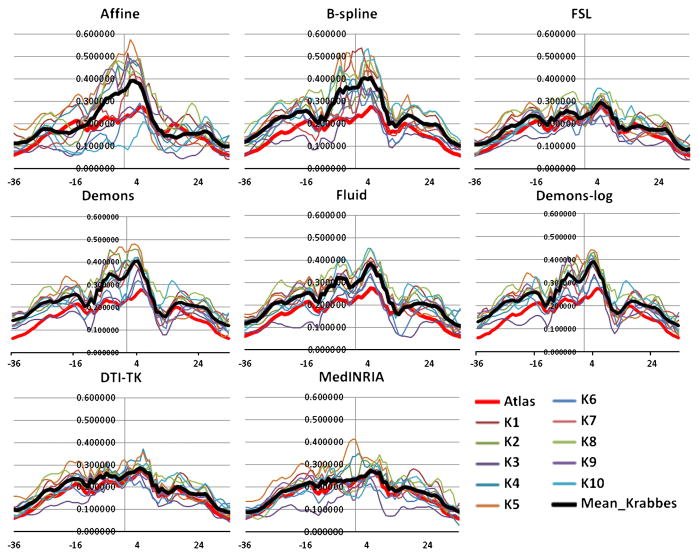
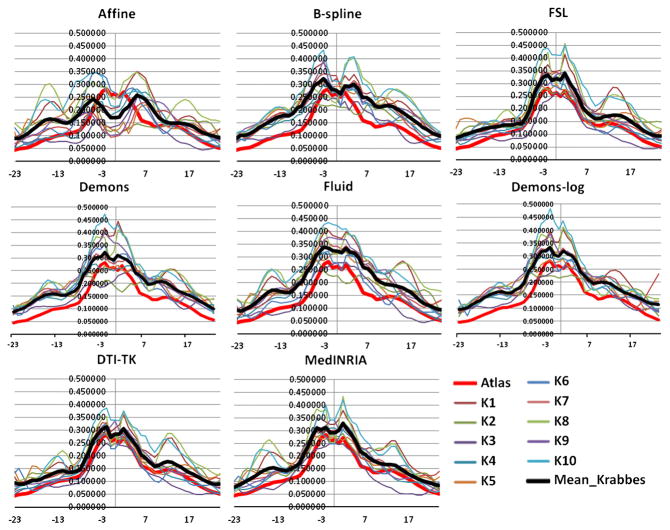
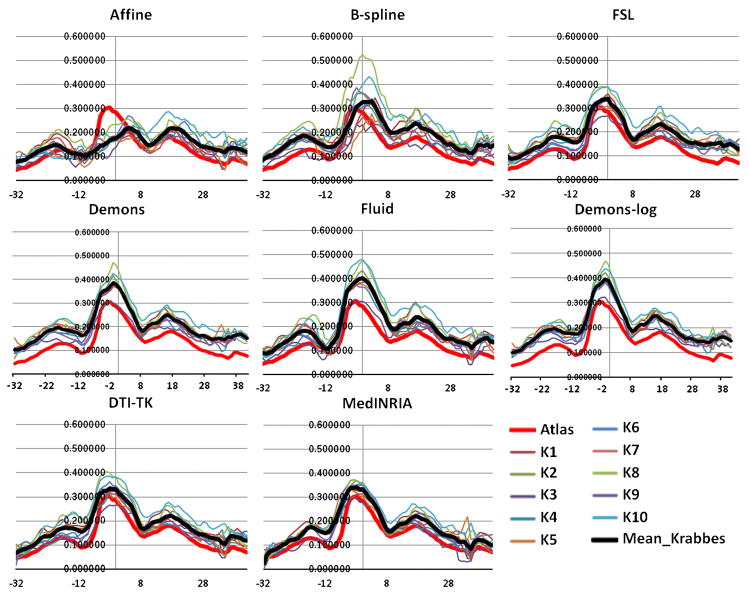
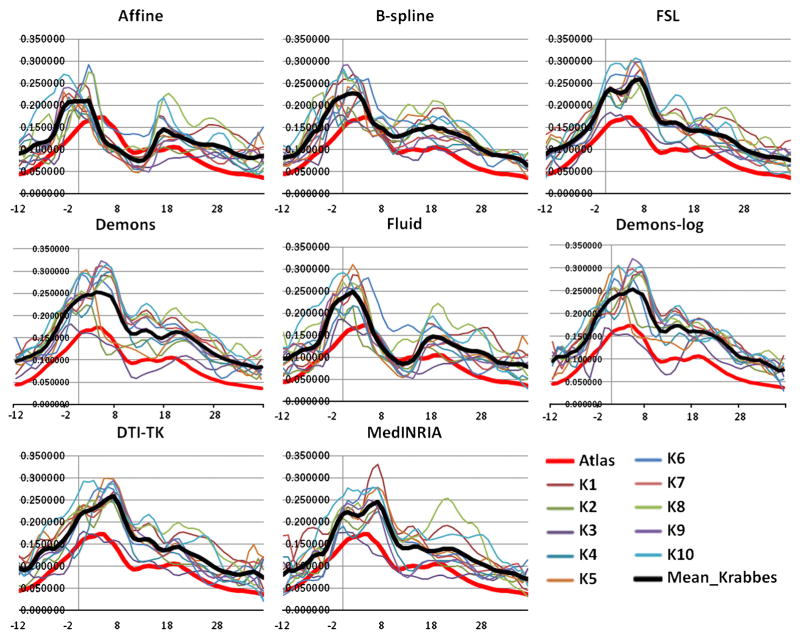
Fiber tractography of the genu, splenium, both hemispheric internal capsules and uncinates is performed on the atlas. Fiber bundles of each subject are then created using the method in Goodlett et al. (2009). The FA profiles along the fiber tracts – genu, splenium, left internal capsule and left uncinate, generated from the seven registration methods are plotted for the atlas and the ten subjects (Figs. 4 to 7).
Figure 4.
Average FA profiles of the SPLENIUM for the atlas and the ten subjects for the eight registration methods. The black profile indicates mean of the Krabbe subjects. X-axis: points along the fiber tracts.
Analysis of the FA profiles gives further information on the performance of the registration methods. Considering all the fiber tracts, the Fluid registration results in slightly higher magnitudes of the subjects’ FA profiles compared to the other methods. The selected tracts are the tracts with the highest FA intensities and hence higher values of FA indicates better mapping of the subject into the atlas and hence better registration. So based on this criteria, Fluid has a slightly better performance. The other aspect that can be interpreted though only visually from the FA profiles is the visual match of the average Krabbe profile with the atlas profile. In that regard, Affine registration, followed by B-spline, clearly shows a poor mapping. FSL and both the tensor based registration methods – DTI-TK and MedINRIA, show a strong similarity of the FA profiles of the subjects to the atlas FA profile, with a slightly better matching for DTI-TK. The mean of the Krabbe subjects (black line) is very similar to the atlas (red line) both in terms of magnitude and shape for these three algorithms. In case of Fluid, Demons and Demons-log the mean of the Krabbe subjects has a very similar shape profile as the atlas but has a different (higher) magnitude. Thus, considering the magnitude of the FA profiles, Fluid shows a higher performance than the other methods, whereas the shape of the FA profiles match visually best for the DTI-TK.
The FA profiles indicate the quasi-Euclidean distance of the tensors to a spherical shape and from the shape and magnitude of the profiles it appears that the tensor based methods are compensating the shape of the tensors (to make them more spherical - isotropic) while trying to map the tensors in to the atlas space. In a certain sense, it appears that these methods are slightly over-fitting the data. Correlation coefficients between the FA profiles in the registered subjects’ dataset and the atlas for all the registration methods is shown in Table 2. No one algorithm shows the best performance for all the tracts. Demons-log shows the best performance for both the internal capsules and the right uncinate fasciculus. DTI-TK and FSL show the best result for the splenium, genu and the left uncinate fasciculus. Hence it is difficult to identify one best algorithm based on the normative tract profile correlation evaluation though summarized over all fiber tracts Demons-log followed by DTI-TK seems to do the best.
Table 2.
Correlation coefficients between FA profile for various fiber tracts in registered subjects and the atlas for the eight registration algorithms. Results significantly different from the best performance algorithm are marked with * (p<5%) and ** (p<1%).
| Fiber Tracts | Affine | B-spline | FSL | Demons | Demon s-log | Fluid | DTI-TK | MedINRI A | Best Performance | |
|---|---|---|---|---|---|---|---|---|---|---|
| GENU | MEAN | 0.5082 | 0.9057 | 0.9506 | 0.9039 | 0.9227 | 0.926 | 0.9487 | 0.9369 | FSL |
| STDEV | 0.2851 | 0.0691 | 0.0325 | 0.0955 | 0.0429 | 0.068 | 0.0315 | 0.0296 | ||
| p-value | 0.0007** | 0.0721 | 0.2017 | 0.1262 | 0.2644 | 0.8362 | 0.2822 | |||
| Rank | 8 | 6 | 1 | 7 | 5 | 4 | 2 | 3 | ||
| SPLENIUM | MEAN | 0.6431 | 0.8594 | 0.8868 | 0.8173 | 0.8386 | 0.8648 | 0.8927 | 0.8368 | DTI-TK |
| STDEV | 0.2884 | 0.0709 | 0.0629 | 0.064 | 0.0559 | 0.0952 | 0.0479 | 0.074 | ||
| p-value | 0.0200* | 0.1042 | 0.7485 | 0.0013 | 0.0114 | 0.2037 | 0.0585 | |||
| Rank | 8 | 4 | 2 | 7 | 5 | 3 | 1 | 6 | ||
| LEFT HEMISPHERE INTERNAL CAPSULE | MEAN | 0.5712 | 0.8445 | 0.9453 | 0.9617 | 0.9693 | 0.9578 | 0.9499 | 0.9318 | Demons-log |
| STDEV | 0.0947 | 0.1456 | 0.0223 | 0.0145 | 0.0104 | 0.0106 | 0.0118 | 0.0272 | ||
| p-value | <0.0001** | 0.0233 | 0.0172 | 0.0546 | 0.0048 | 0.0052 | 0.0015 | |||
| Rank | 8 | 7 | 5 | 2 | 1 | 3 | 4 | 6 | ||
| LEFT HEMISPHERE UNCINATE | MEAN | 0.5568 | 0.8546 | 0.9146 | 0.8923 | 0.8988 | 0.7282 | 0.8995 | 0.8625 | FSL |
| STDEV | 0.133 | 0.051 | 0.0292 | 0.0808 | 0.0993 | 0.0838 | 0.0318 | 0.058 | ||
| p-value | <0.0001** | 0.0018** | 0.7439 | 0.9765 | 0.0001** | 0.195 | 0.0046** | |||
| Rank | 8 | 6 | 1 | 4 | 3 | 7 | 2 | 5 | ||
Based on the correlation coefficients, we used an additional evaluation criterion to determine the number of subjects’ ROIs that the algorithms maps correctly into the atlas. We considered three different correlation values of 0.8, 0.85 and 0.9 as thresholds and correlation co-efficient below the threshold are marked as a failure for mapping the fiber tract into the atlas. Table 3 shows the number of instances the algorithms fail to map the six DTI fiber bundles into the atlas for the ten subjects for a threshold of 0.85. Affine fails for almost all the cases even for the 0.8 threshold. DTI-TK results in minimum number of failures for all the three thresholds and can be considered as the best algorithm based on this criterion. The success of DTI-TK in correctly mapping the six fiber tracts for all the subject cases can be attributed to the fact that the algorithm exploits the whole tensor orientation information for registration compared to the scalar FA values. The Demons-log and the FSL algorithms show the next best performance. This can be attributed to a histogram based intensity normalization step of the subjects to the atlas prior to these two registration methods. The small variation in the intensities of the six selected tracts results in the FA based registration methods mapping certain regions of the subject to the atlas more accurately than the other regions. The tensor based methods use the orientation information and hence have an advantage in mapping fiber tract related information of the subjects to the atlas more accurately.
Table 3.
Number of failures in mapping the subject fiber tracts to the atlas with a correlation value greater than 0.85 for the seven registration algorithms. Best performance: DTI-TK.
| Affine | B-spline | FSL | Demons | Demons- log | Fluid | DTITK | MedINRIA | |
|---|---|---|---|---|---|---|---|---|
| Genu | 9 | 2 | 0 | 2 | 1 | 1 | 0 | 0 |
| Splenium | 9 | 3 | 3 | 7 | 5 | 2 | 2 | 3 |
| Internal Capsule Left | 10 | 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| Internal Capsule Right | 10 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| Uncinate Left | 10 | 5 | 0 | 3 | 2 | 9 | 0 | 2 |
| Uncinate Right | 10 | 7 | 3 | 0 | 0 | 9 | 3 | 2 |
| Total Failed Cases | 58 | 21 | 7 | 12 | 8 | 21 | 5 | 7 |
Discussion
In this paper, we evaluated one linear and seven nonlinear registration methods for use in an atlas based DTI fiber analysis framework on 10 neonates with infantile Krabbe disease. No difference was observed between the two different protocols in terms of their registration accuracy. We used visual evaluation, tensor orientation based criteria, FA profiles based criteria, the correlation of the FA values and the number of failures to evaluate the performance of the registration methods. By visual evaluation, the linear Affine registration method and the B-spline method show a poor matching of the subject to the atlas. The regional matching quality criterion based on the local orientation of the tensors, which is highly relevant to fiber tract analysis, shows that on average, the whole tensor registration using explicit optimization of tensor reorientation – DTI-TK method performed better than the other methods. The criterion based on the correlation values of the subjects’ to the atlas shows that Demons-log, followed by DTI-TK and FSL show a better performance. Considering the number of failure rates in mapping the subjects fiber tracts to the atlas, the DTI-TK algorithm has the lowest failure rate.
From the results obtained based on the various criteria, it appears that all the deformable methods give a satisfactory performance. Depending on the selected criteria, different algorithms show slightly higher performance than the others. Of the above discussed criteria, for DTI fiber tract analysis, the local orientation of the tensors and fiber mapping minimal failure rate are the most crucial. Based on these two criteria, we recommend the DTI-TK registration method based on explicit optimization of tensor reorientation for fiber tract analysis.
As is the case with any evaluation metric, the question can be raised, whether some of these evaluation measures could be used for the purpose of registration itself. The answer of this question with respect to the regional matching criterion, which can be represented in a voxel-wise manner, is currently under investigation in our lab.
Supplementary Material
Figure 3.
Average FA profiles of the GENU for the atlas and the ten subjects for the eight registration methods. The black profile indicates mean of the Krabbe subjects. X-axis: points along the fiber tracts.
Figure 5.
Average FA profiles of the LEFT HEMISPHERIC INTERNAL CAPSULE for the atlas and the ten subjects for the eight registration methods. The black profile indicates mean of the Krabbe subjects. X-axis: points along the fiber tracts.
Figure 6.
Average FA profiles of the LEFT HEMISPHERIC UNCINATE for the atlas and the ten subjects for the eight registration methods. The black profile indicates mean of the Krabbe subjects. X-axis: points along the fiber tracts.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No.60903127); the National Alliance for Medical Image Computing (NAMIC, NIH U54 EB005149); the National Institutes of Health (NIH) Roadmap for Medical Research (U54 EB005149–01); the Autism Centers of Excellence Network at UNC-CH (NIH R01 HD055741), Penn Image Computing & Science Laboratory (PICSL NIBIB NIH R03-EB009321), the Neurodevelopmental Research Center at UNC-CH (NIH P30 HD03110); Ao-Xiang Star Project at Northwestern Polytechnical University, Xi an, Shaanxi, China and the National Institute of Mental Health Conte Center at UNC-CH (MH064065).
We thank Daniel Rueckert and IXICO. The Image Registration Toolkit of Fluid was used under Licence from Ixico Ltd.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander DC, Pierpaoli C, Basser PJ, Gee JC. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans Med Imag. 2001;20(11):1131–1139. doi: 10.1109/42.963816. [DOI] [PubMed] [Google Scholar]
- Andersson JLR, Jenkinson M, Smith S. Non-linear registration, aka Spatial normalization. FMRIB technical report TR07JA2. 2007 from http://www.fmrib.ox.ac.uk/analysis/techrep.
- Arsigny V, Fillard P, Pennec X, Ayache N. Log-euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine. 2006;56(2):411–421. doi: 10.1002/mrm.20965. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophysical Journal. 1994;66 (1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y, Miller M, Winslow RL, Younes L. Large deformation diffeomorphic metric mapping of vector fields. IEEE Trans Med Imag. 2005;24(9):1216–1230. doi: 10.1109/tmi.2005.853923. [DOI] [PubMed] [Google Scholar]
- Catani M, Thiebaut de Schotten M. A diffusion tensor imaging tractography atlas for virtual in vivo dissections. Cortex. 2008;44(8):1105–1132. doi: 10.1016/j.cortex.2008.05.004. [DOI] [PubMed] [Google Scholar]
- Christensen G, Joshi S, Miller M. Deformable templates using large deformation kinematics. IEEE Trans Med Imag. 1997;16:864–877. doi: 10.1109/83.536892. [DOI] [PubMed] [Google Scholar]
- Christensen G, Rabbitt R, Miller M. 3d brain mapping using a deformable neuroanatomy. Phys Med Biol. 1994;39:209–618. doi: 10.1088/0031-9155/39/3/022. [DOI] [PubMed] [Google Scholar]
- Escolar ML, Poe MD, Provenzale JM, Richards KC, Allison J, Wood S, Wenger DA, Pietryga D, Wall D, Champagne M, Morse R, Krivit W, Kurtzberg J. Transplantation of umbilical-cord blood in babies with infantile Krabbe’s disease. N Engl J Med. 2005;352(20):2069–2081. doi: 10.1056/NEJMoa042604. [DOI] [PubMed] [Google Scholar]
- Escolar ML, Poe MD, Smith JK, Gilmore JH, Kurtzberg J, Lin W, Styner M. Diffusion tensor imaging detects abnormalities in the corticospinal tracts of neonates with infantile Krabbe Disease. American Journal of Neuroradiology. 2009;30:1017–1021. doi: 10.3174/ajnr.A1476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gee JC, Alexander DC. Diffusion-tensor image registration. In: Welckert J, Hagen H, editors. Visualization and Image Processing of Tensor Fields. Springer; Berlin: 2005. [Google Scholar]
- Gilmore JH, Zhai G, Lin W, Wilber K, Gerig G. White matter development in newborns assessed with diffusion tensor imaging. International Congress on Schizophrenia Research; 2003. p. 195. [Google Scholar]
- Gilmore JH, Zhai G, Wilber K, Smith JK, Lin W, Gerig G. 3 Tesla magnetic resonance imaging of the brain in newborns. Psychiatry Research: Neuroimaging. 2004;132:81–85. doi: 10.1016/j.pscychresns.2004.04.004. [DOI] [PubMed] [Google Scholar]
- Goodlett CB, Davis B, Jean R, Gilmore J, Gerig G. Improved correspondence for DTI population studies via unbiased atlas building. MICCAI; 2006. pp. 260–267. [DOI] [PubMed] [Google Scholar]
- Goodlett CB, Fletcher PT, Gilmore JH, Gerig G. Group analysis of DTI fiber tract statistics with application to neurodevelopment. NeuroImage. 2009;45:133–142. doi: 10.1016/j.neuroimage.2008.10.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo AC, Petrella JR, Kurtzberg J, Provenzale JM. Evaluation of white matter anisotropy in Krabbe disease with diffusion tensor MR imaging: initial experience. Radiology. 2001;218 (3):809–815. doi: 10.1148/radiology.218.3.r01mr14809. [DOI] [PubMed] [Google Scholar]
- Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. NeuroImage. 2004;23 (Supplement1):151–160. doi: 10.1016/j.neuroimage.2004.07.068. [DOI] [PubMed] [Google Scholar]
- Knickmeyer RC, Gouttard S, Kang C, Evans D, Wilber K, Smith JK, Hamer R, Lin W, Gerig G, Gilmore JH. A structural MRI study of human brain development from birth to 2 years. J Neurosci. 2008;28(47):12176–12182. doi: 10.1523/JNEUROSCI.3479-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z, Goodlett C, Gerig G, Styner M. Evaluation of DTI property maps as basis of DTI atlas building. SPIE - The International Society for Optical Engineering; 2010. pp. 762325–762327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S, Crain BJ, Chacko VP, Van Zijl PCM. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. American Neurological Association. 1999;45:265–69. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- Provenzale JM, Escolar M, Kurtzberg J. Quantitative analysis of diffusion tensor imaging data in serial assessment of Krabbe disease. Ann N Y Acad Sci. 2005 Dec;1064:220–9. doi: 10.1196/annals.1340.040. [DOI] [PubMed] [Google Scholar]
- Rueckert D, Sonoda LI, Hayes C, Hill DLG, Leach MO, Hawkes DJ. Nonrigid registration using Free-Form Deformations: Application to breast MR images. IEEE Transactions on Medical Imaging. 1999;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- Salvador R, Peña A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp. 2005;24(2):144–155. doi: 10.1002/hbm.20076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnabel JA, Rueckert D, Quist M, Blackall JM, Castellano-Smith AD, Hartkens T, Penney GP, Hall WA, Liu H, Truwit CL, Gerritsen FA, Hill DLG, Hawkes DJ. A generic framework for non-rigid registration based on non-uniform multi-level free-form deformations. MICCAI; 2001. pp. 573–581. [Google Scholar]
- Shen D, Davatzikos C. HAMMER: Heirarchical attribute matching mechanism for elastic registration. IEEE TMI. 2002;21(11):1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Studholme C, Hill DLG, Hawkes DJ. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition. 1999 Jan;32(1):71–86. [Google Scholar]
- Studholme C. PhD Thesis. University of London; 1997. Measures of 3D Medical Image Alignment. [Google Scholar]
- Thirion J-P. Image matching as a diffusion process: an analogy with Maxwell’s demons. Med Image Anal. 1998;2(3):243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: efficient non-parametric image registration. NeuroImage. 2009;45(1 Supp 1):S61–S72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Malis E, Perchant A, Ayache N. Insight into efficient image registration techniques and the demons algorithm. Proc. Information Processing in Medical Imaging (IPMI’07), volume 4584 of Lecture Notes in Computer Science; Kerkrade, The Netherlands. 2007. pp. 495–506. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Non-parameteric Diffeomorphic Image Registration with the Demons Algorithm. MICCAI; 2007. pp. 319–326. [DOI] [PubMed] [Google Scholar]
- Vercauteren T, Pennec X, Perchant A, Ayache N. Symmetric log-domain diffeomorphic registration: A demons-based approach. Proceedings of the 11th International Conference on MICCAI 08, volume 5241 of LNCS; September 2008; 2008. pp. 754–761. [DOI] [PubMed] [Google Scholar]
- Wakana S, Jiang H, Nagae-Poetscher M, van Zijl PCM, Mori S. A fiber-tract based atlas of Human white matter anatomy. Radiology. 2004;230:77–87. doi: 10.1148/radiol.2301021640. [DOI] [PubMed] [Google Scholar]
- Wenger DA, Suzuki K, Suzuki Y. Galactosylceramide lipidosis: globoid-cell leukodystrophy (Krabbe disease) In: Scriver CR, Beaudet AL, Sly WS, et al., editors. The Metabolic and Molecular Bases of Inherited Disease. 8. New York: McGraw-Hill; 2001. pp. 3669–3694. [Google Scholar]
- Xu D, Mori S, Solaiyappan M, Van Zijl PCM, Davatzikos C. A framework for callosal fiber distribution analysis. Neuroimage. 2002;17:1131–1143. doi: 10.1006/nimg.2002.1285. [DOI] [PubMed] [Google Scholar]
- Yap P, Wu G, Zhu H, Lin W, Shen D. Fast Tensor Image Morphing for Elastic Registration. MICCAI; 2009. pp. 721–729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo BTT, Vercauteren T, Fillard P, Pennec X, Golland P, Ayache N, Clatz O. DTI registration with exact finite-strain differential. Proceedings of the IEEE International Symposium on Biomedical Imaging: From Nano to Macro (ISBI’08); Paris, France. 2008. [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3D active contour segmentation of anatomical structures: Significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Zhang H, Avants BB, Yushkevich PA, Woo JH, Wang S, McCluskey LF, Elman LB, Melhem ER, Gee JC. High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences in amyotrophic lateral sclerosis. IEEE Transactions on Medical Imaging - Special Issue on Computational Diffusion MRI. 2007;26(11):1585–1597. doi: 10.1109/TMI.2007.906784. [DOI] [PubMed] [Google Scholar]
- Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Medical Image Analysis. 2006;10(5):764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.