The Structure of Working Memory Abilities across the Adult Life Span

Abstract

The present study addresses three questions regarding age differences in working memory: (1) whether performance on complex span tasks decreases as a function of age at a faster rate than performance on simple span tasks; (2) whether spatial working memory decreases at a faster rate than verbal working memory; and (3) whether the structure of working memory abilities is different for different age groups. Adults, ages 20–89 (n=388), performed three simple and three complex verbal span tasks and three simple and three complex spatial memory tasks. Performance on the spatial tasks decreased at faster rates as a function of age than performance on the verbal tasks, but within each domain, performance on complex and simple span tasks decreased at the same rates. Confirmatory factor analyses revealed that domain-differentiated models yielded better fits than models involving domain-general constructs, providing further evidence of the need to distinguish verbal and spatial working memory abilities. Regardless of which domain-differentiated model was examined, and despite the faster rates of decrease in the spatial domain, age group comparisons revealed that the factor structure of working memory abilities was highly similar in younger and older adults and showed no evidence of age-related dedifferentiation.

The present study examines the structure of working memory abilities from the standpoint of both age and individual differences. Our approach builds on the distinction between simple and complex span tasks proposed by Engle and his colleagues (Engle, Tuholski, Laughlin, & Conway, 1999). According to Engle et al.’s original interpretation of this distinction, simple span tasks (e.g., digit span) primarily measure storage whereas complex span tasks (e.g., operation span, reading span) measure executive functions involved in coordinating storage and processing. More recently, however, Unsworth and Engle (2006, 2007a, 2007b), suggested that simple and complex span tasks also differ in the degree to which they rely on primary and secondary memory. Although some investigators reserve the term working memory for the functions and abilities tapped by complex span tasks, we will use the term here to refer to the functions and abilities tapped by both kinds of tasks because, like Unsworth and Engle (2006; 2207a, 2007b), we believe that both simple and complex span tasks rely primarily on the same components of the working memory system, albeit it to different degrees. The major goal of the present effort is to compare different ways of characterizing the abilities associated with these components, in order to better understand the implications of these different characterizations for cognitive aging.

Adult age differences in working memory

In recent years, Baddeley’s model of the working memory system (Baddeley & Hitch, 1974; Baddeley, 1986, 2000) has been studied extensively, and there is now a general consensus regarding the existence of the model’s domain-specific (i.e., verbal and visuospatial) storage components. Baddeley also hypothesized the existence of a central executive component, but this part of his model remains controversial (Miyake & Shah, 1999). Research using simple and complex memory span tasks to study age differences in working memory has provided mixed support for Baddeley’s (1986) model.

For example, Myerson, Hale, Rhee, and Jenkins (1999) had young and older adults perform simple verbal and visuospatial storage tasks as well as two types of complex span tasks, one type involving secondary processing tasks from the same domain as the storage task (e.g., a verbal processing task combined with a verbal storage task), and the other involving secondary tasks from the opposite domain (e.g., a verbal processing task combined with a spatial storage task). When participants had to coordinate storage and processing, their memory spans were significantly lower than when there was no secondary task, but only if the processing task was from the same domain (verbal or spatial) as the memory items. When the processing task was not from the same domain, simple and complex memory spans were approximately equal. Importantly, this pattern of strictly domain-specific interference was observed in both older and younger adults. Moreover, the size of the age difference in complex memory spans was not larger than the age difference in simple spans (see also Jenkins, Myerson, Hale, & Joerding, 2000; Rose, Myerson, Sommers, & Hale, 2009).

These findings seem hard to reconcile with the view that dual-task coordination on complex span tasks depends on executive resources in which older adults are supposedly deficient (e.g., Dempster, 1992; West, 1996). In contrast, a recent meta-analysis by Bopp and Verhaeghen (2005) did find larger age-related differences on complex span tasks compared to simple span tasks, a result consistent with the executive deficit hypothesis. The meta-analysis also showed, however, that the size of the age difference on simple span tasks depends on the type of items to be remembered, with the average age difference in letter spans, for example, being nearly twice the average age difference in digit spans. It follows that in order to compare age differences in simple and complex spans, one should hold the type of memory items constant. Unfortunately, very few studies have compared young and older adults’ performance on simple and complex span tasks under such conditions, and in those that have, the results have been mixed. Some researchers report finding larger age differences on complex span tasks (e.g., Wingfield, Stine, Lahar, & Aberdeen, 1988), whereas others (e.g., Babcock & Salthouse, 1990; Jenkins et al., 2000; Myerson et al., 1999) report finding equivalent age differences on the two types of tasks

The most pronounced effects of the type of memory items are observed when verbal memory spans are compared with spatial memory spans. In both the Myerson et al. (1999) and Jenkins et al. (2000) studies, the difference between young and older adults’ verbal spans was much smaller than the difference between their spatial spans. Evidence for the reliability of this finding is provided by a reanalysis of the WAIS III/WMS III standardization data, which showed that spatial span decreases as a function of age at approximately twice the rate of digit span (Myerson, Emery, White, & Hale, 2003). This difference in the effect of age on verbal and spatial spans is of special interest for two reasons; first, because it parallels the well-established finding that the rate of increase in spatial response times as a function of age is much greater than the rate of increase in verbal response times (e.g., Lawrence, Myerson, & Hale, 1998), and second, because of the strong link between processing speed and working memory (Salthouse, 1996).

The structure of working memory abilities

Comparing rates of change in performance with age or the sizes of age differences on different tasks represents one approach to understanding cognitive aging. Another approach involves comparing the patterns of individual differences in different age groups. This approach, with its focus on the structure of cognitive abilities, provides important information that complements that obtained by examining age differences per se. For example, the fact that spatial spans decrease as a function of age at a faster rate than verbal spans raises the possibility that age-related changes in verbal and spatial spans are independent, in which case the correlation between them would decrease as a function of age. In contrast, stability in the correlation between spatial and verbal spans would suggest that even though individuals’ verbal performance may decrease less than their spatial performance, those who show greater declines than their peers in the spatial domain also show greater declines than their peers in the verbal domain. The differential rates of decrease as a function of age in the two domains also do not preclude the third possibility, which is that spatial and verbal spans actually become more correlated with age, consistent with the dedifferentiation hypothesis (e.g., Balinsky, 1941; Baltes, Cornelius, Spiro, Nesselroade, & Willis, 1990).

Confirmatory factory analysis and structural equation modeling are the techniques of choice for addressing the issue of the structure of abilities, but for the most part, studies using this approach have focused on working memory in young adults. Using these methods, Engle et al. (1999) tested a model that divided young adults’ working memory into a verbal storage component and an executive component for the control of attention. However, their finding of separate executive and (verbal) storage components may not generalize to spatial working memory. Miyake, Friedman, Rettinger, Shah, and Hegarty (2001) reported that in the spatial domain, young adults’ simple and complex memory spans both loaded on a single, unitary construct. Moreover, simple and complex spatial spans were correlated with an independently defined executive function construct to the same degree (see also Oberauer, 2005).

Several recent studies of the structure of young adults’ working memory abilities have examined both verbal and visuospatial working memory simultaneously. Oberauer, Süß, Schulze, Wilhelm, and Wittmann (2000) used a battery of tasks that varied in the demands placed on executive functions and the nature of the memory items (verbal, numerical, and spatial). They reported that verbal and numerical tasks both loaded on a single factor regardless of whether they principally involved storage or whether they placed additional demands on executive functions; spatial tasks loaded on a second factor, and tasks in which performance was measured as response time (rather than accuracy) loaded on a third factor.

In contrast, Kane et al. (2004) reported support for a model that included two domain-specific storage constructs, one verbal and one spatial, as well as a domain-general construct that they hypothesized reflected the ability to resist interference, consistent with the hypothesis of a central executive. It should be noted, however, that when Colom, Abad, Rebollo, and Shih (2005) reanalyzed the Kane et al. data, they found that the correlation between a domain-general executive construct and a domain-general storage construct was .99, which led them to question the distinction between these two constructs, especially because both were correlated with fluid ability to the same degree (see also Ackerman, Beier, & Boyle, 2005; Colom, Shih, Flores-Mendoza, & Quiroga, 2006).

Thus, studies using an individual differences approach to examine the structure of young adults’ working memory abilities have obtained inconsistent results with respect to whether working memory relies on a central executive (i.e., domain-general executive processes) in the same manner in both the verbal and the visuospatial domains. The existence of domain-specific storage components and abilities is better established, although numerical items appear to be handled by the verbal component. The reason for the inconsistent findings regarding domain-general executive processes remains unclear, although the use of different tasks in different studies likely plays a role. The fact that working memory has been measured in different ways in different studies may also be relevant (Oberauer et al., 2000; Unsworth & Engle, 2007b).

We know of only one study, Park et al. (2002), that has examined possible age-related differences in the structure of working memory abilities, albeit as part of a larger effort to determine whether age-related decreases in processing speed and working memory explain the decreases in long-term memory. Within this context, Park et al. compared the structure of working memory abilities in younger (ages 20–49) and older (60–89) adults and concluded that the structure remains stable, even while the abilities themselves decline with age. The measurement model that best described their data included a verbal executive construct and a spatial executive construct, rather than a single, domain-general executive construct like that postulated by Baddeley (1986). Because this kind of domain-differentiated structure has not been observed in studies with young adults, the claim that it remains stable with age is in need of further investigation.

The current study

The effect of age on working memory abilities is approached in two different, but complementary ways in the present study. One approach involves comparing the rates of age-related decrease in performance of four different types of tasks: simple span and complex span tasks using memory items from the verbal and spatial domains. The other approach uses confirmatory factor analysis, controlling for age, to identify the best-fitting models of working memory abilities for the whole sample, and then tests whether or not the relations among the identified working memory abilities differ in younger and older adults. In addition to simple one- and two-factor models, we consider three- and four-factor models based on those proposed by Alloway, Gathercole, and Pickering (2006), Miyake et al. (2001), Kane et al. (2004), and Park et al. (2002), as well as extensions of models proposed by Conway, Cowan, Bunting, Therriaulta, and Minkoff (2002) and Unsworth and Engle (2007a; 2007b), modified to accommodate distinct spatial working memory constructs.

The present study was designed to address three important questions regarding the effect of age on working memory abilities. First, is there evidence that performance on complex span tasks decreases at a faster rate than performance on corresponding simple span tasks in both the verbal and spatial domains, as predicted by the hypothesis of an age-related deficit in executive function? Second, is there evidence that performance on spatial span tasks decreases at faster rates than performance on verbal tasks, as might be expected based on the greater degree of age-related slowing observed in the spatial domain? Third and finally, what do confirmatory factor analyses reveal with respect to the structure of working memory abilities, and does the set of component abilities tapped by working memory tasks or the relations among these abilities change as a function of age?

Method

Participants

The sample consisted of 388 adults, ranging in age from 20 to 89 years (M = 53.6 years, SD = 20.6), all of whom were screened using the Telephone Interview for Cognitive Status (Brandt, Spencer, & Folstein, 1988), and who were part of a larger, ongoing study of the effects of age on listening comprehension. In addition to our working memory battery and a number of other tests, participants were administered the WAIS III Vocabulary subtest. The range of ability among participants was considerable, as evidenced by the fact that their scaled scores on the WAIS-III Vocabulary subtest (Psychological Corporation, 1997) ranged from 5 to 18 (M = 12.5, SD = 2.6). Participant characteristics are provided in Table 1, for which the sample was divided into 5 age groups consisting of approximately equal numbers of participants. One-way ANOVAs revealed that although the groups did not differ in terms of level of education, F (4, 383) = 1.86, p = .117, they did differ in performance on the Vocabulary subtest, F (4, 383) = 5.04, p = .001. Follow-up t-tests revealed that using a Bonferroni family-wise correction, the vocabulary scores of Group 2, which on average had the lowest scores of the 5 groups, differed significantly from those of Group 1, p < .001, but none of the other differences among the groups were significant.

Table 1.

Characteristics of the Five Age Groups Depicted in Figure 4.

Group	Age Range	N	Age	Education	Vocabulary
1	20–31	75	24.9 (3.8)	15.7 (1.7)	13.4 (2.6)
2	32–46	77	38.1 (4.2)	15.7 (2.0)	11.6 (2.6)
3	47–61	79	53.6 (4.4)	15.5 (2.2)	12.3 (2.6)
4	62–75	80	68.5 (3.8)	15.4 (2.7)	12.3 (2.4)
5	76–89	77	81.4 (3.4)	14.9 (2.5)	12.8 (2.5)

Note. Age = Mean age in years; Education = Mean number of grades completed; Vocabulary = Mean of WAIS-III scaled scores based on age norms; Standard Deviations provided in parentheses for Age, Education and Vocabulary.

Apparatus

Stimuli were presented on a 17-in. touch screen LCD monitor that was also used to record manual responses; a digital audio recorder was used to record vocal responses.

Tasks

There were six pairs of simple and complex span tasks: three verbal pairs and three visuospatial pairs. The type of memory item (e.g., digits) was the same for both members of a pair, but differed across pairs. The matching on content within pairs of tasks was intended to facilitate comparisons of the rate of decline on simple and complex span tasks using regression analyses, whereas the diversity of content within each domain was intended to facilitate extraction of shared variance using confirmatory factor analyses.

On all tasks, a green plus sign appeared in the center of the screen prior to each series of memory items; touching the plus sign started the series. For each task, two trials were presented at each series length, and at the end of each trial, a recall cue (a red rectangle) prompted participants to recall the memory items. On all verbal span tasks, participants named each memory item aloud as it appeared, and then recalled the items aloud at the end of the series. On the complex verbal span tasks, they repeated (or counted) the secondary task stimuli aloud, and then reported their secondary task decisions by pressing one of two labeled keys on the computer keyboard. On all spatial span tasks, participants recalled memory items by touching their locations on the monitor. On the complex spatial span tasks, participants reported their secondary task decisions aloud. Importantly, more than 95% of the secondary decisions for all participants were completed within the allowed time frame.

Verbal Domain

Three simple verbal span tasks were administered: Digit Span, Letter Span, and Word Span (see the left-hand panels of Figure 1). Each item appeared for 1500 ms, followed by a blank screen for 500 ms. Series lengths were 2–11 items on the Digit and Letter Span tasks and 2–10 items on the Word Span task.

Figure 1.

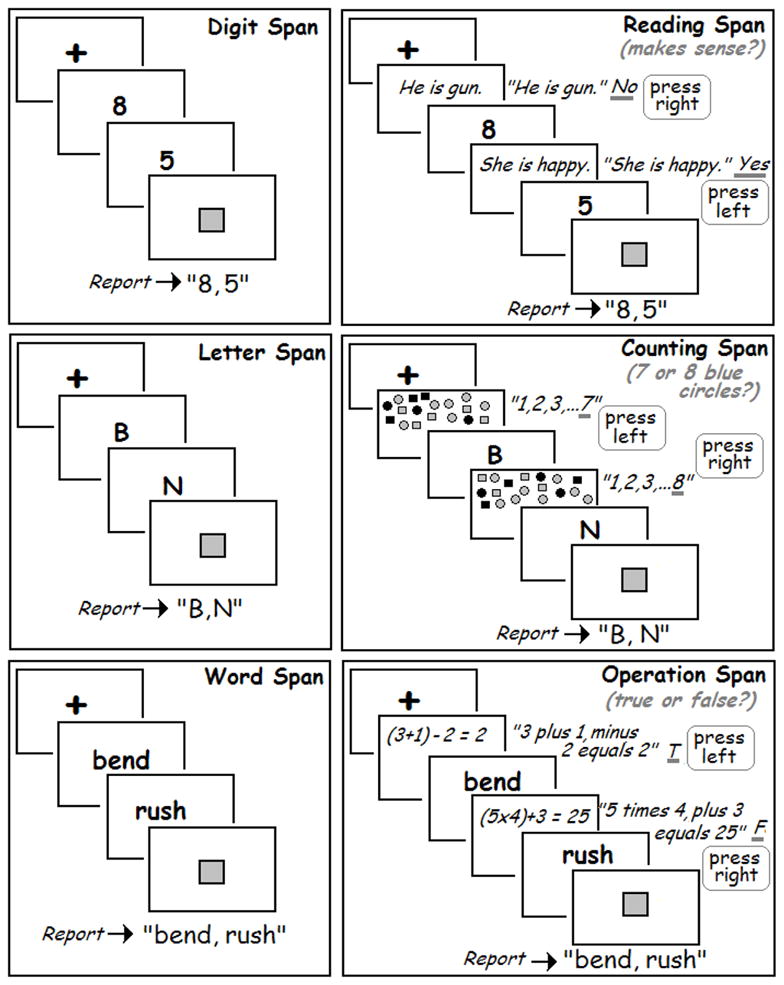
Schematic representations of the six verbal span tasks. The three left panels show the simple working memory tasks requiring storage of digits, letters, and words. The three right panels show the corresponding complex working memory tasks requiring storage of digits, letters, and words, but also require processing irrelevant verbal information interleaved between the presentations of each primary memory item. The actual sentences in the Reading Span task were 7 to 10 words; simplified versions are shown here for purposes of illustration. Also note that the participant stated each memory item aloud as it appeared on the screen in both the simple and complex versions of the task.

Three complex verbal span tasks (adapted from Conway et al., 2005) were also administered: Reading Span, Counting Span, and Operation Span (see the right-hand panels of Figure 1). Each complex span task consisted of one of the three simple span tasks plus a secondary processing task. Stimuli for the secondary tasks were displayed until the participant made a decision, and 250 ms later a memory item was presented. The duration of the items was the same as on the simple span tasks. For Reading Span, Counting Span, and Operation Span, the memory items were digits, letters, and words, respectively.

For the Reading Span task, each memory item was preceded by presentation of a single sentence, and participants indicated whether or not the sentence made sense. For the Counting Span task, each memory item was preceded by an array of colored shapes, and participants indicated whether the array contained 7 or 8 blue circles. For the Operation Span task, each memory item was preceded by presentation of a simple arithmetic problem and a possible solution, and participants indicated whether the solution was correct or incorrect. For all three tasks, series length was 2–7 items.

Spatial Domain

Three simple spatial span tasks were administered: Line Span, Grid Span, and Dot Span (see the left-hand panels of Figure 2). In each case, participants had to remember the locations of a series of stimuli that were presented sequentially in the context of a visuospatial scaffold that remained on the screen throughout the series. Location stimuli appeared for 1500 ms, followed by a blank, unfilled scaffold for 500 ms. For the Line Span, Grid Span, and Dot Span tasks, these scaffolds were a 2 × 3 grid with diagonal lines dividing each cell, a 4 × 5 grid, and a cloud of circles, respectively.

Figure 2.

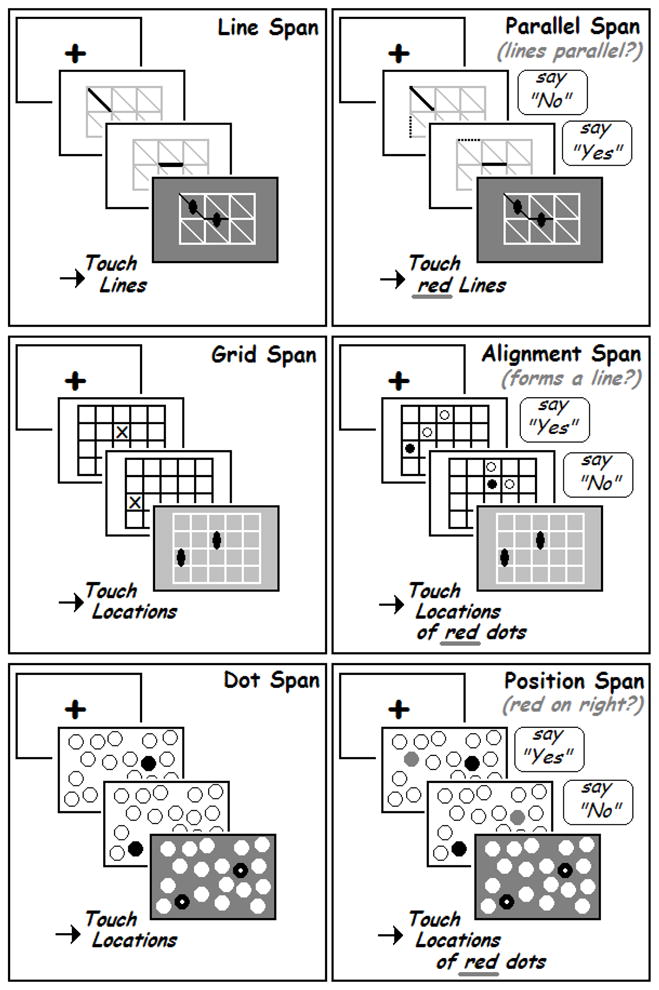
Schematic representations of the six spatial span tasks. The three left panels show the simple working memory tasks requiring storage of the locations of lines, grid positions, and dot positions. The three right panels show the corresponding complex working memory tasks requiring storage of locations of lines, grid positions, and dot positions, but also require processing irrelevant visuospatial information presented simultaneously with the presentations of each primary memory item.

For the Line Span task, lines in the scaffold turned red one at a time, with each successive line beginning at the end of preceding line; at the end of each series, participants had to recall which lines had turned red. For the Grid Span task, participants had to remember the locations of Xs that appeared in the grid. For the Dot Span task, participants had to remember the locations of the circles that turned red. Series lengths were 3–11 items for Line Span and 2–11 items for Grid and Dot Span. Because Line Span was the easiest simple spatial span task, and 2-item series were not presented, participants automatically were given credit for correct performance on this series length.

Three spatial complex span tasks were also administered: Parallel Span, Alignment Span, and Position Span (see the right-hand panels of Figure 2). Each complex span task consisted of one of the three simple span tasks plus a secondary processing task. For Parallel Span, Alignment Span, and Position Span, the location stimuli were red lines, red circles, and red circles, respectively.

For the Parallel Span task, each red line was accompanied by a blue line, and participants indicated whether or not the two lines were parallel. For the Alignment Span task, each red circle was accompanied by two white circles, and participants indicated whether or not the three circles formed a line (horizontal, vertical, or diagonal). For the Position Span task, each red circle was accompanied by a blue circle, and participants indicated whether or not the red circle was to the right of the blue circle. To allow time for making these decisions, the amount of time per presentation was adjusted upwards by 250 ms per secondary task stimulus. Thus, for Alignment Span, memory items remained on the screen for 2000 ms, and for Parallel Span and Position Span, they remained on for 1750 ms. For all three tasks, series length was 2–8 items.

General Procedure

The order of administration of the memory span tasks was Word Span, Letter Span, Operation Span, Digit Span, Reading Span, and Counting Span on the first day of testing, and Grid Span, Alignment Span, Line Span, Dot Span, Parallel Span, and Position Span on the second day. On both days, reaction time tasks were interspersed among the memory span tasks. Within each memory span task, series (i.e., trials) of different lengths were presented according to a pseudo-random sequence, subject to the constraint that all lengths were presented once before any length was repeated; all participants experienced the various series lengths in the same pseudo-random order. Complete data from all 12 tasks were available for all of the participants.

Scoring and analysis

For each span task, we used a proportion correct scoring (PCS) method in which participants received credit for whatever proportion of each series (i.e., trial) was correct, and the score for a particular task was the mean proportion correct, averaged across series (see the Appendix for further details and examples of this method). Although scores obtained using the absolute and proportional scoring systems were highly correlated (rs ranged between .79 and .89), Kane et al. (2004) reported PCS has better psychometric properties, and Unsworth and Engle (2007b) have argued it provides a better measure of secondary memory.

Using the PCS method, split-half reliabilities on the 12 memory span tasks were all very high (median = .80, range = .78 to .86), and scores were approximately normally distributed, with all skewness values less than 1.0 (median = −0.40, range = −0.90 to 0.03), and kurtosis values less than 2.0 (median = 0.34, range = −0.37 to 1.57). Nevertheless, significant multivariate non-normality was observed. Mardia’s normalized kurtosis was 18.87 for the raw data and 19.14 after controlling for age, which exceeded one common recommended threshold (e.g., 3.0; Bentler & Wu, 2002). Therefore, all confirmatory factor analyses were conducted using robust maximum likelihood estimation (i.e., Satorra-Bentler scaling, e.g., Satorra & Bentler, 1994, 2001) after partialling out the effects of age.

Schematic representations of the models we fit are provided in Figure 3. For each model, we report a variety of goodness of fit indices. The recommended number, type, and cut-off values for fit indices has long been a subject of debate (e.g., Bentler, 2007; Hu & Bentler, 1999; Jackson, Gillaspy, & Purc-Stephenson, 2009; McDonald & Ho, 2002), but the following are a fair representation: Measures of absolute fit (chi-square), parsimony corrected fit (Root Mean Square Error of Approximation or RMSEA), and comparative fit (Comparative Fit Index or CFI). We also report the Standardized Root Mean Residual (SRMR), which can be viewed as the average deviation between the correlations in the input matrix and the correlations implied by the model. In good fitting models, chi-square is not significant, the RMSEA is < .05, and the CFI is > .95. We also provide the 90% confidence interval for RMSEA and the probability that RMSEA is less than .05. Finally, we report the Akaike Information Criterion (AIC) values for the different models. Comparisons of AIC values are used in model selection to find the model that can best explain the data using the least number of free parameters (Akaike, 1973, 1987).

Figure 3.

Schematic representations of the one-factor, two-factor, three-factor and four-factor models used to examine the structure of working memory. Arrows represent the correlations to be estimated between constructs. Note that the following abbreviations are used: VS1, VS2, and VS3 denote three Verbal Simple Span tasks; VC1, VC2, and VC3 denote three Verbal Complex Span tasks; SC1, SC2, and SC3 denote three Spatial Complex Span tasks; and, finally, SS1, SS2, and SS3 denote three Spatial Simple Span tasks. In addition, with the exception of Model 2a, these 12 tasks (i.e., the manifest variables) are depicted in the order given here. See text for additional details concerning the constructs (i.e., the latent variables).

For models whose fits were acceptable, we also conducted more localized assessments of model adequacy (Brown, 2006) by examining the standardized residuals. These should be normally distributed, with few values exceeding 2.56 in absolute value, and we report the largest absolute standardized residual to give a sense of the localized fit. Because the same type of memory item (e.g., digits) was used in each of the six pairs of simple and complex span tasks (e.g., digit span and reading span), we specified correlated errors for each pair of tasks. The scale of the latent variables was set by fixing one manifest variable to have a loading of 1.00 for each latent variable: Model 1 (Digit), Model 2a (Digit, Reading), Model 2b (Digit, Parallel), Model 3a (Digit, Reading, Line), Model 3b (Digit, Reading, Line), Model 3c (Digit, Reading, Parallel), and Models 4a, 4b, and 4c (Digit, Reading, Parallel, Line). Confirmatory factor analyses were carried out using LISREL Version 8.71 (Jöreskog & Sörbom, 2004).

Results

As expected, the level of performance (measured as the number of series correctly reported) on each complex span task was lower than on its content-matched, simple span counterpart (e.g., Digit Span and Reading Span), and planned contrasts verified that the differences between simple and complex span performance were all significant; all ts > 15.0, all ps < .001 (see Table 2). Also as expected, the correlations between age and performance on the six spatial tasks, which ranged from −.47 to −.60, all were stronger than those between age and performance on the six verbal tasks, which ranged from −.20 to −.31 (see Table 3).

Table 2.

Mean Number of Series Correct (with Standard Deviations in Parentheses) for Simple and Complex Span Tasks for both the Verbal and Spatial Domains.

Simple Span Tasks		Complex Span Tasks
Verbal Domain
Digit Span	9.69 (2.32)	Reading Span	5.08 (2.22)
Letter Span	7.45 (1.62)	Counting Span	5.49 (2.17)
Word Span	5.61 (1.81)	Operation Span	3.70 (1.59)
Spatial Domain
Line Span	8.85 (3.07)	Parallel Span	6.17 (2.94)
Grid Span	7.13 (2.65)	Alignment Span	5.57 (2.34)
Dot Span	5.91 (2.26)	Position Span	4.17 (2.12)

Table 3.

Correlations between Age and each Span Task and Correlations among all Span Tasks with and without Age Controlled.

Tasks	Age	SD	Verbal Simple			Verbal Complex			Spatial Simple			Spatial Complex
			Digit	Letter	Word	Read	Count	Operate	Line	Grid	Dot	Parallel	Align	Position
Digit	−.198	.083		.790	.688	.588	.548	.576	.342	.311	.345	.356	.365	.380
Letter	−.273	.082	.799		.732	.573	.584	.601	.389	.286	.341	.397	.377	.421
Word	−.293	.099	.703	.753		.477	.495	.631	.335	.275	.320	.331	.343	.373
Read	−.314	.139	.610	.609	.525		.695	.654	.395	.328	.385	.471	.398	.459
Count	−.246	.143	.569	.611	.531	.717		.636	.355	.326	.371	.452	.443	.481
Operate	−.308	.131	.598	.634	.664	.688	.662		.339	.275	.311	.394	.400	.437
Line	−.595	.081	.387	.463	.432	.488	.423	.442		.593	.656	.691	.576	.564
Grid	−.572	.085	.363	.381	.383	.435	.400	.391	.731		.681	.595	.643	.544
Dot	−.542	.083	.392	.423	.416	.478	.436	.416	.765	.779		.620	.617	.604
Parallel	−.494	.130	.401	.467	.420	.544	.503	.478	.777	.707	.721		.644	.679
Align	−.514	.099	.409	.451	.432	.486	.495	.485	.703	.746	.723	.734		.661
Position	−.468	.120	.422	.486	.452	.533	.527	.511	.679	.662	.702	.753	.742

Note: Correlations above the diagonal are partial correlations with the effect of age controlled. Correlations below the diagonal are based on the raw data and thus include the variance associated with age in addition to all other individual differences. SD = Standard Deviation of the Age Residuals, Read, Count, Operate and Align = Reading, Counting, Operation, and Alignment.

Analyses comparing rates of age-related decrease in memory span

Recall that our first question was whether performance on complex span tasks decreases at a faster rate as a function of age than performance on simple span tasks. To answer this question, we first converted the scores for each task (calculated using the PCS method described above) to z-scores, and then compared the regression slopes for each pair of corresponding simple and complex tasks (i.e., those that used the same type of memory items). The four panels of Figure 4 show the regression lines (based on all 388 data points) for each memory span task, as well as the means of the five age groups described in Table 1. Table 4 presents the slopes for the six pairs of corresponding simple and complex span tasks and the statistics, including the p values prior to applying a Bonferroni correction for family-wise error, associated with each of the six comparisons. Only one of these comparisons (Digit Span vs. Reading Span) was significant in the direction predicted by the hypothesis of an age-related deficit in executive function (i.e., faster decrease on the complex span task), and one (Grid Span vs. Alignment Span) was actually significant in the opposite direction.

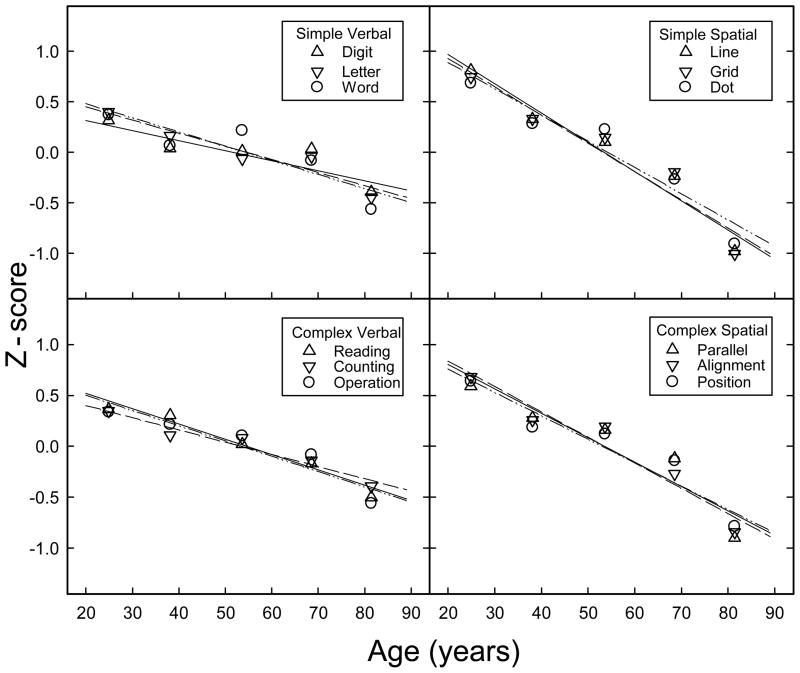
Figure 4.

Data from all of the individuals performing each of the six verbal span tasks were submitted to a linear regression analysis to determine the rate of decrease (if any) as a function of age across the seven decades of age represented in the current sample. The upper left panel displays the best-fitting linear functions for the three simple verbal span tasks (Digit Span, Letter Span, and Word Span). The lower left panel displays the best-fitting linear functions for the three complex verbal span tasks (Reading Span, Counting Span, and Operation Span). The upper right panel displays the best-fitting linear functions for the three simple spatial span tasks (Line Span, Grid Span, and Dot Span). The lower right panel displays the best-fitting linear functions for the three complex spatial span tasks (Parallel Span, Alignment Span, and Position Span). In addition to the linear functions shown in these four panels, the mean performance of seven age groups (binned as described in Table 3) are also shown (solid lines represent the first of each series in the order listed above, dashed lines represent the second of each series, and the dotted-dashed lines represent the third). Slope parameter values for all 12 functions are provided in Table 4.

Table 4.

Linear Regression Slopes (in Z-score Units per Year) and Statistics for Each Comparison between Corresponding Simple and Complex Tasks.

Memory Items	Simple Slope	Complex Slope	F values	p values
Digits	−0.010	−0.015	6.77	.010
Letters	−0.013	−0.012	<1.0	>.50
Words	−0.014	−0.015	<1.0	>.70
Lines	−0.029	−0.024	9.07	.003
Grids	−0.028	−0.025	2.59	>.10
Dots	−0.026	−0.023	3.50	.062

Our second question was whether performance on spatial span tasks decreases at a faster rate as a function of age than performance on verbal tasks. To address this question, we calculated composite mean z-scores for the four different types of tasks and conducted two slope comparisons: one on the slopes for verbal and spatial simple span tasks and one on the slopes for verbal and spatial complex span tasks (see Table 5 for slopes and statistics). For simple span tasks, the slope for the composite spatial score was significantly steeper than the slope for the composite verbal score, and a similar result (spatial slope steeper than verbal slope) was obtained for the complex span tasks, both results consistent with the hypothesis of greater age-related declines in the spatial domain.

Table 5.

Linear Regression Slopes (in Z-score Units per Year) and Statistics for Comparisons between the Verbal and Spatial Composites for Each Task Type (Simple and Complex).

Task Type	Verbal Slope	Spatial Slope	F values	p values
Simple	−0.012	−0.028	50.04	<.0001
Complex	−0.014	−0.024	27.89	<.0001

Confirmatory factor analyses of the relations among working memory abilities

Our third question concerned the structure of working memory abilities and whether the abilities tapped by working memory tasks or the relations among these abilities are different for different age groups, issues appropriately addressed through confirmatory factor analysis. Schematics of the 10 different models that we fit are provided in Figure 3.

Because our focus was on comparing the patterns of individual differences in groups of younger and older adults, and not on age differences per se, all of our confirmatory factor analyses were conducted using partial covariance matrices (with age controlled). We began by examining the structure of working memory abilities in the whole sample by submitting the partial covariance matrix for the whole sample to LISREL, and proceeded to compare the relations among abilities in younger and older groups only after having determined the best-fitting models.

Model 1: One Factor (Working Memory)

For the sake of completeness and for purposes of comparison, we included a simple one-factor model of working memory in our analyses. Not unexpectedly, it did not provide a good fit to the data (see Table 6).

Table 6.

Fit Statistics for the Different Confirmatory Factor Analyses Based on All Participants with Age Controlled.

Model	χ2	df	p	RMSEA	90% CI	RMSEA	RMSEA Prob. <.05	CFI	Largest SRMR	Residual	AIC
1	680.10	48	<.001	.184	.172	.197	<.001	.901	.142	8.73	740.10
2a	571.90	47	<.001	.170	.158	.182	<.001	.918	.159	9.12	633.90
2b	237.06	47	<.001	.102	.089	.115	<.001	.970	.052	8.54	299.06
3a	446.11	45	<.001	.152	.139	.165	<.001	.937	.089	6.40	512.11
3b	59.49	39	.019	.037	.015	.055	.878	.997	.021	6.03	137.49
3c	94.48	45	<.001	.053	.038	.068	.340	.992	.032	8.42	160.48
3d	57.38	35	.010	.041	.020	.059	.783	.997	.018	6.24	143.38
4a	40.90	42	.519	<.0001	.000	.033	.999	>.999	.021	2.41	112.90
4b	30.45	38	.803	<.0001	.000	.024	1.000	>.999	.018	2.40	110.45
4c	38.11	38	.464	.003	.000	.036	.998	>.999	.019	2.14	118.11

Note: χ²= Chi-square value, df = Degrees of Freedom, p = Chi-square p value, RMSEA = Root Mean Square Error of Approximation, 90% CI = 90% Confidence Intervals, Prob. < .05 = Probability that the RMSEA is less than .05, CFI = Comparative Fit Index, SRMR = Standardized Root Mean Residual, Largest Residual = Largest Absolute Standardized Residual, AIC = Akaike Information Criterion.

Model 2a: Two Factors (Storage, Executive)

Following Colom et al. (2005), we fit a two-factor model in which the simple span tasks all loaded on one domain-general storage factor and the complex span tasks loaded on a domain-general executive factor. This model also failed to provide a good fit (Table 6). Notably, the correlation between the storage and executive factors was quite high (.84), which suggests that when domain is not taken into account, these two constructs possess poor discriminant validity (Kline, 2005),

Model 2b: Two Factors (Verbal Working Memory, Spatial Working Memory)

Based on Oberauer et al. (2000), we fit a two-factor model in which memory span tasks are grouped based on domain (verbal vs. spatial), regardless of whether they are simple or complex. Although the CFI was .970, the chi-square was statistically significant, and the RMSEA was .102 (Table 6), which is indicative of an unacceptable model (Thompson, 2004). These results argue that distinguishing between the two domains is not by itself sufficient.

Model 3a: Three Factors (Verbal Storage, Spatial Storage, Central Executive)

This model represents the structure of the working memory system originally proposed by Baddeley (1986), as applied to individual differences by Alloway et al. (2006). In this model, all complex span tasks load on a domain-general executive factor, and verbal and spatial simple span tasks load on two domain-specific storage factors. This model also did not provide an acceptable fit (Table 6), in contrast to the next model (3b), which also involves a domain-general executive component.

Model 3b: Three Factors (Verbal Short-term Memory, Spatial Short-term Memory, Working Memory)

This model represents the structure of working memory originally proposed by Conway et al. (2002), extended here to include spatial as well as verbal span tasks. This three-factor model consists of an executive or working memory factor that loads on all of the complex tasks, regardless of domain, and two domain-specific short-term memory factors, each of which loads on all the tasks from one domain. Unlike Model 3a, Model 3b provided an acceptable fit. Although the chi-square value was statistically significant, the RMSEA was .037 and the CFI was .997 (Table 6). Note also that the SRMR drops substantially compared to the previous models, another indication of this model’s better fit. Nonetheless, the largest absolute standardized residual suggests some localized fitting problems.

Model 3c: Three Factors (Verbal Storage, Executive Control, Spatial Working Memory)

Based on Miyake et al. (2001), we fit a model that consists of two verbal factors, one simple and one complex, and a single spatial factor. This follows their suggestion that all spatial span tasks place a demand on executive functions, and therefore the distinction between simple and complex span tasks does not apply to the spatial domain. Although the chi square was significant, the model also provided an acceptable fit (Table 6), indicating that an adequate model need not include a domain-general executive construct. Despite having a small SRMR, however, this model (like Model 3b) has a very large absolute standardized residual.

Model 3d: Three Factors (Verbal Storage, Attentional Control, Spatial Storage)

Based on Kane et al. (2004), we fit a model that consists of two storage factors, one verbal and one spatial, and a single general factor, attentional control. This follows their suggestion that all working memory tasks rely on attentional control as well as domain-specific storage mechanisms. Although the chi square was significant, the model also provided an acceptable fit (Table 6). Despite having a small SRMR, however, this model (like the other 3-factor models) has a very large absolute standardized residual. What is most striking about the results for this model is that our pattern of factor loadings (see Table 7) is not in complete agreement with the pattern observed by Kane et al. (see their Figure 6, p. 206). That is, although the patterns observed in the two datasets are very similar for the verbal domain (i.e., the complex tasks show stronger loadings associated with the attentional control construct and weaker loadings associated with the storage construct), we obtained a very different pattern of loadings in the spatial domain (i.e., for the spatial tasks, both simple and complex, all of the loadings associated with the attentional control construct were slightly weaker than the loadings associated with the storage construct). It is unclear as to why our findings differ from those of Kane et al., although differences in the tasks may play a role.

Table 7.

Factor Loadings for Model 3d Latent Variables.

Task	Attentional Control	Domain-Specific Storage
Digit Span	.49	.71
Letter Span	.53	.74
Word Span	.44	.67
Reading Span	.82	.18
Counting Span	.80	.22
Operation Span	.72	.30
Line Span	.53	.60
Grid Span	.48	.62
Dot Span	.55	.58
Parallel Span	.40	.64
Alignment Span	.34	.70
Position Span	.39	.74

Figure 6.

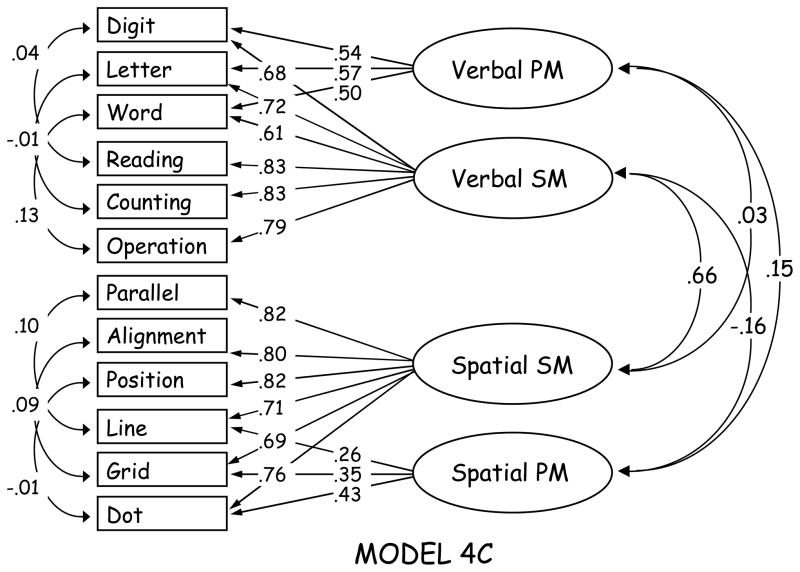
A four-factor model of working memory that is an extension of Conway’s three-factor model each with domain-specific storage and executive constructs is depicted here as Model 4b. Factor correlations, factor loadings, and correlated errors between each simple span task and its corresponding complex span task are provided. For the sake of clarity, error variances are not included in the model shown here. Fit statistics are provided in Table 9.

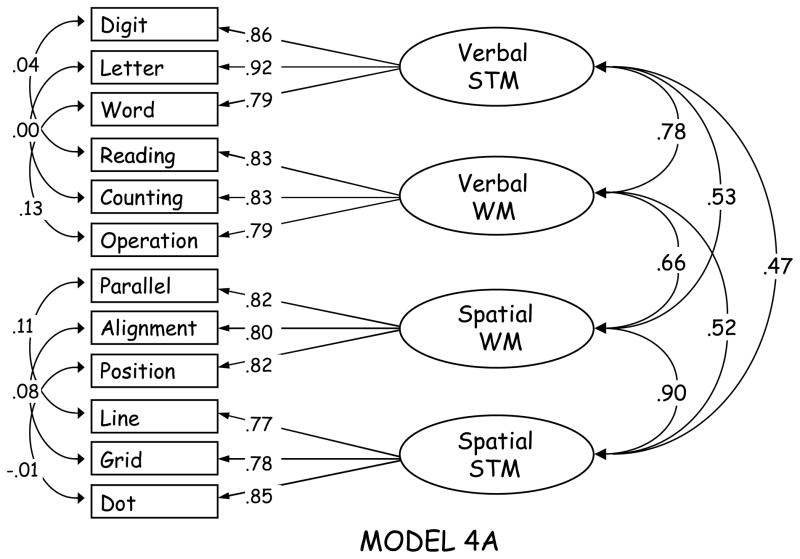
Model 4a: Four Factors (Verbal and Spatial Short-term Memory, Verbal and Spatial Working Memory)

Following Park et al. (2002), we fit a four-factor, domain-differentiated model with one factor for each of the four different types of memory span tasks: verbal simple, verbal complex, spatial simple, and spatial complex. Notably, this model provided a better fit to the data then any of the preceding models, as evidenced by a nonsignificant chi square, a CFI approaching 1.000, and an RMSEA of nearly zero (Table 6). Moreover, the largest absolute standardized residual for this model was rather modest, suggesting good localized fit. As can be seen in Figure 5, however, the two spatial constructs were very highly correlated, raising the issue of discriminant validity (Kline, 2005).

Figure 5.

A four-factor model of working memory previously fit by Park et al. (2002) is depicted here as Model 4a. Factor correlations, factor loadings, and correlated errors between each simple span task and its corresponding complex span task are provided. For the sake of clarity, error variances are not included in the model shown here. Fit statistics are provided in Table 9.

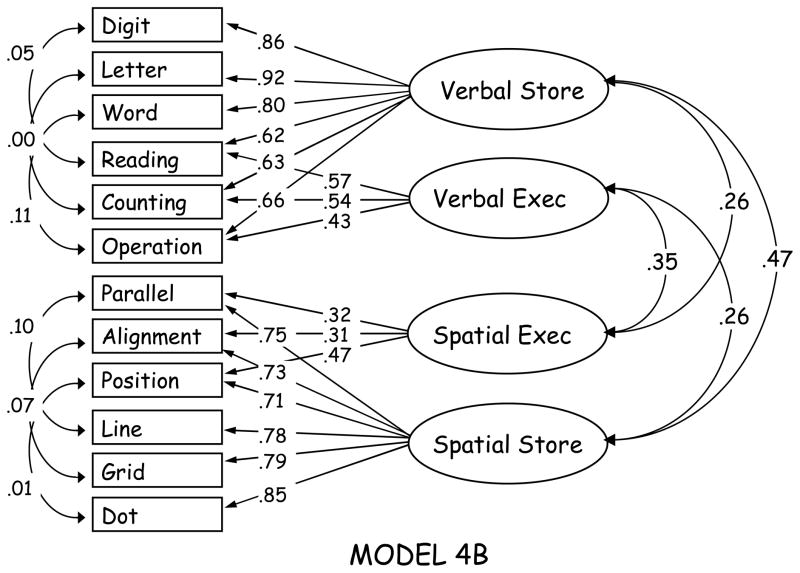
Model 4b: Four Factors (Verbal and Spatial Short-term Memory, Verbal and Spatial Working Memory)

This model is like the preceding one in that verbal and spatial complex span tasks load on separate factors. However, it borrows from Model 3b (Conway et al., 2005) the assumption that all verbal tasks, complex as well as simple, load on a verbal short-term memory factor, and all spatial tasks load on a spatial short-term memory factor. This model provided an excellent fit, as evidenced by nonsignificant chi square, a CFI of approaching 1.000, and an RMSEA of nearly zero (Table 6). Moreover, the largest absolute standardized residual for this model was similar to that for Model 4a, again suggesting good localized fit. Notably, all of the constructs were adequately differentiated, as indicated by moderate cross-domain factor correlations (see Figure 6).

Model 4c: Four Factors (Verbal and Spatial Primary Memory, Verbal and Spatial Secondary Memory)

Based on Unsworth and Engle’s (2007a, 2007b) dual-component theory, we developed a model that reflects their assumption that although simple and complex span tasks both involve primary and secondary memory, complex span tasks rely much more heavily on secondary memory than simple span tasks. Our previous research (Hale & Myerson, 1996; Jenkins et al., 2000; Lawrence et al., 1998; Myerson et al., 1999; Myerson et al., 2003) suggests that one of the most important distinctions in cognitive aging is that between the verbal and spatial domains. Accordingly, we hypothesized that separate primary and secondary memory factors are needed to describe individual and age differences in both domains, resulting in a four-factor model. This model also provided an excellent fit, as evidenced by a nonsignificant chi square, a CFI approaching 1.000, and an RMSEA of nearly zero (Table 6). The largest absolute standardized residual for this model was less than that for any of the other models tested, suggesting good localized fit. The verbal and spatial secondary memory constructs were significantly correlated, but the correlation was not so high as to raise questions as to whether these two constructs are separable (see Figure 7).

Figure 7.

A four-factor model of working memory based on work by Unsworth and Engle (2007a) is depicted here as Model 4c. Factor correlations, factor loadings, and correlated errors between each simple span task and its corresponding complex span task are provided. For the sake of clarity, error variances are not included in the model shown here. Fit statistics are provided in Table 9.

Tests of age invariance

Overall, the three domain-differentiated, four-factor models (Models 4a, 4b, and 4c) emerged as providing the best descriptions of the structure of working memory abilities in the whole sample. Unlike the three-factor models, the four-factor models all provided excellent overall fits as well as no evidence of localized fitting problems. In addition, the AIC values showed a clear improvement for the four-factor models over all of the three-factor models. Although two of the constructs in Model 4a were very highly correlated, this problem could be due to age-related dedifferentiation. If so, this should become apparent when the model is fit to the data from the younger and older adult groups separately. In contrast, Models 4b and 4c had no such problems when fit to the whole sample, but fitting these models to the younger and older groups separately might yet reveal evidence of age-related dedifferentiation.

For the purpose of testing for age invariance, we created a younger adult group and an older adult group of the same size and spanning approximately the same number of years. Specifically, we created a dataset from individuals 20 to 45 years of age and a dataset from individuals aged 65 to 89 years of age, with 150 individuals in each group. Raw correlations for each of these two groups are provided in Table 8. Because performance decreased as a function of age even within these groups (see Figure 3), we again submitted partial covariance matrices to LISREL for analysis. For each of the three four-factor models, we conducted multiple-group confirmatory factor analyses in which the parameters of the model (e.g., factor loadings, factor covariances) were first allowed to be free and then constrained to assess different forms of invariance.

Table 8.

Correlations among all Span Tasks for the Younger and Older Adult Groups.

	Verbal Simple			Verbal Complex			Spatial Simple			Spatial Complex			Young SD
	Digit	Letter	Word	Read	Count	Operate	Line	Grid	Dot	Parallel	Align	Position
Digit		.785	.699	.699	.649	.641	.482	.479	.471	.502	.476	.450	.080
Letter	.793		.768	.712	.710	.697	.515	.381	.452	.572	.469	.499	.086
Word	.684	.737		.616	.583	.705	.453	.387	.389	.445	.416	.439	.101
Read	.491	.445	.440		.713	.687	.551	.523	.548	.643	.533	.560	.147
Count	.430	.439	.401	.714		.629	.496	.467	.522	.568	.536	.534	.147
Operate	.477	.487	.552	.642	.646		.509	.382	.410	.533	.499	.511	.138
Line	.305	.353	.302	.302	.284	.228		.633	.684	.739	.614	.662	.073
Grid	.170	.207	.213	.175	.231	.201	.500		.695	.610	.599	.587	.086
Dot	.282	.278	.290	.266	.293	.262	.599	.649		.625	.646	.631	.090
Parallel	.268	.280	.280	.393	.433	.314	.641	.527	.632		.662	.708	.121
Align	.273	.299	.275	.300	.408	.331	.525	.631	.566	.620		.755	.098
Position	.327	.345	.313	.391	.488	.411	.480	.451	.587	.629	.570		.127
Old SD	.084	.081	.092	.136	.143	.131	.088	.087	.079	.135	.099	.107

Note: Correlations above the diagonal are correlations are for the Young Adult Group and correlations below the diagonal are for the Older Adult Group. Young = Younger Adult Group, Old = Older Adult Group, SD = Standard Deviation of the Residuals, Read, Count, Operate and Align = Reading, Counting, Operation, and Alignment.

The first step in this series of analyses assessed configural invariance (Horn, McArdle, & Mason, 1983). Configural invariance exists if the data from two groups are both well fit by the same set of constructs measured by the same set of manifest variables. The second step assessed a form of metric invariance by constraining the loadings of the manifest variables on the latent variables to be equal across age groups (Invariance 1). Finally, a more restrictive test constrained the covariances between the latent variables to be equivalent in the two age groups (Invariance 2), a form of structural invariance. This approach duplicates that used by Siedlecki (2007). As restrictions are placed on the model, the fit of that model can be tested by itself, and it also can be compared to previous models in the sequence (using a chi-square difference test) to determine if the constraints produce a model that fits significantly worse than a less restrictive model. The chi-square difference tests were calculated using the procedure described by Satorra and Bentler (2001).

Model 4a

First, we examined whether data from the two age groups were both well fit by the same set of four constructs (Verbal and Spatial Short-term Memory, and Verbal and Spatial Working Memory) measured by the same four sets of manifest variables. The model provided excellent fits to the data from both groups, as indicated by a nonsignificant chi-square and very good global fit statistics, as well as a very low RMSEA (see Table 9). Taken together, these results are evidence of configural invariance. Notably, the problematic correlation between the two spatial constructs (observed when the model was fit to the data from the whole sample) turned out not to reflect age-related dedifferentiation: Both the younger and older adult groups had extremely strong correlations (.91 and .89, respectively) between the two spatial constructs, indicative of similar problems with discriminant validity in both groups.

Table 9.

Statistics for Model Fits to Assess Age Invariance.

Model	χ2	df	p	RMSEA	90% CI	RMSEA	RMSEA Prob. <.05	CFI	Δ χ2	df	p
4a
Configural	74.12	84	.771	<.0001	.000	.033	.997	>.999
Invariance 1	84.62	92	.695	<.0001	.000	.036	.995	>.999	10.16	8	.254
Invariance 2	94.12	98	.592	<.0001	.000	.039	.992	>.999	19.56	14	.144
4b
Configural	65.31	76	.804	<.0001	.000	.031	.997	>.999
Invariance 1	86.31	90	.591	<.0001	.000	.040	.989	>.999	20.10	14	.127
Invariance 2	92.95	94	.511	<.0001	.000	.043	.985	>.999	26.53	18	.088
4c
Configural	68.39	76	.721	<.0001	.000	.036	.993	>.999
Invariance 1	84.20	90	.652	<.0001	.000	.038	.993	>.999	15.18	14	.366
Invariance 2	93.80	94	.486	<.0001	.000	.044	.982	>.999	24.07	18	.153

Note: χ²= Chi-square value, df = Degrees of Freedom, p = Chi-square p value, RMSEA = Root Mean Square Error of Approximation, 90% CI = 90% Confidence Intervals, Prob. < .05 = Probability that the RMSEA is less than .05, CFI = Comparative Fit Index, Δ χ²= Chi-square difference. See text for details concerning Invariance 1 and Invariance 2.

Next, we tested for metric invariance by examining the fit of the model when the loadings of the manifest variables on the latent variables were constrained to be equivalent in the younger and older groups. Model 4a satisfied this strict test of age invariance as indicated by a nonsignificant chi-square as well as very good global fit statistics (see Table 9). Equally important, the additional constraints did not produce a significantly poorer fit compared to the configural model. In the final step, we imposed the additional restriction that the factor covariances be equal across the two age groups. This model yielded a nonsignificant chi-square (p = .592) and excellent fit statistics. Moreover, this more constrained model (Invariance 2) did not produce a significantly poorer fit than the configural model.

Model 4b

Again, we tested for configural invariance to determine whether data from the two age groups were both well fit when the same set of four constructs (Verbal and Spatial Short-term Memory, and Verbal and Spatial Working Memory) were defined by the same four sets of manifest variables. This model also provided an excellent fit to the data from both groups, as indicated by a nonsignificant chi-square and very good global fit statistics (Table 9). Thus, configural invariance was observed. Examination of the factor correlations provided no evidence of problems with discriminant validity in either group.

We next examined the fit of Model 4b when the loadings of the manifest variables on the constructs were constrained to be equivalent in the younger and older groups. Like Modal 4a, Model 4b satisfied this test of metric and structural invariance as indicated by a nonsignificant chi-square and very good global fit statistics (Table 9). As with Model 4a, the additional constraints did not produce a significantly poorer fit compared to the configural model. The additional restriction that factor covariances be equal across the two age groups (Invariance 2) produced a nonsignificant chi-square and excellent fit statistics and did not produce a significantly poorer fit than the configural model.

Model 4c

The third and final model under consideration was the domain-differentiated instantiation of Unsworth and Engle’s (2007a) two-component theory of working memory. We tested for configural invariance to determine whether data from the two age groups were both well fit by the same set of four constructs (Verbal and Spatial Primary Memory, and Verbal and Spatial Secondary Memory) measured by the same four sets of manifest variables. Configural invariance was observed with respect to this model also, as evidenced by a nonsignificant chi-square and very good global fit statistics, as well as a very low RMSEA (Table 9). In both groups, the verbal and spatial primary memory constructs were not significantly correlated, and although the two secondary memory constructs were correlated, there was no evidence of problems with discriminant validity in either group.

Even when the loadings of the manifest variables on the latent variables were constrained to be equivalent in the younger and older groups, Model 4c continued to provide an excellent fit, as indicated by a nonsignificant chi square and very good global fit statistics (Table 9). This more constrained model did not produce a significantly poorer fit compared to the configural model. The additional restriction that factor covariances be equal across the two age groups (Invariance 2) produced a nonsignificant chi-square and acceptable fit statistics. It also did not produce a significantly poorer fit than the configural model. Thus, according to the current criteria (Siedlecki, 2007), tests of Model 4c, like the previous tests of Models 4a and 4b, were consistent with age invariance in the relations among working memory abilities.

Discussion

The present study was designed to address three questions regarding the effect of age on working memory abilities: (1) whether performance on complex span tasks decreases as a function of age at a faster rate than performance on simple span tasks; (2) whether performance on spatial span tasks decreases at a faster rate than performance on verbal span tasks; and (3) whether the structure of working memory abilities is different for different age groups. Answering the first two questions was relatively straightforward: When performance on the various span tasks was regressed on age, there was little evidence of faster decrease on complex span tasks, relative to simple span tasks, whereas there was clear evidence of faster decrease on spatial span tasks than on verbal span tasks.

Answering the third question involved two steps. In the first step, confirmatory factor analyses revealed near perfect fits of three four-factor models: a model similar to Park et al.’s (2002) domain-differentiated model of, a domain-differentiated version of a model originally proposed by Conway et al. (2002), and a domain-differentiated instantiation of Unsworth and Engle’s (2007a) two-component theory of working memory. In the second step, we tested whether each model provided comparable fits to data from younger and older adult groups, and found converging evidence of age invariance in the component abilities tapped by working memory tasks and in the relations among these abilities.

Differential decrease in memory spans

Contrary to the hypothesis of an age-related deficit in executive function (e.g., Dempster, 1992; West, 1996), there was little evidence of faster rates of decrease on complex span tasks, relative to simple span tasks. When simple and complex tasks were matched on the type of memory item, only one of the six pairs of matched task, Digit Span and Reading Span, showed the pattern predicted by the executive deficit hypothesis. Previous results indicate that Digit Span decreases exceptionally slowly for a verbal simple span task (Bopp & Verhaeghen, 2005), perhaps because of the extensive practice in remembering digit strings (e.g., zip codes, telephone numbers) provided by daily life. One other difference between content-matched simple and complex span tasks was significant: Performance on Line Span, a simple spatial span task, decreased more steeply than Parallel Span, the corresponding complex span task. However, this difference is the opposite of that predicted by the executive deficit hypothesis

The present cross-sectional results are consistent with previous studies that have used extreme-groups designs in which the same types of memory items were used in both the simple and complex span tasks. Hale and her colleagues (Jenkins et al., 2000; Myerson et al., 1999) found that young and older adults showed equivalent interference with memory for items from the same domain as the secondary processing task, and that neither young adults nor older adults showed interference when the secondary task was from a different domain than the memory items. In addition to these studies of domain-specific interference, Rose et al. (2009) found that although rhythmic tapping produces the kind of domain-general interference that might be expected from disruption of a central executive, the degree of interference was still equivalent in younger and older adults. Taken together, these results are clearly inconsistent with the view that an age related deficit in executive attentional resources produces larger age differences on complex span task than simple span tasks.

The present findings for verbal simple and complex spans differ from those of Park et al. (2002), who reported rates of decrease on complex span tasks (i.e., reading span and computation span) that were more than twice those for simple span tasks (i.e., forward and backward digit span). One possible reason why our results differ from those of Park et al. concerns the nature of the recall response. Emery, Myerson, and Hale (2006) found that although spatial spans are unaffected by whether recall is vocal or manual, having participants make recall responses manually rather than vocally exacerbates the difference between young and older adults’ verbal memory spans. In the Park et al. study, memory items on the simple verbal span tasks were recalled vocally whereas memory items on the complex verbal span tasks were recalled in writing. Although the manual response in the Emery et al. study involved using a touchscreen rather than writing, we suspect the same principle still applies. That is, having to respond manually can exacerbate age-related differences in verbal memory spans, which may explain why Park et al. found that manual recall on their complex verbal span tasks decreased at a faster rate than vocal recall on their simple verbal span tasks.

With respect to domain differences on what they termed short-term memory tasks, however, Park et al.’s (2002) results are consistent with the present findings. Park et al. reported much steeper rates of decrease (in z-score units per year) on Corsi Blocks than on Digit Span tasks (−0.024 and −0.013, respectively). These rates are very similar to the rates of decrease on spatial and verbal simple span tasks in the present study (−0.028 and −0.012, respectively). Moreover, they are nearly identical to those observed in an analysis of the Spatial Span and Digit Span scores of the standardization sample (N = 1050) for the WAIS III/WMS III (Psychological Corporation, 1997). As reported by Myerson et al. (2003), the rates of decrease on the Spatial Span and Digit Span subtests in the standardization sample were −0.025 and −0.013, respectively. Such precise quantitative replication is relatively rare in psychology and testifies to the robustness of the difference in the rates of age-related decrease in verbal and spatial memory spans.

Moreover, the present results show that this domain difference in rates of decrease as a function of age applies to spatial and verbal complex spans (−0.024 and −0.014, respectively) as well as to simple spans, consistent with the results of numerous studies comparing spatial and verbal spans for younger and older groups (for a review, see Jenkins, Myerson, Hale, & Fry, 1999). Taken together with previous findings of domain differences in processing speed (e.g., Hale & Myerson, 1996; Lawrence et al., 1998), our results provide converging evidence of a specific age-related deficit affecting all visuospatial processing, both speeded and unspeeded.

Age invariance in the structure of working memory abilities

Confirmatory factor analyses were used to examine the structure of working memory abilities. Consistent with Park et al. (2002), models with domain-general constructs did not fare as well as well as those with separate constructs for each domain, and there was no evidence of age-related dedifferentiation. For the entire sample of 388 participants, all three domain-differentiated, four-factor models provided excellent fits, as indicated by nonsignificant chi square values and RMSEAs less than .01. One of these models (Model 4a), in which verbal and spatial simple span tasks measure domain-specific short-term memory constructs and verbal and spatial complex span tasks measure domain-specific working memory constructs, is similar to that proposed by Park et al. The second (Model 4b) is similar to that proposed by Conway et al. (2002) for verbal working memory, but extended here to both the verbal and spatial domains. The third (Model 4c) was inspired by Unsworth and Engle’s (2007a) two-component theory of working memory, with the additional assumption that the components in the two domains are distinct, so that the model assumes separate verbal and spatial primary memory constructs as well as separate verbal and spatial secondary memory constructs.

Despite their differences, these models concur on two important points: they all posit a distinction between the verbal and spatial domains, and within each domain, they all further distinguish between two abilities. Although the models differ in how they decompose variance within domains, they are all equally successful in describing the present working memory data, and the key to that success may be the fact that all involve only domain-specific constructs. Moreover, when each of the three domain-differentiated, four-factor models was fit simultaneously to the data from a younger and an older adult group, tests of age invariance revealed that according to the current criteria (Siedlecki, 2007), neither the set of component abilities tapped by the working memory tasks nor the relations among these abilities differed significantly between the two age groups.

It may be noted, of course, that claims of invariance depend on the particular form of invariance (e.g., factorial or structural) and on the nature of the invariance tests that are conducted (e.g., the baseline model used and the goodness of fit index chosen). Psychometricians concerned with whether a particular test instrument measures the same trait or ability in the same way in different groups frequently adopt different procedures from those used here (e.g., Bontempo & Hofer, 2007; Meredith, 1993; Meredith & Teresi, 2006; Widaman & Reise, 1997). For example, establishing measurement invariance can include, among other things, showing that the fit of a model in which the intercepts of the regressions of the manifest variables on the latent variables are constrained to be equal across groups does not differ significantly from the fit of the corresponding configural model. At the level of latent variables, establishing structural invariance can include equivalence of factor means across groups. Furthermore, inferences about invariance can be based on absolute fit or incremental fit, and in the case of incremental fit, it can be based on likelihood ratio tests (i.e., differences in model chi-squares; Widaman & Reise, 1997) or on differences in other goodness of fit estimates (e.g., CFI; Cheung & Rensvold, 2002).

In the present case, all three four-factor models provide relatively poor fits to the data when intercepts and factor means for younger and older groups are constrained to be equal and inferences are based on the traditional chi-square differences approach (all ps ≤ .055 for comparisons of equal intercept models to configural models; all ps < .001 for comparison of equal factor mean models to configural models and to measurement invariant models). Chi-square difference tests, however, suffer from the same sample size dependency as absolute fit chi-squares. When age invariance in working memory abilities is instead evaluated based on RMSEA or CFI, the evidence for invariance is substantial: For all three four-factor models, each form of invariance described by Widaman and Reise (1997) except factor mean equivalence produces RMSEA values less than or equal to .043 and CFI values greater than or equal to .993. Furthermore, the decrement in CFI from the configural model is less than the .01 standard for rejecting the invariance hypothesis suggested by Cheung and Rensvold (2002; see Bowden, Weiss, Holdnack, & Lloyd, 2006, for a relevant application). Only the factor mean invariance model is rejected by all criteria. This latter result is unsurprising but it also quite important—it means that in the context of the other forms of invariance, the age differences found for the manifest variables can be inferred to arise from the specified latent variables and to be uncontaminated by age-specific factors or measurement inequivalence.

The problem of choosing between models with nearly equivalent fit statistics is a difficult one, especially given the consistent evidence of age invariance in the present case, and one which may profit from examination of multiple data sets, as well from consideration of theoretical issues that go beyond those considered here. Although the present results do not indicate which of the four-factor models tested best describes the structure of working memory abilities, nevertheless the bulk of the present evidence indicates that the structure of working memory abilities is highly similar in young and older adults. Indeed, tests based on all three domain-differentiated, four-factor models provided converging evidence of age invariance. Thus, although the jury may be out as to which is more important, the distinction between storage and executive processes (as in Models 4a and 4b) or the distinction between primary and secondary memory processes (as in Model 4c), the evidence clearly suggests that the same distinctions are maintained in younger and older adults.

Reconciling age-invariance and differential decline

How should the relative stability of the relations among working memory abilities revealed by confirmatory factor analysis be interpreted in light of the pattern of age-related decrease revealed by regression analysis? The finding that domain-differentiated models provided better fits than those with domain-general constructs is consistent with the approximately two-fold difference between the rates of decrease in the verbal and spatial domains. Taken together with the absence of age-related dedifferentiation, these findings suggest the following interpretation. Although the cognitive processes involved in verbal and spatial working memory tasks may be analogous, in the sense that these processes perform the same functions, these processes are nonetheless distinct. Not surprisingly, the processes in each domain are more efficient in some people than others, thereby giving rise to the distinctly different abilities in the two domains revealed by confirmatory factor analysis. Moreover, the absence of dedifferentiation indicates that these corresponding processes remain distinct across the adult portion of the life span, and the finding of differential decrease indicates that the spatial processes are more age-sensitive than their verbal counterparts.

At first blush, the finding that the structure of working memory abilities is highly similar in young and older adults may seem surprising given the differential rates of decrease in verbal and spatial working memory.² We would note, however, that our results are strikingly similar to those reported recently by Siedlecki (2007), who studied performance of a large cross-sectional sample of adults on three types of episodic memory tasks (recall, cued recall, and recognition) using three types of material (verbal, spatial, and figural). As in the present study, confirmatory factor analyses revealed considerable similarity in the pattern of individual differences in younger and older adult groups despite the generally slower rates of decrease on verbal episodic memory tasks relative to spatial and figural tasks. Moreover, latent constructs corresponding to recall, cued recall, and recognition could be distinguished in the verbal domain only, a finding analogous to our finding of good discriminant validity with respect to latent constructs corresponding to simple and complex span tasks in the verbal domain, but poor discriminant validity in the spatial domain (for related findings, see Bopp & Verhaeghen, 2007; Miyake et al., 2001).

The fact that we find evidence of a level of age invariance comparable to that observed by Siedlecki (2007) in a task domain (i.e., working memory) quite different from that which Siedlecki examined (i.e., episodic memory) suggests that such age invariance in individual differences in memory abilities may be a general phenomenon (Zelinski & Lewis, 2003). Clearly, over the short term, and especially prior to advanced old age, individual trajectories, and even the trajectories of different abilities in the same individual, may differ (Hertzog, Dixon, Hultsch, & MacDonald, 2004; Sliwinski & Buschke, 2004). Over the longer-term, however, the accumulation of neurological changes, such as loss of white matter integrity and shrinkage of prefrontal cortex (e.g., Head et al., 2004; Head, Rodrigue, Kennedy, & Raz, 2008), may tend to overwhelm the factors responsible for individual differences in rates of change.

Only longitudinal studies can definitively test this hypothesis, and very few have followed individuals over a time interval anything like the approximately 40 years that, on average, separated the younger and older groups in the present study. One study (Arbuckle, Maag, Pushkar, & Chaikelson, 1998) did follow adults over a comparable interval and reported considerable stability of individual differences in scores on the intelligence portion of the Canadian Army M Test. Moreover, Hertzog and Schaie (1986; 1988) found high covariance stability in scores on the Primary Mental Abilities Test (Thurstone & Thurstone, 1949) collected from 14-year longitudinal samples, and Zelinski and Stewart (1998) found that correlations among memory and reasoning abilities were stable over a 16-year period. Taken together, these longitudinal findings suggest that the relative stability of the structure of working memory abilities over the long term is not unique (for an overview, see Zelinski & 2003).

Even if it is true that “nothing makes no difference,” some differences make much more of a difference than others. Although performance on simple span tasks was consistently better than performance on complex span tasks with the same memory items, performance on the two types of task tended to decrease as a function of age at the same rate, contrary to the hypothesis of an age-related deficit in executive function. In contrast, the age-related decrease in performance on spatial span tasks was much steeper than that on verbal span tasks, consistent with the hypothesis of differential decline in the two domains. In addition, confirmatory factor analyses revealed that domain-differentiated models fit much better than models with domain-general constructs, reinforcing the need to distinguish between verbal and spatial working memory abilities. Sometimes, of course, the absence of a significant difference may be very important, and arguably the most striking feature of the present results, especially given the differential decrease in the verbal and spatial domains, may be the similarity of the structure of working memory abilities in younger and older adults. Although we have speculated on how these two findings can co-occur, future longitudinal studies, particularly research examining the relation between cognitive and neurobiological changes over the long term, will be needed to determine the validity of these speculations.

Conclusion

From the perspective of general cognitive psychology, perhaps the most important result of the present study is the finding that the best-fitting models did not include domain-general theoretical constructs, and instead involved separate domain-specific verbal and spatial constructs. Whereas Baddeley (1986) argued that storage was domain-specific, the present results suggest that executive abilities may also be domain-specific. Indeed, the existence of domain-specific verbal and spatial working memory abilities raises the possibility that other domains need to be considered as well in future modeling efforts (e.g., memory for ventral stream object information as distinct from dorsal stream spatial information; Chen, Hale, & Myerson, 2003; Wager & Smith, 2003).

As for whether working memory abilities within each domain are better described in terms of the distinction between storage and processing or the distinction between primary and secondary memory, the present results do not provide a clear answer to this question. One approach that might shed light on this issue would be to apply structural equation modeling techniques to datasets that include working memory measures as well as data from other types of task that index the processes hypothesized to underlie performance on the working memory tasks (e.g., Oberauer, 2005; Unsworth & Spillers, 2010). Although other approaches may also be fruitful, the present results suggest that regardless of the approach used, future studies should examine performance on visuospatial as well as verbal tasks. Moreover, such studies will have to take into account the present finding that domain-differentiated models without domain-general constructs appear to best describe the structure of working memory abilities.

It should be recalled, of course, that our reason for comparing different models of working memory abilities was to understand the implications of the structure of these abilities for cognitive aging. The present results provided no evidence of dedifferentiation in working memory abilities, and there was also no evidence of an age-related deficit in executive ability, at least on the kinds of tasks that we examined. In fact, the results of a series of confirmatory factor analyses using three different four-factor models provided converging evidence of age invariance in the component abilities tapped by working memory tasks as well as in the relations among these abilities. Nevertheless, there was strong evidence that spatial working memory is more age-sensitive than verbal working memory. Thus, despite the obvious importance of verbal working memory for everyday function, it behooves cognitive aging researchers not to neglect the study of spatial working memory. In addition to the need to understand cognition in the domain in which performance declines the most as people age, it is possible that precisely because of the large age differences observed in spatial cognition, research focusing on this domain may be especially revealing of the source of age differences in general.

Appendix

Because participants were not told how many items had been presented and were instructed to report as many items as they could recall, participants could omit items or report more items than were presented. Therefore, a modification the Kane et al. PCS method was used to determine the proportion of items correctly recalled from each series (i.e., each trial).

In the spatial domain, if participants reported more items than had been presented, they were penalized 1 point for each extra item. For example, if a participant reported 5 locations when the series had contained only 4, and 4 of the responses were correct, the proportional score was 3/4 = .75. Note that to obtain the proportional score for each series (i.e., each trial) the total number of points assigned was divided by the total number of items presented in the series. Also, as noted previously, participants were given credit for correct performance on 2-item series on the Line Span task even though this series of this length were not presented.

In the verbal domain only, participants had to report items in the order presented, and this made scoring more complicated in cases where extra items were reported. First, if a participant reported more items than were presented, we ignored these extra responses and scored only those items recalled before the series limit was exceeded. Next, credit for these items was assigned as follows: ½ point for each item recalled that had appeared in the series, plus an additional ½ point for each of these items if it was recalled in the correct order. As in the spatial domain, to obtain the proportional score for each series (i.e., trial), the total number of points assigned was divided by the total number of items presented in the series.

As an example of the scoring method used in the verbal domain, consider the following the 4-item series “P, F, S, H”. If an individual reported “P, F, S, X, H,” the proportional score for the series would be .75 because 3 of the first 4 items recalled had appeared in the series (3 × .5 points = 1.5 points) and each one was recalled in the correct order (for an additional 1.5 points, and a total of 3 out of a possible 4). If, however, the response had been “P, S, F, X”, the proportional score would be .50 because although 3 of the first 4 items recalled had appeared in the series (1.5 points), only the first item was recalled in the correct order (0.5 points, for a total of 2 out of a possible 4).