Abstract
This paper presents a geometrical analysis of how local interactions in a large population of categories packed into a feature space create a global structure of feature relevance. The theory is a formal proof that the joint optimization of discrimination and inclusion creates a smooth space of categories such that near categories in the similarity space have similar generalization gradients. Packing theory offers a unified account of several phenomena in human categorization including the differential importance of different features for different kinds of categories, the dissociation between judgments of similarity and judgments of category membership, and children’s ability to generalize a category from very few examples.
There are an infinite number of objectively correct descriptions of the features characteristic of any thing. Thus, Murphy and Medin (1985) argue that the key problem for any theory of categories is feature selection: picking out the relevant set of features for forming a category and generalizing to new instances. The feature selection problem is particularly difficult because considerable research on human categories indicates that the features people think are relevant depend on the kind of category (Murphy & Medin, 1985; Macario, 1991; Samuelson & Smith, 1999). For example, color is relevant to food but not to artifacts; material (e.g., wood versus plastic) is relevant to substance categories but not typically to artifact categories. This leads to a circularity as pointed out by Murphy and Medin; to know that something is a pea, for example, one needs to attend to its color, but to know that one should attend to its color, one has to know it is a potential pea. Children as young as two and three years of age seem to already know this and exploit these regularities when forming new categories (Colunga & Smith, 2005; Yoshida & Smith, 2003). This paper presents a new analysis of feature selection based on the idea that individual categories reside in a larger geometry of other categories. Nearby categories through processes of generalization and discrimination compete and these local interactions set up a gradient of feature relevance such that categories that are near to each other in the feature space have similar feature distributions over their instances. We call this proposal “packing theory” because the joint optimization of generalization and discrimination yields a space of categories that is like a suitcase of well-packed clothes folded into the right shapes so that they fit tightly together. The proposal, in the form of a mathematical proof, draws on two empirical results: (1) experiments and theoretical analyses showing that the distribution of instances in a feature space is critical to the weighting of those features in adult category judgments and (2) evidence from young children’s category judgments that near categories in the feature space are generalized in similar ways. Distributions of instances In a seminal paper, Rips (1989) reported that judgments of instance similarity to a category and judgments of the likelihood that the instance is a member of the category did not align. The result, now replicated many times, shows that people take into account how broadly known instances vary on particular properties (Kloos & Sloutsky, 2008; Zeigenfuse & Lee, 2009; Rips & Collins, 1993; Holland, Holyoak, Nisbett, & Thagard, 1986; Nisbett, Krantz, Jepson, & Kunda, 1983; Thibaut, Dupont, & Anselme, 2002) With respect to judgments of the likelihood that an instance was a member of the category, people take into account the frequency of features across known instances and do not just judge the likelihood of membership in the category by similarity across all features. Importantly, however, similarity judgments in Rips’ study were not influenced by the frequency distribution of features across category instances (see also, Rips and Collins, 1993; Holland et al., 1986; Nisbett et al., 1983; Thibaut et al., 2002, Stewart & Carter, 2002). Rather, the similarity relations of potential instances to each other and the importance of features to judgments of the likelihood of category membership appear to be separable sources of information about category structure with the distribution of features across known instances most critical in determining the importance of features in decisions about category membership. Figure 1 provides an illustration. The figure shows the feature distribution on some continuous dimension for two categories, A and B. A feature that is highly frequent and varies little within a category is more defining of category membership than one that is less frequent and varies more broadly. Thus, a novel instance that falls just to the right side of the dotted line would be farther from the central tendency of B than A, but may be judged as a member of category B and not as a member of category A. This is because the likelihood of that feature given category B is greater than the likelihood of the feature given category A. This can also be conceptualized in terms of this feature having greater importance to category A than B.
Figure 1.
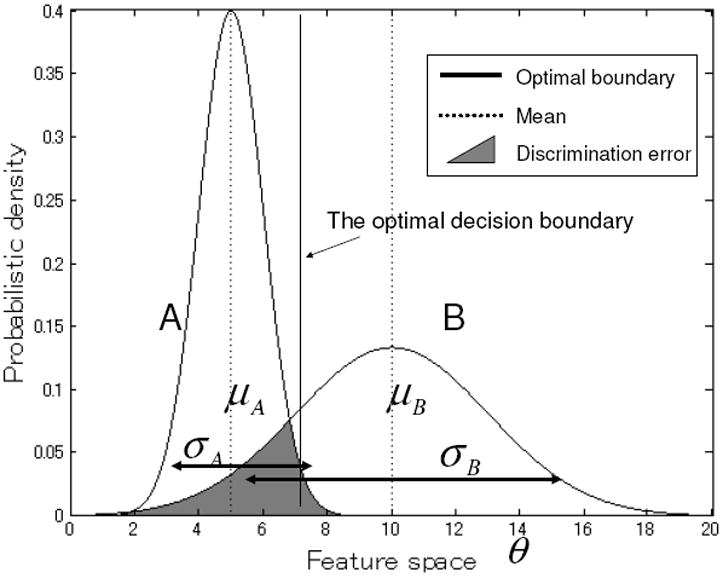
Likelihoods of instances in two categories, A and B, in a hypothetical feature space. The solid line shows the optimal decision boundary between category A and B. The broken line shows mean value of the instances in the feature space for each category.
The potentially separate contributions of similarity and the category likelihoods of features provide a foundation for the present theory. Similarity is a reflection of the proximity of instances and categories in the feature space. The density of instances in this feature space result in local distortions of feature importance in the space, a result of competitions among nearby categories. The result is a patchwork of local distortions that set up a global gradient of feature importance that constrains and promotes certain category organizations over others as a function of location in the global geometry. Further, in this view, the weighting of features is locally distorted, but similarity is not.
Nearby categories
Studies of young children’s novel noun generalizations also suggest that the proximity of categories to each other in a feature space influence category formation. These results derive from laboratory studies of how 2- and 3- year olds generalize a category to new instances given a single exemplar. In these experiments, children are given a novel never-seen-before thing, told its name (“This is a dax”) and asked what other things have that name. The results show that children extend the names for things with features typical of animates (e.g., eyes) by multiple similarities, for things with features typical of artifacts by shape (e.g., solid and angular shapes), and for things with features typical of substances by material (e.g., nonsolid, rounded flat shape). The children systematically extend the name to new instances by different features for different kinds (Jones, Smith & Landau, 1991; Kobayashi, 1998; Jones & Smith, 2002; Yoshida & Smith, 2001; Markman, 1989; Booth and Waxman, 2002; Gathercole & Min, 1997; Imai & Gentner, 1997; Landau, Smith & Jones, 1988, 1992, 1998; Soja, Carey, & Spelke, 1991; see also, Gelman & Coley, 1991; Keil, 1994).
Critically, the features that cue these categories - having eyes or legs, being angular or rounded, being solid or nonsolid - may be treated as continuous rather than as discrete and categorical features. When the degree to which instances present these features is systematically varied so that named exemplars are more or less animal-like or more or less artifact-like (Yoshida & Smith, 2003; Colunga & Smith, 2005, 2008) children show graded generalization patterns: Exemplars with similar features are generalized in similar ways and there is a graded, smooth, shift in the patterns of generalizations across the feature space. Based on an analysis of the structure of early learned nouns, Colunga and Smith (Colunga & Smith, 2005, 2008; Samuelson & Smith, 1999) proposed that children’s generalizations reflected the instance distributions of early learned nouns that categories of the same general kind (artifacts versus animals versus substances) typically have many overlapping features and also have similar dimensions as the basis for including instances and discriminating membership in nearby categories. In brief, categories of the same kind will be similar to each other, located near each other in some larger feature geometry of categories, and have similar patterns of instance distributions. This has potentially powerful consequences: If feature importance is similar for nearby categories, then the location of categories -or even one instance – within that larger space of categories could indicate the relevant features for determining category membership. Thus, children’s systematic novel noun generalizations may reflect the distribution of features for nearby known categories.
The findings in the literature on children’s generalizations from a single instance of a category may be summarized with respect to Figure 2. The cube represents some large hyperspace of categories on many dimensions and features. Within that space we know from previous studies of adult judgments of category structure and from children’s noun generalizations (Soja, Carey, & Spelke, 1991; Samuelson & Smith, 1999; Colunga & Smith, 2005) that solid, rigid and constructed things, things like chairs and tables and shovels) are in categories in which instances tend to be similar in shape but different in other properties. This category generalization pattern is represented by the ellipses in the bottom left corner; these are narrow in one direction (constrained in their shape variability) but broad in other directions (varying more broadly in other properties such as color or texture). We also know from previous studies of adult judgments of category structure and from children’s novel noun generalizations (Soja et al., 1991; Samuelson & Smith, 1999; Colunga & Smith, 2005), that nonsolid, nonrigid things with accidental shapes (things like sand, powder, and water) tend to be in categories well organized by material. This category generalization pattern is represented by the ellipses in the upper right corner of the hyperspace; these are broad in one direction (wide variation in shape) but narrow in other directions (constrained in material and texture). Finally, Colunga and Smith (2005; 2008) found evidence for a gradient of generalization patterns within one local region of feature space of early-learned noun categories. In sum, the evidence suggests that near categories (with similar instances) have similar generalization patterns and far categories (with dissimilar instances) have dissimilar generalization patterns.
Figure 2.
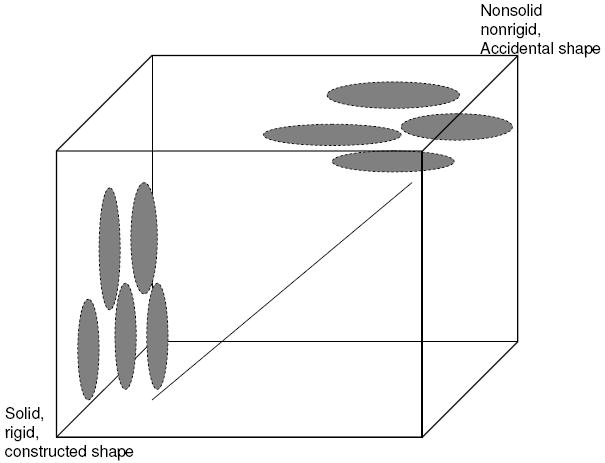
A hyperspace of categories. The ellipses represent categories with particular. generalization patterns (constrained in some directions but allowing variability in others). Packing Theory predicts that near categories in the space will have similar generalization patterns and that there should be a smooth gradient of changing category generalizations as one moves in any direction in the space. Past research shows that categories of solid, rigid and constructed things are generalized by shape but categories of nonsolid, nonrigid, and accidentally shaped things are generalized by material. Packing Theory predicts a graded transition in feature space between these two kinds of category organizations.
At present Figure 2 represents a theoretical conjecture, one based on empirical evidence about one small region of the space of human categories and one that has not been theoretically analyzed. Still, it is a particularly interesting conjecture in the context of Rips’ (1989) insight that the distributions of features are distinct from similarity and determine the relative importance of features in category judgment. Packing theory builds on these two ideas: distributions of instances and proximity of categories in the feature space to suggest how they jointly determine feature selection.
Starting Assumptions
Three theoretical assumptions form the backdrop for Packing Theory. First, as in many contemporary theories of categorization, we take an exemplar approach (Nosofsky, 1986; Ashby & Townsend, 1986; Nosofsky, Palmeri, & McKinley, 1994). We assume that noun categories begin with mappings between names and specific instances with generalization to new instances by some weighted function of feature similarity. Packing is about those weighted features. This means that categories do not have fixed or rule-like boundaries but rather probabilistic boundaries. Second, we assume that at the probabilistic edges of categories, there is competition among categories for instances. Competition characterizes representational processes at the cognitive, sensory, motor, cortical and subcortical levels. In general, activation of a representation of some property, event or object is at the expense of other complementary representations (Duncan, 1996; Beck & Kastner, 2009; Marslen-Wilson, 1987; Swingley & Aslin, 2007). Packing theory proposes that near by categories have similarly shaped generalizations patterns because of the joint optimization of including nearby instances and discriminating instances associated with different categories. Third, the present approach assumes some feature-based representation of categories (McRae, Cree, Seidenberg, & McNorgan, 2005). However, we make no assumptions about the specific nature of these features or these origins. Although we will use perceptual features in ours discussions and simulations, the relevant features could be perceptual, functional or conceptual. Packing Theory is a general theory, about any distribution of many instances in many categories across any set of features and dimensions. Moreover, the theory does not need the right pre-specification of the set of features and dimensions. Optimization within the theory depends only on distance relations in the space (and thus on the number of orthogonal, that is uncorrelated, dimensions but not on any assumptions about what orthogonal directions in that space constitute the dimensions). Further, the predictions are general; along any direction in that space (a direction that might consist of joint changes in two psychological dimensions, angularity and rigidity, for example), one should see near categories having more similar generalization patterns and far categories having more different generalization patterns. To present the theory, we will often use figures illustrating instance and category relations in a two-dimensional space; however, the formal theory as presented in the proof -and the conceptual assumptions behind it -assume a high dimensional space.
Packing Theory
Geometry is principally about how one determines neighbors. If the structure of neighboring categories determines feature selection, then a geometrical analysis should enhance our understanding of why categories have the structure they do. Figure 2 is the starting conjecture for the theory presented here and it suggests that near categories have similar instance distributions whereas as far categories have more dissimilar instance distributions. Thus, a geometry is needed when it represents both local distortions and the more global structure that emerges from a space of such local distortions. Many theorists of categorization have suggested that although Euclidean assumptions work well within small and local stimulus spaces, a Riemann (or non-Euclidian) geometry is better for characterizing the local and global structure of large systems of categories (Tversky & Hutchinson, 1986; Griffiths, Steyvers, & Tenenbaum, 2007; Steyvers & Tenenbaum, 2005). Packing Theory follows this lead. We first present a conceptual understanding of the main idea that packing categories into a space creates a smooth structure and then the formal proof.
Well-Packed Categories
Figure 3 shows three different sets of categories distributed uniformly within a (for exposition only 2-dimensional) feature space. Figure 3a shows a geometry, like that of young children; near categories have similar patterns of feature distributions and far categories have different ones. Such a geometry is not logically necessary (though it may be psychologically likely). One could have a geometry of categories like that in Figure 3b, where each category has its own organization unrelated to those of near neighbors and more specifically, a geometry in which near categories do not share similar feature importance. The two spaces of categories illustrated in Figure 3a and 3b are alike in that in both of these spaces there is little category overlap. That is, in both of these spaces, the categories discriminate among instances. However, the categories in 3b are not smooth in that near categories have different shapes. Moreover, this structure leads to gaps in the space, possible instances (feature combinations) that do not belong to any known category. The categories in Figure 3b could be pushed close together to lessen the gaps. However, given the nonsmooth structure, there would always be some gaps, unless the categories are pushed so close that they overlap as in Figure 3c. Figure 3c then shows a space of categories with no gaps, but also one in which individual categories do not discriminate well among instances. The main point is that if neighboring categories have different shapes there will either be gaps in the space with no potential category corresponding to those instances or there will be overlapping instances. A smooth space of categories, a space in which nearby categories have similar shapes, can be packed in tighter. This is a geometry in which categories include and discriminate among all potential instances.
Figure 3.
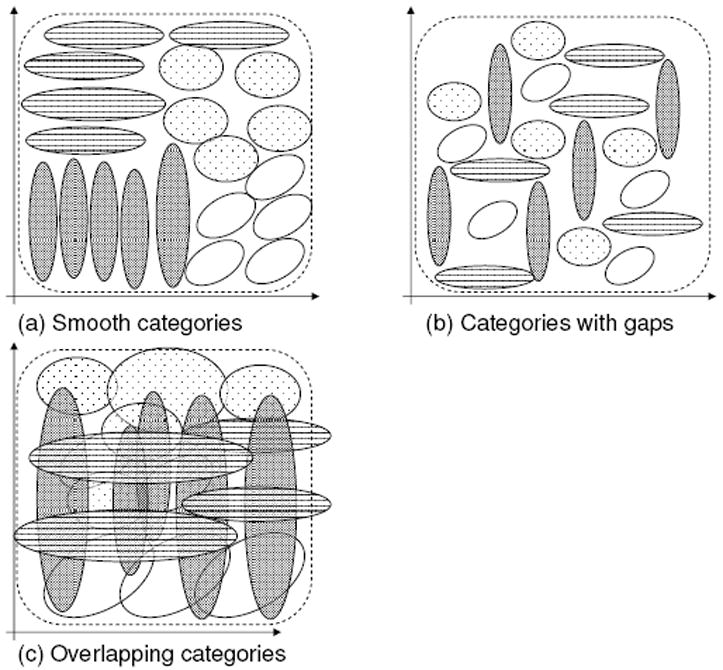
A cartoon of populations of categories in a feature space illustrating three different ways those might categories might fit into the space. Each ellipsis indicates equal-likelihood contour of category. The broken enclosure indicates the space of instances to be categorized.
Packing Theory proposes that a smooth space of categories results from the optimization with respect to two constraints: minimizing gaps and minimizing overlap. These constraints are understood in terms of the joint optimization of including all experienced and potential instances in a category and discriminating instances of nearby categories. The inclusion-discrimination problem is illustrated with respect to the simple case of two categories in Figure 4. Each category has a distribution of experienced instances indicated by the diamonds and the crosses. We assume that the learner can be more certain about the category membership of some instances than others can; that is, the probability that each of these instances is in the category varies. If a category is considered alone, it might be described in terms of its central tendency and estimated category distribution of instances (or covariance of the features over the instances). The solid lines that indicate the confidence intervals around each category illustrate this. However, the learner needs to consider instances not just with respect to a single category, but also with respect to nearby categories. Therefore, such a learner might decrease the weight of influence of any instance on the estimated category structure by a measure of its confusability between the categories. This is plausible because the shared instances in between these nearby categories are less informative as exemplars of categories than the other nonconfusing instances. Thus, the estimation of category structure may “discount” the instances in between the two categories. Doing this results in an estimated category distribution, that is shifted such that the generalization patterns for the two categories are more aligned and more similar, which is shown with dotted lines. This is the core idea of packing theory.
Figure 4.
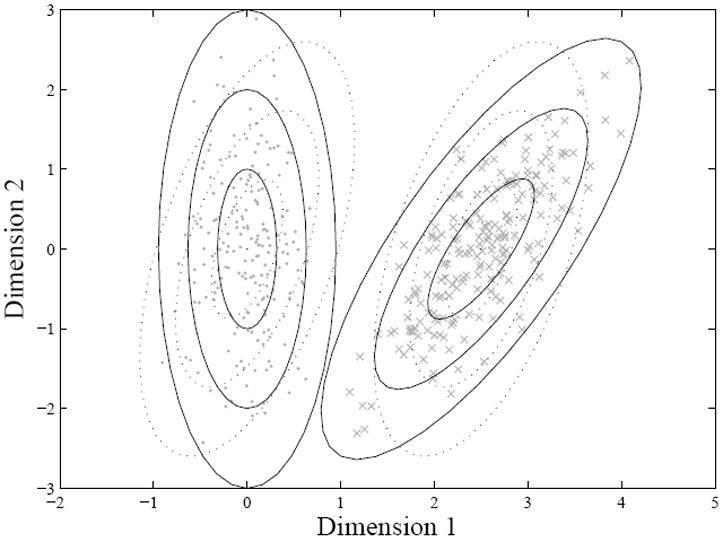
Two categories and their instances on two-dimensional feature space. The dots and crosses show the respective instances of the two categories. The broken and solid ellipses indicate equal-likelihood contours with and without consideration to category discrimination respectively.
Formulation of the Theory
It is relatively difficult to describe the whole structure formed by a large number of categories when they locally interact across all categories at once. N categories have possible pairs of categories. Moving one category to maximize its distance from some other category may influence the other (N − 1) categories, and those other categories’ movements will have secondary effects (even on the first one), and so forth. Thus, two categories that compete with each other in a local region in a feature space influence the whole structure by chains of category interactions. The goal of the theory formulation is to describe the dynamics of category inclusion and discrimination in a general case, and to specify a stable optimal state for the N-categories case. Mathematically, the framework can be classified in one of variant of a broad sense of the Linear Discriminant Analysis (LDA, see Duda, Hart, & Stork, 2000), although we do not necessarily limit the theory to employ only linear transformation or assume homoscedastic category distributions (See also, Ashby & Townsend, 1986 for the similar formulation using normal distribution in psychological field).
Inclusion
We begin with a standard formalization of the distribution of instances in a category as a multidimensional normal distribution; that is, the conditional probabilistic density of an instance having feature θ given category ci is assumed to follow a multi-dimensional normal distribution:
| (1) |
where μi and σi are respectively mean vector and covariance matrix of the features that characterize the instances of category ci. The superscript “T” indicates transposition of the matrix. We identify the central tendency and distribution pattern of these features as the mean vector of the category, and the covariance matrix respectively. The motivation of this formulation of category generalization derives from Shepard (1958) characterization of the generalization gradient as an exponential decay function of given psychological distance.
When we have Ki instances (k = 1, 2, …, Ki) for category ci, the log-likelihood Gi that these instances come from category ci is the joint probability of all instances
| (2) |
where Gik = log {P(xk∣ci)P(ci)}.
Note that log(x) is a monotonic function for all x > 0. Thus we can identify a solution of x that maximizes the log-likelihood. For all categories (i = 1, 2, …, N), the log-likelihood is .
| (3) |
This is the formal definition of the likelihoods of instances with respect to individual categories, which we call inclusion. In this formulation, the mean vectors μ̂i and covariance matrices σ̂i (i = 1, 2, …, N), maximize the log-likelihood (likelihood) as follows:
| (4) |
| (5) |
These maximum likelihood estimates are simply the mean vectors and covariance matrices of all instances of a category.
Discrimination
Consider the simple case with two categories in a one-dimensional feature space as in the example from Rips (1989) in Figure 1. Likelihoods of category A and B are shown as the solid lines: category A has the central tendency on the left side in which the instance is most likely, and category B has the central tendency on the right side. An optimal category judgment for a given instance is to judge it as belonging to the most likely category. Thus the optimal solution is to judge an instance on the left side of the dashed line in Figure 1 to be in category A and otherwise to judge it to be in category B. Meanwhile, the error probability of discrimination in the optimal judgment is the sum of the non-maximum category likelihood, the shaded region in Figure 1. Therefore, we formally define discriminability as the probability of discriminating error in this optimal category judgment.
Although the minimum or maximum function is difficult to solve, we can obtain the upper bound of the discriminating error (log-likelihood) Fij for category ci and cj as follows:
| (6) |
In particular, when likelihoods of categories are normally distributed, it is called the Bhattecheryya bound (Duda, Hart, & Stork, 2000). In fact, the non-maximum likelihood of a given pair is the classification (instance, category) error rate and the non-maximum likelihood has the following upper bound: min(P(θ∣ci), P(θ∣cj)) ≤ P(θ∣ci)α P(θ∣cj)1−α where 0 ≤ α ≤ 1. Thus, Equation 6 is the upper bound of error in the optimal classification with . The term P(θ∣ci)α P(θ∣cj)1−α is the function of α, and a particular α may allow the tightest upper bound with a general case of α. (Equation 6 is called the Chernoff bound). Here, we assume for simplification of formulation.
| (7) |
| (8) |
The first term (μi − μj)T (σi + σj)−1 (μi − μj) indicates the distance between mean vectors of the categories weighted by their covariance matrices, which is zero when μi = μj. And the second and third terms, , indicate the distance between the covariance matrices of categories which is zero when σi = σj. Thus, obviously the discrimination error is maximized when μi = μj and σi = σj, when category ci and cj are identical. Meanwhile the discriminating error is minimized when the distance between two central tendencies or distributions goes to infinity or where tr[X] is trace of the matrix X. The minimum and maximum concern is the one component of discrimination.
The packing metric
The joint optimization of discrimination by reducing the discriminating error and the optimization of the inclusion of instances with respect to the likelihood of known instances results in a solution that is constrained to an inter region between these two extremes. In the general case with N categories, we define the sum of all possible pairs (including symmetric terms) of discriminating error as discriminability.
| (9) |
More formally, we obtain a set of optimal solutions by deriving the differential of Equation 3 (inclusion) and Equation 8 (discrimination). Since the desired organization of categories should maximize both discriminability and inclusion simultaneously, we define the packing metric function as a weighted summation of Equation (3) and Equation (8) with a multiplier:
| (10) |
where C is a particular constant, which indicates a level for discriminability F to satisfy. According to the Lagrange multiplier method, the differential of parameters gives the necessary condition for the optimal solution of X ⊂ {μi, σi, λ} on condition that the discrimination error is a particular criterion F = C. Since the probability of discrimination error is calculated for all possible pairs (categories i, j = 1, 2, …, N), this is the maximization of likelihood with latent variables of the discriminated pairs. The optimization is computed with the EM algorithm, in which the E-step computes the expectation with the unknown pairing probability, and the M-step maximizes the expectation of likelihood function (Dempster, Laird, & Rubin, 1977). Thus, the expected likelihood L, with respect to a variable for the i-th category Xi, is calculated: , where the probability of category pairs are , and the probability from categories to instances , calculated in the following derivation. Note that P(xk∣ci) is a given binary constant variable, either one or zero, in case of supervised learning, and it should be estimated from its likelihood in case of unsupervised learning.
Optimal solutions for covariance matrices
Consider the case in which the mean of a category, but not its covariance, is specified. Packing Theory assumes a covariance for that category derives from the optimization of discrimination and inclusion with respect to the known categories. This is formally given as the solution of the optimal covariance of an unknown category when the mean of the category and the set of means and covariances of the other known categories are given. Thus, in that case, we solve the differential of the packing metric with respect to the covariance matrix. We next derive these differentials to show that these optimal solutions imply a smooth organization of categories in general. As a preview, the following derivations show that a solution that optimizes discrimination and inclusion implies a particular pattern of organization, that of smooth categories, that emerges out of chains of local category interactions. In addition, the form of the optimal solution also suggests how known categories constrain the formation of new categories.
The differential of the functions of likelihoods and discriminability with respect to covariance matrix σi is,
| (11) |
where σ̂ij = 2σi(σi + σj)−1σj and , and
| (12) |
. See Appendix for the detailed derivation of Equation (11) and (12). Since a covariance matrix must be a positive definite, we parameterize the covariance matrix σi using its l-th eigenvector yil and l-th eigenvalue ηil (l = 1, 2, …, D), that is . Solving , we obtain the following generalized eigenvalue problem 1 (See also Appendix):
| (13) |
where Sik = (xik − μi)(xik − μi)T and Ŝij = (μ̄ij − μi)(μ̄ij − μi)T. Because Equation (13) is also an eigenvalue form with a particular constant λ, we identify and, using the relationship between the eigenvector and its matrix σiyil = ηilyil, we obtain the quadratic eigenvalue problem.
| (14) |
where , , , and ID is D-th order identity matrix.
The Equation (13) indicates that the specific structure of category distribution consists of three separate components. The first component in Φi1 which includes Sik represents the deviation of instances from the central tendency of category (scatter matrix of instances). The first term in Φi0 represents the “harmonic mean” of nearby covariance matrices σ̂ij. The second term in Φi0 represents the scatter matrix Ŝij that characterizes local distribution of the central tendencies to nearby categories.
To understand the meaning of these components, we draw the geometric interpretation of these three components, the scatter matrix of instances Sik, the scatter matrix of categories Ŝij, and the harmonic mean of covariance matrices σ̂ij (Figure 5). The probabilistic density Qij weighting to each component exponentially decays in proportion to the “weighted distance” Fij between category ci and cj. This “weighted distance” is with respect to the distance between central tendencies and also the distance between covariance matrices. That means that interactions among categories are limited to a particular local region. In Figure 5b, the likelihood contours of the closest categories to a target category are shown as ellipses, and the probabilistic weighting Qij between the target category (center) and others is indicated by the shading. With respect to this locality, the scatter matrix of categories Ŝij reflects the variance pattern from the center of category ci to other relatively “close” category centers. The harmonic means of covariance matrices σ̂ij indicate the averaged covariance matrices among the closest categories. Note that it is a “harmonic” average, not an “arithmetic” one, because the inverse (reciprocal number) of the covariance matrix (and not the covariance matrix per se) is appropriate for the probabilistic density function with respect to inclusion and discriminability. The point of all this is that categories with similar patterns of covariance matrices that surround another category, will influence the surrounded category, distorting the feature weighting at the edges so that the surrounded category is more similar to the surrounding categories in its instance distributions.
Figure 5.
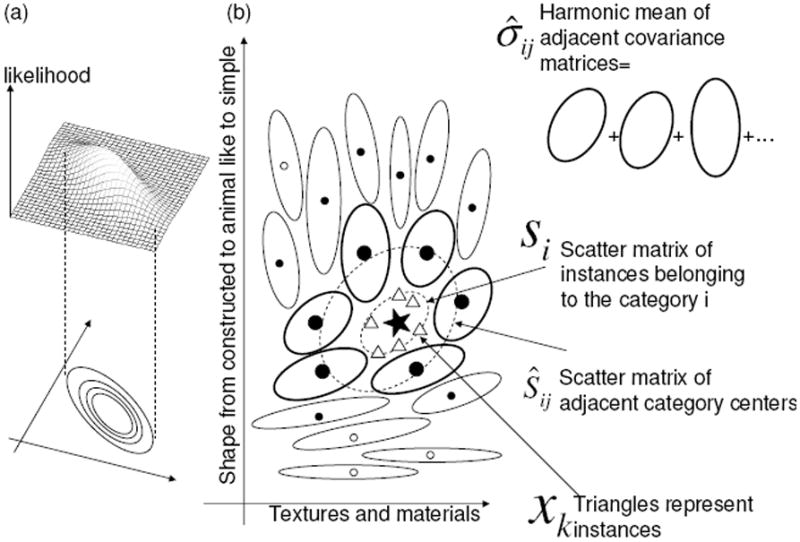
An illustration of the local interactions among adjacent categories according to the packing theory. Each ellipsis indicates equal-likelihood contour of category. The star shows a central tendency of a focal category, and triangles show the few experienced instances of this focal category. The covariance matrix of the focal category is estimated with deviation of instances (triangles; Sik), harmonic mean covariance matrix (ellipses) of adjacent categories (σ̂ij), and deviation of central tendencies (filled circles) of adjacent categories (Ŝij).
These effects depend on the proximity of the categories and the need to discriminate instances at the edge of the distributions of adjacent categories Si is covariance of instances belonging to a category, which is the natural statistical property with respect to the likelihood of instances without discriminability. The magnitude of Qij and Rik are quite influential in determining the weighting between the likelihood of the instances of a category and the discriminability between categories. If Qij → 0(j = 1, 2, …, N). Thus, if the distances of the central tendencies among categories increase (increasing gaps), the estimated category distribution will depend only on the covariance of instances Si. Meanwhile, if the number of experiences instances of categories decreases (i.e., Ki → 0 or Rik → 0(k = 1, 2, …, Ki)) but proximity to other categories remains the same, the estimated category distributions will depend more on discriminability, (Ŝij+σ̄ij)2. That is, when the number of known instances of some category is small, generalization to new instances will be more influenced by the known distributions of surrounding categories. However, when there are already many known instances of a category, the experiences instances - and the known distribution of that category - will have a greater effect on judgments of membership in that category (and a greater effect on surrounding categories).
Optimal solutions for mean vectors
In the previous section, the optimal solution of covariance matrices was derived for a given set of fixed mean vectors. The optimal solutions for mean vectors may also be written as eigenvectors of a quadratic eigenvalue problem. The differential of discriminability and inclusion with respect to the mean vectors are:
| (15) |
and
| (16) |
. Then
| (17) |
The equation is rewritten with N times larger order of matrix as follows.
| (18) |
In Equation 18, each term is as follows: , ,
| (19) |
,
| (20) |
, and
| (21) |
where Q̄ij = Qij(σi + σj)−1.
Since this equation indicates a typical form of the least square error with a constraint, it is also rewritten as a typical quadratic eigenvalue problem as follows (Tisseur & Meerbergen, 2001):
| (22) |
where Σ̄ = R̄Σ−1 R̄ and α2 = μT Φμ. Thus, the optimal mean vector μ is one of the eigenvectors given by this eigenvalue problem. This also suggests a similar structure as in the optimal solution for the covariance. The magnitude of Qij and Rik are quite influential in determining the weighting between the likelihood of the instances of a category and discriminability between categories. If the distances between all pairs of categories are infinite (i.e., Qij → 0(j = 1, 2, …, N)), the optimal mean vector mainly depends on mean vectors of instances (and the matrix assigning instances to categories) which is purely given by a set of instances (i.e., we obtain μ = R̄−1 x̄ by assuming Φ = 0 on Equation (22)). On the other hand, if the number of instances of categories decreases (i.e., Ki → 0 or Rij → 0(k = 1, 2, …, Ki)), the optimal mean vector depends on both central tendency x̄ and distribution Σ of instances (i.e., we obtain Φμ = λ−1Σ−1 x̄ by assuming R̄ = 0). Thus in the latter extreme situation, the central tendencies μ strongly depends on the estimated distribution of instances of each category Σ. In other words, this optimization of central tendencies also indicates the emergence of smooth categories, that is, there is predicted correlation between distances in central tendencies and distributions. This correlation between the distance of two categories and their feature distributions is a solution to the feature selection problem. The learner can know the relevant features for any individual category from neighboring categories.
Analysis 1: Is the Geometry of Natural Categories Smooth?
If natural categories reside in a packed feature space in which both discrimination and inclusion are optimized, then they should show a smooth structure. That is, near-by natural categories should not only have similar instances, but they should also have similar frequency distributions of features across those instances. Analysis 1 provides support for this prediction by examining the relation between the similarity of instances and the similarity of feature distributions for 48 basic level categories.
A central problem for this analysis is the choice of features across which to describe instances of these categories. One possibility that we considered and rejected was the use of features from feature generation studies (McRae et al., 2005; Rosch, Mervis, Gray, Johnson, & Boyes-Braem, 1976; Samuelson & Smith, 1999). In these studies, adults are given a category and asked to list the features characteristic of items in each category (e.g., has legs, made of wood, can be sat on). The problem with this approach is that the features listed by adults as important to those queried categories have (presumably) already been selected by whatever cognitive processes make categories coherent. Thus, there is the danger that the use of these generated features presupposes the very phenomenon one seeks to explain. Accordingly, we chose to examine a broad set of polar dimensions unlikely to be specifically offered as important to any of these categories. The specific features chosen do not need to be the exactly right features nor comprehensive. All they need to do is capture a portion of the similarity space in which instances and categories reside. If they do and if the packing analysis is right, these features should nonetheless define an n-dimensional space of categories, which shows some degree of smoothness: categories with instances similar to each other on these features should also show similar category likelihoods on these features.
To obtain this space, 16 polar opposites (e.g., wet-dry, noisy-quiet, weak-strong) were selected that broadly encompass a wide range of qualities (Osgood, Suci, & Tannenbaum, 1957; Hidaka & Saiki, 2004), that are also (by prior analyses) statistically uncorrelated (Hidaka & Saiki, 2004) but that neither by introspection nor by prior empirical studies seem to be specifically relevant to the particular categories examined in this study. In this way, we let the packing metric select the locally defined features.
The analysis is based on the assumption that categories with more variability in their feature distributions in the world will yield more variability in the subjects’ judgments about the relevant features. Thus, the mean of the subjects’ judgments for any category is used as an estimate of the mean of the feature distributions for the category and the covariance of the subjects’ judgments is used as an estimate of covariance.
Method
Participants
The participants were 104 undergraduate and graduate students at Kyoto University and Kyoto KokaWomen’s University.
Stimuli
Participants were tested in Japanese. The English translations of the 16 adjective pairs in English were dynamic-static, wet-dry, light-heavy, large-small, complex-simple, slow-quick, quiet-noisy, stable-unstable, cool-warm, natural-artificial, round-square, weak-strong, rough hewn-finely crafted, straight-curved, smooth-bumpy, hard-soft. The 48 noun categories, in English, are butterfly, cat, fish, frog, horse, monkey, tiger, arm, eye, hand, knee, tongue, boots, gloves, jeans, shirt, banana, egg, ice cream, milk, pizza, salt, toast, bed, chair, door, refrigerator, table, rain, snow, stone, tree, water, camera, cup, keys, money, paper, scissors, plant, balloon, book, doll, glue, airplane, train, car, bicycle. These nouns were selected to be common with early ages of acquisition (Fenson et al., 1994).
Procedure
Participants were presented with one noun at a time and asked to judge the applicability of the 16 adjective pairs on a 5-point scale. For example, if the adjective pair was small-big, and the noun was chair, participants would be asked to rate the size of typical instances of a chair on the scale of 1 (indicating small) to 5 (indicating big). The presented order of the list of 48 nouns by 16 dimension-rating scale was randomly determined and differed across subjects.
The Smoothness index
The adult judgments generate an initial space defined by the 48 noun categories and the mean and variance of the ratings of these nouns on the 16 polar dimensions. The mean μi and covariance σi of i-th category over instances, is defined as the central tendencies and generalization patterns (Equation 24).
| (23) |
| (24) |
where M is number of subjects (104) and dik is 16 dimensional column vector having k-th subjects’ adjective ratings of i-th category. The smoothness index of the given categories is defined by the correlation of central tendencies and covariance as follows:
| (25) |
where S is the smoothness index, a correlation coefficient between all possible paired distances of central tendencies ∥μi∥ and ∥σij∥. is the Euclidian distance of the paired central tendencies of category i and j (μi is the mean vector given as dimensional column vector). is the Euclidian distance of paired generalization patterns of category i and j (σi is covariance matrix given as dimensional square matrix). ∥μ̄∥ = N−1 Σi,j<i ∥μij∥ and ∥σ̄∥ = N−1 Σi,j<i ∥σij∥ with top bars indicates the mean of ∥μij∥ and ∥σij∥ respectively where N is number of possible combinations of pairs from n categories.
In sum, smoothness is measured as a correlation between the distance of categories, which is measured by the distances of the central tendencies, and the generalization pattern for each category, which is measured by the category’s covariance matrix. Accordingly, we calculated the distances of the central tendencies for each of the 48 categories to each other and the distances of the generalization patterns (the covariance matrices) for each of the 48 categories to each other. If categories that are near in the feature space have similar generalization patterns, than the two sets of distances should be correlated with each other. Because distances between the means of categories A and B are dependent of the distances between the means of categories B and C 3, we sampled independent paired distances in which no category appears in two different pairs. For 48 categories, the number of possible combinations of independent pairs is . We analyzed the median and the empirical distribution of 1000 such samplings. We also transformed the rating data using a logistic function, which corrects for the bounded rating scale. This corrected covariance σ̂ij and mean μ̂i (having range [−∞, ∞]) of dimensions i and j is defined by the following equation:
where μi is mean of i-th dimension (range 1 to 5), and pi is normalized mean having the range from zero to one. As the first differential with respect to corrected mean μ̂i of logistic function pi = (1 + exp(αμ̂i))−1 is proportional to pi(1 − pi) where α is a particular constant, we use this differential to transform mean and variance to theoretically homoscedastic space with mean μ̂i and covariance σ̂ij. The corrected mean μ̂i and covariance σ̂ij are used for the smoothness index instead of the raw mean μi and covariance σij. (See also Generalized Linear Model (McCullagh & Nelder, 1989) for the detail of logistic analysis.) As a supplemental measure, we also calculated smoothness by normalizing variance using a correlation matrix instead of a covariance matrix. The potential value of this approach is that it ignores artificial correlations between means and (the absolute value of) the variance.
Results and Discussion
Figure 6a shows a scatter plot of all possible pairs of categories; the x-axis is the Euclidian distance of the paired corrected mean vectors and the y-axis is the Euclidian distance of the paired corrected covariance matrices. The correlation between these two variables (with no dependence of paired distances) is the Smoothness index (See Equation 25 for its definition). The median correlation was 0.537 (95% confidence interval is from 0.223 to 0.756.). Figure 6b shows the same scatter plot using the correlation matrix instead of the covariance matrix as the measure of category likelihood; here the median correlation was 0.438 (95% confidence interval is from 0.137 to 0.699). These positive correlations between the distances of central tendencies and the distances of category likelihoods provide a first indication that natural categories may be smooth.
Figure 6.
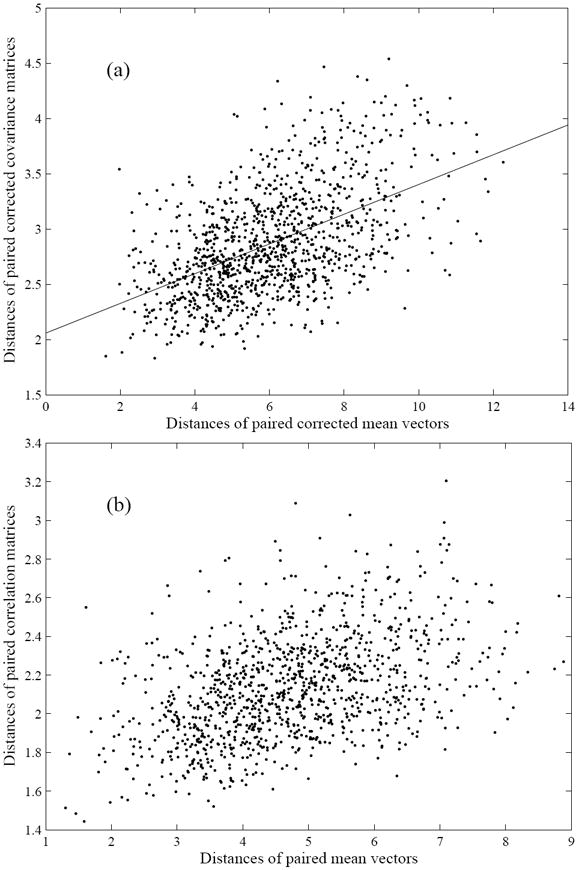
If a space is smooth then the nearness of the categories (distances of the means) and similarity of the generalization patterns should be correlated. The two figures differ in their respective measures of the similarity of the generalization patterns of categories: (a) Scatter plot of the Euclidean distances of the covariance matrices and the Euclidean distances of the means for pairs of categories. This correlation is the smoothness index, S=0.537. (b) Scatter plot of the Euclidean distances of the correlation matrices and the Euclidean distances of the means for pairs of categories, (S=0.438).
Figure 6 raises an additional possible insight. Not only do categories near each other in feature space show similar patterns of feature distribution, but across categories the changes in the feature distributions appear to be continuous, both in terms of location in the feature space and in terms of the feature likelihoods. This seamlessness of transitions within the space of categories is suggested by the linear structure of the scatter plot itself. This can emerge only if there are no big jumps or gaps in feature space or in the category likelihoods.
Critically, the features analyzed in this study were not pre-selected to particularly fit the categories and thus the observed smoothness seems unlikely to have arrived from our choice of features or a priori notions about the kind of features that are relevant for different kinds of categories. Instead, the similarity of categories on any set of features (with suffcient variance across the category) may be related to the distribution of those features across instances.
Categories whose instances are generally similar in terms of their range of features also exhibit similar patterns of feature importance. The mathematical analysis of Packing Theory indicates that this could be because of the optimization of discrimination and generalization in a geometry of crowded categories.
Analysis 2: Learning a New Category
According to Packing Theory, the generalization of a category to new instances depends not just on the instances that have been experienced for that category but also on the distributions of known instances for nearby categories. From one, or very few new instances, generalizations of a newly encountered category may be systematically aligned with the distributions of instances from surrounding categories. This is illustrated in Figure 7: a learner who already knows some categories (shown as solid ellipses in Figure 7a) and observes the first instance (a black star) of a novel category (a broken ellipsis) may predict the unknown generalization pattern shown by the broken ellipsis (Figure 7b). Because nearby categories have similar patterns of likelihoods, the system (via competition among categories and the joint optimization of inclusion and discrimination) can predict the likelihood of the unknown category, a likelihood that would also be similar to other known and nearby categories in the feature space. If categories did not have this property of smoothness, if they were distributed like that in Figure 7c, where each category has a variance pattern unrelated to those of nearby categories, the learner would have no basis on which to predict the generalization pattern. The goal of Analysis 2 is to show that the packing metric can predict the feature distribution patterns of categories unknown to the model. In the simulation, the model is given the mean and covariance of 47 categories (from Analysis 1) and then is given a single instance of the 48th category. The model’s prediction of the novel probabilistic density is calculated by an optimal solution with respect to the configuration of surrounding known noun categories.
Figure 7.
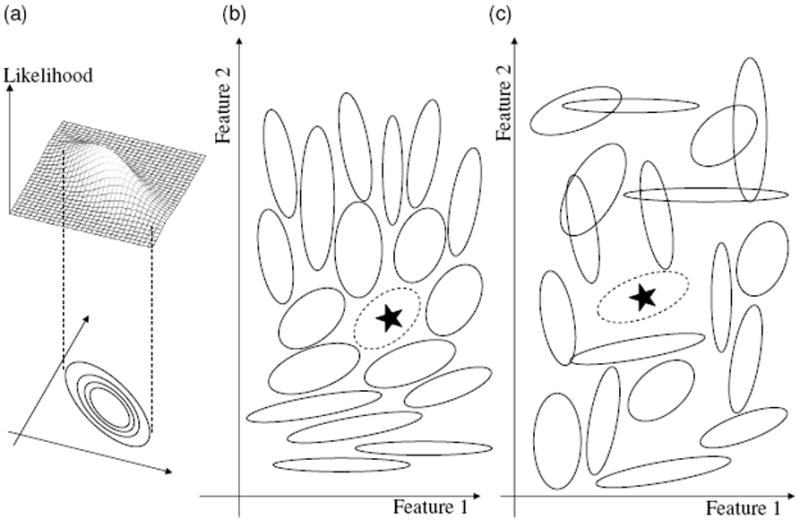
(a) Each ellipsis indicates the equal-likelihood contour. Two schematic illustrations of a (b) smooth (c) and non-smooth space of categories. The broken ellipsis in each figure indicates the equal-likelihood contour of the unknown category, and the star indicates a given first instance of that category. The solid ellipses indicate equal-likelihood contour of known categories. A smooth space of categories provides more information for predicting the likelihood of the novel category contour.
Method
On each trial of the simulation, one target category is assigned as unknown; the other 47 categories serve as the background categories that are assumed to be already learned. Each of the background-knowledge categories is assumed to have a normal distribution, and the model predicts the covariance matrix of the target category of the base on the given mean vectors and covariance matrices of the categories that comprise the model’s background knowledge. Because children are unlikely to have complete knowledge of any category, the mean and covariance for the background categories are estimated from a random sampling of 50% of the adult judgments. This is done 50 times with each of the 48 noun categories from Analysis1 serving as the target category.
Estimation of a novel category from the first instance
Within the packing model, the variance (and covariance) of the probabilistic density function is a critical determiner of the feature dimensions that are most important for a local region and category. Thus, to predict the distribution of instances for the target category, a category for which only one instance is given, we derive the covariance estimation for the whole category. To do this, we let the scatter matrix of category i be zero (i.e., Si ≈ 0) by assuming the first instance is close to the true mean (i.e., Ki = 1 and xil = μi). In addition, we assume that the unknown likelihood of the novel category takes the form Gi − log(C) where C is a particular constant. In particular, in case. Based on this assumption, we can obtain the covariance matrix of category Ci (σi) by solving the Equation (13). Then the optimal covariance of the novel category is given as follows:
| (26) |
where is derived from the constraint . Thus, estimated σi in Equation (26) optimize the packing metric, and it is considered as a special case of the general optimal solution when the covariance matrix of instances is collapsed to be zero (because there is the only instance). This equation indicates that a novel category with only instance can be estimated with harmonic mean of nearer known covariance matrices (σ̂ij) and nearer scatter matrix of weighted means (Ŝij). This directly means the covariance matrix of the novel category is estimated from the other covariance matrices of nearby categories.
We used Equation (26) in order to calculate a covariance matrix of a novel category σi from an instance sampled from the category (Ki = 1, xk = μi) and other known categories (μj and σj, j = 1, 2, …, i − 1, i + 1, …, 48). The scaling constant in Equation (26) is assumed to have the same determinant of covariance matrix as the target category as the adult judgment has (i.e, C = |Si| so as to have |σi| = |Si|).
Control comparisons
The packing metric predicts the distribution of instances in the target category by taking into account its general location (indicated by the one given instance) and the distributions of known instances for nearby categories. It is thus a geometric solution that derives not from what is specifically known about the individual category but from its position in a geometry of many categories. Accordingly, we evaluate this central idea and the packing model’s ability to predict the unknown distribution of instances by comparing the predictions of the packing model to two alternative measures of the distribution of instances in feature space for that target category that take into account only information about the target category and not information about neighboring categories. These two alternative measures are: (1) the actual distribution of all instances of the target category as given by the subjects in Analysis 1 and (2) three randomly selected instances from that subject generated distribution of instances. The comparison of the predictions of the packing metric to the actual distribution answers the question of how well the packing metric generates the full distribution given only a single instance but information about the distributions of neighboring categories. The second comparison answers the question of whether a single instance in the context of a whole geometry of categories provides better information about the shape of that category than more instances with no other information.
Results and Discussion
The predicted covariance of the target category by the packing model correlates strongly with the actual distribution of instances as generated by the subjects in Analysis 1. Specifically, the correlations between the packing metric predictions for the target category and measures of the actual distributions from Analysis 1 were 0.876, 0.578 and 0.559 for the covariances and variances (136 dimensions), the variances considered alone (16 dimensions) and the covariances considered alone (120 dimensions). These are robust correlations overall; moreover, they are considerably greater than those derived from an estimation of the target category from three randomly chosen instances. For this “control” comparison, we analyzed the correlation of covariance matrix for each category calculated from randomly chosen three instances of adults’ judgment with that calculated from the whole set of instances. Their average correlations of 50 different random set of samples were 0.2266 in variances (S.D.=0.2610), 0.2273 in covariance (S.D.=0.1393) and 0.4456 in both variance and covariance (S.D.=0.0655). The packing metric –given one instance and information about neighboring categories– does a better job predicting category shape than a prediction from three instances. In sum, the packing metric can generate the distribution of instances in a category using its location in a system of known categories. This result suggests that a developing system of categories should, when enough categories and their instances are known, enable the learner to infer the distribution of newly encountered categories from very few instances. A geometry of categories –and the local interactions among them– creates knowledge of possible categories.
There are several open questions with respect to the joint optimization of inclusion and discrimination should influence category development in children who will have sparser instances and sparser categories than do adults. The processes presumed by Packing Theory may be assumed to always be operation as they seem likely to reflect core operating characteristics (competition) of the cognitive system. But their effects will depend on the density of categories and instances in local regions of the space. An implication of the simulation is that the accuracy of novel word generalizations will be monotonic increasing function of number of categories. But here is what we do not know: As children learn categories, are some regions dense (e.g., dense animal categories) and other sparse (e.g., tools)? Are some regions of the space -even those with relatively many categories -sparse in the sense of relatively few experienced instances of any one category? Knowing just how young children’s category knowledge “scales up” is critical to testing the role of the joint optimization proposed by Packing Theory in children’s category development.
The formal analyses show that for the bias inherent in the joint optimization of discrimination and inclusion require many categories (crowding) and relatively many instances in these categories. This crowding will also depend on the dimensionality of the space as crowding is more likely in a lower than in a higher dimensional space, and we do not know the dimensionality of the feature space for human category judgments. This limitation does not matter for testing general predictions since the optimization depends only on distance relations in the space (and thus on the number of orthogonal, that is uncorrelated, dimensions but not on any assumptions about what orthogonal directions in that space constitute the dimensions) and since the prediction of smoothness should hold in any lower-dimensional characterization of the space. The specification of the actual dimensionality of the space also may not matter for relative predictions about more and less crowded regions of people’s space of categories. Still, insight into the dimensionality of the feature space of human categories would benefit an understanding of the development of the ability to generalize a new category from very few instances.
General Discussion
A fundamental problem in category learning is knowing the relevant features for to-be-learned categories. Although this is a difficult problem for theories of categorization, people, including young children, seem to readily solve the problem. The packing model provides a unified account of feature selection and fast mapping that begins with the insight that the feature distributions across the known instances of a category play a strong role, one that trumps overall similarity, in judgments as to whether some instance is a member of that category. This fact is often discussed in the categorization literature in terms of the question of whether instance distributions or similarity matter to category formation (Rips, 1989; Rips & Collins, 1993; Holland et al., 1986; Nisbett et al., 1983; Thibaut et al., 2002). The packing model takes role of instance distributions and ties it to similarity in a geometry of category in which nearby categories having similar category-relevant features, showing how this structure may emerge and how it may be used to learn new categories from very few instances. The packing model thus provides a bridge that connects the roles of instance distributions and similarity. The fitting of categories into a feature space is construed as the joint optimization of including known and possible instances and discriminating the instances belonging to different categories. The joint optimization of inclusion and discrimination aligns nearby categories such that their distributions of instances in the feature space are more alike. The chain reaction of these local interactions across the population of categories creates a smooth space. Categories that are similar (near in the space) have similar distributions of instances; categories that are dissimilar (far in the space) have more dissimilar distributions of instances.
In this way, the packing model provides the missing link that connects similarity to the likelihood of instances. Both similarity and feature distributions are deeply relevant to understanding how and why human categories have the structures that they do. However, the relevance is not with respect to the structure of a single category, but with respect to the structure of a population of categories. Smoothness implies a higher order structure, a gradient of changing feature relevance across the whole that is made out of, but transcends, the specific instances and the specific features of individual categories. It is this higher order structure that may be useable by learners in forming new categories. This higher order structure in the feature space aligns with what are sometimes called “kinds” or “superordinate categories” in that similar categories (clothes versus food for example) will have similar features of importance and be near each other in the space. However, there are no hard and fast boundaries and the packing does not directly represent these higher order categories. Instead, they are emergent in the patchwork of generalization gradients across the feature space. How such a space of probabilistic likelihoods of instances as members of basic level categories relates to higher and lower levels of categories (and the words one learns to name those categories) is an important question to be pursued in future work.
Packing Theory in relation to other topographic approaches
The packing model shares some core ideas with other topographic approaches such as self-organizing maps (SOM, see Kohonen, 1995; see also Tenenbaum, 2000; etc.). The central assumption underlying the algorithms used in SOM is that information coding is based on a continuous and smooth projection that preserves a particular topological structure. More particularly, within this framework, information coders (e.g., receptive fields, categories, memories) that are near each other code similar information whereas coders that are more distant code different types of information. Thus, SOM and other topographical representations posit a smooth representational space, just as the packing metric.
However, there are differences between the packing model and algorithms, such as SOM. In the packing metric, categories may be thought of as the information coders, but unlike the information coders in SOM, these categories begin with their own feature importance and their own location in the map, which is specified by the feature distributions of experienced instances. Within the packing model, local competition “tunes” feature importance across causes of the population of categories and creates a smooth space of feature relevance. SOM also posits a competition among information unites but of a fundamentally different kind. In the SOM algorithm, information coders do not explicitly have “their own type” of information. Rather it is the topological relation among information coders that implicitly specifies their gradients of data distribution. In the SOM learning process, the closest information units to an input is gradually moved to better fit the data point, and nearby points are moved to fit similar inputs. Thus nearby units end up coding similar inputs.
Topological algorithms such as SOM assume that a smooth structure is a good way to represent information and this assumption is well supported by the many successful applications of these algorithms (Kohonen, 1995). However, just why a smooth structure is “good” is not well specified. The packing metric might provide an answer from a psychological perspective. The packing neither assumes topological relations nor a smooth structure, but rather produces them through the joint optimization of discriminability and inclusion. Thus, a smooth space might be a good form of representation because of the trade off between discrimination and generalization.
Packing Theory in relation to other accounts of fast mapping
Fast Mapping is the term sometimes used to describe young children’s ability to map a noun to a whole category given just one instance (Carey & Bartlett, 1978). Packing Theory shares properties with two classes of current explanations of fast mapping in children: connectionist (Colunga & Smith, 2005; Roger & McClelland, 2004, see also, Hanson & Negishi, 2002 for a related model) and Bayesian approaches (Kemp, Perfors, & Tenenbaum, 2007; Xu & Tenenbaum, 2007). Like connectionist accounts, the packing model views knowledge about the different organization of different kinds as emergent and graded. Like rationalist accounts, the packing model is not a process model. Moreover, since the packing model is build upon a statistical optimality, it could be formally classified as a rationalist model (Anderson, 1990). Despite these differences, there are important similarities across all three approaches. Both the extant connectionist and Bayesian accounts of children’s smart noun generalizations consider category learning and generalization as a form of statistical inference. Thus, all three classes of models are sensitive to the feature variability within a set of instances. All agree on the main idea behind the packing model that feature variability within categories determines biases in category generalization. All three also agree that the most important issue to be explained is higher order feature selection, called variously second order generalizations (Smith, Jones, Landau, Gershkoff-Stowe, & Samuelson, 2002; Colunga & Smith, 2005), overhypotheses (Kemp, Perfors, & Tenenbaum, 2007), and smoothness (the packing model). Using the terms of Colunga and Smith (2005), the first order of generalization is about individual categories and it is a generalization over instances. The second order generalization is generalization of distribution of categories over categories. The central goal of all three approaches is to explain how people form higher-order generalizations.
There are also important and related differences among these approaches. The first set of differences concern whether or not the different levels are explicitly represented in the theory. Colunga and Smith’s (2005) connectionist account represents only input and output associations, the higher order representations of kind – that shape is more relevant for solid things than for nonsolid things, for example – are implicit in the structure of the input-output associations. They are not explicitly represented and they do not pre-exist in the learner prior to learning. In contrast, the Bayesian approach for the novel word generalization (Kemp et al., 2007; Xu & Tenenbaum, 2007) has assumed categories structured as a hierarchical tree. The learner knows from the start that there are higher order and lower order categories in a hierarchy. Although the packing model is rationalist in approach, it is emergentist in spirit: Smoothness is not an a priori expectation and is not explicitly represented as higher order variable but is an emergent and graded property of the population as a whole. As it stands, the Packing model also makes no explicit distinction between learned categories at different levels such as the learning of categories of animal as dog, for example. The present model is considered only basic level categories and thus is moot on this point. However, one approach that the packing metric could take with respect to this issue is to represent all levels of categories in the same geometry, with many overlapping instances, letting the joint optimization of inclusion and discrimination find the stable solution given the distributional evidence on the inclusion and discrimination of instances in the overlapping categories. This approach might well capture some developmental phenomena. For example, children’s tendency to agree that unknown animals are “animals” but that well known ones (e.g., dogs) are not. Within this extended framework, one might also want to include, outside of the packing model itself, real-time processes that perhaps activate a selected map of categories in working memory or that perhaps contextually shift local feature gradients, enabling classifiers to flexibly shift between levels and kinds of categories and to form ad hoc categories (Barsalou, 1985; Spencer, Perone, Smith, & Samuelson, in preparation).
The second and perhaps most crucial difference between packing theory and the other two accounts is the ultimate origin of the higher order knowledge about kinds. For connectionist accounts, the higher order regularities are latent structure in the input itself. If natural categories are smooth, by this view, it is solely because the structure of the categories in the world is smooth and the human learning system has the capability to discover that regularity. However, if this is so, one needs to ask (and answer) why the to-be-learned categories have the structure that they do. For the current Bayesian accounts, a hierarchical representational structure (with variabilized over-hypotheses) is assumed and fixed (but see the other approach that learns the structure (Kemp & Tenenbaum, 2008). These over-hypotheses create a tree of categories in which categories near the tree will have similar structure. Again, why the system would have evolved to have such an innate structure is not at all clear. Moreover, the kind of mechanisms or neural substrates in which such hierarchical pre-ordained knowledge resides is also far from obvious.
The packing model provides answers and new insights to these issues that put smoothness neither in the data nor as a pre-specified outcome. Instead, smoothness is emergent in the local interactions of fundamental processes of categorization, inclusion, and discrimination. As the proof and analyses show, the joint optimization of discriminability and inclusion leads to smooth categories, regardless of the starting point. The packing model thus provides answer as to why categories are the way they are and why they are smooth. The answer is not that categories have the structure they do in order to help children learn them; the smoothness of categories in feature space is not a pre-specification of what the system has to learn as in the current Bayesian accounts of children’s early word learning (although the smoothness of geometry of categories is clearly exploitable). Rather, according to Packing Theory, the reason categories have the structure they do lies in local function of categories, in the first place: to include known and possible instances but to discriminate among instances falling in different categories. The probabilistic nature of inclusion and discrimination, the frequency distributions of individual categories, the joint optimization of discrimination, and inclusion in a connected geometry of many categories creates a gradient of feature relevance that is then useable by learners. For natural category learning, for categories that are passed on from one generation to the next, the optimization of inclusion and discrimination over these generations may make highly common and early-learned categories particularly smooth. Although the packing model is not a process model, processes of discrimination and inclusion and processes of competition in a topographical representation are well studied at a variety of levels of analysis and thus bridges between this analytic account and process accounts seem plausible.
Testable Predictions
The specific contribution of this paper is a mathematical analysis that shows that the joint optimization of inclusion and discrimination yields a smooth space of categories and that given such a smooth space that optimization can also accurately predict the instance distributions of a new category specified only by the location of a single instance. What is needed beyond this mathematical proof is empirical evidence that shows that the category organizations and processes proposed by the packing model are actually observable in human behavior. The present paper provide a first step by indicating that the feature space of early-learned noun categories may be smooth (and smooth enough to support fast mapping). Huttenlocher et al (2007) have reported empirical evidence that also provides support for local competitions among neighboring categories. Huttenlocher et al’s (2007) method provides a possible way to test specific predictions from Packing Theory in adults.
The local interactions that create smoothness also raise new and testable hypotheses about children’s developing category knowledge. Because these local competitions depend on the frequency distributions over known instances and the local neighborhood of known categories, there should be observable and predictable changes as children’s category knowledge “scales up”. Several developmental predictions follow: (1) Learners who know (or are taught) a sufficiently large and dense set of categories, should form and generalize a geometry of categories that is smoother than that given by the known instances. (2) The generalization of any category trained with a specific set of instances should depend on the instance distributions of surrounding categories and be distorted in the direction of the surrounding categories; thus, children should show smoother category structure and smarter novel noun generalizations in denser category regions than sparser ones. (3) The effects of learning a new category on surrounding categories or surrounding on new categories should depend in formally predictable ways on the feature distributions of those categories.
Conclusion
Categories (and their instances) do not exist in isolation but reside in a space of many other categories. The local interactions of these categories create a gradient of higher order structure - different kinds with different feature distributions. This structure emergent from the interactions of many categories in a representational space constrains the possible structure of both known and unknown categories. Packing Theory captures these ideas in the joint optimization of discrimination and generalization.
Acknowledgments
This study is based on in part on the PhD thesis of the first author. The authors thank Dr. Jun Saiki and Dr. Toshio Inui for their discussion on this work. This study was supported by grants from NIH MH60200.
Appendix: Derivation of differential with respect to covariance matrix
We derive Equation (11) and (12) by expanding and . For the derivation, we use the vectorizing operator v(X) which form a column vector from a given matrix X (See also Magnus & Neudecker, 1988; Turkington, 2002 for the matrix algebra). A useful formula on vectorizing operator is as follows. For A: m × n matrix and B: n × p matrix,
where Im is m-th order identity matrix and ⊗ denotes Kronecker product. Moreover, we use the following formulae in order to expand the differential with respect to a matrix (See also Turkington, 2002). For d × d matrices X, Y, Z and a constant matrix A which is not function of X,
where xk and λk are respectively k-th eigenvector and eigenvalue of a d-th order real symmetric matrix X. We derive Equation (11) from Equation (8) using formulae above,
where σ̄ij = σi + σj and Δμij = μi − μj. And note that and are used for the last line. Thus, we obtain Equation (11). Likewise the derivation of Equation (11), we derive Equation (12) from Equation (2) as follows.
Next, we derive Equation (13) using formula for the differential with respect to eigenvector as follows.
Since |ηilID − σi| = 0 is obvious by definition, is necessary in order to obtain non-obvious solution for . Therefore, we obtain Equation (13).
Footnotes
Since the matrix in Equation (13) includes σ̂ij or Ŝij which has σi inside, it is not a typical eigenvalue problem, which has a fixed matrix. Equation (13) can be considered an eigenvalue problem only when σi is given. Thus, iterative method for eigenvalue problems such as the power iteration method would be preferable to calculate numerical values.
Although too few instances may cause a non-full-rank covariance matrix whose determinant is zero (i.e., |σi| = 0), in this special case, we still assume a particular variability |σi| = C. See also Method in Analysis 4.
In fact, for arbitrary points A, B, and C, the triangle inequality |AB| + |BC| > |CA| is true, where |AB| is a metric between point A and B.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Anderson JR. The adaptive character of thought. Hillsdale, NJ: Lawrence Erlbaum Associates; 1990. [Google Scholar]
- Ashby GF, Townsend JT. Varieties of perceptual independence. Psychological Review. 1986;93:154–179. [PubMed] [Google Scholar]
- Barsalou LW. Ideals, central tendency, and frequency of instantiation as determinants of graded structure in categories. Journal of experimental psychology Learning, memory, and cognition. 1985;11:629–654. doi: 10.1037//0278-7393.11.1-4.629. [DOI] [PubMed] [Google Scholar]
- Beck DM, Kastner S. Top-down and bottom-up mechanisms in biasing competition in the human brain. Vision Research. 2009;49:1154–1165. doi: 10.1016/j.visres.2008.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Booth AE, Waxman S. Word learning is ‘smart’: Evidence that conceptual information affects preschoolers’ extension of novel words. Cognition. 2002;84:B11–B22. doi: 10.1016/s0010-0277(02)00015-x. [DOI] [PubMed] [Google Scholar]
- Carey S, Bartlett E. Acquiring a single new word. Papers and reports on child language development. 1978;15:17–29. [Google Scholar]
- Colunga E, Smith L. From the lexicon to expectations about kinds: A role for associative learning. Psychological Review. 2005;112:347–382. doi: 10.1037/0033-295X.112.2.347. [DOI] [PubMed] [Google Scholar]
- Colunga E, Smith LB. Flexibility and variability: Essential to human cognition and the study of human cognition. New Ideas in Psychology. 2008;26(2):174–192. [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the em algorithm. Journal of Royal Statistical Society Series B. 1977;39:1–38. [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern classification. 2. New York: John Wiley & Sons; 2000. [Google Scholar]
- Duncan J. Cooperating brain systems in selective perception and action. Attention and performance XVI: information integration. 1996;18:193–222. [Google Scholar]
- Fenson L, Dale PS, Reznick JS, Bates E, Thal DJ, Pethick SJ. Variability in early communicative development. Monogr Soc Res Child Dev. 1994;59:1–173. [PubMed] [Google Scholar]
- Gathercole VCM, Min H. Word meaning biases or language-specific effects? evidence from english, spanish, and korean. First Language. 1997;17(49):31–56. [Google Scholar]
- Gelman SA, Coley JD. Perspectives on language and thought: Interrelations in development. In: German SA, Byrnes JP, editors. chap Language and categorization: the acquisition of natural kind terms. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Griffiths TL, Steyvers M, Tenenbaum JB. Topics in semantic representation. Psychological Review. 2007;114:2. doi: 10.1037/0033-295X.114.2.211. [DOI] [PubMed] [Google Scholar]
- Hanson SJ, Negishi M. On the emergence of rules in neural networks. Neural computation. 2002;14:2245–2268. doi: 10.1162/089976602320264079. [DOI] [PubMed] [Google Scholar]
- Hidaka S, Saiki J. A mechanism of ontological boundary shifting. The twenty sixth annual meeting of the cognitive science society. 2004:565–570. [Google Scholar]
- Holland JH, Holyoak KJ, Nisbett RE, Thagard PR. Induction. Cambridge, MA: MIT Press; 1986. [Google Scholar]
- Huttenlocher J, Hedges LV, Lourenco SF, Crawford LE, Corrigan B. Estimating stimuli from contrasting categories: Truncation due to boundaries. Journal of Experimental Psychology: General. 2007;136(3):502–519. doi: 10.1037/0096-3445.136.3.502. [DOI] [PubMed] [Google Scholar]
- Imai M, Gentner D. A cross-linguistic study of early word meaning: universal ontology and linguistic influence. Cognition. 1997;62:169–200. doi: 10.1016/s0010-0277(96)00784-6. [DOI] [PubMed] [Google Scholar]
- Jones SS, Smith L. How children know the relevant properties for generalizing object names. Developmental Science. 2002;5:219–232. [Google Scholar]
- Jones SS, Smith LB, Landau B. Object properties and knowledge in early lexical learning. Child development. 1991;62:499–516. [PubMed] [Google Scholar]
- Keil FC. Mapping the mind: Domain specificity in cognition and culture. In: Hirschfeld LA, Susan SA, Gelman A, editors. chap The birth and nurturance of concepts by domains: The origins of concepts of living things. MA: Cambridge University Press; 1994. [Google Scholar]
- Kemp C, Perfors A, Tenenbaum JB. Learning overhypotheses with hierarchical bayesian models. Developmental Science. 2007;10(3):307–321. doi: 10.1111/j.1467-7687.2007.00585.x. [DOI] [PubMed] [Google Scholar]
- Kemp C, Tenenbaum JB. The discovery of structural form. Proceedings of the National Academy of Sciences. 2008;105(31):10687–10692. doi: 10.1073/pnas.0802631105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kloos H, Sloutsky VM. What’s behind different kinds of kinds: Effects of statistical density on learning and representation of categories. Journal of Experimental Psychology: General. 2008;137:52–75. doi: 10.1037/0096-3445.137.1.52. [DOI] [PubMed] [Google Scholar]
- Kobayashi H. How 2-year-old children learn novel part names of unfamiliar objects. Cognition. 1998;68:B41–B51. doi: 10.1016/s0010-0277(98)00044-4. [DOI] [PubMed] [Google Scholar]
- Kohonen T. Self-organizing maps. Heidelberg: Springer; 1995. [Google Scholar]
- Landau B, Smith LB, Jones S. Syntactic context and the shape bias in children’s and adults’ lexical learning. Journal of Memory and Language. 1992 Dec;31(6):807–825. [Google Scholar]
- Landau B, Smith LB, Jones SS. Object shape, object function, and object name. Journal of Memory and Language. 1998;38:1–27. [Google Scholar]
- Macario JF. Young children’s use of color in classification: Foods and canonically colored objects. Cognitive Development. 1991;6:17–46. [Google Scholar]
- Magnus JR. Linear structure. Oxford: Oxford University Press; 1988. [Google Scholar]
- Markman EM. Categorization and naming in children: Problems of induction. Cambridge, MA: MIT Press; 1989. [Google Scholar]
- Marslen-Wilson WD. Functional parallelism in spoken word-recognition. Cognition. 1987;25:71–102. doi: 10.1016/0010-0277(87)90005-9. [DOI] [PubMed] [Google Scholar]
- McCullagh P, Nelder JA. Generalized linear models. 2. Chapman & Hall; 1989. [Google Scholar]
- McRae K, Cree GS, Seidenberg MS, McNorgan C. Semantic feature production norms for a large set of living and nonliving things. Behavior Reserch Methods, Instruments, & Computers. 2005;37:547–559. doi: 10.3758/bf03192726. [DOI] [PubMed] [Google Scholar]
- Murphy G, Medin DL. The role of theories in conceptual coherence. Psychological Review. 1985;92:289–316. [PubMed] [Google Scholar]
- Nisbett R, Krantz D, Jepson C, Kunda Z. The use of statistical heuristics in everyday inductive reasoning. Psychological Review. 1983;90:339–363. [Google Scholar]
- Nosofsky RM. Attention, similarity and the identification-categorization relationship. Journal of Experimental Psychology: Learning Memory, and Cognitition. 1986;15:39–57. doi: 10.1037//0096-3445.115.1.39. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Palmeri TJ, McKinley SC. Rule-plus-exception model of classification learning. Psychological Review. 1994;101:53–79. doi: 10.1037/0033-295x.101.1.53. [DOI] [PubMed] [Google Scholar]
- Osgood CE, Suci GJ, Tannenbaum PH. The measurement of meaning. Urbana, IL: University of Illinois Press; 1957. [Google Scholar]
- Rips LJ. Similarity, typicality, and categorization. In: Vosniadou S, Ortony A, editors. Similarity and analogical reasoning. Cambridge, England: Cambridge University Press; 1989. [Google Scholar]
- Rips LJ, Collins A. Categories and resemblance. Journal of Experimental Psychology: General. 1993;122:468–486. doi: 10.1037//0096-3445.122.4.468. [DOI] [PubMed] [Google Scholar]
- Rogers TT, McClelland JM. Semantic cognition: A parallel distributed processing approach. Cambridge, MA: The MIT Press; 2004. [DOI] [PubMed] [Google Scholar]
- Rosch E, Mervis CB, Gray WD, Johnson DM, Boyes-Braem P. Basic objects in natural categories. Cognitive Psychology. 1976;8:382–439. [Google Scholar]
- Samuelson LK, Smith LB. Early noun vocabularies: do ontology, category structure and syntax correspond? Cognition. 1999;73:1–33. doi: 10.1016/s0010-0277(99)00034-7. [DOI] [PubMed] [Google Scholar]
- Shepard RN. Stimulus and response generalization: Tests of a model relating generalization to distance in psychological space. Journal of Experimental Psychology. 1958;55:509–523. doi: 10.1037/h0042354. [DOI] [PubMed] [Google Scholar]
- Smith LB, Jones SS, Landau B, Gershkoff-Stowe L, Samuelson L. Object name learning provides on-the-job training for attention. Psychological Science. 2002;13:13–19. doi: 10.1111/1467-9280.00403. [DOI] [PubMed] [Google Scholar]
- Soja NN, Carey S, Spelke ES. Ontological categories guide young children’s inductions of word meanings: object terms and substance terms. Cognition. 1991;38:179–211. doi: 10.1016/0010-0277(91)90051-5. [DOI] [PubMed] [Google Scholar]
- Spencer JP, Perone S, Smith LB, Samuelson L. Non-bayesian noun generalization from a capacity-limited system. Manuscript in preparation. in preparation. [Google Scholar]
- Stewart N, Chater N. The effect of category variability in perceptual categorization. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2002;28:893–907. doi: 10.1037//0278-7393.28.5.893. [DOI] [PubMed] [Google Scholar]
- Steyvers M, Tenenbaum JB. The large-scale structure of semantic networks: Statistical analyses and a model of semantic growth. Cognitive Science. 2005;29:41–78. doi: 10.1207/s15516709cog2901_3. [DOI] [PubMed] [Google Scholar]
- Swingley D, Aslin RN. Lexical competition in young children’s word learning. Cognitive Psychology. 2007;54:99–132. doi: 10.1016/j.cogpsych.2006.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tenenbaum JB, Silva V de, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science. 2000;290:2319–2323. doi: 10.1126/science.290.5500.2319. [DOI] [PubMed] [Google Scholar]
- Thibaut JP, Dupont M, Anselme P. Dissociations between categorization and similarity judgments as a result of learning feature distributions. Memory & Cognition. 2002;30(4):647–656. doi: 10.3758/bf03194966. [DOI] [PubMed] [Google Scholar]
- Tisseur F, Meerbergen K. The quadratic eigenvalue roblem. SIAM Review. 2001;43(2):235–286. [Google Scholar]
- Turkington DA. Matrix calculus and zero-one matrices: Statistical and econometric applications. Cambridge, MA: Cambridge University Press; 2002. [Google Scholar]
- Tversky A, Hutchinson JW. Nearest neighbor analysis of psychological spaces. Psychological Review. 1986;93:3–22. [Google Scholar]
- Xu F, Tenenbaum J. Word learning as bayesian inference. Psychological Review. 2007;114:245–272. doi: 10.1037/0033-295X.114.2.245. [DOI] [PubMed] [Google Scholar]
- Yoshida H, Smith LB. Early noun lexicons in english and japanese. Cognition. 2001;82:63–74. doi: 10.1016/s0010-0277(01)00153-6. [DOI] [PubMed] [Google Scholar]
- Yoshida H, Smith LB. Shifting ontological boundaries: how japanese- and english- speaking children generalize names for animals and artifacts. Developmental Science. 2003;6:1–34. [Google Scholar]
- Zeigenfuse MD, Lee MD. Finding the features that represent stimuli. Acta Psychologica. 2009;133:283–295. doi: 10.1016/j.actpsy.2009.07.014. [DOI] [PubMed] [Google Scholar]


