Abstract
A number of settings arise in which it is of interest to predict Principal Component (PC) scores for new observations using data from an initial sample. In this paper, we demonstrate that naive approaches to PC score prediction can be substantially biased towards 0 in the analysis of large matrices. This phenomenon is largely related to known inconsistency results for sample eigenvalues and eigenvectors as both dimensions of the matrix increase. For the spiked eigenvalue model for random matrices, we expand the generality of these results, and propose bias-adjusted PC score prediction. In addition, we compute the asymptotic correlation coefficient between PC scores from sample and population eigenvectors. Simulation and real data examples from the genetics literature show the improved bias and numerical properties of our estimators.
Keywords and phrases: PCA, PC Scores, Random Matrix, PC Regression
1. Introduction
Principal component analysis (PCA) [19] is one of the leading statistical tools for analyzing multivariate data. It is especially popular in genetics/genomics, medical imaging, and chemometrics studies where high-dimensional data is common. PCA is typically used as a dimension reduction tool. A small number of top ranked principal component (PC) scores are computed by projecting data onto spaces spanned by the eigenvectors of sample covariance matrix, and are used to summarize data characteristics that contribute most to data variation. These PC scores can be subsequently used for data exploration and/or model predictions. For example, in genome-wide association studies (GWAS), PC scores are used to estimate ancestries of study subjects and as covariates to adjust for population stratification [24, 27]. In gene expression microarray studies, PC scores are used as synthetic “eigen-genes” or “meta-genes” intended to represent and discover gene expression patterns that might not be discernible from single-gene analysis [30].
Although PCA is widely applied in a number of settings, much of our theoretical understanding rests on a relatively small body of literature. Girshick [12] introduced the idea that the eigenvectors of sample covariance matrix are maximum likelihood estimators. Here a key concept in a population view of PCA is that the data arise as p-variate values from a distinct set of n independent samples. Later, the asymptotic distribution of eigenvalues and eigenvectors of the sample covariance matrix (i.e., the sample eigenvalues and eigenvectors) were derived for the situation where n goes to infinity and p is fixed [2, 13]. With the development of modern high-throughput technologies, it is not uncommon to have data where p is comparable in size to n, or substantially larger. Under the assumption that p and n grow at the same rate, that is p/n → γ > 0, there has been considerable effort to establish convergence results for sample eigenvalues and eigenvectors (see review [5]). The convergence of the sample eigenvalues and eigenvectors under the “spiked population” model proposed by Johnstone [18] has also been established[7, 23, 26]. For this model it is well known that the sample eigenvectors are not consistent estimators of the eigenvectors of population covariance (i.e., the population eigenvectors) [17, 23, 26]. Furthermore, Paul [26] has derived the degree of discrepancy in terms of the angle between the sample and population eigenvectors, under Gaussian assumptions for 0 < γ < 1. More recently, Nadler [23] has extended the same result to the more general γ > 0 using a matrix perturbation approach.
These results have considerable potential practical utility in understanding the behavior of PC analysis and prediction in modern datasets, for which p may be large. The practical goals of this paper focus primarily on the prediction of PC scores for samples which were not included in the original PC analysis. For example, gene expression data of new breast cancer patients may be collected, and we might want to estimate their PC scores in order to classify their cancer sub-type. The recalculation of PCs using both new and old data might not be practical, e.g. if the application of PCs from gene expression is used as a diagnostic tool in clinical applications. For GWAS analysis, it is known that PC analysis which includes related individuals tends to generate spurious PC scores which do not reflect the true underlying population substructures. To overcome this problem, it is common practice to include only one individual per family/sibship in the initial PC analysis. Another example arises in cross-validation for PC regression, in which PC scores for the test set might be derived using PCA performed on the training set [16]. For all of these applications, the predicted PC scores for a new sample are usually estimated in the “naive” fashion, in which the data vector of the new sample is multiplied by the sample eigenvectors from the original PC analysis. Indeed, there appears to be relatively little recognition in the genetics or data mining literature that this approach may lead to misleading conclusions.
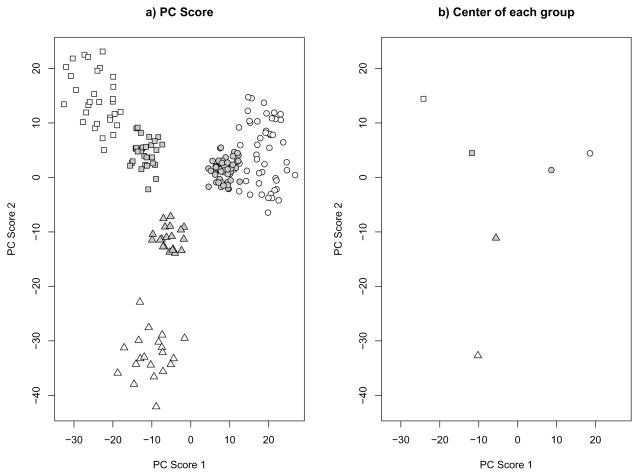
For low dimensional data, where p is fixed as n increases or otherwise much smaller than n, the predicted PC scores are nearly unbiased and well-behaved. However, for high-dimensional data, particularly with p > n, they tend to be biased and shrunken towards 0. The following simple example of a stratified population with three strata illustrates the shrinkage phenomenon for predicted PC scores. We generated a training data set with n = 100 and p = 5000. Among the 100 samples, 50 are from stratum 1, 30 are from stratum 2 and the rest from stratum 3. For each stratum, we first created a p-dimensional mean vector μk (k = 1, 2, 3). Each element of each mean vector was created by drawing randomly with replacement from {−0.3, 0, 0.3}, and thereafter considered a fixed property of the stratum. Then for each sample from the kth stratum, its p covariates were simulated from the multivariate normal distribution MVN(μk, 4I), where I is the p×p identity matrix. A test dataset with the same sample size and μk vectors was also simulated. Figure 1 shows that the predicted PC scores for the test data are much closer to 0 compared to the scores from the training data. This shrinkage phenomenon may create a serious problem if the predicted PC scores are used to classify new test samples, perhaps by similarity to previous apparent clusters in the original data. In addition, the predicted PC scores may produce incorrect results if used for downstream analyses (e.g., as covariates in association analyses).
Fig 1.
Simulation results for p=5000 and n=(50,30,20). Different symbols represent different groups. White background color represents the training set and grey background color represents the test set. A) First 2 PC score plot of all simulated samples. B) Center of each group.
In this paper, we investigate the degree of shrinkage bias associated with the predicted PC scores, and then propose new bias-adjusted PC score estimates. As the shrinkage phenomenon is largely related to the limiting behavior of the sample eigenvectors, our first step is to describe the discrepancy between the sample and population eigenvectors. To achieve this purpose, we follow the assumption that p and n both are large and grow at the same rate. By applying and extending results from random matrix theory, we establish the convergence of the sample eigenvalues and eigenvectors under the spiked population model. We generalize Theorem 4 of Paul [26], which describes the asymptotic angle between sample and population eigenvectors, to non-Gaussian random variables for any γ > 0. We further derive the asymptotic angle between PC scores from sample eigenvectors and population eigenvectors, and the asymptotic shrinkage factor of the PC score predictions. Finally we construct estimators of the angles and the shrinkage factor. The theoretical results are presented in Section 2.
In section 3, we report simulations to assess the finite sample accuracy of the proposed asymptotic angle and shrinkage factor estimators. We also show the potential improvements in prediction accuracy for PC regression by using the bias adjusted PC scores. In section 4, we apply our PC analysis to a real genome-wide association study, which demonstrates that the shrinkage phenomenon occurs in real studies and that adjustment is needed.
2. Method
2.1. General Setting
Throughout this paper, we use T to denote matrix transpose, to denote convergence in probability, and to denote almost sure convergence. Let Λ = diag(λ1, λ2, …, λp), a p × p matrix with λ1 ≥ λ2 ≥ ··· ≥ λp, and E = [e1, …, ep], a p × p orthogonal matrix.
Define the p × n data matrix, X as [x1, …, xn], where xj is the p-dimensional vector corresponding to the jth sample. For the remainder of the paper, we assume the following:
Assumption 1
X = EΛ1/2Z, where Z = {zij} is a p × n matrix whose elements zijs are i.i.d random variables with E(zij) = 0, and .
Although the zijs are i.i.d, Assumption 1 allows for very flexible covariance structures for X, and thus the results of this paper are quite general. The population covariance matrix of X is Σ = EΛET. The sample covariance matrix S equals
The λks are the underlying population eigenvalues. The spiked population model defined in [18] assumes that all the population eigenvalues are 1, except the first m eigenvalues. That is, λ1 ≥ λ2 ··· ≥ λm > λm+1 = ··· = λp = 1. The spectral decomposition of the sample covariance matrix is
where D = diag(d1, d2, …, dp) is a diagonal matrix of the ordered sample eigenvalues and U = [u1, …, up] is the corresponding p × p sample eigen-vector matrix. Then the PC score matrix is P = [p1, p2, …, pn], where is the vth sample PC score. For a new observation xnew, its predicted PC score is similarly defined as UT xnew with the vth (PC) score equal to .
2.2. Sample Eigenvalues and Eigenvectors
Under the classical setting of fixed p, it is well known that the sample eigenvalues and eigenvectors are consistent estimators of the corresponding population eigenvalues and eigenvectors [3]. Under the “large p, large n” framework, however, the consistency is not guaranteed. The following two lemmas summarize and extend some known convergence results.
Lemma 1
Let p/n → γ ≥ 0 as n → ∞.
- When γ = 0,
(1) -
When γ > 0,
(2) where k is the number of λv greater than , and ρ(x) = x(1+γ/(x − 1)).
The result in ii) is due to Baik and Silverstein [7], while the proof of i) can be found in section (6.3). The result in i) shows that when γ = 0, the sample eigenvalues converge to the corresponding population eigenvalues, which is consistent with the classical PC result where p is fixed. The result in ii) shows that for any non-zero γ, dv is no longer a consistent estimator of λv. However, a consistent estimator of λv can be constructed from Equation (2). Define
Then ρ−1(dv) is a consistent estimator of λv when . Furthermore, Baik et al. [6] have shown the -consistency of dv to ρ(λv), and Bai and Yao [4] have shown that dv is asymptotically normal.
Lemma 2
Suppose p/n → γ ≥ 0 as n → ∞. Let < ., . > be an inner product between two vectors. Under the assumption of multiplicity one,
- if 0 < γ < 1, and the zijs follow the standard normal distribution, then
(3) -
removing the normal assumption on the zijs, the following weaker convergence result holds for all γ ≥ 0
(4) Here .
The inner product between unit vectors is the cosine angle between these two. Thus, Lemma 2 shows the convergence of the angle between population and sample eigenvectors. For i), Paul [26] proved it for γ < 1; while Nadler [23] obtained the same conclusion for γ > 0 using the matrix perturbation approach under the Gaussian random noise model. We relax the Gaussian assumption on z and prove ii) for γ ≥ 0 in section 6.4. The result of ii) is general enough for the application of PCA to, for example, genome-wide association mapping, where each entry of X is a standardized variable of SNP genotypes, which are typically coded as {0, 1, 2}, corresponding to discrete genotypes.
2.3. Sample and Predicted PC Scores
In this section, we first discuss convergence of the sample PC scores, which forms the basis for the investigation of the shrinkage phenomenon of the predicted PC scores. For the sample PC scores, we have
Theorem 1
Let , the normalized vth PC score derived from a corresponding population eigenvector, ev, and , the normalized vth sample PC score. Suppose p/n → γ ≥ 0 as n → ∞. Under the multiplicity one assumption,
| (5) |
The proof can be found in section 6.7. In PC analysis, the sample PC scores are typically used to estimate certain latent variables (largely the PC scores from population eigenvectors) that represent the underlying data structures. The above result allows us to quantify the accuracy of the sample PC scores. Note that here < gv, p̃v > is the correlation coefficient between gv and p̃v. Compared to Equation (3) in Lemma 2, the angle between the PC scores is smaller than the angle between their corresponding eigenvectors.
Before we formally derive the asymptotic shrinkage factor for the predicted PC scores, we first describe in mathematical terms the shrinkage phenomenon that was demonstrated in the Introduction. Note that the first population eigenvector e1 satisfies
for a random vector x that follows the same distribution of the xjs. For the data matrix X, its first sample eigenvector u1 satisfies
Assuming that u1 and the new sample xnew are independent of each other, we have
| (6) |
Since the follow the same distribution,
| (7) |
By (6) and (7), we can show that
which demonstrates the shrinkage feature of the predicted PC scores. The amount of the shrinkage, or the asymptotic shrinkage factor, is given by the following theorem:
Theorem 2
Suppose p/n → γ ≥ 0 as n → ∞, . Under the multiplicity one assumption,
| (8) |
where pvj is the jth element of pv.
The proof is given in section 6.8. We call (λv − 1)/(λv + γ − 1), the (asymptotic) shrinkage factor for a new subject. As shown, the shrinkage factor is smaller than 1 if γ > 0. Quite sensibly, it is a decreasing function of γ and an increasing function of λv. The bias of the predicted PC score can be potentially large for those high dimensional data where p is substantially greater than n, and/or for the data with relatively minor underlying structures where λv is small.
2.4. Rescaling of sample eigenvalues
The previous theorems are based on the assumption that all except the top m eigenvalues are equal to 1. Even under the spiked eigenvalue model, some rescaling of the sample eigenvalues may be necessary with real data.
For a given data, let its ordered population eigenvalues Λ* = {ζλ1, …, ζλm, ζ, …, ζ}, where ζ ≠ = 1, and its corresponding sample eigenvalues . We can show that Equations (4), (8), and (5) still hold under such circumstances. However, is no longer a consistent estimator of λv, because
To address this issue, Baik and Silverstein [7] have proposed a simple approach to estimate ζ. In their method, the top significant large sample eigenvalues are first separated from the other grouped sample eigenvalues. Then ζ is estimated as the ratio between the average of the grouped sample eigenvalues and the mean determined by the Marchenko-Pastur law [22]. To separate the eigenvalues, they have suggested to use a screeplot of the percent variance versus component number. However, for real data, we may not be able to clearly separate the sample eigenvalues in such a manner and readily apply the approach. Thus we need an automated method which does not require a clear separation of the sample eigenvalues.
The expectation of the sum of the sample eigenvalues when ζ = 1 is
Thus, the sum of the rescaled eigenvalues is expected to be close to ( ). Let and d̂v be a properly rescaled eigenvalue, then d̂v should be very close to . Note that for fixed m and λv. Thus prv is a properly adjusted eigenvalue. However, for finite n and p, the difference between p and ( ) can be substantial, especially when the first several λvs are considerably larger than 1. To reduce this difference, we propose a novel method which iteratively estimates the ( ) and d̂v.
Initially set d̂v,0 = prv
- For the lth iteration, set λ̂v,l = ρ−1(d̂v,l−1) for , and λ̂v,l = 1 for . Define kl as the number of λ̂v,ls that are greater than 1, and let
- If converges, let
and stop. Otherwise, go to step 2.
The consistency of d̂v to ρ(λv) is shown in the following theorem.
Theorem 3
Let d̂v be the rescaled sample eigenvalue from the proposed algorithm. Then, for with multiplicity one,
Since , φ(ρ−1(d̂v,))2 is a consistent estimator of φ(λv)2. Combining this fact with Theorems 2 and 3, we can obtain the bias adjusted PC score
and the asymptotic correlation coefficient between gv and p̃v
3. Simulation
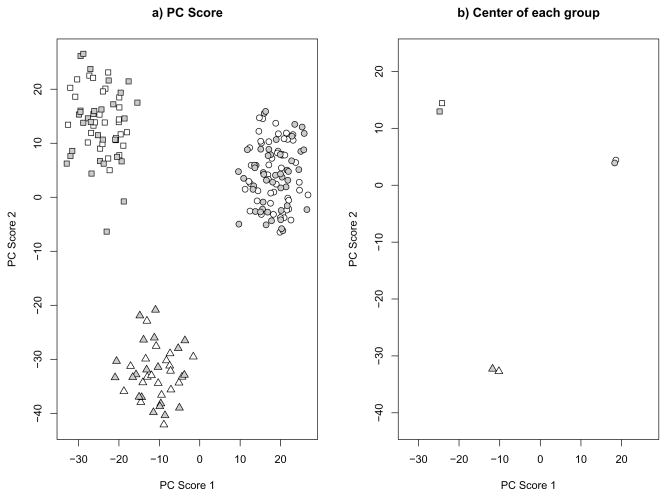
First, we applied our bias adjustment process to the simulated data described in the Introduction. Our estimated asymptotic shrinkage factors are 0.465 and 0.329 for the first and second PC scores, respectively. The scatter plot of the top two bias adjusted PC scores is given in Figure 2. After the bias adjustment, the predicted PC scores of the test data are comparable to those of the training data. This indicates that our method is effective in correcting for the shrinkage bias.
Fig 2.
Shrinkage Adjusted PC scores of the data in Figure 1. Different symbols represent different groups. White background color represents the training set and grey background color represents the test set. A) plots of all simulation samples. B) Center of each group.
Next, we conducted a new simulation to check the accuracy of our estimators. For the jth sample (j = 1, …, n), its ith variable was generated as
where λ1 > λ2 > 1 and zij ~ N (0, 22). Under this setting, λ1 and λ2 are the first and the second population eigenvalues. The first and second population eigenvectors are e1 = {1, 0,…, 0} and e2 = {0, 1, 0, …, 0} respectively. We set the standard deviation of zij to 2 instead of 1, which allows us to test whether the rescaling procedure works properly. We tried different values of γ and n, but set λ1 and λ2 to and , respectively.
We split the simulated samples into test and training sets, each with n samples. We first estimated the asymptotic shrinkage factor based on the training samples. We then calculated the predicted PC scores on the test samples. To assess the accuracy of shrinkage factor estimator for each PC, we empirically estimated the shrinkage factor by the ratio of the mean predicted PC scores of the test samples to the mean PC scores of the training samples. That is, for the vth PC, the empirical shrinkage factor is estimated by . On the training samples, we also estimated the empirical angle between the sample and (known) population eigenvectors, as well as the empirical angle between PC scores from sample and population eigenvectors. The asymptotic theoretical estimates were also calculated. Tables 1 and 2 summarize the simulation results. Our asymptotic estimators provide accurate estimates for the angles and the shrinkage factor.
Table 1.
Cosine angle estimates of eigenvectors and PC scores based on 1000 simulations. “Angle” indicates the theoretical asymptotic cos (angle), “Estimate1” indicates the empirical cos(angle) estimator, ‘Estimate2” indicates the asymptotic cos(angle) estimator. For each estimator, each entry represents mean of 1, 000 simulation results with standard error in parentheses.
| γ | n | PC 1 |
PC 2 |
||||
|---|---|---|---|---|---|---|---|
| Angle | Angle Estimate1 | Angle Estimate2 | Angle | Angle Estimate1 | Angle Estimate2 | ||
| Eigenvectors | |||||||
| 1 | 100 | 0.93 | 0.93(0.013) | 0.91(0.027) | 0.82 | 0.81(0.053) | 0.80(0.052) |
| 200 | 0.93(0.009) | 0.92(0.014) | 0.81(0.030) | 0.81(0.032) | |||
| 20 | 100 | 0.70 | 0.69(0.037) | 0.70(0.031) | 0.51 | 0.50(0.053) | 0.50(0.058) |
| 200 | 0.69(0.023) | 0.70(0.022) | 0.51(0.036) | 0.51(0.041) | |||
| 100 | 100 | 0.53 | 0.53(0.034) | 0.53(0.031) | 0.37 | 0.35(0.043) | 0.35(0.047) |
| 200 | 0.53(0.024) | 0.53(0.024) | 0.36(0.029) | 0.36(0.033) | |||
| 500 | 100 | 0.38 | 0.38(0.029) | 0.38(0.028) | 0.25 | 0.24(0.033) | 0.24(0.037) |
| 200 | 0.38(0.020) | 0.38(0.020) | 0.25(0.021) | 0.25(0.024) | |||
| PC Scores | |||||||
| 1 | 100 | 0.99 | 0.99(0.004) | 0.98(0.016) | 0.94 | 0.93(0.036) | 0.91(0.048) |
| 200 | 0.99(0.003) | 0.99(0.006) | 0.94(0.019) | 0.93(0.024) | |||
| 20 | 100 | 0.98 | 0.97(0.083) | 0.98(0.008) | 0.89 | 0.86(0.105) | 0.87(0.055) |
| 200 | 0.97(0.055) | 0.98(0.005) | 0.88(0.073) | 0.88(0.036) | |||
| 100 | 100 | 0.97 | 0.97(0.079) | 0.97(0.009) | 0.88 | 0.85(0.109) | 0.86(0.060) |
| 200 | 0.97(0.058) | 0.97(0.006) | 0.86(0.076) | 0.87(0.039) | |||
| 500 | 100 | 0.97 | 0.96(0.084) | 0.97(0.010) | 0.87 | 0.83(0.117) | 0.84(0.069) |
| 200 | 0.96(0.058) | 0.97(0.007) | 0.86(0.076) | 0.86(0.038) | |||
Table 2.
Shrinkage factor esimates based on 1000 simulation. “Factor” indicates the theoretical asymptotic factor, “Estimate1” indicates the empirical shrinkage factor estimator, ‘Estimate2” indicates the asymptotic shrinkage factor estimator. For each estimator, each entry represents mean of 1, 000 simulation results with standard error in parentheses.
| γ | n | PC 1 |
PC 2 |
||||
|---|---|---|---|---|---|---|---|
| Factor | Factor Estimate1 | Factor Estimate2 | Factor | Factor Estimate1 | Factor Estimate2 | ||
| 1 | 100 | 0.88 | 0.88(0.017) | 0.87(0.076) | 0.75 | 0.75(0.044) | 0.76(0.063) |
| 200 | 0.88(0.013) | 0.87(0.054) | 0.75(0.027) | 0.75(0.044) | |||
| 20 | 100 | 0.51 | 0.51(0.037) | 0.51(0.038) | 0.33 | 0.34(0.033) | 0.32(0.038) |
| 200 | 0.51(0.025) | 0.51(0.026) | 0.34(0.022) | 0.33(0.028) | |||
| 100 | 100 | 0.30 | 0.30(0.024) | 0.30(0.030) | 0.17 | 0.17(0.019) | 0.17(0.023) |
| 200 | 0.30(0.017) | 0.30(0.023) | 0.18(0.013) | 0.17(0.017) | |||
| 500 | 100 | 0.16 | 0.15(0.014) | 0.16(0.020) | 0.08 | 0.08(0.010) | 0.08(0.013) |
| 200 | 0.15(0.010) | 0.16(0.014) | 0.08(0.007) | 0.08(0.009) | |||
Finally, we conducted simulation to demonstrate an application of the bias adjusted PC scores in PC regression. PC regression has been widely used in microarray gene-expression studies [9]. In this simulation, we let p = 5, 000, and our set up is very similar to the first simulation of Bair et al. [8]. Let xij denote the gene expression level of the ith gene for the jth subject. We generated each xij according to
and the outcome variable yj as
where n is the number of samples, g is the number of genes that are differentially expressed and associated with the phenotype, ε ~ N(0, 22) and εy ~ N(0, 1). A total of eight different combinations of n and g were simulated. For the training data, we fit the PC regression with the first PC as the covariate and computed the mean square error (MSE). For the test samples with the same configuration of the training samples, we applied the PC model built on the training data to predict the phenotypes using the un-adjusted and adjusted PC scores. The results are presented in Table 3. We see that the MSE of the test set without bias adjustment is appreciably higher than that of the test set with bias adjustment, and the MSE of the test set with bias adjustment is comparable with the MSE of the training set.
Table 3.
Mean Square Error(MSE) of the PC regression based on gene-expression microarray data simulation with and without shrinkage adjustment. 1,000 simulation were conducted. Each entry in the table represents mean of the MSE with standard error in parentheses
| n | g | Test Data without Adjustment | Test Data with Adjustment | Training Data |
|---|---|---|---|---|
| 100 | 150 | 1.97(0.256) | 1.70(0.284) | 1.61(0.284) |
| 100 | 300 | 1.63(0.230) | 1.17(0.167) | 1.12(0.158) |
| 100 | 500 | 1.43(0.204) | 1.07(0.157) | 1.03(0.147) |
| 100 | 1000 | 1.22(0.182) | 1.03(0.148) | 0.99(0.142) |
| 200 | 150 | 1.73(0.159) | 1.33(0.133) | 1.30(0.131) |
| 200 | 300 | 1.39(0.139) | 1.08(0.105) | 1.07(0.110) |
| 200 | 500 | 1.24(0.131) | 1.04(0.105) | 1.01(0.101) |
| 200 | 1000 | 1.10(0.114) | 1.02(0.101) | 1.00(0.101) |
4. Real data example
Here we demonstrate that the shrinkage phenomenon appears in real data, and can be adjusted by our method. For this purpose, genetic data on samples from unrelated individuals in the Phase 3 HapMap study [http://hapmap.ncbi.nlm.nih.gov/] were used. HapMap is a dense genotyping study designed to elucidate population genetic differences. The genetic data are discrete, assuming the values 0, 1, or 2 at each genomic marker (also known as SNPs) for each individual. Data from CEU individuals (of northern and western European ancestry) were compared with data from TSI individuals (Toscani individuals from Italy, representing southern European ancestry).
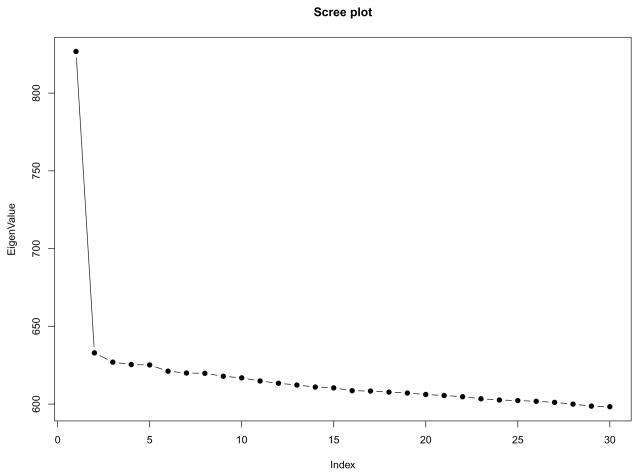
Some initial data trimming steps are standard in genetic analysis. We first removed apparently related samples, and removed genomic markers with more than a 10% missing rate, and those with frequency less than 0.01 for the minor genetic allele. To avoid spurious PC results, we further pruned out SNPs that are in high linkage disequlibrium (LD) [11]. Lastly, we excluded 7 samples with PC scores greater than 6 standard deviations away from the mean of at least one of the top significant PCs (i.e., with Tracy-Widom (TW) Test p-value < 0.01) [24, 27]. The final dataset contained 178 samples (101 CEU, 77 TSI) and 100, 183 markers. We mean-centered and variance-standardized the genotypes for each marker [27]. The screeplot of the sample eigenvalues is presented in Figure 3. The first eigenvalue is substantially larger than the rest of the eigenvalues, although the TW test actually identifies two significant PCs. Figure 3 suggests that our data approximately satisfies the spiked eigenvalue assumption.
Fig 3.
Scree plot of the first 30 sample eigenvalues, CEU+TSI dataset
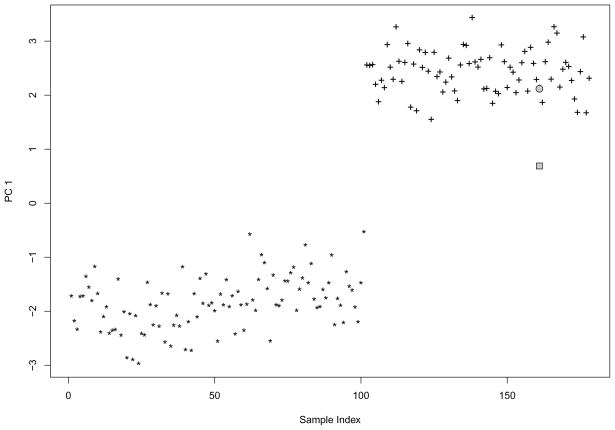
We estimated the asymptotic shrinkage factor and compared it with the following jackknife-based shrinkage factor estimate. For the first PC, we first computed the scores of all samples. Next, we removed one sample at a time and computed the (unadjusted) predicted PC score. We then calculated the jackknife estimate as the square root of the ratio of the means of the sample PC score and the predicted PC score. The jackknife shrinkage factor estimate is 0.319, which is close to our asymptotic estimate 0.325. Figure 4 shows the PC scores from the whole sample, the predicted PC score of an illustrative excluded sample, and its bias-adjusted predicted score. Clearly, the predicted PC score without adjustment is very biased towards zero, while the bias adjusted PC score is not.
Fig 4.
An instance with and without shrinkage adjustment, performed on Hapmap CEU(*) and TSI(+). “*” and “+” represent PC scores using all data. The 161th sample was excluded from PCA, and PC score for it was predicted. The grey rectangle represents the predicted PC score without shrinkage adjustment and the grey circle represents the predicted PC score after the shrinkage adjustment
5. Discussion and conclusions
In this paper we have identified and explored the shrinkage phenomenon of the predicted PC scores, and have developed a novel method to adjust these quantities. We also have constructed the asymptotic estimator of correlation coefficient between PC scores from population eigenvectors and sample eigenvectors. In simulation experiments and real data analysis, we have demonstrated the accuracy of our estimates, and the capability to increase prediction accuracy in PC regression by adopting shrinkage bias adjustment. For achieving these, we consider asymptotics in the large p, large n framework, under the spiked population model.
We believe that this asymptotic regime applies well to many high dimensional datasets. It is not, however, the only model paradigm applied to such data. For example, the large p small n paradigm [1, 14], which assumes p/n → ∞, has also been explored. Under this assumption, Jung and Marron [20] have shown that the consistency and the strong inconsistency of the sample eigenvectors to population eigenvectors depend on whether p increases at a slower or faster rate than λv. It may be argued that for real data where p/n is “large,” we should follow the paradigm of Ahn et al. [1], Hall et al. [14]. However, for any real study, it is unclear how to test whether p increases at a faster rate than λv, or vice versa, making the application of Ahn et al. [1], Hall et al. [14] difficult in practice. Furthermore, the scenario where p and λv grow at the same rate is scientifically more interesting, for which we are aware of no theoretical results. In contrast, our asymptotic results can be straightforwardly applied. Further, our simulation results indicate that for p/n as large as 500, our asymptotic results still hold well. We believe that the approach we describe here applies to many datasets.
Although the results from the spiked model are useful, it is likely that observed data has more structure than allowed by the model. Recently, several methods have been suggested to estimate population eigenvalues under more general scenarios [10, 29]. However, no analogous results are available for the eigenvectors. In data analysis, jackknife estimators, as demonstrated in the real data analysis section, can be used. However, resampling approaches are very computationally intensive, and it remains of interest to establish the asymptotic behavior of eigenvectors in a variety of situations.
We note that inconsistency of the sample eigenvectors does not necessarily imply poor performance of PCA. For example, PCA has been successfully applied in genome-wide association studies for accurate estimation of ethnicity [27], and in PC regression for microarrays [21]. However, for any individual study we cannot rule out the possibility of poor performance of the PC analysis. Our asymptotic result on the correlation coefficient between PC scores from sample and population eigenvectors provides us a measure to quantify the performance of PC analysis.
For the CEU/TSI data, SNP pruning was applied to adjust for strong LD among adjacent SNPs. Such SNP pruning is a common practice in the analysis of GWAS data, and has been implemented in the popular GWAS analysis software Plink [28]. The primary goal of SNP pruning is to avoid spurious PC results unrelated to population substructures. Technically, our approach does not rely on any independence assumption of the SNPs. However, strong local correlation may affect eigenvalues considerably. Thus the value in SNP pruning may be viewed as helping the data better accord with the assumptions of the spiked population model. From the CEU/TSI data and our experience in other GWAS data, we have found that the most common pruning procedure implemented in Plink is sufficient for us to then apply our methods.
6. Proofs
Note that EΛ1/2ZZT Λ1/2ET and Λ1/2ZZT Λ1/2 have the same eigenvalues, and ET U is the eigenvector matrix of Λ1/2ZZT Λ1/2. Since eigenvalues and angles between sample and population eigenvectors are what we concerned about, without loss of generality (WLOG), in the sequel, we assume Λ to be the population covariance matrix.
6.1. Notations
We largely follow notations in Paul [26]. We denote λv(S) as the vth largest eigenvalue of S. Let suffice A represent the first m coordinates and B represent the remaining coordinates. Then we can partition S into
We similarly partition the vth eigenvector into (uA,v, uB,v) and ZT into [ ]. Define Rv as ||uB,v|| and let , then we get ||av|| = 1.
Applying singular value decomposition (SVD) to , we get
| (9) |
where M = diag(μ1, …, μp−m) is a (p − m) × (p − m) diagonal matrix of ordered eigenvalues of SBB, V is a (p − m) × (p − m) orthogonal matrix, and H is an n × (p − m) matrix. For n ≥ p − m, H has full rank orthogonal columns. When n < p−m, H has more columns than rows, hence it does not have full rank orthogonal columns. For the later case, we make H = [Hn, 0] where Hn is an n × n orthogonal matrix.
6.2. Propositions
We introduce two propositions for later use. The proofs of the 2 propositions can be found in section 6.5 and 6.6.
Proposition 1
Suppose Y is an n×m matrix with fixed m and each entry of Y is i.i.d random variable which satisfies the moment condition of zij in Assumption 1. Let C be an n × n symmetric non-negative definite random matrix and independent of Y. Further assume ||C|| = O(1). Then
as n → ∞
Proposition 2
Suppose y is an n dimensional random vector which follows the same distribution of the row vectors of Y and independent of SBB. Let f(x) be a bounded continuous function on [ ] and f(0) = 0. Suppose F = diag(f(μ1), …, f(μp−m)), where are ordered eigenvalues of M which is defined on (9), then
as n → ∞, where Fγ(x) is a distribution function of Marchenko-Pastur law with parameter γ [22].
6.3. Proof of Part i) of Lemma 1)
6.3.1. When p is fixed
By the strong law of large numbers, . Since eigenvalues are continuous with respect to the operator norm, the lemma follows after applying continuous mapping theorem.
6.3.2. When p → ∞
For every small ε > 0, there exist p̃(n) and γε such that p̃(n)/n → γε > 0, λv(1 + γε/(λv − 1)) < λv + ε for all v ≤ m, , and . For simplicity, we denote p̃(n) as p̃. Suppose Zp̃ is a p̃ × n matrix that satisfies the moment condition of zij in Assumption 1. Define an augmented data matrix and its sample covariance matrix S̃ = X̃X̃T. Let S be a p × p upper left submatrix of S̃. We also let Ŝ be an (m + 1) × (m + 1) upper left submatrix of S̃. For v ≤ (m + 1), by the interlacing inequality (Theorem 4.3.15 of Horn and Johnson [15]),
Since for v ≤ m, and for v = m + 1, we have
Thus,
| (10) |
Similarly by the interlacing inequality, we get
Since , and , we conclude that
| (11) |
6.4. Proof of Part ii) of Lemma 2
Our proof of Lemma 2 (ii) closely follows the arguments in Paul [26]. From [26], it can be shown that
| (12) |
and
| (13) |
where ΛA = diag {λ1, …, λm}.
6.4.1. When
We can show that
| (14) |
and
| (15) |
where eA,v is a vector of the first m coordinates of the vth population eigen-vector ev, ρv is , and zAv is a vector of vth row of ZA. The proofs can be found in 6.4.3. Note that ev is a vector with 1 in its vth coordinate and 0 elsewhere. WLOG, we assume that 〈ev, uv〉 ≥ 0. Since . By (13) and (15), we can show that
| (16) |
From Lemma B.2 of [26],
| (17) |
Thus
| (18) |
It concludes the proof of the first part of Lemma 2 ii).
6.4.2. When
Here we only need to consider γ > 0 because no eigenvalue satisfies this condition when γ = 0. We first show that , which implies , hence . For any ε > 0 and x ≥ 0, define
and
then by Propositions 1 and 2,
| (19) |
By monotone convergence theorem,
| (20) |
RHS of (20) is
| (21) |
where and . Since (21) equals ∞ for any a ≤ ρv ≤ b, we conclude that
| (22) |
Therefore , which proves the second part of Lemma 2 ii).
6.4.3. Proof of (14) and (15)
Define
, 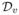 = SAA+SAB(dvI−SBB)−1 SBA −(ρv/λv)ΛA, αv = ||
= SAA+SAB(dvI−SBB)−1 SBA −(ρv/λv)ΛA, αv = ||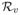
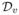 || + |dv − ρv|||
|| + |dv − ρv|||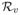 ||, and βv = ||
||, and βv = ||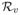
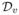 eA,v||.
eA,v||.
With the exactly same argument of [26], it can be shown that
where rv = − (1 − 〈eA,v, av〉)eA,v − 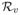
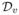 (av − eA,v)+(dv − ρv)
(av − eA,v)+(dv − ρv)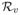 (av − eA,v). By Lemma 1 of [25], rv = op(1), if αv = op(1) and βv = op(1).
(av − eA,v). By Lemma 1 of [25], rv = op(1), if αv = op(1) and βv = op(1).
When γ = 0,
and the remainder of 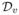 is
is
| (23) |
Since and ,
By Proposition 1,
| (24) |
hence 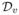 = op(1).
= op(1).
When γ > 0, 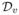 can be written as
can be written as
| (25) |
The first term of RHS is op(1) by the weak law of large number. The second and third terms are op(1) by Propositions 1 and 2. For the fourth term, ρv − dv = op(1) and its remainder part is Op(1). Therefore, 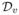 = op(1). By combining the above results and
= op(1). By combining the above results and 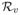 = Op(1) plus dv − ρv = op(1), we prove the Equation (14).
= Op(1) plus dv − ρv = op(1), we prove the Equation (14).
For (15): When γ = 0, (15) can be proved by the exactly same way used to show (24). When γ > 0, , and , hence . Therefore the result follows according to Propositions 1 and 2.
6.5. Proof of Proposition 1
Let μ1 ≥ μ2 ≥ ··· ≥ μn be the ordered eigenvalues of C, and cij be the (i, j)th element of C. Suppose ys is the sth column of Y, and yij is the (i, j)th element of Y. We further define and for s ≠ t. The conditional mean of ψ(s, s) given C is
| (26) |
Thus, E(ψ(s, s)) = E(E(ψ(s, s)|C)) = E(0) = 0.
Next, the conditional variance of ψ(s, s) given C is
| (27) |
where . Since ||C|| = O(1), . Therefore, Var(ψ(s, s)|C) ≤ O(1/n) and Var(ψ(s, s)) = Var(E(ψ(s, s)|C)) + E(Var(ψ(s, s)|C)) ≤ 0 + O(1/n) → 0 as n → ∞. By Chebyshev inequality, we can conclude that
We can similarly show , which we omit here.
6.6. Proof of Proposition 2
Consider an expansion
We show that both (a) and (b) converge to 0 in probability.
Since , μk = 0 for k > min(p−m, n), and f(x) is continuous and bounded on [ ], there exists K > 0 such that supi |f (μi)| < K a.s. Let C = HFHT, then trace(C) = trace(F). By Proposition 1, (a) = op(1).
-
Let Fp−m be an empirical spectral distribution of SBB, then
which shows that (b) = op(1).
Combining (a) and (b), we finish the proof.
6.7. Proof of Theorem 1
WLOG we assume 〈gv, p̃v〉 ≥ 0. Let ev = {eA,v, eB,v}, then eA,v is the vector with 1 in vth coordinate and 0 elsewhere, and eB,v is the zero vector. Since SAAuA,v + SABuB,v = dvuA,v, we have
| (28) |
6.8. Proof of Theorem 2
First, we show the square of the denominator converges to ρ(λv). Since , and for i ≠ j,
| (29) |
Next we show the square of numerator converges to φ(λv)2(λv − 1)+1. Define , then uv can be expressed as
Partition . From (14), , therefore and Since xnew and uv are independent, we have
| (30) |
| (31) |
6.9. Proof of Theorem 3
Since ρ−1(prv) → λv for v ≤ k, WLOG we assume that k0 = k, where k is the number of λv bigger than . Set
| (32) |
The first and second partial derivatives of h(x) are
| (33) |
| (34) |
so h(x) is a concave function of x given rv. From the fact that ρ−1(rvp) > 1 for v ≤ k, we know h(p) > 0. Because of the concave nature of this function, h(x) = 0 has an unique solution τ on [p, ∞), which converges to. Thus d̂v = τrv. Define d̃v = rvω where , and set dv as the sample eigenvalue when σ2 = 1. The sum of all dv is
| (35) |
thus
| (36) |
and
| (37) |
| (38) |
Since dv → ρ(λv) for v ≤ k,
| (39) |
Now, we show that τ = ω + op(1). Plugging ω into h(x) and combining the fact that ρ−1(d̃v) = λv + op(1), we get
| (40) |
From the facts that h(x) is a continuous concave function, ω > p, and h(p) > 0, we conclude that
| (41) |
Therefore
| (42) |
for v ≤ k, which concludes the proof.
Contributor Information
Seunggeun Lee, Email: slee@bios.unc.edu.
Fei Zou, Email: fzou@bios.unc.edu.
Fred A. Wright, Email: fwright@bios.unc.edu.
References
- 1.Ahn J, Marron JS, Muller KM, Chi YY. The high-dimension, low-sample-size geometric representation holds under mild conditions. Biometrika. 2007;94:760–766. [Google Scholar]
- 2.Anderson TW. Asymptotic theory for principal component analysis. Ann Math Statist. 1963;34:122–148. [Google Scholar]
- 3.Anderson TW. Wiley Series in Probability and Statistics. 3. Hoboken, NJ: Wiley-Interscience [John Wiley & Sons]; 2003. An introduction to multivariate statistical analysis. [Google Scholar]
- 4.Bai Z, Yao J-f. Central limit theorems for eigenvalues in a spiked population model. Ann Inst Henri Poincaré Probab Stat. 2008;44:447–474. [Google Scholar]
- 5.Bai ZD. Methodologies in spectral analysis of large-dimensional random matrices, a review. Statist Sinica. 1999;9:611–677. [Google Scholar]
- 6.Baik J, Ben Arous G, Péché S. Phase transition of the largest eigenvalue for nonnull complex sample covariance matrices. Ann Probab. 2005;33:1643–1697. [Google Scholar]
- 7.Baik J, Silverstein JW. Eigenvalues of large sample covariance matrices of spiked population models. J Multivariate Anal. 2006;97:1382–1408. [Google Scholar]
- 8.Bair E, Hastie T, Paul D, Tibshirani R. Prediction by supervised principal components. J Amer Statist Assoc. 2006;101:119–137. [Google Scholar]
- 9.Bovelstad H, Nygard S, Storvold H, Aldrin M, Borgan O, Frigessi A, Ling-jaerde O. Predicting survival from microarray data a comparative study. Bioinformatics. 2007;23:2080–2087. doi: 10.1093/bioinformatics/btm305. [DOI] [PubMed] [Google Scholar]
- 10.El Karoui N. Spectrum estimation for large dimensional covariance matrices using random matrix theory. Ann Statist. 2008;36:2757–2790. [Google Scholar]
- 11.Fellay J, Shianna K, Ge D, Colombo S, Ledergerber B, Weale M, Zhang K, Gumbs C, Castagna A, Cossarizza A, et al. A Whole-Genome Association Study of Major Determinants for Host Control of HIV-1. Science. 2007;317:944–947. doi: 10.1126/science.1143767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Girshick M. Principal components. J Amer Statist Assoc. 1936;31:519–528. [Google Scholar]
- 13.Girshick M. On the sampling theory of roots of determinantal equations. Ann Math Statist. 1939;10:203–224. [Google Scholar]
- 14.Hall P, Marron JS, Neeman A. Geometric representation of high dimension, low sample size data. J R Stat Soc Ser B Stat Methodol. 2005;67:427–444. [Google Scholar]
- 15.Horn R, Johnson C. Matrix analysis. Cambridge Univ Pr; 1990. [Google Scholar]
- 16.Jackson J. A user’s guide to principal components. Wiley-Interscience; 2005. [Google Scholar]
- 17.Johnstone I, Lu A. On Consistency and Sparsity for Principal Components Analysis in High Dimensions. J Amer Statist Assoc. 2009;104:682–693. doi: 10.1198/jasa.2009.0121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Johnstone IM. On the distribution of the largest eigenvalue in principal components analysis. Ann Statist. 2001;29:295–327. [Google Scholar]
- 19.Jolliffe I. Principal component analysis. Springer; New York: 2002. [Google Scholar]
- 20.Jung S, Marron JS. PCA consistency in High dimension, low sample size context. Ann Statist. 2009;37:4104–4130. [Google Scholar]
- 21.Ma S, Kosorok MR, Fine JP. Additive risk models for survival data with high-dimensional covariates. Biometrics. 2006;62:202–210. doi: 10.1111/j.1541-0420.2005.00405.x. [DOI] [PubMed] [Google Scholar]
- 22.Marčenko V, Pastur L. Distribution of eigenvalues for some sets of random matrices. Sbornik: Mathematics. 1967;1:457–483. [Google Scholar]
- 23.Nadler B. Finite sample approximation results for principal component analysis: a matrix perturbation approach. Ann Statist. 2008;36:2791–2817. [Google Scholar]
- 24.Patterson N, Price A, Reich D. Population structure and eigenanalysis. PLoS Genet. 2006;2:e190. doi: 10.1371/journal.pgen.0020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Paul D. Asymptotics of the leading sample eigenvalues for a spiked covariance model. Technical Report. 2005 http://anson.ucdavis.edu/debashis/techrep/eigenlimit.pdf.
- 26.Paul D. Asymptotics of sample eigenstructure for a large dimensional spiked covariance model. Statist Sinica. 2007;17(4):1617–1642. [Google Scholar]
- 27.Price A, Patterson N, Plenge R, Weinblatt M, Shadick N, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 28.Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira M, Bender D, Maller J, Sklar P, de Bakker P, Daly M, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. The American Journal of Human Genetics. 2007;81(3):559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rao NR, Mingo JA, Speicher R, Edelman A. Statistical eigen-inference from large Wishart matrices. Ann Statist. 2008;36:2850–2885. [Google Scholar]
- 30.Wall M, Rechtsteiner A, Rocha L. Singular value decomposition and principal component analysis. A practical approach to microarray data analysis. 2003:91–109. [Google Scholar]