A conditional Granger causality model approach for group analysis in functional MRI

Abstract

Granger causality model (GCM) derived from multivariate vector autoregressive models of data has been employed for identifying effective connectivity in the human brain with functional MR imaging (fMRI) and to reveal complex temporal and spatial dynamics underlying a variety of cognitive processes. In the most recent fMRI effective connectivity measures, pairwise GCM has commonly been applied based on single voxel values or average values from special brain areas at the group level. Although a few novel conditional GCM methods have been proposed to quantify the connections between brain areas, our study is the first to propose a viable standardized approach for group analysis of an fMRI data with GCM. To compare the effectiveness of our approach with traditional pairwise GCM models, we applied a well-established conditional GCM to pre-selected time series of brain regions resulting from general linear model (GLM) and group spatial kernel independent component analysis (ICA) of an fMRI dataset in the temporal domain. Datasets consisting of one task-related and one resting-state fMRI were used to investigate connections among brain areas with the conditional GCM method. With the GLM detected brain activation regions in the emotion related cortex during the block design paradigm, the conditional GCM method was proposed to study the causality of the habituation between the left amygdala and pregenual cingulate cortex during emotion processing. For the resting-state dataset, it is possible to calculate not only the effective connectivity between networks but also the heterogeneity within a single network. Our results have further shown a particular interacting pattern of default mode network (DMN) that can be characterized as both afferent and efferent influences on the medial prefrontal cortex (mPFC) and posterior cingulate cortex (PCC). These results suggest that the conditional GCM approach based on a linear multivariate vector autoregressive (MVAR) model can achieve greater accuracy in detecting network connectivity than the widely used pairwise GCM, and this group analysis methodology can be quite useful to extend the information obtainable in fMRI.

Introduction

In the past decade, the main focus of most functional magnetic resonance imaging (fMRI) studies has been the localization of neural activation relying on general linear model (GLM) analysis associated with the measurements of the Blood Oxygen Level Dependent (BOLD) signal [Goebel et al., 2003; Logothetis, 2002; Roebroeck et al., 2005]. Nowadays, most interest in neuroscience has advanced from mapping sites of activation towards identifying the functional and effective connectivity that weave them together into dynamic neural systems [Goebel et al., 2003; Londei et al., 2007]. These are complex networks with a large number of correlated variables. Impressive progress in methodology has been made since the first description of the BOLD effect, and functional integration has been proposed to investigate interactions in the correlation between brain areas engaged in specific tasks and at resting conditions. Brain areas involved in various cognitive tasks can now be identified accurately and reliably. Brain networks have been primarily studied in terms of functional connectivity and effective connectivity. Functional connectivity analysis methods identify correlations between remote neurophysiological events. Effective connectivity measures the causal influence one neuronal system exerts over another that might show how the network operates to mediate cognitive demands [Friston, 1995]. Recently, there have been several attempts to investigate the direct causality among different activated brain regions [e.g., Duann et al., 2009; Kaas et al., 2010; Sato et al., 2006; Stilla et al., 2007] and within resting state networks [Stevens et al., 2009; Uddin et al., 2009] by using a Granger causality model (GCM) on fMRI data in either the time [Londei et al., 2006; Kayser et al., 2009; Hemmelmann et al., 2009] or the spectral domain [Demirci et al., 2009; Havlicek et al., 2009; Sato et al., 2009]. Understanding the detailed connections between brain areas is important to understand information processing in the human brain, and the pairwise GCM [e.g., Abler et al., 2006; Sridharan et al., 2008; Chen et al., 2009; Zhou et al., 2009a] provides information about the dynamics and directionality of fMRI BOLD signal in cortical circuits. However, several limitations still remain in previous applications of fMRI [Deshpande et al., 2009; Friston, 2009, Liao et al., 2009; Zhou et al., 2009b].

Recent fMRI studies have always applied GCM based on two methods. The first involves either single voxel values or average values from regions of interest (ROIs) to derive Granger causality maps on single subjects in task-related fMRI studies. The other is based on related independent components (ICs) from group spatial independent component analysis (ICA) over multiple subjects in resting-state fMRI studies. Most of the methods for evaluating Granger causality rely on pairwise analysis and follow two early studies on single subjects [Goebel et al., 2003; Roebroeck et al., 2005]. It attempts to demonstrate that Granger causality techniques can be applied to fMRI data and promise further insights into the neural mechanisms of cognitive processing [Goebel et al., 2003; Roebroeck et al., 2005; Florin et al., 2010]. Subsequently, a number of reports in larger studies [e.g., Graaf et al., 2009; Graham et al., 2009; Jabbi et al., 2008; Peterson et al., 2009; Upadhyay et al., 2009; Witt et al., 2009] have confirmed and extended the utility of Granger causality in fMRI analyses during the past three years. However, these approaches face three major limitations when applied to fMRI data: (i) The pairwise GCM ignores interactions between other ROIs in the underlying neuronal network which may lead to an oversimplification of the multivariate neuronal relationships that exist during the majority of cognitive tasks. (ii) Independent component (IC) time series can represent the conjoint pattern of hemodynamic activity across each distributed neural network in group analysis of functional network connectivity, but little is known about possible directional connectivity within each network itself [Uddin et al., 2009]. (iii) Multivariate causality relationships are difficult to interpret and compare across subjects in group analysis, and normalization in both GLM and group ICA processes will lead to significant information lost in time series. A few researchers have taken advantage of multivariate measures of Granger causality application to infer direct connectivity from fMRI data of various cognitive tasks and resting conditions [Deshpande et al., 2009, Zhou et al., 2009b], but these multivariate autoregressive models are still not presently accepted as a standard technique and are not widely used. To overcome these problems in the temporal domain, we have developed a conditional GCM approach for analyzing selected brain ROIs resulting from GLM or group kernel ICA of fMRI datasets. In our study, a non-seed based ROI over multiple normalized subjects is treated as a group of time series for the conditional GCM application. This method provides accurate information about the multivariate influences among time series, whereas the pairwise GCM cannot clearly distinguish between direct causal influences from one region to another and indirect ones mediated through a third region.

Effective connectivity in two functional networks selected by GLM and ICA were investigated in a group analysis to demonstrate the utility of this conditional GCM approach. We first applied the conditional GCM to an fMRI study with standard block design that involved a group of 12 subjects performing emotional facial tasks. The GLM analysis showed that both left and right amygdalae responded to the face matching task and that only the left amygdala response habituated to the emotion matching condition but not to identity matching. The conditional GCM results confirmed the detection of a cognitive causal relationship and revealed the reason for the habituation during the emotion processing. Secondly, ICA was performed on a group dataset of 25 subjects in a resting-state fMRI study which detected the default mode network (DMN) and other resting-state networks (RSNs). This study was then analyzed using multivariate conditional GCM to elucidate the nature of the interregional connections in addition to the relationship among the RSNs. This procedure allowed us to detect particular patterns of DMN dynamics that can be classified as the afferent and efferent influences of the medial prefrontal cortex (mPFC) and posterior cingulate cortex (PCC). Our conditional GCM approach was successful in harnessing the ability of fMRI to evaluate the connection and direct causality in cortical circuits across multiple subjects. The resulting characterized connectivity can greatly enhance our understanding of cognitive processes that are usually difficult to identify in brain network studies.

Methods

We first applied the conditional GCM approach for group analysis on our previously published fMRI data (referred to herein as University of Florida data), allowing us to investigate the activated regions potentially responsible for the left amygdala response habituation in a sequence of four emotion blocks during the task with general linear model (GLM). Subsequently, a group kernel-ICA approach was applied to the resting-state data from the group of 25 subjects from New York University (referred to below as New York University data [Uddin et al., 2009; Zuo et al., 2009]) for further GCM analysis within brain regions of DMN, which is an important network of RSNs.

Subjects and Tasks

University of Florida data

Twelve right-handed volunteers with normal vision were recruited. The subjects did not report any neurological or psychiatric history and had not taken psychoactive medications within the 6 months prior to participating in the study. The research protocol for the human study was approved by the University of Florida's Institutional Review Board.

The subjects performed a face matching task. Three conditions were used: (1) Emotion condition: in which participants were asked to match faces by their expressed emotion between a target face and two probe faces positioned below the target face; (2) Identity condition: in which participants were asked to match the identify of neutral faces; (3) Control condition: in which the participant was asked to match pixilated patterns derived from neutral face pictures. The task started with a 3-second instruction screen followed by blocks of six 3-second trials of the same condition. The block condition was presented in a fixed sequence that repeated four times. The entire run consisted of twelve 21-second task blocks interspersed with thirteen 9-second rest blocks and lasted for 369s (123 time points per subject). Further details regarding the fMRI protocol are available in the original publications [Wright et al., 2006; Zhou et al., 2009a].

New York University data

An unrestricted dataset from the New York University (NYU) CSC TestRetest resource (http://www.nitrc.org/projects/nyu_trt/) was used for the resting-state fMRI study. This dataset includes 25 right handed native English-speaking, healthy participants (10 males; mean age 29.44+/-8.47). Resting state EPI-images and anatomical images were collected according to protocols approved by the institutional review boards of NYU and the NYU School of Medicine [Shehzad et al., 2009].

Imaging Methods

University of Florida data

The fMRI data was collected with a Siemens Allegra 3.0 Tesla MR scanner. Structure images were acquired using a T1 MPRAGE sequence in the sagittal plane at 1.0 mm³ resolution, TR = 1780 ms, TE = 4.38 ms, flip angle = 8°. Functional images were acquired using a T2* weighted echo planar imaging BOLD sequence in the axial orientation (parallel to the AC-PC line), covering the entire brain with 36 slices, 3.8 mm thick with no gaps using TR = 3000 ms, TE = 30 ms, flip angle = 90°, a 240 mm² FOV and a 64×64 voxel matrix, resulting in a 3.75 mm in-plane resolution. A total of 125 volumes were scanned during the matching task experiment and the first two volumes were discarded before analysis to allow for T1 equilibration.

New York University data

Resting-state fMRI data were also acquired on a Siemens Allegra 3.0 Tesla scanner. For each participant, resting-state fMRI images were collected on three occasions, but only the first scan was selected for our study. Each scan consisted of 197 continuous EPI functional volumes (TR=2000ms; TE=25ms; flip angle=90, 39 slices, matrix=64×64; FOV=192mm; acquisition voxel size= 3×3×3 mm³) and a high-resolution T1-weighted volume using magnetization prepared gradient echo sequence (TR=2500ms; TE=4.35ms; T1=900ms; flip angle =8; 176 slices, FOV=256mm). All participants were instructed to remain relaxed with their eyes open during each scan [Shehzad et al., 2009].

Data Preprocessing

University of Florida data

Imaging data were analyzed using Brain Voyager QX (Brain Innovation, Maastricht, Netherlands). Anatomical and functional images were coregistered and normalized to Talairach space [Talairach et al., 1988] for all subjects. Functional images underwent 3D motion correction, linear trend removal, and slice timing correction. Spatial smoothing was applied using a Gaussian filter of 6 mm full-width half maximum and no temporal smoothing was applied to the functional data.

Regional activations were estimated using a GLM. Statistical maps based on group activation pattern with 12 subjects were created using random effects analysis. Individual voxel time series were regressed onto the model combined with these predictors, and clusters of voxels with significant differences between predictors had a statistical threshold of t(11) > 4.0 (P < 0.002) and a minimum cluster size of 50 mm³. Two experimental conditions (Emotion and Identity) were contrasted with the Control condition in order to identify activation within specific brain regions. Further significant differences in modeled signal activations are summarized in the original publication [Zhou et al., 2009b]. For the habituation investigation, the BOLD response to the emotion condition was calculated separately for four repetitions, averaged across subjects, and compared with the conditional GCM results across subjects in group analysis.

New York University data

Resting-state fMRI data preprocessing was carried out by SPM8 (www.fil.ion.ucl.ac.uk/spm). This involved: (1) slice timing to correct difference in image acquisition time between slices; (2) realigning all EPI functional volumes to reduce head motion correction; (3) spatial normalization to transform all T1 weighted volumes to MNI152 standard brain space; (4) spatial registration to map all EPI functional volumes to individual T1 weighted image with spatial resolution of 3×3×4 mm³; (5) remove linear trends; (6) remove high-frequency (>0.1 Hz) components; (7) spatial smoothing with an 8 mm FWHM Gaussian kernel [Greicius et al., 2004; Shehzad et al., 2009].

For all subjects, the first two functional volumes were excluded. Then, all the left spatial smoothed fMRI images were processed by data reduction using principal components analysis (PCA), group kernel-ICA, and components reconstruction. PCA and components reconstruction were performed by the modified GIFT software (http://icatb.sourceforge.net/gift) [Calhoun et al. 2001], and there were 43 components retained after data reduction. ICA, one of the blind source separation approaches, is a powerful model–free method for task-related fMRI data analysis and has been successfully applied to investigate resting state networks from fMRI data [Calhoun et al., 2006/2009; Grubera et al., 2009]. The conventional ICA model used in GIFT software assumes that the source signals are statistically independent and non-Gaussian. It has an unknown but linear mixing process [Calhoun et al. 2001], which makes the calculated component of ICA less adaptable to non-linear signals such as the BOLD signals of human brain. The kernel-ICA method, proposed here to deal with non-linear problems, overcomes the weakness of conventional linear method by transforming the original data into a higher feature space and processing projection data through the “kernel trick” [Bach et al., 2002; Marinazzo et al., 2010]. We implemented the original kernel-ICA [Bach et al., 2002] in lieu of widely used kernel PCA + ICA methods [Grubera et al., 2009] in resting-state fMRI study. The kernel-ICA method is based on an entire function space of candidate nonlinearities, which can compute canonical correlations in a reproducing kernel Hilbert space. The cost functions have desirable mathematical properties to yield statistical dependence, which can be computed by kernel canonical correlation analysis. Our results suggest that kernel-ICA is a flexible and robust method to extract the DMN of resting-state fMRI. After the kernel-ICA analysis, a group of t-map 3D images representing different resting state networks were obtained to reveal the active voxels in each one. Finally, the time series of each voxel in four single ROIs of DMN were extracted semi-automatically by region-growing methods for further connectivity analysis in order to investigate the DMN of RSNs.

Conditional Granger Causality Model

The Granger causality approach allows for the determination of the causal relationships among activated brain regions selected by the GLM or kernel-ICA methods in fMRI studies. The concept of causality introduced by Wiener [Wiener et al., 1956] and formulated by Granger [Granger, 1969] has played an important role in investigating the relationships among stationary time series. Pairwise GCM approaches have been widely used in previous fMRI studies [e.g., Goebel et al., 2003; Roebroeck et al., 2005; Londei et al., 2007; Bressler et al., 2010]. However, without the pre-selection of the interacting factors and related hypothesis, the pairwise GCM approaches do not clearly distinguish between direct causal influences between one brain region and another and indirect influences from a third factor. This could lead to erroneous conclusions about the relationships between regions in fMRI studies. Therefore, a conditional GCM approach has been introduced in the application of our previous study with a single subject [Zhou et al., 2009b] to overcome the previous problems. We then applied the conditional GCM methodology to group data to demonstrate its effectiveness and ability to provide more details about relationships between regions in group data.

The formulation below follows the Geweke method [Geweke, 1984] for group GCM analysis in fMRI studies. Consider a multiple stationary discrete zero-mean stochastic processes W_t = [w_1t, w_2t, …, w_nt]^T of dimension n, where T denotes the matrix transposition. Suppose that W_t has been decomposed into three vectors X_t, Y_t and Z_t with dimensions a, b, and c (e.g. a is voxel number of one single ROI), respectively: W_t = (X_t^T, Y_t^T, Z_t^T)^T where a + b + c = n. Here, X_t and Y_t are two sets of original time series over multiple subjects with no overlap, and Z_t represents all time series indices other than X_t and Y_t in the network. The measure given by Geweke [Geweke, 1984] for the linear dependence of X_t on Y_t, conditional on Z_t, in the temporal domain is:

$$f_{Y\to X\mid Z}=ln\frac{var({\mathbf{\text{X}}}_{\mathbf{\text{t}}}\mid {\mathbf{\text{X}}}_{\mathbf{\text{t}}-\mathbf{1}},{\mathbf{\text{Z}}}_{\mathbf{\text{t}}-\mathbf{1}})}{var({\mathbf{\text{X}}}_{\mathbf{\text{t}}}\mid {\mathbf{\text{X}}}_{\mathbf{\text{t}}-\mathbf{1}},{\mathbf{\text{Y}}}_{\mathbf{\text{t}}-\mathbf{1}}\mathbf{,}{\mathbf{\text{Z}}}_{\mathbf{\text{t}}-\mathbf{1}})}\mathbf{,}$$ (1)

which is consistent with Granger's definition of a prima facie cause [Granger, 1980]. If all the other information included in Z_t is lost, then only pairwise Granger causality between X_t and Y_t can be calculated by the following: $f_{Y\to X}=ln\frac{var({\mathbf{\text{X}}}_{\mathbf{\text{t}}}\mid {\mathbf{\text{X}}}_{\mathbf{\text{t}}-\mathbf{1}})}{var({\mathbf{\text{X}}}_{\mathbf{\text{t}}}\mid {\mathbf{\text{X}}}_{\mathbf{\text{t}}-\mathbf{1}}\mathbf{,}{\mathbf{\text{Y}}}_{\mathbf{\text{t}}-\mathbf{1}})}$ which is named the pairwise GCM method. Geweke [Geweke, 1982] also proposed that a measure of linear influence exists between the time series of two discrete zero-mean stochastic processes. Actual physical data may contradict the key assumption that the spectra of X_t and Z_t are identical due to practical estimation errors; however, the problem can be solved by using the spectral matrix procedure and its spectral factorization [Wilson, 1972; Dhamala et al., 2008].

In this study, we present a framework to calculate the direct influence of both task-related and resting-state fMRI data with a conditional GCM approach based on multivariate autoregressive (MVAR) modeling of fMRI time series in the context of conditional Granger causality. Most commonly, fMRI data acquired by averaging over multiple voxels were directly treated as a time series in brain connectivity studies and the averaging operation may lead to a loss of information in the vector time series of an ROI. The PCA method is a possible suitable approach, which is a data-reduction step in cases when large numbers of voxels are of interest and can still adequately account for its activity [Zhou et al., 2009b]. Group kernel-ICA also has the same performance in addition to the detection of RSNs in a resting-state fMRI study for further group analysis with conditional GCM approach. Subsequently, time series prediction is achieved by the fitting of MVAR models. In order to implement Eq.1, two MVAR models are involved. These two models can be developed from an efficient parametric method [Kaminski et al., 2001], which is obtained by first modeling the multivariate data as a stationary MVAR process W_t:

$$\left(\begin{array}{l}{w}_{1t}\\ w_{2t}\\ ⋮\\ w_{nt}\end{array}\right)=\sum _{k=1}^m\left(\begin{array}{cccc}{A}_{11k}& A_{12k}& \cdots & A_{1\mathit{\text{nk}}}\\ A_{21k}& A_{22k}& \cdots & A_{2\mathit{\text{nk}}}\\ ⋮& ⋮& \cdots & ⋮\\ A_{n1k}& A_{n2k}& \cdots & A_{\mathit{\text{nnk}}}\end{array}\right)\left(\begin{array}{l}{w}_{1(t-k)}\\ w_{2(t-k)}\\ ⋮\\ w_{n(t-k)}\end{array}\right)+\left(\begin{array}{l}{\varepsilon }_{1t}\\ {\varepsilon }_{2t}\\ ⋮\\ {\varepsilon }_{nt}\end{array}\right),$$ (2)

where A_ijk is the auto regression (AR) coefficient between channels i and j at lag k and constitutes the ij^th element of the AR coefficient matrix A_k, The coefficient ε_t is a white noise residual with zero mean and covariance matrix Σ, and m is the order of the model which can be determined by criterion such as Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC). Here, we used order one as determined by the application of AIC to raw time series for our fMRI studies. Because a single time point in the summary time series corresponds to the area under the corresponding epoch, the resulting model represents epoch-to-epoch prediction [Deshpande et al., 2009]. In order to evaluate the conditional causal influence of Y_t on the X_t in the frequency domain of this multivariate setting, we first rewrite Eq.2 as follows to get one three-variable MVAR model:

$$\left(\begin{array}{l}{\mathbf{\text{X}}}_{\mathbf{\text{t}}}\\ {\mathbf{\text{Y}}}_{\mathbf{\text{t}}}\\ {\mathbf{\text{Z}}}_{\mathbf{\text{t}}}\end{array}\right)=\sum _{k=1}^m\left(\begin{array}{ccc}{\mathbf{\text{A}}}_{\mathbf{\text{aak}}}& {\mathbf{\text{A}}}_{\mathbf{\text{abk}}}& {\mathbf{\text{A}}}_{\mathbf{\text{ack}}}\\ {\mathbf{\text{A}}}_{\mathbf{\text{bak}}}& {\mathbf{\text{A}}}_{\mathbf{\text{bbk}}}& {\mathbf{\text{A}}}_{\mathbf{\text{bck}}}\\ {\mathbf{\text{A}}}_{\mathbf{\text{cak}}}& {\mathbf{\text{A}}}_{\mathbf{\text{cbk}}}& {\mathbf{\text{A}}}_{\mathbf{\text{cck}}}\end{array}\right)\left(\begin{array}{l}{\mathbf{\text{X}}}_{\mathbf{\text{a}}(\mathbf{\text{t}}-\mathbf{\text{k}})}\\ {\mathbf{\text{Y}}}_{\mathbf{\text{b}}(\mathbf{\text{t}}-\mathbf{\text{k}})}\\ {\mathbf{\text{Z}}}_{\mathbf{\text{c}}(\mathbf{\text{t}}-\mathbf{\text{k}})}\end{array}\right)+\left(\begin{array}{l}{\mathbf{\varepsilon }}_{\mathbf{\text{at}}}\\ {\mathbf{\text{ɛ}}}_{\mathbf{\text{bt}}}\\ {\mathbf{\text{ɛ}}}_{\mathbf{\text{ct}}}\end{array}\right)$$ (3)

where Z_t is the time series vector excluding X_t and Y_t, and ε_ct is the white noise vector excluding ε_at and ε_bt.

The other MVAR model used for detecting the prediction of X_t can be performed based on only the past knowledge of Z_t and X_t:

$$\left(\begin{array}{l}{\mathbf{\text{X}}}_{\mathbf{\text{t}}}\\ {\mathbf{\text{Z}}}_{\mathbf{\text{t}}}\end{array}\right)=\sum _{k=1}^p\left(\begin{array}{ll}{\mathbf{\text{B}}}_{\mathbf{\text{aak}}}& {\mathbf{\text{B}}}_{\mathbf{\text{ack}}}\\ {\mathbf{\text{B}}}_{\mathbf{\text{cak}}}& {\mathbf{\text{B}}}_{\mathbf{\text{cck}}}\end{array}\right)\left(\begin{array}{l}{\mathbf{\text{X}}}_{\mathbf{\text{a}}(\mathbf{\text{t}}-\mathbf{\text{k}})}\\ {\mathbf{\text{Z}}}_{\mathbf{\text{c}}(\mathbf{\text{t}}-\mathbf{\text{k}})}\end{array}\right)+\left(\begin{array}{l}{\mathbf{\eta }}_{\mathbf{\text{at}}}\\ {\mathbf{\eta }}_{\mathbf{\text{ct}}}\end{array}\right),$$ (4)

Then, η_at is the error prediction of X_t excluding the possible causal influence from Y_t, whereas ε_at is the prediction error of X_t including the possible causal influence from Y_t. If the variance of ε_at is less than the variance of η_at, then Y_t is said to have a conditional causal influence on X_t after taking into account the causal influence from Z_t. The conditional Granger causality can be quantified as $f_{Y\to X\mid Z}=ln\frac{var({\mathbf{\eta }}_{\mathbf{\text{at}}})}{var({\mathbf{\varepsilon }}_{\mathbf{\text{at}}})}$.

Subsequently, one gets the overall spectral matrix according to S(f) = H(f)ΣH*(f), $H(f)=I-\text{∑}_{k=1}^m{A}_{k}exp(i2\pi \mathit{\text{fk}})$ is the transfer function [Chen et al., 2006; Rogers et al., 2010]. To avoid fitting the AR model twice [Chen et al., 2006] and thereby eliminating the problems associated with such repeated fitting, we chose suitable entries from the spectral matrix to form a new spectral matrix that corresponds to X_t and Z_t. The two sets of spectral matrices and their associated H and Σ are used to compute the spectral representation of Granger causality from Y_t to X_t conditioned on Z_t. Integrating the spectrum over frequency yields the time domain counter which is used throughout this work.

Simulation has been reported comparing the conditional GCM approach and pairwise GCM approach in our previous study [Zhou et al., 2009a]. In applying the theory of conditional GCM to the task-related and resting-state fMRI data, the vector time series of one activated ROI can be associated with X_t and another one with Y_t. Z_t represents all the remaining ROIs vector time series other than X_t and Y_t. All the vector time series of the BOLD signal from selected ROIs lasts for in-order multiple subjects in our group analysis. Finally, a permutation procedure was used to test the statistical significance of the computed conditional GCM approach [Nichols et al., 2001] in group analysis. Specifically, 500 synthetic datasets were created by random rearrangement of the subject order for all vectors. A distribution of Granger causality values in the time domain was obtained after the conditional Granger causality computation in each permutation. The Granger causality values under the threshold of distribution were not considered to be significant.

Results

To address the performance of conditional GCM approach on BOLD data in both task-related and resting-state fMRI studies and to ensure that we could obtain meaningful results in multiple subjects, we analyzed data from multiple subjects performing the emotion task and during the resting state.

Emotional Pathway (University of Florida data)

Significant differences in modeled signal activations are summarized in our previous publications regarding depression [Wright et al., 2006; Zhou et al., 2009a]. Since the amygdala has been described as an emotion processing module specialized to enable both the experience of fear and the recognition of fear in others, we tried to investigate the amygdala response in the emotion pathway from the fMRI data. According to recent literature [Etkin et al., 2006], emotional conflict is resolved through top-down inhibition of amygdalar activity by the anterior cingulated cortex (ACC).

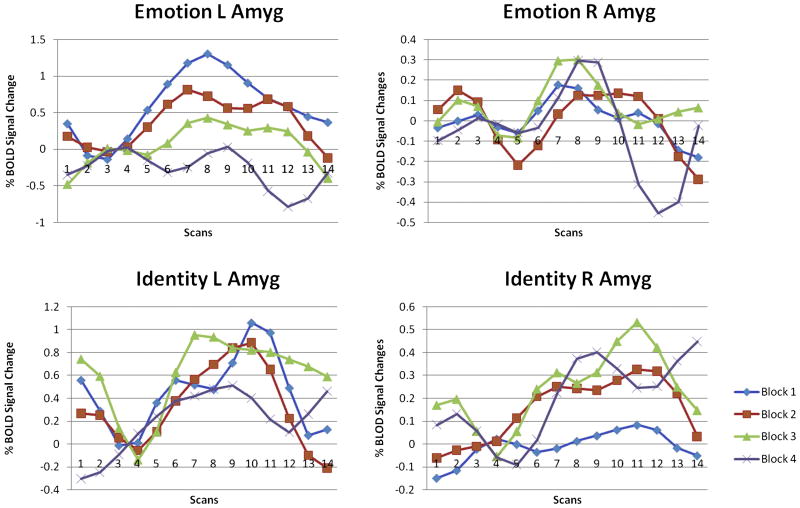
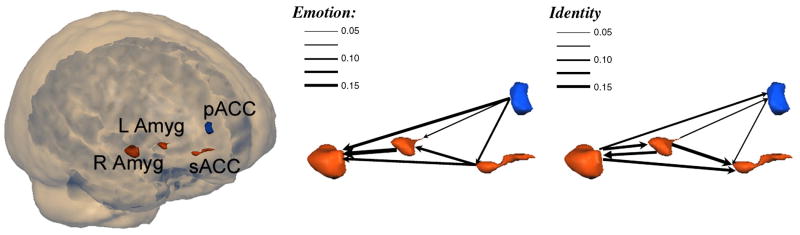
In this current depression study, conditional GCM analysis allowed us to further investigate the connections among the pregenual cingulate cortex (pACC), subgenual cingulate cortex (sACC), left amygdala, and right amygdala in the selected four activated brain ROIs. For each ROI, we validated the GLM results by plotting the average BOLD response to each condition, as previously described [Wright et al., 2006]. The percentage signal change was calculated for each block relative to the preceding resting signal and then averaged across blocks and participants for each condition. In order to investigate habituation, the BOLD response to each condition was calculated separately for each of the four repetitions of that block, averaged across participants. We used the mean % BOLD signal change values for 18 second time points as the peak response after block onset. The BOLD response at the left amygdala decreases over time in the emotion condition but not in the identity condition and no obvious changes have been found at the right amygdala (Fig.1). The Granger causal connectivity network (Fig.2) was constructed such that the thickness of connecting arrows indicated the strengths of the causal influences (p<0.05) in both emotion and identity conditions. The conditional GCM approach results show that both the sACC and pACC have a strong directional influence upon the right amygdala during the emotion task but less upon the left amygdala (Fig.2), and they indicate that there might be a distinct pattern of emotion processing at the left amygdala.

Figure 1.

BOLD response at both amygdalae in both conditions. Only the left amygdala decreases over time in the emotion condition but not in the identity condition. BOLD responses are derived from left and right amygdala activation clusters for the contrasts emotion vs. control and identity vs. control.

Figure 2.

“Glass brain” showing main clusters of activation with a threshold of t(11)>4.0. Left inferior prefrontal sulcus, right amygdala, and anterior cingulate cortex activations for the group illustrated on this rendered 3D brain. The Granger causal connectivity network was constructed in which the thickness of connecting arrows indicated the strengths of the causal influences in both conditions (p<0.05).

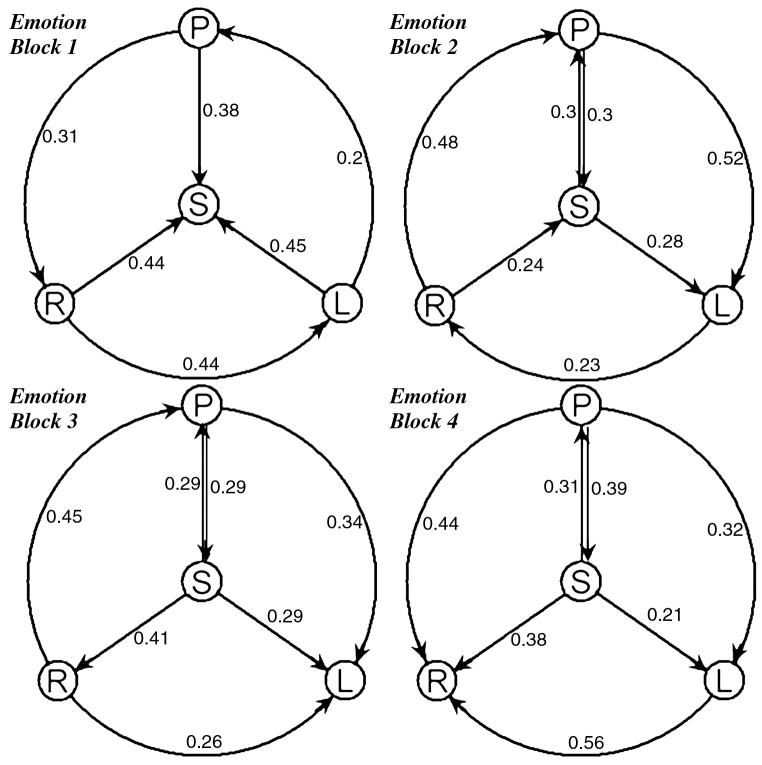
The initial BOLD response at the left amygdala is greater during the emotion task than during the identity task but then it rapidly diminishes. We then focus on the left amygdalar response during the 4 repeated emotion tasks with conditional GCM analysis. A significant habituation apparent to repeated emotional tasks was found in the left amygdala. The current findings of Granger causality from ACC to the left amygdala fit the model, which was proposed by Wright [Wright et al., 2001]. The connectivity and directed influence between ACC and amygdala have been calculated, and the influence from ACC to left amygdala has been extracted to illustrate the inhibition phenomenon of the left amygdala response (Fig.3).

Figure 3.

The directed influence with the sub-network, which is composed of ACC (sACC and pACC) and amygdala (left and right). All Granger causalities have been calculated within itself over four repeated blocks in the emotion condition. P means pACC, S means sACC, R means right amygdala and L means left amygdala. The connecting arrows indicate Granger causal directionality.

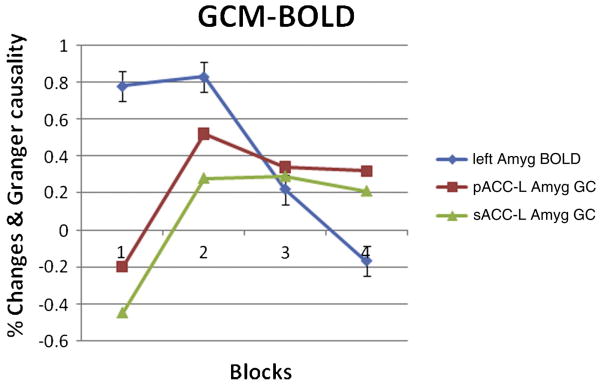
Both pACC and sACC have apparent direct causality changes to the left amygdala during last three (2^nd to 4^th) repeated emotion tasks in conditional GCM analysis, but no obvious habituation was detected in the right amygdala. This result conflicts with Wright et al. [2001] who described the right amygdala as a rapid but general relevance detector and the left amygdala as slower but capable of distinguishing emotional valence. But we believe the reason is that habituation of the right amygdalar response in the current study is difficult to detect because it occurs too rapidly within the first block. We have also found the causality from ACC to the left amygdala in this study, and the causality is a possible reason for its habituation (Fig.4). Although no increase in ACC activation had been detected, the Granger causality would still produce a response in the left amygdala. It has also predictably shown that the left amygdala has a slow response to emotional valence. In addition, the habituation causes difficulty in finding the left amygdala activation in block design tasks; meanwhile, right amygdala activation is always easily detected in block design tasks. Since the block design task is not suited for the investigation of both amygdalae, an event-related study would be more constructive for future fMRI studies of emotion.

Figure 4.

Habituation. The peak BOLD response habituates at the left amygdala in the emotion condition. Peak response = mean % signal change values for 9-18s time points. Responses derived from left amygdala cluster and Granger causality from pACC/sACC to left amygdala is presented for the contrast. Negative number indicates opposite Granger causality directionality.

Default Mode Network (New York University data)

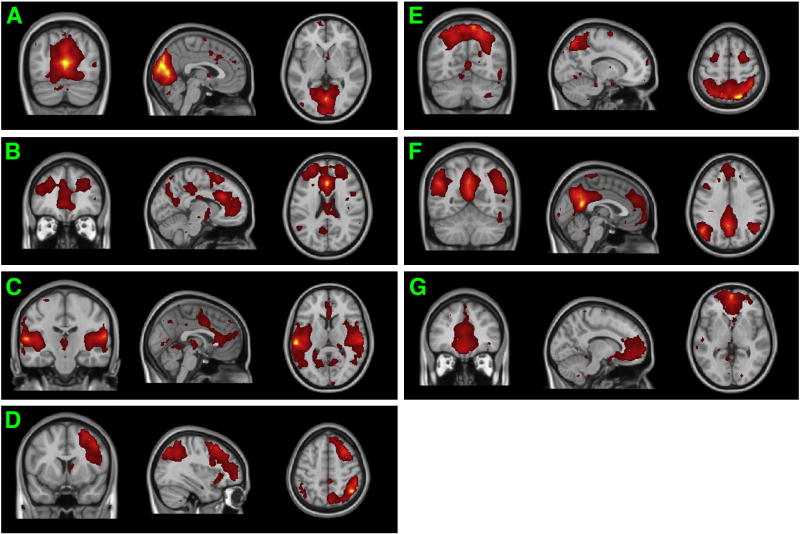
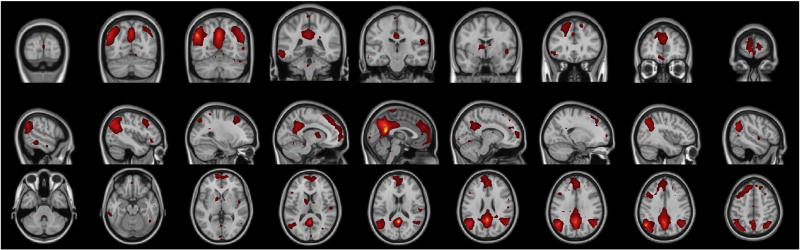
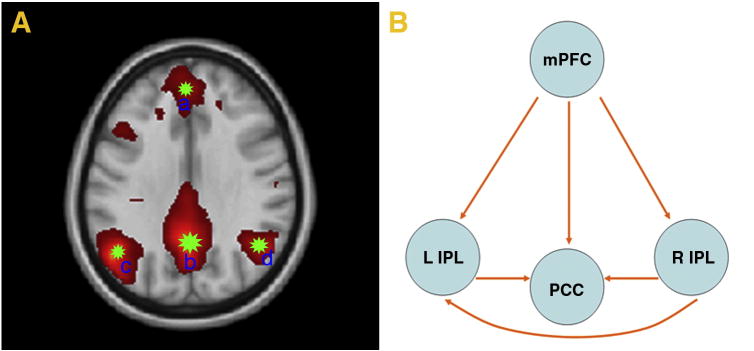
The brain during the resting-state has generated much research interest. Most previous studies have found low frequency fluctuation among certain regions of cortex during rest and have argued that there are RSNs in the human brain. RSNs can be applied to study the functional connectivity of specific diseases in the human brain such as Alzheimer's disease, autism, and schizophrenia [e.g. Buckner et al., 2008]. The spatial maps of seven (7) RSNs illustrated in Fig.5, were selected for further analysis according to 43 ICs decomposed by kernel-ICA and the large number of previous RSN studies. The RSN a is the network related to visual processing. The RSN b is the core network with the function of task control. The RSN c is the network corresponded to auditory system. The RSN d is the central-executive network. The RSN e is the network for motor and integration of sensory information. The RSN f is the DMN, as shown in Table 1 and Fig.6. The RSN g is the self-referential network related to self-knowledge and knowledge represent and other high level neural activity [Lowe et al., 1998; Buckner et al., 2008; Eckert et al., 2008; Sridharan et al., 2008; Jafri et al., 2009; Mantini et al., 2009; Liao et al., 2009b]. The DMN is a preferentially fundamental active brain system, which can integrate information from RSNs related to both primary function and higher level cognition [Buckner et al., 2008;], and it has been suggested to be involved in episodic memory [Vincent et al. 2006] and self-projection [Buckner et al., 2007]. In our study, the DMN is mainly composed of the medial temporal lobes, bilateral inferior parietal lobes (IPL), medial prefrontal cortex (mPFC), and posterior cingulate cortex (PCC), which is consistent with the findings of Buckner [Buckner et al., 2008]. To the best of our knowledge, this is the first study dedicated to analyze the conditional causal influences over DMN components and other RSNs. As shown in Fig.7A, our study semi-automatically chose four ROIs based on kernel-ICA results (peak T score point MNI152 coordinates) for further conditional causality analysis, which is consistent with existing research [Uddin et al., 2009]. Here, we chose the DMN detected by group kernel-ICA method from New York University data to examine our conditional GCM methodology. Previous studies of resting-state functional connectivity in the DMN based on ICA and GCM are usually focused on its relationship with other RSNs, but our current research will focus on both the connectivity and causality between brain ROIs within the DMN and the relationship among RSNs.

Figure 5.

RSNs detected by kernel-ICA. RSN a is visual network. RSN b is the core network. RSN c is auditory network. RSN d is central-executive network. RSN e is motor-sensory network. RSN f is DMN. RSN g is self-referential network.

Table 1.

Clusters of major activated brain regions of DMN. Minimum cluster size: 75 voxels. Voxels above threshold were converted from MNI to Talairach coordinates. Within each area, the maximum t-value and its coordinates are provided.

Major Regions of DMN	Hemisphere	Brodmann area	Talairach coordinates	Voxel No.	T score
medial prefrontal cortex	L, R	9	6, 45, 24	97	11.0
posterior cingulate cortex	L, R	31	-3, -57, 29	178	22.2
inferior parietal lobes	L	40	-53, -56, 40	190	6.7
inferior parietal lobes	R	40	45,-54, 44	231	7.8

Minimum cluster size: 75 voxels. Voxels above threshold were converted from MNI to Talairach coordinates. Within each area, the maximum t-value and its coordinates are provided.

Figure 6.

DMN is mainly composed of medial temporal lobes, bilateral inferior parietal lobes (IPL), medial prefrontal cortex (mPFC), and posterior cingulate cortex (PCC) etc.

Figure 7.

Four ROIs and causality within DMN. A. Time series in each ROIs are extracted from seed a, seed b, seed c, seed d by region growing method. B. The lines with arrows represent the coupling Granger causality.

Subsequently, we used the conditional GCM approach to determine the functional connectivity of four (4) selected brain regions at resting-state. We hypothesized that all of these regions individually would reveal important differences in resting functional connectivity between each couple. Here, we were particularly interested in the internal relationship of DMN in lieu of the external influence with other RSNs. A conditional Granger causal connectivity network was constructed in which the arrowheads of connecting lines indicated the directionality of causal influences (Fig.7B). As demonstrated in Fig.6, our study showed significant Granger causality between brain regions of the DMN for the entire group of subjects. Lines between-region pairs not reaching significance (p < 0.05) in the Granger causality measures are not shown. We examined the relationship between each coupling of activated brain regions in the DMN sub-networks.

Furthermore, the details of coupling Granger causality for directional intrinsic connectivity (F_X→Y∣Z − F_Y→X∣Z) based on conditional GCM approach are provided in the temporal domain in Table 2.

Table 2.

Conditional Granger causality results within DMN based on conditional GCA (F_X→Y∣Z).

Brian Regions	mPFC	PCC	L IPL	R IPL
mPFC	-	0.1432*	0.1846*	0.2099*
PCC	0.1150	-	0.0943	0.1464
L IPL	0.1175	0.1163*	-	0.1204
R IPL	0.1828	0.1757*	0.1784*	-

Direction of influence is from the activated region at the left to the region at the top. Values are shown for temporal interactions determined to be significant (* means p<0.05) by the permutation procedure described in Method. -, the pairing of a region with itself, because the Granger causality is measured only between different regions.

The dominant direction of the influence term F_X→Y∣Z − F_Y→X∣Z) was applied in previous ICA + GCM studies in resting-state fMRI [Liao et al. 2009; Uddin et al. 2009]. We examined the pairwise GCM (Table 3) and conditional GCM approaches within DMN. The later results indicate that the former results are real directional causalities. Hence, we suggest considering the directed influence term (F_X→Y∣Z) in lieu of the dominant direction of the influence term. If both causalities were significant, then we should also consider whether to include the coherency term in fMRI studies with GCM. There is a distinction between implementation because in most fMRI studies Granger causality is implemented in the time domain, while coherency is implemented in the frequency domain [Kayser et al. 2009]. All events of coherence in the time domain integrated from the frequency domain (as Granger causality calculation throughout this work) within the DMN were added and found to be significant between selected brain regions (Table 3). After performing experiments on this data, the ideal approach to resting-state fMRI data analysis is likely to involve a complementary combination of both Granger causality and coherence (Table 3). Furthermore, the brain regions selected by ICA could be divided into different sub-regions corresponding to different Brodmann Areas. The general RSNs relationship information is omitted and can be found in previous studies [e.g. Liao et al. 2009; Uddin et al. 2009].

Table 3.

Pair-wised GCA results including coherency between coupling variables.

Brian Regions	mPFC	PCC	L IPL	R IPL
mPFC	-	0.3225	0.3520	0.4714
PCC	0.1296/0.1703	-	0.5635	0.6663
L IPL	0.1512/02393	0.1310/0.1138	-	0.6203
R IPL	0.2239/0.2302	0.2191/0.1486	0.2327/0.1198	-

BOLD font is coherency and others are Granger causality (F_X→Y∣Z / F_Y→X∣Z).The directionality of each pairing of two regions are as shown in the way of following: PCC-mPFC (0.1296/0.1703) means the pGCA result from PCC to mPFC is 0.1296 and the causality from mPFC to PCC is 0.1703.

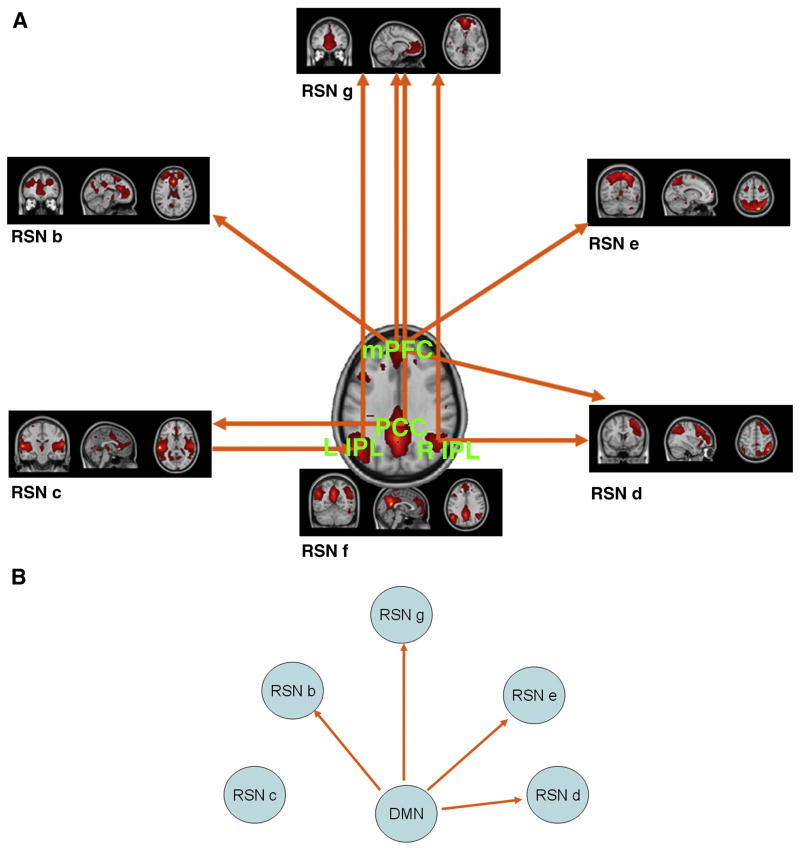
In order to analyze the different contributions of the sub-regions in the DMN at resting state, the conditional GCM analysis was applied to determine the effective connectivity between each of the four ROIs within the DMN and other RSNs (RSN a-e and g) conditional on other sub-regions of the DMN. Fig.8a demonstrates significant Granger causality between DMN components and RSNs with significance (p< 0.05) in the same way of the above analysis. The RSN a is excluded due to the absence of significance. The details are provided in Table 4. In addition, Fig.8b showed significant Granger causality in the terms of (F_Y→X∣Z and F_X→Y∣Z) and between the entire DMN and each RSN conditional on other RSNs by conditional GCM analysis. The details are provided in Table 5.

Figure 8.

A. Causality between DMN components and other RSNs. The lines with arrows represent the coupling Granger causality. RSN a is excluded for the detection of no significance; B. Causality between entire DMN and other RSNs. The lines with arrows represent the coupling Granger causality. RSN a is excluded for the detection of no significance.

Table 4.

Granger causality results between DMN sub-regions and other RSNs based on CGCA.

Brain Regions	RSN a	RSN b	RSN c	RSN d	RSN e	RSN g
PCC→	0.149211	0.134608	0.160091*	0.100641	0.130188	0.181068*
PCC←	0.133617	0.120793	0.118263	0.123054	0.147352	0.116751
mPFC→	0.154574	0.202055*	0.108448	0.182086*	0.193076*	0.223168*
mPFC←	0.130457	0.121733	0.116011	0.147916	0.116550	0.146441
L IPL→	0.109890	0.109592	0.099917	0.147077	0.150169	0.142707*
L IPL←	0.110938	0.117271	0.128859*	0.138780	0.139610	0.117328
R IPL→	0.168068	0.134026	0.167369	0.205572*	0.174455	0.132687*
R IPL←	0.152073	0.136483	0.165011	0.147496	0.152995	0.107149

Direction → of influence is from the activated region at the left to the region at the top and direction ← of influence is from the activated region at the top to the region at the left.

^*are shown the significant Granger causality between brain regions (p<0.05) by the permutation procedure described in Method.

Table 5.

Granger causality results within RSNs based on CGCA (F_X→Y∣Z and F_Y→X∣Z).

Brain RSNs	RSN a	RSN b	RSN c	RSN d	RSN e	RSN g
DMN (RSN f)→	0.454626	0.494301*	0.471885	0.521473*	0.486932*	0.617325*
DMN (RSN f)←	0.401168	0.382614	0.432934	0.442348	0.423257	0.391084

Direction → of influence is from the activated region at the left to the region at the top and direction ← of influence is from the activated region at the top to the region at the left.

^*are shown the significant Granger causality between brain regions (p<0.05) by the permutation procedure described in Method.

In summary, many detailed Granger causal connections were detected within and without the DMN, which is one of the most important RSNs. Using a conditional GCM approach on resting-state data, we individually assessed the functional connectivity of each component of the DMN and found that the interactions were predominantly directional, with bidirectional interactions among four selected brain regions (bilateral inferior parietal lobes, medial prefrontal cortex, and posterior cingulate cortex). Unlike other descriptions of the DMN as a whole, the idea that the role of a brain region is determined by how it interacts with other regions is particularly relevant. It may be that the relationship between activities in the DMN, in lieu of the DMN itself, is most functionally relevant in a resting-state fMRI study.

Discussion

Mapping functional neuron connectivity is an essential step towards unraveling the brain mechanisms of cognition and emotion. The incorporation of a conditional GCM approach in fMRI provides the possibility of better identifying the anatomical foundation that mediates cognitive and affective processing in the human brain. Efforts have been undertaken to address various aspects of the application of GCM to fMRI data during the past five years and many clinical studies based on GCM and ICA have been recently published [e.g. Demirci et al., 2009; Londei et al. 2009; Peterson et al. 2009]. A key issue in functional and effective connectivity analysis of fMRI data involves defining ROIs and representing the information in given ROIs in group analysis over multiple subjects. The classical pairwise GCM approach is often applied to an ROI based on average time series or independent components by group spatial ICA. The former representation is prone to significant information loss while the latter representation is only effective in connectivity studies between RSNs. The proposed conditional GCM approach performs a standard procedure for further group GCM analysis to extract components from ROIs selected by either GLM or ICA from task-related or resting-state fMRI datasets. These components account for full data variance after data normalization procedure and are suited in conditional Granger causality calculations. Although these are preliminary observations and connectivity measures do not always reflect the true neuronal connectivity, it is evident that the modified procedure may be quite useful to extend the information that is currently within reach. Conditional GCM can provide more accurate information [Zhou et al., 2009a] in the brain network for GCM approaches relative to previous work. It facilitates group analysis of conditional Granger causality over multiple subjects based on multidimensional vector time series in lieu of 1-dimension time series.

The proposed conditional GCM approach appears valid and it can be applied to an in vivo fMRI dataset in human brain research. Both task-related and resting-state fMRI datasets have been examined in the current study. Using the face matching fMRI data from University of Florida, we were able to distinguish direct connectivity from indirect connectivity and further identify patterns of both amygdalae within the emotion pathway. Moreover, habituation of the left amygdala was discussed in emotional processing based on our conditional GCM approach. Using the resting-state fMRI data from NYU, we demonstrated that the conditional GCM approach can provide more detailed information in functional connectivity within one special RSN in addition to the relationships between RSNs. Furthermore, the differential contributions of DMN sub-regions to the competitive relationships were examined and explained in a clarified pattern. The most important conclusion from our study is that the integration of multivariate conditional GCM analysis can be utilized as a powerful tool for identifying large scale functional connectivity patterns from a relatively short time series of fMRI data. It could be helpful in measuring brain effective and functional connectivity over multiple subjects and in finding a correlation between such measurements and behavioral or physiological parameters.

Conditional GCM analysis in Task-related fMRI

A systemic level of understanding of neurobiological disturbances in emotion related disorders (e.g. depression) remains poorly developed. In this paper, depression was chosen as an example of how the conditional GCM approach has worked in a task-related fMRI experiment. Efforts to develop and validate strategies for investigating the interaction of functional brain networks supporting emotion may greatly facilitate that effort. Meanwhile, recent fMRI research has gone beyond simply localizing brain activation, and more research has been focused on mapping neural connectivity and detecting the underlying dynamics. Previous studies suggest three main regions of altered brain activity in depression. Activity in the amygdala correlates positively with depression symptoms [Drevets et al., 1998]. The orbitofrontal cortex (OFC), which has a high probability of direct connectivity with the sACC, is also more active in depression but its activity correlates inversely with the associated symptoms [Kennedy et al., 2001; Mayberg et al., 2000]. This is speculated to represent a compensatory response to an initial functional lesion possibly in the amygdala. Finally, activity at the pACC appears to predict the response to drug treatment [Mayberg et al., 1997; Brannan et al., 2000; Saxena et al., 2003].

In our face matching study, emotion specific activations were found using the conjunction of the contrast between [emotion vs. identity] and [emotion vs. control] which occurred at the left inferior frontal sulcus. The pACC BOLD response showed a greater decrease from baseline during emotion matching than during identity matching [Wright et al., 2006]. The BOLD response at the sACC and amygdala was not specific to either the emotion or identity conditions and appeared when contrasting either face-matching condition against the control. The activation was more statistically significant at the right amygdala (peak t(11)=7.25 for emotion). However, no significant activation was found at OFC in our study. The four main activated brain ROIs were selected for subsequent conditional GCM analysis. Directional causality in emotion related brain pathways was investigated by looking for changes over time in BOLD responses. Note that the ACC response increased over time and was reportedly associated with the amygdala. We investigated the connections among the pACC, sACC, inferior frontal sulcus, and right amygdala using Granger causality analysis in our previous study [Zhou et al., 2009b]. In this study, we found that both the pACC and sACC send projections to the amygdala [Mayberg, 2003; Vogt, 2005], and DTI fiber tracking was recently used to show connections between the sACC and amygdala [Johansen-Berg et al., 2006]. The inferior frontal sulcus can be considered a part of the dorsolateral prefrontal cortex, which is associated with working memory and executive functions. Ochsner [Ochsner et al., 2005] has described this region of the prefrontal cortex as having an involvement in indirect emotional regulation since there is no strong anatomic connection between this region and the amygdala. We investigated this local brain network based on the conclusions described above and used the conditional GCM approach on the PC vectors to clarify the relationship among these mentioned regions.

The detailed description of the related brain regions have been reported in our previous reports [Zhou et al. 2009b]. At the left amygdala, the mean amplitude of the BOLD response decreased over time for emotion but not identity matching. This suggests that, while both face matching conditions activate the amygdala, there is still a distinct pattern of emotion processing at the left amygdala. Although the emotion condition initially evoked greater left amygdala activation than the identity condition, it is our conjecture that habituation prevented this difference from being detected with the statistical approach used in this study. Furthermore, both the pACC and sACC have apparent direct causality changes to the left amygdala during repeated emotion tasks in conditional GCM analysis, but no obvious habituation was detected in the right amygdala. A previous study found greater habituation when repeating passively viewed faces in the right amygdala compared with the left amygdala; the activation in the left amygdala distinguished fearful and happy faces [Wright et al., 2001]. It is possible that the habituation of the right amygdala response in the current study occurs rapidly within the first block making it difficult to detect. The results of our current study have further confirmed that the left amygdala has a slow response to emotional valence, and the habituation should cause difficulty in finding the left amygdala activation in block design tasks, while the right amygdala activation are always easily detected in block design tasks. Since the block design task is not suited for the investigation of both amygdalae, an event-related study of habituation during explicit and incidental emotion processing may shed more light on the lateralization of the speed and specificity of emotion processing at the amygdala.

Conditional GCM analysis in Resting-state fMRI

In most of the previous resting-state fMRI studies, the DMN was considered as a homogenous network [e.g. Uddin et al., 2009]. Although few works have been dedicated to investigate the different contributions of mPFC and PCC in DMN, some studies have found that brain regions from different RSNs would show decreased or increased function connectivity around PCC at resting-state [Uddin et al., 2009; Zhang et al., 2009]. However, the inner and outer dynamics of DMN are still not fully understood. We reasoned that causal circuitry of RSNs with DMN are a fundamental RSN for integration of information possibly detected by the conditional GCM approach and hypothesized that all of these regions would individually reveal important differences in rest functional connectivity between each couple. To test this hypothesis, we examined the relationship between each coupled pair of activated brain regions in the DMN sub-networks. Here, we were particularly interested in the intrinsic relationship of the DMN since the conditional GCM approach has not yet been applied to study the effective connectivity within and without the DMN. We found that the efferent influence from mPFC to PCC is consistent with three previous studies. The first study reported correlated influence between the vmPFC and PCC, indicating the complexity within DMN [Greicius et al., 2003]. Another study presented significant causal relationship from the anterior node to the posterior node in DMN [Uddin et al., 2009], which is strikingly confirmed by our CGA results. The third study reported that mPFC shows decreased connectivity with PCC in Alzheimer's disease (AD) subjects [Zhang et al., 2009], which suggests that the GCM approaches can be applied for AD study. Moreover, the specific pattern of the DMN dynamic discovered in our study shows that PCC performs afferent causal while mPFC performs efferent causal influence within the DMN.

Differential contributions of the sub-regions within the DMN compared to the competitive relationships were examined and an interesting pattern of DMN dynamics was established. Our study showed that the nodes of DMN play different roles and are affected by the core network (RSN b), the auditory system (RSN c), the central-executive network (RSN d), motor-sensory network (RSN e), and the self-referential network (RSN g). Previous studies indicates that the dynamic aspect of the DMN is related to the mentally diverse level involving multiple sensory and cognitive representations [Buckner et al., 2008; Liao et al., 2009; Uddin et al., 2009]. In addition, our results demonstrate a different pattern to one of the previous studies [Liao et al., 2009]: a potential trend of brain activity that both PCC and mPFC perform more efferent causal influence than afferent causal influence with other RSNs, especially in mPFC. This interesting finding is very similar to Uddin's results that the anterior node is more active than the posterior node in the causal circuitry between DMN and other brain regions [Uddin et al., 2009]. The causality between the RSN b and mPFC is in agreement with the finding that showed the core network to have an important role in cognitive control related to switching between the DMN and task-related networks [Sridharan et al., 2008]. The interaction from the RSN c to the left IPL indicates that the auditory system may not be resting and affected by the noise from the MRI scanner since there is no significant causality between the RSN c and the entire DMN according to our results. A possible reason for the efferent causality from mPFC to the RSN d and the RSN e is that the DMN may monitor the external environment at the resting state [Buckner et al. 2008; Gusnard et al. 2001]. The causality between the DMN components and the RSN g confirms that the self-referential network is a high level active brain system which had been previously assumed to be an intermediary between sensory and higher-order processing [Gusnard et al. 2001; Raichle et al. 2001].

Conclusion

The technology and procedure for group analysis based on conditional GCM approach has shown to be useful in measuring complex connectivity with direct influences from one brain region to another in fMRI studies. The major strength of this methodology lies in its ability to investigate the real causality relations in brain connectivity studies. By analyzing two paradigms, the present study shows that the conditional GCM approach can be used as standard statistical approach for both group-wise effective and functional connectivity studies of fMRI datasets. In addition to DCM and psychophysiological interaction (PPI) methods, the conditional GCM methodology can also be applied to explore a wide range of cognitive tasks involved in fMRI studies. Such a new approach may be widely expanded to statistical interference within task-related and resting state fMRI datasets for effective connectivity analysis. Mapping an entire individual brain can provide valuable information for understanding the depth and dynamics of brain networks. This will be a big step towards discovering neural mechanisms underlying various mental diseases and emotional disorders.