Abstract
We introduce a quantitative framework for assessing the generation of crossovers in DNA shuffling experiments. The approach uses free energy calculations and complete sequence information to model the annealing process. Statistics obtained for the annealing events then are combined with a reassembly algorithm to infer crossover allocation in the reassembled sequences. The fraction of reassembled sequences containing zero, one, two, or more crossovers and the probability that a given nucleotide position in a reassembled sequence is the site of a crossover event are estimated. Comparisons of the predictions against experimental data for five example systems demonstrate good agreement despite the fact that no adjustable parameters are used. An in silico case study of a set of 12 subtilases examines the effect of fragmentation length, annealing temperature, sequence identity and number of shuffled sequences on the number, type, and distribution of crossovers. A computational verification of crossover aggregation in regions of near-perfect sequence identity and the presence of synergistic reassembly in family DNA shuffling is obtained.
Directed evolution methods use the process of natural selection to combinatorially evolve enzymes, proteins, or even entire metabolic pathways with improved properties. These methods typically begin with the infusion of diversity into a small set of parent nucleotide sequences through DNA recombination and/or mutagenesis. The resulting combinatorial DNA library then is subjected to a high-throughput selection or screening procedure, and the best variants are isolated for another round of recombination or mutagenesis. The cycles of recombination/mutagenesis, screening, and isolation continue until a protein or enzyme with the desired level of improvement is found. In the last few years remarkable success stories of directed evolution have been reported (1), ranging from many-fold improvements in industrial enzyme activity and thermostability (2) to the design of vaccines (3) and viral vectors for gene delivery (4).
DNA shuffling (5), along with its variants, is one of the earliest and most commonly used DNA recombination protocols. It consists of random fragmentation of parent nucleotide sequences with DNase I and subsequent fragment reassembly through primerless PCR. Library diversity is generated during reassembly when two fragments originating from different parent sequences anneal and subsequently extend. This gives rise to a crossover, the junction point in a reassembled sequence where a template switch takes place from one parent sequence to another. The key advantage of DNA shuffling is that many parent sequences can be recombined simultaneously (i.e., family DNA shuffling; ref. 6), generating multiple crossovers per reassembled sequence. However, crossovers tend to aggregate in regions of high sequence identity due to the annealing-based reassembly.
A key challenge in directed evolution is that only an infinitesimally small fraction of the diversity afforded by DNA sequences can be characterized regardless of the efficiency of the screening procedure used. For example, a 500-bp gene implies 4500 ≈ 10301 alternatives, but even the most efficient screening methods are restricted to 107–108 alternatives. Therefore, it is important to know how diversity is generated and allocated in the combinatorial DNA library and which regions are the most promising. This paper addresses the first question in the context of DNA shuffling protocols and examines how fragmentation length, annealing temperature, sequence identity, and number of shuffled parent sequences affect the number, type, and distribution of crossovers along the length of reassembled sequences. This predictive framework provides a step toward optimizing directed evolution protocols in response to an enzyme or protein design challenge. In this paper, annealing events during reassembly are modeled as a network of reactions, and equilibrium thermodynamics is used to quantify their conversions and selectivities.
Modeling of Annealing Events
During annealing, fragments compete to anneal with a growing template. This competition is quantified by using equilibrium thermodynamics to infer (i) what fraction of these fragments will anneal at a given temperature, (ii) how these annealing events will be distributed between those involving high or low overlap lengths, and (iii) what portion of these annealing events will involve mismatches. An annealing event between fragments originating from the same parent sequence yields a homoduplex (assuming in-frame annealing), whereas the annealing of two fragments from different parents gives a heteroduplex. Mismatches at exactly the 3′ end will prevent extension and thus are not counted.
The thermodynamics of duplex formation can be analyzed by using nearest-neighbor parameters that describe the enthalpic and entropic contributions of specific nucleotide pairs in the overlapping region (7–12). The change ΔG in free energy associated with an annealing event can be approximated by summing the free energy gains associated with all 2-nt matches and the free energy penalties associated with the mismatches. Additional corrections also are included for the duplex initiation free energy cost, salt concentration, and dangling end stabilization (13). Enthalpic and entropic parameters at 37°C for the contribution of pairs of matches and mismatches are shown in Table 2, which is published as supplemental material on the PNAS web site, www.pnas.org.
Given this free energy predictive capability the extent of duplex formation can be tracked at different temperatures. Specifically, consider the reaction associated with the annealing of a fragment F with a template A, forming a duplex AF.
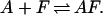 |
Assuming equilibrium, the equilibrium constant K(T) links the mole fractions of the template, fragment, and duplex at different temperatures.
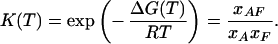 |
Here x denotes mole fractions and 0 denotes initial
values of the species in the reaction mixture so that
xA = x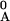 −
xAF and
xF = x
−
xAF and
xF = x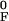 −
xAF. Let a(T) be
the annealing curve defined as the fraction of templates that have
annealed at temperature T, [a(T)
= xAF/x
−
xAF. Let a(T) be
the annealing curve defined as the fraction of templates that have
annealed at temperature T, [a(T)
= xAF/x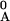 = 1 −
xA/x
= 1 −
xA/x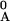 ].
Upon rearrangement these equations can be solved for
xF,
xA,
xAF, and
a(T). The temperature at which half of the
templates have hybridized to form duplexes [i.e.,
a(T) = 1/2] is defined as the melting
temperature Tm. Comparisons of the
predictions obtained with the described free energy modeling framework
against those found by an empirical formula commonly used for
hybridization experiments (14) are in good agreement (see Table 3,
which is published as supplemental material). Plots of
a(T) versus T reveal that there is a
relatively narrow temperature range, centered around
Tm, where the majority of annealing
events take place (sigmoidal curve). In general, longer overlaps imply
higher melting temperatures whereas shorter overlaps, mismatches, and
low GC content depress Tm.
].
Upon rearrangement these equations can be solved for
xF,
xA,
xAF, and
a(T). The temperature at which half of the
templates have hybridized to form duplexes [i.e.,
a(T) = 1/2] is defined as the melting
temperature Tm. Comparisons of the
predictions obtained with the described free energy modeling framework
against those found by an empirical formula commonly used for
hybridization experiments (14) are in good agreement (see Table 3,
which is published as supplemental material). Plots of
a(T) versus T reveal that there is a
relatively narrow temperature range, centered around
Tm, where the majority of annealing
events take place (sigmoidal curve). In general, longer overlaps imply
higher melting temperatures whereas shorter overlaps, mismatches, and
low GC content depress Tm.
During the annealing step of DNA shuffling, not a single, but many different fragments with varying lengths, overlaps, and mismatches are competing for a given template.
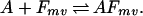 |
Here m refers to a fragment originating from parent sequence m and v implies an overlap length of v nucleotides with the template on annealing. After adjusting the expression for a(T) to reflect the multiplicity of annealing choices and resolving the system of equations the temperature-dependent selectivity
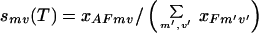 |
for a particular fragment and overlap choice mv is estimated. The presence of multiple fragment and overlap choices “spreads” the melting curve over a wider range of temperatures, implying that annealing events occur over the entire temperature range (typically 94–55°C). The free energy differences between annealing choices and relative fragment concentrations determine which annealing choice dominates at a given temperature. For instance, at high temperatures fragments with large overlaps that match perfectly with the template dominate all other ones because of the large enthalpic gains that they provide on annealing. As the temperature is lowered, the melting temperatures of fragments with progressively smaller overlaps and even one or two mismatches is reached, resulting in selectivities that are much more uniform.
Because annealing selectivities are temperature dependent, duplex formation must be assessed cumulatively over the entire annealing temperature range. To this end, the annealing step is modeled as a sequence of pseudoequilibrium states progressively contributing duplexes as the temperature is lowered from 94°C to 55°C. Mathematically, this implies integration of the temperature-dependent selectivities smv(T) times the annealing rate da(T)/dT over the annealing temperature schedule.
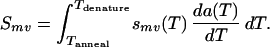 |
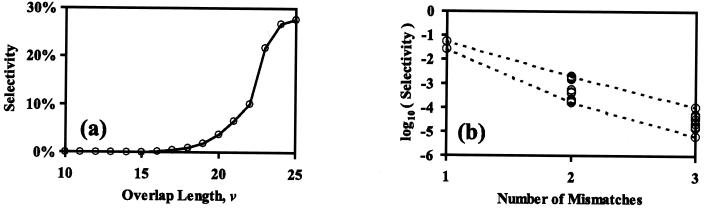
Given a pool of fragments competing for a template and an annealing temperature schedule, Smv quantifies the overall annealing selectivities. The effect of the length of overlap and number/severity of mismatches is illustrated in Fig. 1. The first plot (Fig. 1a) addresses the case when there are no mismatches. It clearly shows that there is strong preference toward annealing events involving the maximum overlap. However, a non-negligible portion of annealing events involve shorter overlaps. The second plot (Fig. 1b) considers the effect of the number and type of mismatches on annealing selectivities for a given overlap length. Although the great majority of annealing events involve no mismatches (homoduplexes) there are some mismatch-bearing annealing events (heteroduplexes), which upon extension give rise to crossovers. Note that, in the present implementation, the type of a mismatch affects its selectivity whereas its distance from the 3′ end does not. Next, the individual annealing statistics are used to infer crossover generation in the reassembled sequences.
Figure 1.
Selectivity versus overlap lengths (a) and selectivity for different degrees, types, and locations of mismatches (b). Both charts use the subtilisin E gene, positions 760–784, and mismatches are evenly distributed in the overlapping region.
Fragment Reassembly
The reassembly process is modeled as a successive sequence of annealing events. Specifically, the selectivity of an annealing event is assumed to depend only on the identity of the fragment added immediately before. For clarity of presentation, only fragments of a unique length L will be used in the reassembly analysis. Nevertheless, fragments with varying lengths can be incorporated in a straightforward manner as described (15, 16).
The key idea of the reassembly procedure is to postulate a set of
recursive relations that resolve the question of what is the
probability Πx that a full-length
reassembled sequence of B nucleotides has x
crossovers. To this end, we define
P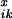 denoting the probability that
reassembly from position i to the end B of the
DNA sequence will yield exactly x crossovers, given that the
fragment ending at position i − 1 originated from
parent sequence k. The selectivities
Smv, defined earlier, can then be calculated for
different annealing choices. When a fragment from parent sequence
m anneals with a fragment from sequence k either
a homoduplex (m = k) or heteroduplex
(m ≠ k) is formed. Homoduplex formation
implies that no crossover is generated and the recursion must still
track x crossovers over the remainder of the reassembly.
However, heteroduplex formation implies that only x −
1 remaining crossovers must be subsequently tracked. The annealing of a
fragment of length L with an overlap v implies
the addition of L − v nucleotides,
extending the template to position (i − 1) +
(L − v). This position becomes the new
reassembly point completing the recursion. Summation over all parent
sequences m and overlap lengths v encompasses all
possible reassembly pathways.
denoting the probability that
reassembly from position i to the end B of the
DNA sequence will yield exactly x crossovers, given that the
fragment ending at position i − 1 originated from
parent sequence k. The selectivities
Smv, defined earlier, can then be calculated for
different annealing choices. When a fragment from parent sequence
m anneals with a fragment from sequence k either
a homoduplex (m = k) or heteroduplex
(m ≠ k) is formed. Homoduplex formation
implies that no crossover is generated and the recursion must still
track x crossovers over the remainder of the reassembly.
However, heteroduplex formation implies that only x −
1 remaining crossovers must be subsequently tracked. The annealing of a
fragment of length L with an overlap v implies
the addition of L − v nucleotides,
extending the template to position (i − 1) +
(L − v). This position becomes the new
reassembly point completing the recursion. Summation over all parent
sequences m and overlap lengths v encompasses all
possible reassembly pathways.
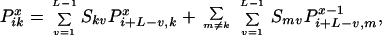 |
 |
Resolution of this recursion requires boundary conditions at the start and end of the gene or gene fragment under consideration. At the onset of reassembly, the initial fragment covers the range i = 1 to i = L, implying that subsequent annealing events add nucleotides starting from position i = L + 1. This initial fragment comes from parent m with probability equal to the relative concentration Cm of parent m in the reaction mixture. This implies that the probability Πx that the reassembled sequences contains x crossovers is the parent relative concentration averaged probability of having x crossovers past position L + 1.
 |
The boundary conditions for the end position B ensure that no crossovers occur beyond position i = B.
 |
 |
Because reassembly is a bidirectional process, the reassembly algorithm also is executed in the reverse direction with the complementary DNA sequences and the results are combined. A flowchart outlining the proposed reassembly procedure is shown in Fig. 6, which is published as supplemental material.
Interestingly, the original application of the reassembly algorithm overestimated the total number of crossovers, especially for shuffling sequences that share very high sequence identity. Closer inspection revealed that this was due to the formation of heteroduplexes with fragments involving perfect sequence identity with the growing template. Even though they are indeed crossovers, according to the formal crossover definition, they are completely undetectable experimentally and more importantly they do not contribute any diversity. Therefore, the term silent crossovers was proposed for them, and the reassembly algorithm was revised to exclude them. Specifically, if the annealing of a fragment from parent m to a growing template ending with a fragment from parent k is equivalent to the continuation of the template with nucleotides from parent k, no crossover is counted.
The proposed reassembly procedure allows the estimation of the fraction of the reassembled sequences containing x = 0, 1, … crossovers. By redefining what constitutes a desirable crossover different types of crossovers can be assessed separately. For example, in the family DNA shuffling of sequences A, B, and C the statistics of all six possible types of crossovers AB, BA, AC, CA, BC, and CB can be tracked independently. In addition, one could even track homoduplex extension events such as AA, BB, or CC. Next, the statistics of the distribution of these crossovers along the reassembled sequences is examined.
Specifically, the question addressed is what is the probability that a given position i in a reassembled sequence is the site of a crossover (i.e., end point of a heteroduplex annealing event). This probability depends on the parent origin of the fragment ending at position i − 1. Thus, the probability that a fragment from parent k ends exactly at position i − 1 is defined as Tik. A recursion is then established in a similar manner as before. A fragment from parent m ends at position i − 1 if and only if it was added to a fragment from parent k ending at position i − L + v with an overlap v. The probability for this particular duplex formation event can be quantified by multiplying the selectivity Smv times the probability Ti−L+v,k that the template is positioned appropriately.
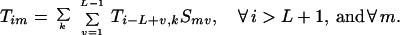 |
Boundary conditions ensure that the first nucleotide added to the original fragment comes from a parent sequence k with a probability proportional to its relative concentration. Furthermore, no fragment may end before position i = L.
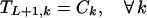 |
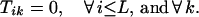 |
Once the probability Tik that a particular
type of template k ends immediately before position
i is known, it can be multiplied by the selectivity of a
crossover-generating annealing event Smv
and summed over all possible annealing choices to infer the probability
P that position i is the
site of a crossover.
that position i is the
site of a crossover.
 |
Again, by tailoring the definition of a crossover, the
distribution of different types of crossovers (i.e., AB, BC, or AC)
along the sequence can be assessed separately. A consistency check
reveals that the average number of crossovers calculated based on the
probabilities P quantifying crossover
density along the DNA sequence,
(ΣiP
quantifying crossover
density along the DNA sequence,
(ΣiP ), is
identical to the one obtained based on the crossover number
distribution calculated earlier
(ΣxxΠx).
Given this versatile algorithmic framework the statistics of any type
of crossover can be quantified both in terms of variability among the
reassembled sequences and along the length of the gene. Predictions
obtained based on the above described analysis are next contrasted
against experimental data from DNA shuffling experiments reported in
the literature.
), is
identical to the one obtained based on the crossover number
distribution calculated earlier
(ΣxxΠx).
Given this versatile algorithmic framework the statistics of any type
of crossover can be quantified both in terms of variability among the
reassembled sequences and along the length of the gene. Predictions
obtained based on the above described analysis are next contrasted
against experimental data from DNA shuffling experiments reported in
the literature.
Comparisons with Experimental Results
Although directed evolution studies are being reported in the literature with an accelerating pace, only a few studies report DNA sequencing results for naive (i.e., unselected) DNA libraries. Partial DNA sequencing results allowing for the estimation of the number of crossovers in a small subset of the reassembled sequences are found for the following five studies. Computer simulation of DNA shuffling of these systems provides the basis for the comparisons. Every effort was made to ensure that the fragment length, annealing temperature, and salt and DNA concentrations matched the ones in the experimental study. When no information was provided, default values from the original DNA shuffling protocol (5) were adopted.
The first system considered is two 465-bp IL-1β genes (human and murine) (5) with a sequence identity of only 75%. An extremely low annealing temperature of 25°C was used to boost the generation of crossovers. Nine colonies were sequenced for a total of 17 crossovers, implying an average of 1.9 per sequence. Simulation results are in close agreement with experiment, predicting an average of 1.5 crossovers.
The next system involved the family DNA shuffling of four class C cephalosporinase genes, 1.2 kb in length with pairwise sequence identities ranging from 58% to 82% (6). It was reported that neither of the two active clones sequenced contained any fragments from the Yersinia enterocolitica gene (third gene). The question is whether this occurred because fragments originating from this gene have a detrimental effect on activity or simply because pieces from this gene are disproportionately misrepresented in the naive library due to the lack of sufficiently long stretches of near-perfect sequence identity with the other three genes. The average sequence identity of each one of the four genes against the remaining three are 70%, 70%, 65%, and 59%, respectively. Simulation results predict that 36% of the naive sequences contain at least one crossover. The fraction of crossover bearing sequences containing at least one piece from each one of the four genes is 85%, 95%, 7%, and 19%, respectively. This indicates that Y. enterocolitica (third one) is by far the least even though it is not the one with the lowest sequence identity. This suggests a possible explanation for the absence of any piece of Y. enterocolitica in the most active clones.
The next system studied involved two genes for glycinamide ribonucleotide transformylase, Escherichia coli (purN) and human (hGART) (17) with a very low sequence identity of 50%. Here the following staggered portions of the two genes were shuffled (E. coli positions 1–434) and (human positions 164–611), implying that crossovers could only be formed in the 271-bp shared region (47% sequence identity). This arrangement requires that all reassembled genes of full length start with the E. coli gene and end with the human gene, yielding odd numbers of crossovers. In the experimental study only single crossover clones were observed of 10 sequenced clones. This is consistent with the simulation prediction that the ratio of the number of reassembled sequences with three or more crossovers to the number of sequences with a single crossover is less than 10−9. A system with a relatively high sequence identity is analyzed next. It involves the DNA shuffling of two biphenyl oxygenases sharing a sequence identity of 87% (18). For this system, an average of 3.3 crossovers per sequence is observed experimentally (six sequenced clones), whereas the simulation suggests a slightly smaller average of 2.8.
The last study is the only one where the simulation results deviated from the experimentally observed crossover averages. It involved the DNA shuffling of a 1.3-kb gene for wild-type subtilisin E and that of a clone (1E2A) differing by only 10 point mutations (19). Slightly larger fragments in the range of 20 to 50 bases were used in place of the default fragment length range of 10 to 50 bases. One would expect that a large average number of crossovers would be generated in this system because only 10 point mutations are present, implying a sequence identity of 99.2%. However, this is not observed experimentally as only an average of 1.9 crossovers per sequence is reported (19). The simulation results, on the other hand, are consistent with the intuitive expectation, predicting an average of 3.6 crossovers per reassembled sequence. The randomly chosen sequences may not have been representative of the entire DNA library. For instance, recombinations between mutations at positions 520 and 732 in clone 1E2A must be occurring independently because the stretch of perfect identity is much wider than even the maximum fragment size. However, a crossover occurs in only 10% of the reported sequences instead of the 50% frequency expected for independent reassembly. With the exception of this last example, simulation predictions are in good agreement with the published experimental results without adjustable model parameters.
Subtilase Case Study
Subtilases are serine proteases (20) extensively engineered with directed evolution experiments (21, 22). A set of 12 subtilases including subtilisins E, BPN′, Carlsberg, 147, ALP I, PB92, and Sendai; serine proteases C and D; proteinases K and R; and thermitase is next considered to highlight the effect of fragmentation length, annealing temperature, sequence identity, and number of shuffled sequences on the number, type, and distribution of crossovers. We chose to mirror recent subtilase-directed evolution experiments (22) by analyzing the shuffling of only a 500-bp subgenomic region. The average pairwise sequence identity is 58% ranging from 44% to 90%. First, a high sequence identity 80% pair (subtilisin E, subtilisin BPN′) is considered.
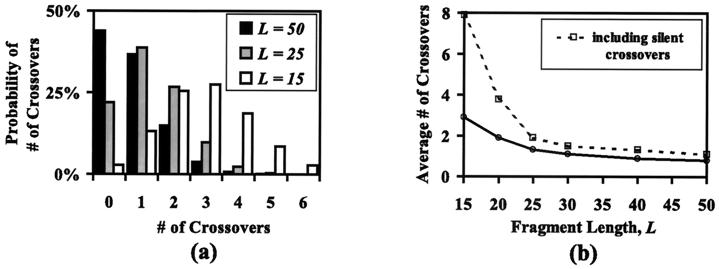
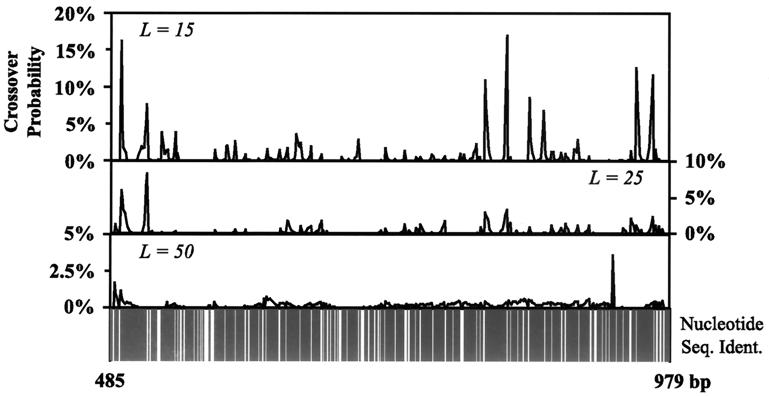
As shown in Fig. 2a, for a fragmentation length of L = 50 bases, 44% of the reassembled sequences involve no crossovers, 37% one crossover, 15% two crossovers, and diminishing percentages for sequences with more than two crossovers. As the fragment length is reduced, a nonlinear increase of crossovers is observed. This nonlinear increase in the average number of crossovers as a function of L is more clearly depicted in Fig. 2b. Interestingly, the same plot (dashed line) reveals a dramatic increase of silent crossovers for very small fragment lengths (i.e., L ≤ 20). Fig. 3 illustrates the distribution of crossovers superimposed against the sequence identity along the sequence. It shows that crossovers are preferentially aggregated in regions of near perfect sequence identity forming a characteristic double peak. The double peak implies that annealing events make full use of the available sequence identity, giving rise to two distinct double peaks at the two flanking positions of the sequence identity stretch. Larger fragments afford a wider range of overlaps flattening the two peaks whereas smaller fragments are capable of generating crossovers in relatively narrow regions of high sequence identity. However, in DNA shuffling not a single fragmentation length L is used but rather a distribution of fragment sizes, typically in the range of 10 to 50 bases, with a size distribution described by an exponentially decaying function (15, 16). When a range of fragment sizes is used for the above example, computational results reveal that the crossover statistics are almost identical with the case of using a single “effective” fragment size, which for the 10- to 50-base range is 25 bases.
Figure 2.
(a) Crossover number distribution for DNA shuffling of subtilisin E and subtilisin BPN′ for L = 15, 25, and 50 bases. (b) Average number of crossovers per sequence for the same system plotted versus fragment length in bases. The dotted line includes silent crossovers.
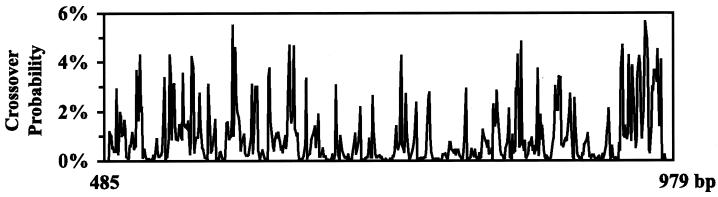
Figure 3.
Probability of generating a crossover along the length of the sequence for the (subtilisin E, subtilisin BPN′) system for L = 15, 25, and 50 bases along the subregion 485–979. Black columns in the bottom strip chart denote identical nucleotides for both sequences, and white lines denote mismatches.
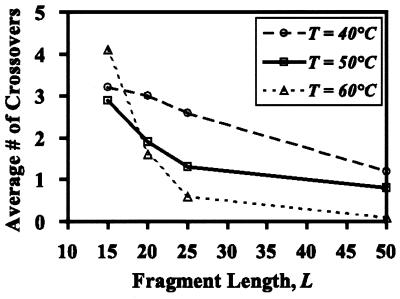
Next, the effect of annealing temperature on crossover generation is studied. What is found is that two underlying mechanisms exist with which annealing temperature affects the crossover statistics (see Fig. 4). Specifically, for medium to large fragments, lower annealing temperatures imply that the melting temperatures of more annealing choices containing mismatches (i.e., heteroduplexes) are encountered, yielding more crossovers upon extension. However, for very small fragments at high temperatures the entropic contribution to the free energy of annealing dominates, blurring the distinction between homoduplexes and heteroduplexes, causing a sharp increase in the total number of crossovers. Clearly, as in the case of fragment length, the annealing temperature cannot be arbitrarily reduced because at some point fragments cease to exhibit strong affinity for annealing in-frame, and out-of-frame additions start to overwhelm the reassembly process.
Figure 4.
Effect of annealing temperature to the number of crossovers produced for the high sequence identity subtilase pair (subtilisin E, subtilisin BPN′).
The limits of DNA shuffling are explored by choosing the low sequence identity pair (serine protease D, proteinase K), which has a 46% sequence identity. As expected, very few crossovers are predicted (see Table 1) with only a single narrow region at the end of the sequence coinciding with a short stretch of high sequence identity. Subsequently, the high sequence identity pair (subtilisin E, subtilisin BPN′) is shuffled in silico together with the low sequence identity pair (serine protease D, proteinase K) in equal ratios. The key question is whether the low identity pair will simply dilute the fragment pool that can form heteroduplexes depressing crossover generation by a factor of 2, or if synergism in the reassembly will dominate. Even though the average pairwise sequence identity for the four subtilase system is as low as 58%, a comparable number of crossovers with the (subtilisin E, subtilisin BPN′) single pair case is found (see Table 1). This implies that synergistic reassembly is taking place alluding to the contribution of “bridging” crossovers by the low sequence identity pairs. The full power of synergistic reassembly is revealed when all 12 subtilases are included, providing a computational verification of what is seen experimentally with family DNA shuffling, especially for smaller fragments. Even though the average pairwise sequence identity is only 58% at least as many crossovers are generated (see Table 1) as for the high sequence identity 80% pair. More importantly these crossovers span the entire sequence range (see Fig. 5). Admittedly though, the distribution is still multimodal with peaks tracking the location of high sequence identity, a signature of the annealing-based reassembly characteristic of DNA shuffling.
Table 1.
Average numbers of crossovers per sequence calculated for various fragment lengths L and parent sets
| L (bases) | High seq. ident. pair | Low seq. ident. pair | Set of 4 subtilases | Set of 12 subtilases |
|---|---|---|---|---|
| 15 | 2.9 | 0.5 | 2.3 | 4.8 |
| 25 | 1.3 | 0.1 | 0.8 | 1.4 |
| 50 | 0.8 | 0.0 | 0.5 | 0.8 |
Figure 5.
Crossover probability distributions for in silico family DNA shuffling of all 12 subtilases (L = 15).
Summary and Discussion
In this paper a quantitative framework for assessing the number, type, and distribution of crossovers is proposed in the context of DNA shuffling. This predictive framework allows one to explore “what if” scenarios in terms of fragmentation, length, annealing temperature, and parent choices in the context of DNA shuffling. Comparisons of predictions against experimental data reveals good agreement, particularly in light of the fact that there are no adjustable parameters. The only parameters are the free energy contributions used unchanged from literature sources (see Table 2). Therefore, no reparameterization is needed when experimental conditions or the sequences to be shuffled change, thus providing a versatile framework for comparing different protocol choices and setups. Interestingly, the application of in silico DNA shuffling revealed the presence and quantified the frequency of silent crossovers and synergistic reassembly.
The free energy-based reassembly framework is flexible enough to consider the case of out-of-frame additions. By scoring all possible out-of-frame additions based on their associated free energy of annealing the fraction of reassembled sequences that are out-of-frame can be quantified. By setting maximum limits on this target, minimum allowable fragment lengths and annealing temperatures then can be inferred. In addition, if necessary, the amount of backcrossing with the wild type needed to keep out-of-frame reassembled sequences in check also can be estimated. Ongoing work on combining nonhomologous recombination protocols (17) with DNA shuffling in the context of SCRATCHY (23) has revealed counterintuitive mechanisms for crossover generation and valuable insights for the engineering of directed evolution protocols tailored to desired crossover profiles.
Our future vision is an integrated system that combines the crossover allocation estimator proposed in this paper with a targeting system that will identify contiguous or not motifs through statistical inference (24) that are likely to give rise to active enzymes or functional proteins. An optimizer then will be used to identify which directed evolution protocol or nonobvious combinations of protocols and setups will produce crossover profiles most “in tune” with the motif targets. Alternatively, one may combine the crossover allocation estimator with different hypotheses being put forward for the type of crossovers that are likely to yield active enzymes or functional proteins. Such hypotheses include multipool swapping (25) and the recently proposed minimum schema disruption (C. A. Voigt, S. L. Mayo, F. H. Arnold, and Z. Wang, personal communication).
Supplementary Material
Acknowledgments
Financial support by the Life Science Consortium at Penn State and National Science Foundation Career Award CTS-9701771 is gratefully acknowledged.
References
- 1.Petrounia I P, Arnold F H. Curr Opin Biotechnol. 2000;11:325–330. doi: 10.1016/s0958-1669(00)00107-5. [DOI] [PubMed] [Google Scholar]
- 2.Schmidt-Dannert C, Arnold F H. Trends Biotechnol. 1999;17:135–136. doi: 10.1016/s0167-7799(98)01283-9. [DOI] [PubMed] [Google Scholar]
- 3.Patten P A, Howard R J, Stemmer W P C. Curr Opin Biotechnol. 1997;8:724–733. doi: 10.1016/s0958-1669(97)80127-9. [DOI] [PubMed] [Google Scholar]
- 4.Powell S K, Kaloss M A, Pinskstaff A, McKee R, Burimski I, Pensiero M, Otto E, Stemmer W P, Soong N W. Nat Biotechnol. 2000;18:1279–1282. doi: 10.1038/82391. [DOI] [PubMed] [Google Scholar]
- 5.Stemmer W P C. Proc Natl Acad Sci USA. 1994;91:10747–10751. doi: 10.1073/pnas.91.22.10747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Crameri A, Raillard S, Bermudez E, Stemmer W P C. Nature (London) 1998;391:288–291. doi: 10.1038/34663. [DOI] [PubMed] [Google Scholar]
- 7.SantaLucia J., Jr Proc Natl Acad Sci USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Allawi H T, SantaLucia J., Jr Biochemistry. 1997;36:10581–10594. doi: 10.1021/bi962590c. [DOI] [PubMed] [Google Scholar]
- 9.Allawi H T, SantaLucia J., Jr Biochemistry. 1998;37:2170–2179. doi: 10.1021/bi9724873. [DOI] [PubMed] [Google Scholar]
- 10.Allawi H T, SantaLucia J., Jr Biochemistry. 1998;37:9435–9444. doi: 10.1021/bi9803729. [DOI] [PubMed] [Google Scholar]
- 11.Allawi H T, SantaLucia J., Jr Nucleic Acids Res. 1998;26:2694–2701. doi: 10.1093/nar/26.11.2694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Peyret N, Seneviratne P A, Allawi H T, SantaLucia J., Jr Biochemistry. 1999;38:3468–3477. doi: 10.1021/bi9825091. [DOI] [PubMed] [Google Scholar]
- 13.Bommarito S, Peyret N, SantaLucia J., Jr Nucleic Acids Res. 2000;28:1929–1934. doi: 10.1093/nar/28.9.1929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Howley P M, Israel M F, Law M, Martin M A. J Biol Chem. 1979;254:4876–4883. [PubMed] [Google Scholar]
- 15.Moore G L, Maranas C D. J Theor Biol. 2000;205:483–503. doi: 10.1006/jtbi.2000.2082. [DOI] [PubMed] [Google Scholar]
- 16.Moore G L, Maranas C D, Gutshall K R, Brenchley J E. Comp Chem Eng. 2000;24:693–699. [Google Scholar]
- 17.Ostermeier M, Shim J H, Benkovic S J. Nat Biotechnol. 1999;17:1205–1209. doi: 10.1038/70754. [DOI] [PubMed] [Google Scholar]
- 18.Kumamaru T, Suenaga H, Mitsuoka M, Watanabe T, Furukawa K. Nat Biotechnol. 1998;16:663–666. doi: 10.1038/nbt0798-663. [DOI] [PubMed] [Google Scholar]
- 19.Zhao H, Arnold F H. Proc Natl Acad Sci USA. 1997;94:7997–8000. doi: 10.1073/pnas.94.15.7997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Siezen R J, Leunissen J A. Protein Sci. 1997;6:501–523. doi: 10.1002/pro.5560060301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chen K, Arnold F H. Bio/Technology. 1991;9:1073–1077. doi: 10.1038/nbt1191-1073. [DOI] [PubMed] [Google Scholar]
- 22.Ness J E, Welch M, Giver L, Bueno M, Cherry J R, Borchert T V, Stemmer W P C, Minshull L. Nat Biotechnol. 1999;17:893–896. doi: 10.1038/12884. [DOI] [PubMed] [Google Scholar]
- 23.Ostermeier M, Nixon A E, Benkovic S J. Bioorg Med Chem. 1999;7:2139–2144. doi: 10.1016/s0968-0896(99)00143-1. [DOI] [PubMed] [Google Scholar]
- 24.Neuwald A F, Liu J S, Lipman D J, Lawrence C E. Nucleic Acids Res. 1997;25:1665–1677. doi: 10.1093/nar/25.9.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bogarad L D, Deem M W. Proc Natl Acad Sci USA. 1999;96:2591–2595. doi: 10.1073/pnas.96.6.2591. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.