Abstract
The human response to uncertainty has been well studied in tasks requiring attention and declarative memory systems. However, uncertainty monitoring and control have not been studied in multi-dimensional, information-integration categorization tasks that rely on non-declarative procedural memory. Three experiments are described that investigated the human uncertainty response in such tasks. Experiment 1 showed that following standard categorization training, uncertainty responding was similar in information-integration tasks and rule-based tasks requiring declarative memory. In Experiment 2, however, uncertainty responding in untrained information-integration tasks impaired the ability of many participants to master those tasks. Finally, Experiment 3 showed that the deficit observed in Experiment 2 was not because of the uncertainty response option per se, but rather because the uncertainty response provided participants a mechanism via which to eliminate stimuli that were inconsistent with a simple declarative response strategy. These results are considered in the light of recent models of category learning and metacognition.
Keywords: Metacognition, Categorization, Procedural memory, Non-declarative memory, Uncertainty
Introduction
Humans have feelings of confidence and doubt, of (not) knowing, and of (not) remembering. They respond appropriately to these feelings by deferring to respond and rethinking their situation. These responses form the basis of the literature on uncertainty monitoring and metacognition (Benjamin, Bjork, & Schwartz, 1998; Dunlosky & Bjork, 2008; Flavell, 1979; Koriat, 1993; Koriat & Goldsmith, 1996; Metcalfe & Shimamura, 1994; Nelson, 1992; Scheck & Nelson, 2005; Schwartz, 1994; Serra & Dunlosky, 2005). Metacognition refers to the monitoring and control of primary cognitive processes (Nelson, 1996, Nelson & Narens, 1990, 1994) and indicates important aspects of mind, including hierarchical cognitive control (Nelson & Narens, 1990), self-awareness (Gallup, 1982), and consciousness (Koriat, 2007; Nelson, 1996). It is acknowledged to be a sophisticated cognitive capacity that is critical to humans’ cognitive self-regulation in many situations.
In tasks requiring attention and declarative memory systems, it has been well established that humans are able to monitor the status of ongoing cognitive processing within those systems accurately and adaptively. In contrast, uncertainty monitoring has not been well studied in tasks that rely on non-declarative procedural memory. In fact, it has occasionally been documented, though mostly informally, that performance in more implicit, procedural tasks is hidden from the normal sources of conscious monitoring and from the participant’s own evaluation of his or her performance. This was reported informally in early research on artificial-grammar learning (Brooks, 1978; Reber, 1967) and was also observed in early research on the so-called weather prediction task, an influential task within cognitive neuroscience (Knowlton, Mangels, & Squire, 1996). In both lines of research, it was clear that participants progressively improved in performance, while still self-reporting a lack of task knowledge and a failure of proficient performance. More recently, Bechara, Damasio, Tranel, and Damasio (1997) and Persaud, McLeod, and Cowey (2007) illustrated the same dissociation more metacognitively. Their participants made high- or low-confidence wagers about their performance in the Iowa gambling task. Even as their levels of correct responding strongly improved, participants persisted in making low-confidence wagers about their task answers because their own metacognitive assessments were still non-confident and non-optimistic. In all these cases, there was a failure of metacognition and uncertainty monitoring facing ongoing processing within procedural, implicit cognition.
In this article, we describe three experiments in which we have compared uncertainty monitoring and control in carefully matched categorization tasks that primarily differ only in whether they recruit explicit, declarative memory systems or implicit, procedural memory. Experiment 1 compares uncertainty monitoring in these two tasks. The results of this experiment make two primary contributions. First, they extend the literature on metacognition and uncertainty monitoring to category learning and categorization, an area in which almost no data exist. Second, they provide among the first careful comparisons of uncertainty monitoring in declarative- and procedural-memory tasks. Experiments 2 and 3 focus on metacognitive control during perceptual categorization. The results of these experiments show that an option to respond “uncertain” can change the qualitative nature of a task that depends on implicit, procedural memory, but not of a matched control task that depends on declarative memory.
Two category-learning tasks
The multiple-systems perspective that has been influential recently in the categorization literature often contrasts two different types of category-learning tasks. Rule-based (RB) category-learning tasks are those in which the category structures can be learned via some explicit reasoning process. The rule that maximizes accuracy (i.e., the optimal rule) is frequently easy to describe verbally (Ashby, Alfonso-Reese, Turken, & Waldron, 1998). In the most common applications, only one stimulus dimension is relevant, and the observer’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. The key requirement in RB tasks is that the optimal strategy can be discovered by logical reasoning that is easy for humans to describe verbally. Many previous perceptual uncertainty-monitoring experiments have used RB tasks with only a single relevant dimension.
In contrast, information-integration (II) category-learning tasks are those in which accuracy is maximized only if information from two or more stimulus components (or dimensions) is integrated at some pre-decisional stage (Ashby & Gott, 1988). Perceptual integration could take many forms – from treating the stimulus as a Gestalt to computing a weighted linear combination of the dimensional values. Typically, the optimal strategy in II tasks is difficult or impossible to describe verbally (Ashby et al., 1998). RB-based strategies can be (and frequently are) applied in II tasks, but they produce sub-optimal accuracy.
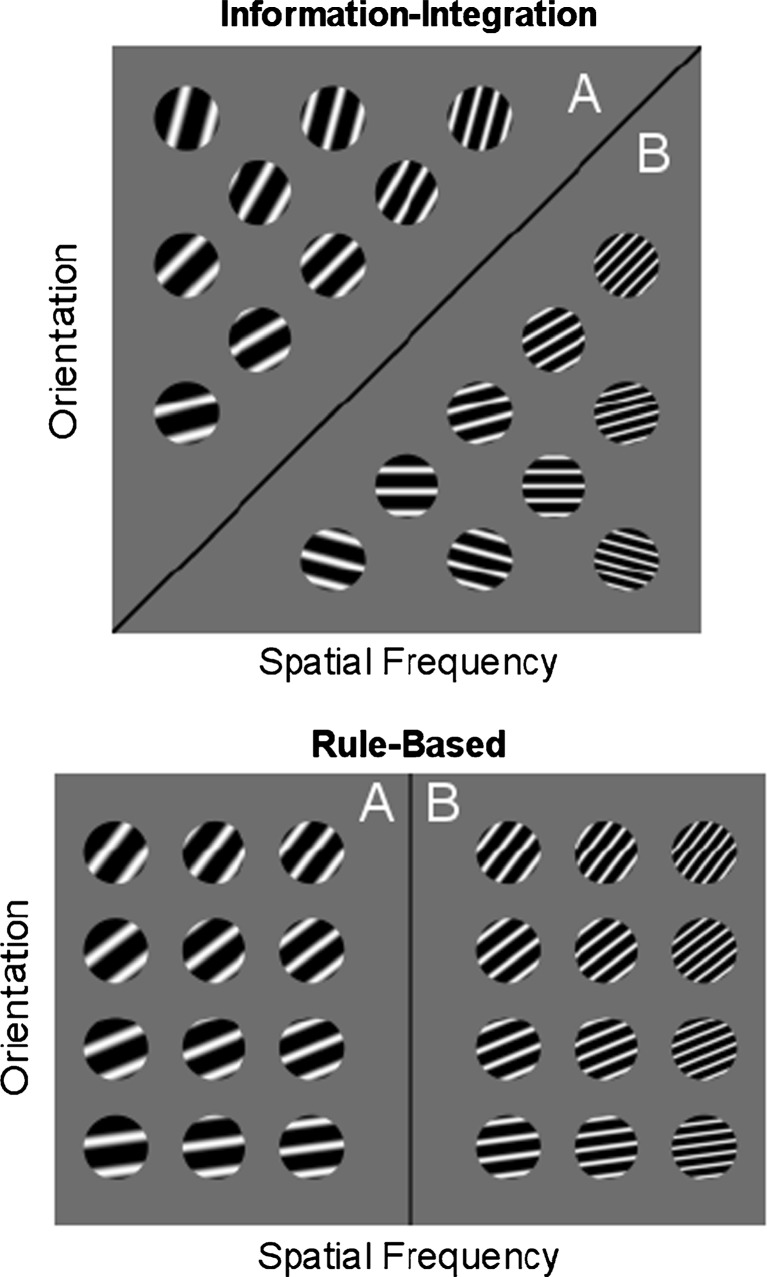
RB and II category structures similar to those used in the Experiment 1 reported here are illustrated in Fig. 1. As in this figure, each stimulus in our Experiment 1 was a circular sine-wave grating, and all stimuli were of identical size, shape and contrast. On each trial, one randomly selected disk was presented, and on categorization trials (i.e., when no uncertainty response was allowed) the participant’s task was to assign this disk to category A or B by pressing the appropriate response key. The disks varied across trials only in bar width (i.e., spatial frequency) and orientation. Participants received feedback about the accuracy of their response on each trial. The categories used in Experiment 1 were similar to those shown in Fig. 1, except that in Experiment 1 each category included many more disks and in some conditions perfect accuracy was impossible because of category overlap. The optimal decision bound in each condition is denoted by the solid line. Note that in the RB condition, the optimal strategy for separating the disks into the two categories is easily verbalized (“disks with thick bars are in category A; whereas disks with thin bars are in category B”). In contrast, the optimal strategy in the information-integration condition has no verbal description.1
Fig. 1.
Example stimuli and their relative distributions in information-integration and rule-based categories. Information-integration categories utilize both dimensions simultaneously to divide stimuli into “A” and “B” categories, whereas these rule-based categories require information about only one dimension (in this figure, spatial frequency)
There is now overwhelming evidence that learning in RB and II tasks is mediated by functionally separate systems (Ashby et al., 1998; Ashby & O'Brien, 2005; Ashby & Maddox, 2005). This evidence suggests that RB category learning depends most heavily on declarative memory systems (e.g., working memory), whereas II learning is mediated primarily by procedural memory (Ashby & O’Brien, 2005). First, a dual task requiring working memory and executive attention significantly impairs RB but not II learning (Filoteo, Lauritzen, & Maddox, 2010; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). Second, feedback processing requires attention and effort in RB but not II categorization (Maddox, Ashby, Ing, & Pickering, 2004a). Third, II but not RB learning is impaired by feedback delays as short as 2.5 seconds (Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005). Fourth, observational training impairs II but not RB learning, relative to feedback training (Ashby, Maddox, & Bohil, 2002). Fifth, unsupervised learning is possible with RB categories, but there is no evidence of any unsupervised learning with II categories (Ashby, Queller, & Berretty, 1999). Sixth, as in traditional procedural-memory tasks (Willingham, Wells, Farrell, & Stemwedel, 2000), II categorization is impaired if the response buttons are switched, but not if the hands are switched on the same buttons. In contrast, RB categorization is unaffected by either type of switch (Ashby, Ell, & Waldron, 2003a; Maddox, Bohil, & Ing, 2004b; Maddox, Glass, O’Brien, Filoteo, & Ashby, 2010; Spiering & Ashby, 2008b). In addition to these dissociations, many other qualitative differences have been reported that are consistent with the hypothesis that RB learning recruits declarative memory systems and II learning recruits procedural memory (e.g., Ashby, Noble, Filoteo, Waldron, & Ell, 2003b; Ashby & O’Brien, 2007; Ell & Ashby, 2006; Maddox, Filoteo, Hejl, & Ing, 2004; Maddox, Filoteo, Lauritzen, Connally, & Hejl, 2005; Nomura et al., 2007; Spiering & Ashby, 2008a).
It is important to note that these dissociations are not the result of task difficulty differences. First, in a number of cases, the experimental manipulation impaired an easy RB task more than a difficult II task (Ashby et al., 2003b; Filoteo et al., 2010; Maddox et al., 2004a; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). If the dissociations between RB and II categorization are due to differences in difficulty, then any manipulation that impairs performance (e.g., adding a dual task) should interfere more strongly with the difficult II task than with the simple RB task. Instead, the opposite result often occurs. Second, although the RB task shown in Fig. 1 is easier for healthy young adults to learn than the II task, there are several ways to equate the difficulty of the RB and II tasks (e.g., use a more difficult explicit rule). Many of the studies cited in the previous paragraph included conditions that equated difficulty using one of these methods, and in every such case, the reported dissociation was still observed.
In sharp contrast to all of the knowledge that has been gained about the roles of declarative and procedural memory systems in RB and II category learning, very little is known about how much access metacognitive and uncertainty-monitoring processes have to the functional workings and response outputs of these systems. Yet many real-world skills, such as medical diagnostic imaging, airport security screening, and military drone/satellite surveillance, depend critically on the success of metacognition in monitoring and sustaining the consistency, reliability, stability, and quality of responses emerging from these different systems of differentiation and categorization. For these reasons, we have evaluated the access of uncertainty-monitoring processes to both systems.
To do so, we incorporated a simple, uncertainty-monitoring paradigm that has been used extensively in recent comparative studies of human and animal metacognition (Beran, Smith, Coutinho, Couchman, & Boomer, 2009; Smith, 2009; Smith, Beran, & Couchman, 2010; Smith, Beran, Redford, & Washburn, 2006; Smith, Redford, Beran, & Washburn, 2010; Smith et al., 1995; Smith, Shields, Schull, & Washburn, 1997; Son & Kornell, 2005; Washburn, Gulledge, Beran, & Smith, 2010). More specifically, many of the uncertainty-monitoring studies performed to date have used simple A–B discrimination tasks in which the participant makes one of two primary responses based on the class membership of the to-be-categorized stimulus. In addition, participants are given an uncertainty response with which they can decline to complete any trials of their choosing. In fact, humans and some nonhuman species (dolphins, macaques), but not other nonhuman species (capuchin monkeys, pigeons), use this uncertainty response proactively and adaptively to decline the most difficult trials that are nearest the discrimination breakpoint or decision boundary between the two discriminative classes. Humans also universally attribute their use of the uncertainty response to their conscious uncertainty about the status of the trial. This uncertainty-response methodology was ideally suited to the A–B categorization tasks used in all of these experiments. The value added in our experiments was that we included this uncertainty response in two carefully matched and controlled discrimination tasks that are known to tap different category-learning utilities and even different structural systems in the brain.
Although most research on metacognition has focused on more standard memory tasks (e.g., Dunlosky & Bjork 2008), it seems intuitive that humans should be able to monitor uncertainty effectively in RB categorization tasks, since these tasks rely on explicit cognitive processes. By definition, the declarative memory systems central to RB categorization are accessible to conscious awareness (e.g., Eichenbaum, 1997). Thus, we expected that uncertainty responses would be used optimally and adaptively in the RB tasks. In contrast, II tasks require procedural memory that is nondeclarative (Rolls, 2000; Squire & Schacter, 2002). Thus, participants in II tasks do not have conscious access to the memory traces they are encoding and consolidating throughout the learning process and, therefore, they might also lack conscious access to their ongoing states of uncertainty and confidence as they perform the trials in the II task. In fact, it is documented that participants performing related implicit/procedural tasks do express a pervasive disbelief that they can perform correctly – and even a lack of confidence regarding the correct responses they make in such tasks (Brooks, 1978; Reber, 1967). Thus, we considered it a clear possibility that uncertainty responses would be used inappropriately to manage difficulty and uncertainty within the II task context. This would be an important finding because it would mean that one of humans’ basic categorization systems is hidden from the evaluative/monitoring light of metacognitive oversight.
Experiment 1
Experiment 1 used a 2 × 2 design in which two types of category structure (i.e., RB vs. II) were crossed with two levels of category overlap (i.e., 0% or 5% overlap). In the 5% overlap condition, optimal accuracy was 95% correct because the two category-exemplar distributions slightly intermingled and overlapped one another. In other words, a participant who perfectly used the optimal decision strategy in these conditions would sometimes receive negative feedback because some A-correct stimuli were on the B side of the optimal decision bound. In contrast, perfect accuracy was possible in the 0% overlap condition. For each type of category structure (RB vs. II), the 0% and 5% overlap conditions used exactly the same stimuli. The only difference was that in the 5% condition, feedback was based on category membership, whereas in the 0% condition, feedback was based on the response of the ideal observer. For example, in the 0% II condition, all stimuli above the optimal II bound were assigned to Category A, and all stimuli below the optimal bound were assigned to Category B. Similarly, in the 0% RB condition, all stimuli to the left of the optimal RB bound were assigned to Category A, and all stimuli to the right were assigned to Category B. Thus, perfect accuracy was theoretically possible in both 0% overlap conditions.
All conditions began with 300 training trials in which participants responded by assigning each stimulus to Category A or B and then received feedback about the accuracy of this response. Uncertainty responses were not allowed during the training period. The training blocks were followed by 300 transfer trials in which participants were now allowed to respond “A”, “B”, or “uncertain”. To encourage uncertainty responses, participants were told that their goal during the transfer phase was to maximize the number of points they received. They were told they would receive +1 point for every correct response, –5 points for every error, and 0 points if they responded “uncertain”. The asymmetric payoffs were chosen because many humans are generally reluctant to give an uncertainty response. In fact, many participants are actually often overconfident and interpret an expression of doubt as a sign of weakness in a task. For these reasons, without a substantial penalty for errors, it can be difficult to elicit uncertainty responses from participants.
Method
Participants
There were 31 and 23 participants in the 5% overlap II and RB conditions, respectively, and 49 and 38 participants in the 0% overlap II and RB conditions, respectively. All 5% overlap participants were from the University of California Santa Barbara community, and all 0% overlap participants were from the State University of New York at Buffalo community. All participants reported normal or corrected-to-normal vision and received partial course credit in exchange for participation. Each participant completed an approximately 60-minute session.
Stimuli and apparatus
The stimuli were circular sine-wave gratings that continuously varied on two dimensions (spatial frequency and orientation; see Fig. 1). Each stimulus subtended approximately 5 degrees of visual angle at a distance of 76 cm from the monitor. The coordinates of each stimulus, (x 1 , x 2), were transformed into physical spatial frequency (f) and orientation (o) values according to f = (1/30)x 1 + (1/4) and o = (π/200)x 2 + (π/9). These transformations were chosen to approximately equate salience between the two dimensions. The stimuli were presented on a gray background using Matlab and functions from Brainard’s (1997) Psychophysics Toolbox. Responses were made with keys labeled on a keyboard.
A total of 600 stimuli were generated for the training and transfer conditions of the experiment. For the II condition, different stimuli were used in the two phases. During the first 150 training trials, the stimuli (75 from each category) were sampled from rows that were near and parallel to the category bound (as in the first block of the hard-to-easy condition of Spiering & Ashby, 2008a). These stimuli had the same optimal boundary as in Fig. 1, but Spiering and Ashby (2008a) found that beginning with difficult-to-categorize stimuli improved II learning. The stimuli in the last 150 training trials in the 5% overlap condition were sampled randomly from two bivariate normal distributions (75 from each category; parameters are included in Table 1). For the 300 transfer trials in the II condition, an additional 300 stimuli (150 from each category) were sampled randomly from the two category distributions.
Table 1.
Category mean, variance, and covariance parameters
| Category Structure | μ A | μ B | σ 2 o | σ 2 f | cov o,f |
|---|---|---|---|---|---|
| II | 40, 60 | 60, 40 | 175 | 175 | 103 |
| RB | 35.9, 50 | 65.1, 50 | 72 | 278 | 0 |
Mean, variance, and covariance parameters of the bivariate normal distributions used to generate stimuli for the II and RB categories; o denotes orientation and f denotes spatial frequency. Means are (o, f) coordinate pairs; variances and covariances are equal for the A and B categories in both category structures. All values reported are prior to orientation and spatial frequency transformations.
The stimuli for the 5% overlap RB condition were composed in much the same way, except that the stimuli were rotated 45 degrees counter-clockwise in spatial frequency–orientation space so that the relevant dimension was spatial frequency. It was unnecessary to facilitate training with extra difficult trials because participants find RB tasks intrinsically easier to master. Therefore, an additional sample of 75 stimuli from each category distribution was used for the RB condition instead of the initial 150 training-row trials, yielding a total of 300 training and 300 transfer trials.
As mentioned above, the stimuli for the 0% overlap condition were identical to those in the 5% overlap condition except that they were strictly divided at the optimal category boundary. This reassignment of category membership created A and B categories that were slightly unequal in size because of the random sampling procedure that was used to select stimuli in the 5% overlap condition. To correct this, an iterative procedure was used in which the heavy category (i.e., the category with n too many stimuli) had n stimuli randomly excised, and the light category (the category with n too few stimuli) was augmented with a new sample of n stimuli from the corresponding source bivariate normal distribution until both categories had exactly 300 stimuli. The RB categories were simple 45-degree counter-clockwise rotations of these new non-overlapped II stimuli. As in the 5% overlap RB condition, the 0% overlap RB condition did not include training-row stimuli and simply re-sampled the training stimuli from phase two.
Procedure
All participants completed the experimental session in a dimly lit room seated in front of a monitor and keyboard. Instructions and informed consent were administered prior to the beginning of the experiment. Participants were told that the first half of the experiment would only allow category assignment responses (i.e., A or B on the keyboard) and were asked to maximize accuracy. The feedback during this portion of the experiment was a sine-wave (i.e., pure) tone for correct responses and a sawtooth (harsh) tone for incorrect responses. A beep tone was also included for “too slow” responses and “incorrect key” presses along with the corresponding descriptive text to signal the source of the error to the participant. For the second half of the experiment, participants were told that an uncertainty response option (i.e., the ? key on the keyboard) would be allowed and that the nature of the feedback would change. The feedback was now presented visually in the form of points (green, +1 for correct responses; red, –5 for incorrect responses, late responses, or wrong-key responses; black, +0 for uncertainty responses). In all cases, the participant’s current total score was also shown on each trial. For this portion of the experiment, participants were asked to maximize their scores and try their best to beat a target score of 100 points. For all trials, participants were asked to make a response within 2 seconds of the stimulus onset.
To familiarize participants with the training and experimental portions of the experiment, a 20-trial practice session preceded the training and experimental trials, which was broken up into two blocks of ten trials each. The practice stimuli were randomly sampled from the A and B training row stimuli. The first ten trials mimicked the first half (training) portion of the experiment where only category-assignment responses were allowed and feedback was administered aurally through headphones. The second ten trials mimicked the experimental portion, which included an uncertainty response option and feedback administered visually in the form of points and a total score.
After the practice trials, participants completed 600 trials divided into eight blocks with 75 trials each. The first four blocks were training, and the last four were transfer. On every trial, a fixation cross appeared for 1,500 ms followed by a response-terminated stimulus with feedback proceeding immediately after the response (1,000 ms duration of audio feedback, 2,000 ms for visual), at which point the fixation–stimulus–response–feedback sequence would repeat. As a reminder, the participants were given on-screen instructions about the uncertainty response and the score feedback prior to Block 5.
Results
In the 5% overlap condition, two participants failed to achieve a 65% correct rate during the last 150 trials, and one participant responded “Uncertain” on more than 70% of trials. In the 0% overlap condition, 11 participants failed to reach the accuracy criterion of 65% correct, two participants indiscriminately responded “uncertain,” and one participant never responded “B”. These participants were excluded from further analysis.
Model-based analyses
Before the category and uncertainty responses can be analyzed, it is important to determine whether participants learned to use an optimal strategy. This is especially important in the II conditions. More specifically, before deciding how participants monitor uncertainty in II tasks, it is important to verify that they were using a nondeclarative decision strategy. To answer this question, we fit a variety of different decision-bound models (Ashby, 1992; Maddox & Ashby, 1993) to the final 150 responses of each participant. This allowed us to assess each participant’s steady-state response strategy. These models assumed (1) an II strategy, (2) an RB strategy, or (3) a random-guessing strategy. Some details of these models are given in the Appendix.
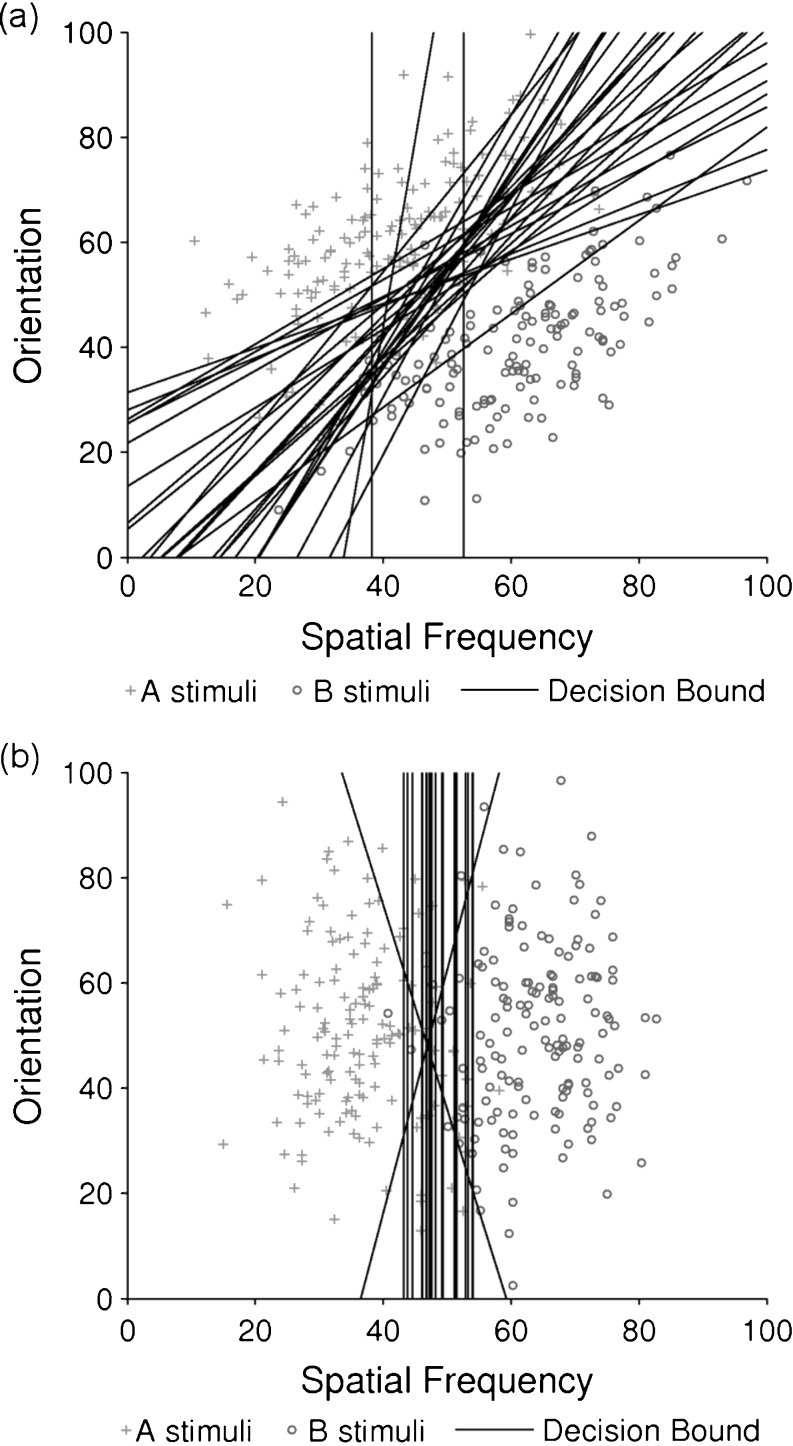
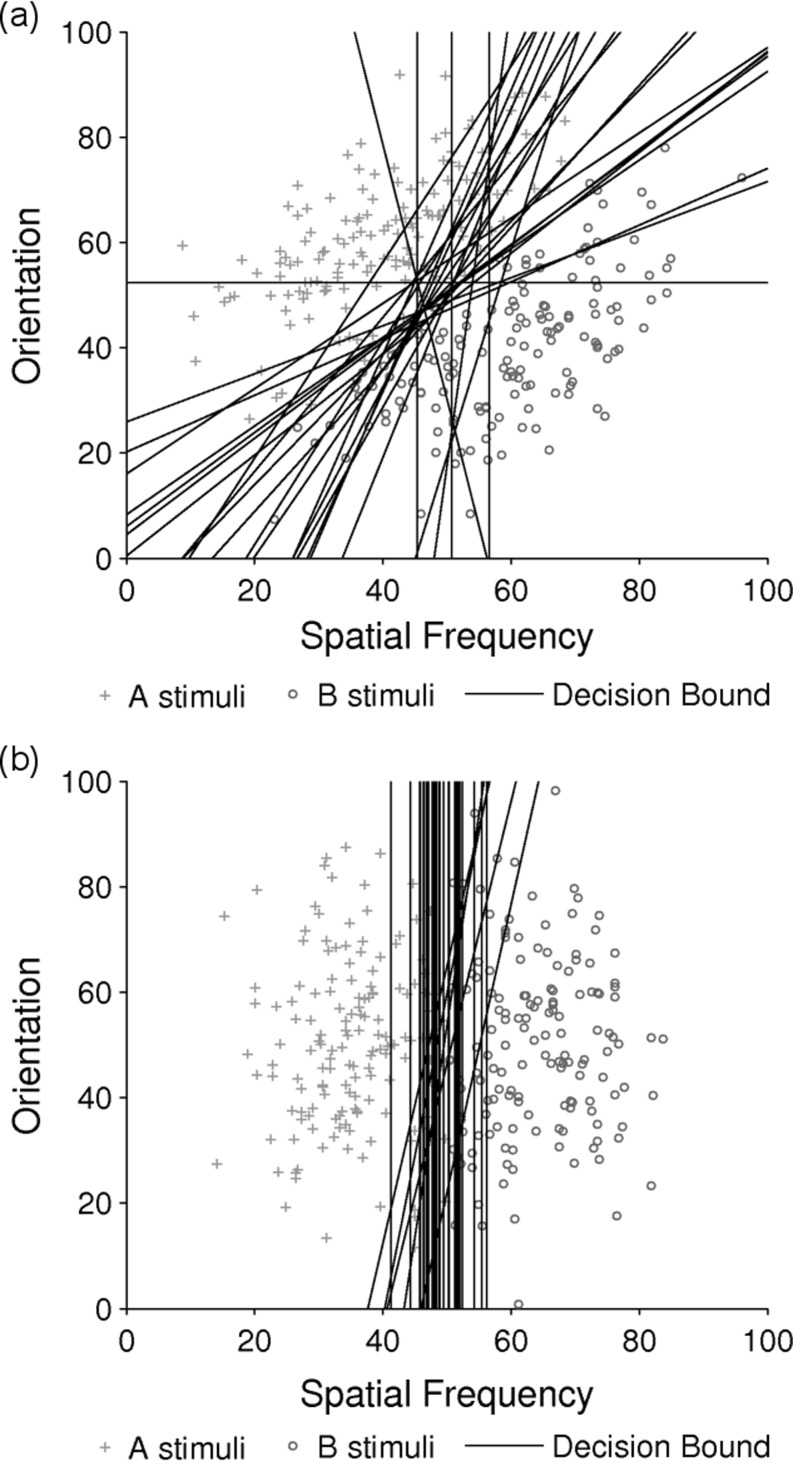
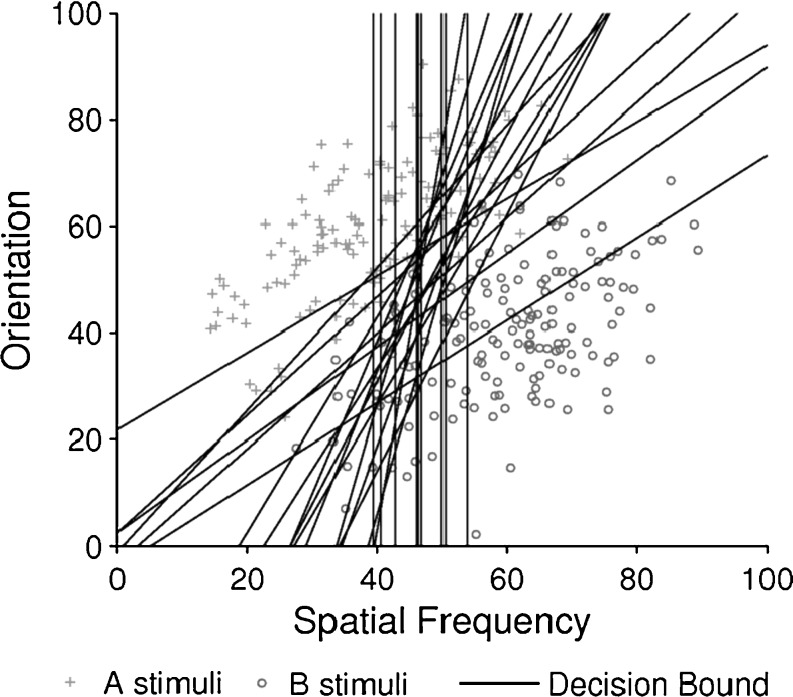
In the II conditions, the responses of 27 of the 29 participants in the 5% overlap condition were best fit by a model that assumed an II strategy; the remaining two participants were best fit by an RB model. Similarly, the responses of 22 of the 26 participants in the 0% overlap II condition were best fit by an II model, with the remaining four participants being best fit by an RB model. In the RB conditions, the responses of 21 of the 23 participants in the 5% overlap condition and 33 of 38 participants in the 0% overlap condition were best fit by an RB model (of the optimal type); the responses of all other participants were best fit by an II model. Figures 2 and 3 show the best-fitting bound for every participant in the 5% and 0% overlap condition, respectively, plotted with a sample of 300 stimuli. Note that the few best-fitting II bounds in both RB conditions were nearly vertical and closely matched the optimal RB boundary. These participants were included in all analyses using their individual best-fitting bounds when applicable.
Fig. 2.
Best-fitting bounds for participants’ final 150 trials plotted with 300 stimuli for illustrative purposes in (a) the II and (b) RB conditions of the 5% overlapped categories in Experiment 1
Fig. 3.
Best-fitting bounds for participants’ final 150 trials plotted with 300 stimuli for illustrative purposes in (a) the II and (b) RB conditions of the 0% overlapped categories in Experiment 1
Accuracy- and uncertainty-based analyses
For each participant, we analyzed the accuracy and the frequency of uncertainty responses during the final 150 trials. This provided a sufficient number of trials to analyze for each response-type and to assess performance at a point when learning had stabilized and participants had adopted their mature task strategies within the scope of the experiment. The difference in the number of uncertainty responses between participants in the II and RB conditions was not significant in either the 5% [II: M = 23.3, standard deviation (SD) = 17.9; RB: M = 14.4, SD = 16.1; t(50) = 1.86, p = 0.069] or the 0% overlap condition [II: M = 13.2, SD = 18.3; RB: M = 9.0, SD = 9.45; t(62) = 1.20, p = 0.23].
It is possible that the lack of difference in the number of uncertainty responses in the II and RB conditions is related to how well participants were trained in those tasks. In the 5% overlap condition, accuracy during the last 150 trials of training was lower for the II condition (M = 73.2%, SD = 8.95%) than the RB condition (M = 87.1%, SD = 4.98%); similarly, in the 0% overlap condition, accuracy was also lower in the II condition (M = 72.3%, SD = 8.06%) than in the RB condition (M = 89.9%, SD = 7.74%). To investigate the possibility that uncertainty responses are related to participants’ task competency (as measured by training accuracy), we computed correlations between average accuracy in the last 150 trials of training (i.e., before uncertainty responses were allowed) and the proportion of uncertainty responses during the last 150 trials of the experiment. This correlation was not significantly different from zero for any group [5% overlap condition – II group: r(27) = 0.012, p = 0.95, RB group: r(21) = –0.22, p = 0.31; 0% overlap condition – II group: r(24) = 0.002, p = 0.99, RB group: r(36) = 0.15, p = 0.31]. Thus, the RB versus II difficulty difference did not affect the participants’ use of the uncertainty response.
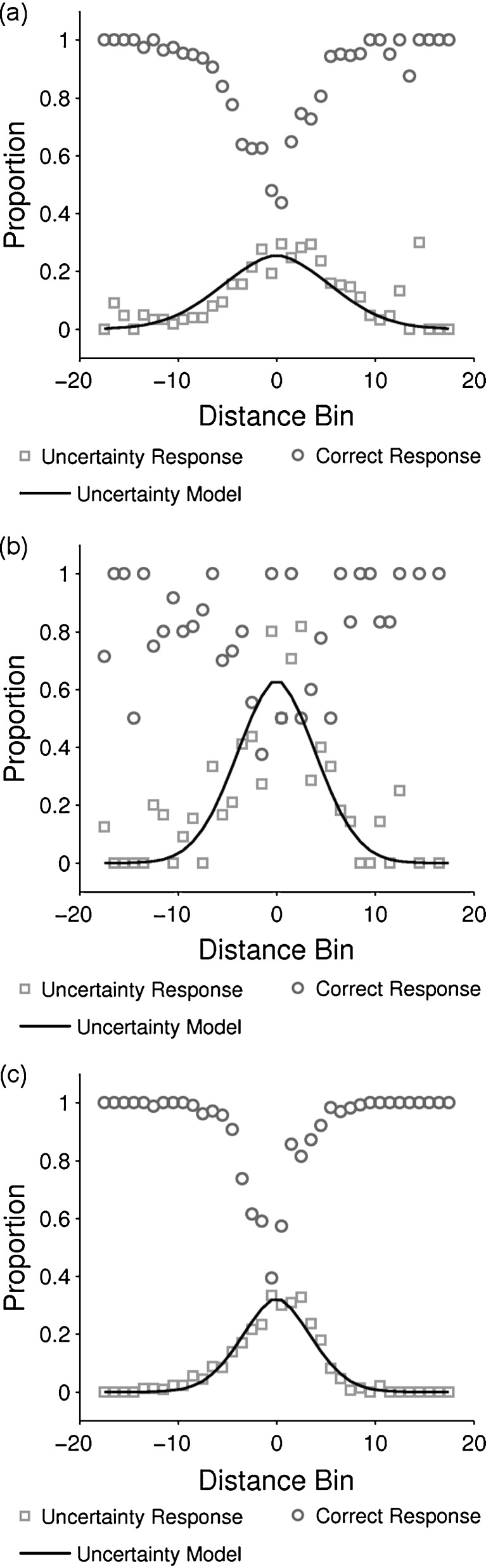
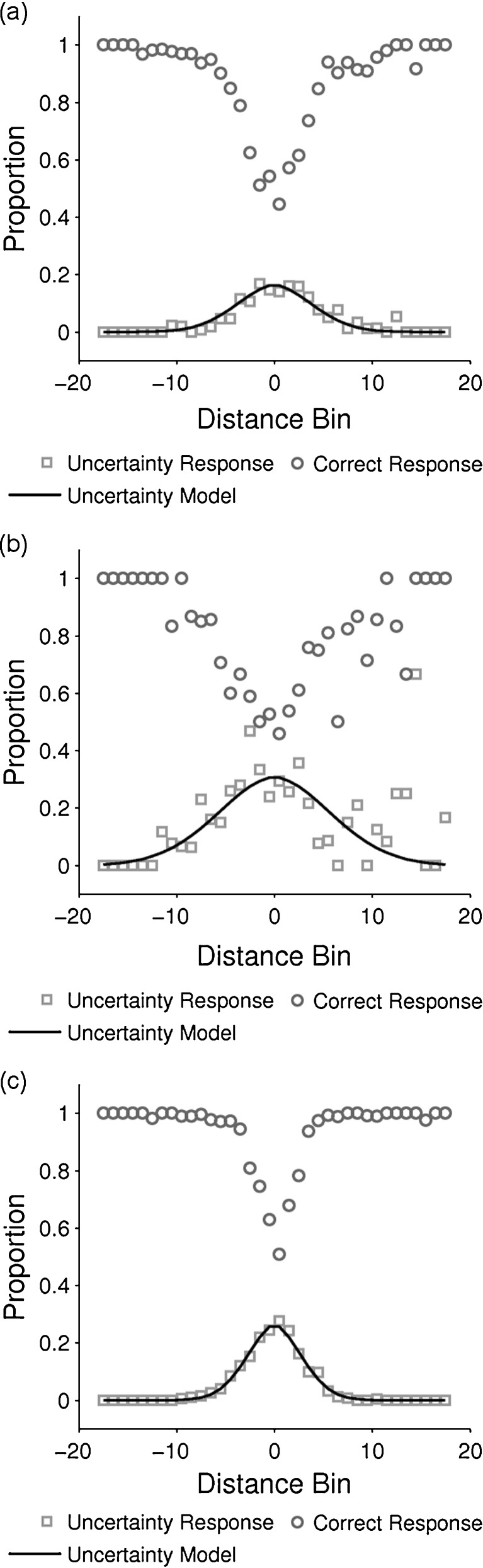
The model-based analyses provided a best-fitting bound for each participant, which was used to divide that participant’s response space into A and B response regions. This partition was used to investigate how accuracy and uncertainty responding changed as the distance between the stimulus and the decision bound increased. For each response (i.e., all A, B, and “uncertain” responses), we calculated the Euclidian distance from the stimulus coordinates to the best-fitting bound. Next, these distances were binned equally into 36 intervals so that there were 18 intervals on each side of the bound. Within each interval, the proportion of correct categorization responses (excluding trials that produced uncertainty responses) was computed, along with the proportion of all trials that produced uncertainty responses. Figures 4 and 5 (open squares and circles) show the accuracy and uncertainty results for the 5% and 0% overlap conditions, respectively. The solid line curves are described below. Note that the abscissa in both figures is binned distance, not metric Euclidean distance. In all cases, accuracy decreased and uncertainty responding increased as stimuli moved closer to the decision bound. This same result has previously been reported in one-dimensional uncertainty experiments.
Fig. 4.
Average accuracy and uncertainty responses in the 5% overlap conditions of Experiment 1 for: (a) 27 II-responders in the II condition; (b) 2 rule-responders in the II condition; (c) 23 responders in the rule-based condition. The abscissa is binned distance from category bound and the ordinate is accuracy/response frequency
Fig. 5.
Average accuracy and uncertainty responses in the 0% overlap condition of Experiment 1 for: (a) 22 II-responders in the II condition; (b) 4 rule-responders in the II condition; (c) 38 rule-responders in the rule-based condition. The abscissa is binned distance from category bound and the ordinate is accuracy/response proportion
Figures 4 and 5 suggest that uncertainty responding was strongly driven by distance-to-bound in both the RB and II conditions. To confirm this, we constructed a model which assumed that for any one stimulus, the only factors determining whether the participant responded “uncertain” were distance-to-bound and noise (i.e., perceptual and criterial).
Let X denote the signed distance between the presented stimulus and the decision bound (in stimulus units) – that is, X is a positive distance for all stimuli on the A side of the bound and a negative distance for all stimuli on the B side. The model assumes that each participant uses a decision strategy of the following type:
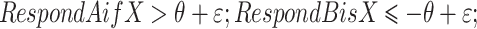 |
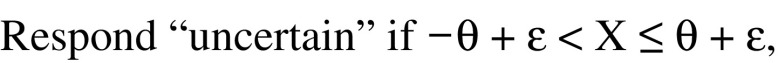 where ε is a normally distributed random variable with mean 0 and variance σ2 that models the effects of perceptual and criterial noise, and 2θ is the mean width of the uncertainty region. Given this decision rule, the probability of responding “uncertain” is
where ε is a normally distributed random variable with mean 0 and variance σ2 that models the effects of perceptual and criterial noise, and 2θ is the mean width of the uncertainty region. Given this decision rule, the probability of responding “uncertain” is
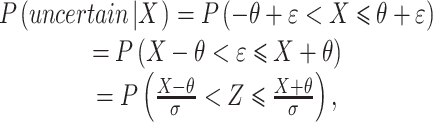 |
1 |
where Z has a standard normal distribution.
This model was fit to the mean uncertainty response proportions for each group of participants who used the same type of decision strategy in each condition. The parameters θ and σ were estimated using the method of weighted least squares (i.e., where each error is weighted by sample size). The best fits of this model are denoted by the solid line curves in Figs. 4 and 5. Numerical estimates of θ and σ, as well as the weighted sum of squared errors (SSEs), are listed in Table 2 for each condition of Experiment 1 and for each response strategy used within that condition. Note that, in general, the model provides accurate fits, and there is no real difference in the quality of these fits between the RB and II conditions. The only poor fits are to the responses from participants who used an RB strategy in an II condition (i.e., middle panels of Figs. 4 and 5). In these cases, the model makes no systematic errors, but the data are highly variable, so some of the mispredictions are large. These poor fits should be interpreted cautiously, however, since they are based on extremely small sample sizes (i.e., 2 and 4 participants in the 5% and 0% overlap conditions, respectively). Overall, however, the good fits of this simple model suggest that participants in all conditions used similar strategies when deciding whether to respond “uncertain”, and that the only variable they evaluated was the distance to the decision bound. The model was also fit to individual participant response data. These data were highly variable because of the relatively small sample sizes but, in general, the model fit well in the sense that no systematic errors in the individual fits were observed across participants for any experiment.
Table 2.
Summary of uncertainty model fits from Experiments 1 and 2
| Condition | Response Strategy | Experiment 1 (5% overlap) | Experiment 1 (0% overlap) | Experiment 2 (all trials) | |
|---|---|---|---|---|---|
| II | II | SSE | 0.770 | 0.093 | 0.299 |
| r 2 | 0.616 | 0.906 | 0.818 | ||
| θ | 5.759 | 3.376 | 3.851 | ||
| σ | 13.9 | 10.115 | 10.991 | ||
| II | RB | SSE | 6.014* | 2.574 | 1.998† |
| r 2 | 0.723 | 0.227 | 0.890 | ||
| θ | 9.467 | 6.509 | 14.346 | ||
| σ | 9.042 | 13.47 | 12.359 | ||
| RB | II, RB | SSE | 0.175 | 0.019 | |
| r 2 | 0.953 | 0.989 | |||
| θ | 4.112 | 3.198 | |||
| σ | 7.361 | 6.248 |
The first row describes results for participants in the II conditions who used an II response strategy. The second row shows results for participants in the II conditions who used an RB strategy. Row three includes fits for all participants in the RB conditions of Experiment 1.
* Excluded 3 bins in right tail with no data (bins 36, 34, 32)
† Excluded 1 bin in right tail with no data (bin 35)
Previous uncertainty studies reported large individual differences in the use of the uncertainty response. For example, Smith et al. (2006) found both reluctant and generous uncertainty responders who used the uncertainty response option rarely and frequently, respectively. This phenomenon was also observed in our data despite the high cost of errors and despite quite similar accuracy levels across participants. For example, several participants never responded “uncertain”, and one responded “uncertain” on 70% of all trials.
Discussion
Our results from Experiment 1 make two unique contributions to the literature on uncertainty monitoring. First, the RB results show that variation along an irrelevant dimension did not disrupt the ability of participants to monitor uncertainty. Second – and more importantly – the II results show that participants can effectively monitor uncertainty even in a task that depends primarily on a nondeclarative memory system. While one might assume uncertainty monitoring is inversely related to task fluency, our participants’ use of the uncertainty response was notably unrelated to their raw training accuracy after 300 training trials in any condition, indicating that differences in II and RB training accuracy alone do not predict uncertainty, at least for accuracies above 70%. Our results also suggest that uncertainty monitoring is not strongly affected by whether the categories overlap. With overlapping categories, even optimal responding causes errors. Even so, participants appeared to use the same strategy of responding “uncertain” to stimuli that were near the category boundary, regardless of whether the categories overlapped, and in all cases the frequency of an uncertainty response decreased at roughly the same rate as the stimulus moved away from that boundary. This was true for both RB and II category structures.
Experiment 2
In Experiment 1, participants received extensive training with the II categories before they were allowed to ever respond “uncertain”. The reasoning underlying this training is closely linked to our primary aim of determining whether humans can monitor uncertainty in tasks that depend on nondeclarative memory. Thus, we provided participants with preliminary training in order to maximize the probability that they would adopt a nondeclarative (i.e., II) strategy. However, a second key goal in human metacognition research is to understand how metacognitive judgments – in this case about uncertainty – are used to control future decisions (Nelson & Narens, 1990). Koriat, Ma’ayan, and Nussinson (2006) reported results suggesting that metacognitive monitoring and control are interacting processes that mutually inform each other. Experiment 1 was a poor design for studying this interactive process because participants were not allowed to act on their uncertainty until learning was mostly complete. In Experiment 2, participants were given the option of responding “uncertain” from the first trial.
To the best of our knowledge, metacognitive control has not been studied in any procedural-learning tasks.2 Even so, there are results from the categorization literature which suggest that allowing participants to act on their feelings of uncertainty from the first trial might reduce the likelihood that they ever adopt a nondeclarative strategy. In particular, Spiering and Ashby (2008a) showed that II category learning is impaired if participants are initially trained only on exemplars that are easy to categorize (i.e., far from the category bound). Not only was accuracy lower for this group than for a group that began with the most difficult items, but participants who began with easy items were also less likely to adopt II strategies. An “uncertain” response allows a participant to avoid responding to a stimulus. The results of Experiment 1 show that participants are more likely to choose this option for stimuli near the category bound. Thus, providing the opportunity to respond “uncertain” from trial 1 potentially allows participants to avoid ever responding to difficult stimuli. The Spiering and Ashby (2008a) results suggest that participants who choose this option might be less likely to adopt II strategies. Experiment 2 tests this hypothesis.
Experiment 2 was identical to the 5% overlap II condition in Experiment 1 except that the initial training trials were removed. Instead, participants were given the option of responding “uncertain” on all 600 trials of the experiment. Since all participants adopted an RB strategy or a strategy closely resembling an RB strategy (i.e., Figs. 2b and 4b) in the RB conditions of Experiment 1, we did not have any reason to assume that an "uncertain" option on all trials would affect participants' ability to adopt an optimal strategy. In addition, many participants begin with RB response strategies in II conditions. For these reasons, we did not run an RB condition in Experiment 2.
Method
Participants
There were 31 participants in the experiment, and all were from the University of California at Santa Barbara community. All participants reported normal or corrected-to-normal vision. Each participant completed one session of approximately 60 minutes in duration and was given partial course credit for volunteering.
Stimuli and apparatus
A new sample of 600 stimuli (300 in the A category and 300 in the B category) was randomly selected from the overlapped II distributions used in Experiment 1. All other aspects of stimulus generation and presentation were identical to those in Experiment 1. Note that this experiment did not use the training rows procedure that was used in Experiment 1.
Procedure
The procedures were identical to those of Phase 2 of Experiment 1 (i.e., when participants were given the option of responding “uncertain”).
Results
Each participant’s data were screened for accuracy and uncertainty response frequency as before, but the exclusion criterion for uncertainty response frequency was increased to 80% (slightly more liberal than in Experiment 1). One participant exceeded the uncertainty response frequency criterion, and four participants failed to reach the criterion on accuracy of 65% correct. These participants were therefore excluded from further analyses.
Model-based analyses
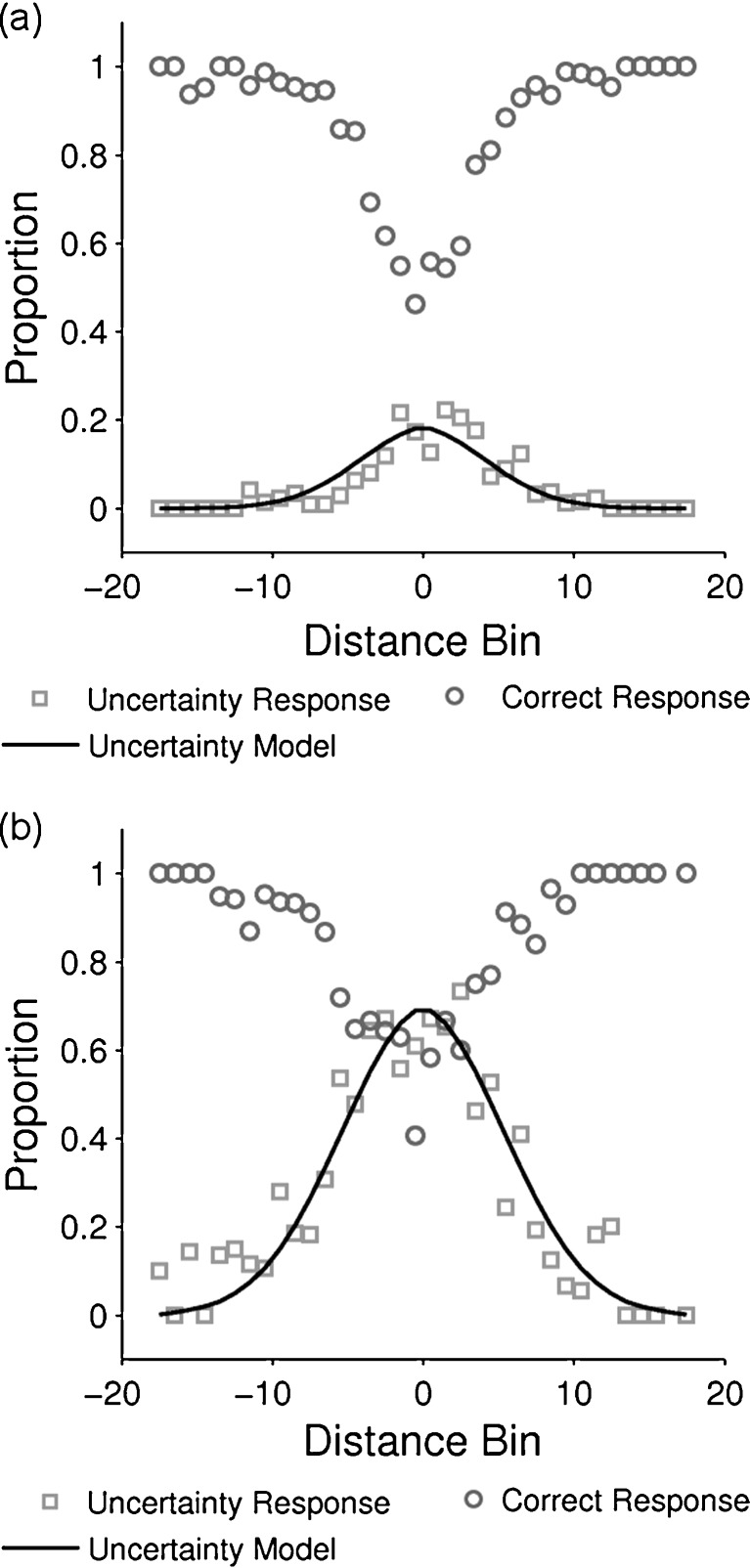
The same three types of decision-bound models used in Experiment 1 were fit to the responses of each successive 150-trial block, separately for every participant. In the crucial last block, the responses of 17 of the 26 participants were best fit by a model that assumed an II response strategy, and the responses of the remaining nine participants were best fit by a model that assumed an RB strategy. Figure 6 shows these best-fitting bounds plotted with a sample of 300 stimuli.
Fig. 6.
Best-fitting bounds for the final 150 trials in both the information integration responding and the rule-based responding participants plotted with 300 stimuli from Experiment 2
Accuracy and uncertainty-based analyses
Accuracy and uncertainty statistics were computed for the last 150 trials of the experiment. Participants who used an II strategy and those who used an RB strategy both appeared to produce uncertainty curves similar in shape to those of the participants in Experiment 1, but there was clearly a strong relation between categorization strategy (RB vs. II) and the frequency of uncertainty responding (Fig. 7). Fits of the Equation 1 uncertainty model revealed that the participants in Experiment 2 who used a sub-optimal RB strategy had the most liberal criterion for responding uncertain (i.e., the largest θ parameter estimates) of any group of participants in either experiment (see Table 2). It should also be noted that this same trend was seen in Experiment 1 – that is, the group of Experiment 1 participants with the most liberal criterion for responding uncertain were the RB responders in the II condition.
Fig. 7.
Average accuracy and uncertainty responses in Experiment 2 for: (a) 17 II-responders in the last 150 trials; (b) 9 rule-responders in the last 150 trials. The abscissa is binned distance from category bound and the ordinate is accuracy/response proportion
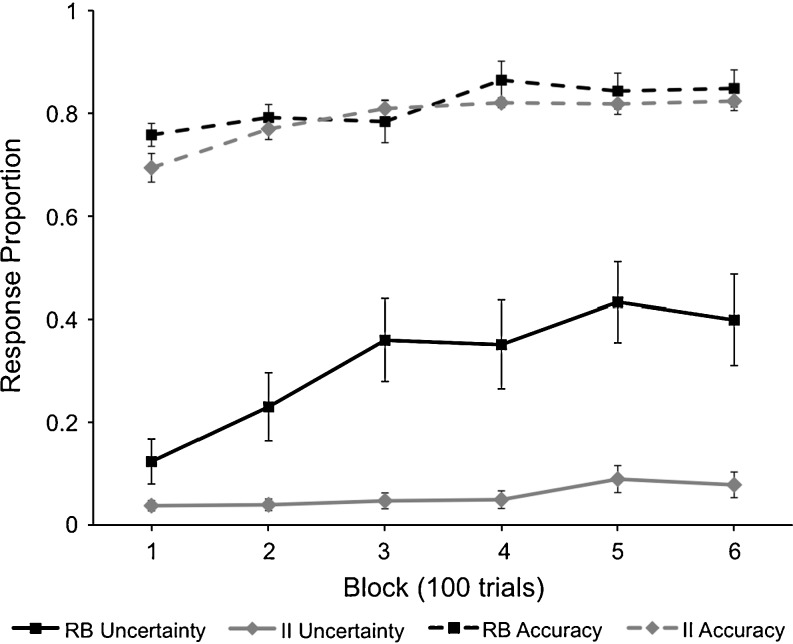
During the last 150 trials of the experiment, participants best fit by an RB model responded “uncertain” more frequently (M = 63.2, SD = 35.2) than those best fit by an II model (M = 12.8, SD = 15.2), and this difference was highly significant [t(24) = 5.13, p < .001]. Since this experiment allowed uncertainty responses beginning with the first trial, we also investigated how uncertainty responding evolved over time and training for the two response strategy groups. Figure 8 shows the mean categorization-response accuracy and the mean proportion of uncertainty responding during each 100-trial block of the experiment separately for the RB and II responders. The figure clearly demonstrates the relatively constant use of uncertainty responses throughout the experiment for the II responders and a clear increase in uncertainty responding for the RB responders. In addition, the RB responders used the uncertainty response more frequently than the II responders on every block. Figure 8 also shows that the accuracy of the RB responders was generally higher than that of the II responders, although only by a couple of percentage points. These conclusions were tested more rigorously with a mixed-effects analysis of variance (ANOVA) in which strategy (II or RB) was crossed with block (1–6). The results revealed main effects of strategy [F(1,24) = 29.75, p < .001] and block [F(5,120) = 7.756, p < .001] as well as a significant interaction [F(5,120) = 6.39, p < .001]. Separate one-way ANOVAs also revealed that uncertainty response use differed across blocks for RB responders [F(5,40) = 6.20, p < .001], but not for II responders [F(5,80) = 2.02, p = .085].
Fig. 8.
Mean uncertainty response proportion and accuracy of the information-integration (II) and rule-based (RB) responders across six 100-trial blocks of Experiment 2
In order to further assess the relationship between accuracy and uncertainty responding, we calculated correlations between accuracy and uncertainty responses during the final 150 trials of the experiment. For both groups of participants, this correlation was significantly positive [RB: r(7) = 0.89, p = .002; II r(15) = .58, p = .016].
Because of the increased use of the uncertainty response, RB responders received corrective feedback on fewer trials than II responders. In fact, the RB responders received feedback on an average of only 408 trials of the experiment, whereas II responders received feedback on an average of 565 trials. This raises the possibility that II responders adopted an II strategy only because they received more overall feedback than RB users. To test this hypothesis, we fit the decision-bound models to the first 408 feedback trials for the 17 participants identified as II responders above. Thus, in this analysis, all participants received the same average number of feedback trials. The models were fit to blocks of 136 trials. During the last block, 15 of the 17 II-responders were still best fit by a model that assumed an II response strategy. The RB model fit best for only two of these participants. Thus, participants who adopted an II decision strategy did not do so because of an overall greater number of feedback trials.
Discussion
Allowing participants to respond “uncertain” from the first trial had important effects both on the use of the uncertainty response and on the nature of category learning. Most importantly, the success that participants had in learning to use a strategy of the optimal type depended on the frequency with which they responded “uncertain”. Participants who frequently responded “uncertain” mostly used simple one-dimensional RB rules that ignored one of the two relevant dimensions. In contrast, participants who rarely used the uncertainty response mostly adopted a strategy of the optimal type. The most plausible explanation of this coordination between uncertainty responding and categorization strategy is that participants who frequently used the uncertainty response avoided difficult-to-categorize stimuli near the category bound, which allowed them to maintain an acceptably high level of accuracy with a suboptimal RB decision strategy. For example, if a one-dimensional RB strategy were to be used on every trial with the Experiment 2 categories, then the highest accuracy that would be theoretically possible is 75.6% correct. Figure 8 shows that during blocks 4–6, the mean accuracy of RB responders was above 80%. Thus, RB responders were clearly using the uncertainty response to avoid many of the most difficult stimuli as a way to improve accuracy with an inferior response strategy.
Figure 8 also shows that the RB responders used the uncertainty response with increasing frequency throughout the experimental session. This is interesting because the best-fitting RB model provided ever-improving fits to the responses of these participants. In other words, as the experiment progressed, the response strategy of the RB responders became more and more rule-based. This result supports the conclusion of Koriat et al. (2006) that metacognitive monitoring and control processes continuously interact and also illustrates a downward spiral that can accompany increasing use of the uncertainty response. As participants avoid more and more difficult stimuli, a simple, but suboptimal strategy begins working better and better, which encourages participants to avoid still more of the difficult stimuli. According to an influential model of metacognition (Nelson & Narens, 1990), metacognitive monitoring is used to build a mental model of the task at hand. Therefore, one interpretation of our results is that the ability to respond “uncertain” allowed participants to construct an incorrect model of the categories that assumed only one stimulus dimension was relevant.
Evidence can also be found in Experiment 1 that participants strategically adopted the uncertainty response as a way to maintain high accuracy. In three of the four conditions of that experiment, the frequency of uncertainty responses was positively correlated with accuracy during the final 150 trials (all p < 0.01); this correlation was nonsignificant only in the II condition when overlap was 0% (p = 0.214). Experiment 2 revealed an identical trend. Although the II and RB responders were similarly using the uncertainty response to improve accuracy, by the end of Experiment 2, the RB responders were doing so more fervently, supporting the idea that the RB responders were increasingly using the uncertainty response to maintain high accuracy with a suboptimal response strategy throughout the duration of the experiment.
In summary, the results of Experiment 2 suggest that many participants used the uncertainty response to change the qualitative character of the II task into an RB task. This is a remarkable result because to the best of our knowledge, this is the first instance in which participants have used a metacognitive-monitoring response to change the underlying affordances of their primary task so that it fits their overall cognitive system more comfortably.
Experiment 3
The results of Experiment 2 suggest that granting participants the uncertainty-response option allowed them to change the qualitative nature of the task. This hypothesis leads to two strong predictions. First, changing the qualitative nature of the task should be more likely with II than RB categories, basically because humans are dimensionally analytical and rule preferring, and there is, therefore, no reason for participants to change the nature of an RB task. Second, we hypothesized that many Experiment 2 participants changed the II task into an RB task by using the uncertainty response to remove the most difficult stimuli from the experiment. If so, then the qualitative change was not because the availability of an uncertainty response option activated an uncertainty monitoring module, which then somehow caused the qualitative change, but rather that the uncertainty response simply provided participants a mechanism via which to eliminate stimuli that were inconsistent with a simple RB response strategy.
The aim of Experiment 3 was to test these predictions using the same II and RB categories as in Experiment 1. There was no uncertainty response option. However, feedback was withheld for the same (relative) stimuli on which the RB responders of Experiment 2 responded uncertain. Thus, in the II condition of Experiment 3, participants made categorization responses to the same stimuli that elicited categorization responses in Experiment 2, and they received no feedback during all trials in which the stimulus elicited an uncertainty response from the participants of Experiment 2. Thus, if our interpretation of the Experiment 2 results is correct, then participants in the RB condition of Experiment 3 should respond optimally, whereas participants in the II condition should respond similarly to the II participants of Experiment 2.
Method
Participants
There were 15 participants in the RB condition and 26 participants in the II condition, all from the University of California at Santa Barbara community. All participants reported normal or corrected-to-normal vision. Each participant completed one session of approximately 60 minutes in duration and was given partial course credit for volunteering.
Stimuli and apparatus
A sample of 600 overlapped RB stimuli was created for the RB condition by rotating the II stimuli used in Experiment 2 by 45 degrees counter-clockwise so that the optimal bound was on the spatial frequency dimension. The II condition re-used the exact set of stimuli from Experiment 2. The remaining aspects of stimulus generation and presentation were identical to Experiment 2.
Procedure
Participants were instructed that they would receive feedback only after some responses. On every trial during the RB condition, the distance between the stimulus and the optimal bound was computed, and the stimulus was assigned to a bin using a procedure identical to the binning procedure used in the previous analyses. We used the modeled uncertainty curve from the RB responders in Experiment 2 to determine the probability of withholding feedback in each distance bin. Specifically, the probability of withholding feedback on a particular trial was proportional to the height of the modeled uncertainty curve at the distance bin containing the stimulus.
In the II condition, the stimuli in Experiments 2 and 3 were identical. For this reason, the probability of withholding feedback in the II condition for each stimulus was set equal to the proportion of times the nine RB responders in Experiment 2 responded uncertain given that same stimulus. None of these probabilities exceeded 0.889 (i.e., every stimulus had a non-zero probability of receiving feedback) though many probabilities were zero, and feedback was guaranteed. For each participant in the II condition, a feedback schedule was generated before the experiment to determine exactly which stimuli would receive feedback. This was to ensure that no participant received either fewer or more feedback trials than any RB responder from Experiment 2.
Stimuli were response-terminated. When feedback was given, it was presented visually for 2,000 ms as “Correct” in green text to correct responses and “Incorrect” in red text to incorrect responses. When feedback was withheld, no text appeared after the response for a period of 2,000 milliseconds. Otherwise, all aspects of timing and presentation were identical to those in the previous two experiments.
Results
Model-based analyses
For the RB condition, no participant failed to meet the minimum accuracy criterion of 65%; thus, all participants were included in subsequent analyses. The same three types of decision-bound models used in Experiments 1 and 2 were fit to the last 150 responses of each participant. Every participant was best fit by a model that assumed an RB response strategy on the spatial frequency dimension.
For the II condition, four participants failed to meet the minimum accuracy criterion and were excluded from further analyses. As above, decision-bound models were fit to the last 150 responses of each participant. Of the remaining 22 participants, ten were best fit by a model assuming an RB strategy, and 12 were best fit by a model assuming an II strategy.
Accuracy-based analyses
Recall that maximum possible accuracy was 95% for the overlapped categories. Overall accuracy for each participant in the RB condition was 84.6% during the final 150 trials, with two participants in the 65–74% accuracy range, two in the 75–84% range, and 11 in the 85% + range. On average, RB participants received feedback on 410 of 600 trials, which closely matches the 408 trials of feedback for the RB responders in Experiment 2.
In the II condition, the RB responders had an overall accuracy of 74.3% in the last 150 trials, while the II responders had a higher overall accuracy of 80.4%. The accuracy of RB and II responders on feedback trials was 79.2% and 83%, respectively. The maximum possible accuracy with no-feedback trials is 82.4% if using an RB strategy and 94.8% if using an II strategy. In order to compare the distribution of RB and II responders in this experiment with the responders from Experiments 1 and 2, we computed a chi-square test for homogeneity and found that the distribution of RB and II responders was significantly different in the II condition of Experiment 3 than in that of Experiment 1 [χ 2(1, N = 51) = 10.34, p = 0.001] but not different than in that of Experiment 2 [χ 2(1, N = 48) = .59, p = 0.44]. Finally, participants in the II condition received an average of 410 trials of feedback, which again closely matches the 408 trials for the RB responders in Experiment 2.
Discussion
Reducing the number of feedback trials in an RB categorization task to match the distribution of corrective feedback observed by RB responders in Experiment 2 apparently caused no detrimental learning effects. Withholding feedback increased the difficulty of the task, especially since feedback was most often withheld for stimuli near the category bound. Despite this increased difficulty, however, participants learned the optimal response strategy, and their accuracy during the last 150 trials was within about 10% of the maximum possible accuracy.
On the other hand, reducing the number of feedback trials in an II categorization task to match the distribution of feedback observed by the RB responders in Experiment 2 clearly affected participants’ ability to learn the optimal response strategy. With II categories, the percentage of RB users was significantly higher in Experiment 3 than in Experiment 1 and not different from that in Experiment 2. Even so, some Experiment 3 II participants were able to learn the optimal response strategy. Because an II strategy yielded a higher maximum accuracy than an RB strategy, many participants were still able to learn the optimal strategy and improve their accuracy despite the reduction in feedback.
It is important to note that simply withholding feedback randomly in an II categorization task does not necessarily impair learning: Vandist, De Schryver, and Rosseel (2009) demonstrated intact II category learning during a single session while providing feedback on only 50% of the trials, and Ashby and O’Brien (2007) observed normal II category learning across five sessions where participants received feedback on only 25% of the trials per session. Nearly half of our II participants failed to learn the optimal strategy while receiving feedback on 68% of all trials. Hence, it was not strictly the reduction in feedback that impaired learning; it was the landscape of feedback encountered by the participants that induced them to persist with a suboptimal strategy.
Participants in the II conditions of Experiments 2 and 3 adopted similar response strategies, despite the fact that Experiment 2 participants had the option of responding uncertain, whereas Experiment 3 participants did not. Thus, it was not the uncertainty response per se that caused the RB responders in Experiment 2 to persist with a suboptimal RB strategy but, rather, it was a strategic choice to use the uncertainty response to eliminate many of the most difficult-to-categorize stimuli.
The results of Experiment 3 also show that withholding feedback on trials when the more difficult stimuli are presented does not necessarily change the response strategy of participants. A qualitative change in strategy occurred in Experiments 2 and 3 with II categories but not in Experiment 3 with RB categories that were created by rotating the Experiment 2 categories by 45 degrees. This supports the hypothesis that the Experiment 2 participants were systematically leveraging increased uncertainty responding toward a preferred RB construal of the II task.
General discussion
The results of our study make two important contributions. First, they suggest that uncertainty monitoring in tasks that depend on nondeclarative (i.e., procedural) memory is similar to uncertainty monitoring in declarative-memory tasks. Second, we found evidence that metacognitive control processes can change the qualitative nature of the task by selectively rejecting stimuli that do not conform to an altered world view. In the language of Nelson and Narens (1990), this result suggests that metacognitive monitoring and control processes can build a severely biased mental model by carefully avoiding aspects of the environment that do not conform to this preferred model.
The results of Experiment 1 show that uncertainty responding in trained II categorization closely resembles uncertainty responding in trained and untrained RB categorization. This is true for overlapping categories in which perfect accuracy is impossible as well as non-overlapping categories in which perfect accuracy is technically possible. These results confirm that uncertainty-monitoring and metacognitive processes do finally catch up with implicit, procedural learning processes, somehow gaining veridical information about them and about the sufficiency and efficiency of their task-solution algorithms. One very adaptive aspect of human cognition is that even the more implicit and procedural components of category learning and discrimination are subject to the error checking and quality controls of metacognition.
Because much prior research has established that learning in II tasks is nondeclarative (i.e., procedural), a natural question arising from our results is how the monitoring functions manage to contact and oversee processes that in other respects are so hidden from introspection, verbalization, consciousness, and declaration. Much evidence implicates the basal ganglia as a critical site of learning in II tasks (for a review, see for example, Ashby & Ennis, 2006). The basal ganglia do not project directly to the prefrontal cortex; thus, the Crick–Koch hypothesis (Crick & Koch, 1998), for example, predicts that people do not have conscious access to activity in the basal ganglia. This prediction is supported by evidence that many basal ganglia-mediated behaviors are nondeclarative (Squire & Zola, 1996). As with other procedural skills (Willingham et al., 2000), II category learning includes a distinct motor component (Ashby et al., 2003a; Maddox et al., 2004b; Spiering & Ashby, 2008b), which has led to the proposal that the cortical target of the basal ganglia-mediated procedural-learning system that dominates in II tasks is in premotor cortex (Ashby, Ennis & Spiering 2007). The premotor cortex does project directly to prefrontal cortex, so the Crick–Koch hypothesis predicts that we should have conscious awareness of activity in the premotor cortex. During trials when a stimulus is near the category bound, it seems plausible that the basal ganglia categorization system might activate the premotor targets associated with the two competing categorization responses almost equally. Therefore, one possibility is that a cortical uncertainty-monitoring network is activated any time there is significant response competition in the premotor cortex. Such a system could produce uncertainty data of the type seen in our experiments, even if it had no access to the details of processing within the (basal ganglia-mediated) procedural-learning system. Obviously, this account is highly speculative, and more work is needed to understand the nature of uncertainty monitoring in nondeclarative tasks. An important feature of this mechanism, however, is that the metacognitive feeling is based on indirect or secondary cues and contents – not on primary, privileged access to the real discriminative processes ongoing in the striatum. This indirect-access account has an intriguing resonance with the work of Reder and her colleagues (e.g., Reder & Schunn, 1996) on implicit metacognitive monitoring of feelings-of-knowing.
A second important conclusion that can be drawn from our experiments is that allowing an uncertainty response reduces the proportion of participants who learn to use a strategy of the optimal type in II category-learning tasks. In Experiment 2, participants who frequently responded “uncertain” were much more likely to use one-dimensional RB rules than participants who seldom responded “uncertain”. This result is consistent with a recent report that II category learning, but not RB learning, is facilitated if participants begin training with the most difficult category exemplars (Spiering & Ashby, 2008a). The idea is that participants who begin with exemplars that are easy to categorize tend to find simple rules that succeed. When more difficult exemplars are later introduced, many of these participants perseverate with the simple rule, even when their error rates increase. In contrast, participants who begin with the most difficult exemplars quickly give up on simple rules because none of these yield an acceptable level of accuracy.
Allowing participants the option of responding “uncertain” allows them to avoid categorizing the most difficult exemplars. As a result, they can choose to use a simple rule, respond to stimuli that conform to that rule, and respond “uncertain” on all other trials. In this way, they can maintain reasonable accuracy with a preferred strategy that fits well their underlying cognitive system that emphasizes dimensional analysis and explicit categorization rules. The results of Experiment 2 suggest that many participants took this approach. In a sense, therefore, one sees that the II task in Experiment 2 was subject to a kind of Uncertainty Principle – that is, the very presence of the uncertainty response during the learning of the II task let participants qualitatively change the population of stimuli they directly encountered and therefore changed the reinforcement landscape they directly experienced, so that in actuality, the explicit RB task approach became perfectly feasible. Experiment 3 showed that a similar change in strategy did not occur with RB tasks because the cognitive organization of that task was already well suited to humans’ cognitive system. This experiment also showed that the uncertainty response played only an indirect role in this process – that is, the change in strategy was not due to uncertainty monitoring per se, but rather to the opportunity that the uncertainty response provided to eliminate stimuli that were incompatible with an RB strategy.
In conclusion, our results show that humans can effectively monitor uncertainty in II tasks but that the option of responding uncertain can shift the balance between explicit and implicit category-learning systems. Unfortunately, little is known about other factors that can shift this balance (although see Ashby & Crossley, 2010). As a result, we stress the continuing need to study the coordination between implicit and explicit category-learning systems in the mind and brain, the competition between them, and the tradeoffs between them at different stages of category learning and for different tasks.
Acknowledgments
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Appendix
Two different decision-bound models that assumed an RB decision strategy were fit to each participant’s data. We also fit one model that assumed an II strategy, and two different models that assumed random guessing. For more details, see Ashby (1992) or Maddox and Ashby (1993).
Rule-based models
The one-dimensional classifier
This model assumes that participants set a decision criterion on a single stimulus dimension. For example, a participant might base his or her categorization decision on the following rule: “Respond A if the bar width is small, otherwise respond B”. Two versions of the model were fit to the data. One version assumed a decision based on bar width, and the other version assumed a decision based on orientation. These models have two parameters: a decision criterion along the relevant perceptual dimension and the variance of perceptual and criterial noise.
Let xi denote the value of stimulus Si on the relevant dimension. Then the one-dimensional classifier assumes that the probability of responding B on a trial when stimulus Si is presented equals
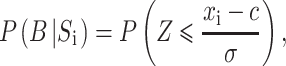 |
where Z is a random variable with a standard z distribution (i.e., normal with mean 0 and variance 1), c is the decision criterion on the relevant stimulus dimension, and σ is the variance of perceptual and criterial noise.
Information-integration models
The general linear classifier (GLC)
The GLC assumes that participants divide the stimulus space using a linear decision bound. Categorization decisions are then based upon which region each stimulus is perceived to fall in. These decision bounds require linear integration of both stimulus dimensions, thereby producing an II decision strategy. The GLC has three parameters: the slope and intercept of the linear decision bound and noise variance.
If stimulus Si has coordinates (xi, yi) on the two stimulus dimensions, then the GLC predicts that the probability of responding B on a trial when stimulus Si is presented equals
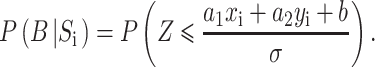 |
Only two of the three parameters a1, a2, and b are free since only two parameters are required to specify a line.
Random guessing models
Fixed random guessing model
This model assumed that the participant responded randomly, essentially flipping an unbiased coin on each trial to determine the response. Thus, the predicted probability of responding “A” (and “B”) was 0.5 for each stimulus. This model has no free parameters.
General random guessing model
This model assumed that the participant responded randomly, essentially flipping a biased coin on each trial to determine the response. Thus, the predicted probability of responding “A” was a free parameter in the model that could take on any value between 0 and 1. This model is useful for identifying participants who are biased towards pressing one response key.
Goodness-of-fit measure
Model parameters were estimated using the method of maximum likelihood, and the statistic used for model selection was the Bayesian Information Criterion (BIC; Schwarz, 1978), which is defined as:
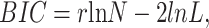 |
where r is the number of free parameters, N is the sample size, and L is the likelihood of the model given the data. The BIC statistic penalizes models for extra free parameters. To determine the best fitting model within a group of competing models, the BIC statistic is computed for each model, and the model with the smallest BIC value is the winning model.
Footnotes
Note that the rule “Respond A if the bars are thin and steep, and B if the bars are thick and shallow” is a conjunction rule that does not match the optimal bound. Conjunction rules describe rectangular response regions, not diagonal regions. Many previous studies have reported that conjunction rules provide poor accounts of human responding in II tasks (Ashby & O’Brien, 2007; Maddox, Bohil, & Ing, 2004; Maddox, Filoteo, Hejl, & Ing, 2004; Maddox & Ing, 2005; Smith, Beran, Crossley, Boomer, & Ashby, 2010).
Although we do know of at least one study that examined metacognitive control in a categorization task that recruits the nondeclarative perceptual representation memory system (Redford, 2010).
This research was supported in part by National Institute of Health Grant R01 MH3760-2 and by support from the U.S. Army Research Office through the Institute for Collaborative Biotechnologies under grant W911NF-07-1-0072. Correspondence concerning this article should be addressed to F. Gregory Ashby, Department of Psychology, University of California, Santa Barbara, CA 93106. (e-mail: ashby@psych.ucsb.edu).
References
- Ashby FG. Multidimensional models of categorization. In: Ashby FG, editor. Multidimensional models of perception and cognition. Hillsdale, NJ: Erlbaum; 1992. pp. 449–483. [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295X.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashby F. G., Crossley M. J. Interactions between declarative and procedural-learning categorization systems. Neurobiology of Learning and Memory. 2010;94:1–12. doi: 10.1016/j.nlm.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashby FG, Ell SW, Waldron EM. Procedural learning in perceptual categorization. Memory & Cognition. 2003a;31:1114–1125. doi: 10.3758/BF03196132. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ennis JM. The role of the basal ganglia in category learning. The Psychology of Learning and Motivation. 2006;46:1–36. doi: 10.1016/S0079-7421(06)46001-1. [DOI] [Google Scholar]
- Ashby FG, Ennis JM, Spiering BJ. A neurobiological theory of automaticity in perceptual categorization. Psychological Review. 2007;114:632–656. doi: 10.1037/0033-295X.114.3.632. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Gott RE. Decision rules in the perception and categorization of multidimensional stimuli. Journal of Experimental Psychology. Learning, Memory, and Cognition. 1988;14(1):33–53. doi: 10.1037/0278-7393.14.1.33. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT. Human category learning. Annual Review of Psychology. 2005;56:149–178. doi: 10.1146/annurev.psych.56.091103.070217. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT, Bohil CJ. Observational versus feedback training in rule-based and information-integration category learning. Memory & Cognition. 2002;30:666–667. doi: 10.3758/BF03196423. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Noble S, Filoteo JV, Waldron EM, Ell SW. Category learning deficits in Parkinson's disease. Neuropsychology. 2003b;17:115–124. doi: 10.1037/0894-4105.17.1.115. [DOI] [PubMed] [Google Scholar]
- Ashby FG, O'Brien JB. Category learning and multiple memory systems. Trends in Cognitive Sciences. 2005;9:83–89. doi: 10.1016/j.tics.2004.12.003. [DOI] [PubMed] [Google Scholar]
- Ashby FG, O'Brien JB. The effects of positive versus negative feedback on information-integration category learning. Perception & Psychophysics. 2007;69:865–878. doi: 10.3758/BF03193923. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Queller S, Berretty PM. On the dominance of unidimensional rules in unsupervised categorization. Perception & Psychophysics. 1999;61:1178–1199. doi: 10.3758/BF03207622. [DOI] [PubMed] [Google Scholar]
- Bechara A, Damasio H, Tranel D, Damasio AR. Deciding advantageously before knowing the advantageous strategy. Science. 1997;275:1293–1295. doi: 10.1126/science.275.5304.1293. [DOI] [PubMed] [Google Scholar]
- Benjamin AS, Bjork RA, Schwartz BL. The mismeasure of memory: When retrieval fluency is misleading as a metamnemonic index. Journal of Experimental Psychology: General. 1998;127:55–68. doi: 10.1037/0096-3445.127.1.55. [DOI] [PubMed] [Google Scholar]
- Beran MJ, Smith JD, Coutinho MVC, Couchman JJ, Boomer J. The psychological organization of “uncertainty” responses and “middle” responses: A dissociation in capuchin monkeys (Cebus apella) Journal of Experimental Psychology: Animal Behavior Processes. 2009;35:371–381. doi: 10.1037/a0014626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH. Psychophysics software for use with MATLAB. Spatial Vision. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Brooks LR. Nonanalytic concept formation and memory for instances. In: Rosch E, Lloyd BB, editors. Cognition and categorization. Hillsdale, NJ USA: Erlbaum; 1978. pp. 169–211. [Google Scholar]
- Crick F, Koch C. Consciousness and neuroscience. Cerebral Cortex. 1998;8:97–107. doi: 10.1093/cercor/8.2.97. [DOI] [PubMed] [Google Scholar]
- Dunlosky J, Bjork RA, editors. Handbook of memory and metamemory. New York: Psychology Press; 2008. [Google Scholar]
- Eichenbaum H. Declarative memory: Insights from cognitive neurobiology. Annual Review of Psychology. 1997;48:547–572. doi: 10.1146/annurev.psych.48.1.547. [DOI] [PubMed] [Google Scholar]
- Ell SW, Ashby FG. The effects of category overlap on information-integration and rule-based category learning. Perception & Psychophysics. 2006;68:1013–1026. doi: 10.3758/BF03193362. [DOI] [PubMed] [Google Scholar]
- Filoteo JV, Lauritzen JS, Maddox WT. Removing the frontal lobes: The effects of engaging executive functions on perceptual category learning. Psychological Science. 2010;21:415–423. doi: 10.1177/0956797610362646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flavell JH. Metacognition and cognitive monitoring: A new area of cognitive-developmental inquiry. The American Psychologist. 1979;34:906–911. doi: 10.1037/0003-066X.34.10.906. [DOI] [Google Scholar]
- Gallup GG. Self-awareness and the emergence of mind in primates. American Journal of Primatology. 1982;2:237–248. doi: 10.1002/ajp.1350020302. [DOI] [PubMed] [Google Scholar]
- Knowlton BJ, Mangels JA, Squire LR. A neostriatal habit learning system in humans. Science. 1996;273:399–402. doi: 10.1126/science.273.5280.1399. [DOI] [PubMed] [Google Scholar]
- Koriat A. How do we know that we know? The accessibility model of the feeling of knowing. Psychological Review. 1993;100:609–639. doi: 10.1037/0033-295X.100.4.609. [DOI] [PubMed] [Google Scholar]
- Koriat A. Metacognition and consciousness. In: Zelazo PD, Moscovitch M, Thompson E, editors. The Cambridge handbook of consciousness (pp. 289–325) Cambridge, UK: Cambridge University Press; 2007. [Google Scholar]
- Koriat A, Goldsmith M. Monitoring and control processes in the strategic regulation of memory accuracy. Psychological Review. 1996;103:490–517. doi: 10.1037/0033-295X.103.3.490. [DOI] [PubMed] [Google Scholar]
- Koriat A, Ma’ayan H, Nussinson R. The intricate relationships between monitoring and control in metacognition: Lessons for the cause-and-effect relation between subjective experience and behavior. Journal of Experimental Psychology: General. 2006;135:36–69. doi: 10.1037/0096-3445.135.1.36. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG. Comparing decision bound and exemplar models of categorization. Perception & Psychophysics. 1993;53:49–70. doi: 10.3758/BF03211715. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Bohil CJ. Delayed feedback effects on rule-based and information-integration category learning. Journal of Experimental Psychology. Learning, Memory, and Cognition. 2003;29:650–662. doi: 10.1037/0278-7393.29.4.650. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Ing AD, Pickering AD. Disrupting feedback processing interferes with rule-based but not information-integration category learning. Memory & Cognition. 2004a;32:582–591. doi: 10.3758/BF03195849. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Bohil CJ, Ing AD. Evidence for a procedural-learning-based system in perceptual category learning. Psychonomic Bulletin. 2004b;11:945–952. doi: 10.3758/BF03196726. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Filoteo JV, Hejl KD, Ing AD. Category number impacts rule-based but not information-integration category learning: Further evidence for dissociable category learning systems. Journal of Experimental Psychology. Learning, Memory, and Cognition. 2004;30:227–235. doi: 10.1037/0278-7393.30.1.227. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Filoteo JV, Lauritzen JS, Connally E, Hejl KD. Discontinuous categories affect information-integration but not rule-based category learning. Journal of Experimental Psychology. Learning, Memory, and Cognition. 2005;31:654–669. doi: 10.1037/0278-7393.31.4.654. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Glass BD, O’Brien JB, Filoteo JV, Ashby FG. Category label and response location shifts in category learning. Psychological Research. 2010;74:219–236. doi: 10.1007/s00426-009-0245-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maddox WT, Ing AD. Delayed feedback disrupts the procedural-learning system but not the hypothesis testing system in perceptual category learning. Journal of Experimental Psychology. Learning, Memory, and Cognition. 2005;31:100–107. doi: 10.1037/0278-7393.31.1.100. [DOI] [PubMed] [Google Scholar]
- Metcalfe J, Shimamura A. Metacognition: Knowing about knowing. Cambridge, MA: Bradford Books; 1994. [Google Scholar]
- Nelson TO, editor. Metacognition: Core readings. Toronto: Allyn and Bacon; 1992. [Google Scholar]
- Nelson TO. Consciousness and metacognition. The American Psychologist. 1996;51:102–116. doi: 10.1037/0003-066X.51.2.102. [DOI] [Google Scholar]
- Nelson TO, Narens L. Metamemory: A theoretical framework and new findings. Psychology of Learning and Motivation. 1990;26:125–141. doi: 10.1016/S0079-7421(08)60053-5. [DOI] [Google Scholar]
- Nelson TO, Narens L. Why investigate metacognition? In: Metcalfe J, Shimamura AP, editors. Metacognition: Knowing about knowing. Cambridge, MA: MIT Press; 1994. pp. 1–25. [Google Scholar]
- Nomura EM, Maddox WT, Filoteo JV, Ing AD, Gitelman DR, Parrish TB, Mesulam M-M, Reber PJ. Neural correlates of rule-based and information-integration visual category learning. Cerebral Cortex. 2007;17(1):37. doi: 10.1093/cercor/bhj122. [DOI] [PubMed] [Google Scholar]
- Persaud N, McLeod P, Cowey A. Post decision wagering objectively measures awareness. Nature Neuroscience. 2007;10:257–261. doi: 10.1038/nn1840. [DOI] [PubMed] [Google Scholar]
- Reber AS. Implicit learning of artificial grammars. Journal of Verbal Learning and Verbal Behavior. 1967;6:855–863. doi: 10.1016/S0022-5371(67)80149-X. [DOI] [Google Scholar]
- Reder, L. M., & Schunn, C. (1996). Metacognition does not imply awareness: Strategy choice is governed by implicit learning and memory. In L.M. Reder (Ed.), Implicit memory and metacognition (pp. 45-77).
- Redford JS. Evidence of metacognitive control by humans and monkeys in a perceptual categorization task. Journal of Experimental Psychology. Learning, Memory, and Cognition. 2010;36:248–254. doi: 10.1037/a0017809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolls ET. Memory systems in the brain. Annual Review of Psychology. 2000;51:599–630. doi: 10.1146/annurev.psych.51.1.599. [DOI] [PubMed] [Google Scholar]
- Scheck P, Nelson TO. Lack of pervasiveness of the underconfidence-with-practice effect: Boundary conditions and an explanation via anchoring. Journal of Experimental Psychology: General. 2005;134:124–128. doi: 10.1037/0096-3445.134.1.124. [DOI] [PubMed] [Google Scholar]
- Schwartz BL. Sources of information in metamemory: Judgments of learning and feelings of knowing. Psychonomic Bulletin & Review. 1994;1:357–375. doi: 10.3758/BF03213977. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- Serra MJ, Dunlosky J. Does retrieval fluency contribute to the underconfidence-with-practice effect? Journal of Experimental Psychology. Learning, Memory, and Cognition. 2005;31:1258–1266. doi: 10.1037/0278-7393.31.6.1258. [DOI] [PubMed] [Google Scholar]
- Smith JD. The study of animal metacognition. Trends in Cognitive Sciences. 2009;13:389–396. doi: 10.1016/j.tics.2009.06.009. [DOI] [PubMed] [Google Scholar]
- Smith JD, Beran MJ, Couchman JJ. Animal metacognition. In: Zentall T, Wasserman E, editors. Comparative cognition: Experimental explorations of animal intelligence. Oxford, UK: Oxford University Press; 2010. [Google Scholar]
- Smith JD, Beran MJ, Crossley MJ, Boomer JT, Ashby FG. Implicit and explicit category learning by macaques (Macaca mulatta) and humans (Homo sapiens) Journal of Experimental Psychology: Animal Behavior Processes. 2010;36:54–65. doi: 10.1037/a0015892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JD, Beran MJ, Redford JS, Washburn DA. Dissociating uncertainty responses and reinforcement signals in the comparative study of uncertainty monitoring. Journal of Experimental Psychology: General. 2006;135(2):282–297. doi: 10.1037/0096-3445.135.2.282. [DOI] [PubMed] [Google Scholar]
- Smith JD, Redford JS, Beran MJ, Washburn DA. Rhesus monkeys (Macaca mulatta) adaptively monitor uncertainty while multi-tasking. Animal Cognition. 2010;13:93–101. doi: 10.1007/s10071-009-0249-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith JD, Schull J, Strote J, McGee K, Egnor R, Erb L. The uncertain response in the bottlenosed dolphin (Tursiops truncatus) Journal of Experimental Psychology: General. 1995;124:391–408. doi: 10.1037/0096-3445.124.4.391. [DOI] [PubMed] [Google Scholar]
- Smith JD, Shields WE, Schull J, Washburn DA. The uncertain response in humans and animals. Cognition. 1997;62:75–97. doi: 10.1016/S0010-0277(96)00726-3. [DOI] [PubMed] [Google Scholar]
- Son LK, Kornell N. Metaconfidence judgments in rhesus macaques: Explicit vs. implicit mechanisms. In: Terrace HS, Metcalfe J, editors. The missing link in cognition: Origins of self-reflective consciousness. New York: Oxford University Press; 2005. pp. 296–320. [Google Scholar]
- Spiering BJ, Ashby FG. Initial training with difficult items facilitates information-integration but not rule-based category learning. Psychological Science. 2008;19:1169–1177. doi: 10.1111/j.1467-9280.2008.02219.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiering BJ, Ashby FG. Response processes in information-integration category learning. Neurobiology of Learning and Memory. 2008;90:330–338. doi: 10.1016/j.nlm.2008.04.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squire LR, Schacter DL. The neuropsychology of memory. 3. New York: Guilford Press; 2002. [Google Scholar]
- Squire LR, Zola SM. Structure and function of declarative and nondeclarative memory systems. Proceedings of the National Academy of Sciences of the United States of America. 1996;93:13515–13522. doi: 10.1073/pnas.93.24.13515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandist K, De Schryver M, Rosseel Y. Semisupervised category learning: The impact of feedback in learning the information-integration task. Attention, Perception, & Psychophysics. 2009;71:328–341. doi: 10.3758/APP.71.2.328. [DOI] [PubMed] [Google Scholar]
- Waldron EM, Ashby FG. The effects of concurrent task interference on category learning: Evidence for multiple category learning systems. Psychonomic Bulletin & Review. 2001;8:168–176. doi: 10.3758/BF03196154. [DOI] [PubMed] [Google Scholar]
- Washburn DA, Gulledge JP, Beran MJ, Smith JD. With his memory magnetically erased, a monkey knows he is uncertain. Biology Letters. 2010;6(2):160–162. doi: 10.1098/rsbl.2009.0737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willingham DB, Wells LA, Farrell JM, Stemwedel ME. Implicit motor sequence learning is represented in response locations. Memory & Cognition. 2000;28:366–375. doi: 10.3758/BF03198552. [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT. Dual-task interference in perceptual category learning. Memory & Cognition. 2006;34:387–398. doi: 10.3758/BF03193416. [DOI] [PubMed] [Google Scholar]