A Bayesian population PBPK model for multiroute chloroform exposure

Abstract

A Bayesian hierarchical model was developed to estimate the parameters in a physiologically based pharmacokinetic (PBPK) model for chloroform using prior information and biomarker data from different exposure pathways. In particular, the model provides a quantitative description of the changes in physiological parameters associated with hot-water bath and showering scenarios. Through Bayesian inference, uncertainties in the PBPK parameters were reduced from the prior distributions. Prediction of biomarker data with the calibrated PBPK model was improved by the calibration. The posterior results indicate that blood flow rates varied under two different exposure scenarios, with a two-fold increase of the skin's blood flow rate predicted in the hot-bath scenario. This result highlights the importance of considering scenario-specific parameters in PBPK modeling. To demonstrate the application of a probability approach in toxicological assessment, results from the posterior distributions from this calibrated model were used to predict target tissue dose based on the rate of chloroform metabolized in liver. This study demonstrates the use of the Bayesian approach to optimize PBPK model parameters for typical household exposure scenarios.

Introduction

Physiologically based pharmacokinetic (PBPK) modeling has been used in toxicology, epidemiology, and in exposure and risk assessment as an adjunct to studies on the toxic modes of action of xenobiotics (Gibb et al., 2002; Zeise et al., 2002; Andersen, 2003). The power of PBPK modeling is achieved at the expense of using a large number of parameters, some of which may vary significantly among individuals (e.g., tissue weights and blood flows) and few of which are known with precision (e.g., bioavailability, metabolic/excretion rates) (Zeise et al., 2002). Therefore, every PBPK model requires some level of calibration or optimization of its parameters. Parameters in PBPK models are usually calibrated based on biomarker data by regression or a maximum likelihood approach using available software package such as ACSL (AEgis Technologies, 2008) or Simusolv (Steiner et al., 1990). However, it is not practical to simultaneously calibrate a large number of parameters using these methods. Thus, optimizations are often conducted by changing the values of a few parameters while fixing other parameters at point values. These optimization methods provide point estimates of parameters with the best fit to the experimental data based on the selected objective functions. The accuracy of point estimates in such a process is highly susceptible to variability and uncertainty in the fixed parameters. Interpretation of the results can be misleading when the estimates are uncertain or the values of the parameters that were fixed are inaccurate (Louis, 1991).

The Bayesian pharmacokinetic population model has received much attention in the past 10 years, beginning with the work of Bois et al. (1996a,b). The Bayesian approach provides a formal way to incorporate prior knowledge on model parameters together with observed data in the modeling process. The analysis starts with the construction of prior probability distributions of the model parameters of interest, usually based on studies available in the literature. These distributions are then evaluated on the basis of their likelihood given observed data to compute posterior distributions of the model parameters. Hierarchical modeling with Bayesian MCMC simulation is suitable for population PBPK models because the development of these models often involves non-linear processes, small datasets, high uncertainty, and biological variability (Bernillon and Bois, 2000). This approach is flexible; new information (such as additional experiment data, different PBPK models, and refined prior distributions), can easily be incorporated into existing models to improve the parameter estimation process. These methods have been used in many PBPK modeling applications to assess population pharmacokinetics in chemicals including trichloroethylene (Bois, 2000a,b; Hack et al., 2006), methylene chloride (Jonsson et al., 2001), toluene (Jonsson and Johanson, 2001), and dichloromethane (Marino et al., 2006). Recently, a Bayesian chloroform PBPK model for rats and mice was developed based on gas uptake and labeling index data (Liao et al., 2007).

In this study, a Bayesian framework developed by Bois (2000a,b) was adapted to evaluate the uncertainty and variability in PBPK parameters for multiple route exposures to chloroform. The specific aims of this study were (1) to optimize PBPK modeling parameters through Bayesian techniques, (2) to study the impact of interindividual variability on pharmacokinetics of chloroform, and (3) to study the impact of hot-water immersion on scenario-dependent PBPK modeling parameters.

Since the identification of chloroform and other trihalomethanes in chlorinated drinking water, human exposure to these disinfectant by-products (DBPs) has become a public health concern. The most significant routes for chloroform exposure are ingestion and inhalation (ATSDR, 1997). However, using chlorinated water causes significant inhalation and dermal exposure to chloroform as well (Wallace, 1997). Wilkes et al. (1996) estimated that exposure from showering represents 40–50% of the total exposure from tap water used domestically. Jo et al. (1990) estimated that the absorbed dose of chloroform from a 10-min shower is equivalent to drinking 21 of chlorinated water. A recent modeling study showed that dermal absorption of chloroform from 10-min showering contributed 30% of the total internal dose (area under the concentration curve in the blood) for an average adult (Haddad et al., 2006). The experiments conducted by Gordon et al. (1998) and Xu et al. (2002) used real-time breath analysis techniques to examine the dermal-only intake of chloroform from hot-water bathing. Their results showed that dermal absorption contributes significantly to the total exposure to chloroform.

A chloroform PBPK model was first developed by Corley et al. (1990) to describe the inhalation and ingestion exposure of mice, rats, and humans. Roy et al. (1996) developed a distributed parameter (DP) skin model to simulate the uptake of volatile organic compounds (VOCs) through dermal exposure. The Roy DP model was then incorporated into the Corley model to evaluate dermal and inhalation chloroform exposures for humans. Corley et al. (2000) later used the 1990 model to examine the dermal uptake of chloroform through bath water with a one-compartment skin model. Levesque et al. (2000) also developed a PBPK model for dermal and inhalation uptake of chloroform for competition swimmers. In all these modeling efforts, there were limited attempts to incorporate the effects of water temperature on blood flow rates, but Corley et al. (2000) did consider the re-distribution of blood flow between the skin and the rapidly perfused tissues in model parameter optimization. In Levesque's model, the physiological properties of the swimming scenarios, including cardiac output, inhalation rate, and blood flow rate, were significantly impacted by the exercise level, as described by Johanson and Naslund (1988). However, changes due to exercise could not be directly applied to the hot-bath scenario. The recommended metabolic equivalent (MET) value for sit bath, 1.5, is similar to knitting or typing (Ainsworth, 2002). Earlier studies show that hot-water bathing significantly changes the skin blood flow rate, but does not significantly change heart rate or blood pressure (Miwa et al., 1994; Koda et al., 1995; Allison and Reger, 1998; Allison et al., 1998; Boone et al., 1999). Gordon et al. (1998) pointed out that temperature-dependent parameters should be used to calculate dermal uptake during hot-water bathing.

In this study, a Bayesian hierarchical model was used to estimate the uncertainty and variability in human PBPK parameters associated with multiple-route exposures to chloroform. A chloroform PBPK model was modified from the earlier published PBPK models to focus more specifically on inhalation-only exposures in a running shower stall, and on dermal-only exposures from hot-water bathing. Scaling functions were used to determine the anatomic parameters in this PBPK model. Physiological and biochemical parameters with higher levels of uncertainty and variability were optimized using a Bayesian MCMC method. This approach combined prior parameter distributions from published literature with data from laboratory-controlled human exposures to refine or update posterior distributions of the parameters. In particular, the influences of hot-water bath effects on tissue blood flow rates (BFs) and on activity-based parameters (METs) were analyzed. Although other Bayesian analyses of human PBPK models have been published (Gelman et al., 1996; Bois et al., 1996a,b; Bois, 1999, 2000a,b; Jonsson et al., 2001; Sohn et al., 2004; Hack et al., 2006, Liao et al., 2007), this study represents the first attempt to simultaneously update parameters with biomarker data obtained from household exposure scenarios.

Materials and methods

Experimental Data

Xu and Weisel conducted a human exposure study to characterize the inhalation and dermal uptake of chloroform and haloketones during showering and bathing (Xu and Weisel, 2005a,b). Six subjects (Table 1), three males and three females, participated in two series of experiments: inhalation-only exposure in a shower chamber and dermal-only exposure in bath water. In the inhalation-only experiments, individual subjects were exposed to chloroform in air as they stood near the shower water stream for 30 min. To avoid dermal contact with the water, the subjects wore water-proof clothing and shoes during the experiment. The average concentration of chloroform in air during the inhalation exposure was 180 μg/m³. In the dermal-only experiments, each subject was exposed to water containing 40 μg/l of chloroform in a bathtub at 38±1°C. The subject was submerged in the water, except for the head, for 30 min. Dermal exposure was isolated from potential inhalation exposure by using a mouth breathing face mask that was equipped with two one-way breathing valves, one that provided a purified air supply and the other that collected/monitored exhaled breath samples. Before each exposure, two breath samples were collected to determine the level of chloroform in the exhaled breath. The air collected by this method is approximately 95% alveolar, with the balance of air from the upper airway. After each exposure, breath samples were collected at various time points for 2 h. Four samples of exhaled breath during the inhalation-only exposure and six samples of exhaled breath during the dermal-only exposure were collected. A detailed setting of the experimental design and analysis methods can be found in Xu and Weisel (2005a,b).

Table 1.

Basic demographic information and physical measurements of human subjects.

Subject	Gender	Age (year)	Bodyweight (kg)	Height (cm)
M1	M	29	59.0	167
M2	M	28	63.5	170
M3	M	39	70.0	181
F1	F	27	55.0	155
F2	F	25	62.0	165
F3	F	27	55.0	162

PBPK Model

A multiroute chloroform PBPK model was developed for this study. The PBPK model was adapted from an earlier model by Corley et al. (1990) with the DP skin model developed by Roy et al. (1996) (see Figure 1). The model incorporated six tissue compartments: slowly perfused tissues, rapidly perfused tissues, liver, kidney, fat, and skin. In this model, the body is described as a set of well-mixed compartments, each of which represent a specific or lumped body compartment, which are similar with respect to blood flow and partitioning of chloroform between blood and tissues. Tissue compartments are assumed to be homogeneous and the distribution is flow limited, except for the stratum corneum (described in the skin model section, below). Pulmonary exchanges are simulated by assuming instantaneous equilibrium between alveolar air, venous blood, and arterial blood. The exhaled breath is assumed to be a mixture of alveolar air (95–99%) and ambient air (1–5%). This model uses saturable Michaelis–Menten kinetics for chloroform metabolism that occurs in the liver and the kidney, in which the metabolic constant of kidney metabolism is expressed as a fraction of that in the liver (Corley et al., 1990).

Figure 1.

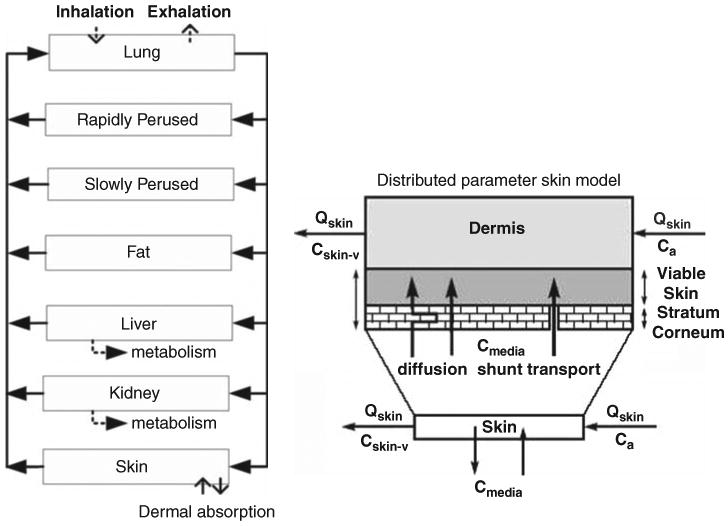
PBPK model structure (left panel) for prediction chloroform exposure through inhalation or dermal route; and the distributed parameter model for skin compartment (right panel) (adapted from Roy et al., 1996).

Skin Model

Traditional one-compartment skin models usually assume a homogenous distribution in the skin compartment and do not consider accumulation of the chemical in the barrier layer (stratum corneum). Thus, the rate of transport through the skin depends on permeability, which is only true when chloroform in the skin is in equilibrium with the concentration of media. However, dermal mass flux does not reach steady-state diffusion for many common dermal exposure scenarios (Xu et al., 2002). Therefore, traditional skin models cannot predict the time lag of the exhaled breath sample after exposure. In the DP skin model (Roy et al., 1996), the skin consisted of two compartments, the outer compartment (representing the stratum corneum) and the inner compartment (representing the viable skin) (see Figure 1). In the outer compartment, the stratum corneum was considered as a barrier layer and epidermis as a reservoir. The chemical concentration in the stratum corneum changes with distance from the stratum corneum-media interface. Once the chemical reached the inner compartment, the viable skin was considered as a homogeneous, well-mixed tissue. Dermal absorption was estimated through unsteady state dermal mass flux, as described by the Fickian diffusion equation (Roy et al., 1996). The equations used to describe the dermal absorption rate are presented in Appendix A. A detailed description of the DP model can be found in Roy et al. (1996).

Biochemical Processes

Partition and metabolic coefficients were assumed to be the same for the two exposure scenarios. Values of partition coefficients (PCs) were obtained from ILSI (1997). The metabolism of chloroform was assumed to occur only in the liver and the kidney through Michaelis–Menten kinetics. Metabolic parameters (V_max and K_m) in the liver were determined in vitro using human tissues (Corley et al., 1990). Enzyme activities in the kidney tissue were observed in hamsters, mice, and rats, but there was no enzyme activity observed in the human kidney tissue. Therefore, Corley et al. assumed that the metabolic activity for human kidney tissue was present but below the detection limit and was incorporated into the model by relating kidney metabolism and liver metabolism (Corley et al., 1990).

PBPK Parameters

The uncertainty of PBPK model parameters is highly related to the characteristics and quality of the original source of information. The information used for generated PBPK model parameters is often characterized by a high degree of uncertainty regarding the processes studied and significant variation in the values observed, measured, and registered (Nestorov, 2001). Physiological parameters, such as tissue volumes and blood flow rates, are relatively well characterized compared with the biochemical parameters for PBPK models, as most of these parameters can be measured separately from the exposure experiments. Therefore, the scaling functions were used to estimate the tissue volumes (discussed in further detail in the Materials and methods section).

A preliminary sensitivity analysis (SA) for the PBPK model parameters was performed based on the literature values. The purpose of the SA was to compare and select sensitive biochemical and scenario-dependent PBPK parameter to be included in MCMC analysis, starting with the likely sensitive parameters based on earlier sensitivity analysis on PBPK model parameters for similar compounds (Clewell et al., 1994, 2000). If the selected model parameter was a sensitive model parameter, then all the parameters in that category were included in the MCMC analysis (i.e., blood:air PC for PC category). If the selected model parameter showed a low sensitivity, then all of the parameters in that category were tested. The equation used for the sensitivity analysis can be found in Appendix B.

It was found that the sensitivity of the parameters (Table 2) varied with the exposure scenario (inhalation or dermal). For example, skin blood flow is more sensitive in the case of dermal exposure than the inhalation exposure. The sensitivity of the parameters also varied with time. For example, the metabolic parameters (liver clearance: CL and kidney clearance: A) become more sensitive in the post-exposure period (after 30 min). This analysis only provided a local sensitivity of the model parameters, as it only varied one parameter while holding other parameters constant. The parameters included in the MCMC analysis were those with multiple sensitivity coefficients >0.1 (which means varying the parameter value by 1% has a 0.1% impact on the response). On the basis of the sensitivity analysis, blood flow rates, PCs, and metabolic parameters were all included in the MCMC analysis.

Table 2.

Sensitivity analysis of the model parameters during a 30-min inhalation-only or dermal-only exposure.

Time	PBA	CL	A	BF_SK	MET
Inhalation
5	−0.744	−0.088	−0.055	0.017	0.212
10	−0.716	−0.101	−0.059	0.046	0.266
20	−0.689	−0.096	−0.061	0.045	0.231
28	−0.679	−0.108	−0.067	0.055	0.236
31	−0.431	−0.21	−0.119	0.147	0.465
35	−0.402	−0.201	−0.123	0.177	0.279
40	−0.395	−0.165	−0.154	0.17	0.123
60	−0.446	−0.219	−0.156	0.119	0.234
90	−0.4	−0.251	−0.152	0.072	0.224
120	−0.335	−0.264	−0.161	0.088	−0.024
Dermal
5	0.119	−0.072	−0.046	0.902	0.051
10	0.031	−0.085	−0.053	0.799	−0.014
20	−0.123	−0.097	−0.06	0.627	−0.171
28	−0.225	−0.103	−0.064	0.516	−0.287
31	−0.258	−0.105	−0.065	0.48	−0.325
35	−0.319	−0.11	−0.069	0.4	−0.392
40	−0.481	−0.12	−0.075	0.222	−0.569
60	−1.032	−0.139	−0.096	−0.376	−1.213
90	−1.319	−0.19	−0.126	−0.745	−1.55
120	−1.038	−0.234	−0.15	−0.551	−1.452

Abbreviations: PBA, blood:air partition coefficient; CL, liver clearance; A, ratio of kidney/liver clearance; BF_SK, percentage of cardiac output to skin compartment; MET, metabolic equivalent.

Only selected parameters were presented.

Uncertainty/Variability Characterized through Scaled Functions

To account for known physiological dependencies among some model parameters, tissue volumes, ventilation rates, cardiac output, and blood flow rates were calculated through scaling functions that were based on the demographic information for each subject (Gallegos and Wenzel, 1984; Layton, 1993; ICRP, 2002). Tissue volumes were calculated to account for age, gender, and body weight (BW). Total fractional tissue volumes were sum to 0.92; this value represents the fraction of perfusable tissues in the body (Tan et al., 2006). The inhalation rate is calculated based on the person's age, gender, and the metabolic equivalent of tasks (MET) value associated with the activity pursued (see e.g., Georgopoulos et al., 2005 and references therein). The cardiac outputs were correlated with alveolar ventilation rate through a semi-empirical function, which accounts for MET, body weight, and oxygen consumption values (Barash et al., 2000). Scaled functions used to describe the interindividual variability among the tissue volumes, correlations between the ventilation rates and cardiac outputs, can be found in Appendix C.

The blood flow rates to various tissue compartments were expressed as percentages of the total cardiac output (as they were summed to unity). Although the correlations between tissue volumes and the blood flow to the tissue has been reported (Price et al., 2003), in this study, the tissue blood flows as percentages of the total cardiac output were assumed to be independent from other physiological parameters, such as body size. (Note that the estimation of cardiac output was still correlated with age, gender, BW, and MET). As blood flow rates for the dermal (hot-water bath) scenario should be different from those for the inhalation scenario, two sets of blood flow rates were used in this study, one for inhalation-only exposure, the other for dermal-only exposure.

Figure 2 compares simulation results (the dashed line) derived from the point literature values (as the population means of the prior distributions) to simulation results (solid lines) derived from the parameters calculated from the scaling functions (shown in Appendix C). The scaled parameter values provide more interindividual variability than the unscaled values, but not enough to account for the interindividual variability observed in the data. Therefore, in addition to the scaling functions, the Bayesian approach was used to optimize/calibrate the parameters of the PBPK model for chloroform.

Figure 2.

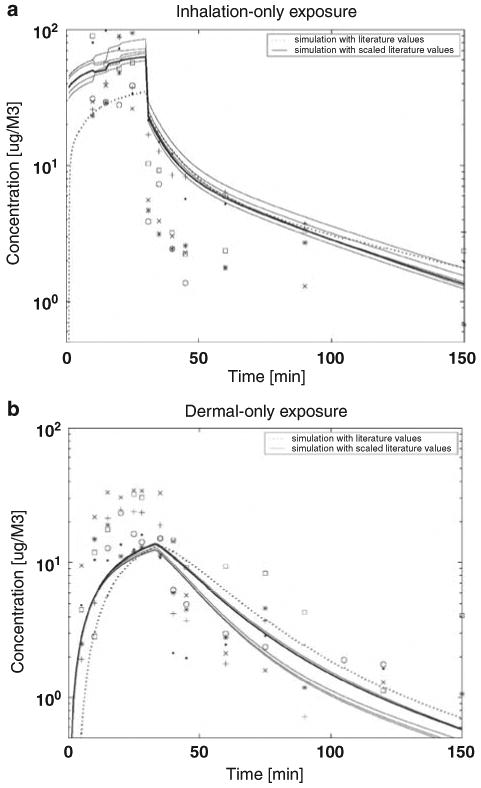
Comparison of model simulations of chloroform time series data in exhaled breath for (a) inhalation-only (top panel) and (b) dermal-only (bottom panel) exposure using two input parameter vectors; default literature point estimates (dash line) and default values with age-gender scaling functions as inputs (solid line).

Uncertainty/Variability Characterized Using a Bayesian Approach

A three-level hierarchical Bayesian approach (Figure 3) used for our analyses assumed that the general population varied with respect to the PBPK model parameters. Specific distributional families were assumed to describe the variability, but the specific values of the population-level parameters for those distributional families were considered uncertain. This approach is hierarchical in the sense that the uncertain population-level parameters are at the top level; they define the variability of the lower-level individual parameter values, which in turn predict the exhaled concentrations in each individual as a function of chloroform exposure level.

Figure 3.

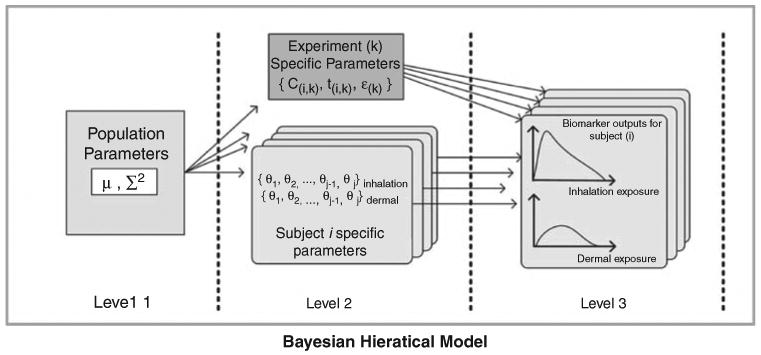
Three-level hierarchical population model for MCMC analysis.

(I) Definition of Prior Distributions (Level 1)

In our analyses, the interindividual variability for any given model parameter was described by a log-normal distribution with the population mean μ₁ and the variance ${\sum }_1^2$. The prior distribution of μ₁ is modeled by drawing μ₁ from a log-normal distribution with mean M₁ and variance ${\mathit{\text{S}}}_1^2$. The values of M₁ are usually obtained from the literature review or measurement, where the value of ${\mathit{\text{S}}}_1^2$ reflects the uncertainty of M₁. For example, for an average adult, the reported values of blood flow to tissue compartments are in agreement (ICRP, 2002; Price et al., 2003); however, a wide range of values of permeability of chloroform are reported, from both in vitro and in vivo studies (Nakai et al., 1999). Therefore, the prior uncertainty of the values of blood flow to tissue (μ_BFs) is assumed smaller than the permeability of chloroform (μ_perm). Thus, S_BFi is smaller than S_perm to reflect the uncertainty of the population means. The population variance ${\sum }_1^2$ is modeled by an inverse gamma distribution with 1 degree of freedom and centered at ${\mathit{\delta }}_0^2$, which is assumed to reflect the variability of reported parameter values.

It is somewhat difficult to gauge the likely uncertainty associated with a specific parameter, as most data were reported as point values. For well-studied parameters in the literature, the uncertainty was determined based on the values reported. For example, the smallest uncertainty value, 1.3, which represents 30% coefficient of variation (CV), was assigned to PCs and blood flow rates in the inhalation scenario. Larger values of uncertainty were assigned to blood flow rates in the dermal (hot-water bathing) scenario than in the inhalation scenario. For parameters that have been reported to vary widely, larger uncertainty values were used. For example, an uncertainty factor of 5 was assigned to permeability and the V_max/K_m (clearance) ratio, because the experimental data on the former varies over a wide range, and there is high uncertainty involved in cross-species and in vitro/in vivo extrapolation of the latter. The highest values were assigned to these parameters that are considered the most uncertain (Bois, 2000b). Specifically, an uncertainty factor of 10 was assigned to A (kidney/liver metabolism proportion) and to the thickness of the stratum corneum (the effective length of the diffusion path) to reflect the scarcity of relevant information. The values of M₁, ${\mathit{\text{S}}}_1^2$ and ${\mathit{\delta }}_0^2$ are summarized in Table 3. In general, the prior uncertainty and variability are comparable or larger than the reported values in the literature.

Table 3.

Prior and posterior distributions of population chloroform PBPK model parameters selected for the Bayesian MCMC studies.

Parameter	Unit	Prior distribution			Posterior distribution
		Population mean			Population mean
		Population geometric mean (M)	Uncertainty geometric SD (S)	Interindividual variability (Σ) geometric SD	Population geometric mean (M)	Uncertainty geometric SD (S)	Interindividual variability (Σ) geometric SD
Perm	cm/min	0.00083	5	5	0.0011	1.34	1.26
Lsc	[μM]	25	10	2	20.5	1.18	1.15
CL	(L/min-kg 0.7)	0.584	5	5	1.81	2.37	1.27
A	—	0.033	10	5	0.015	1.75	1.27
PBA	—	7.43	1.5	1.5	10.85	1.16	1.14
PSW	—	1.94	1.5	1.5	1.96	1.25	1.17
PC_Fat	—	37	1.5	1.5	26.43	1.47	1.2
PC_SP	—	1.62	1.3	1.3	1.96	1.13	1.09
PC_RP	—	2.3	1.3	1.3	2.22	1.17	1.11
PC_liver	—	2.3	1.3	1.3	2.33	1.14	1.11
PC_kidney	—	1.5	1.3	1.3	1.48	1.14	1.1
BF_Fat_inha	% of CO	0.05	1.5	1.5	0.093	1.34	1.16
BF_inha_SP	% of CO	0.156	1.3	1.2	0.178	1.14	1.11
BF_inha_RP	% of CO	0.26	1.3	1.2	0.223	1.12	1.11
BF_inha_liver	% of CO	0.25	1.3	1.2	0.254	1.14	1.09
BF_inha_kidney	% of CO	0.25	1.3	1.2	0.205	1.14	1.1
BF_inha_skin	% of CO	0.034	1.3	1.2	0.045	1.14	1.1
BF_Fat_dermal	% of CO	0.05	2	1.5	0.077	2.01	1.21
BF_dermal_SP	% of CO	0.156	1.5	1.3	0.14	1.25	1.13
BF_dermal_RP	% of CO	0.26	1.5	1.3	0.227	1.35	1.1
BF_dermal_liver	% of CO	0.25	1.5	1.3	0.221	1.26	1.21
BF_dermal_kidney	% of CO	0.25	1.5	1.3	0.254	1.37	1.13
BF_dermal_skin	% of CO	0.034	2	1.3	0.089	1.5	1.17
MET_inha	—	1.6	1.5	1.5	1.42	1.15	1.12
MET_dermal	—	1.6	1.5	1.5	1.55	1.14	1.12

Note: Prior distributions are log-normal truncated at ± 3 SD. Blood flow rates are constrained to sum of cardiac output.

This table lists the model parameters that were optimized using the Bayesian approach. Included are the prior estimates of mean and variance, along with optimized (posterior) results.

Abbreviations: L_sc, stratum corneum thickness [μm]; CL, clearance = V_maxC/K_m; A, scaling factor for kidney V_max; PBA, partition coefficient (PC) blood:air; PSW, PC skin:water; PC SP, partition coefficient between slowly perfused tissues and blood; PC RP, partition coefficient between rapidly perfused tissues and blood; BF, blood flow rate as percentage of cardiac output (CO); MET, metabolic equivalent task.

(II) Interindividual variability (Level 2)

At the individual level, the PBPK parameters were updated for each subject, based on the subject-specific demographic information and the exposure data. Tissue volume, ventilation rates, and cardiac output were calculated using the scaling functions. The tissue blood flow rates, as the percentage of cardiac output, were constrained to sum to 1. This was done by first simultaneously sampling the fractional blood flow for all tissues from assigned distributions, and then dividing the fractional blood flow for each tissue by the sum of all the fractional blood flows. To reduce the correlations between V_max and K_m in the liver, the clearance (CL) was updated in the Bayesian model. CL is calculated as oxidative capacity (V_maxC) divided by affinity (K_m) (Marino et al., 2006). The optimized CL was adjusted based on the subject's body weight and used in the PBPK model. The prior population mean of CL was distributed log-normally with a geometric mean equal to 0.584 [/min/l/Kg0.7] derived from Roy et al. (1996).

Other parameters, such as PCs, were random samples from the corresponding population distributions listed in Table 3. To evaluate the intra-individual variability and population variability under different exposure scenarios, two sets of BFs and METs were used. Prior population means (M₁) of both sets of BFs and METs were the same, whereas a larger uncertainty $({\mathit{\text{S}}}_1^2)$ was assigned during the hot-bath scenario. The likelihood of obtaining the observations (data) was calculated separately using either the inhalation-only or dermal-only data. For other parameters, one set of prior distributions was assigned for the parameters and data likelihood was updated using both inhalation-only and dermal-only data. Equal weight was given to both experiments in the data likelihood calculation, as the number of data points was similar in both exposure studies.

(III) Likelihood calculation (Level 3)

Level 3 links the individual parameters to the measured data through a residual error model. Differences between the observed and the predicted exhaled breath concentrations are assumed to be log-normally distributed. The individual parameter vector is used to simulate the time-series exhaled chloroform concentrations using experimental conditions appropriate for each individual, and the value of the data likelihood is then calculated. The measurements are assumed to be normally distributed around the simulated data (in log-scale) (Bortot et al., 2002). Two separate residue errors ( ${\mathit{\sigma }}_{\mathcal{\text{I}}}^2$ and ${\sigma }_D^2$) are used as the inhalation and dermal exposure experiments followed different protocols. Non-informative priors are used for ${\mathit{\sigma }}_{\mathcal{\text{I}}}^2$ and ${\sigma }_D^2$ (Bois et al., 1999). These two residual errors incorporate both experiment and modeling errors.

Markov chain Monte Carlo (MCMC) computation is used to sample from the distributions of model parameters. For population parameters (the first level of the hierarchical model), Gibbs sampling is used to randomly draw samples from the distributions. For individual parameters, the Metropolis–Hasting algorithm is used to sample from the distributions, as seen in the work of Bois (2000b) and Marino et al. (2006). Five MCMC chains are used. For population mean and individual parameters, the initial values for the five chains were the prior population mean, prior population mean ± one prior standard deviation, and prior population mean ± two prior standard deviations, respectively. For population variance, the initial values for the five chains were set to the prior population variance. The program was written in Matlab (The Mathworks Inc, 2008).

Results

Once the MCMC chains converge to a stationary distribution, the “converged” parts of the chains provide a random sampling from the posterior distributions. The first 3000 iterations of the five MCMC chains were taken as “burn-in,” and the results of these iterations were discarded to ensure the chain was well mixed. The methods of Brooks and Gelman (1998) were used to diagnose the convergence of MCMC chains. Corrected Scale Reduction Factors (R) were calculated for the five chains, using every fifth sample from the last 15,000 iterations. The MCMC chains are considered converged when the estimates of CSRF are close to 1; a value of 1.2 is a rule of thumb often used as a cut-point for determining convergence. The values of R for most parameters are below 1.1, and the largest is 1.23. After the chains converged, one chain was randomly chosen and continued for 50,000 iterations, which were used to define the population and individual posterior distributions.

Comparison of Model Simulation with Biomarker Data

The observed data were compared with the corresponding model predictions for the inhalation and dermal exposure scenarios with three sets of PBPK model parameters (Figure 4). The three sets of model input parameters (see subsection entitled “Uncertainty/variability characterized through scaled functions”) were (1) literature values (as prior mean values listed in Table 3, (2) geometric means of posterior population parameters (as the posterior mean values in Table 3), and (3) parameter vectors drawn from individual posterior distributions. On the basis of the data likelihood calculation, the individual input vectors provide the best estimation, and the means of posterior population parameters are usually better at representing the data than the default-scaled parameters for individuals.

Figure 4.

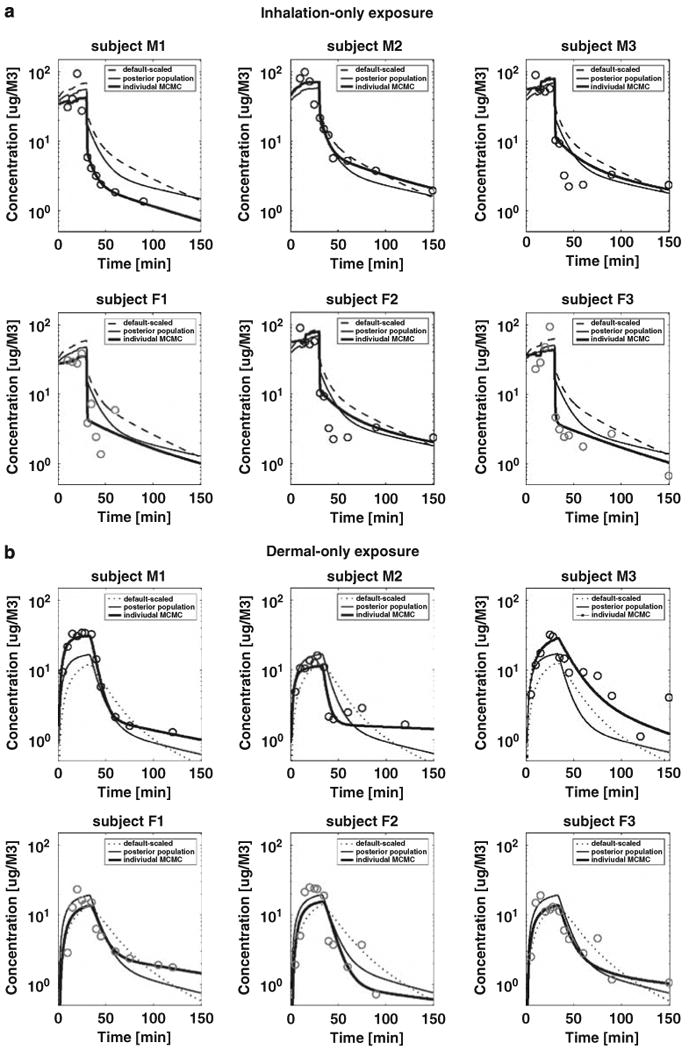
Comparison of PBPK model for chloroform simulations to time series profiles of chloroform in exhaled breath during 30-min (a) inhalation-only (top panel) and (b) dermal-only (bottom panel) exposures for six subjects. Three sets of input parameters are used (1) default-scaled literature values (default scaled), (2) mean of posterior population parameters from MCMC results (posterior population), and (3) individual input vector drawn from individual MCMC results (individual MCMC).

In general, the predictions for both the inhalation-only and the dermal-only scenarios agreed reasonably well with the experimental data. For the inhalation scenario, the predicted exhaled concentrations for subject F1 were consistently higher than the observed data. In the dermal scenario, the predictions for subject F2 were consistently lower than the observed data. Another area of disagreement resulted from random experimental measurement errors. For example, in the inhalation-only scenario, the highest observed exhaled concentrations appeared at 10 min (subject M3) or 20 min (subject F2) after exposure began, whereas the peaks should appear at the end of the 30-min exposure duration. Assuming that the population distribution of exhaled concentrations can be estimated from the results of the six subjects, all the data fall within the range that is defined by the mean ± three standard deviations. Therefore, no data points were eliminated during the simulation in this study. By using the Bayesian statistical approach, both prior information and data likelihood were considered, and the deviation from the questionable data points is quantitatively captured in the posterior distributions of the error terms.

Posterior Parameter Distributions

The posterior distributions of population geometric mean (M), geometric standard deviation (S), and population variance (Σ) are shown in Table 3. The geometric mean represents the parameter value for an average person (Bois, 2000b), and the geometric standard deviation (S) represents the uncertainty of M. The population variance (Σ) represents the population variability, which is captured by the assumption that parameter values are not the same in every individual in the population of interest. During the MCMC analysis, the uncertainty of population mean (S), and the variability of the population mean (Σ) were updated separately. Therefore, a distinction can be made between uncertainty and variability. Uncertainty is reflected in the fact that perfect information exists about what those distributions are. In this study, the uncertainty and variability of the population PBPK model parameters were all reduced from their prior distributions (Figure 5). This result indicates the reduction in uncertainty associated with the values of those population-level parameters, accomplished with the Bayesian updating.

Figure 5.

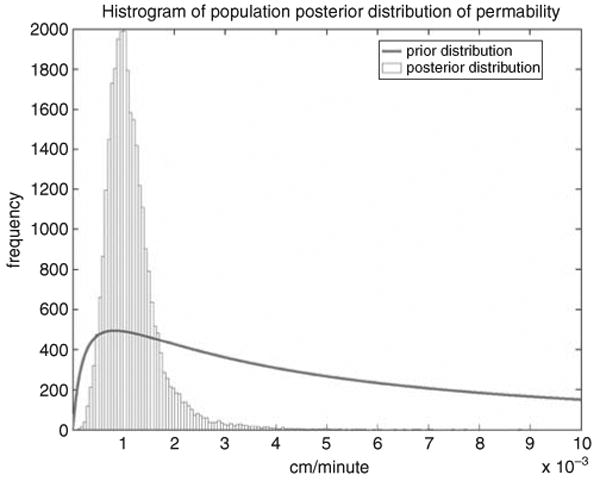
Demonstration of the reduction in uncertainty associated with the population-level permeability distribution. The posterior distribution of the permeability is much tighter than the corresponding prior.

The geometric means (posterior point estimates) of several population PCs are close to their prior estimates; this is not true for fat. The PCs for fat shifts from 37.7 to 27.8; this 30% decrease may be due to the joint uncertainty of the scaled fat volume (compared with default 23.1% of body mass) and the fat/blood PC. However, for some parameters, the posterior point estimates differ 50% or more from their prior estimates. For example, the permeability shifts from 0.00833 to 0.013 cm/min, and the clearance (CL) shifts from 0.58 to 2.16, an almost four-fold increase. For the average stratum corneum thickness (the effective length of the diffusion path), a factor of 10 for prior population uncertainty is used, which allows the “data to speak” (Bois, 2000a,b). The posterior point estimate is 20 μm, whereas the below-neck range of thickness is 10 to 40 μm (Roy et al., 1996). The kidney/liver metabolism proportional constant A has a posterior point estimate of 0.015, approximately half of the value derived from Corley's experiments (Corley et al., 1990).

Tissue blood flow rates as the percentage of cardiac output were updated separately for inhalation and dermal exposures. For the inhalation and dermal scenario, the posterior means of the tissue blood flow rates at the population level are close to their prior estimates (defined by ±20% from the prior data), except for fat and skin (Table 3). The posterior means of the tissue blood flow rates for inhalation exposure are close to those for dermal exposure, except for the skin, which is half of the value for the dermal scenario. The posterior means of the tissue blood flow rates at the individual level are usually similar under the two exposure scenarios (defined by ± 20% from the inhalation results), except for kidney and skin (Table 4).

Table 4.

Comparison of the individuals' posterior distributions for model parameters with different exposure scenarios.

		Sub M1	Sub M2	Sub M3	Sub F1	Sub F2	Sub F3
BF Fat	(I)	(0.09, 1.40)	(0.08, 1.42)	(0.09, 1.40)	(0.09, 1.40)	(0.09, 1.43)	(0.10, 1.40)
	(D)	(0.08, 1.79)	(0.10, 1.87)	(0.07, 1.79)	(0.09, 1.85)	(0.08, 1.78)	(0.08, 1.81)
BFSP	(I)	(0.14, 1.23)	(0.17, 1.23)	(0.17, 1.23)	(0.16, 1.23)	(0.20, 1.21)	(0.16, 1.23)
	(D)	(0.12, 1.32)	(0.16, 1.33)	(0.15, 1.39)	(0.18, 1.33)	(0.12, 1.32)	(0.16, 1.30)
BFRP	(I)	(0.18, 1.22)	(0.23, 1.21)	(0.2, 1.20)	(0.19, 1.21)	(0.22, 1.20)	(0.19, 1.22)
	(D)	(0.25, 1.37)	(0.22, 1.37)	(0.22, 1.34)	(0.24, 1.36)	(0.24, 1.36)	(0.22, 1.34)
BF liver	(I)	(0.27, 1.27)	(0.22, 1.24)	(0.24, 1.23)	(0.26, 1.24)	(0.21, 1.22)	(0.28, 1.22)
	(D)	(0.24, 1.34)	(0.22, 1.33)	(0.2, 1.30)	(0.22, 1.36)	(0.24, 1.32)	(0.19, 1.28)
BFkidney	(I)	(0.19, 1.22)	(0.21, 1.22)	(0.2, 1.21)	(0.2, 1.21)	(0.20, 1.21)	(0.20, 1.22)
	(D)	(0.28, 1.39)	(0.26, 1.40)	(0.25, 1.35)	(0.28, 1.41)	(0.26, 1.37)	(0.25, 1.36)
BF skin	(I)	(0.04, 1.25)	(0.05, 1.25)	(0.05, 1.24)	(0.04, 1.24)	(0.05, 1.24)	(0.04, 1.25)
	(D)	(0.10, 1.49)	(0.11, 1.47)	(0.07, 1.52)	(0.09, 1.52)	(0.10, 1.48)	(0.09, 1.48)
MET	(I)	(1.47, 1.31)	(1.64, 1.29)	(1.39, 1.29)	(1.38, 1.32)	(1.50, 1.29)	(1.38, 1.33)
	(D)	(1.55, 1.27)	(1.96, 1.27)	(1.31, 1.28)	(1.62, 1.29)	(1.78, 1.26)	(1.53, 1.27)

Abbreviations: BF tissue, percentage of cardiac output to tissues; I, inhalation exposure scenario; D, dermal exposure scenario.

For the MET value, the posterior point estimates are within 10% of the prior estimates for both scenarios, with the posterior MET for the dermal scenario being slightly higher than the inhalation scenario. Pairwise linear correlations between estimated parameters of the PBPK model for chloroform were calculated from the population posterior distributions. The highest correlation is 0.53 (between percentages of cardiac output to liver and fat). During model development, many of the known possible correlations among the PBPK parameters have been considered. These include those between inhalation rate and cardiac output, percentages of cardiac output, and V_max/K_m ratio. Tissue blood flow rates were adjusted proportionally to ensure that the total flows were summed to cardiac output. Cardiac output and inhalation rate were estimated using MET-correlated scaling functions. The clearance was directly optimized instead of optimizing V_max and K_m separately. The correlation found will be considered for future applications, such as developing a regression equation between parameters that are correlated. Without properly delineating these correlations; however, model simulation will produce incorrect predictions as these parameters should not be sampled independently.

Discussion

In this study, a Bayesian method was applied to optimize certain population PBPK parameters as the use of scaled physiological parameter alone is not enough to account for the interindividual variability observed in the data (see subsection “Uncertainty/variability characterized through scaled functions”). Scaling functions were used to describe the population variability of physiological parameters, to account for the known correlations in the estimation of physiological parameters, and to reduce the number of parameters that needed to be optimized. For parameters independent of the exposure scenario, biomarker data from both inhalation and dermal experiments were joined to expand the data size for optimization. For parameters dependent on the exposure scenario, the optimization process was performed within the same framework (hierarchical Bayesian model and PBPK model) for mechanistic consistency.

The results of the influence of hot-water bath effects on physiological parameters on both population and individual levels are shown in Tables 3 and 4. Increases in the geometric means of the percentage of cardiac output (%CO) to the skin compartments at both the population and individual levels were estimated. It is known that human skin blood flow rates increase under elevated environmental temperatures (Song et al., 1990; Charkoudian, 2003). Although animal studies show reduced renal blood flow rates because of heat stress (Kanter, 1960; Kenney and Musch, 2004), the results of this study show a slight increase of renal blood rates flow in humans at a moderately higher water temperature (38°C). In addition to the blood flow rates, MET is the only other model parameter that provides information on physiological changes due to hot-water bathing for the same individuals. At the population level (Table 3), it is observed that the dermal MET is slightly higher than the inhalation MET. At the individual level (Table 4), the same pattern is observed with the exception of subject M3, who had the lowest dermal MET. One possible reason for this is the interindividual variability on the baseline values of VO₂ and AVO_diff. In addition, as the two experiments were conducted on two different days, the baseline value of each subject may vary from the showering occasion to the bathing occasion. Therefore, at the individual level, the comparison is highly baseline dependent. As there is no repeated biomarker measurement at specific time points and all the data points were included in the optimization process, it should be noted that the posterior distribution will likely be impacted by the data uncertainty. Furthermore, owing to the limitations of the sample size, the observation of the population parameters may not prove conclusive, and further investigation may be needed to reduce the data uncertainty. Table 5 summarizes the change of cardiovascular responses resulting from the whole-body bathing in different water temperatures for human subjects. However, these studies provide limited information on the effects of hot-water bathing on the blood flow rates in the whole body scale.

Table 5.

Literature review of cardiovascular responses to hot-water bathing.

Parameters	Literature review	Mean of posterior distributions
BF fat	NA	↑
BF slowly perfused	NA	↓
BF rapidly perfused	NA	Similar
BF liver	↓ (4)	↓
BF kidney	NA	↑
BF skin	↑ (4)(5)	↑
MET	NA	↑
Hear rate	↑ (1)(5)	NA
Blood pressure	↓ (2)(4)	NA
Oxygen consumption	↑	NA
Ventilation rate	Same (3)(5)	NA
Cardiac output	↑ (2)(3)	Ventilation rate and cardiac outputs were calculated with scaling functions Increased METs value will result in the increase of both ventilation rates and cardiac outputs

Abbreviations: BF tissue, blood flow rate as the percentage of cardiac output; NA, data not available.

References: (1) Allison and Reger, 1998; (2) Allison et al., 1998; (3) Boone et al., 1999; (4) Koda et al., 1995; (5) Miwa et al., 1994.

Earlier studies show that dermal absorption during bathing is strongly influenced by water temperature. Breath measurements from Gordon et al. (1998) showed that subjects bathing in hot water (38–41°C) exhaled approximately 30 times more chloroform than they did when bathing in cold water (28–32°C). Corley et al. (2000) used PBPK modeling to study the temperature effect on dermal-only absorption of chloroform based on data from Gordon et al. (1998). This study found that blood flow to the skin and the effective skin permeability coefficient (Kp) both had temperature dependence. Kp was determined to be 0.001 cm/min for exposure at 40°C, when CO to the skin was held at 18% (Corley et al., 2000). The results of this study show that there is 9% CO to the skin in the dermal-only exposure scenario, which is twice than that of the inhalation-only scenario, but that the CO is below the 18% used by Corley et al. These results are estimates that were averaged over the entire time course: 150 min total time (30 min exposure/immersion time, plus 120 min post-exposure time). Therefore, the current results reflect the “trends” of physiological changes in hot-water bathing, specially the larger increase of the blood flow rate to the skin. Future studies using time-dependent and temperature-dependent PBPK modeling parameters could provide more detailed information regarding physiological changes.

A wide range of values of permeability (Kp) of chloroform has been used in PBPK modeling to evaluate dermal absorption of chloroform during showing (Roy et al., 1996; Corley et al., 2000; Levesque et al., 2000; Xu et al., 2002; Haddad et al., 2006). Thus, the uncertainty of the population mean is set at 5, whereas the mean is set as 0.0008 cm/min. The posterior mean for Kp in this study was 0.0011 cm/min. This value is less than half of the values reported in Levesque et al. (2000) and Xu et al. (2002), but it is in agreement with the 0.0005–0.001 cm/min estimated by Corley et al. (2000) and 0.0002–0.0015 cm/min by Xu and Weisel (2005a). The posterior variability and uncertainty are both significantly reduced from the priors.

The regional stratum corneum thickness has been reported to range from 10.5 μm on the back to 600 μm on the sole, and the thickness of the stratum corneum recommended for the whole body is 10–40 μm (USEPA, 1992, 1997). The population variability of stratum corneum thickness was set at 2, and the uncertainty of population mean was set at 10. These values reflect the varying layers of thickness of stratum corneum over the whole body. The posterior point estimate of the population mean of L_sc is 20.5 μm, which is at the low end of USEPA recommended values. The posterior variability and uncertainty are both 1.15, which is significantly reduced by the priors from the Bayesian optimization.

In this study, scaling functions were used for describing the interindividual difference in physiological parameters. A similar approach has been applied to earlier MCMC analysis such as Jonsson and Johanson (2001). This approach can reduce the number of MCMC parameters while reflecting the average tissue values for different sub-population based on age, gender, and BW. Alternatively, other body size measurement such as body mass index (BMI) or body surface area (BSA) could be used. However, BW is commonly used in allometric scaling and more readily available in various datasets than BMI and BSA. The utility of the model with BW as covariate may be greater in the future. BW, BSA, and BMI are usually highly correlated with each other. For VOCs (such as chloroform), the concentration equilibrium between blood and tissues is assumed to be reached instantaneously, and the product of the tissue volume and the corresponding PC can be thought of as the effective distribution volume for the tissue compartment. As the tissue PCs were included as MCMC parameters, the uncertainty related to the scaling functions on the estimation of tissue volumes can impact the estimation of the PC. Most posterior mean estimates of the PCs are very close to the priors with the exception of the estimate for the fat, which is considerably lower than the corresponding prior. The difference may be because the size of the fat compartment in the original model is smaller than those predicted by the scaling function in this study, or because the fat tissue is heterogeneously perfused, or because the fat compartment in the model may correspond to the well-perfused portion of the fat tissues (Jonsson et al., 2001).

A three-fold difference of posterior point estimates between the highest and the lowest individual CL ratios for liver has been observed. This variation may be a result of population variation in hepatic concentrations of CYP2E1 (Raucy, 1995), or may reflect the fact that P450 CYP2E1 is polymorphic in humans, and the different genotypes may cause interindividual differences in enzyme expression (Bogaards et al., 1993) and in the toxicity of its substrates (Bolt et al., 2003). Population variations in CYP2E1 enzyme expression also vary due to physical/hormonal status, alcohol consumption, drug interferences, and ethnic differences (Bolt et al., 2003). Ethnic differences were found in CYP2E1 enzyme expression because of genetic factors between European and Japanese populations (Kim et al., 1996).

Metabolic activity of chloroform in kidney microsomes was not detectable in humans (Corley et al., 1990). However, enzyme activities in the kidney were observed in hamsters, mice, and rats. For each of these species, Corley et al. calculated a proportional parameter A that relates the metabolic activity in the kidney to the activity in the liver. For humans, the value of A was estimated to be 0.033 by assuming that the metabolic activity was at the detection limit. As kidney metabolism was included in the original chloroform PBPK model for the human (Corley et al., 1990), and the sensitivity analysis showed that model outputs were sensitive to the kidney metabolism (see the Materials and methods section), kidney metabolism was included in the MCMC analysis. The value of A, 0.033, was used as the prior population mean in the hierarchical model. The corresponding population variability was set at 5 and the uncertainty of population mean was set at 10. These values reflect the lack of precise prior information of chloroform metabolism in the human kidney. With a large prior variability and uncertainty, the optimization is primarily driven by data likelihood. The posterior point estimate of the population mean of A is 0.015, about half of the value derived from the experiments by Corley et al. (1990). The posterior variability and the uncertainty are significantly reduced from the priors in the Bayesian optimization. This result suggests that there is some information from the exhalation data to update the prior assumptions of the chloroform metabolism in the human kidney. It should be noted that it is difficult to discriminate between both types of clearance (liver and kidney) when using exhaled air alone. Therefore, it would be ideal to validate the model, in addition to exhaled breath, with urine (if validated urinary biomarker available for chloroform exposure) and plasma data to have full confidence in the prediction of kidney clearance. For other VOCs such as PERC (Clewell et al., 2005), it was possible to identify the kidney clearance because there were data on the time-course data of a metabolite (TCA) in the urine. But for chloroform, there is no metabolite excretion and it is not possible to distinguish between the kidney and the liver contributions to metabolism using only blood and exhaled breath data on the parent compound. Nevertheless, this result demonstrates that PBPK modeling in combination with Bayesian optimization can be used to test toxicological assumptions when data are available.

To demonstrate the application of a probability approach in toxicological assessment, results from the posterior distributions from this calibrated model were used to predict the averaged rate of amount of chloroform metabolized per liver (ng/g/h). The distributions of the rate of metabolism were computed with 500 vectors drawn from every 10th vector of the final 5000 MCMC runs. The overlapped distributions among the individuals indicate that the interindividual variability of the metabolism rate is not overly large. The median individual rate of metabolism was compared with those calculated by the default-scaled literature parameters (see Figure 6). These figures provide a comparative measure of the rate of metabolism in the liver from different model inputs. The differences between median individual rate of metabolism and those calculated from literature parameters were similar for inhalation-only scenario and larger for dermal-only scenario. This indicates the importance of considering scenario-specific parameters to derive the target tissue dose with PBPK modeling. For inhalation and dermal exposure, the alveolar exhaled breath and blood concentration are good surrogates for target tissue dose (R² over 0.9). However, it is important to realize that relationship of the chemical blood concentration to rate of metabolism is very different for ingestion pathway, in which all of the portal blood flow from GI tract is subject to pre-systemic liver clearance (Clewell et al., 2008). Clewell et al. (2008) show that the pairwise correlation between the blood concentration and the rate of metabolism was only 0.48 when the ingestion pathway were considered for a multiroute household chloroform exposure scenario.

Figure 6.

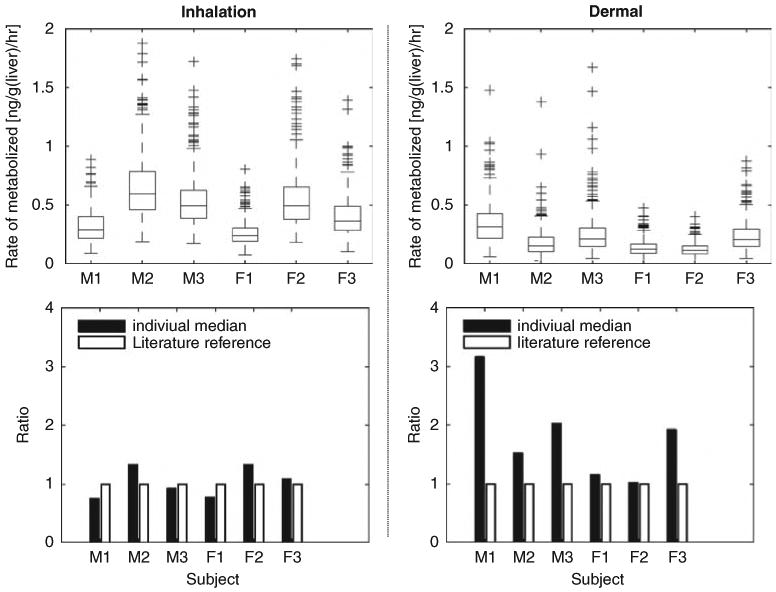
Right column present the predictions of the hepatic rate of metabolism for inhalation scenario; and results for dermal scenario are on the left column. For each scenario, the upper figure presents the boxplots of average rate of chloroform metabolized in liver (ng/g/h) for 24 h. The box has lines at the lower quartile, median, and upper quartile values. The whiskers are lines extending from each end of the box to show the extent of the rest of the data. Lower figure compares the location of the 50th percentile (50%) (as shown in the upper figure) to those calculated using default literature reference values.

Conclusions

In this study, a Bayesian method was applied to estimate scenario-dependent (i.e. cardiac output) and scenario-independent (i.e., tissue PCs) parameters using biomarker data from different exposure studies. Twenty-five model parameters were optimized using a Bayesian hierarchical modeling approach. The uncertainty in the parameters was significantly reduced in the posterior distributions for most model parameters. The agreement between model prediction and observed data were improved significantly when the parameters from the Bayesian MCMC results were used, compared with the simulation that used the default literature values and the default-scaled literature values that included additional scaling parameters based on age, gender, and body mass. The results from the MCMC analysis showed that tissue blood flow rates varied in the two exposure scenarios. Two-fold increases in skin blood flow rates during the hot-water bath exposure were observed at both population and individual levels. Thus, the Bayesian approach provides a good model “calibration” tool, when it considers information from different studies and experiments. The results of the MCMC analysis yield information about the variability of model parameters under the hot-water scenario, and can improve further PBPK modeling applications to assess risk associate with the human exposure to DBPs because of showering and bathing behavior.

Appendix A

The rate of change of the amount of chemical uptake in viable skin compartment in the DP skin model is described as:

$$\frac{dA\mathit{\text{m}}{t}_{\text{vs}}}{\text{dt}}=Q_{\text{sk}}(C_{\text{art}}-\frac{C_{\text{vs}}}{P_{\text{vs}}})+J(L_{\text{sc}},t)\times SA$$

The mass flux at interface between stratum corneum and viable skin is calculated as:

$$J_{\text{sc},n+1}=-D_{\text{sc}}\left(\frac{C_{\text{sc},n+1}-C_{\text{sc},n}}{L_{\text{sc}}/(n+1)}\right)$$

The rate of change of the concentration in Nth layer of stratum corneum is calculated using the central difference formula:

$$\frac{d{C}_{\text{sc},n}}{\text{dt}}=\frac{D_{\text{sc}}}{{(L_{\text{sc}}/n+1)}^2}\times (C_{\text{sc},n+1}-2C_{\text{sc},n}+C_{\text{sc},n-1})$$

And, the stratum corneum diffusivity can be calculated as:

$$D_{\text{sc}}=\frac{\mathit{\text{Perm}}\times L_{\text{sc}}}{P_{\text{sc},\text{water}}}$$

D_sc = effective stratum corneum diffusivity [cm²/min]

Perm = stratum corneum permeability [cm/min]

L_sc = stratum corneum thickness [cm]

P_sc,water = partition coefficient between stratum corneum and water [unitless]

C_sc,n = chemical concentration in the nth layer of stratum corneum

N = number of layer defined in the stratum corneum

J_sc = dermal mass flux

Appendix B

The sensitivity coefficient were calculated as follows: Sensitivity coefficient (Clewell et al., 2003):

$$[(A-B)/B]/[(C-D)/D]$$

where

A is the exhaled conc with 1% increased parameter value,

B is the exhaled conc at the starting parameter value,

C is the parameter value after 1% increase, and

D is the original parameter value.

Appendix C

Age, gender, and bodyweight-dependent scaling functions for selected PBPK model parameters.

Equations used to calculate the cardiac output (Q_cardiac) and inhalation rate (Q_Pulmonary)

$$Q_{\text{cardiac}}=\frac{V{O}_2}{AV{O}_{\text{diff}}}$$

$$V{O}_2=ME\mathit{\text{T}}\times BM\times F$$

where

VO₂ = oxygen consumption (ml/kg/min)

AVO_diff = difference in volume of oxygen between arterial and venous blood (40–60 ml/l for adult, a uniform distribution between 40 and 60 was used in the model)

MET = metabolic equivalent of tasks (unitless)

BM = body mass, assumed to be same as body weight (BW)

F = conversion factor (3.5) from oxygen consumption to MET (ml/kg/min/MET)

$$Q_{\text{Pulmonary}}=BM\mathit{\text{R}}\ast ME\mathit{\text{T}}\ast H\ast VQ$$

where BMR = basal metabolic rate (e.g., 1.16 MJ/day for 30 year old, 70 kg male)

H = oxygen update factor, the volume of oxygen consumed in the production of 1 MJ energy expended (e.g., 0.21 m³/MJ for 30 year old, 70 kg male)

VQ = ventilatory equivalent (unitless), the ratio of minute volume to oxygen uptake (i.e., 27.5 for 30 year old, 70 kg male)

Scaling functions used to calculate tissue volumes

Body surface area (SA) [cm²]

Male, age .ge. 18: SA = 252 × BW

Female, age .ge. 14: SA = 288 × (1−0.00201 × (age–14) × BW

Fat tissue mass (assume the fat density = 0.93)

Male, age .ge. 18: Volume_fat = (0.21 + 0.000307 × (age–18)) × BW²/100/0.93

Female, age .ge. 14: Volume_fat = 0.003732 × (1 + 0.0055 × (age–14) × BW²)/0.93

Other tissues (assume the density = 1)

Skin tissue mass

Male, age .ge. 15: Volume_skin = 0.0367 × BW

Female, age .ge. 15: Volume_skin = 0.044 × BW

Kidney: Volume_kidney = 8.38 × BW^0.85 × 0.001

Liver: Volume_liver = 92 × BW^0.7 × 0.001

Rapidly perfused: ${\mathit{\text{Volume}}}_{\text{RP}}=(0.1-\frac{{\mathit{\text{Volume}}}_{\text{kidney}}+{\mathit{\text{Volume}}}_{\text{liver}}}{BW})\times BW$

Slowly perfused: ${\mathit{\text{Volume}}}_{\text{SP}}=(0.82-\frac{{\mathit{\text{Volume}}}_{\text{fat}}+{\mathit{\text{Volume}}}_{\text{skin}}}{BW})\times BW$