Abstract
Living organisms perform and control complex behaviours by using webs of chemical reactions organized in precise networks. This powerful system concept, which is at the very core of biology, has recently become a new foundation for bioengineering. Remarkably, however, it is still extremely difficult to rationally create such network architectures in artificial, non-living and well-controlled settings. We introduce here a method for such a purpose, on the basis of standard DNA biochemistry. This approach is demonstrated by assembling de novo an efficient chemical oscillator: we encode the wiring of the corresponding network in the sequence of small DNA templates and obtain the predicted dynamics. Our results show that the rational cascading of standard elements opens the possibility to implement complex behaviours in vitro. Because of the simple and well-controlled environment, the corresponding chemical network is easily amenable to quantitative mathematical analysis. These synthetic systems may thus accelerate our understanding of the underlying principles of biological dynamic modules.
Keywords: design principle, feedback loop, in vitro, oscillation, reaction networks
Introduction
Recent advances in the study of the dynamics of living systems have highlighted the role of reaction networks (RNs; Barabási and Oltvai, 2004). These architectures, in their various genetic, metabolic or signalling implementations, encode many decision-making processes, and thus control cell behaviour (Hartwell et al, 1999).
The study of biological networks usually focuses on the relation between the global dynamics of the RN and its topology (the way the reactions involved are connected to each other; Milo et al, 2002; Novák and Tyson, 2008), with less emphasis on the chemical processes themselves (Bailey, 2001). Synthetic biologists have used these topological inferences to reorganize biological elements into artificial in vivo circuits, successfully obtaining the desired dynamic functions: for instance, introducing three repressor genes arranged with their corresponding promoter in a triangular negative-feedback loop in Escherichia coli resulted in oscillations in gene expression (Elowitz and Leibler, 2000); in another study, the presence of a positive-feedback loop was shown to increase the robustness of the oscillatory behaviour (Stricker et al, 2008). However successful and promising these attempts have been, the ability to target and predict the overall dynamic behaviour is strongly impaired (Purnick and Weiss, 2009) by the difficulty of precisely characterizing the kinetics and thermodynamics of the reactions occurring inside a cell (Rosenfeld et al, 2005; Koide et al, 2009).
In vitro systems provide a way towards the rational building of RNs in a chemically simpler and more controlled context. At present, however, our ability to assemble rationally test-tube RNs lags far behind that for in vivo systems. Serious challenges remain, including the cascadability of the various modules (Ackermann et al, 1998), the precise control of the sequence of events (Dadon et al, 2008) and the correct balance between production and destruction of the dynamic species (Noireaux et al, 2003; Kim et al, 2006; Kim and Winfree, 2011).
Among various biological RNs, gene regulatory networks have attracted special interest because of their conceptual simplicity and modularity. Taking them as a prototypical example of biological RNs, we noticed that their architecture relies mostly on a limited set of basic events: activation, inhibition and destruction. We then searched for an experimental model that would allow the generic in vitro implementation of these three basic events without the need for the complex gene expression machinery. In a second step, we used these components to assemble an efficient biochemical oscillator (Box 1).
Designing reaction networks.
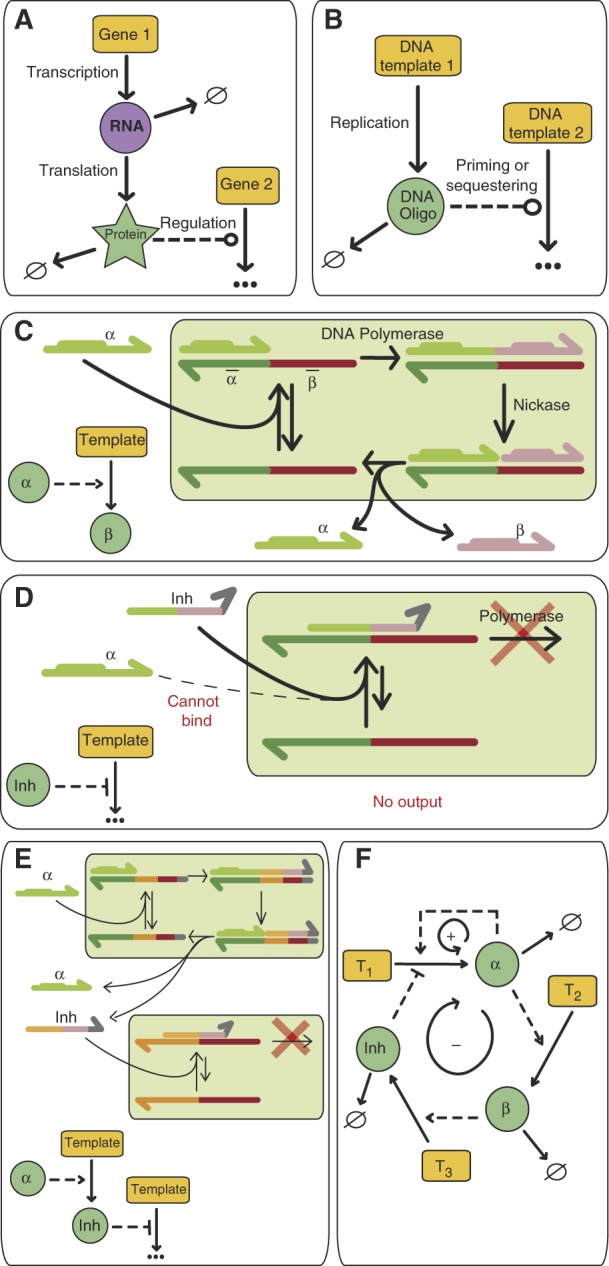 |
‘--->‘ Indicates an activation interaction, ‘---∣' shows inhibition; ‘---o' represents either activation or inhibition; ‘ → ∅' indicates decay. (A) Schematic description of the canonical gene regulation pathway. (B) A similar architecture is implemented, but genes are replaced by single-stranded DNA templates, while dynamic species (RNA and proteins) are replaced by small oligomers obtained from replication of the templates. (C) Molecular description of the activation mechanism. The input oligomer α binds to the template and is elongated by a polymerase. α displays a recognition sequence (in bold), which allows a nicking endonuclease to nick the newly extended strand. This step releases the input α, the output strand β and the template, ready for a new turnover. (D) Inhibition mechanism. The inhibitor Inh is designed to bind strongly to the template but, due to a pair of mismatches at its 3′ end, it is not recognized as a polymerization primer. Therefore, the template is reversibly sequestered as an unproductive partial duplex (E) Cascading. Previous activation or inhibition blocks can be connected to each other by simply matching their sequences (shown here using a colour code). (F) Implementation, within this framework, of an oscillator comprising a positive-feedback loop (+) and a delayed negative-feedback loop (−).
Results and discussion
The first element, activation, is achieved by a modification of an isothermal linear oligodeoxy-nucleotide (hereafter ‘oligomer') amplification scheme based on the repeated extension/nicking of one strand of a short DNA duplex (Walker et al, 1992). As the reaction occurs close to the melting temperature (Tm) of the duplexes, ‘input' and ‘output' strands dynamically dehybridize from the template. This, together with the use of a polymerase with strand-displacement ability prevents product inhibition. It also ensures that this element is dynamic and adjusts the output production rate according to changes in input concentration.
Inhibition is implemented by oligomers capable of repressing, instead of activating, the production of outputs by a template. To that purpose, we propose the use of 3′-mismatched oligomers, which are poor substrates for polymerases lacking proofreading ability; however, given a sufficient number of matching base pairs, they can still form stable duplexes with the templates. Such ‘inhibitors' displace the correct inputs, but fail to trigger the production of any output.
Destruction, i.e., the continuous removal of the dynamic species, is compulsory in order to build complex behaviour. In a closed system this sink function must be chemically controlled. RecJf, a 5′ → 3′, single-strand specific, processive exonuclease (Han et al, 2006), hydrolyzes oligomers into inactive monomers and is suitable for this purpose. Templates should not be destroyed, so they are protected by phosphorothioate bonds at their 5′ end.
In this overall scheme, inputs, outputs and inhibitors are chemically similar (all are short oligomers), so these network components can be arbitrarily connected: the output of one template simply becomes the input or the inhibitor of another (Box 1).
Chemical oscillators are prototypical examples of interesting nonlinear systems, but their in vitro design is still difficult (Epstein and Pojman, 1998; another successful approach is reported by Kim and Winfree, in this issue). We used the aforedescribed components to form a network that includes both a positive and a negative-feedback loop; hence, it is expected to produce robust oscillations (Stricker et al, 2008). We then proceeded to the step-by-step experimental assembly of this system, nicknamed ‘Oligator'.
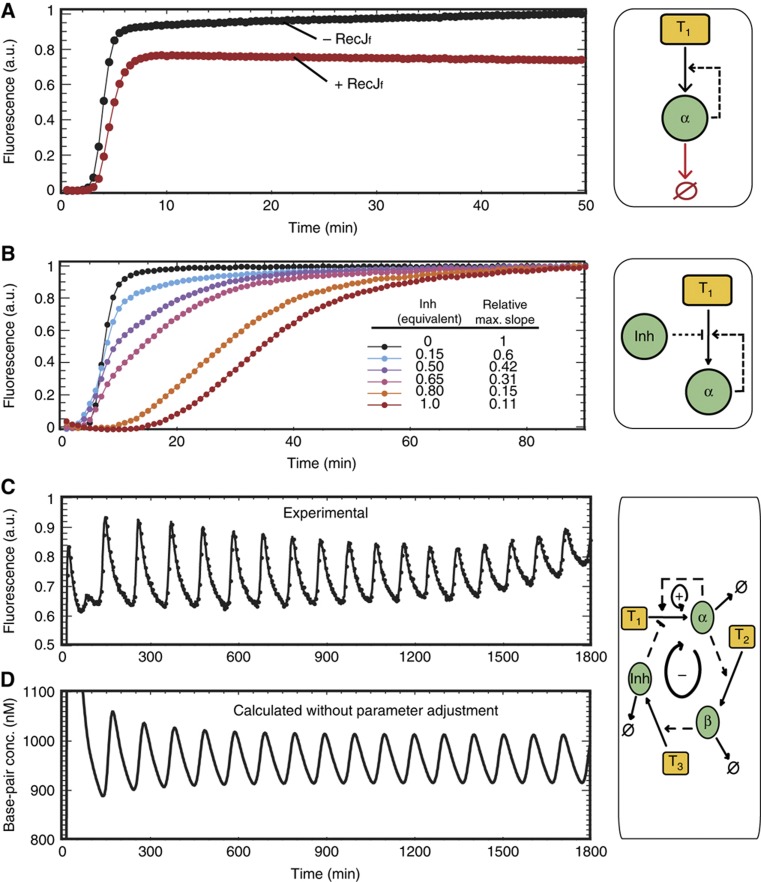
We first built a one-node network, implementing the positive-feedback loop, by using a single template (T1) that consists of a dual repeat of its input's (α) complementary sequence. This template is incubated in the presence of a polymerase and a nicking enzyme, and we monitor the reaction using a double-strand intercalating dye. As expected, this elementary network produces an exponential amplification of α. However, when the same reaction is combined with the exonuclease destruction reaction, a steady state, where α is dynamically produced and destroyed, is reached after the initial transient phase (Figure 1A).
Figure 1.
Experimental assembly. All the reactions shown were performed at 38.5°C, initiated with 0.1 nM α and monitored (ex. 490 nM; em. 510 nM) using EvaGreen-induced fluorescence. (A) One-node positive-feedback loop (autocatalytic module). In the presence of Bst Polymerase (80 U ml−1) and nicking enzyme Nt.bstNBI (200 U ml−1), template T1 (60 nM) performs an exponential amplification of its input α. The fluorescence reaches a plateau when the template gets saturated with α. The low subsequent increase is due to the accumulation of single-stranded α, weakly fluorescent in these conditions. In the presence of exonuclease RecJf (30 U ml−1), the reaction reaches a flat steady state instead. (B) Inhibited amplification. Increasing amounts of inhibitor (from 0 to 1 eq. of T1) decrease the amplification rate of the previous system (−RecJf). (C) Oscillator. Production of Inh is connected to the presence of α as in Figure 1F. This three-templates (T1 and T3: 30 nM; T2: 5 nM) three-enzymes (Bst, Nt.BstNBI, RecJf) system produces sustained fluorescent oscillations with a period of 100 min, in good agreement with the predicted evolution of the total concentration of base pairs (D).
Next, we complemented the network with an inhibitory interaction. We designed the 3′-mismatched inhibitor (Inh) to displace α from T1: Inh's higher binding constant and toeholds (Zhang and Winfree, 2009) allow it to bind strongly and quickly to T1 even in the presence of α. Experimentally, increasing (Inh) significantly decreased the amplification rate of α (Figure 1B). However, Inh can be destroyed in the presence of the exonuclease, resulting in an eventual release of the inhibition (Supplementary Figure S1).
Finally, we connected the production of Inh to the presence of α to close the negative-feedback loop. Because stable oscillations require a delay in this loop (Novák and Tyson, 2008), we inserted an intermediate species, β, between α and Inh: template T2 produces β from α and template T3 gives Inh from β. Altogether, T1, T2 and T3 experimentally encode the network shown in Figure 1F.
After assembling all components and triggering the reaction, sustained oscillations indeed emerge (Figure 1C). Depending on experimental conditions, we could detect up to 40 cycles with a period ranging from one to several hours; eventually, the reaction either stabilized or diverged. Note that, in a closed system, only transient oscillations can be expected: in any case, the exhaustion of available chemical fuel (here dNTPs) will eventually lead to the stabilization of the system, but other causes can also participate (Supplementary information S4 and Supplementary Figure S8).
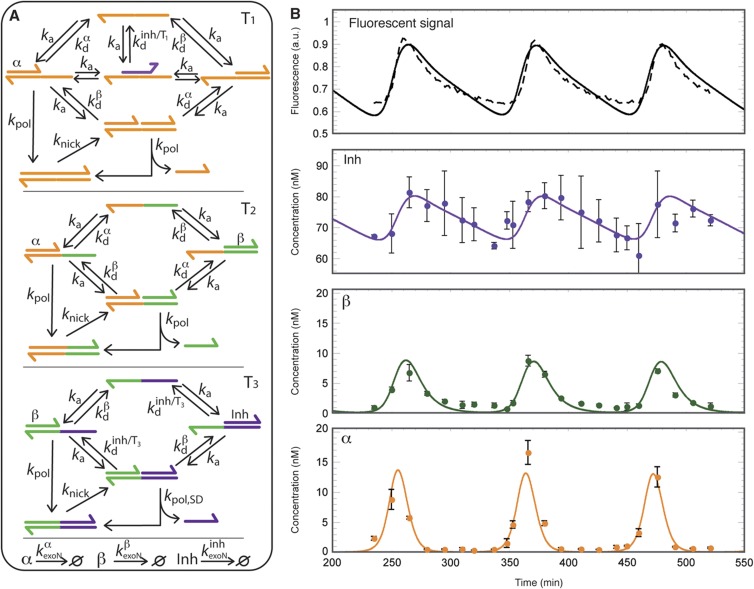
The kinetic behaviour of this system can be described by a combination of hybridization/melting equilibria and irreversible enzymatic reactions, as shown in Figure 2A. Assuming first order kinetics for all the enzymatic reactions (See Supplementary information S5 for validation), we directly obtain a realistic yet simple ‘raw model' that depends only on 11 kinetic parameters (Supplementary information S5 and Supplementary Figures S9 and S10). Moreover, all these parameters could be independently measured in separate experiments: melting curves gave the thermodynamic hybridization constants; the kinetic association rates for each template/oligomer pair were extracted from temperature jump experiments (Supplementary information S1, Supplementary Figure S2 and Supplementary Table SII); and finally the three enzymatic catalyses were analysed one by one: each satisfyingly conformed to the standard Michaelis–Menten model, from which a first-order rate constant, valid for small substrate concentrations, was calculated (Table I and Supplementary information S2, Supplementary Figures S3–S5 and Supplementary Table SIII). Using these independent experimental parameters, it became possible to numerically integrate the ‘raw model'. In Figure 1D, we plot the calculated evolution of the total concentration of base pairs in solution, which is assumed to be proportional to the fluorescent signal emitted by the intercalating dye: the period and overall behaviour agrees remarkably well with the experimental data.
Figure 2.
Measurement and simulation. (A) Schematic representation of the reactions included in the kinetic model. For clarity, the oligomers α, β and Inh have been omitted when not bound to a template. (B) Fluorescence signal (top panel, dashed line) and discrete concentration measurements of total individual oligomers α, β and Inh taken between t=235 and 520 min (Supplementary information S3). The plots show the mean of three replicates ±s.d. The solid curves are the best simultaneous agreement (‘optimized model') for fluorescence signal and oligomer concentrations, respectively (Supplementary information S5).
Table 1. Kinetic and thermodynamic parameters.
| Parameter | Measured valuesa | |
|---|---|---|
| aAll error bars are 1 s.d. formal errors calculated from least-square fitting and concentration measurement uncertainties. | ||
| Kinetic association constant (106 M−1 min−1) | ka | 26±6 |
| Kinetic dissociation | kdα=ka/Kaα | 2.3±0.7 |
| constants (min−1) | kdβ=ka/Kaβ | 0.81±0.4 |
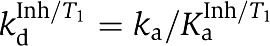 |
0.0057±0.002 | |
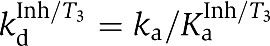 |
0.0021±0.001 | |
| Enzymatic pseudo first-order rates (min−1) | ||
| Bst polymerase | kpolα | 17±4 |
| kpol,SDInh | 6.9±3 | |
| Nt.BstNBI nickase | 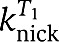 |
3.0±1 |
| RecJf exonuclease | kexoα | 0.32±0.1 |
| kexoβ | 0.37±0.1 | |
| kexoInh | 1.2±0.2 | |
However, this fluorescent signal only gives a global indication of the amount of DNA in the system, and results from contributions of many species. To precisely describe the system, one needs to know individually the evolution of each dynamic species α, β and Inh. To do so, samples were taken and quenched at various time intervals over three cycles. The low concentration of the oligomers made gel analysis difficult (Supplementary Figure S6), but we could successfully use a DNA amplification method to individually quantify α, β and Inh in each aliquot (Figure 2B and Supplementary information S3, Supplementary Figure S7 and Supplementary Table SIV): we found that all three concentrations oscillate over time, with α first reaching its maximum, followed by β, then Inh. Inh then slowly decays, until α is able to recover and the cycle starts again.
Without any adjustment in the parameters, the agreement between calculated and measured values was only qualitative. This is not surprising given the relatively large experimental uncertainties associated with the parameter values. We thus built an ‘optimized model' that includes these uncertainties, by allowing all parameters to drift within a 30% window around their input values. Similarly, the rates of similar but distinct reactions (e.g., polymerization of α.T1 versus that of β.T3) were allowed to take independent values within the same 30% window. This created a slightly more complex, but also more realistic model, whose final parameters were optimized by fitting, simultaneously, all the data in Figure 3. Under these conditions, the ‘optimized model' precisely describes the period, amplitude and phase position of the experimental observables (average parameter drift 15%, resulting in a χ2 of 1–3 for the adjustment of concentration evolutions; Figure 2B and Supplementary information S5 and Supplementary Table SV).
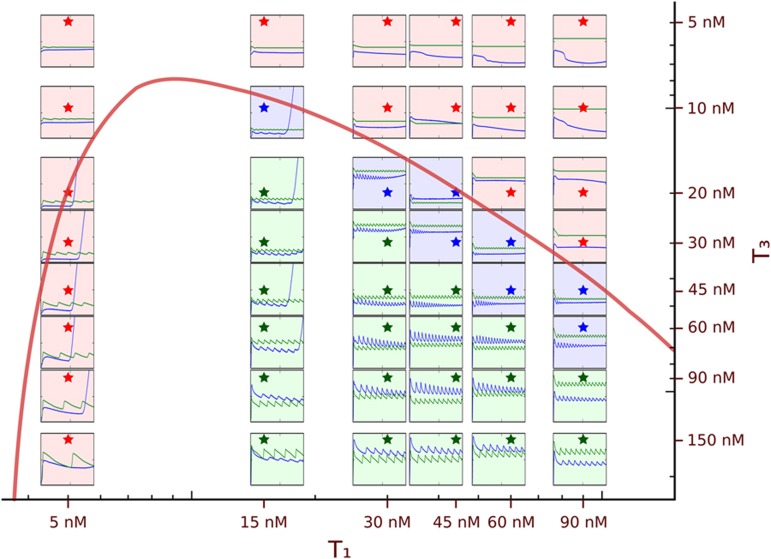
Figure 3.
Phase diagram in the [T1]–[T3] 2D space. The red curve shows the computed border, within which stable oscillations are expected. Each frame shows the fluorescence (a.u.) from t=0 to 1800 min, at [T1] and [T3] corresponding to the position of the star in the matrix. Blue line: experiments; green line: genuine predictions made with the set of parameters of the ‘optimized model' (a constant value was added to avoid overlap of the two lines). Green, blue and red frames correspond to sustained, damped or non-oscillating experiments, respectively.
While the structure of the network is encoded at the DNA sequence level, it is possible to tune its behaviour by changing the template concentrations. To test the robustness of our predictions in other locations of its control parameter space, we used the optimized model to calculate the phase diagram in the [T1]–[T3] plane (Figure 3). A stable steady state is predicted for low values of T3, but, increasing [T3], critical values distributed along a hyperbolic-shaped curve are reached. Beyond these values the steady state becomes unstable: the concentrations spontaneously oscillate. Amplitudes and periods continuously increase with [T3] and no other stable points are observed. In parallel, we experimentally explored the same area by reproducing the oscillating experiment with 48 different [T1]/[T3] conditions (Figure 3). We observed a good qualitative agreement with calculations, over a large area of the [T1]–[T3] plane (see Supplementary Figure S13 for investigation along the [T2] axis). Moreover, within the oscillatory region, the periods were correctly predicted in most cases.
DNA strands, with their predictable base pairing, together with computable thermodynamic (Santalucia and Hicks, 2004) and kinetic (Zhang and Winfree, 2009) features enable unambiguous encoding at the molecular level. This has been used to create spatial static structures at the nanometre scale (Seeman, 2003; Rothemund, 2006), as well as chemical (Yin et al, 2008; Soloveichik et al, 2010) and biochemical (Bath et al, 2005; Win et al, 2009) machines. Here, we have extended this strategy to the experimental assembly of dynamic systems by implementing complete RNs.
To do so we have used a topological design strategy inspired from biological RNs. However, we have built the system using only simple in vitro biochemical reactions based on DNA polymerization/depolymerization. In this first demonstration, we selected a network topology that was compatible with oscillations and could be implemented with a minimum number of templates (only three). We chose the parameters (Tm of the sequences, enzyme concentrations or working temperature) using mixed empirical and computational approaches: we first designed the activating oligomers with a Tm close to—or below—the working temperature, to insure that oligomers dynamically hybridize and dehybridize; we then tested various sequences for their capacity to inhibit the self-amplification of the activator, as in Figure 2C; subsequently, we assembled the whole network and searched for experimental conditions compatible with oscillations; we were then able to measure the kinetic and thermodynamic parameters in these conditions and used the model to guide our search towards a more stable oscillatory behaviour. For this specific topology to produce oscillations, we found that the inhibitor should possess a Tm much higher than the activator (typically 10°C higher).
While we have not yet entirely clarified all the design rules of such systems and especially the role of the network's structure, it should be emphasized that this in vitro approach gives a large freedom to the molecular network designer. The connectivity of the network can be simply reorganized by matching the sequence of the various sub-elements. The thermodynamic parameters can be tuned by adjusting their length and/or GC content and, importantly, this can be done in a predictive manner using well-known algorithms. Finally, the kinetic parameters can be controlled by adjusting the concentrations of enzymes and/or by positioning toehold sequences on the templates (Zhang and Winfree, 2009). This versatility suggests that more elaborate systems, containing maybe tens of nodes, might be feasible. This would open the unexplored territory of large synthetic networks, displaying complex dynamic functions (Purnick and Weiss, 2009).
Therefore, we expect that such designs will be useful to rapidly assess various hypotheses concerning the structure–function relationships at the level of RNs (Nakajima et al, 2005; Novák and Tyson, 2008). Recently, the design requirements to obtain oscillations have been experimentally investigated in E. coli (Stricker et al, 2008; Mather et al, 2009), focusing on the role of the positive and negative feedback. Comparing such in vivo results with equivalent in vitro prototypes will provide more insight on the role of various design features of biological networks. For example, one might use the approach reported here to quickly evaluate the importance of loops, delay mechanisms or other nonlinear phenomena on the occurrence and robustness of oscillations.
An important aspect of in vivo systems, e.g., gene regulatory networks, is that they are chemically much more complex than the simple biochemical reactions used in this study. Moreover, biological networks take place in the intricate context of the cellular inner medium and are intrinsically connected to its metabolic functions. Therefore, mathematical analyses of biological networks generally involve a coarse description and rough estimates of the parameters. In contrast, we have shown that the Oligator's behaviour can be predicted accurately from a straightforward kinetic model and a small set of easy-to-obtain parameters. After refinement, the numerical analysis provides a reliable and precise understanding of its dynamics (Supplementary Figures S11 and S12). This fact has proven extremely valuable during the assembly process, allowing us to find our way in a complex multi-parameter space. It also opens the possibility to assess the importance of quantitative aspects on the emergence of complex dynamic functions.
Materials and methods
All reactions (except quantitative isothermal amplifications described in Supplementary information S3) were assembled in buffer A containing 45 mM Tris–HCl, 50 mM NaCl, 10 mM KCl, 10 mM (NH4)SO4, 7 mM MgCl2, 6 mM DTT, pH=8.0, 100 μg ml−1 BSA (New England Biolabs), 410 mM Trehalose (included to stabilize RecJf during long experiments), complemented with 1 × EvaGreen (Biotium) and dNTPs (100 μM each) when necessary. Oligonucleotides α, β, Inh, T1, T2, T3 were obtained from IDT and ordered with HPLC purification. Templates T1, T2 and T3 were phosphorylated at their 3′ end to prevent any unexpected polymerization and bore two phosphorothioates at their 5′ end to protect them from hydrolysis by RecJf. Bst DNA polymerase, large fragment, Nt.BstNBI nickase and RecJf were purchased from NEB. When not specified otherwise, they were used at 16, 200 and 30 U ml−1, respectively. Fluorescence was recorded with a real-time thermocycler (either a MiniOpticon (Bio-Rad), an iQ5 (Bio-Rad) or a 7500 Real-Time PCR System (Applied Biosystems)) set at a constant temperature of 38.5°C. Melt curves at 260 nM were recorded with a V630BIO UV-vis spectrometer (JASCO) equipped with a Peltier cell. The model in SBML format can be accessed in BioModels Database under the ID ‘MODEL1010260000'.
Sequence design
The length of α was fixed at 11 bases and its sequence (5′-TCGAGTCTGTT-3′) chosen to (1) have a nicking enzyme recognition sequence (in bold) (2) have a melting temperature (Tm=39.5°C, calculated in buffer A at 100 nM strand concentration) close to the working temperature and (3) display no secondary structure. β (5′-ATGAGTCATGC-3′, Tm=37.9°C) was designed with similar constraints and the absence of cross-binding with α or 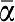 . T1 and T2 were consequently assigned the complementary sequences 3′-
. T1 and T2 were consequently assigned the complementary sequences 3′-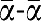 -5′ and 3′-
-5′ and 3′-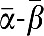 -5′, respectively. Inh (AGTCTGTTTCGAGTAA, Tm=50.2°C) was made to bind T1 with a Tm higher than α, but with two mismatches at its 3′ end. It was also designed not to be cut by the nicking enzyme. T3 was consequently 3′-
-5′, respectively. Inh (AGTCTGTTTCGAGTAA, Tm=50.2°C) was made to bind T1 with a Tm higher than α, but with two mismatches at its 3′ end. It was also designed not to be cut by the nicking enzyme. T3 was consequently 3′-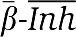 -5′ (See Supplementary Table SI for template sequences).
-5′ (See Supplementary Table SI for template sequences).
Supplementary Material
Acknowledgments
We acknowledge T Fukuba, H Kinoshita, H Nakamura, H Kimura for support and E Winfree for discussing his submission of a related study. This work was carried out under the support of the Radioisotope Center of The University of Tokyo, with the help of K Watanabe and K Tao, and funded by JSPS (Japan) and CNRS (France). RP thanks Keio University for support.
Author contributions: KM performed the experiments, RP dealt with the numerical simulation, TF and YS provided assistance and comments, and YR proposed the original concept and carried out experiments.
Footnotes
The authors declare that they have no conflict of interest.
References
- Ackermann J, Wlotzka B, McCaskill JS (1998) In vitro DNA-based predator-prey system with oscillatory kinetics. Bull Math Biol 60: 329–353 [Google Scholar]
- Bailey JE (2001) Complex biology with no parameters. Nat Biotech 19: 503–504 [DOI] [PubMed] [Google Scholar]
- Barabási AL, Oltvai ZN (2004) Network biology: understading the cell's functional organization. Nat Rev Genet 5: 101–113 [DOI] [PubMed] [Google Scholar]
- Bath J, Green SJ, Turberfield AJ (2005) A free-running DNA motor powered by a nicking enzyme. Angew Chem Int Ed 44: 435–4361 [DOI] [PubMed] [Google Scholar]
- Dadon Z, Wagner N, Ashkenasy G (2008) The road to non-enzymatic molecular networks. Angew Chem Int Ed 47: 6128–6136 [DOI] [PubMed] [Google Scholar]
- Elowitz MB, Leibler S (2000) A synthetic oscillatory network of transcriptional regulators. Nature 403: 335–338 [DOI] [PubMed] [Google Scholar]
- Epstein IR, Pojman JA (1998) An Introduction to Nonlinear Chemical Dynamics: Oscillations, Waves, Patterns, and Chaos. London: Oxford University Press [Google Scholar]
- Han ES, Cooper DL, Persky NS, Sutera VA, Whitaker RD, Montello ML, Lovett ST (2006) RecJ exonuclease: substrates, products and interaction with SSB. Nucl Acids Res 34: 1084–1091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartwell LH, Hopfield JJ, Leibler S, Murray AW (1999) From molecular to modular cell biology. Nature 402: C47–C52 [DOI] [PubMed] [Google Scholar]
- Kim J, White KS, Winfree E (2006) Construction of an in vitro bistable circuit from synthetic transcriptional switches. Mol Syst Biol 2: 6810.1038/msb4100099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Winfree E (2011) Synthetic in vitro transcriptional oscillators. Mol Syst Biol 7: 46510.1038/msb.2010.119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koide T, Pang WL, Baliga NS (2009) The role of predictive modeling in rationally re-engineering biological systems. Nat Rev Microbiol 7: 297–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mather W, Bennett MR, Hasty J, Tsimring LS (2009) Delay-induced degrade-and-fire oscillations in small genetic circuits. Phys Rev Lett 102: 068105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milo R, Shen-Orr S, Itzkovitz S, Kashtan N, Chklovskii D, Alon U (2002) Network motifs: simple building blocks of complex networks. Science 298: 824–827 [DOI] [PubMed] [Google Scholar]
- Nakajima N, Imai K, Ito H, Nishiwaki T, Murayama Y, Iwasaki H, Oyama T, Kondo T (2005) Invitro reconstitution of circadian oscillation of cyanobacterial KaiC phosphorylation. Science 308: 414–415 [DOI] [PubMed] [Google Scholar]
- Noireaux V, Bar-Ziv R, Libchaber A (2003) Principles of cell-free genetic circuit assembly. Proc Natl Acad Sci USA 100: 12672–12677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novák B, Tyson JJ (2008) Design principles of biochemical oscillators. Nat Rev Mol Cell Biol 9: 981–991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purnick PE, Weiss R (2009) The second wave of synthetic biology: from modules to systems. Nat Rev Mol Cell Biol 10: 410–422 [DOI] [PubMed] [Google Scholar]
- Rosenfeld N, Young JW, Alon U, Swain PS, Elowitz MB (2005) Gene regulation at the single cell level. Science 307: 1962–1965 [DOI] [PubMed] [Google Scholar]
- Rothemund PW (2006) Folding DNA to create nanoscale shapes and patterns. Nature 440: 297–302 [DOI] [PubMed] [Google Scholar]
- SantaLucia J, Hicks D (2004) The thermodynamics of DNA structural motifs. Annu Rev Biophys Biomol Struct 33: 415. [DOI] [PubMed] [Google Scholar]
- Seeman NC (2003) DNA in a material world. Nature 421: 427–431 [DOI] [PubMed] [Google Scholar]
- Soloveichik D, Seelig G, Winfree E (2010) DNA as a universal substrate for chemical kinetics. Proc Natl Acad Sci USA 107: 5393–5398 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker J, Cookson S, Bennett MR, Mather WH, Tsimring LS, Hasty J (2008) A fast, robust and tunable synthetic gene oscillator. Nature 456: 516–519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker GT, Little MC, Nadeau JG, Shank DD (1992) Isothermal in vitro amplification of DNA by a restriction enzyme/DNA polymerase system. Proc Natl Acad Sci USA 89: 392–396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Win MN, Liang JC, Smolke CD (2009) Frameworks for programming biological function through RNA parts and devices. Chem Biol 16: 111–122 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin P, Choi HM, Calvert CR, Pierce NA (2008) Programming biomolecular self-assembly pathways. Nature 451: 318–322 [DOI] [PubMed] [Google Scholar]
- Zhang DZ, Winfree E (2009) Control of DNA strand displacement kinetics using toehold exchange. J Am Chem Soc 131: 17303–17314 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.