Autosomal recessive disease in children of consanguineous parents: inferences from the proportion of compound heterozygotes

Abstract

This short communication deals with the questions of how to calculate the expected proportion of compound heterozygous patients among affected offspring of consanguineous parents, and how, from an observed proportion of compound heterozygotes, to calculate both the proportion of homozygotes not identical by descent and the frequency of pathogenic alleles in the population. This estimate of allele frequency may be useful when dealing with populations with a considerable number of consanguineous matings.

Introduction

In a recent search for offspring of consanguineous matings affected by autosomal recessive diseases, we came across four compound heterozygous patients among 38 affected children. This raised the question of whether this was an unexpectedly high proportion or not.

In the past, when we reported about a first compound heterozygous cystic fibrosis (CF) patient with consanguineous parents, we showed that the proportion of affected children with two alleles not identical by descent (non-IBD) can be considerable (Ten Kate et al. 1991). However, alleles non-IBD may still be identical by state (IBS). So the affected compound heterozygous children are just a subset of the affected children who do not have both alleles IBD notwithstanding parental consanguinity.

Therefore, we wondered what proportion of non-IBD patients with consanguineous parents represent compound heterozygotes, and what proportion is non-IBD but still IBS. Secondly, we wanted to know whether it is possible to calculate the overall pathogenetic allele frequency for an autosomal recessive disorder on the basis of knowledge of the proportion of compound heterozygotes among affected children of consanguineous parents. This might be a useful application as the current global prevalence of consanguineous marriage is estimated at 10.4%, (Bittles and Black 2009), with much higher percentages in many non-Western countries.

Methods

We start our exploration with the well-known formula to calculate the probability of the presence of a given autosomal recessive disease X in the children of a consanguineous couple (Li, 1955).

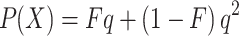1

In this formula, F is the inbreeding coefficient and q is the total frequency of all pathogenic alleles causing disorder X. The fraction Fq represents the proportion of affected children whose alleles are IBD, and the fraction (1−F)q ² corresponds with the proportion of affected children whose alleles are not IBD.

The fraction (1−F)q ² is composed of two parts—one part comprising the compound heterozygotes (CH), and the other part combining all homozygotes non-IBD (HN). The relative frequencies of the two sets within the fraction (1−F)q ² are (in reversed order)

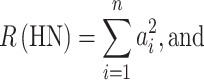2

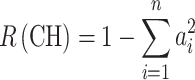3

In Eqs. 2 and 3, a _i represents the relative frequency of the i^th allele. So its square, a _i ², is the relative frequency of homozygotes of the i^th allele non-IBD.

From Eqs. 1 and 3, it follows that the proportion of compound heterozygotes, P(CH), among affected children of consanguineous parents is

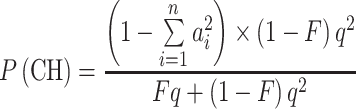4

We can now calculate the expected proportion of compound heterozygotes, P(CH), if we know F, q, and the relative frequencies of the pathogenic alleles. Conversely, knowing P(CH) by observation, as mentioned in the introduction, we can estimate R(CH), R(HN), and P(HN), if we know F and q, as follows:

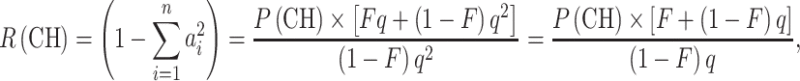5

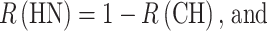6

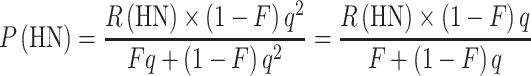7

We can also calculate q from (4) or (5) if we know P(CH), F and R(CH) or the relative frequencies of the pathogenic alleles.

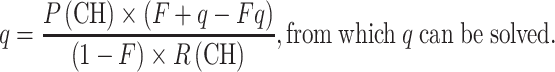8

Results

Table 1 shows the dependency of the proportion of compound heterozygotes among affected offspring of consanguineous parents, P(CH), upon the parameters F, q, and R(CH) (see Eqs. 3 and 4). The examples given illustrate that P(CH) is positively correlated with R(CH) and q, and negatively with F,—as expected.

Table 1.

Expected proportions of compound heterozygotes among affected children of consanguineous parent, P(CH), given some values of F, q, and R(CH), the relative frequency of these compound heterozygotes among non-IBD affected children

F	q	R(CH)	P(CH)
1/8	0.01	0.1	0.007
		0.5	0.033
	0.05	0.1	0.026
		0.5	0.130
1/16	0.01	0.1	0.013
		0.5	0.065
	0.05	0.1	0.043
		0.5	0.214
1/64	0.01	0.1	0.039
		0.5	0.193
	0.05	0.1	0.076
		0.5	0.380

Table 2 shows the results of calculations of the frequencies of homozygotes IBD and non-IBD among affected children of first cousins, and the total frequency of pathogenic alleles in the population in case of 10% compound heterozygotes and with different numbers and relative frequencies of pathogenic alleles. As the proportion of compound heterozygotes is fixed at 10% in this table, the row sum of the proportions of homozygotes IBD and non-IBD (third and fourth columns) add up to 90%. The table shows that knowledge of the proportion of compound heterozygotes, the inbreeding coefficient, and the number and relative frequencies of pathogenic alleles (first and second columns) allows one to calculate the total frequency of pathogenic alleles of a gene in the population (fifth column). Not unexpectedly, the higher the frequency of the major allele, the higher is the frequency of homozygotes non-IBD and the higher the total frequency of pathogenic alleles in the population for a given frequency of compound heterozygotes among affected offspring of consanguineous matings. The same trend can be observed for children of second cousins (data not shown) and other levels of inbreeding.

Table 2.

Frequencies of homozygotes IBD and non-IBD among children with an autosomal recessive disease whose parents are first cousins when 10% of these children are compound heterozygotes as well as total frequency of pathogenic alleles in the population for different numbers and relative frequencies of alleles

Input		Output
Alleles		Frequencies among affected children		Total frequency of pathogenic alleles in the population
Number	Relative frequency	Homozygotes IBD	Homozygotes non-IBD
5	0.9; 0.07; 0.02; 0.007; 0.003	0.458	0.442	0.079
	0.7; 0.2; 0,05; 0.03; 0.02	0.786	0.114	0.018
	0.5; 0.3; 0.1; 0.07; 0.03	0.845	0.055	0.012
	0.4; 0.3; 0.2; 0,08; 0.02	0.858	0.042	0.011
	0.2; 0.2; 0.2; 0.2; 0.2	0.875	0.025	0.010
3	0.9; 0.07; 0.03	0.457	0.443	0.079
	0.7; 0.2; 0.1	0.783	0.117	0.018
	0.33333; 0.33333; 0.33333	0,850	0.050	0.012
2	0.9; 0.1	0.444	0.456	0.083
	0.7; 0.3	0.762	0.138	0.021
	0.5; 0.5	0.800	0.100	0.017

Discussion

Since our observation of a compound heterozygous CF patient with consanguineous parents back in 1990, many more observations of compound heterozygotes in consanguineous families have been reported (summarized in Petukhova et al. 2009). Such patients present a problem to researchers using autozygosity mapping for identification of recessive disease genes. Still, finding compound heterozygosity among affected children of consanguineous couples has potential advantages. It may comfort parents, who thought or were told that their consanguinity was causally related to the disorder in their children, to learn now that their consanguinity cannot be blamed for it. The same applies to some extent for parents who can be told that there is a considerable chance that the homozygosity in their affected child is not caused by alleles IBD. Moreover, the mere existence of compound heterozygotes and the presence of non-IBD homozygotes among affected offspring of consanguineous parents may be of help in disputes with opponents of consanguineous matings, who are abundantly present in countries where consanguineous matings are not customary. As we have shown here, we can also learn more from the frequency of compound heterozygotes, as this frequency is related to the inbreeding coefficient, the number and relative frequencies of alleles, and their total frequency.

While preparing the manuscript of this communication, we came across the paper of Petukhova et al. (2009). These authors developed a formula to calculate the frequency of compound heterozygotes in the presence of inbreeding as we did, but unfortunately assumed equal frequencies of disease-causing mutations. As we have shown here, this is a serious omission and, moreover, far from realistic. A second difference with their paper is that we did not only calculate the frequency of compound heterozygotes, but turned the problem upside down by looking for inferences following from observed frequencies of compound heterozygotes.

One may question the usefulness of being able to make these calculations. If F is known in a certain (sub)population, then the most straightforward way to estimate q would be via the prevalence of the disease in that (sub)population. In practice, however, F and the prevalence of the disease in a population are seldom known with any certainty. Most of the times, they are unknown or the estimates are debatable because of large variances or possible biases. Arriving at accurate and dependable estimates of both parameters takes a lot of effort and resources. For this reason, any method to estimate q from other sources, such as the one we describe, is an improvement. While estimating F in a population requires knowledge of the prevalence of consanguineous matings and the distribution of different degrees of consanguinity among them, estimating F from a small number of consanguineous families known to a laboratory in general is less of a challenge.

Once the total frequency of pathogenic alleles is known, the frequency of an autosomal recessive disease in a population, P(D), can be inferred from the total frequency of disease-causing alleles, especially when the frequency of consanguineous matings, c, is known as well, using the equation

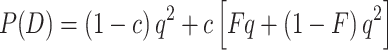9

Others have taken a different approach to calculate the frequency of a disease in the population by looking at the proportion of consanguineous parents among affected children and inferring from there, taking into account the frequency of consanguineous matings, the total pathogenic allele frequency and the total frequency of recessives in the general population (Romeo et al. 1985; Koochmeshgi et al. 2002). This method might result in a biased estimate if the presence of consanguinity of the parents alerts the physician to think of the possibility of a recessive disorder and diagnose accordingly, while this might not have been the case in the absence of consanguinity. Starting from the proportion of compound heterozygotes gives an unbiased estimate and therefore at least represents an additional tool to determine disease frequency in the general population.

Of course our method has some limitations too. Firstly, inferences can only be made about the population to which the cases belong. If a population is non-homogeneous as to the frequency of consanguineous matings, population stratification has to be taken into account. Secondly, for any recessive disorder, the number of compound heterozygotes among affected children of consanguineous parents will be limited. This means that estimates of the proportion of compound heterozygotes will tend to have rather wide confidence intervals, which will persist in derived figures. Nevertheless, a provisional estimate of the frequency of pathogenic alleles using our method can be useful before embarking on larger studies, or as a check when other data are already available.