Abstract
Purpose
A framework for the evaluation of paediatric population models is proposed and applied to two different paediatric population pharmacokinetic models for morphine. One covariate model was based on a systematic covariate analysis, the other on fixed allometric scaling principles.
Methods
The six evaluation criteria in the framework were 1) number of parameters and condition number, 2) numerical diagnostics, 3) prediction-based diagnostics, 4) η-shrinkage, 5) simulation-based diagnostics, 6) diagnostics of individual and population parameter estimates versus covariates, including measurements of bias and precision of the population values compared to the observed individual values. The framework entails both an internal and external model evaluation procedure.
Results
The application of the framework to the two models resulted in the detection of overparameterization and misleading diagnostics based on individual predictions caused by high shrinkage. The diagnostic of individual and population parameter estimates versus covariates proved to be highly informative in assessing obtained covariate relationships. Based on the framework, the systematic covariate model proved to be superior over the fixed allometric model in terms of predictive performance.
Conclusions
The proposed framework is suitable for the evaluation of paediatric (covariate) models and should be applied to corroborate the descriptive and predictive properties of these models.
KEY WORDS: model evaluation, morphine, paediatric pharmacokinetic population modeling
INTRODUCTION
Whereas many diagnostic and validation tools are available for the evaluation of population models in the adult population, these tools may not always directly suffice in the paediatric population due to the heterogeneity of this special population and the scarcity of the datasets. In this study, a framework including six evaluation criteria is presented for the systematic assessment of the descriptive and predictive properties of paediatric (covariate) models that takes these specific issues into consideration.
In paediatric population pharmacokinetic (PK) models, the influence of the many physiological changes that take place in the paediatric age range are reflected in covariate relationships that are usually based on body-weight and/or age. However, since body-weight and age are naturally correlated in the paediatric population, there is a debate on how to incorporate the influence of the physiological changes in paediatric population PK models. Body-weight and age may be regarded as regular covariates whose predictive properties on PK parameters are evaluated together with other covariates in a systematic covariate analysis by formally testing them for significance and only retaining them in the model if they statistically improve the model fit (1–3). Alternatively, body-weight can be included a priori into paediatric PK models by the use of a body-weight-based allometric equation with a fixed exponent of 0.75 for clearance and 1 for distribution volume. These equations can subsequently be augmented by estimated age-based functions of various forms (3–5).
In recent years, two different population PK models for morphine and its two major pharmacologically active metabolites, morphine-3-glucuronide (M3G) and morphine-6-glucuronide (M6G), in children younger than 3 years have been published (1,4). The model by Knibbe et al. (1) was developed using a systematic covariate analysis. The model by Bouwmeester et al. (4) was developed using fixed allometric scaling principles in conjunction with estimated age-based functions. As these models were developed using similar datasets, these models provide both an example for the assessment of the developed framework for the evaluation of paediatric (covariate) models, as well as an opportunity to directly compare the performance of these two fundamentally different paediatric covariate models.
MATERIALS AND METHODS
Models and Data
Figure 1 shows a schematic representation of the two models that are evaluated in the current analysis. In the model by Knibbe et al. (1), the maturation of the formation and elimination clearances of the morphine glucuronides was found to be best described by a body-weight-based exponential equation with an estimated exponent of 1.44. Within this exponential equation, the formation clearance of the glucuronides was found to be significantly reduced in neonates younger than 10 days. Distribution volumes were estimated to scale linearly with body-weight. This model will be referred to as the systematic covariate model.
Fig. 1.
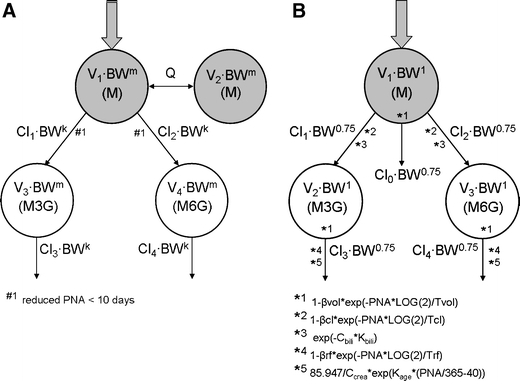
Schematic representation of the systematic covariate model (1) (A) and the fixed allometric model (4) (B). M = morphine, M3G = morphine-3-glucuronide, M6G = morphine-6-glucuronide, V = distribution volume of the designated compartment, Cl = clearance of designated route, Q = inter-compartmental clearance, PNA = postnatal age, k and m = exponential scaling constants, β = fraction below adult values at birth and T = maturation half-life for distribution volume (vol), formation clearance of the metabolites (cl), and elimination clearance of the metabolites (rf), C = plasma concentration and K = scaling constant for bilirubin (bili) and creatinine (crea).
In the model by Bouwmeester et al. (4), body-weight was included a priori using an allometric equation with fixed exponents of 0.75 for clearance and 1 for distribution volume. Three exponential equations based on postnatal age (PNA) augmented the model: one equation for distribution volumes, one for the formation of the morphine metabolites and one for the elimination of the metabolites. Bilirubin concentration and creatinine concentrations were also incorporated into the model as covariates for the formation and elimination of the glucuronides, respectively. This model will be referred to as the fixed allometric model.
The systematic covariate model (Knibbe et al. (1)) was developed using two datasets (6,7), while the fixed allometric model (Bouwmeester et al. (4)) was developed using only one of these two datasets (6). To allow for a direct comparison, the systematic covariate model was refit with the data from the one common dataset. This dataset will be referred to as the internal dataset of this study and consists of post-operative term neonates, infants and children up to the age of 3 years on a continuous or intermitted intravenous morphine regimen (6).
For the external evaluation of the two paediatric covariate models in the current analysis, five previously published datasets (7–11) were used. These external datasets included the same patient population as the internal dataset with the exception that their PNA ranged up to only 1 year instead of 3 years. In addition, two external datasets included preterm neonates (7,8), which is a younger age range than the age range in the internal dataset (6) used for model building. An overview of all datasets is given in Table I.
Table I.
Overview of the Internal Dataset (Int.1) and the External Datasets (Ext.1–5) Used for Model Building and External Model Evaluation
| Dataset | Patient population | Number of patients | Postnatal age in days (median, IQR) | Body-weight in g (median, IQR) |
|---|---|---|---|---|
| Int.1.(6) | Post-operative term neonates, infants and children. | 183 | 97 (8–286) | 4,700 (3,100–8,000) |
| Ext.1.(9) | Post-operative term neonates and infants | 28 | 14 (0–70) | 3,100 (2,550–4,000) |
| Ext.2.(10) | Post-operative term neonates and infants | 9 | 10.5 (3–135) | 3,800 (3,000–5,000) |
| Ext.3.(11) | Term neonates and infants on artificial ventilation | 12 | 13 (6–80) | 3,050 (2,675–6,900) |
| Ext.4.(7) | Preterm and term neonates on artificial ventilation | 63 | 0.4 (0.2–0.5) | 1,180 (862.5–1,760) |
| Ext.5.(8) | Preterm neonates on artificial ventilation | 41 | 1 (1–2) | 1,035 (892.5–1,295) |
Int. internal dataset, Ext. external dataset, M morphine, M3G morphine-3-glucuronide, M6G morphine-6-glucuronide
Model Evaluation
All model fitting and model-based simulations in the current study were performed using NONMEM VI (ICON, Ellicott City, MD).
The framework for the evaluation of paediatric population models is composed of the following six evaluation criteria and tools:
Total number of parameters and condition number of the model: The latter was obtained by taking the ratio of the largest and smallest eigenvalue of the covariance matrix of the estimate from the NONMEM output.
Numerical diagnostics by means of a bootstrap analysis using the PsN software package (12): One hundred datasets were resampled with replacement from the internal dataset and refit to the models. The parameter estimates for fixed and random effects obtained in every separate run were summarized in terms of mean and relative standard errors (RSE) for each parameter. Runs that did not minimize successfully were excluded from the analysis.
Prediction-based diagnostics by means of basic goodness-of-fit plots: Both the individual and population predicted concentrations were plotted versus the concentrations that were actually observed in these datasets. Plots were made for both the internal and external datasets and for the population as a whole as well as for stratified subsets based on age (0–1 month, 1 month–1 year, 1–3 years). Mirror plots were created to serve as a reference for these predicted versus observed plots (13).
η-shrinkage as defined by Karlsson et al. (13), which was calculated for all model parameters for which inter-individual variability was estimated.
Simulation-based diagnostics by means of normalized prediction distribution errors (NPDE) (14): Both the internal and merged external datasets were simulated 1,000 times with inclusion of the inter-individual variability and residual error. Using the NPDE add-on package for R (version 1.2) (15), a cumulative distribution was assembled for each observation with the 1,000 simulated concentrations; subsequently, the value of the cumulative distribution at the observed concentration was determined. An inverse function of the normal cumulative density function was then applied to these data to obtain what are called the normalized prediction distribution errors. The NPDEs are presented in a total distribution, versus time and versus the concentration. This analysis was also performed on the population as a whole and on the stratified subsets described in item 3.
-
Individual and population parameter estimates versus the most predictive covariate in the model: In both models, body-weight was the most predictive covariate. Total morphine clearance was defined as the sum of Cl1 and Cl2 for the systematic covariate model (see Fig. 1a) and of Cl0, Cl1, and Cl2 for the fixed allometric model (see Fig. 1b). The elimination clearances of the metabolites (Cl3 and Cl4) and the distribution volume of the central morphine compartment (V1) were directly compared between the two models.
To numerically quantify the bias and precision of the model-predicted parameter values compared to the observed parameter values in the internal datasets, Mean Prediction Error (MPE, Eq. 1) and the Root Mean Square Error (RMSE, Eq. 2) were calculated for both models.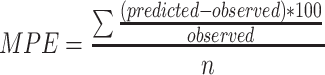
1 
2 In these equations, predicted parameter values were the population predicted values for each individual by both models, and the observed parameter values were the individually observed post hoc parameter values for that individual. MPE and RMSE were calculated separately for the strata described before.
A table with MPE and RMSE was also constructed for the external datasets. This table was also stratified based on age with the following strata: preterm neonates (PNA <1 month and postmenstrual age (PMA) at birth <36 weeks), term neonates (PNA <1 month and PMA at birth ≥36 weeks), toddlers (PNA 1 month–1 year).
RESULTS
Table II (A and B) lists the parameter estimates as obtained with the fit of the internal dataset by the systematic covariate model and the fixed allometric model, respectively.
Table II.
Parameter Estimates from the Model Fit, Number of Model Parameters and Parameter Estimates from the Bootstrap Procedure for the Systematic Covariate Model (A) and for the Fixed Allometric Model (B) Obtained with the Internal Dataset. Parameter Names are Explained in Fig. 1
| Parameters systematic covariate model | Model fit | Bootstrap (98 out of 100 successful) |
|---|---|---|
| Value (RSE%) | Mean value (RSE%) | |
| A | ||
| Fixed effects (n = 10) | ||
| k = exponential scaling factor on clearance | 1.49 (3.6) | 1.49 (3.42) |
| m = exponential scaling factor on distribution volume | 1 fixed | 1 fixed |
| Cl1 PNA < 10d (ml/min/kgk) | 3.68 (9.0) | 3.68 (8.15) |
| Cl1 PNA > 10d (ml/min/kgk) | 8.04 (11.0) | 8.01 (10.1) |
| Cl2 PNA < 10d (ml/min/kgk) | 0.423 (11.1) | 0.42 (14.4) |
| Cl2 PNA >10d (ml/min/kgk) | 0.623 (10.2) | 0.62 (13.0) |
| Cl3 (ml/min/kgk) | 1.84 (9.9) | 1.85 (9.73) |
| Cl4 (ml/min/kgk) | 0.955 (9.0) | 0.95 (12.6) |
| Qeq (ml/min) | 40.8 (24.1) | 43.8 (42.7) |
| V1 = V4 (l/kg) | 1.64 (8.2) | 1.65 (9.44) |
| V2 = V3 (fraction of V1) | 0.157 (21.2) | 0.161 (27.0) |
| Inter-individual variability (n = 5) | ||
| ω2 Cl1 | 0.0809 (24.0) | 0.0774 (22.9) |
| ω2 Cl2 | – | – |
| ω2 Cl3 | 0.256 (27.1) | 0.263 (29.1) |
| ω2 Cl4 | 0.110 (15.2) | 0.110 (15.5) |
| ω2 Cl3-Cl4 covariance | 0.128 (18.2) | 0.126 (19.8) |
| ω2 V1 | 0.162 (17.9) | 0.168 (20.7) |
| Residual error (n = 3) | ||
| σ2, prop (morphine) | 0.440 (14.7) | 0.431 (14.0) |
| σ2, prop (M3G) | 0.261 (27.2) | 0.243 (26.0) |
| σ2, prop (M6G) | 0.0894 (15.7) | 0.0894 (16.4) |
| Parameters fixed allometric model | Model fit | Bootstrap (46 out of 100 successful) |
| Value (RSE%) | Value (RSE%) | |
| B | ||
| Fixed effects (n = 14) | ||
| Cl0 (l/h/70 kg0.75) | 3.12 (117) | 2.59 (43.4) |
| Cl1 (l/h/70 kg0.75) | 64.3 (18.0) | 55.2 (32.3) |
| Cl2 (l/h/70 kg0.75) | 3.63 (14.0) | 3.99 (65.6) |
| Cl3 (l/h/70 kg0.75) | 17.4 (16.0) | 7.23 (38.0) |
| Cl4 (l/h/70 kg0.75) | 5.8 (20.2) | 5.43 (23.4) |
| V1 (l/70 kg) | 136 (59.3) | 147 (34.9) |
| V2 (l/70 kg) | 23 fixed | 23 fixed |
| V3 (l/70 kg) | 30 fixed | 30 fixed |
| Βcl | 0.834 (6.41) | 0.894 (8.35) |
| Tcl (days) | 88.3 (37.4) | 65.2 (176) |
| Βrf | 0.832 (9.74) | 0.814 (10.7) |
| Trf (days) | 129 (49.8) | 136 (45.4) |
| Βvol | 0.391 (28.4) | 0.388 (38.1) |
| Tvol (days) | 26.3 (72.2) | 26.7 (58.9) |
| Kage | 0.0141 (140) | 0.0201 (36.3) |
| Kbili | -0.00203 (33.2) | -0.00207 (35.3) |
| Inter-individual variability (n = 16) | ||
| ω2 Cl0 | 1.37 (104) | 1.80 (69.9) |
| ω2 Cl1 | 0.346 (20.9) | 0.916 (74.9) |
| ω2 Cl2 | 0.675 (29.3) | 1.21 (75.8) |
| ω2 Cl3 | 0.185 (20.8) | 0.764 (41.7) |
| ω2 Cl4 | 0.545 (32.1) | 1.39 (87.6) |
| ω2 V1 | 0.351 (29.1) | 1.54 (121) |
| full omega block on all eta’s except Cl0 | Data not shown | Data not shown |
| Residual error (n = 5) | ||
| σ2, prop morphine | 0.128 (11.6) | 0.503 (105) |
| σ2, add M3G (ng/ml) | 50.3 (36.2) | 136 (217) |
| σ2, prop M3G | 0.118 (27.0) | 2.21 (80.0) |
| σ2, add M6G (ng/ml) | 0.198 (26.0) | 1.31 (148) |
| σ2, prop M6G | 0.0925 (16.9) | 0.249 (53.0) |
With a total of 18 model parameters, the systematic covariate model described the fixed and random effects with fewer parameters than the fixed allometric model, which contains 35 model parameters. The condition number of the systematic covariate model was 293, which is well below the critical value for the indication of serious ill-conditioning of 1,000 (16). For the fixed allometric model, the condition number was 10,698, which is more than ten-fold higher than the critical value.
In Table II (A and B) the parameter estimates obtained with the bootstrap analyses are presented as well. The parameter estimates of the bootstrap deviated more from the values obtained in the initial model fit for the fixed allometric model compared to the systematic covariate model. For both the model fit and the bootstrap procedure with the fixed allometric model, the overall precision of the parameter estimates was lower than the systematic covariate model as expressed by the higher relative standard error (RSE) of the parameter estimates. Additionally, for the bootstrap, using the fixed allometric model only 46 out of 100 model refits minimized successfully, whereas 98 out of 100 model refits successfully minimized using the systematic covariate model.
Figure 2 shows the individual predicted concentrations versus observed concentrations for morphine and its metabolites as obtained with the internal dataset for both the systematic covariate model (A) and the fixed allometric model (B). This figure shows a slightly better description of individual concentrations by the fixed allometric model compared to the systematic covariate model, especially for the mother compound morphine.
Fig. 2.
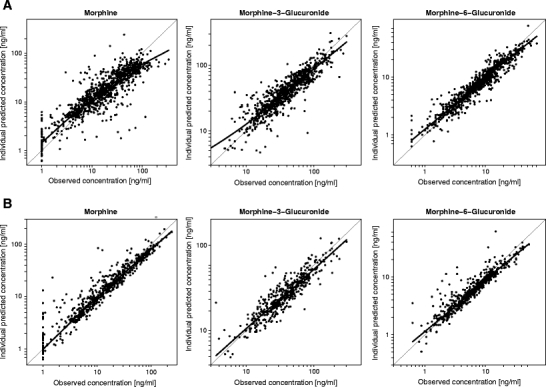
Individual predicted concentrations versus observed concentrations including a loess curve of morphine and its metabolites in the internal dataset Predictions by the systematic covariate model are depicted in panel A, and predictions by the fixed allometric model in panel B.
Figure 3 shows the population predicted concentrations versus observed concentrations obtained with the internal as well as the five external datasets. This figure shows the systematic covariate model to be superior to the fixed allometric model in the predictions of population concentrations in the datasets. The predictions for the systematic covariate model are only slightly biased, and since this bias is also observed in the mirror plots (data not shown), this is not indicative of model misspecification. For the fixed allometric model, on the other hand, significant bias towards under-prediction can be observed that did not correspond to trends observed in the mirror plots (data not shown).
Fig. 3.
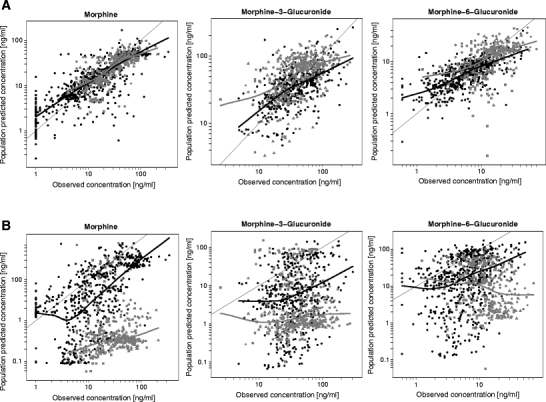
Population predicted concentrations versus observed concentrations including loess curves of morphine and its metabolites for the systematic covariate model (A) and fixed allometric model (B). Data points in black originate from the internal dataset and data points in grey from the external datasets. Different symbols are used for different external datasets: ■ = Ext. 1(9), ● = Ext 2(10), ♦ = Ext 3(11),* Ext 4(7), ▲ = Ext 5(8).
For both models, stratification into the different age groups of the plots of the predicted versus observed concentrations showed no differences in model performance (data not shown).
Table III shows the percentage of η-shrinkage for the parameters for which inter-individual variability was identified in each of the two models. Both models have parameters for which shrinkage is relatively high (>20%), indicating that the individual data in the internal dataset is not rich in information about these parameters.
Table III.
Percentage η-Shrinkage in Both Models for the Parameters for Which Inter-individual Variability was Identified
| Cl0 | Cl1 | Cl2 | Cl3 | Cl4 | V1 | |
|---|---|---|---|---|---|---|
| Systematic covariate model (%) | – | 29.6 | – | 8.26 | 5.76 | 30.3 |
| Fixed allometric model (%) | 52.3 | 10.8 | 13.2 | 21.0 | 18.9 | 17.7 |
For both models, the results of the NPDE analysis with the internal dataset are depicted in Fig. 4. For the systematic covariate model, no trends in time or versus concentration are observed. The mean of the distribution of NPDEs is close to 0, while the variance is slightly lower than 1. The trends observed in the plots for the fixed allometric model are indicative of an under-prediction, which appears to be relatively constant over time but to increase with decreasing concentrations.
Fig. 4.
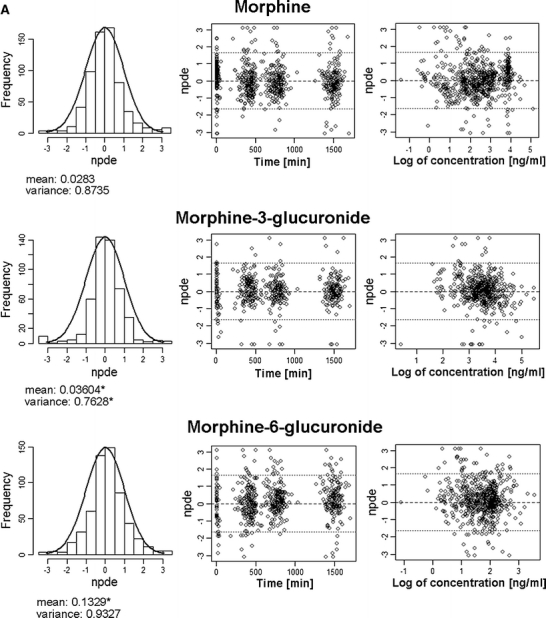

Result of the NPDE analysis for morphine and its metabolites using the internal dataset with the systematic covariate model (A) and the fixed allometric model (B). In the histograms the distributions of the NPDEs for morphine and its metabolites in the total dataset are shown. The solid line depicts a normal distribution, and the values below specify the mean and variance of the observed NPDE distribution in the histogram. A statistically significant deviation of the distribution from a mean of 0 and a variance of 1 is indicated with an asterisk (*). The distributions of NPDEs in time after first dose and against the observed concentrations are also shown. As for the systematic covariate model, log-transformed data have been used; the last plot shows the NPDE against the log-value of the observed concentration.
The results of the NPDE analysis with the external datasets confirmed the results obtained with the internal dataset for both models (data not shown). Stratification into different age groups also revealed similar results for the three age groups for each of the models (data not shown).
The plots of the individual post hoc parameter estimates and population predicted parameter estimates for total morphine clearance, the clearances of the metabolites and distribution volume of the central morphine compartment versus body-weight for both models are shown in Fig. 5. For the systematic covariate model, total morphine clearance is composed of Cl1 and Cl2 (see Fig. 1a), which both have different population values for children older and younger than 10 days, resulting in two different lines of population parameter estimates. For the fixed allometric model, total morphine clearance is composed of Cl0, Cl1 and Cl2 (see Fig. 1b). The larger number of additional covariates (age, and bilirubin and creatinine concentration) on the structural parameters in the fixed allometric model results in scattered lines for the population parameter estimates of this model. This figure shows that for the systematic covariate model, the population predicted values describe the individual post hoc values without bias for all parameters, whereas for the fixed allometric model, the population predicted values are biased compared to the individual post hoc values for all parameters.
Fig. 5.
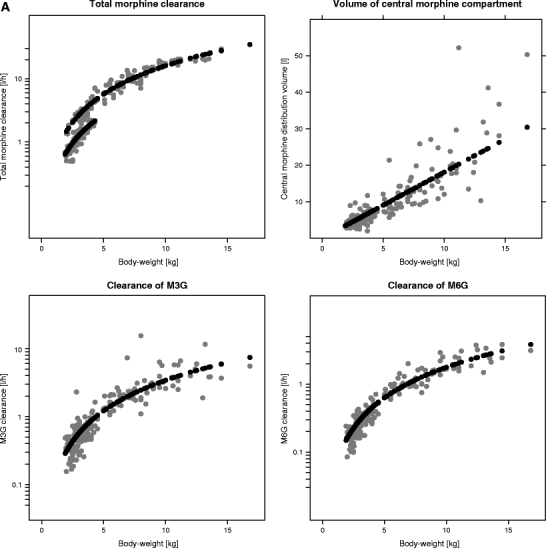
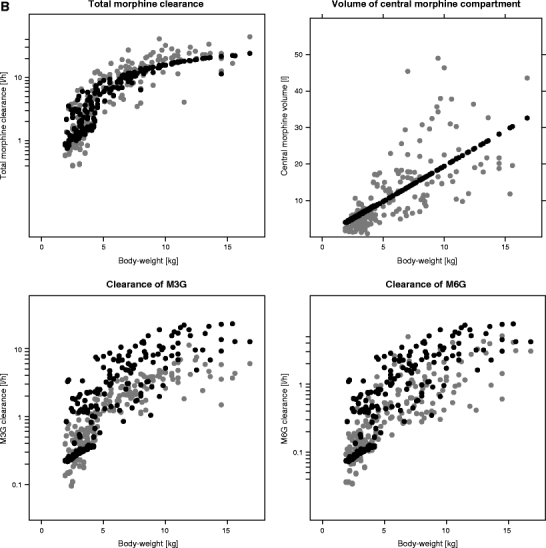
Individual post hoc parameter estimates (grey) and population predicted parameter estimates (black) for total morphine clearance (Cl1 + Cl2 for the systematic covariate model and Cl0 + Cl1 + Cl2 for the fixed allometric model), the elimination clearances of the metabolites (Cl 3 and Cl 4) and distribution volume of the central morphine compartment (V 1) versus body-weight for the systematic covariate model (A) and the fixed allometric model (B).
Table IV numerically quantifies the bias (MPE) in the population predicted parameter values compared to the individually observed parameter values for both models. The RMSE in this table quantifies the precision of the population prediction. It can be seen that for the systematic covariate model, mean bias in the population predictions stays well below 25% and remains relatively constant over the age ranges for all parameters. For the fixed allometric model, bias in the population predictions reaches up to 250%, and, especially in the clearance of the metabolites, an increasing trend towards over-prediction is observed with increasing age.
Table IV.
Bias (MPE) and Precision (RMSE) of the Predicted Parameter Values in the Internal Datasets Stratified by Age Group
| Parameter | Age group | Systematic covariate model | Fixed allometric model | ||
|---|---|---|---|---|---|
| MPE | RMSE | MPE | RMSE | ||
| Total morphine clearance | neonatesa | 4.26 | 0.426 | 10.8 | 0.922 |
| toddlersb | -0.74 | 1.65 | 12.7 | 5.00 | |
| infantsc | 4.63 | 3.28 | -2.56 | 7.90 | |
| M3G clearance | neonatesa | 19.7 | 0.291 | -19.5 | 2.50 |
| toddlersb | 1.85 | 0.888 | 23.8 | 15.5 | |
| infantsc | 14.5 | 3.82 | 188 | 9.03 | |
| M6G clearance | neonatesa | 12.5 | 0.0784 | -69.0 | 0.825 |
| toddlersb | 0.262 | 0.230 | 100 | 5.27 | |
| infantsc | 4.93 | 0.852 | 253 | 2.84 | |
| Distribution volume of central morphine compartment | neonatesa | 23.2 | 1.30 | 90.6 | 2.93 |
| toddlersb | 15.9 | 3.43 | 22.4 | 7.26 | |
| infantsc | 5.90 | 9.27 | 9.35 | 13.4 | |
MPE mean prediction error, RMSE root mean square error
aneonates, PNA <30 days, n = 61
btoddlers, PNA = 1 month-1 year, n = 87
cinfants, PNA >1 year n = 35
Table V shows the mean bias and precision in the predictions of the model parameters in the external dataset stratified in three age groups. As can be expected, for both models, the bias in the parameter predictions of the external datasets is generally larger than for the internal dataset; however, for the systematic covariate model, it still remains below 35.6%, whereas for the fixed allometric model, the values are between 26.6% and 296%.
Table V.
Bias (MPE) and Precision (RMSE) of the Predicted Parameter Values in the External Datasets Stratified by Age Group
| Parameter | Age Group | Systematic covariate model | Fixed allometric model | ||
|---|---|---|---|---|---|
| MPE | RMSE | MPE | RMSE | ||
| Total morphine clearance | preterm neonatesa | 17.4 | 0.0667 | 192 | 0.444 |
| term neonatesb | 29.74 | 0.274 | 85.5 | 3.91 | |
| toddlersc | 29.3 | 1.64 | -26.6 | 4.22 | |
| M3G clearance | preterm neonatesa | -16.3 | 0.102 | 114 | 0.225 |
| term neonatesb | 31.0 | 0.463 | 108 | 0.928 | |
| toddlersc | 5.48 | 0.818 | 172 | 1.34 | |
| M6G clearance | preterm neonatesa | -12.5 | 0.0447 | 46.8 | 0.779 |
| term neonatesb | 35.6 | 0.0818 | 31.1 | 0.502 | |
| toddlersc | 12.5 | 0.285 | 93.5 | 0.490 | |
| Distribution volume of central morphine compartment | preterm neonatesa | -12.9 | 0.945 | -115 | 1.46 |
| term neonatesb | -10.3 | 2.03 | -296 | 3.50 | |
| toddlersc | 3.45 | 3.47 | -93.1 | 3.22 | |
MPE mean prediction error, RMSE root mean square error
apreterm neonates, (PNA <30 days and PMA at birth <36 weeks), n = 80
bterm neonates, (PNA <30 days and PMA at birth ≥36 weeks), n = 40
cinfants, PNA = 1 month–1 year,n = 33
DISCUSSION
In childhood, many physiological changes take place in quick succession, and the paediatric population is very heterogeneous. Additionally, studies in this population are often performed during routine clinical practice, which increases the variability in both dosing and sampling schemes, while due to limitations in sample size and frequency, often only sparse data are obtained. All these factors influence the evaluation of population and covariate models for this young population. In the current study, a framework of six different evaluation criteria is proposed for the evaluation of paediatric models. Most tools in the framework are not necessarily new, but in the context of paediatric model, evaluation adaptations to the standard methods are sometimes required, or a shift in emphasize on the various tools is essential.
As an example, two previously published paediatric population PK models for morphine that were based on the same dataset but fundamentally different covariate models were evaluated with this framework. The systematic covariate model was developed by regarding body-weight and age as regular covariates in a systematic covariate analysis (1). The fixed allometric model was based on allometric principles including body-weight a priori using exponential functions with fixed exponents and estimating an age-based function (4).
In itself, the number of parameters in a model is not an evaluation criterion; however, according to the rule of parsimony, a model should have the lowest possible number of parameters. Large deviations of bootstrap parameter values from the original value, low precision in parameter estimates as expressed by high RSE values in the model fit and bootstrap procedures, small number of successful bootstrap runs and a condition number higher than 1,000 are all generally indicative of model inaccuracy, model instability, and ill-conditioning (16–19). Testing covariates for significance and only retaining a covariate when it significantly improves the model adheres to the rule of parsimony and does not introduce specific assumptions into the model, and the resulting model is always supported by data. In the current example, it is shown that the systematic covariate model performs well on all the criteria of ill-conditioning. In case covariates in a model are not formally tested for significance, there is a risk of over-parameterization. The results for the fixed allometric model in this example suggest the fixed allometric model to be an unstable model for which precise parameter estimates cannot be obtained. It should also be noted in this respect that with the increased number of fixed and random model parameters in the fixed allometric model, the degrees of freedom in this model are increased as well. More degrees of freedom improve the description of data by a model, but do not necessarily improve the predictions by that model.
As stated before, paediatric PK analyses are often based on sparse data. This is an important aspect to consider when evaluating paediatric population PK models, because when data are uninformative due to scarcity, the estimated variability parameters may shrink to zero, causing the individual post hoc parameter estimates to move towards the population predictions. This shrinkage phenomenon makes individual parameter estimates and the diagnostics based on them less reliable or even misleading (13,20). Population predictions, however, are solely based on the fixed effects described in the structural and covariate model. As the random effects are not considered in the population predictions, diagnostics based on population predictions are not sensitive to shrinkage and are therefore more reliable than individual predictions. The two models in the current study illustrate how diagnostics based on individual predictions can be misleading when shrinkage is high, as was the case for some of the parameters in both models (Table III). The plots of the individual predicted versus observed concentrations in Fig. 2 inadvertently suggest the fixed allometric model to perform better than the systematic covariate model, since, especially for morphine, the data points are closer to the line of unity. However, in Fig. 3, large differences in the predictive performance between the two models are revealed for both the internal and external datasets when considering population predicted concentrations instead of the individual predicted concentrations. For the systematic covariate model, there are no signs of model misspecification. The fixed allometric model, on the other hand, shows significant bias towards under-prediction throughout the total concentration range. Since diagnostics based on population predictions are generally more reliable, these should always be included in the evaluation of paediatric (covariate) models.
Simulation-based diagnostics known as posterior predictive checks (PPC) are diagnostics that create a reference distribution of an observation of interest by performing multiple model simulations with inclusion of both fixed and random effects and subsequently compare the actual observations to this reference distribution (21). A visual predictive check (VPC) is a commonly used and easily interpretable form of a PPC that graphically presents the reference distribution and observed data (22). A VPC can be used for the evaluation of paediatric models as well; however, when data are obtained during routine clinical practice and variability in individual dosing and sampling schemes are high, the NPDE methodology (14) is often easier to perform and interpret. Shrinkage does not influence the results of simulation-based diagnostics (13). The results of the NPDE analysis of the models in the current example demonstrate that the systematic covariate model can quite accurately predict median concentrations for morphine and the glucuronides, but that it slightly over-predicts the variability in the overall dataset. This over-prediction of the variability is constant over time and over the concentration range. If this model were to be used in simulation exercises, the predictions would be unbiased, and the inferences made on the variability in the population would be on the conservative side, as the variability is predicted to be higher than it actually is. Based on the trend towards under-prediction by fixed allometric model, it can be concluded that significant bias in the predictions would occur if this model would be used in simulation exercises. The under-prediction of concentrations by the fixed allometric model increases the risk of overdosing when deriving morphine doses based on this model. These NPDE results substantiate the results obtained in the population predicted versus observed plots in Fig. 3.
Due to the heterogeneity in the paediatric population, it is very important to not only perform diagnostics on the population as a whole, but to also look at various subpopulations by stratifying the datasets based on bodyweight or age. For both models in the example, stratification showed the same descriptive and predictive performance in all age groups. For the systematic covariate model, the predictive performance of the model was adequate in all age ranges. The trends towards under-prediction identified for the fixed allometric model was also similar across all age ranges. Despite the fact that stratification of the diagnostics did not reveal new information in the current examples, this adjustment of the various validation tools remains imperative for the detection of previously unidentified age-related misspecifications.
To corroborate the obtained covariate relationships in paediatric models, the plots of individual and population parameter values versus the covariate presented here in Fig. 5, together with a numerical representation of bias and precision in Table IV, have proven to be highly informative. Even in case of high shrinkage, this diagnostic will enable the identification of bias in the population predictions of parameters. In this study, in both models, bodyweight was the most important covariate for clearances and distribution volumes. For the systematic covariate model, population predicted parameter values are adequately centered in the range of individual predicted values for all parameters and across the entire body-weight and age ranges. However, for the fixed allometric model, the population predicted parameter values are biased compared to the individual predicted values. For some parameters, this bias exists over the total weight and age ranges; for others, only over part of these ranges. The results in the plots in Fig. 5 and Table IV provide an explanation for the adequate individual concentration predictions by the fixed allometric model and the highly biased population predictions by this model, as observed with the other evaluation tools. Structural model misspecifications in the population parameter values result in biased population predictions that are corrected by the error models to yield good individual predictions. This type of diagnostic is hardly ever published; however, the information contained in these plots and tables is crucial and should become a standard diagnostic tool with paediatric population PK models.
Especially in drug development, population PK models in paediatric subpopulations are often used for extrapolations to younger age ranges. When a model is used for this purpose, the obtained covariate relationships should be thoroughly evaluated, for instance by using the diagnostic in Fig. 5 and Table IV. In the current study, two out of five external datasets (Ext 4 and Ext 5) include preterm patients, a younger and smaller population than the population in the internal dataset. For both models, the results of the various tools in the framework were similar irrespective of the age range in the dataset that was used, indicating that the inclusion of a new patient population in the external validation did not influence to overall results.
A systematic covariate analysis is a data-driven approach; therefore, the extrapolation potential of the resulting model cannot be known a priori. It is clear that for the systematic covariate model in the current analysis extrapolations to older (heavier) children is not possible as the body-weight-based exponential equation for clearance predicts rapidly increasing clearances at higher weight ranges. Figure 5 indicates that for this model, population parameter predictions are unbiased in the lower weight ranges, suggesting that extrapolation to smaller children could be possible. The extensive evaluation procedures in the current example prove this to be the case in this particular example.
It is claimed that the allometric equations used in the fixed allometric model are based on ‘sound biological principles’ (23) and that the methodology based on these equations therefore yields mechanistic models that can be used for extrapolations outside the studied age or weight ranges. It is argued that the influence of size (parameterized by body-weight) and maturation (parameterized by age) on the parameters in paediatric population PK models are disentangled by using the fixed allometric equations augmented by age-based functions (5,24). However, the theory of allometry is based on the empirical observation that over a wide weight range, metabolic rates of animal species increase with body-weight to the power of 0.75 (25). The fixed allometric exponents have no biological or physiological meaning, although reports exist that propose possible physiological explanations (26–28). Conversely, a large body of evidence exists against the existence of one unique value for the allometric clearance exponent (29–35) and against the application of these allometric equations in human paediatric PK models (36,37). Additionally, the maturation function based on age only reflects a mathematical residue of the age effect that remains after the inclusion of the correlated covariate body-weight. In the current study, in the fixed allometric model, the model-predicted increase in clearance comes to a plateau with increasing body-weight. Therefore, this model cannot be excluded for extrapolations to higher weight ranges. The predictive properties of this model in preterm neonates is very poor, albeit comparable to the predictions in the older children that comprised the learning dataset. As a result, the extrapolation potential of fixed allometric models in general can neither be confirmed nor disputed based on the results in the current study.
CONCLUSION
The framework of six evaluation criteria proposed in the current study takes into consideration the specific issues encountered in the evaluation of paediatric population models. The application of this framework to two models for morphine and its two major metabolites in children younger than 3 years with fundamentally different covariate models demonstrates how to detect over-parameterization, which is a risk with models based on sparse data. Additionally, it illustrates the importance of diagnostics that are based on population predictions rather than individual predictions, as high shrinkage due to sparse data may yield misleading individual prediction-based diagnostics. Finally, the diagnostic comparing population parameter predictions with individually observed parameter values proved to be highly informative in assessing obtained covariate relationships, as in the current example it detected the cause of model misspecification by the fixed allometric model. Stratification of the various diagnostics did not yield much additional information in the current examples; however, due to the heterogeneity of the paediatric population, this adaption of standard validation tools may be of value for other paediatric models.
The differences observed in model performance between the systematic covariate model and the fixed allometric model in the current study do not imply that any of the two methodologies for covariate model development is superior over the other. The current study does, however, highlight the importance of corroborating results in evaluation procedures. It also illustrates that information in data should not be ignored and that one should never be guided by theories alone.
ACKNOWLEDGMENTS
We would like to thank Dr. Caroline van der Marel, Dr. Richard van Lingen, Dr. Anne Lynn and Dr. Imti Choonara for kindly sharing their data with us.
This study was performed within the framework of Dutch Top Institute Pharma project number D2-10.
The work of C.A.J. Knibbe is supported by the Innovational Research Incentives Scheme (Veni grant, July 2006) of the Dutch Organization for Scientific Research (NWO).
All authors declare no conflict of interest.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
ABBREVIATIONS
- IQR
inter quartile range
- M3G
morphine-3-glucuronide
- M6G
morphine-6-glucuronide
- MPE
mean prediction error
- NPDE
normalized prediction distribution error
- PD
pharmacodynamics
- PK
pharmacokinetics
- PMA
postmenstrual age
- PNA
postnatal age
- RMSE
root mean square error
- RSE
relative standard error
REFERENCES
- 1.Knibbe CA, Krekels EH, van den Anker JN, et al. Morphine glucuronidation in preterm neonates, infants and children younger than 3 years. Clin Pharmacokinet. 2009;48(6):371–385. doi: 10.2165/00003088-200948060-00003. [DOI] [PubMed] [Google Scholar]
- 2.Peeters MY, Prins SA, Knibbe CA, et al. Propofol pharmacokinetics and pharmacodynamics for depth of sedation in nonventilated infants after major craniofacial surgery. Anesthesiology. 2006;104(3):466–474. doi: 10.1097/00000542-200603000-00013. [DOI] [PubMed] [Google Scholar]
- 3.de Cock RF, Piana C, Krekels EH, Danhof M, Allegaert K, Knibbe CA. The role of population PK-PD modelling in paediatric clinical research. Eur J Clin Pharmacol. 2010. [DOI] [PMC free article] [PubMed]
- 4.Bouwmeester NJ, Anderson BJ, Tibboel D, Holford NH. Developmental pharmacokinetics of morphine and its metabolites in neonates, infants and young children. Br J Anaesth. 2004;92(2):208–217. doi: 10.1093/bja/aeh042. [DOI] [PubMed] [Google Scholar]
- 5.Anderson BJ, Allegaert K, Holford NH. Population clinical pharmacology of children: modelling covariate effects. Eur J Pediatr. 2006;165(12):819–829. doi: 10.1007/s00431-006-0189-x. [DOI] [PubMed] [Google Scholar]
- 6.van Dijk M, Bouwmeester NJ, Duivenvoorden HJ, et al. Efficacy of continuous versus intermittent morphine administration after major surgery in 0–3-year-old infants; a double-blind randomized controlled trial. Pain. 2002;98(3):305–313. doi: 10.1016/S0304-3959(02)00031-3. [DOI] [PubMed] [Google Scholar]
- 7.Simons SH, van Dijk M, van Lingen RA, et al. Routine morphine infusion in preterm newborns who received ventilatory support: a randomized controlled trial. JAMA. 2003;290(18):2419–2427. doi: 10.1001/jama.290.18.2419. [DOI] [PubMed] [Google Scholar]
- 8.van Lingen RA. Pain assessment and analgesia in the newborn: an integrated approach. 2000.
- 9.van der Marel CD, Peters JW, Bouwmeester NJ, Jacqz-Aigrain E, van den Anker JN, Tibboel D. Rectal acetaminophen does not reduce morphine consumption after major surgery in young infants. Br J Anaesth. 2007;98(3):372–379. doi: 10.1093/bja/ael371. [DOI] [PubMed] [Google Scholar]
- 10.Lynn AM, Nespeca MK, Bratton SL, Shen DD. Intravenous morphine in postoperative infants: intermittent bolus dosing versus targeted continuous infusions. Pain. 2000;88(1):89–95. doi: 10.1016/S0304-3959(00)00313-4. [DOI] [PubMed] [Google Scholar]
- 11.Choonara I, Lawrence A, Michalkiewicz A, Bowhay A, Ratcliffe J. Morphine metabolism in neonates and infants. Br J Clin Pharmacol. 1992;34(5):434–437. doi: 10.1111/j.1365-2125.1992.tb05652.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lindbom L, Pihlgren P, Jonsson EN. PsN-Toolkit–a collection of computer intensive statistical methods for non-linear mixed effect modeling using NONMEM. Comput Meth Programs Biomed. 2005;79(3):241–257. doi: 10.1016/j.cmpb.2005.04.005. [DOI] [PubMed] [Google Scholar]
- 13.Karlsson MO, Savic RM RM. Diagnosing model diagnostics. Clin Pharmacol Ther. 2007;82(1):17–20. doi: 10.1038/sj.clpt.6100241. [DOI] [PubMed] [Google Scholar]
- 14.Brendel K, Comets E, Laffont C, Laveille C, Mentre F. Metrics for external model evaluation with an application to the population pharmacokinetics of gliclazide. Pharm Res. 2006;23(9):2036–2049. doi: 10.1007/s11095-006-9067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Comets E, Brendel K, Mentre F. Computing normalised prediction distribution errors to evaluate nonlinear mixed-effect models: the npde add-on package for R. Comput Meth Programs Biomed. 2008;90(2):154–166. doi: 10.1016/j.cmpb.2007.12.002. [DOI] [PubMed] [Google Scholar]
- 16.Montgomery DC, Peck EA. Introduction to linear regression analysis. New York: Wiley; 1982. [Google Scholar]
- 17.Dartois C, Lemenuel-Diot A, Laveille C, Tranchand B, Tod M, Girard P. Evaluation of uncertainty parameters estimated by different population PK software and methods. J Pharmacokinet Pharmacodyn. 2007;34(3):289–311. doi: 10.1007/s10928-006-9046-9. [DOI] [PubMed] [Google Scholar]
- 18.Ette EI. Stability and performance of a population pharmacokinetic model. J Clin Pharmacol. 1997;37(6):486–495. doi: 10.1002/j.1552-4604.1997.tb04326.x. [DOI] [PubMed] [Google Scholar]
- 19.Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Statist Sci. 1986;1(1):54–75. doi: 10.1214/ss/1177013815. [DOI] [Google Scholar]
- 20.Savic RM, Karlsson MO. Importance of shrinkage in empirical bayes estimates for diagnostics: problems and solutions. AAPS J. 2009;11(3):558–569. doi: 10.1208/s12248-009-9133-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yano Y, Beal SL, Sheiner LB. Evaluating pharmacokinetic/pharmacodynamic models using the posterior predictive check. J Pharmacokinet Pharmacodyn. 2001;28(2):171–192. doi: 10.1023/A:1011555016423. [DOI] [PubMed] [Google Scholar]
- 22.Holford N. The visual predictive check—superiority to standard diagnostic (Rorschach) plots. PAGE 14 Abstr 738. 2005. (www.page-meeting.org/?abstract=738)
- 23.Anand KJ, Anderson BJ, Holford NH, et al. Morphine pharmacokinetics and pharmacodynamics in preterm and term neonates: secondary results from the NEOPAIN trial. Br J Anaesth. 2008;101(5):680–689. doi: 10.1093/bja/aen248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Anderson BJ, Holford NH. Mechanism-based concepts of size and maturity in pharmacokinetics. Annu Rev Pharmacol Toxicol. 2008;48:303–332. doi: 10.1146/annurev.pharmtox.48.113006.094708. [DOI] [PubMed] [Google Scholar]
- 25.Kleiber M. Energy Metabolism. Annu Rev Physiol. 1944;6:123–154. doi: 10.1146/annurev.ph.06.030144.001011. [DOI] [PubMed] [Google Scholar]
- 26.West GB, Brown JH, Enquist BJ. A general model for the origin of allometric scaling laws in biology. Science. 1997;276(5309):122–126. doi: 10.1126/science.276.5309.122. [DOI] [PubMed] [Google Scholar]
- 27.West GB, Brown JH, Enquist BJ. The fourth dimension of life: fractal geometry and allometric scaling of organisms. Science. 1999;284(5420):1677–1679. doi: 10.1126/science.284.5420.1677. [DOI] [PubMed] [Google Scholar]
- 28.Mcmahon T. Size and shape in biology. Science. 1973;179(79):1201–1204. doi: 10.1126/science.179.4079.1201. [DOI] [PubMed] [Google Scholar]
- 29.Dodds PS, Rothman DH, Weitz JS. Re-examination of the “3/4-law” of metabolism. J Theor Biol. 2001;209(1):9–27. doi: 10.1006/jtbi.2000.2238. [DOI] [PubMed] [Google Scholar]
- 30.Mahmood I. Application of fixed exponent 0.75 to the prediction of human drug clearance: an inaccurate and misleading concept. Drug Metabol Drug Interact. 2009;24(1):57–81. doi: 10.1515/DMDI.2009.24.1.57. [DOI] [PubMed] [Google Scholar]
- 31.Agutter PS, Wheatley DN. Metabolic scaling: consensus or controversy? Theor Biol Med Model. 2004;1:13. doi: 10.1186/1742-4682-1-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bokma F. Evidence against universal metabolic allometry. Funct Ecol. 2004;18:184–187. doi: 10.1111/j.0269-8463.2004.00817.x. [DOI] [Google Scholar]
- 33.Glazier DS. Beyond the ‘3/4-power law’: variation in the intra- and interspecific scaling of metabolic rate in animals. Biol Rev. 2005;80(4):611–662. doi: 10.1017/S1464793105006834. [DOI] [PubMed] [Google Scholar]
- 34.White CR, Cassey P, Blackburn TM. Allometric exponents do not support a universal metabolic allometry. Ecology. 2007;88(2):315–323. doi: 10.1890/05-1883. [DOI] [PubMed] [Google Scholar]
- 35.Kolokotrones T, Van S, Deeds EJ, Fontana W. Curvature in metabolic scaling. Nature. 2010;464(7289):753–756. doi: 10.1038/nature08920. [DOI] [PubMed] [Google Scholar]
- 36.Mahmood I. Prediction of drug clearance in children from adults: a comparison of several allometric methods. Br J Clin Pharmacol. 2006;61(5):545–557. doi: 10.1111/j.1365-2125.2006.02622.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mahmood I. Prediction of drug clearance in children: impact of allometric exponents, body weight, and age. Ther Drug Monit. 2007;29(3):271–278. doi: 10.1097/FTD.0b013e318042d3c4. [DOI] [PubMed] [Google Scholar]


