Abstract
Much research concerning attention has focused on changes in the perceptual qualities of objects while attentional states were varied. Here, we address a complementary question—namely, how perceived location can be altered by the distribution of sustained attention over the visual field. We also present a new way to assess the effects of distributing spatial attention across the visual field. We measured magnitude judgments relative to an aperture edge to test perceived location across a large range of eccentricities (30°), and manipulated spatial uncertainty in target locations to examine perceived location under three different distributions of spatial attention. Across three experiments, the results showed that changing the distribution of sustained attention significantly alters known foveal biases in peripheral localization.
Keywords: Peripheral localization, Peripheral vision, Space perception, Visual-spatial attention, Sustained attention, Distributed attention
Over the course of a day, we continually alter the degree to which our attention is focused or dispersed across the visual field. This ability to voluntarily adjust the focus of attention allows humans to maximize information processing given the optical and processing limitations of the visual system. Despite much progress in understanding how different attentional states change the way information is processed, this progress has also highlighted new complexities and interactions between attentional operations and the resulting perceptions.
Studies looking at rates of processing have shown that visually attending to a stimulus location or feature speeds target detection time (Carrasco, Giordano, & McElree, 2006; Posner & Peterson, 1990; Posner, Snyder, & Davidson, 1980; Treisman & Gelade, 1980). Other lines of study have shown that directing voluntary attention toward an object can alter object perception. For example, accuracy in speeded target discrimination tasks increases when voluntary attention is directed to a cued location and the target is presented there (Prinzmetal, McCool, & Park, 2005). Another study examined changes in the physical appearance of objects when voluntary attention was focused on or away from an object and found that directing the locus of attention toward a circular array of moving dots increased the perceived size of the array (Anton-Erxleben, Henrich, & Treue, 2007). Spatial attention has also been shown to increase the processing abilities of the visual system, enhancing spatial resolution (Carrasco, Williams, & Yeshurun, 2002; Yeshurun & Carrasco, 1998), texture segmentation (Yeshurun, Montagna, & Carrasco, 2008), and contrast thresholds (Carrasco, Ling, & Read, 2004) relative to conditions when attention is directed away from a target item.
In contrast to studies looking at reaction time and accuracy measures, less is known about what effect attention may have on the perceived locations of objects themselves. To date, most studies examining the effect of attention on spatial localization have used visual cues to direct attention preferentially to one region of space or another (Kosovicheva, Fortenbaugh, & Robertson, 2010; Suzuki & Cavanagh, 1997; Tsal & Bareket, 1999, 2005) or have used dual-task methods that manipulated attentional load or resources (Adam, Davelaar, van der Gouw, & Willems, 2008; Adam, Ketelaars, Kingma, & Hoek, 1993; Prinzmetal, 2005; Prinzmetal, Amiri, Allen, & Edwards, 1998). One line of studies (Prinzmetal, 2005; Prinzmetal et al., 1998) tested the perceived location of target dots briefly presented within a circular region while participants completed easy or hard dual tasks at fixation. Participants were required to move a cursor to the perceived location of the target dot, and the results showed that increasing attentional demands at fixation increased the variability but not the mean perceived location. However, another study using a dual-task paradigm (Adam et al., 2008) found evidence for a foveal bias in perceived location that was modulated by the difficulty of the secondary task at fixation. Here, participants were required to move a cursor to the perceived location of a target presented along the horizontal meridian. The secondary task was a digit identification task at fixation in which participants were required to report one, two, or three numbers presented prior to the target onset. Results showed that participants mislocalized the targets as being closer to the point of fixation than they really were (i.e., a foveal bias) and that the degree of foveal bias increased with the true distance of the target from fixation. Furthermore, increasing the demand of the secondary task from one to three letters or reducing the target duration both increased the size of the foveal bias for a given target location.
While the studies discussed above provide important information on the effects of attentional processing on perceived target location, in all cases targets were presented within 10° of fixation. Thus, by the criteria of Bishop and Henry (1971), these studies only provided information about localization effects within the parafoveal region of the central visual field. However, a significant amount of research has shown systematic biases in the localization of targets presented in both the parafoveal and peripheral regions of the visual field. In one early study, Mateeff and Gourevich (1983) presented small, circular targets that were briefly flashed at various eccentricities above a stable numbered scale along the horizontal meridian. They found a foveal bias when estimating the target’s location, consistent with the results of Adam et al. (2008). That is, while the numbered scale used to reference the target location was visible throughout a trial, observers reported the location of the target to be at a smaller distance from the fovea than it actually was, and this tendency to underestimate the eccentricity of the stimulus increased as targets were presented more peripherally. Though one study (Mapp, Barbeito, Bedell, & Ono, 1989) failed to replicate these findings (but see Rose & Halpern, 1992), other studies (Eggert, Ditterich, & Straube, 2001; Müsseler & van der Heijden, 2004; Müsseler, van der Heijden, Mahmud, Deubel, & Ertsey, 1999) using relative and absolute localization judgments of successively presented peripheral targets found results consistent with a foveal bias.
Of particular interest to the present article are the results of studies looking at the effect of placing landmarks or distractor items in the visual display while participants report the perceived location of briefly presented peripheral targets. Results from these studies (Diedrichsen, Werner, Schmidt, & Trommershäuser, 2004; Eggert et al., 2001; Kerzel, 2002; Makovski, Swallow, & Jiang, 2010; Uddin, Kawabe, & Nakamizo, 2005; Werner & Diedrichsen, 2002; Yamada, Kawabe, & Miura, 2008) have shown that in many cases, distortions in perceived location are shifted toward the location of the distractor items, reducing the foveal bias that is otherwise seen when the distractors are located at further eccentricities than the target. Currently, there is a proposal that the underlying cause of this attraction effect is due to attention being shifted toward the location of the distractor item (Kerzel, 2002; Yamada, et al., 2008). Under this model, the largest foveal biases occur when attention is focused at the point of fixation and no landmarks or distractors are present in the display. However, alternative models for these effects have been proposed, including a spatial memory averaging hypothesis in which the perceived location of the target stimulus is a weighted average of the true location of the target and salient neighboring landmarks (Hubbard & Ruppel, 2000). Given that alternative stimulus-based proposals exist for alterations in perceived location when landmarks are present, and that prior studies on attention have manipulated stimulus qualities, it is important to develop new paradigms that can manipulate aspects of visual attention without introducing distractors or altering the physical qualities of landmarks in the display.
The purpose of the present study was to further explore changes in perceived location over a large range of eccentricities under different attentional conditions. However, in contrast to studies that have used dual-task or cuing paradigms in which multiple objects beside the target are present in the display, we investigated how changes in the distribution of sustained attention could alter the perceived location of targets across the visual field in the absence of foveal distractor items and landmarks. A single target dot was briefly presented (150 ms) in the parafoveal or peripheral visual field across several eccentricities. We used a measure similar to those reported initially by Temme, Maino, and Noell (1985) and Mateeff and Gourevich (1983), in which participants made verbal magnitude judgments about the perceived location of a target dot briefly flashed along one of the cardinal axes. In addition, we manipulated the distribution of voluntary attention across the visual field by telling participants before each block along which of the four cardinal axes the target could appear. The number of relevant axes was systematically varied: (1) all four axes, to induce a broad distribution of attention (attend all); (2) the vertical or horizontal meridian (between blocks), to induce a more narrowed, elongated distribution of attention (attend meridian); and (3) one of the four axes (between blocks) to induce an even more narrowed distribution of attention (attend axis). The attention manipulation was therefore a sustained attention task related to the area of space that the participants attended throughout a block of trials, while allowing for comparison between different regions of the visual field under the different attention conditions. As this paradigm was designed to test perceived location, and not detection ability, white target dots were presented on a black background to maximize stimulus contrast. This assured that the target’s visibility was always above threshold.
Magnitude estimates were made relative to the edge of a circular aperture placed over the monitor, and thus, all targets were presented within the same defined area. This removed the need for visible scales across the regions or multiple stimuli on each trial. While the ability of individuals to accurately make magnitude judgments varies, the present study was designed to examine how magnitude judgments to the exact same stimulus location change as attentional distribution varies. Moreover, while this is a type of relative judgment task, it differs from previous designs (Mateeff & Gourevich, 1983; Müsseler & van der Heijden, 2004; Müsseler et al., 1999) in which localization judgments were made relative to a comparison object or landmark present within the display. It was also not possible for participants to direct attention solely to the edge of the aperture to make a magnitude judgment. Rather, their judgments had to be based on the entire length of the axis on which a target appeared. This is the aspect of the design that enabled us to manipulate the distribution of attention rather than just shifts of attention from one region of the display to another within a block of trials and to control for any extra distractor objects in the display.
Based on previous findings (Mateeff & Gourevich, 1983), it was hypothesized that participants would show a foveal bias: underestimating perceived target locations, with the degree of error increasing with the true eccentricity of the target. More importantly, if sustained attention not only alters perceived stimulus qualities but also perceived location, as suggested by the results of Adam et al. (2008), foveal biases should be reduced or eliminated as attention is focused on smaller regions of visual space.
Experiment 1
Method
Participants
Twelve healthy undergraduates (9 females; mean age 19.4 ± 1.1 years) participated in the main experiment for course credit. An additional 4 undergraduates (3 females; mean age 21.5 years) participated at a later time in the eye-movement control condition for course credit. All reported normal or corrected-to-normal vision and no ocular disorders. Participants with corrected-to-normal vision wore contact lenses. Glasses, astigmatism, or any indication of ocular disease were means for exclusion. This research was approved by the University of California’s Committee for the Protection of Human Subjects and followed the tenets of the Declaration of Helsinki.
Materials and procedure
Participants sat 25.4 cm from the computer monitor (ViewSonic G225f, refresh rate = 100 Hz). A chin-and-forehead rest stabilized head position. A large black piece of cardboard, 91.5 × 61.5 cm, with a circular aperture (14.67 cm or 30° radius) cut out, was centered over the computer screen. The experiment was run in a dark room. The only border visible to the participants was the edge of the circular aperture due to the glow of the computer screen. Aside from adjusting the distance to the computer screen, care was taken before running each participant to assure that the height and lateral placement of the monitor were centered such that the participant could fixate a cross at the center of the screen with his or her eyes in primary position. A digital level was used to check that the monitor was not tilted, and participants verbally confirmed with the lights on that the monitor appeared centered.
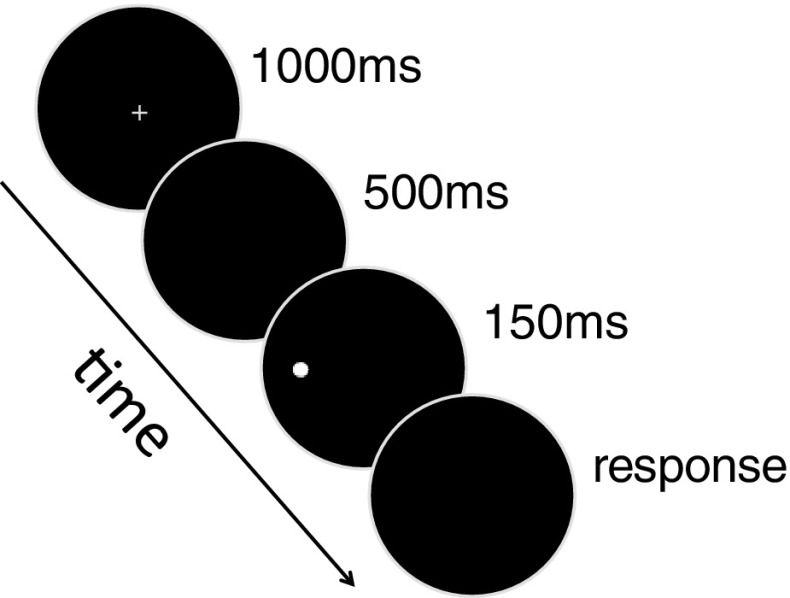
All experimental parameters were executed using Presentation software (Version 11.1, www.neurobs.com). Figure 1 shows an example of a trial sequence. On every trial, participants first viewed a blue fixation cross (1° in visual angle, 10 cd/m2) for 1,000 ms on a black background (0.3 cd/m2). After a 500-ms blank, a white target dot (1° diameter; 84 cd/m2) appeared for 150 ms in the participant’s peripheral visual field, and participants verbally estimated how far out from fixation the target appeared to be by giving magnitude estimates between 0 (central fixation) and 100 (edge of aperture). The experimenter sat next to the participant in the room and recorded all of the responses. The ISI was long enough to eliminate apparent motion between the fixation cross and target dot, but short enough that participants were able to maintain fixation on the cross. The fixation cross was colored blue to help eliminate apparent motion.
Fig. 1.
Trial sequence. The monitor was covered with a large black piece of cardboard with a circular aperture (30° radius) cut out. Every trial began with a blue fixation cross in the center of the screen. This was followed by a blank screen, and then a 1°-diameter target was briefly presented at one of seven equally spaced eccentricities between 4° and 28° along one of the four cardinal axes. The fixation cross and target are shown at a larger scale here for clarity
After the experimenter recorded the participant’s response for a given trial, there was a fixed intertrial interval of 500 ms before the next trial started. As participants made verbal responses that were recorded by the experimenter, it was not possible to determine reaction times in this task. This is because any measure of reaction time would be contaminated with variations in how long it took the experimenter to enter the participant’s response on a given trial.
There were seven blocks of trials with three levels of attentional distribution along the horizontal and vertical meridians, as follows. (1) Attend axis condition: four blocks in which the target appeared only along the left, right, upper, or lower axis. (2) Attend meridian condition: two blocks in which the target appeared only along the horizontal or vertical meridian. (3) Attend all condition: one block in which the target appeared randomly along any of the four axes. Before beginning each block, participants were verbally informed about the axis/axes on which the target could appear, and a large white cross was also displayed at this time, with the axis/axes that the participants were to attend to highlighted in blue. In every block, seven eccentricities were tested along each axis (4°, 8°, 12°, 16°, 20°, 24°, and 28°), for a total of 28 possible target locations in the attend all block, 14 target locations in each of the attend meridian blocks, and 7 target locations in each of the attend axis blocks. Because the possible axes on which the target might appear did not change within a block and the target locations spanned almost the entire length of each axis, the task manipulated the distribution of sustained attention across the visual field over long periods of time, as opposed to other studies of voluntary attention in which participants were cued to move the focus of their attention to a different location on every trial. Target locations were randomly tested with five repeats per location. Before beginning the experiment, participants first completed 10 practice trials in the attend all condition to familiarize them with the task. Participants were also informed that they should respond as quickly and accurately as possible. It was explained that the study was designed to examine where participants perceived the target locations and that it was important for them to give a response as soon as possible after the target was presented. Feedback was given regarding response times after the practice trials. Block order was randomized across participants to control for possible learning effects across blocks.
Eye-movement control condition
Four new, naïve participants completed the task at a later time while eye movements were monitored. The paradigm for this test was exactly the same as in the main experiment, with one exception. A commercial infrared camera (LTCMW304C5 by LTS, Houston, TX) was set up in front of the aperture with a monitor off to the side such that the experimenter was able to continuously monitor the right eye of the participant. If participants made an eye movement before a magnitude estimate was given during a trial, the experimenter pressed the space bar, a tone was sounded, and no magnitude estimate was recorded for that trial. The discarded trial was then repeated at a random time later during that block. This assured that five valid repeats for each target location tested were still obtained at the end of each block.
Results
Localization errors
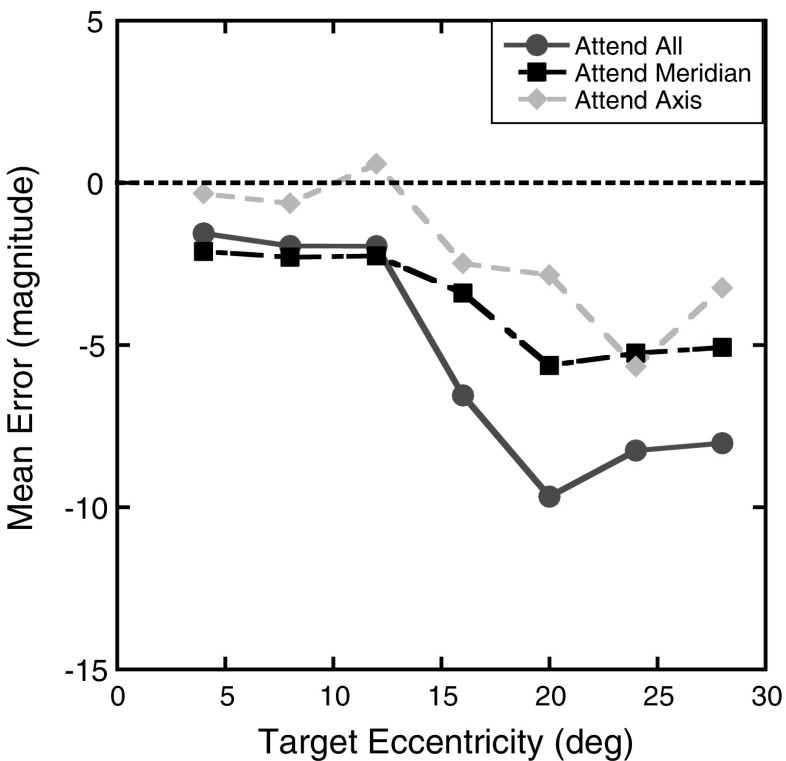
The task required participants to give magnitude estimates of the perceived target location relative to the aperture’s edge and fixation. This type of relative judgment is essentially a percentage reflecting the ratio of the perceived target eccentricity relative to the perceived total extent of the stimulus space (i.e., the perceived eccentricity of the aperture edge). For the seven target eccentricities tested here (4°, 8°, 12°, 16°, 20°, 24°, and 28°) with the aperture edge located at 30° eccentricity, the true magnitudes of the targets relative to the aperture edge were 13.3, 26.7, 40, 53.3, 66.7, 80, and 93.3, respectively. Magnitude errors were calculated by subtracting the true magnitude of each target location from participants’ magnitude estimates. Thus, a negative magnitude error indicates an underestimation of the true target location (i.e., a foveal bias), and a positive magnitude error indicates an overestimation (i.e., a peripheral bias). Since the true eccentricity of the aperture edge and target locations were known, it was possible to recover errors in terms of degrees of visual angle as well. Therefore, to aid in comparisons with previous studies and to provide a more meaningful unit of measurement, all figures show errors in degrees of visual angle as well as magnitude units. Figure 2 shows the mean magnitude errors as a function of eccentricity and axis for each of the three attention conditions. As can be seen, participants showed a foveal bias with a general tendency to underestimate the distance of the target from fixation. A 3 (attention) × 4 (axis) × 7 (eccentricity) repeated measures ANOVA (using the Greenhouse–Geisser correction when appropriate) was run on the mean magnitude errors. This analysis resulted in a main effect of eccentricity, with participants showing larger underestimations the farther the target was from fixation, F(2.1, 22.6) = 4.58, p = .02. Underestimations also increased the more attention was distributed across the visual field, as seen in the significant main effect of attention condition, F(2, 22) = 6.83, p < .01. A main effect of axis was also found, with greater underestimations along the horizontal than along the vertical meridian, F(3, 33) = 12.62, p < .01. All two-way interactions also reached significance, showing that the degree of underestimation with eccentricity depended on the axis and attention condition [Attention × Eccentricity: F(12, 132) = 2.93, p < .01; Attention × Axis: F(6, 66) = 2.74, p = .02; Eccentricity × Axis: F(18, 198) = 2.96, p < .01]. The patterns of errors across the eccentricities tested differed along the horizontal and vertical meridians in the three attention conditions. However, the three-way interaction did not reach significant levels, F(36, 396) = 1.38, p = .08. A trend analysis showed an overall linear increase in foveal bias with eccentricity, F(1, 11) = 8.02, p = .02. Tests for quadratic and cubic trends did not reach significant levels (p > .86 for both).
Fig. 2.
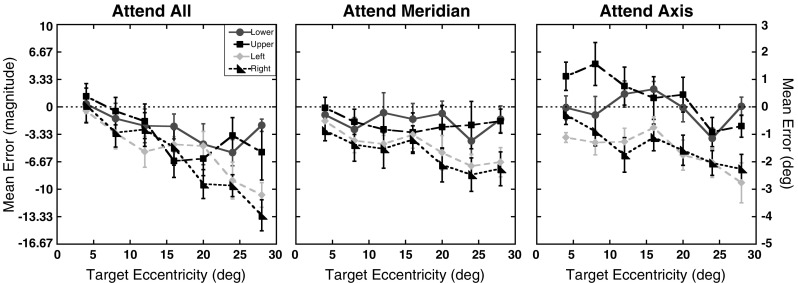
Experiment 1 magnitude errors: Mean magnitude errors for each of the four axes tested as a function of target eccentricity (in degrees) for the three attention conditions. The right y-axis shows the errors in units of degrees of visual angle. Results for the lower on-screen axis are shown as circles, those for the upper axis as squares, for the left axis as diamonds, and for the right axis as triangles. Error bars represent ±1 SE. The dotted lines at 0 represent the expected performance if no distortion exists
Uncertainty in perceived location
Since the attention conditions were designed to manipulate uncertainty in where targets could appear within a block of trials but not in the location where they did appear on a given trial, the targets were presented at the maximum contrast possible (Weber contrast = 278%). However, to test for systematic changes in positional uncertainty, analyses were conducted on the standard deviations of the participants’ magnitude errors. Figure 3 shows the standard deviations of the magnitude errors as a function of eccentricity and axis for the three attention conditions. The standard deviations were submitted to a 3 (attention) × 4 (axis) × 7 (eccentricity) repeated measures ANOVA. As can be seen in Fig. 3, standard deviations did not significantly differ across the three attention conditions, F(2, 22) = 0.21, p = .81. However, there were significant main effects of axis, F(3, 33) = 4.24, p = .01, and eccentricity, F(6, 66) = 3.57, p < .01. None of the interactions reached significant levels (ps > .46). A trend analysis on the standard deviations revealed a significant quadratic trend for eccentricity, F(1, 11) = 10.10, p < .01. The linear and cubic trends were not significant (linear: p = .86; cubic: p = .15). Post-hoc comparisons, using the Sidak–Bonferroni correction for multiple comparisons (αS-B = .0085), revealed that the main effect of axis was driven by larger standard deviations along the upper axis relative to the left and right axes (ps ≤ .008), but not along the lower axis (p = .04). Standard deviations did not differ among the other three axes (ps ≥ .21).
Fig. 3.
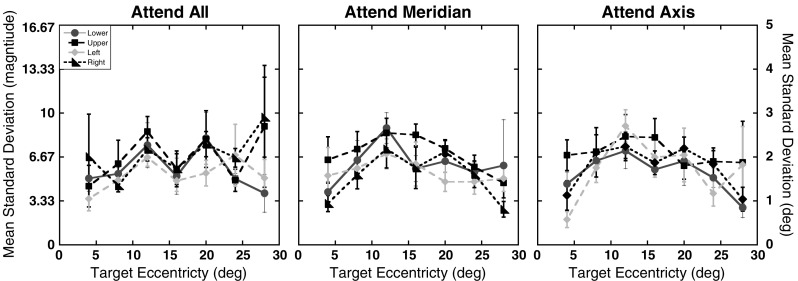
Experiment 1 positional uncertainty: Standard deviations of the magnitude errors as a function of target eccentricity (in degrees) and axis tested for the three attention conditions. The same formatting is used here as in Fig. 2. Error bars represent ±1 SE
Spatial metric(s) underlying localization errors
While the localization errors showed differences in spatial distortion that varied with attentional distribution, eccentricity, and axis tested, it was not possible to determine from the errors alone whether this distortion reflected a deviation from a linear mapping, a change in scaling, or some combination of the two. To assess the underlying source of these changes, a hierarchical modeling scheme was applied in fitting a two-parameter power function to the raw participant data. The predefined origin (the fixation point) was presented on every trial, eliminating the need for a constant parameter in the model. For every participant, power functions as shown in Eq. 1 were fit to the 35 magnitude estimates (7 Eccentricities × 5 Repeats) for each of the 12 conditions (3 Attention Conditions × 4 Axes).
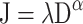 |
1 |
In this equation, J = the magnitude estimate, D = the targets’ true magnitude, λ = a global scaling factor that compresses or expands all values by a constant amount, and α = an exponent that determines whether the metric is linear (i.e., when α = 1). For every participant, two functions were fit, one in which both the λ and α parameters were free to vary and one in which the α parameter was fixed at α = 1 (GraphPad Prism, San Diego, CA). The quality of fits was assessed by comparing the change in the amount of variance explained relative to the change in degrees of freedom using an F ratio. For the one-parameter model, the average adjusted R 2 was .91 (range: .42 to .97). For the two-parameter model, the average adjusted R 2 was .92 (range: .6 to .98). Across the 12 conditions for each of the 12 participants, 51% of the 144 functions showed a significantly better fit by the two-parameter model. While half of the models did show a better fit when exponents were allowed to vary from 1, the increase in variability explained was modest: The average R 2 results showed only a 1% increase on average for the two-parameter model over a one-parameter model. Given the high level of explained variance for the one-parameter model and the only modest increase in variance explained when the exponent was treated as a free parameter, these results suggest that the magnitude estimates were best fit by a linear model. The estimates from this model were therefore used in further analyses.
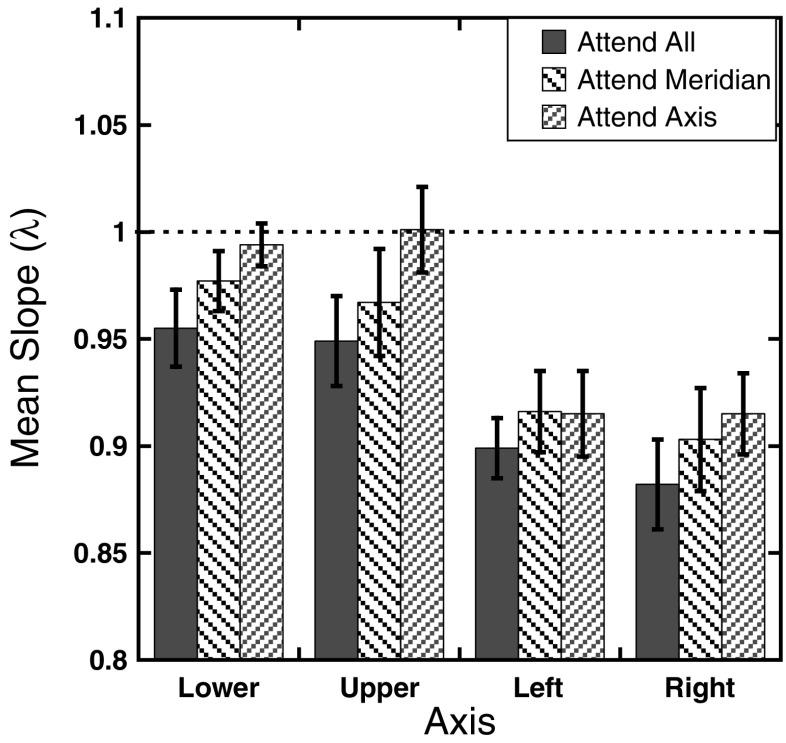
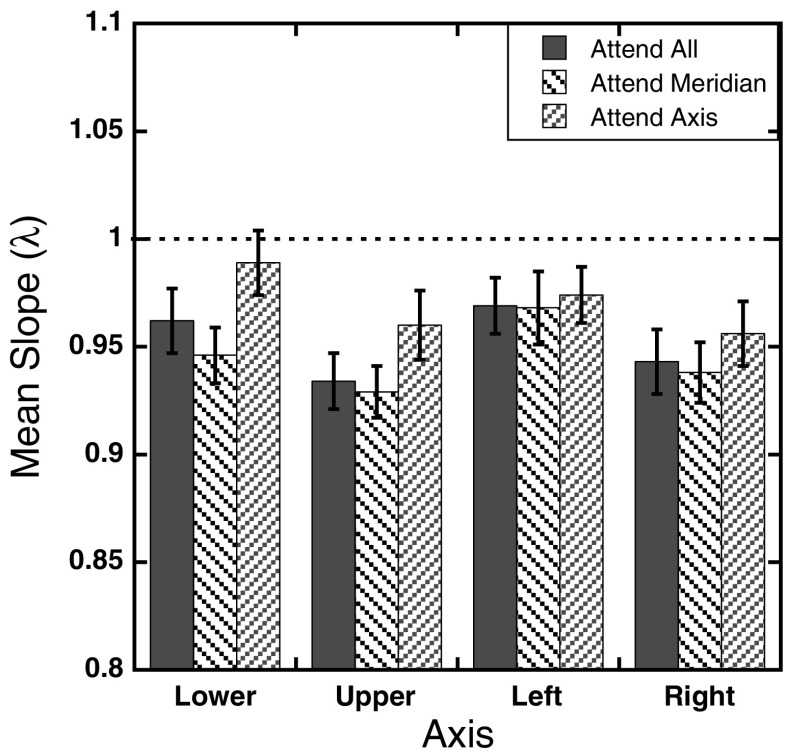
Figure 4 shows the mean estimated slopes (λ) across the three attention conditions for each of the four axes tested. To further examine the effect of attention on perceived location, a 3 (attention) × 4 (axis) repeated measures ANOVA was used to analyze the estimated slopes, with Greenhouse–Geisser corrections applied where appropriate. The results show a main effect of attention, with slopes increasing monotonically as attention was focused on smaller regions of space, F(2, 22) = 6.79, p < .005. There was also a main effect of axis, F(3, 33) = 16.69, p < .001. The Attention × Axis interaction was not significant, F(3.42, 37.64) = 0.73, p = .56.
Fig. 4.
Experiment 1 slope parameters: Mean estimated slope parameters, λ, as a function of axis tested for the three attention conditions after fitting the individual magnitude estimates to the function J = λD. Error bars represent ±1 SE. The dotted line at 1 represents the expected performance if the mapping is undistorted
Discussion
Attentional effects on foveal bias
Previous studies found that targets flashed in the peripheral visual field tend to be mislocalized toward the fovea (Mateeff & Gourevich, 1983; Müsseler et al., 1999). The results of Experiment 1 both replicate this finding and extend it to include measurements based on magnitude estimates relative to a stable external visual boundary (i.e., an aperture’s edge). More importantly, the results demonstrate that changes in the distribution of sustained voluntary attention across the visual field, independent of other landmarks present in a display, can alter the degree to which such targets are mislocalized. As seen in Fig. 2, the Attention × Eccentricity interaction reflects the different rates of underestimation with eccentricity across attention conditions. This effect is most evident when comparing the magnitude errors in the attend all and attend axis conditions, with small errors for the close eccentricities but large underestimations at the farther eccentricities in the attend all condition. In contrast, errors for the attend axis condition were small for both close and far eccentricities. Interestingly, the magnitude estimates in the attend meridian condition showed a pattern that was similar to the attend all condition for the closer target eccentricities (<12°) but resembled the attend axis condition for the farther eccentricities.
The effect of attentional distribution on perceived location is further seen in the slope estimates of Fig. 4, which show a global decrease in scaling when attention is distributed across the entire visual field relative to when attention is focused on a specific region. Previous studies (Adam et al., 2008; van der Heijden, van der Geest, de Leeuw, Krikke, & Müsseler, 1999) reported that the degree to which participants underestimate the distance of a target from fixation is approximately 10% of the eccentricity of that target. In both of these studies, targets were only presented along the horizontal meridian, and inspection of Fig. 4 shows a similar degree of underestimation for targets presented along the horizontal meridian, here with slopes around 0.90. Similar degrees of underestimation were not, however, found for targets along the vertical meridian. These results will be discussed more fully below.
One concern that could be raised about the magnitude errors is whether the differential distributions of the eccentricity effects across attention conditions are the result of a true distortion in perceived location or arise from degradation in stimulus quality due to changes in sampling and cortical processing in the peripheral visual field (Banks, Sekuler, & Anderson, 1991; Bishop & Henry, 1971; Goldstein, 2002; Horton & Hoyt, 1991; Johnston, 1986; Mullen, Sakurai, & Chu, 2005). The analyses of the standard deviations addressed this question and showed a quadratic, inverted-U trend, verifying that the linear increase in foveal bias across eccentricities cannot be explained by uncertainty in perceived target location per se. Rather, the results are more consistent with the participants using the fixation point and edge of the aperture as landmarks, with uncertainty in estimates reaching a maximum at the points most distant from these two landmarks. However, unlike previous studies (Diedrichsen et al., 2004; Kerzel, 2002; Uddin et al., 2005; Werner & Diedrichsen, 2002; Yamada et al., 2008), which showed that the presence of landmarks or distractor elements in a display can reduce foveal bias (i.e., they induce a bias in localization toward the landmark), the results of the present study show that the edge of the aperture and point of fixation served only to reduce variability in responses. Errors in localization consistently showed the largest foveal bias for target locations closest to the aperture edge. Thus, the edge of the aperture was not able to serve as a landmark in the same manner that has been reported previously in the literature. Importantly, the lack of any main effect or interaction with attention condition in the analysis of the standard deviations suggests that uncertainty in perceived location did not vary systematically as attention was spread across the visual field.
Vertical/horizontal differences
While the three-way interaction for the magnitude errors did not reach significant levels, a trend was observed. Specifically, the pattern of results seen in Fig. 2 suggests that there was a qualitative difference in performance along the horizontal and vertical meridians across the three attention conditions. Magnitude errors tended to be smaller along the vertical meridian in all three attention conditions, and the rates at which magnitude errors changed with eccentricity also tended to be smaller along the vertical meridian. The largest dissociation in performance along the horizontal and vertical meridians is seen in the attend axis condition. Here, participants actually overestimated target locations along the upper axis for most of the points, and there was almost no error along the lower axis. Differences in foveal bias across the two meridians are also visible in the slope parameters. As can be seen in Fig. 4, slope estimates were higher for the upper and lower axes than the left and right axes across the three attention conditions. Moreover, the slope estimates for the attend axis condition show a near-perfect scaling across eccentricities along the vertical meridian, with slopes approaching a value of 1 (lower axis = 0.994, upper axis = 1.001). In contrast, slopes estimates along the horizontal meridian ranged from 0.882 to 0.916.
This result is important, as it shows that participants were able to give accurate verbal estimates of the target locations, at least under some circumstances. This increases confidence that errors along the other axes and different attention conditions reflect distortions in perceived target locations and not just an inability to give accurate verbal judgments, since the same eccentricities were tested in all cases.
No predictions were made prior to testing about variations in localization performance across the two meridians. In the peripheral localization literature, no definitive evidence exists for differences in performance across the two meridians. One study by Temme et al. (1985) found that for eccentricities larger than 20°, overestimations in perceived eccentricity were greater along the upper axis than the lower axis, and larger overall along the vertical meridian than along the horizontal meridian. However, this study differed from the present study in that participants made judgments relative to their perceived visual field extent, and the results show a consistent peripheral bias in perceived location. Moreover, another study (Bock, 1993) that found peripheral biases in perceived eccentricity using a pointing task found comparable biases across the two meridians, though only locations within the central 10° were tested. While it is not clear why performance varied across the horizontal and vertical meridians in the present task, both neurobiological and visual distinctions between the two meridians and across the lower and upper axes have been found in a variety of tasks (Carrasco, Giordano, & McElree, 2004; Carrasco, Talgar, & Cameron, 2001; McAnany & Levine, 2007; Previc, 1998; Previc & Intraub, 1997). At least one study (Mackeben, 1999) also found greater cuing benefits when stimuli were presented along the horizontal rather than the vertical meridian in a letter identification task. Similarly, here the largest changes in localization errors across the three attention conditions occurred along the horizontal meridian. However, it has also been shown that individual differences exist in the degree to which attentional facilitation occurs in different regions of the visual field for a given eccentricity (Altpeter, Mackeben, & Trauzettel-Klosinski, 2000; Mackeben, 1999). Since most studies on localization in the visual periphery have only tested along the horizontal meridian, it is not possible to determine whether the present results reflect an inherent anisotropy across the meridians in this type of task, a property of the participant population used in the study, or some combination of the two. While the horizontal–vertical anisotropy may appear to add undue complexity to the question of how attention changes representations of visual space, these results show that different effects of attention along the horizontal and vertical meridians can be isolated by analyzing parameters that tease apart the underlying spatial metric.
Potential confounds
One concern about the present data is whether or not eye-movement patterns differed across the three attention conditions, because it is well documented that eye movements toward target locations can improve localization performance (Adam et al., 1993; Enright, 1995; Uddin, 2006). However, previous studies that have examined localization and attention with and without eye movements have found only modest benefits for localization performance with eye movements at the target duration used in the present study (Adam et al., 1993, 2008). This is supported by another study examining shifts of attention and eye movements that found typical saccade latencies of around 200 ms (Hoffman & Subramanian, 1995). In the present study, the presentation time of the target was kept very brief (150 ms) to help prevent participants from making eye movements to the targets once they appeared. A more problematic issue is whether participants moved their eyes before the target appeared. While the instructions emphasized maintaining fixation at the center of the screen, the optimal strategy to locate an object in a given region would be to fixate in the center of the region along which the target might appear. For the attend all and attend meridian conditions, eye movements were not of great concern, since the optimal location corresponded to the center of the screen. Eye movements are of greater concern in the attend axis conditions, in which participants knew the direction in which the target would appear. Thus, while the timing of target presentations was the same across the attention conditions, it is possible that in the attend axis condition, when participants knew the direction in which the target would appear, they made eye movements along the tested axis prior to target onset on some trials, and this reduced their errors. The eye-movement control condition was run in order to address this concern.
Figure 5 shows the mean errors for the eye-movement control condition as a function of eccentricity and attention condition. Given the small number of participants who completed this task, statistical analyses on the data were not completed. However, inspection of Fig. 5 shows that the pattern of errors replicates the overall pattern found in the main experiment, with errors increasing with increasing eccentricity and larger errors found as attention was distributed across more of the visual field. If participants did move their eyes along the attended axis in the main experiment, and this in turn led to reductions in foveal bias, the data from the eye-movement control condition should not show significant differences across the three attention conditions; rather, the same degree of underestimations would be expected across the three attention conditions. The fact that the expected differences were found in the control condition therefore suggests that the differences in localization errors across the three attention conditions in the main experiment cannot be explained by systematic differences in eye-movement patterns.
Fig. 5.
Experiment 1 eye-movement control condition: Mean magnitude errors for the 4 participants who completed this condition as a function of target eccentricity (in degrees) for the three attention conditions. Means are shown for the attend all condition as circles, for the attend meridian condition as squares, and for the attend axis condition as diamonds. The dotted line at 0 represents the expected performance if no distortion exists
Another potential confound in the original design is that the number of possible target locations covaried with the attention manipulation. While participants were informed before each block that the target could appear anywhere along the attended axes, and they should therefore maintain attention across the space, it is possible that variations in the number of target locations tested influenced the participants’ responses. Because the number of target locations tested in each block and changes in the distribution of attention cannot be untangled in the present design, a second experiment was conducted to address this issue.
Experiment 2
The second experiment followed the same procedure as the first, with the following exceptions. In the attend all condition, only four eccentricities were tested along each axis, resulting in a total of 16 target locations tested. The same seven eccentricities tested in Experiment 1 were tested in the two attend meridian conditions, resulting in a total of 14 target locations in each of the two blocks. Finally, in the four attend axis blocks, 14 eccentricities were tested along each axis. Thus, the total number of target locations tested in each block of trials was either 16 or 14 locations. If the attention effects found in Experiment 1 are the result of changes in the number of target locations tested within a block, no differences across the three attention conditions should be found. On the other hand, if changes in the errors seen in Experiment 1 are due to changes in the distribution of attention across the axes being attended, the same pattern of errors observed in Experiment 1 should be observed here.
Method
Participants
Eleven undergraduates (7 females; mean age 19.6 ± 1.0 years) participated in this experiment for course credit. None of the participants had participated in the previous experiment, and the same exclusion criteria were applied as before. All gave informed consent as approved by the University of California before participating.
Materials and procedure
The same stimulus parameters and apparatus were used as in Experiment 1. For the attend all condition, the eccentricities tested were: 4°, 12°, 20°, and 28°. In the attend meridian condition, seven eccentricities tested were: 4°, 8°, 12°, 16°, 20°, 24°, and 28°. Finally, in the attend axis condition, eccentricities were sampled every 2°, to include: 2°, 4°, 6°, 8°, 10°, 12°, 14°, 16°, 18°, 20°, 22°, 24°, 26°, and 28°. As the total number of targets across all attention conditions increased from 84 in Experiment 1 to 100 in this experiment, the number of repetitions for each target location was reduced to four per block. Therefore, there were a total of 400 experimental trials in this experiment. As before, all participants completed 10 practice trials before beginning the experiment, and block order was varied across participants.
Results
Localization errors
Magnitude errors were calculated in the same way as in Experiment 1, and the mean localization errors are shown in Fig. 6. Only four eccentricities (4°, 12°, 20°, and 28°) were tested in all three attention conditions. The mean magnitude errors for these four eccentricities were therefore run in a 3 (attention) × 4 (axis) × 4 (eccentricity) repeated measures ANOVA (using the Greenhouse–Geisser correction when appropriate). As in the previous experiment, there was a significant effect of attention, with larger underestimations observed when attention was distributed across the visual field, F(2, 20) = 11.87, p < .001. Magnitude errors also increased with eccentricity, F(3, 30) = 13.31, p < .001. In contrast to Experiment 1, no difference was found in magnitude errors across the four axes tested, F(2.04, 20.42) = 1.03, p = .40. Moreover, none of the interactions were significant (ps ≥ .32). Also contrary to the first experiment, a trend analysis for the Eccentricity factor showed a significant linear trend, F(1, 10) = 25.13, p = .001, and a significant cubic trend, F(1, 10) = 6.11, p = .03. The quadratic trend was not significant, F(1, 10) = 1.67, p = .23.
Fig. 6.
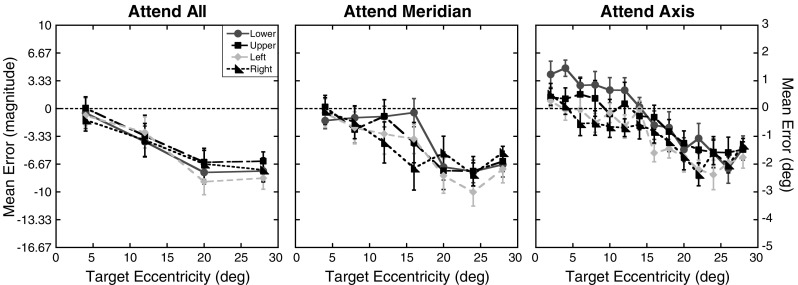
Experiment 2 magnitude errors: Mean magnitude errors for each of the four axes tested as a function of target eccentricity (in degrees) for the three attention conditions. The right y-axis shows the errors in units of degrees of visual angle. Results for the lower on-screen axis are shown as circles, those for the upper axis as squares, for the left axis as diamonds, and for the right axis as triangles. Error bars represent ±1 SE. The dotted lines at 0 represent the expected performance if no distortion exists
Uncertainty in perceived location
As in Experiment 1, analyses on the standard deviations were conducted to assess whether positional uncertainty increased with eccentricity or across the different attention conditions. Figure 7 shows the mean standard deviations as a function of axis and eccentricity for the three attention conditions. A 3 (attention) × 4 (axis) × 4 (eccentricity) repeated measures ANOVA was used to analyze the mean standard deviations for the four eccentricities tested in all attention conditions, with Greenhouse–Geisser corrections applied where necessary. Analyses revealed a significant effect of eccentricity, F(3, 30) = 24.81, p < .001. There was no main effect of axis, F(3, 30) = 1.50, p = .24, or of attention, F(2, 20) = 0.40, p = .68. The Axis × Attention interaction was also not significant, F(6, 60) = 1.06, p = .39. However, the Attention × Eccentricity interaction was significant, with a shift in the peak standard deviations from 12° in the attend all condition to 20° in the attend meridian and attend axis conditions, F(6, 60) = 2.57, p = .03. The Axis × Eccentricity interaction was also significant, F(9, 90) = 2.50, p = .01. The three-way interaction was not significant, F(18, 180) = 1.36, p = .16. As in Experiment 1, a trend analysis run on the main effect of eccentricity showed a significant quadratic trend, F(1, 10) = 51.44, p < .001. The linear and cubic trends were not significant [linear: F(1, 10) = 0.13, p = .72; cubic: F(1, 10) = 0.03, p = .87].
Fig. 7.
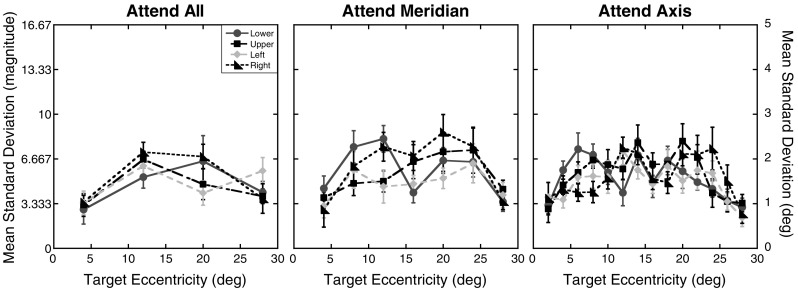
Experiment 2 positional uncertainty: Standard deviations of the magnitude errors as a function of target eccentricity (in degrees) and axis tested for the three attention conditions. The same formatting is used here as in Fig. 6. Error bars represent ±1 SE
Spatial metric(s) underlying localization errors
To assess the spatial metric the participants used to make magnitude judgments across eccentricities, the same fitting procedure described in Experiment 1 was applied. For the one-parameter model, the average adjusted R 2 was .92 (range: .66 to .98). For the two-parameter model, the average adjusted R 2 was .93 (range: .77 to .99). Across the 12 conditions for each of the 11 participants, only 39% of the 132 functions showed a significantly better fit by the two-parameter model. In part, this difference can be explained by the smaller number of eccentricities tested in the attend all condition. With only four eccentricities, the increase in the number of free parameters increases the risk of model overfitting. Regardless, given that 61% of the conditions showed a better fit with the one-parameter model, these results suggest that the magnitude estimates are best fit by a linear model, as found in Experiment 1. The estimates from this model were therefore used in further analyses.
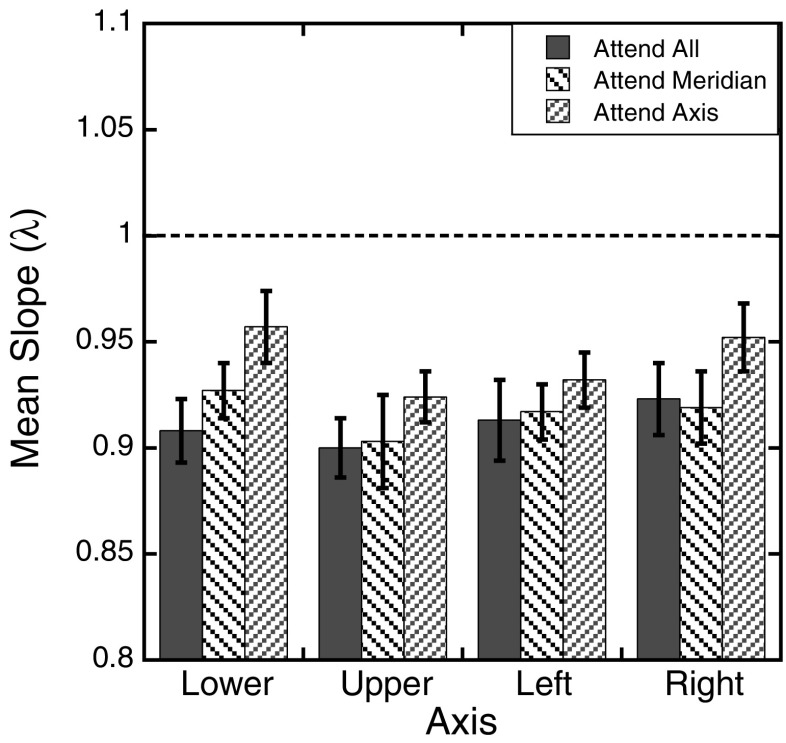
Figure 8 shows the mean estimated slopes (λ) across the three attention conditions for each of the four axes tested. A 3 (attention) × 4 (axis) repeated measures ANOVAs was used to analyze the estimated slopes. The results showed a main effect of attention, with slopes increasing as attention was focused on smaller regions of space, F(2, 20) = 4.87, p = .02. As expected given the pattern of the magnitude errors, the slopes did not differ across the four axes tested, F(3, 30) = 1.27, p = .30. The Attention × Axis interaction was also not significant, F(6, 60) = 0.52, p = .79.
Fig. 8.
Experiment 2 slope parameters: Mean estimated slope parameters, λ, as a function of axis tested for the three attention conditions after fitting the individual magnitude estimates to the function J = λD. Error bars represent ±1 SE. The dotted line at 1 represents the expected performance if the mapping is undistorted
Discussion
The findings of Experiment 2 support the hypothesis that changes in the distribution of attention modulate foveal biases in peripheral localization. In contrast to Experiment 1, the number of target locations were equated as best possible across the three attention conditions. Significant reductions in foveal biases were again found in the attend axis condition relative to the attend all and attend meridian conditions. This is supported by changes in both the magnitude errors themselves and the slope parameters.
There were a couple of differences found in the pattern of errors across the two experiments. Inspection of Figs. 2 and 6 suggests a reduction in foveal bias for the farthest eccentricity tested in the attend all condition along the horizontal meridian. While there were a total of 16 target locations in this block across the four axes, only four distinct eccentricities were tested. Given the small number of distinct eccentricities, it is plausible that in this condition participants were more likely to be aware that the same eccentricities across each axis were repeatedly tested. This, in turn, may have caused a reduction in target uncertainty once the target appeared over the course of the block. This interpretation is supported by a slight reduction in the average standard deviations of responses in the attend all condition across the two experiments, which is not seen for the other two attention conditions.
A more significant difference across the two experiments is the lack of a main effect of axis or an interaction between axis and attention condition for either the magnitude errors or the slope parameters. In the first experiment, foveal biases were significantly smaller along the vertical than the horizontal meridian. In the present experiment, no differences in magnitude errors were observed in the attend all condition across the two meridians. Across all attention conditions, the magnitude of errors along the horizontal meridian closely matched those found in the first experiment, with the exception of the farthest eccentricity tested in the attend all condition. The largest changes in magnitude errors across the two experiments occurred for target locations along the vertical meridian. In the attend axis condition, an overestimation of target locations was still observed for the target eccentricities closest to the point of fixation along the lower axis. However, for the farther eccentricities tested, magnitude errors showed comparable foveal biases across all axes tested. The lack of a horizontal–vertical anisotropy is also clearly seen in the slope parameters. While the slope parameters for the left and right axes matched those found in Experiment 1, the slope parameters for the upper and lower axes showed a large reduction in this experiment that is apparent across all three attention conditions. The only difference between the first experiment and the present one was the number of locations tested in each attention condition, and there is no apparent reason why changes in the number of target locations across the three attention conditions would influence the horizontal–vertical anisotropy found in Experiment 1. However, as noted previously, there are known individual differences in attentional facilitation across the visual field (Altpeter et al., 2000; Mackeben, 1999). The lack of any significant variation in localization performance across the two meridians in this experiment therefore suggests that the previous dissociation may have been due to individual differences on the part of the participants.
In sum, the present results support the hypothesis that changes in the distribution of attention across the visual field modulate foveal biases when localizing peripheral targets. One further question is whether the degree to which targets locations are underestimated depends on the relative location of the targets within the display or the true eccentricity of the targets. Magnitude errors were comparable in size across the previous two experiments, and both of these experiments were run at the same viewing distance so the magnitudes and target eccentricities remained constant. Given a fixed aperture width, it is possible to dissociate the true magnitudes of the targets from the target eccentricities by manipulating the viewing distance to the screen. The final experiment used this technique to look at the influence of target eccentricity and relative location on the magnitude of foveal biases.
Experiment 3
This experiment was the same as Experiment 1, except for one change in the design: The viewing distance of the participants was doubled from 25.4 to 50.8 cm. This change essentially halved the eccentricities of the target locations. If the degree to which participants underestimate the locations of targets depends on the true eccentricity of the target item (independent of the relative position along each axis in the display), localization errors should here be smaller overall than the errors observed in the first experiment but should match the pattern observed within the first four testing locations (i.e., 4°–16°). On the other hand, if the degree of foveal bias depends on the relative location of the targets within the display, the localization errors in this experiment should be of the same magnitude and follow the same pattern as the results from the first experiment.
Method
Participants
Fourteen undergraduates (7 females; mean age 20.4 ± 3.3 years) participated in this experiment for course credit. None of the participants had participated in the previous experiments, and the same exclusion criteria were applied as before. All gave informed consent as approved by the University of California before participating.
Materials and procedure
The same stimulus parameters and apparatus were used as in Experiment 1. Participants viewed the monitor from 50.8 cm. Given that targets were presented on a flat monitor, doubling the viewing distance did not exactly halve the eccentricities of the targets. The new eccentricities of the seven target locations along each axis were: 2.0°, 4.0°, 6.1°, 8.2°, 10.3°, 12.6°, and 14.9° of visual angle. The aperture, with a radius of 14.67 cm, was now located at 16.1° eccentricity. Thus, the true magnitudes of the targets in this experiment were 12.4, 25, 37.7, 50.7, 64.1, 78, and 92.5, respectively. As before, all participants completed 10 practice trials before beginning the experiment. To better control for learning effects, 14 participants completed the experiment, and block order was counterbalanced across participants with the constraint that each of the seven blocks be presented twice at a given temporal order. In other words, 2 of the participants completed the attend all condition in the first block, 2 completed it during the second block of trials, and sop forth.
Results
Localization errors
Magnitude errors were calculated in the same way as in Experiment 1, and the mean localization errors are shown in Fig. 9. A 3 (attention) × 4 (axis) × 7 (eccentricity) repeated measures ANOVA (using the Greenhouse–Geisser correction when appropriate) was used to analyze mean magnitude errors. As in the previous experiment, there was a significant effect of attention, with larger underestimations observed when attention was distributed across the visual field, F(2, 26) = 16.52, p < .001. There was also a main effect of axis, F(3, 39) = 4.75, p = .01, but the main effect of eccentricity did not reach significant levels, F(1.68, 21.77) = 3.05, p = .07. However, eccentricity did interact with attention condition, F(5.48, 71.22) = 3.42, p = .006, and the axis tested, F(18, 234) = 3.00, p < .001. The Attention × Axis interaction was also significant, F(6, 78) = 3.53, p = .004, and the three-way interaction was not significant, F(36, 468) = 1.07, p = .36. Contrary to the first experiment, a trend analysis for the Eccentricity factor did not reach significant levels for the linear trend, F(1, 13) = 3.81, p = .07. The quadratic and cubic trends were also not significant [quadratic: F(1, 13) = 1.04, p = .33; cubic: F(1, 13) = 0.44, p = .52].
Fig. 9.
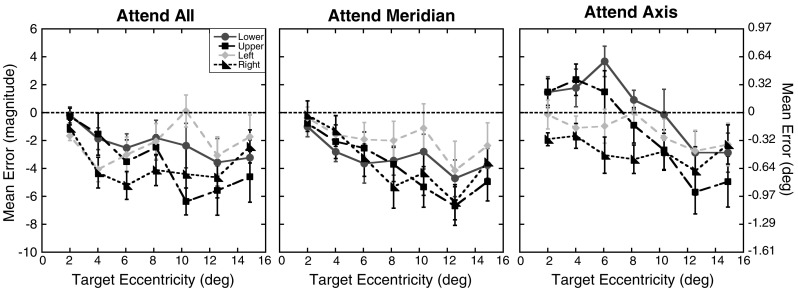
Experiment 3 magnitude errors: Mean magnitude errors for each of the four axes tested as a function of target eccentricity (in degrees) for the three attention conditions. The right y-axis shows the errors in units of degrees of visual angle. Results for the lower axis are shown as circles, those for the upper axis as squares, for the left axis as diamonds, and for the right axis as triangles. Error bars represent ±1 SE. The dotted lines at 0 represent the expected performance if no distortion exists
Uncertainty in perceived location
As in Experiment 1, analyses on the standard deviations were conducted to assess whether positional uncertainty increased with eccentricity or across the different attention conditions. Figure 10 shows the mean standard deviations as a function of axis and eccentricity for the three attention conditions. A 3 (attention) × 4 (axis) × 7 (eccentricity) repeated measures ANOVA was used to analyze the mean standard deviations, with Greenhouse–Geisser corrections applied where necessary. The pattern of results mirrored that found in Experiment 1. Analyses revealed a significant effect of eccentricity, F(2.24, 29.08) = 14.09, p < .001, and a main effect of axis, F(3, 39) = 4.43, p = .01. There was no main effect of attention, F(2, 26) = 0.11, p = .90, although the Axis × Attention interaction did show a trend, F(6, 78) = 2.09, p = .06. The Axis × Eccentricity interaction was not significant, F(18, 234) = 0.95, p = .52, nor was the Attention × Eccentricity interaction, F(12, 156) = 1.32, p = .21. Finally, the three-way interaction was not significant, F(36, 468) = 1.22, p = .19. A trend analysis run on the main effect of eccentricity showed significant linear and quadratic trends [linear: F(1, 13) = 15.55, p = .002; quadratic: F(1, 13) = 38.26, p < .001]. The cubic trend did not reach significance, F(1, 13) = 4.39, p = .06.
Fig. 10.
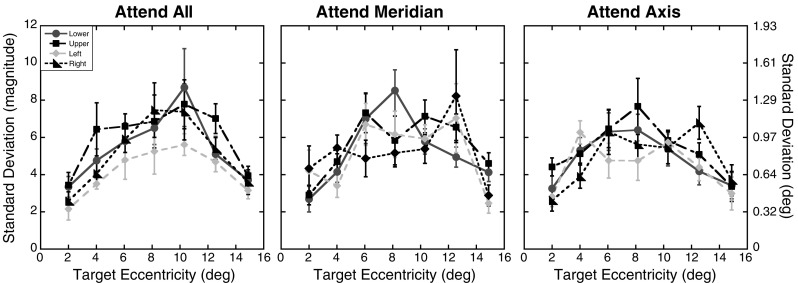
Experiment 3 positional uncertainty: Standard deviations of the magnitude errors as a function of target eccentricity (in degrees) and axis tested for the three attention conditions. The same formatting is used here as in Fig. 9. Error bars represent ±1 SE
Spatial metric(s) underlying localization errors
The spatial metric used by participants to make magnitude judgments across eccentricities was assessed with the same fitting procedure described in Experiment 1. For the one-parameter model, the average adjusted R 2 was .94 (range: .73 to .98). For the two-parameter model, the average adjusted R 2 was .95 (range: .84 to .98). Across the 12 conditions for each of the 14 participants, 52% of the 168 functions showed a significantly better fit by the two-parameter model. As in Experiment 1, while half of the models showed a better fit when exponents were allowed to vary from 1, the increase in variability explained was modest. The average R 2 results showed only a 1% increase on average for the two-parameter model over a one-parameter model. Given the high level of explained variance for the one-parameter model and the modest increase in variance explained when the exponent was treated as a free parameter, these results suggest that the magnitude estimates are best fit by a linear model, as found in Experiment 1. The estimates from this model were therefore used in further analyses.
Figure 11 shows the mean estimated slopes (λ) across the three attention conditions for each of the four axes tested. A 3 (attention) × 4 (axis) repeated measures ANOVAs was used to analyze these slopes. The results showed a main effect of attention, with slopes increasing as attention was focused on smaller regions of space, F(2, 26) = 7.19, p = .003. There was also a main effect of axis, F(3, 39) = 4.6, p = .007. The Attention × Axis interaction was not significant, F(6, 78) = 1.58, p = .16.
Fig. 11.
Experiment 3 slope parameters: Mean estimated slope parameters, λ, as a function of axis tested for the three attention conditions after fitting the individual magnitude estimates to the function J = λD. Error bars represent ±1 SE. The dotted line at 1 represents the expected performance if the mapping is undistorted
Discussion
The results of the last experiment mirror those found in Experiment 1 in several respects. First, the foveal bias was replicated with a new group of participants and at a new viewing distance. As seen in Fig. 9, across both meridians and the three attention conditions participants showed consistent underestimations in perceived target location, and the degree of underestimation tended to increase with eccentricity. Second, the degree to which participants exhibited a foveal bias was modulated by the extent to which they distributed their attention across the display, again confirming the main finding in Experiment 1. Relative to the attend all and attend meridian conditions, the foveal bias was significantly reduced in the attend axis condition. The pattern of variability in magnitude estimates for a given target also showed an inverted-U pattern similar to that observed in the previous experiments, with the smallest variability seen in estimates to the targets closest to the fovea and aperture edge.
There are a few ways in which the pattern of errors in the present study diverged from those observed in Experiment 1. First, magnitude error tended to be smaller in this experiment relative to the first, particularly when the errors were calculated in degrees of visual angle. The rate at which errors increased across eccentricities was also smaller than in the previous experiments. This is reflected in the main effect of eccentricity not reaching significant levels and the higher slope estimates along the horizontal meridian. However, in the present experiment, the locations of the targets in degrees of visual angle were approximately half the size of those in the first experiment. This suggests that the size of the foveal bias exhibited by participants depends to some extent on the retinal location of the target, and not just on the relative location of the targets within the display. To more easily compare the magnitude errors across Experiments 1 and 3, Fig. 12 shows the mean errors in degrees of visual angle as a function of eccentricity and experiment for the three attention conditions. As can be seen in Fig. 12, both the pattern and size of errors across eccentricities are similar in both experiments in the attend axis and attend meridian conditions. Thus, despite a global reduction in the size of magnitude errors found in Experiment 3, the absolute size of these errors in terms of degrees of visual angle was comparable when target eccentricities were matched. Less consistency in the patterns of errors across eccentricities was found in the attend all condition, with participants showing a more constant level of underestimation in this experiment than Experiment 1. One possible explanation for the difference in patterns may be how participants utilized the edge of the aperture as a landmark. Several studies (Diedrichsen et al., 2004; Kerzel, 2002; Uddin et al., 2005; Werner & Diedrichsen, 2002; Yamada et al., 2008) have found a reduction in foveal bias or a bias in perceived location toward a peripherally placed distractor item. Importantly, the degree to which such a distractor influences the perceived location of a target depends on the distance between the target and distractor. While the physical distance of the targets relative to the aperture edge did not vary across experiments, the distance in terms of degrees of visual angle did. It is possible that by reducing the angular distance of the targets to the aperture edge in the last experiment, an attraction effect as found in previous studies was introduced for the more peripheral targets. Such an effect would counteract the foveal bias and lead to the pattern of errors observed in the present study. Moreover, errors for the farthest target tested showed a slight reduction relative to the second farthest target across all attention conditions, which is consistent with a larger attraction effect toward the aperture edge for the most peripheral target locations, as noted in Adam et al. (2008).
Fig. 12.
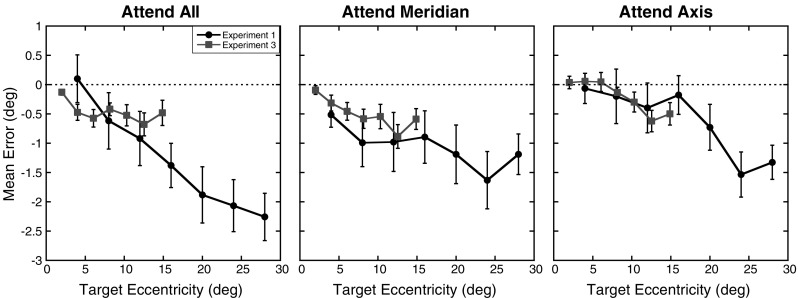
Comparison of errors across Experiments 1 and 3: Mean errors in degrees of visual angle as a function of experiment and target eccentricity (in degrees) for the three attention conditions. Errors from Experiment 1 are shown as circles, while the errors from Experiment 3 are shown as squares. Error bars represent ±1 SE. The dotted lines at 0 represent the expected performance if no distortion exists
As seen in Fig. 9, the magnitude errors are nearly identical for the most peripheral target across all axes and attention conditions in the third experiment, despite varying degrees and patterns of errors across the other eccentricities tested. As seen in Fig. 12, this pattern was not observed in Experiment 1, with errors in the attend all condition increasing even for the farthest target. While the exact form of the attentional distribution in the attend all condition is unknown, this difference could be related to qualitative differences in the spread of attention across one and two dimensions as well as changes in the effect of attention across eccentricities.
As in Experiment 2, a horizontal–vertical anisotropy was not observed in this experiment. This is reflected in the patterns of magnitude errors shown in Figs. 2 and 9 and the slope parameter estimates in Figs. 4 and 11. Of particular note is the change in scaling across the left axis. In the attend all and attend meridian conditions, the smallest errors appear for targets along the left axis. In contrast, errors along the right axis continue to show some of the largest underestimations. Though the initial variations were striking, the lack of a replication of this finding across the second and third experiments suggests that differences in performance along the horizontal and vertical meridians are most likely due to variations in the individual participants who completed the task rather than to some underlying bias in localization performance across the two meridians. If such underlying biases do exist, it may also be that a more sensitive measure than verbal magnitude estimates would be needed to reliably measure such effects. More importantly, across all three experiments, changes in scaling were found across the three attention conditions while differences in scaling across the horizontal and vertical meridians were only found in Experiment 1.
General discussion
The three experiments in this study used a new method that blends approaches used to study localization across eccentricities (Mateeff & Gourevich, 1983; Temme et al., 1985), but added variations that produce differences in the distribution of attention to determine how attention affects the underlying metric of visual space. Importantly, the “objects” in the field were kept constant (in this case, the only objects were the surrounding aperture edge and fixation point). We found that the distribution of spatial attention itself modulates the metric of visual space. The results showed significant and replicable distortions of the spatial metric as a function of how attention was allocated over the visual field, consistent with previous reports using different types of attentional manipulations (Adam et al., 2008; Bocianski, Müsseler, & Erlhagen, 2010). We also provided support in the third experiment for the idea that the size of errors and the degree to which they are modulated by the distribution of attention depend on the retinal location of targets, not just on their relative location within a display.
One question that may be raised is the extent to which memory played a role in the present findings. It is known that spatial distortions occur when observers are asked to remember the layout of a scene (Intraub, 2002; Intraub, Hoffman, Wetherhold, & Stoehs, 2006; Intraub & Richardson, 1989). Foveal biases have also been demonstrated when observers are asked to report the location of a previously seen target (Sheth & Shimojo, 2001), and distortions in memory are known to increase as the interval between target presentation and response increases (Diedrichsen et al., 2004; Werner & Diedrichsen, 2002). The study by Sheth and Shimojo is of particular importance, because the general bias to remember locations as being closer to the fovea than they really were matches the observed pattern of responses in the present studies. The participants in the present studies were encouraged to respond as quickly as possible and were explicitly told that the purpose of the study was to determine where they perceived target location and not where they remembered them to be. However, magnitude estimates without a visible scale on which to rely take a longer time to formulate than other measures, such as reaction times and relative comparisons. As a result, it is difficult to rule out a memory component. It beyond the scope of this article to determine whether the foveal biases observed here and in other studies of peripheral localization (Mateeff & Gourevich, 1983) are due to processes of retaining spatial representations in memory. The primary interest of the present study was to examine how changes in the distribution of attention alter localization performance in the periphery. To our knowledge, there is no evidence in the spatial memory literature that the modulations in errors observed in the present experiment vary with how participants distribute their attention across the display.
Models of attention and localization
While the results of the three experiments all suggest that changes in the distribution of sustained attention across the visual field lead to consistent modulations in the magnitude of peripheral mislocalization, questions remain as to how these findings fit with current theories of how attention influences location perception. The following section describes some of the relevant models and their applicability to the present findings.
Many models of attention, such as feature integration theory (Treisman & Gelade, 1980), have postulated that attention is required for accurate localization and identification to occur. However, it has also been shown that while directing attention to a location can significantly improve the precision of localization (Prinzmetal, 2005; Prinzmetal et al., 1998; Tsal & Bareket, 1999, 2005), localization is still possible when attention is directed away from the location of a target. This finding led Tsal and colleagues to propose the attentional receptive field hypothesis (Shalev & Tsal, 2002; Tsal & Bareket, 1999, 2005; Tsal & Shalev, 1996). Under this model, coarse localization is possible when attention is directed away from a target location. However, because position information is pooled over many receptive fields, the ability of the visual system to localize positions is limited by its ability to perform computations across multiple, overlapping receptive fields. Using theoretical receptive fields, the attentional receptive field hypothesis predicts that information about length and position from any one receptor is determined by the size of that receptive field. Precision can be improved, however, by comparing responses across multiple receptive fields, and this process is thought to occur, or at least to improve, when attention is directed toward the location of the target. While this model can capture findings of increased length of stimuli (Tsal & Shalev, 1996) or increased dispersion in localization responses (Tsal & Bareket, 1999, 2005) when attention is directed away from a target, it is not clear how the model in its current form can account for systematic biases to localize a target toward or away from the fovea and for changes in mean perceived location under different attentional conditions.
It is of interest to note that in one study (Tsal & Bareket, 1999), changes in localization errors consistent with the present study were found. In this previous study, participants were required to localize briefly presented targets within large circles that were either located at the center of the screen or offset 9° to the left or right side. Pointing responses were used to indicate the perceived target location. Participants were also cued to the possible circle in which the target could appear. The results showed peripheral biases for the validly cued targets presented in the peripheral circles that were not seen in the invalidly cued condition. The researchers suggest that the introduction of a peripheral bias may have been due to the participants making eye movements in the direction of the target when it was validly cued. While peripheral biases are not usually found in localization tasks using computer-based displays, other studies using manual responses with different experimental setups have found such biases when eye movements were controlled (Bock, 1993; Temme et al., 1985; Uddin, 2006). Of more relevance to the present study is the direction of the shift in errors. As attention shifted from another circle in the invalidly cued condition to the circle in which the target actually appeared (the validly cued condition), localization errors shifted peripherally. While the present study found consistent foveal biases, the direction in which errors moved from the attend all condition to the attend axis condition was also more peripheral (i.e., a reduction in foveal bias).
Another possible mechanism that may be able to account for the present findings has to do with spatially localized changes in the baseline activity of neurons in attended regions of space. Increases in baseline activity when attention is directed to specific regions of space have been found using both single-cell recordings in monkeys (David, Hayden, Mazer, & Gallant, 2008; Luck, Chelazzi, Hillyard, & Desimone, 1997) and functional magnetic resonance imaging (fMRI) in humans (Driver & Frith, 2000; Kastner, Pinsk, De Weerd, Desimone, & Ungerleider, 1999; Silver, Ress, & Heeger, 2007). In the present study, no visual cues were used to manipulate spatial attention. Rather, within a given block of trials, spatial uncertainty in where the target might appear was altered to affect the distribution of attention. Thus, it seems plausible that the underlying mechanisms responsible for altering perceived location in the present paradigm are not stimulus locked but rather occur in the absence of visual stimulation. Previous work in fMRI has shown such spatially specific increases in baseline activity prior to target onset (Kastner et al., 1999; Silver et al., 2007). Moreover, while the spatial extent over which baseline activity can be modulated is not fully understood, shifts in baseline activity over an entire quadrant of the visual field have been previously measured (Kastner et al., 1999). This suggests that changes in baseline activity across the regions tested in the present study are plausible.
Recently, a model has been proposed that includes such baseline variations in activity to account for changes in localization performance. This model is an extension of the dynamic neural field model, which was originally developed to describe the evolution of spatial coding within the motor (Schöner, Kopecz, & Erlhagen, 1997) and visual (Jancke, et al. 1999) systems. The model has since been proposed to account for systematic mislocalization of successively presented targets in the peripheral visual field (Bocianski, Müsseler, & Erlhagen, 2008; Bocianski et al., 2010). In brief, the model proposes that the first stimulus activates a population of spatially tuned neurons. Across this population, the interaction profiles are asymmetrically distributed such that neurons receive the maximum input from other neurons located toward the fovea. This asymmetry leads to a “drift” of population activity, and thus perceived position, over time toward the fovea. Local interactions between populations of neurons representing the first and second stimuli then cause the position coding of the second stimulus to be further skewed toward the fovea. Importantly, the interactions are both local and change from predominantly excitatory to inhibitory over time, which means that how the first stimulus influences the perceived position of the second stimulus is both dependent on the distance between the two stimuli and the time between their presentations.
In a follow-up study, Bocianski et al. (2010) showed that attention can modulate errors in the same relative localization task. In one condition, participants were informed on which side of the display the stimuli would appear (predictable left/right condition). Here, no significant errors in relative localization were found. In contrast, a significant foveal bias was observed when participants were unsure whether a given pair of stimuli would appear to the left or the right of fixation on each trial, replicating previous findings (Müsseler et al., 1999). In a second experiment, the researchers compared the unpredictable (left/right) condition with another in which the stimulus pair could appear to the left or right of fixation and above or below the horizontal meridian. This created four locations that the observers had to attend to, and relative mislocalizations were found to be even greater in this condition. There are obvious similarities between the attentional manipulation used by Bocianski et al. (2010) and the one employed in the present study. While the position of the second stimulus varied slightly compared to the first stimulus (which was always located at 5°, slightly above the horizontal meridian), the general locations of the two stimuli varied from one location in the predictable condition, to two locations in the unpredictable condition, and finally to four in the distributed condition. In the present study, much larger ranges of possible target locations were tested within a block of trials. However, across the three attention conditions, participants knew that they either had to attend to one, two, or four axes at a time. Similar to the findings of Bocianski et al. (2010), we also found the greatest foveal bias when participants were required to distribute their attention across the largest region of space, and foveal biases were systematically reduced as attention was focused over smaller regions.
To explain this reduction in foveal bias, Bocianski et al. (2010) introduce a tonic surround-suppression input into the model, representing a spatially structured change in baseline activity at attended locations. This surround-suppression input both increases activity of neurons responsive to the attended location and suppresses the baseline firing rates of neurons responsive to other locations. One consequence of this change in connections is that errors in the relative position coding of the second stimulus are reduced, consistent with the behavioral findings of Bocianski et al. (2010). However, another consequence is that the introduction of this baseline activity reduces the position drift of the first stimulus (Bocianski et al., 2010, Fig. 7). The introduction of the surround-suppression resting state activity can therefore also accommodate the attentional modulations found in the present study, where only one target was presented on each trial. If one assumes that the strength of the baseline activity increases as attention is focused on smaller regions of space, the model outlined above predicts corresponding reductions in foveal biases at attended locations.
Source of the foveal bias
While the dynamic neural field model including tonic baseline shifts (Bocianski et al., 2010) is best able to account for the present findings, there is one aspect of the model that is lacking. This is the source of the foveal bias that was observed across all of the attention conditions and experiments in the present study. In order to accommodate a foveal bias in the original model, Bocianski et al. (2008) altered the Gaussian weight profiles of the interactions such that they were skewed toward more foveal connections, creating the foveal “drift” of perceived position. While this drift creates the foveal bias observed across many peripheral localization studies, it does not explain why such a drift exists to begin with. In the behavioral literature, several studies have investigated the source of foveal bias. In many tasks of peripheral localization, fixation points are used, and it is known that targets can be misperceived toward the locations of landmarks in a display (Hubbard & Ruppel, 2000; Makovski et al., 2010; Yamada et al., 2008). While it could be argued that a fixation cross serves as a landmark and that foveal biases are the result of memory averaging across the fixation cross and target, research has shown that foveal biases persist when no physical stimulus is present at the point of fixation (Kerzel, 2002; van der Heijden et al., 1999). It should be noted that maintaining fixation throughout an experiment is not a passive process. Under normal viewing conditions one’s eyes are continuously moving, and it has been suggested that attention shifts precede eye movements (Hoffman & Subramanian, 1995). Thus, it seems plausible that the source of the original “drift” in the model of Bocianski et al. (2008) is due to attention being actively maintained at the point of fixation prior to target onset. This would alter the model somewhat, by assuming that tonic baseline shifts are always present and spatially structured, and that variations across tasks determine the focus of this baseline as well as the spread. For example, when participants know where the target will appear, the focus of attention is moved from fixation prior to target onset. In the present study, participants were required to attend to entire axes in the display. Here, one might assume that the distribution of attention is spread along each tested axis, with the form of attention changing across the three attention conditions. In particular, in the attend all condition participants needed to distribute their attention across all four axes for optimal performance. If such a distribution leads to focal baseline changes at the point of fixation that dissipate with increased eccentricity, one should find the strongest foveal bias and drift in position coding. As attention is focused on fewer axes, participants should be able to focus their attention more directly along the axes being tested, thereby reducing attentional focus at the point of fixation. This would serve to essentially flatten the distribution of the baseline function and eliminate the foveal bias. This interpretation is consistent with the results of Tsal and Bareket (1999, 2005), who found greater dispersion in estimated locations along the radial line connecting the target to the point of fixation, as compared to the orthogonal direction. Though this result may appear contradictory at first, if one assumes that the distribution of attention is spread from the point of fixation out toward the cued location, biases in perceived location due to changes in baseline activity will occur along this line more than in the orthogonal direction. This will result in errors in the perceived distance of the target from fixation and will not affect the radial position.
Conclusions
One of the most important functions of vision is that it allows us to act, not only on objects that may be the focus of attention, but also within the environments in which we perceive ourselves. Even on the darkest night, attention can be focused in space to help guide us through the environment. The present results demonstrate that the location where we believe items to be can be changed by the very act of attending toward or away from that direction. While objects and other visual cues can change the metric of perceived space, the results presented in these three experiments demonstrate that attentional distribution can also modulate location perception, suggesting a dynamic interaction between the form of space, the representation of objects, and attention.
Author Note
This research was supported by the Veterans Administration, National Institutes of Health Grant EY-016975-05 (to L.C.R.) and an NSF-GRF grant (to F.C.F.). L.C.R. has a Senior Research Career Scientist award from the Veterans Administration and is affiliated with the VA Clinical Sciences Research Service, Department of Veterans Affairs Medical Center, Martinez, CA. The authors thank Thomas Wickens for help with data modeling, Bill Prinzmetal for many helpful discussions, and Anna Enzminger for help with data collection.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
References
- Adam JJ, Davelaar EJ, van der Gouw A, Willems P. Evidence for attentional processing in spatial localization. Psychological Research. 2008;72:433–442. doi: 10.1007/s00426-007-0126-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adam JJ, Ketelaars M, Kingma H, Hoek T. On the time course and accuracy of spatial localization: Basic data and a two-process model. Acta Psychologica. 1993;84:135–159. doi: 10.1016/0001-6918(93)90024-L. [DOI] [PubMed] [Google Scholar]
- Altpeter E, Mackeben M, Trauzettel-Klosinski S. The importance of sustained attention for patients with maculopathies. Vision Research. 2000;40:1539–1547. doi: 10.1016/S0042-6989(00)00059-6. [DOI] [PubMed] [Google Scholar]
- Anton-Erxleben K., Henrich C., Treue S. Attention changes perceived size of moving visual patterns. Journal of Vision. 2007;7(11):1. doi: 10.1167/7.11.5. [DOI] [PubMed] [Google Scholar]
- Banks MS, Sekuler AB, Anderson SJ. Peripheral spatial vision: Limits imposed by optics, photoreceptors, and receptor pooling. Journal of the Optical Society of America A. 1991;8:1775–1787. doi: 10.1364/JOSAA.8.001775. [DOI] [PubMed] [Google Scholar]
- Bishop PO, Henry GH. Spatial vision. Annual Review of Psychology. 1971;22:119–160. doi: 10.1146/annurev.ps.22.020171.001003. [DOI] [PubMed] [Google Scholar]
- Bocianski D, Müsseler J, Erlhagen W. Relative mislocalization of successively presented stimuli. Vision Research. 2008;48:2204–2212. doi: 10.1016/j.visres.2008.06.016. [DOI] [PubMed] [Google Scholar]
- Bocianski D, Müsseler J, Erlhagen W. Effects of attention on a relative mislocalization with successively presented stimuli. Vision Research. 2010;50:1793–1802. doi: 10.1016/j.visres.2010.05.036. [DOI] [PubMed] [Google Scholar]
- Bock O. Localization of objects in the peripheral visual field. Behavioural Brain Research. 1993;56:77–84. doi: 10.1016/0166-4328(93)90023-J. [DOI] [PubMed] [Google Scholar]
- Carrasco M, Giordano AM, McElree B. Temporal performance fields: Visual and attentional factors. Vision Research. 2004;44:1351–1365. doi: 10.1016/j.visres.2003.11.026. [DOI] [PubMed] [Google Scholar]
- Carrasco M, Giordano A, McElree B. Attention speeds processing across eccentricity: Feature and conjunction searches. Vision Research. 2006;46:2028–2040. doi: 10.1016/j.visres.2005.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M, Ling S, Read S. Attention alters appearance. Nature Neuroscience. 2004;7:308–313. doi: 10.1038/nn1194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M, Talgar C, Cameron EL. Characterizing visual performance fields: Effects of transient covert attention, spatial frequency, eccentricity, task and set size. Spatial Vision. 2001;15:61–75. doi: 10.1163/15685680152692015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrasco M., Williams P., Yeshurun Y. Covert attention increases spatial resolution with or without masks: Support for signal enhancement. Journal of Vision. 2002;2(6):467–479. doi: 10.1167/2.6.4. [DOI] [PubMed] [Google Scholar]
- David SV, Hayden BY, Mazer JA, Gallant JL. Attention to stimulus features shifts spectral tuning of V4 neurons during natural vision. Neuron. 2008;59:509–521. doi: 10.1016/j.neuron.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diedrichsen J, Werner S, Schmidt T, Trommershäuser J. Immediate spatial distortions of pointing movements induced by visual landmarks. Perception & Psychophysics. 2004;66:89–103. doi: 10.3758/BF03194864. [DOI] [PubMed] [Google Scholar]
- Driver J, Frith C. Shifting baselines in attention research. Nature Reviews. Neuroscience. 2000;1:147–148. doi: 10.1038/35039083. [DOI] [PubMed] [Google Scholar]
- Eggert T, Ditterich J, Straube A. Mislocalization of peripheral targets during fixation. Vision Research. 2001;41:343–352. doi: 10.1016/S0042-6989(00)00263-7. [DOI] [PubMed] [Google Scholar]
- Enright JT. The non-visual impact of eye orientation on eye–hand coordination. Vision Research. 1995;35:1611–1618. doi: 10.1016/0042-6989(94)00260-S. [DOI] [PubMed] [Google Scholar]
- Goldstein EB. Sensation and perception. 6. Pacific Grove: Wadsworth; 2002. [Google Scholar]
- Hoffman JE, Subramanian B. The role of visual attention in saccadic eye movements. Perception & Psychophysics. 1995;57:787–795. doi: 10.3758/BF03206794. [DOI] [PubMed] [Google Scholar]
- Horton JC, Hoyt WF. The representation of the visual field in human striate cortex: A revision of the classic Holmes map. Archives of Ophthalmology. 1991;109:816–824. doi: 10.1001/archopht.1991.01080060080030. [DOI] [PubMed] [Google Scholar]
- Hubbard TL, Ruppel SE. Spatial memory averaging, the landmark attraction effect, and representational gravity. Psychological Research. 2000;64:41–55. doi: 10.1007/s004260000029. [DOI] [PubMed] [Google Scholar]
- Intraub H. Anticipatory spatial representation of natural scenes: Momentum without movement? Visual Cognition. 2002;9:93–119. doi: 10.1080/13506280143000340. [DOI] [Google Scholar]
- Intraub H, Hoffman JE, Wetherhold J, Stoehs S. More than meets the eye: The effect of planned fixations on scene representation. Perception & Psychophysics. 2006;68:759–769. doi: 10.3758/BF03193699. [DOI] [PubMed] [Google Scholar]
- Intraub H, Richardson M. Wide-angle memories of close-up scenes. Journal of Experimental Psychology. Learning, Memory, and Cognition. 1989;15:179–187. doi: 10.1037/0278-7393.15.2.179. [DOI] [PubMed] [Google Scholar]
- Jancke D, Erlhagen W, Dinse HR, Akhavan AC, Giese M, Steinhage A, et al. Parametric population representation of retinal location: Neuronal interaction dynamics in cat primary cortex. The Journal of Neuroscience. 1999;19:9016–9028. doi: 10.1523/JNEUROSCI.19-20-09016.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston A. A spatial property of the retino-cortical mapping. Spatial Vision. 1986;1:319–331. doi: 10.1163/156856886X00115. [DOI] [PubMed] [Google Scholar]
- Kastner S, Pinsk MA, De Weerd P, Desimone R, Ungerleider LG. Increased activity in human visual cortex during directed attention in the absence of visual stimulation. Neuron. 1999;22:751–761. doi: 10.1016/S0896-6273(00)80734-5. [DOI] [PubMed] [Google Scholar]
- Kerzel D. Memory for the position of stationary objects: Disentangling foveal bias and memory averaging. Vision Research. 2002;42:159–167. doi: 10.1016/S0042-6989(01)00274-7. [DOI] [PubMed] [Google Scholar]
- Kosovicheva A. A., Fortenbaugh F. C., Robertson L. C. Where does attention go when it moves? Spatial properties and locus of the attentional repulsion effect. Journal of Vision. 2010;10(12):1–13. doi: 10.1167/10.12.33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luck SJ, Chelazzi L, Hillyard SA, Desimone R. Neural mechanisms of spatial selective attention in areas V1, V2, and V4 of macaque visual cortex. Journal of Neurophysiology. 1997;77:24–42. doi: 10.1152/jn.1997.77.1.24. [DOI] [PubMed] [Google Scholar]
- Mackeben M. Sustained focal attention and peripheral letter recognition. Spatial Vision. 1999;12:51–72. doi: 10.1163/156856899X00030. [DOI] [PubMed] [Google Scholar]
- Makovski T., Swallow K. M., Jiang Y. V. The visual attractor illusion. Journal of Vision. 2010;10(1):1–16. doi: 10.1167/10.1.1. [DOI] [PubMed] [Google Scholar]
- Mapp A, Barbeito R, Bedell HE, Ono H. Visual localization of briefly presented peripheral targets. Biological Cybernetics. 1989;60:261–265. doi: 10.1007/BF00204123. [DOI] [PubMed] [Google Scholar]
- Mateeff S, Gourevich A. Peripheral vision and perceived visual direction. Biological Cybernetics. 1983;49:111–118. doi: 10.1007/BF00320391. [DOI] [PubMed] [Google Scholar]
- McAnany JJ, Levine MW. Magnocellular and parvocellular visual pathway contributions to visual field anisotropies. Vision Research. 2007;47:2327–2336. doi: 10.1016/j.visres.2007.05.013. [DOI] [PubMed] [Google Scholar]
- Mullen KT, Sakurai M, Chu W. Does L/M cone opponency disappear in human periphery? Perception. 2005;34:951–959. doi: 10.1068/p5374. [DOI] [PubMed] [Google Scholar]
- Müsseler J, Van der Heijden ACH. Two spatial maps for perceived visual space: Evidence from relative mislocalization. Visual Cognition. 2004;11:235–254. doi: 10.1080/13506280344000338. [DOI] [Google Scholar]
- Müsseler J, van der Heijden ACH, Mahmud SH, Deubel H, Ertsey S. Relative mislocalization of briefly presented stimuli in the retinal periphery. Perception & Psychophysics. 1999;61:1646–1661. doi: 10.3758/BF03213124. [DOI] [PubMed] [Google Scholar]
- Posner MI, Peterson SE. The attention system of the human brain. Annual Review of Neuroscience. 1990;13:25–42. doi: 10.1146/annurev.ne.13.030190.000325. [DOI] [PubMed] [Google Scholar]
- Posner MI, Snyder CR, Davidson BJ. Attention and the detection of signals. Journal of Experimental Psychology: General. 1980;109:160–174. doi: 10.1037/0096-3445.109.2.160. [DOI] [PubMed] [Google Scholar]
- Previc FH. The neuropsychology of 3-D space. Psychological Bulletin. 1998;124:123–164. doi: 10.1037/0033-2909.124.2.123. [DOI] [PubMed] [Google Scholar]
- Previc FH, Intraub H. Vertical biases in scene memory. Neuropsychologia. 1997;35:1513–1517. doi: 10.1016/S0028-3932(97)00091-2. [DOI] [PubMed] [Google Scholar]
- Prinzmetal W. Location perception: The X-Files parable. Perception & Psychophysics. 2005;67:48–71. doi: 10.3758/BF03195012. [DOI] [PubMed] [Google Scholar]
- Prinzmetal W, Amiri H, Allen K, Edwards T. The phenomenology of attention: Part 1. Color, location, orientation, and “clarity. Journal of Experimental Psychology: Human Perception & Performance. 1998;24:261–282. doi: 10.1037/0096-1523.24.1.261. [DOI] [Google Scholar]
- Prinzmetal W, McCool C, Park S. Attention: Reaction time and accuracy reveal different mechanisms. Journal of Experimental Psychology: General. 2005;134:73–92. doi: 10.1037/0096-3445.134.1.73. [DOI] [PubMed] [Google Scholar]
- Rose D, Halpern DL. Stimulus mislocalization depends on spatial frequency. Perception. 1992;21:289–296. doi: 10.1068/p210289. [DOI] [PubMed] [Google Scholar]
- Schöner G, Kopecz K, Erlhagen W. The dynamic neural field theory of motor programming: Arm and eye movements. In: Morasso P, Sanguineti V, editors. Self-organization, computational maps, and motor control. Amsterdam: Elsevier; 1997. pp. 271–310. [Google Scholar]
- Shalev L, Tsal Y. Detecting gaps with and without attention: Further evidence for attentional receptive fields. European Journal of Cognitive Psychology. 2002;14:3–26. doi: 10.1080/09541440143000005. [DOI] [Google Scholar]
- Sheth BR, Shimojo S. Compression of space in visual memory. Vision Research. 2001;41:329–341. doi: 10.1016/S0042-6989(00)00230-3. [DOI] [PubMed] [Google Scholar]
- Silver MA, Ress D, Heeger DJ. Neural correlates of sustained spatial attention in human early visual cortex. Journal of Neurophysiology. 2007;97:229–237. doi: 10.1152/jn.00677.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki S, Cavanagh P. Focused attention distorts visual space: An attentional repulsion effect. Journal of Experimental Psychology: Human Perception and Performance. 1997;23:443–463. doi: 10.1037/0096-1523.23.2.443. [DOI] [PubMed] [Google Scholar]
- Temme LA, Maino JH, Noell WK. Eccentricity perception in the periphery of normal observers and those with retinitis pigmentosa. American Journal of Optometry and Physiological Optics. 1985;62:736–743. doi: 10.1097/00006324-198511000-00003. [DOI] [PubMed] [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12:97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Tsal Y, Bareket T. Effects of attention on localization of stimuli in the visual field. Psychonomic Bulletin & Review. 1999;6:292–296. doi: 10.3758/BF03212332. [DOI] [PubMed] [Google Scholar]
- Tsal Y, Bareket T. Localization judgments under various levels of attention. Psychonomic Bulletin & Review. 2005;12:559–566. doi: 10.3758/BF03193805. [DOI] [PubMed] [Google Scholar]
- Tsal Y, Shalev L. Inattention magnifies perceived length: The attentional receptive field hypothesis. Journal of Experimental Psychology: Human Perception and Performance. 1996;22:233–243. doi: 10.1037/0096-1523.22.1.233. [DOI] [PubMed] [Google Scholar]
- Uddin MK. Visual spatial localization and the two-process model. Kyushu University Psychological Research. 2006;7:65–75. [Google Scholar]
- Uddin MK, Kawabe T, Nakamizo S. Attention shift not memory averaging reduces foveal bias. Vision Research. 2005;45:3301–3306. doi: 10.1016/j.visres.2005.03.006. [DOI] [PubMed] [Google Scholar]
- van der Heijden A, van der Geest J, de Leeuw F, Krikke K, Müsseler J. Sources of position-perception error for small isolated targets. Psychological Research. 1999;62:20–35. doi: 10.1007/s004260050037. [DOI] [PubMed] [Google Scholar]
- Werner S, Diedrichsen J. The time course of spatial memory distortions. Memory & Cognition. 2002;30:718–730. doi: 10.3758/BF03196428. [DOI] [PubMed] [Google Scholar]
- Yamada Y, Kawabe T, Miura K. Mislocalization of a target toward subjective contours: Attentional modulation of location signals. Psychological Research. 2008;72:273–280. doi: 10.1007/s00426-007-0109-3. [DOI] [PubMed] [Google Scholar]
- Yeshurun Y, Carrasco M. Attention improves or impairs visual performance by enhancing spatial resolution. Nature. 1998;396:72–75. doi: 10.1038/23936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeshurun Y, Montagna B, Carrasco M. On the flexibility of sustained attention and its effects on a texture segmentation task. Vision Research. 2008;48:80–95. doi: 10.1016/j.visres.2007.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]