Spatio-temporal dynamics of an encapsulated gas bubble in an ultrasound field

Abstract

Coupled equations describing the radial and translational dynamics of an encapsulated gas bubble in an ultrasound field are derived by using the Lagrangian formalism. The equations generalize Church’s theory by allowing for the translation motion of the bubble and radiation losses due to the compressibility of the surrounding liquid. The expression given by Church for the inner bubble radius corresponding to the unstrained state of the bubble shell is also refined, assuming that the shell can be of arbitrary thickness and impermeable to gas. Comparative linear analysis of the radial equation is carried out relative to Church’s theory. It is shown that there are substantial departures from predictions of Church’s theory. The proposed model is applied to evaluate radiation forces exerted on encapsulated bubbles and their translational displacements. It is shown that in the range of relatively high frequencies encapsulated bubbles are able to translate more efficiently than free bubbles of the equivalent size.

I. INTRODUCTION

Interest in theoretical models describing the dynamics of encapsulated gas bubbles in an ultrasound field is motivated by increasingly growing use of contrast agents in ultrasound biomedical applications. Of special interest are models in the form of a Rayleigh-Plesset-type equation as they are more amenable to theoretical analysis, more convenient for numerical simulations, and can with comparative ease be applied to model the dynamics of more than one bubble. The first of such models was proposed by de Jong et al.^1,2 They modified the Rayleigh-Plesset equation by phenomenologically introducing an additional restoring force due to the stiffness of the bubble shell and an additional damping due to internal friction inside the shell. The modified equation was used to model the radial oscillation of Albunex contrast agent. Subsequently, Frinking and de Jong³ proposed another version of this equation that was intended to model the radial dynamics of thick-shelled contrast agents such as Quantison and Myomap. It should be emphasized that both of the above-mentioned models are based on qualitative arguments rather than rigorous theoretical derivations.

A more sophisticated and theoretically justified model was developed by Church.⁴ He considered a spherical encapsulated gas bubble enclosed in an incompressible solid elastic shell and surrounded by an incompressible viscous Newtonian liquid. The viscous damping inside the shell was also taken into account. Using a consistent theoretical approach, Church derived a Rayleigh-Plesset-type equation describing the radial motion of the bubble. The only ad hoc assumption that he used concerns determination of the inner radius of the bubble shell corresponding to the unstrained state of the shell.

More recently, using a modified Herring equation⁵ along with some elements of Church’s theory, the behavior of a contrast agent bubble was modeled by Morgan et al.⁶ and Dayton et al.⁷ In the latter work, the radial equation was also supplemented with a translational equation to estimate the magnitude of radiation force on contrast agents and compare the theoretical results with experiments.

All the above-mentioned papers show that, as a matter of fact, any modification of the Rayleigh-Plesset equation, based on reasonable assumptions, can be fitted to provide good agreement with specific experiments. However, models that involve ad hoc parameters cannot guarantee reliable predictions for cases different from that to which they were fitted, even if distinctions are physically insignificant. This fact is well illustrated by Frinking and de Jong’s³ article, where an effective bulk modulus, K_eff, is introduced to describe the elasticity of the encapsulating shell of contrast agents such as Quantison, Myomap, and Albunex. All of these agents consist of air bubbles encapsulated by a shell of human albumin. They differ only in diameter and the shell thickness. For Quantison, which has a mean diameter of 3.2 μm and the shell thickness of which is 200–300 nm and proportional to the bubble diameter, Frinking and de Jong obtained K_eff=17.4 MPa. For Myomap, which has a mean diameter of 10 μm and the shell of which is approximately three times thicker than the Quantison shell, K_eff =78.4 MPa. Measurements for Albunex filtered with 12-, 8-, 5-, and 3-μm pore size mechanical filters yielded the following values of K_eff, respectively: 1.3, 2.0, 6.2, and 9.8 MPa. These results are believed to be explained by the fact that the thickness of the Albunex shell, which is about 15–20 nm, is independent of the bubble diameter, the latter being about 3.8 μm. It is evident that such a model is very inconvenient, especially if we are going to simulate the dynamics of a contrast agent cluster consisting of bubbles of different size. When a model is based on real physical parameters, distinctions in the behavior of the above-mentioned contrast agents should arise in a natural way, just varying sizes instead of fitting K_eff to every new set of the bubble geometrical adjectives.

Models accounting for the translational motion of contrast agents deserve special notice. They have not received proper consideration so far. If a model incorporates translation, this makes it more complicated. However, such a model provides an additional means for adjusting the parameters responsible for the radial dynamics of a contrast agent bubble, among other things. With an adequate expression for the drag force, the translational displacement of a contrast agent bubble is determined mainly by the intensity of its radial oscillation, i.e., the translational displacement can serve as a direct measured performance of the radial oscillation. In many cases, the translational displacement can be measured more precisely than the radius-time curves, especially since the translational displacement is in fact a time-average quantity. Hence, fitting theoretical and experimental displacements can be used to improve values of the model parameters which were initially estimated by other methods, such as radius-time curves, scattering spectra, etc. It should also be remembered that in many applications, such as targeted drug delivery, the translational dynamics of contrast agents is of great independent interest.

The purpose of this paper is to derive rigorously coupled equations governing the spatio-temporal dynamics of an encapsulated gas bubble in an ultrasound field. The present derivation improves Church’s theory by allowing for the translation motion of the bubble and radiation losses due to the compressibility of the surrounding liquid. The expression given by Church for the inner bubble radius corresponding to the unstrained state of the encapsulating shell is also refined, assuming that the shell can be of arbitrary thickness and impermeable to gas.

II. THEORY

Let us consider an encapsulated gas bubble surrounded by a liquid and undergoing radial and translational motions in response to an imposed acoustic field. It is assumed that the surrounding liquid is a slightly compressible Newtonian liquid and the bubble shell behaves as a viscoelastic solid. It is also assumed that the bubble translates along a straight line that is specified by the wave vector of the acoustic field. To describe the motion of the bubble, spherical coordinates (r,θ,ε) are introduced, the origin of which is at the moving center of the bubble. The geometry of the system is shown in Fig. 1. The aim of this section is to derive coupled equations of radial and translational bubble motions by using the Lagrangian formalism. Using the Lagrangian procedure is not new in fluid arid bubble dynamics.^8–15 However, with respect to encapsulated bubbles, this approach has not been used much so far.¹⁶

FIG. 1.

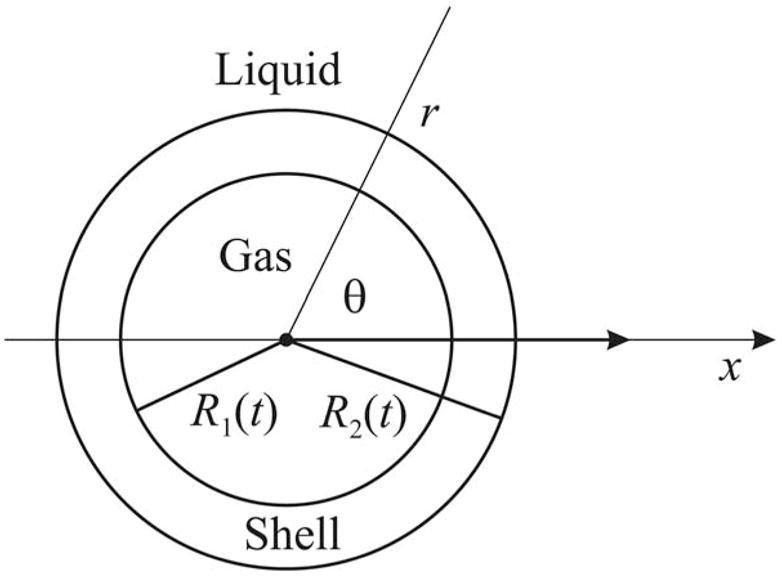
Schematic sketch of an encapsulated bubble.

A. Lagrangian equations

The Lagrangian equations are given by¹⁷

$$\frac{d}{dt}\frac{\partial L}{\partial {\stackrel{.}{q}}_i}-\frac{\partial L}{\partial q_i}=-\frac{\partial F}{\partial {\stackrel{.}{q}}_i},$$ (1)

where L is the Lagrangian function, q_i and q̇_i are called generalized coordinates and velocities, respectively, and F is the dissipative function that is entered to account for dissipative effects such as viscosity. The Lagrangian function is defined as L=T–U, where T and U are the kinetic and potential energies of the system, respectively. Expressions for T, U, and F are sequentially calculated in the following subsections.

B. Kinetic energy

The kinetic energy can be represented as

$$T=\frac{1}{2}{m}_b{\stackrel{.}{x}}^2+T_L+T_S,$$ (2)

where m_b is the mass of the bubble, x(t) is the position of the center of the bubble in an inertial frame, the overdot denotes the time derivative, T_L is the kinetic energy of the liquid, and T_S is the kinetic energy of the shell.

It is shown in Ref. 18 that the kinetic energy of a slightly compressible liquid that encloses a spherical bubble with the time-varying radius R₂(t), assuming also that the bubble can translate, is given by

$$T_L=2\pi {\rho }_L\left(R_2^3{\stackrel{.}{R}}_2^2+\frac{1}{6}{R}_2^3{\stackrel{.}{x}}^2+\frac{2}{c}{R}_2^2{\stackrel{.}{R}}_2\stackrel{.}{f}(t)+\frac{1}{c}{\int }_0^t{[f^{\prime }(\tau )]}^{2}d\tau \right)+O(c^{-2}),$$ (3)

where ρ_L is the equilibrium density of the liquid, c is the sound speed in the liquid, and $f(t)=-{\stackrel{.}{R}}_2(t)R_2^2(t)$. Note that if we substitute the explicit expression for ḟ(t) into Eq. (3), we will get a second-order time derivative of the radius in the third term in brackets, which is inadmissible in the Lagrangian formalism. To avoid this problem, ḟ(t) in will be T_L treated just as a function of time and the explicit expression for f(t) will be used only in final equations. We will see below that this approach gives a correct result.

Assuming that the volume of the bubble shell, V_S, remains constant in the process of bubble motion and that the effect of translation on the deformation of the shell is negligible, the velocity inside the shell can be written as

$$v_S=\frac{R_1^2{\stackrel{.}{R}}_1}{r^2},$$ (4)

where R₁(t) is the inner radius of the bubble shell. The kinetic energy of the shell is then calculated as

$$T_S=\frac{1}{2}{\int }_{V_S}{\rho }_S{v}_S^{2}dV=2\pi {\rho }_S{R}_1^3{\stackrel{.}{R}}_1^2\left(1-\frac{R_1}{R_2}\right),$$ (5)

where ρ_S is the density of the shell. Applying to the shell the same approach that was used in Ref. 18 for calculating Eq. (3), it can be shown that compressibility corrections to Eq. (5) can not be lower order than $c_l^{-2}$, where c_l denotes the longitudinal speed of sound in the shell. Note also that the assumption of incompressible shell gives the following equations, which will be used below,

$$R_2^3-R_1^3=R_{20}^3-R_{10}^3,R_1^2{\stackrel{.}{R}}_1=R_2^2{\stackrel{.}{R}}_2,\frac{{dR}_2}{{dR}_1}=\frac{R_1^2}{R_2^2},$$ (6)

where R₁₀ and R₂₀ are, respectively, the inner and the outer radii of the bubble shell at rest.

C. Potential energy

The total potential energy of the system can be written as the following sum:

$$U=U_g+U_{\text{st}}+U_{\text{ex}}+U_L+U_S.$$ (7)

U_g is the internal energy of the gas core. Assuming that the behavior of the gas is adiabatic, one has¹⁹

$$U_g=\frac{P_{g0}{V}_{g0}}{\gamma -1}{\left(\frac{R_{10}}{R_1}\right)}^{3(\gamma -1)},$$ (8)

where P_g0 is the equilibrium pressure of the gas within the bubble, $V_{g0}=(4\pi /3)R_{10}^3$ is the equilibrium gas volume, and γ is the ratio of specific heats.

The term U_st describes contributions due to surface tension at the gas-shell and the shell-liquid interfaces,

$$U_{\text{st}}=4\pi R_1^2{\sigma }_1+4\pi R_2^2{\sigma }_2.$$ (9)

Here σ₁ and σ₂ denote the surface tension coefficients for the corresponding interfaces.

U_ex is the contribution due to work done by the external pressure on the outer bubble surface. This contribution can be represented as

$$U_{\text{ex}}=\frac{4\pi }{3}{R}_2^3[P_0+P_{\text{ac}}(x,t)],$$ (10)

where P₀ is the hydrostatic pressure in the liquid and P_ac(x,t) is the acoustic pressure at the location of the bubble.

U_L is the potential energy of the surrounding liquid due to its compressibility. It is shown in Ref. 18 that U_L is given by

$$U_L=\frac{2\pi {\rho }_L}{c}{\int }_0^t{[f^{\prime }(\tau )]}^{2}d\tau +O(c^{-2}).$$ (11)

Finally, U_S is the elastic energy of the shell defined by

$$U_S={\int }_{V_S}\mathcal{E}dV,$$ (12)

where ε is the elastic energy density which is given by²⁰

$$\mathcal{E}={\mu }_S{(u_{ij}-\frac{1}{3}{\delta }_{ij}{u}_{kk})}^2+\frac{1}{2}{K}_S{u}_{kk}^2.$$ (13)

Here μ_S and K_S are respectively the shear modulus and the bulk modulus of the shell, δ_ij is the Kronecker delta, u_ij is the linear strain tensor, and summation over double indices is implied. The linear strain tensor is defined as

$$u_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right),$$ (14)

with u_i denoting the ith component of the displacement vector. Since the shell is assumed to be incompressible, which results in u_kk =0, and in view of spherical symmetry, Eq. (13) takes the form

$$\mathcal{E}={\mu }_S{(u_{ij})}^2={\mu }_S\left[{\left(\frac{\partial u}{\partial r}\right)}^2+\frac{2u^2}{r^2}\right],$$ (15)

where u is the radial displacement. Using again the fact that the shell is incompressible, u can be written as

$$u=\frac{R_1^2}{r^2}(R_1-R_{1e}),$$ (16)

where R_1e is the unstrained equilibrium position of the gas-shell interface. Note that R_1e does not coincide with R₁₀. The expression for R_1e is calculated below.

Substitution of Eqs. (15) and (16) into Eq. (12) yields

$$U_S=8\pi {\mu }_S(R_{20}^3-R_{10}^3)\frac{R_1{(R_1-R_{1e})}^2}{R_2^3}.$$ (17)

As with T_S, it can be shown that compressibility corrections to Eq. (17) are on the order $c_1^{-2}$ and therefore they are neglected here.

D. Dissipative function

The total dissipative function of the system can be represented as

$$F=F_L+F_S={\int }_{V_L}{f}_{L}dV+{\int }_{V_S}{f}_{S}dV.$$ (18)

where V_L is the volume occupied by the liquid, F_L and F_S are the dissipative functions of the liquid and the shell, and f _L and f _S are the densities of the dissipative functions.

For the surrounding liquid, f _L, can be written as^20,21

$$f_L={\eta }_L{(v_{ij}-\frac{1}{3}{\delta }_{ij}{v}_{kk})}^2+\frac{1}{2}{\zeta }_L{v}_{kk}^2,$$ (19)

where η_L and ζ_L are, respectively, the shear and the bulk viscosity coefficients of the liquid, and v_ij is the rate-of-strain tensor of the liquid, defined as

$$v_{ij}=\frac{1}{2}\left(\frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right),$$ (20)

with v denoting the liquid velocity. Neglecting the compressibility of the liquid, one has v_kk = ∇ · v= 0 so Eq. (19) reduces to

$$f_L={\eta }_L{(v_{ij})}^2.$$ (21)

To satisfy the boundary condition of adhesion of the liquid particles to the bubble surface, which is expressed as

$$\mathit{v}={\stackrel{.}{R}}_2{\mathit{e}}_r+\stackrel{.}{\mathit{x}}=({\stackrel{.}{R}}_2+\stackrel{.}{x}cos\theta ){\mathit{e}}_r-\stackrel{.}{x}sin\theta {\mathit{e}}_{\theta }\text{at}r=R_2,$$ (22)

the liquid velocity can be represented as v=∇ϕ+∇×ψ, where the scalar potential ϕ must obey the Laplace equation, Δϕ =0. Expressions for ϕ and ψ satisfying these two conditions are given by

$$\varphi =-\frac{R_2^2{\stackrel{.}{R}}_2}{r}+\frac{R_2^3\stackrel{.}{x}cos\theta }{4r^2},$$ (23)

$$\mathit{\psi }=\frac{3}{4}{R}_2\stackrel{.}{x}sin\theta {\mathit{e}}_{\epsilon }.$$ (24)

The liquid velocity are then calculated as

$$\mathit{v}=\left[\frac{R_2^2{\stackrel{.}{R}}_2}{r^2}+\frac{\stackrel{.}{x}}{2}\left(\frac{3R_2}{r}-\frac{R_2^3}{r^3}\right)cos\theta \right]{\mathit{e}}_r-\frac{\stackrel{.}{x}}{4}\left(\frac{3R_2}{r}+\frac{R_2^3}{r^3}\right)sin\theta {\mathit{e}}_{\theta }.$$ (25)

Considering the form of Eq. (25), (v_ij)² can be written as²⁰

$${(v_{ij})}^2=v_{rr}^2+v_{\theta \theta }^2+v_{\epsilon \epsilon }^2+2v_{r\theta }^2={\left(\frac{\partial v_r}{\partial r}\right)}^2+\frac{1}{r^2}{\left(v_r+\frac{\partial v_{\theta }}{\partial \theta }\right)}^2+\frac{1}{r^2}{\left(v_r+v_{\theta }\frac{cos\theta }{sin\theta }\right)}^2+\frac{1}{2}{\left(\frac{1}{r}\frac{\partial v_r}{\partial \theta }+\frac{\partial v_{\theta }}{\partial r}-\frac{v_{\theta }}{r}\right)}^2.$$ (26)

On substitution of Eq. (25) into Eq. (26), one has

$${(v_{ij})}^2=\frac{6R_2^4{\stackrel{.}{R}}_2^2}{r^6}+\frac{9R_2^6{\stackrel{.}{x}}^2}{8r^8}+\frac{9R_2^2{\stackrel{.}{R}}_2\stackrel{.}{x}}{r^4}\left(\frac{R_2}{r}-\frac{R_2^3}{r^3}\right)cos\theta +\frac{{\stackrel{.}{x}}^2}{8}\left(\frac{27R_2^2}{r^4}-\frac{54R_2^4}{r^6}+\frac{18R_2^6}{r^8}\right){cos}^2\theta .$$ (27)

Finally, integrating this equation over V_L, one finds

$$F_L=8\pi {\eta }_L{R}_2{\stackrel{.}{R}}_2^2+3\pi {\eta }_L{R}_2{\stackrel{.}{x}}^2.$$ (28)

Calculation of the dissipative function for the shell is much easier. For f_S, one has ²⁰

$$f_S={\eta }_S{(v_{ij})}^2={\eta }_S\left[{\left(\frac{\partial v_S}{\partial r}\right)}^2+\frac{2v_S^2}{r^2}\right],$$ (29)

where η_S is the shear viscosity of the shell and v_S is given by Eq. (4). Integrating Eq. (29), one obtains

$$F_S=8\pi {\eta }_S(R_{20}^3-R_{10}^3)\frac{R_1{\stackrel{.}{R}}_1^2}{R_2^3}.$$ (30)

E. Equations of motion

Calculating the functions L and F by using the equations obtained above, substituting the resulting expressions into Eq. (1), taking R₁ and x as generalized coordinates, and using Eq. (6) to express R₂ in terms of R₁, one obtains the following equations of bubble motion:

$$R_1{\ddot{R}}_1\left[1+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\frac{R_1}{R_2}\right]+{\stackrel{.}{R}}_1^2\left[\frac{3}{2}+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\times \left(\frac{4R_2^3-R_1^3}{2R_2^3}\right)\frac{R_1}{R_2}\right]-\frac{1}{c}\frac{{\rho }_L}{{\rho }_S}(R_2^2{\stackrel{\cdots }{R}}_2+6R_2{\stackrel{.}{R}}_2{\ddot{R}}_2+2{\stackrel{.}{R}}_2^3)=\frac{{\rho }_L}{{\rho }_S}\frac{{\stackrel{.}{x}}^2}{4}+\frac{P_{g0}}{{\rho }_S}{\left(\frac{R_{10}}{R_1}\right)}^{3\gamma }-\frac{2{\sigma }_1}{{\rho }_S{R}_1}-\frac{2{\sigma }_2}{{\rho }_S{R}_2}-\frac{P_0+P_{ac}(x,t)}{{\rho }_S}-\frac{4{\stackrel{.}{R}}_1}{{\rho }_S{R}_1{R}_2^3}[{\eta }_L{R}_1^3+{\eta }_S(R_{20}^3-R_{10}^3)]-\frac{4{\mu }_S(R_{20}^3-R_{10}^3)}{{\rho }_S{R}_2^3}\times \left(1-\frac{R_{1e}}{R_1}\right)\left[1+\frac{1}{2}\left(1-\frac{R_{1e}}{R_1}\right)\left(1-\frac{3R_1^3}{R_2^3}\right)\right],$$ (31)

$$m_b\ddot{x}+\frac{2\pi }{3}{\rho }_L\frac{d}{dt}(R_2^3\stackrel{.}{x})=-\frac{4\pi }{3}{R}_2^3\frac{\partial }{\partial x}{P}_{ac}(x,t)-6\pi {\eta }_L{R}_2\stackrel{.}{x}.$$ (32)

Equation (31) governs the radial pulsation of the bubble and Eq. (32) its translation. The first term on the right-hand side of the translational equation is the acoustic radiation force and the second term is the viscous drag force in the form of the Stokes law, which is only natural as we used the no-slip boundary condition on the bubble surface. However, it is common practice to replace the Stokes drag force with a more accurate equation resulting from experimental measurements.

If the c⁻¹ term on the left-hand side, the translational term ρ_Lẋ²/(4ρ_S) on the right-hand side, and the (1–R_1e/R₁) correction within the square brackets in the elastic term on the right-hand side are omitted, Eq. (31) becomes identical to that obtained by Church.⁴ Note that Church’s theory implicitly supposes that the deformation of the shell is small and therefore the elastic term in Church’s radial equation is taken only to the first order in (1–R_1e/R₁). The (1–R_1e/R₁) correction in the elastic term partly extends the range of Eq. (31) towards finite deformations.

When the sound is off and the bubble is at rest, from Eq. (31) it follows that

$$P_{g0}=P_0+\frac{2{\sigma }_1}{R_{10}}+\frac{2{\sigma }_2}{R_{20}}+4{\mu }_S\left(1-\frac{R_{10}^3}{R_{20}^3}\right)\left(1-\frac{R_{1e}}{R_{10}}\right)\times \left[1+\frac{1}{2}\left(1-\frac{R_{1e}}{R_{10}}\right)\left(1-\frac{3R_{10}^3}{R_{20}^3}\right)\right].$$ (33)

Church used this equation, neglecting the (1–R_1e/R₁) correction in the elastic term, to get an expression for R_1e. Assuming that the encapsulating layer is thin and fully permeable to gas, he set P_g0 = P₀ and obtained

$$R_{1e}^{Ch}=R_{10}\left[1+\frac{1}{4{\mu }_S}\left(\frac{2{\sigma }_1}{R_{10}}+\frac{2{\sigma }_2}{R_{20}}\right)\frac{R_{20}^3}{R_{20}^3-R_{10}^3}\right].$$ (34)

However, for thick-shelled contrast agents, such as Quantison and Myomap,³ it is unlikely that such an approximation will be appropriate. In the following subsection, a more correct calculation of R_1e is given.

Next, ẋ in Eqs. (31) and (32) is in fact the velocity of the bubble with respect to the velocity of the surrounding liquid. That is, if there is a stream in the bulk liquid, due to the propagation of the acoustic wave, acoustic streaming, and so forth, ẋ should be replaced with ẋ– v_ex, where v_ex denotes the liquid velocity unrelated to the presence of the bubble.

It is easy to see that the compressibility correction, the c⁻¹ term in Eq. (31), is similar to that obtained by Prosperetti for a free bubble.²² The striking feature of this term is the appearance of the third-order derivative R⃛₂. This is just a consequence of using Taylor series expansions to express time-retarded quantities, e.g., R̈₂(t–R₂/c) ≈ R̈₂(t) – (R₂/c) R⃛₂(t). The third derivative can be eliminated as follows. It is easily shown by using Eq. (6) that

$$R_2^2{\stackrel{\cdots }{R}}_2+6R_2{\stackrel{.}{R}}_2{\ddot{R}}_2+2{\stackrel{.}{R}}_2^3=R_1^2{\stackrel{\cdots }{R}}_1+6R_1{\stackrel{.}{R}}_1{\ddot{R}}_1+2{\stackrel{.}{R}}_1^3,$$ (35)

i.e., R₂ in the compressibility correction can be replaced with R₁. Further, since the compressibility correction is already of order c⁻¹, the right-hand side of Eq. (35) can be evaluated from Eq. (31) omitting the c⁻¹ term. This results in

$$R_1^2{\stackrel{\cdots }{R}}_1+6R_1{\stackrel{.}{R}}_1{\ddot{R}}_1+2{\stackrel{.}{R}}_1^3={\left[1+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\frac{R_1}{R_2}\right]}^{-1}\times \left\{R_1\frac{dG}{dt}+2R_1{\stackrel{.}{R}}_1{\ddot{R}}_1\left[1+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\frac{R_1^4}{R_2^4}\right]+2{\stackrel{.}{R}}_1^3\left[1+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\frac{R_1^4(2R_2^3-R_1^3)}{R_2^7}\right]\right\},$$ (36)

where G denotes the right-hand side of Eq. (31). On substitution of this equation into Eq. (31), the third derivative vanishes.

F. Expression for R_1e

The radius R_1e (as well as R_2e for the outer interface) corresponds to the unstrained state of the shell material when any internal stresses within the shell are absent. Knowledge of R_1e is necessary because by definition the displacement vector is reckoned from the unstrained position. Clearly R₁₀ does not meet the unstrained state since even if the sound is off, stresses within the shell are not zero as there exists surface tension at the interfaces and in general P₀ ≠ P_g0.

To calculate R_1e, we need to know the strain distribution inside the shell when the sound is off. Solution to this problem can be found, for example, in Ref. 20. Applying it to the present case, one has

$$u=ar+b/r^2,$$ (37)

where

$$a=\frac{R_{10}^3(P_{g0}-2{\sigma }_1/R_{10})-R_{20}^3(P_0+2{\sigma }_2/R_{20})}{3K_S(R_{20}^3-R_{10}^3)},$$ (38)

$$b=\frac{(P_{g0}-P_0-2{\sigma }_1/R_{10}-2{\sigma }_2/R_{20})R_{10}^3{R}_{20}^3}{4{\mu }_S(R_{20}^3-R_{10}^3)}.$$ (39)

These equations give the strain distribution inside a resting spherical layer with inner and outer radii of R₁₀ and R₂₀. At r = R₁₀, the deformation is equal to u₁ = R₁₀–R_1e. Setting u = u₁ and r = R₁₀ in Eq. (37) and using Eq. (33), one obtains

$$R_{1e}=R_{10}\left[1-\frac{1}{4{\mu }_S}\left(P_0+\frac{2{\sigma }_2}{R_{20}}\right)\frac{R_{20}^3}{R_{10}^3}\right].$$ (40)

Similarly, for R_2e, one has

$$R_{2e}=R_{20}\left[1-\frac{1}{4{\mu }_S}\left(P_0+\frac{2{\sigma }_2}{R_{20}}\right)\right].$$ (41)

Equations (40) and (41) show that R_1e < R₁₀ and R_2e < R₂₀, i.e., the internal gas pressure expands the shell outwards with respect to its unstrained position. Note that $R_{1e}^{Ch}>R_{10}$, i.e., Church’s approximation predicts an opposite effect, namely that the shell shrinks due to surface tension with respect to its unstrained position. This discrepancy can be important because it affects the sign of the elastic term in Eq. (31). Note also that for the case of a free bubble, when $R_{20}^3-R_{10}^3=0$ the elastic term in Eq. (31) tends to zero as it must, whereas in Church’s theory this term tends to a finite quantity as is seen from Eq. (34).

Completing this main section, some remarks concerning the limits of validity of the proposed model should be made. Although no explicit restrictions are imposed on the amplitude of radial oscillation, the model, like the others mentioned in the Introduction, in fact is valid for moderate acoustic pressures at best. First, it ignores nonlinear elastic effects in the shell. Second, if compression is strong enough, the shell buckles. Even if the buckling is reversible, it is evident that the dynamics of the shell will change. If the buckling is irreversible, then the response of the bubble to repeating acoustic pulses can change. Third, the shell can break up during expansion and the bubble will lose gas. Finally, the bubble can also lose gas due to the shell permeability, the radial and translational motions of the bubble can be affected by a constrained environment of a blood vessel, etc. All these effects are still beyond the capabilities of existing models.

III. LINEAR ANALYSIS

Let us assume that the amplitude of the radial oscillation is small. Then we can write

$$R_1=R_{10}+\xi (t),R_2=R_{20}+\frac{R_{10}^2}{R_{20}^2}\xi (t),$$ (42)

where it is assumed that |ξ| <R₁₀. Substituting Eqs.(42) into Eq. (31) and linearizing it with respect to ξ, one obtains the equation of a linear harmonic oscillator:

$$\ddot{\xi }+\delta \stackrel{.}{\xi }+{\omega }_0^2\xi =-\frac{P_{ac}(t)}{\alpha {\rho }_S{R}_{10}}.$$ (43)

It is assumed in Eq. (43) that P_ac(t) is of the form P_ac(t) = P_a exp (iωt), where P_a is the acoustic pressure amplitude and ω is the angular driving frequency. The coefficient α, the damping constant δ, and the undamped linear resonance frequency ω₀ are given by

$$\alpha =1+\left(\frac{{\rho }_L-{\rho }_S}{{\rho }_S}\right)\frac{R_{10}}{R_{20}},$$ (44)

$$\delta ={\delta }_{\eta }+{\delta }_r,$$ (45)

$${\delta }_{\eta }=\frac{4}{\alpha {\rho }_S{R}_{10}^2{R}_{20}^3}[{\eta }_L{R}_{10}^3+{\eta }_S(R_{20}^3-R_{10}^3)],$$ (46)

$${\delta }_r=\frac{{\rho }_L{R}_{10}{\omega }^2}{\alpha c{\rho }_S},$$ (47)

$${\omega }_0=\frac{1}{R_{10}\sqrt{\alpha {\rho }_S}}{\left\{3\gamma P_{g0}-\frac{2{\sigma }_1}{R_{10}}-\frac{2{\sigma }_2{R}_{10}^3}{R_{20}^4}+\frac{4{\mu }_S(R_{20}^3-R_{10}^3)}{R_{20}^3}\left[1-D\left(1+\frac{3R_{10}^3}{R_{20}^3}\right)\right]\right\}}^{1/2},$$ (48)

$$D=\frac{1}{4{\mu }_S}\left(P_0+\frac{2{\sigma }_2}{R_{20}}\right)\frac{R_{20}^3}{R_{10}^3}.$$ (49)

It is instructive to compare these quantities to those obtained by Church.⁴ Differences are observed for δ_r, and ω₀:

$${\delta }_r^{Ch}={\omega }^2{R}_{20}/c,$$ (50)

$${\omega }_0^{Ch}=\frac{1}{R_{10}\sqrt{\alpha {\rho }_S}}{\left\{3\gamma P_0-\frac{2{\sigma }_1}{R_{10}}-\frac{2{\sigma }_2{R}_{10}^3}{R_{20}^4}+\frac{4{\mu }_S(R_{20}^3-R_{10}^3)}{R_{20}^3}\left[1+Z\left(1+\frac{3R_{10}^3}{R_{20}^3}\right)\right]\right\}}^{1/2},$$ (51)

$$Z=\frac{1}{4{\mu }_S}\left(\frac{2{\sigma }_1}{R_{10}}+\frac{2{\sigma }_2}{R_{20}}\right)\frac{R_{20}^3}{R_{20}^3-R_{10}^3}.$$ (52)

It should be noted that Eq. (50) was not formally derived by Church as part of Eq. (31); it was introduced by ad hoc assumption, modifying the relevant expression for a free bubble. The difference between Eqs. (48) and (51) is accounted for by Church’s assumption that P_g0 = P₀ and his resulting expression for R_1e, Eq. (34). Figures 2 and 3 show the ratios ${\delta }_r/{\delta }_r^{Ch}$ and ${\omega }_0/{\omega }_0^{Ch}$ as functions of R₂₀. The solid lines in the figures correspond to the shell thickness R_S =R₂₀− R₁₀=20 nm (Albunex bubble), and the dashed lines to R_S =200 nm (Quantison bubble). The values of the physical parameters required for these calculations were taken from Church’s work:⁴ P₀ =101.3 kPa, ρ_L =1000 kg/m³, η_L =0.001 Pa s, c=1500 m/s, ρ_S =1100 kg/m³, η_S =1.77 Pa s, μ_S =88.8 MPa, σ₁ =0.04 N/m, and σ₂ =0.005 N/m. Figures 2 and 3 show that the discrepancy with Church’s theory increases as the bubble radius decreases and the shell thickness increases, but is not very significant for bubbles with R₂₀> 1 μm. However, it is known that the real resonance frequency of a system with dissipation differs from ω₀ and depends on δ. The behavior of δ_r, and ω₀ suggests that the damped (real) resonance frequency of an encapsulated bubble differs more significantly from that given by Church’s theory. To clarify this point, let us consider a solution to Eq. (43). This is

FIG. 2.

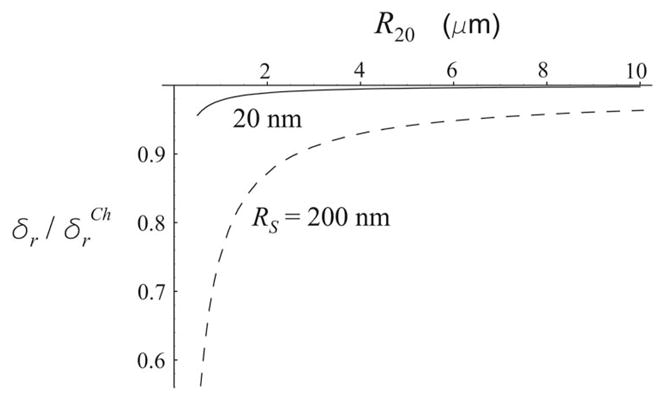
The ratio of the radiation damping constants ${\delta }_r/{\delta }_r^{Ch}$ as a function of equilibrium bubble radius for two values of the shell thickness R_S.

FIG. 3.

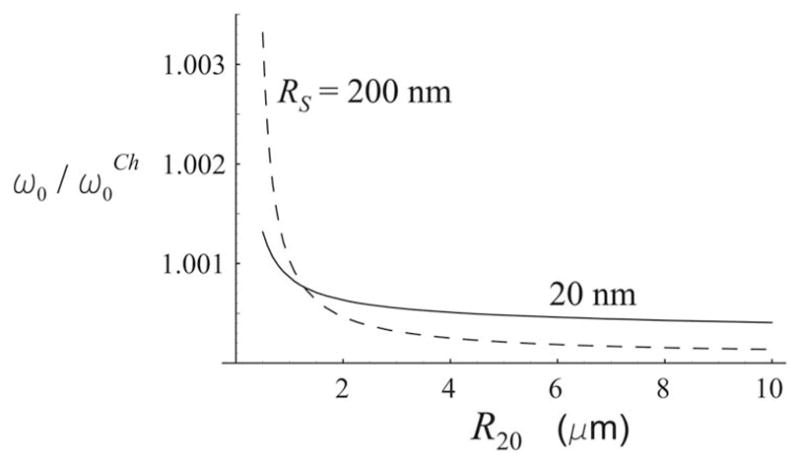
The ratio of the undamped resonance frequencies ${\omega }_0/{\omega }_0^{Ch}$ as a function of equilibrium bubble radius for two values of the shell thickness R_S.

$$\xi (t)=Aexp(i\omega t+i\phi ),$$ (53)

where

$$\phi =arctan[\omega \delta /({\omega }^2-{\omega }_0^2)],$$ (54)

$$A=P_{a}Q(\omega )/(\alpha {\rho }_S{R}_{10}{\omega }_0^2),$$ (55)

$$Q(\omega )={\omega }_0^2/{[{({\omega }^2-{\omega }_0^2)}^2+{\omega }^2{\delta }^2]}^{1/2}.$$ (56)

The resonance response corresponds to a maximum of Q(ω). If δ is independent of ω, the damped resonance frequency is equal to ${\omega }_r=\sqrt{{\omega }_0^2-{\delta }^2/2}$. However, in the present case δ_r is frequency dependent and therefore ω_r is defined by a more complicated expression

$${\omega }_r=\frac{1}{\beta \sqrt{3}}{(\sqrt{{\beta }^2{\sigma }_{\eta }^2+4\beta {\delta }_{\eta }+6{\beta }^2{\omega }_0^2+1}-2\beta {\delta }_{\eta }-1)}^{1/2},$$ (57)

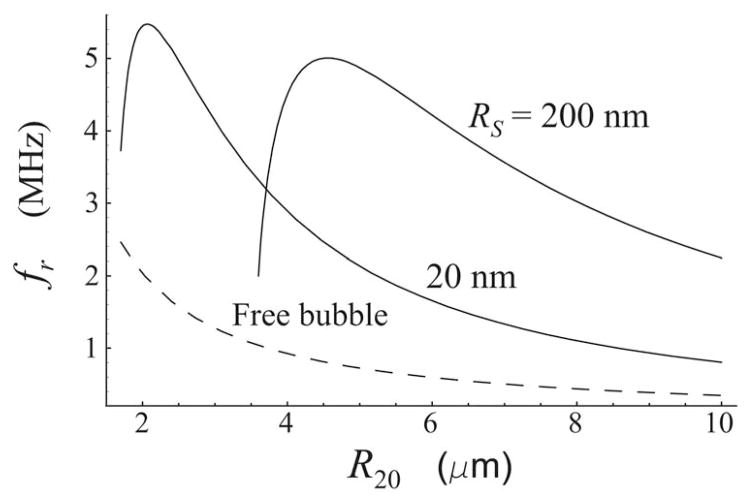
where β=δ_r/ω²=ρ_LR₁₀/(αcρ_S). The value of the damped resonance frequency given by Church’s theory, ${\omega }_r^{Ch}$, is obtained from Eq. (57) by replacing ω₀ with ${\omega }_0^{Ch}$ and β with β^Ch=R₂₀/c. Figure 4 shows the ratio ${\omega }_r/{\omega }_r^{Ch}$ as a function of R₂₀ for the same values of the parameters as in Fig. 3. Figure 5 presents the absolute values of the damped resonance frequency f _r = ω_r/2π; the dashed line corresponds to a free bubble of the equivalent size. It is seen from Fig. 4 that the ratio ${\omega }_r/{\omega }_r^{Ch}$ is really noticeably larger than the ratio ${\omega }_0/{\omega }_0^{Ch}$ in Fig. 3. Figure 5 points to one more feature of damped oscillations, which is not considered in Church’s analysis, namely that strong damping can lead to the absence of resonance. This occurs when the expression in brackets in Eq. (57) becomes negative, which in turn results from the fact that δ_η very strongly increases as the bubble radius decreases. It is for this reason that the solid lines in Fig. 5 go down and stop at small values of R₂₀, and the corresponding lines in Fig. 4 are terminated at approximately 3.5 and 2 μm. Figure 6 illustrates the process of vanishing resonance response, showing the function Q(ω) at R_S =20 nm for various values of R₂₀. It is seen that when R₂₀ is smaller than a threshold value, the resonance peak is absent and the amplitude of the radial oscillation monotonically decreases as the driving frequency increases. Figure 5 also shows that the thicker the bubble shell, the larger the threshold bubble radius.

FIG. 4.

The ratio of the damped resonance frequencies ${\omega }_r/{\omega }_r^{Ch}$ as a function of equilibrium bubble radius for two values of the shell thickness R_S.

FIG. 5.

Damped resonance frequency f _r = ω_r/2π versus equilibrium bubble radius for two values of the shell thickness R_S. The dashed line corresponds to a free bubble of the equivalent size.

FIG. 6.

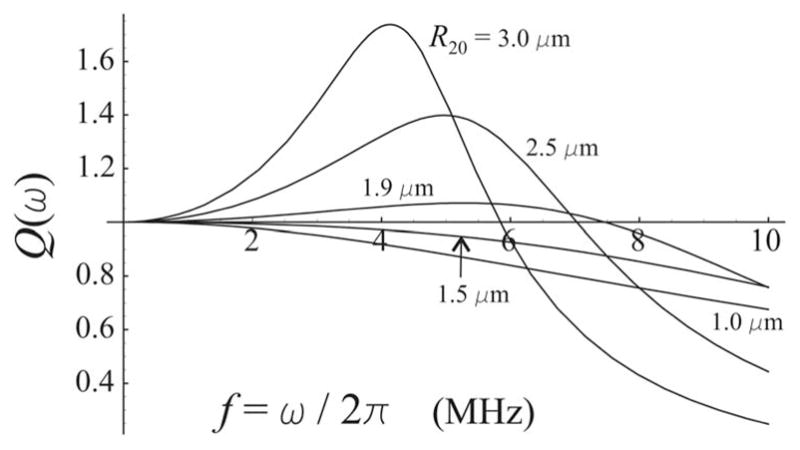
Behavior of the resonance function Q(ω) at R_S =20 nm for various values of the equilibrium bubble radius R₂₀.

IV. COMPARISON WITH ZERO-THICKNESS ENCAPSULATION MODELS

Most of the existing models having the form of a Rayleigh-Plesset-type equation can be referred to as zero-thickness encapsulation models, since these, explicitly or implicitly, assume the bubble shell to be very thin and describe only the dynamics of the outer bubble radius. If we neglect the translational term in Eq. (31) and assume that ρ_S ≈ ρ_L, the deformation of the shell is small, and R_S Lt; R₁₀, R₂₀, Eq. (31) reduces to an equation of the above-named type:

$${\rho }_L\left(R\ddot{R}+\frac{3}{2}{\stackrel{.}{R}}^2\right)=P_{g0}{\left(\frac{R_0}{R}\right)}^{3\gamma }-\frac{2\sigma }{R}-P_0-P_{\text{ac}}-4{\eta }_L\frac{\stackrel{.}{R}}{R}-12{\eta }_S{R}_S\frac{\stackrel{.}{R}}{R^2}-12{\mu }_S{R}_S\frac{R_0}{R}\left(\frac{1}{R_0}-\frac{1}{R}\right),$$ (58)

where R denotes the outer bubble radius and σ=σ₁ + σ₂. It is easy to see that Eq. 3583 is practically identical to the equation proposed by de Jong et al. for Albunex microspheres^1,2 provided that

$$S_p=6R_S{\mu }_S\text{and}{S}_f=48\pi R_S{\eta }_S,$$ (59)

where S_p and S_f are, respectively, the shell elasticity parameter and the shell friction parameter that appear in de Jong et al.’s model. Using Eqs. (59) and the results of de Jong et al., we can estimate values of μ_S and η_S for albumin-shelled bubbles. Assuming R_S =15 nm, one has μ_S =88.8 MPa and η_S =1.77 Pa s, in agreement with Church’s estimates.⁴ By using Ref. 23, the parameters S_p and S_f can also be evaluated for lipid-shelled bubbles. For example, setting R_S =1 nm as is proposed by Morgan et al.⁶ for lipid coatings, one finds μ_S =333.3 MPa and η_S =2.4 Pa s. Note that the value of η_S is of the same order of magnitude as that obtained by Morgan et al.⁶ by fitting experimental radius-time curves. As regards the elastic term used in the model of Morgan et al., Marmottant et al.²³ have recently shown that it is incorrect. Therefore comparison of the value of μ_S is impossible.

Marmottant et al.²³ also showed that for lipid-shelled bubbles, the elastic behavior of the bubble shell can occur only for very small oscillations of the bubble radius about its equilibrium value. For larger oscillations, the shell buckles when the bubble is compressed and breaks up when the bubble expands. Therefore a continuous elastic model like Eq. (58) is not a good approximation for lipid-shelled contrast agents. However, for bubbles with a sufficiently thick encapsulation, such as polymer- or albumin-shelled contrast agents, Eqs. (31) and (32) can be quite adequate.

V. RADIATION FORCE AND TRANSLATIONAL MOTION

In this section, we apply Eqs. (31) and (32) to calculate the radiation force experienced by an encapsulated bubble and the translational displacement of the bubble due to this force. Let us first consider radiation force in a weak field, assuming that the radial oscillation of the bubble is described by Eq. (43). The radiation force exerted on the bubble can be calculated as

$${\mathit{F}}_{\text{en}}=-\frac{4\pi }{3}\langle R_2^3(t)\nabla P_{ac}(\mathit{r},t)\rangle ,$$ (60)

where 〈〉 means the time average and r is the position vector of the bubble centroid. Substituting R₂(t) from Eq. (42), one obtains

$${\mathit{F}}_{\text{en}}=-4\pi R_{10}^2\langle \xi (t)\nabla P_{ac}(\mathit{r},t)\rangle .$$ (61)

In the case of a plane traveling wave, P_ac(r,t) = P_a exp (iωt −ik·r), where k=ω/c is the wave vector. Substituting this expression into Eq. (43), one finds ξ(t) to be

$$\xi (t)=\frac{P_{ac}(\mathit{r},t)}{\alpha {\rho }_S{R}_{10}({\omega }^2-{\omega }_0^2-i\omega \delta )}.$$ (62)

Substitution of Eq. (62) into Eq. (61) finally yields

$$F_{\text{en}}=\frac{2\pi P_a^2{R}_{10}\omega \delta k}{\alpha {\rho }_S[{({\omega }^2-{\omega }_0^2)}^2+{\omega }^2{\delta }^2]}.$$ (63)

The radiation force on a free bubble of the equivalent radius is given by²⁴

$$F_{\text{fr}}=\frac{2\pi P_a^2{R}_{20}\omega {\delta }_{f}k}{{\rho }_L[{({\omega }^2-{\omega }_{0f}^2)}^2+{\omega }^2{\delta }_f^2]},$$ (64)

where

$${\delta }_f=\frac{{\omega }^2{R}_{20}}{c}+\frac{4{\eta }_L}{{\rho }_L{R}_{20}^2},$$ (65)

$${\omega }_{0f}=\frac{1}{R_{20}\sqrt{{\rho }_L}}{\left(3\gamma P_0+\frac{2(3\gamma -1)\sigma }{R_{20}}\right)}^{1/2}.$$ (66)

Figure 7 displays the ratio F_fr/F_en as a function of driving frequency for three bubbles with different values of equilibrium radius and shell thickness. The presence of encapsulation decreases the amplitude of the radial oscillation of contrast agent bubbles. For this reason, it is commonly supposed that the radiation force on an encapsulated bubble should be considerably smaller than that on a free bubble of the equivalent size. Figure 7 reveals, however, that this is not true throughout the whole frequency range. At relatively low frequencies, near the resonance of the free bubble, the radiation force on the free bubble is really much larger than that on the encapsulated bubbles. However, for higher frequencies, in the range of resonances of the encapsulated bubbles, the radiation force on the encapsulated bubble exceeds that on the free bubble. Curve 3 shows that this effect can occur even for a thick-shelled bubble with R_S =200 nm if its outer radius is large enough.

FIG. 7.

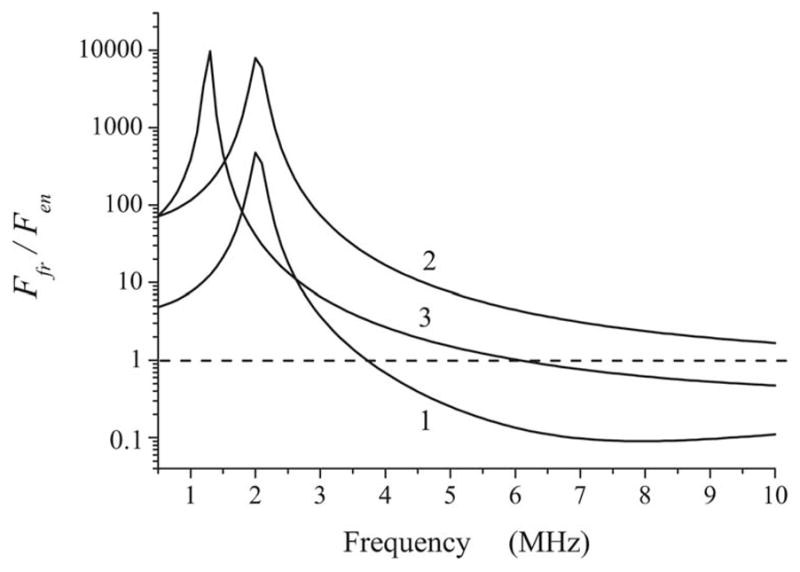
Comparison of radiation force experienced by an encapsulated bubble in a weak field with that on a free bubble of the equivalent size at various driving frequencies. (1) R₂₀=2 μm, R_S =15 nm; (23 R₂₀=2 μm, R_S =200 nm; and (3) R₂₀=3 μm, R_S =200 nm.

Figure 8 shows the translational displacement of a free bubble (dashed line) and two equivalent encapsulated bubbles with R_S =15 nm and 200 nm under stronger driving. The bubbles are subjected to a single 20-cycle acoustic pulse with a pressure amplitude of 150 kPa. The displacement is fixed after the termination of the pulse. The outer radius of all the bubbles is 2 μm. The simulation was carried out by numerically calculating Eqs. (31) and (32). It is again seen that at high frequencies the displacement of the encapsulated bubbles is considerably larger, this time even for the 2-μm-radius bubble with R_S =200 nm. Thus, it is found that in the range of relatively high frequencies encapsulated bubbles are able to translate more efficiently than free bubbles of equivalent size.

FIG. 8.

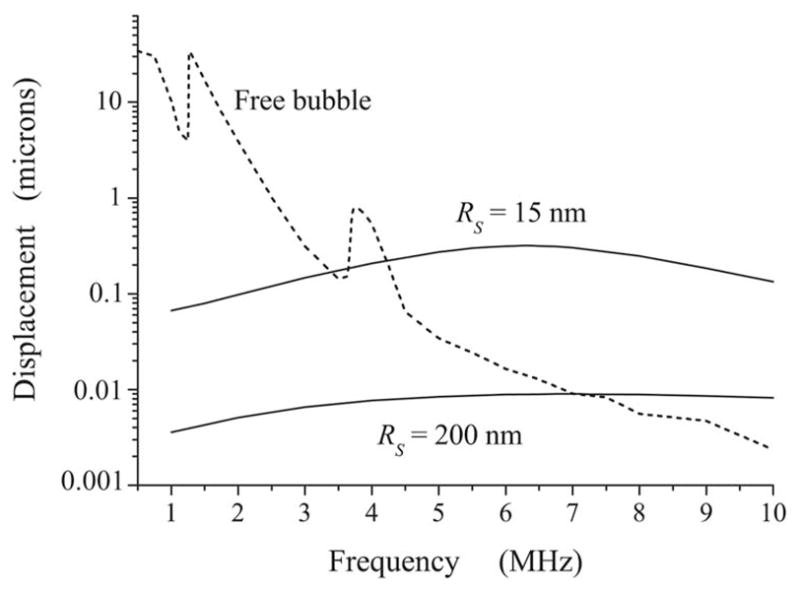
Translational displacement versus driving frequency for a free and an encapsulated bubble. The driving field is a single 20-cycle acoustic pulse with a pressure amplitude of 150 kPa. The displacement is fixed after the termination of the pulse. The outer radius of the bubbles is 2 μm.

VI. CONCLUSIONS

In this work coupled equations describing the radial and translational dynamics of an encapsulated gas bubble are derived. It is assumed that the encapsulating layer is an incompressible elastic solid with viscous damping and the surrounding medium is a slightly compressible viscous Newtonian liquid. The proposed model improves Church’s theory⁴ by allowing for the translation motion of the bubble and radiation losses due to the compressibility of the surrounding liquid. It is also shown that the expression obtained by Church for the inner bubble radius corresponding to the unstrained state of the encapsulating shell gives an incorrect result when the shell thickness tends to zero. The expression for the unstrained radius is recalculated by using equations from the theory of elasticity.

Comparative analysis of the linearized radial equation is carried out relative to Church’s theory. In the course of the analysis, the expression for the acoustic damping constant of an encapsulated bubble is refined, and it is shown that Church’s theory underestimates the damped resonance frequencies of encapsulated bubbles. It is also shown that the viscous damping in the bubble shell can lead to the absence of resonance response. This effect is observed when the bubble radius is smaller than a threshold value; the thicker the bubble shell, the larger the threshold bubble radius. Below the threshold radius, the amplitude of the radial oscillation monotonically decreases as the driving frequency increases.

The acoustic radiation force experienced by an encapsulated bubble in a weak field is calculated analytically and compared with the radiation force on a free bubble of the equivalent size. It is shown that for high frequencies, the radiation force on the encapsulated bubble exceeds that on the free bubble. For the case of stronger driving, comparison of the radiation forces is carried out by numerically calculating the translational displacement of the bubbles, using the nonlinear coupled equations of the radial and translational motions. It is shown again that at high frequencies the displacement of encapsulated bubbles is considerably greater than that of free bubbles of equivalent size.