Abstract
Elevations in systolic blood pressure are believed to be closely linked to the pathogenesis and progression of renal diseases. It has been hypothesized that the afferent arteriole (AA) protects the glomerulus from the damaging effects of hypertension by sensing increases in systolic blood pressure and responding with a compensatory vasoconstriction (Loutzenhiser R, Bidani A, Chilton L. Circ Res 90: 1316–1324, 2002). To investigate this hypothesis, we developed a mathematical model of the myogenic response of an AA wall, based on an arteriole model (Gonzalez-Fernandez JM, Ermentrout B. Math Biosci 119: 127–167, 1994). The model incorporates ionic transport, cell membrane potential, contraction of the AA smooth muscle cell, and the mechanics of a thick-walled cylinder. The model represents a myogenic response based on a pressure-induced shift in the voltage dependence of calcium channel openings: with increasing transmural pressure, model vessel diameter decreases; and with decreasing pressure, vessel diameter increases. Furthermore, the model myogenic mechanism includes a rate-sensitive component that yields constriction and dilation kinetics similar to behaviors observed in vitro. A parameter set is identified based on physical dimensions of an AA in a rat kidney. Model results suggest that the interaction of Ca2+ and K+ fluxes mediated by voltage-gated and voltage-calcium-gated channels, respectively, gives rise to periodicity in the transport of the two ions. This results in a time-periodic cytoplasmic calcium concentration, myosin light chain phosphorylation, and cross-bridge formation with the attending muscle stress. Furthermore, the model predicts myogenic responses that agree with experimental observations, most notably those which demonstrate that the renal AA constricts in response to increases in both steady and systolic blood pressures. The myogenic model captures these essential functions of the renal AA, and it may prove useful as a fundamental component in a multiscale model of the renal microvasculature suitable for investigations of the pathogenesis of hypertensive renal diseases.
Keywords: renal microcirculation, smooth muscle mechanics, calcium transport, nonlinear system
the rates of blood flow and filtration in a nephron are regulated by two major mechanisms. One is the tubuloglomerular feedback (TGF) system, a negative feedback loop in which alterations in tubular fluid chloride concentration alongside the macula densa cells result in compensatory adjustments in the muscle tension of the afferent arteriole (AA). The second is the myogenic mechanism, which is an intrinsic property of the AA. This mechanism induces a compensatory vasoconstriction of the AA when the vessel is presented with an increase in transmural pressure. The relative contributions of these two mechanisms to the autoregulation of nephron blood flow and filtration rate depend on a number of factors, including genetic factors, hormonal status, and arterial blood pressure.
In the rat kidney, the myogenic response has been found to operate at 0.1–0.3 Hz (4, 19, 20, 39), whereas the TGF mechanism operates at much lower frequencies (<0.05 Hz). These findings have been interpreted to imply that renal autoregulatory compensation is limited by the upper bound of the myogenic frequency response and that pressure fluctuations with frequencies higher than ∼0.3 Hz are transmitted passively through the renal vasculature.
However, in recent years evidence has emerged which demonstrates that the renal myogenic mechanism can respond to pulse pressure fluctuations in blood flow. Rather than fully responding to each pressure pulse, the AA exhibits a sustained vasoconstriction that is determined by the systolic pressure (28, 29). This surprising behavior arises from a marked asymmetry in the kinetics of vasoconstriction and relaxation. Loutzenhiser and coworkers (28, 29) developed a simple phenomenological model of AA kinetics which predicted changes in AA radius as a function of renal blood pressure; the predictions of the model agreed with their measurements. The modulation of baseline vascular resistance by systolic pressure is thought to protect the renal microvasculature from hypertension-induced injury, the incidence of which is correlated with both autoregulatory dysfunction and systolic pressure (2, 3).
The goal of the present study was to develop a detailed mathematical model of the myogenic response of a small segment of the AA wall, including the endothelium and the surrounding smooth muscle cell. The model, which is intended to be incorporated into models of integrative renal hemodynamic regulation, is used to examine the response of a segment of the AA to changes in mean and pulsatile pressure. The simulations reveal model behaviors that agree well with experimental data and that lend support to the hypothesis that the AA myogenic response plays an important role in protecting the glomerular capillary against elevated systolic pressures.
MATHEMATICAL MODEL
Our AA wall model represents the response of both the smooth muscle cell and the endothelium. The model is based on a model for cerebral arterioles in the cat that was developed by Gonzalez-Fernandez and Ermentrout (14). To account for the differences in physical dimensions and in dynamical behaviors between the cerebral arterioles and the renal afferent arteriole, we adjusted a number of the model parameters in the Gonzalez-Fernandez and Ermentrout model (see below). We also incorporated into the model a new myogenic response mechanism that is based on the hypothesis that the dependence of calcium channel openings on voltage is shifted by changes in transmural pressure, such that vessel diameter decreases with increasing pressure and vice versa.
Key model equations are summarized below; detailed derivations for the equations can be found in the appendix and in Ref. 14. The model simulates the interactions among voltage-sensitive Ca2+ channels, Ca2+-sensitive and voltage-sensitive K+ channels, and the membrane potential. The model AA wall undergoes contractions that are controlled by the free cytosolic calcium concentration, denoted Cai. The rate of change of Cai is given by
| (1) |
where α = 1/(zCaβVcellF), zCa = 2 is the valence of the calcium ion, β is the fraction of cell volume occupied the cytosol, Vcell is the cell volume, F is the Faraday constant, gCa is the maximum whole-cell membrane conductance for the calcium current, kCa is the first-order rate constant for cytosolic calcium extrusion, Kd is the ratio of the forward and backward reaction rates of the calcium-buffer system, and BT is the total buffer concentration. The equilibrium distribution of open calcium channel states m∞ is described as a function of membrane potential v (13, 27)
| (2) |
where v1 is the voltage at which half of the channels are open, and v2 determines the spread of the distribution.
Oscillations in Cai vary the phosphorylation rate of the 20-kDa myosin light chains (MLC), which are involved in the formation of cross bridges between overlapping myosin and actin filaments. The formation of cross bridges causes smooth muscle contraction. Because the kinetics of that phosphorylation, which is calcium dependent, is much faster than other vasomotion processes considered here, we assume that the fraction of phosphorylated MLC to total MLC, denoted by ψ, is given by (34)
| (3) |
where Cai,m is a constant. The phosphorylated myosin interacts with actin to form cross bridges and develop stress (25). Let ω denote the fraction of cross bridges formed; then we describe the net formation of cross bridges by means of the ordinary differential equation given by
| (4) |
Variations in the number of cross bridges induce variations in a contractile force, which in turn gives rise to variations in AA diameter. To simulate the resulting vasomotion, we consider the blood vessel to be a thick-walled cylinder. The motion of the vessel wall is driven, in part, by the transmural pressure, muscle activity, and wall deformation, which give rise to forces described below and in the appendix. Let ri and ro denote the inner and outer vessel radius, respectively. Let Δp denote the transmural pressure, and let x denote the average circumferential length, i.e., x = π(ri + ro). The transmural pressure causes the vessel to relax or contract, which then gives rise to a tension force in the angular (θ) direction. That force, which we denote by fΔp, is given by
| (5) |
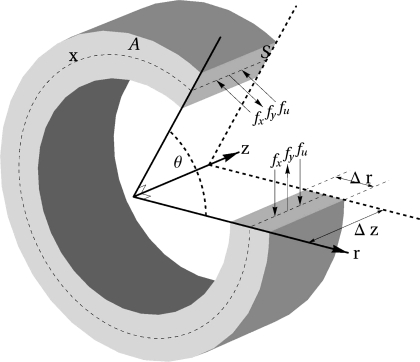
where A, the wall cross-sectional area, is given by A = π(ro2 − ri2) (14). A schematic diagram of the model AA wall is shown in Fig. 1.
Fig. 1.
Longitudinal (S) and transverse (A) sections of the vessel cylinder. x denotes the circumferential length. Coordinates r, θ, and z denote the radial, angular, and axial directions. The hoop forces fx, fy, and fu are perpendicular to S.
Wall deformation gives rise to additional stresses along the θ direction of the wall. Let y and u be the circumferential lengths associated with the contractile and series elastic components, respectively. We assume that those stresses consist of the following components: a contractile component of length y, in series with an elastic component of length u; these two components are in parallel with an elastic component of length x = y + u (recall that x is the average circumference). We consider the resulting hoop forces on a surface S, which is bounded by the inner and outer radii of the vessel; S is assumed to be perpendicular to the angular (θ) direction, and to have unit length along the axial (z) direction. Then, given the stresses σx, σy, and σu (given in the appendix), the hoop forces on S are
| (6) |
where we and wm are weights representing the contribution by the elastic and muscular components of the hoop forces. The rate of change of the parallel elastic component's length is given by
| (7) |
where τ is a pseudo-time constant associated with the wall internal friction.
For a given number of cross bridges, the velocity of the contractile component (y) is assumed to depend on the balance between the muscle load experienced by the contractile component, given by the elastic stress σu and the contractile stress σy. For σu ≤ σy, the velocity is also proportional to phosphorylation level (7, 8, 33). Thus, following Ref. 14, we have
| (8) |
for σu > σy, the contractile component lengthens:
| (9) |
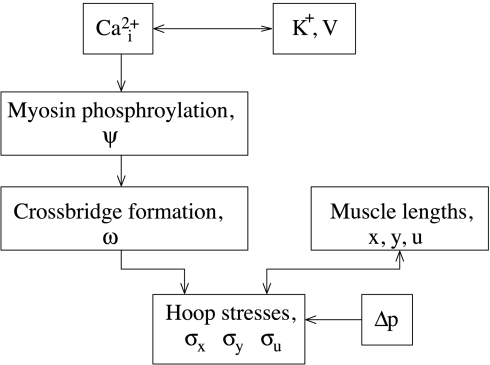
Figure 2 provides a flow chart that illustrates the steps by which periodic oscillations in cytosolic calcium concentration give rise to spontaneous vasomotion of the model AA wall.
Fig. 2.
Flow chart that illustrates the steps by which periodic oscillations in cytosolic calcium concentration (Cai2+) give rise to spontaneous vasomotion of the model afferent arteriole wall. Δp, Transmural pressure.
Myogenic Response
A notable feature of the AA myogenic mechanism is the asymmetry in its response times for vasoconstriction and vasodilation. Loutzenhiser and coworkers (28, 29) observed that the initial delay in the activation of a pressure-dependent vasoconstriction was ∼0.3 s, with the time-profile of the response approximated by an exponential having a time constant of 4 s. In contrast, vasodilation exhibited an initial delay of ∼1 s, with a response approximated by two exponentials having time constants of 1 and 14 s, respectively.
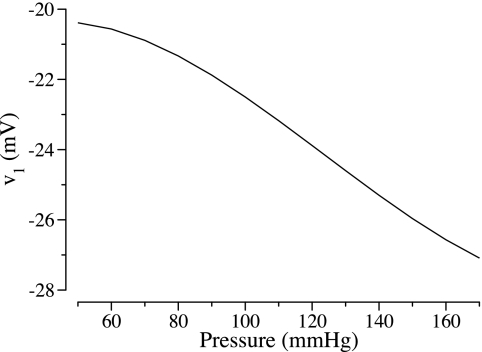
Based on the hypothesis that the dependence of calcium channel openings on voltage is shifted by changes in transmural pressure, Gonzalez-Fernandez and Ermentrout (14) described the voltage associated with the opening of half of the calcium channels (denoted v1) as a decreasing function of transmural pressure Δp (see Fig. 6 in Ref. 14). However, our implementation of their model fails to predict the aforementioned asymmetry in the kinetics of the AA vasomotion (see discussion). To attain that asymmetry (28, 29), we hypothesize that, as transmural pressure Δp changes from Δp1 to Δp2, v1 undergoes transient changes (see below), with the final v1 value, denoted v1,* representing a decreasing function (in units of mV) of Δp2 (in units of mmHg); thus we hypothesize that v1* is given by
| (10) |
where the parameters c1,* c2,* c3,* c4,* and Δp* are given in Table 6. Figure 3 shows v1* as a function of Δp. For a given transmural pressure, Eq. 10 yields an AA radius that is in general agreement with experimental measurements by Loutzenhiser and coworkers (28).
Fig. 6.
Average vessel inner diameter as a function of steady-state transmural pressure, with and without a myogenic response.
Table 6.
Myogenic mechanism parameters
| Parameter | Value | Unit |
|---|---|---|
| c1* | 3.81 × 10−6 | mV·mmHg−3 |
| c2* | −2.71 × 10−4 | mV·mmHg−2 |
| c3* | −6.53 × 10−2 | mV·mmHg−1 |
| c4* | −22.5 | mV |
| Δp* | 100 | mmHg |
| c1fast | −2.79 × 10−7 | mV·mmHg−3·s2 |
| c2fast | 4.18 × 10−4 | mV·mmHg−2·s1 |
| c3fast | −2.85 × 10−1 | mV·mmHg−1 |
| c4fast | −2.53 × 10−2 | mV·mmHg−1 |
Parameters that differ from those in Ref. 14.
Fig. 3.
Steady-state voltage at which half of the channels are open (v1) as a function of transmural pressure, as given by Eq. 10.
To obtain response times that are consistent with experiments, the rate of change of v1 depends not only on the Δp values, but also on the rate of change of Δp. We further assume that as Δp changes, the response in v1 consists of a fast component and a slow component, i.e.,
| (11) |
where Rfast and Rslow are determined by Δp and its rate of change.
Consider first an increase in Δp (i.e., Δp2 > Δp1); the response in v1 begins after an initial delay of 0.3 s. The fast component of the response, Rfast, which lasts for the same time interval as the increase in Δp, yields a rapid decrease in v1 that overshoots beyond v1.* Rfast is a function of the rate of increase in Δp, given in units of mV/s, by
| (12) |
where c1fast, c2fast, and c3fast are given in Table 6. The overshoot generated by Rfast is necessary for the model to generate a sufficiently rapid vasoconstriction response. The slow component, Rslow, exponentially increases to v1*, if we let
| (13) |
We set k1 = ln(2)/0.2 s−1 to yield an exponential decay with a half-life of 0.2 s. Unlike the fast component which lasts for the same time interval as the pressure increase, the slow component continues after the pressure increase has ended.
We assume that a decreasing Δp also induces a two-component response in v1. The fast component Rfast, which begins after an initial delay of 1 s and which lasts for the same time interval as the decrease in Δp, increases v1 rapidly to vmid which lies between v1 and v1;* Rfast is given in units of mV/s by
| (14) |
where c4fast is given in Table 6. The slow component elevates v1 exponentially to v1*:
| (15) |
where we set k2 = ln(2)/10 s−1 to yield an exponential decay with a half-life of 10 s. The slow component continues after the pressure decrease has ended. This two-component response is constructed to generate a slow vasodilation response.
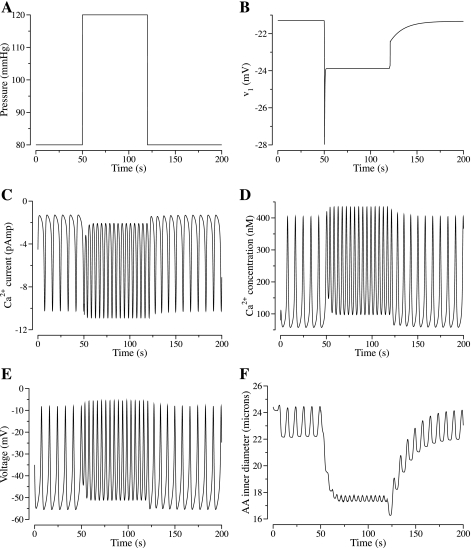
To illustrate the response of v1 to changes in Δp, we display in Fig. 4, A and B, the time course of v1 as Δp changes rapidly from 80 to 120 mmHg during an interval of 0.1 s, then, after 70 s, decreases rapidly back to 80 mmHg over 0.1 s. This simulation will be discussed further in results.
Fig. 4.
A: step perturbation in transmural pressure. B–F: time courses of the resulting v1, Ca2+ current, intracellular free calcium concentration Cai, membrane potential v, and AA inner diameter.
Parameters
A large number of parameters are used in this model to describe the AA wall's geometrical dimensions, membrane transport properties, and muscle mechanical properties. The values of these parameters are given in Tables 1–5. Myogenic mechanism parameters are given in Table 6. Most of these parameters are taken from Ref. 14 and the references therein. A selected subset of parameters in Ref. 14 has been modified to account for the differences in physical dimensions and in dynamic behaviors between the cerebral arterioles modeled in Ref. 14 and the renal AA of this study; modified parameters are marked with asterisks in Tables 1–5.
Table 1.
Afferent arteriole geometric dimensions
| Parameter | Value | Unit |
|---|---|---|
| S* | 2.00 × 10−4 | cm2 |
| A* | 1.38 × 10−6 | cm2 |
| ro* | 12.0 × 10−4 | cm |
| ri* | 10−3 | cm |
| we | 1/9.00 | Dimensionless |
| wm | 0.700 | Dimensionless |
| τ | 0.500 | dyn·s·cm−1 |
Parameters that differ from those in Ref. 14.
Table 2.
Arteriolar membrane parameters
| Parameter | Value | Unit |
|---|---|---|
| v2 | 25.0 | mV |
| v4 | 14.5 | mV |
| v5 | 8.00 | mV |
| v6 | −15.0 | mV |
| vL | −70.0 | mV |
| vK | −90.0 | mV |
| vCa | 80.0 | mV |
| Ca3 | 400 | nM |
| Ca4 | 150 | nM |
| ϕn* | 0.900 | s−1 |
Parameter that differs from that in Ref. 14.
Table 3.
Arteriolar cell parameters
| Parameter | Value | Unit |
|---|---|---|
| gL | 7.85 × 10−14 | C·s−1·mV−1 |
| gK | 3.14 × 10−13 | C·s−1·mV−1 |
| gCa | 1.57 × 10−13 | C·s−1·mV−1 |
| C* | 7.85 × 10−14 | C·mV−1 |
| Kd | 103 | nM |
| BT | 105 | nM |
| α | 8.00 × 1015 | nM·C−1 |
| β | 0.550 | Dimensionless |
| kCa* | 190 | s−1 |
Parameters that differ from those in Ref. 14.
Table 4.
Arteriolar vessel mechanical parameters
| Parameter | Value | Unit |
|---|---|---|
| x0* | 0.0150 | cm |
| x1 | 1.20 | Dimensionless |
| x2 | 0.130 | Dimensionless |
| x3 | 2.22 | Dimensionless |
| x4 | 0.712 | Dimensionless |
| x5 | 0.800 | Dimensionless |
| x6 | 0.0100 | Dimensionless |
| x7 | 0.321 | Dimensionless |
| x8 | 0.890 | Dimensionless |
| x9 | 9.05 × 10−3 | Dimensionless |
| u1 | 41.8 | Dimensionless |
| u2 | 4.74 × 10−2 | Dimensionless |
| u3 | 5.84 × 10−2 | Dimensionless |
| y0 | 0.928 | Dimensionless |
| y1 | 0.639 | Dimensionless |
| y2 | 0.350 | Dimensionless |
| y3 | 0.788 | Dimensionless |
| y4 | 0.800 | Dimensionless |
Parameter that differs from that in Ref. (14).
Table 5.
Arteriolar smooth muscle parameters
| Parameter | Value | Unit |
|---|---|---|
| Cai,m* | 277 | nM |
| q | 3.00 | Dimensionless |
| Cai, ref | 400 | nM |
| σy0#* | 1.46 × 107 | dyn·cm−2 |
| σ0#* | 1.69 × 107 | dyn·cm−2 |
| ψm | 0.300 | Dimensionless |
| kψ* | 0.250 | s−1 |
| vref | 0.240 | s−1 |
| a | 0.281 | Dimensionless |
| b | 5.00 | Dimensionless |
| c | 0.0300 | Dimensionless |
| d | 1.30 | Dimensionless |
Parameters that differ from those in Ref. 14.
MODEL RESULTS
Using the base-case parameter set given in Tables 1–5, we investigated the dynamic behaviors of the model AA wall. In this study, we set the baseline transmural pressure, Δp, to 100 mmHg, a value consistent with a AA wall segment located at the proximal portion of the vessel. The Δp for a wall segment in the distal AA would be smaller owing to the pressure drop along the AA. We first considered the dynamics of the model's ionic transport and membrane potential. Figure 5, A and B, depicts the oscillations of electrical current across the membrane carried by Ca2+ and by K+ (i.e., ICa and IK, respectively, given by Eq. 26) and the corresponding transmembrane potential v. The asynchrony between the ionic currents ICa and IK gives rise to the oscillations of the action potential. The inward-directed Ca2+ current depolarizes the cell, which results in an increase in the membrane potential. The outward-directed K+ current then follows and repolarizes the cell, resulting in a decrease in the membrane potential. Because both the Ca2+ and K+ channels are voltage dependent, variations in membrane electrical potential v affect those currents. As v decreases, the equilibrium distributions of open Ca2+ and K+ channel states (denoted m∞ and n∞; see Eqs. 2 and 24) both decrease. Consequently, the magnitudes of currents ICa and IK decrease, which result in periodic oscillations in the transmembrane potential and the ionic currents.
Fig. 5.
Base-case oscillation profiles. A: oscillations in Ca2+ and K+ currents (denoted ICa and IK, respectively) and membrane potential v. B: oscillations in equilibrium distribution of open Ca2+ and K+ channel states (denoted m∞ and n∞, respectively). C and D: oscillations in intracellular free Ca2+ concentration and AA inner diameter, respectively.
Oscillations in ICa result in oscillations in the intracellular free calcium concentration, Cai, which give rise to cross-bridge formation and smooth muscle contractions. Figure 5, C and D, shows the time courses of the intracellular free calcium concentration Cai and the vessel's inner diameter, respectively. The calcium concentration oscillations (Fig. 5C) lag behind those of the membrane potential (Fig. 5A), whereas the peaks and troughs of the membrane potential correspond in time to those of the vessel diameter (Fig. 5D). The frequency of these oscillations is ∼175 mHz, and the amplitude of the vessel diameter oscillations is ∼1 μm. These predictions are consistent with experimental measurements (28).
Responses to Different Steady-State Transmural Pressure Values
We examined the model AA wall's behaviors for differing steady-state transmural pressure values. For the first set of simulations, we neglected the myogenic response. That is, we assumed that the voltage-dependence of calcium channel openings is unaffected by changes in transmural pressure. In all simulations, we set v1 to −22.5 mV, the value that corresponds to Δp = 100 mmHg. The dynamic behaviors of the model vessels were computed for a range of transmural pressure Δp values. The vessel's time-averaged inner diameters for differing Δp are shown in Fig. 6. As transmural pressure is elevated, the tension force due to pressure (i.e., fΔp, Eq. 5) increases. Thus, in the absence of the myogenic response, the model vessel reacts passively to changes in transmural pressure, expanding from an average inner diameter of ∼17.3 μm at Δp = 60 mmHg to ∼24.2 μm at Δp = 160 mmHg.
In the next set of simulations, we incorporated the myogenic response by allowing dependence of calcium channel openings on membrane potential to be shifted by changes in transmural pressure (see Eq. 10). We computed the time-averaged vascular diameters for differing transmural pressure values; see Fig. 6. As Δp increases from 60 to 160 mmHg, v1 decreases from −20.6 to −26.6 mV. The more negative v1 values obtained for larger Δp generated larger inward-directed calcium currents and thus higher calcium concentrations, which resulted in the formation of cross bridges and muscle contraction. The increased pressure-induced tension force (i.e., increased fΔp) and the increased contractile force competed, with the net result being a vasoconstriction. In contrast to the previous case, which neglected the myogenic response, the model predicts a vasodilation when Δp is reduced to 60 mmHg: the vessel's average inner diameter increases from the base-case value of 19.95 μm at Δp = 100 mmHg to 26.8 μm at Δp = 60 mmHg; when Δp is increased to 160 mmHg, the vessel's average inner diameter decreases by 28.0% from base case (19.95 μm) to 14.4 μm. For sufficiently low or sufficiently high transmural pressure (Δp <40 mmHg or Δp >160 mmHg), no oscillations of significant amplitude were obtained in the vascular diameter.
The shifting of calcium channel openings by transmural pressure results in changes in calcium current and membrane potential. We computed the time-averaged membrane potential for differing transmural pressure; see Fig. 7. As Δp increases, v1 decreases and the inward-directed calcium current increases, which depolarizes the membrane. This result is consistent with experimental observations (17, 37) that report the depolarization of vascular muscle cells when transmural pressure is elevated. When the membrane calcium conductance, gCa, is reduced by a factor of 10, membrane potential becomes nearly insensitive to transmural pressure; see Fig. 7.
Fig. 7.
Average membrane potential as a function of steady-state transmural pressure, obtained for base-case membrane Ca2+ conductance gCa and for gCa reduced by a factor of 10.
Responses to Step Perturbations in Transmural Pressure
We examined the model's vasoconstriction kinetics by simulating a rapid increase in transmural pressure from 80 to 160 mmHg. A true step change in pressure was approximated by a smooth rise having a duration of 0.1 s. The vasodilation kinetics were then assessed when transmural pressure was reduced from 160 to 80 mmHg. We computed the model AA wall's vasodilation response, which we defined by
| (16) |
where ri(t) denotes the inner radius at time t, r̄0 denotes the time-averaged inner radius before the pressure change, and r̄max denotes the maximum response, i.e., the time-averaged inner radius value that the model AA wall approaches after the pressure change. The time courses for the responses, expressed as the percentage of the maximum response, are exhibited as solid curves in Fig. 8. To facilitate the interpretation of these responses, we also provide (as dashed curves) in Fig. 8, A and B, the time courses of the spontaneous vasomotion corresponding to steady-state pressures of 80 and 160 mmHg, respectively.
Fig. 8.
Kinetics of AA vasoconstrictive response to pressure increase (80–160 mmHg; A) or decrease (160–80 mmHg; B). Solid line, oscillations in AA inner diameter given as percentage of maximal response; dashed line, oscillations in AA inner diameter in the absence of pressure changes.
Note that the maximum responses approached 100% in both simulations, but the response did not start at 0% in Fig. 8A, the case where pressure was increased from 80 to 160 mmHg. Instead, at t = 0, both the spontaneous vasomotion and the vasoconstriction response were determined to be at −13.5% of the maximum contractile response (see Fig. 8A). That is because the model AA wall undergoes spontaneous vasomotion even in the absence of pressure changes. In this simulation, the AA radius was below its average radius, corresponding to 80 mmHg at t = 0. Immediately after the pressure increase, the AA wall underwent a passive dilation, inasmuch as the myogenic response did not begin until 0.3 s after the pressure change. That delay was followed by an almost monotonic contractile response, with the AA radius reaching 90% of the maximum contractile response in ∼11.3 s. As shown in Fig. 8B, the vasodilation response exhibited a longer initial delay (∼1 s), and a generally slower response time: 90% of maximal dilation was attained in ∼45.2 s. Because the amplitude of the vasomotion decreases with increasing pressure, as shown in the sensitivity studies at the end of results, the amplitude of the oscillations at Δp = 160 mmHg is insignificant.
We then simulated the vessel's responses to a rapid, steplike increases or decreases in transmural pressure. In this simulation, Δp began to increase from 80 to 120 mmHg at t = 50 s, remained constant at 120 mmHg for ∼70 s, and then began to decrease from 120 to 80 mmHg at t = 120 s. Figure 4 shows the time course of the transmural pressure, and the resultant v1, Ca2+ current, intracellular free calcium concentration, membrane potential, and vascular inner diameter.
As Δp increased from 80 to 120 mmHg, v1 exhibited an overshoot response (after an initial delay of 0.3 s), in which it decreased rapidly from −21.3 to −28.0 mV (see Fig. 4B). As v1 decreased, a larger Ca2+ current was induced, depolarizing the cell. After the overshoot response, v1 returned to the target value −23.9 mV, which corresponds to Δp = 120 mmHg. Compared with the response at 80 mmHg, the magnitude of the average calcium current, and thus the average calcium concentration, is higher at Δp = 120 mmHg; consequently, the magnitude of the average membrane potential (v) is reduced (see Fig. 4, C–E). As a result of the higher calcium concentration, a higher fraction of cross bridges is formed, which gives rise to smooth muscle contractions, exhibited in a decrease in vascular diameter from an average of ∼23.1 to 17.5 μm (see Fig. 4F).
As Δp decreased from 120 to 80 mmHg, v1 increased, after an initial delay of 1 s, from −23.9 to −22.5 mV, in a first-phase response of duration 0.1 s. That was then followed by a longer second-phase response, during which v1 further increased to −21.3 mV, the target value that corresponds to Δp = 80 mmHg. The elevation in v1 gave rise to a smaller Ca2+ current, a lower calcium concentration, and a smaller fraction of cross bridges formed. A vasodilation thus resulted, with average ri increases from ∼8.76 to 11.5 μm. Compared with vasoconstriction, vasodilation occurred over a substantially longer time interval. These results demonstrate the asymmetry in response times for vasoconstriction and vasodilation, in agreement with measurements by Loutzenhiser et al. (28, 29).
Responses to Pressure Pulses
We then assessed the model vessel's response to pressure oscillations having differing frequencies. We first considered steplike pressure pulses, having a frequency of 1 Hz, with transmural pressure varying between 100 and 120 mmHg. The period of those oscillations is substantially shorter than the response times of the vessel's myogenic mechanism; in that sense, the frequency of these pressure signals can be considered high. The time course of the transmural pressure and the changes in the vessel's inner diameter are shown in Fig. 9, A1 and B1. The response to a single pressure pulse of 20-s duration is included for comparison. That response is qualitatively similar to that shown in Fig. 4.
Fig. 9.
A1: single-step pressure perturbation, followed by a period pulse train at 1 Hz. A2: similar pressure perturbations, but with a slower period pulse train at 0.05 Hz. B1 and B2: corresponding changes in AA inner diameter.
Instead of responding to the high-frequency pressure variations passively without attenuation, the model vessel exhibited a sustained vasoconstriction. Vasoconstriction occurred because the response to the pressure stimulus continues during the 1-s delay in vasodilation. Thus, when presented with a train of such pulses, the contractile responses are additive. Also, results in Fig. 9B1 show that similar sustained vasoconstriction responses were obtained for both the single-step perturbation and the high-frequency pressure signals, even though the average pressure increase in the high-frequency signals was only half of that of the single-step perturbation. (If we consider pressure increases >100 mmHg, then the average pressure increase in the high-frequency signals was 10 mmHg, because the pressure was 100 mmHg for half of the interval over which the signal was applied, and the pressure was 120 mmHg for the other half of the time, whereas the pressure increase corresponding to the single-step perturbation was 20 mmHg, because the pressure was set to 120 mmHg for the entire 100-s interval.)
In contrast, when presented with a train of pressure pulses of a lower frequency of 0.05 Hz, the inner vessel diameter exhibited clearly distinguishable oscillations instead of a sustained vasoconstriction; see Fig. 9, A2 and B2.
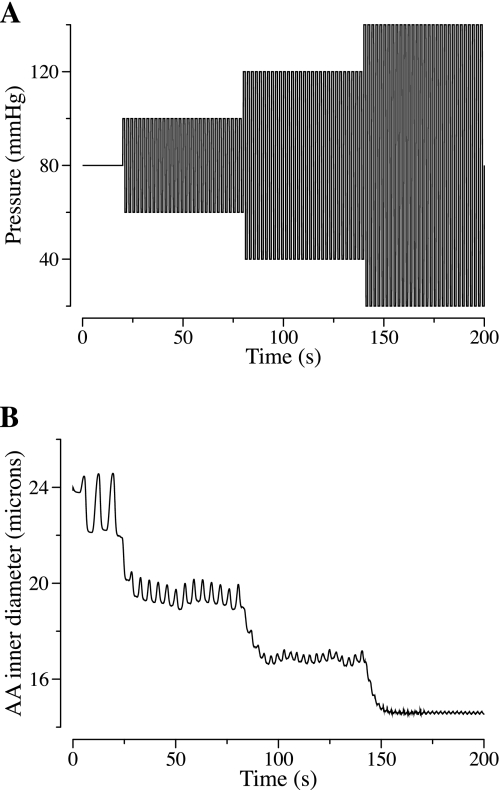
To further examine the hypothesis that myogenic tone is determined, in large part, by systolic pressure rather than mean pressure, we conducted a simulation in which the transmural pressure was perturbed by high-frequency (0.5 Hz) oscillations, of increasing amplitude but constant mean pressure. Specifically, transmural pressure first oscillated for 60 s between 60 and 100 mmHg, then for 60 s between 40 and 120 mmHg, then for another 60 s between 20 and 140 mmHg. The model response is shown in Fig. 10. An increase in systolic pressure elicited AA vasoconstriction, which occurred progressively with increasing range in pressure oscillations, and which occurred despite a constant mean pressure of 80 mmHg, owing to a corresponding decrease in diastolic pressure.
Fig. 10.
A: oscillatory pressure perturbation with amplitude (and systolic pressure) increasing by steps, while a mean constant pressure of 80 mmHg is maintained. B: corresponding AA inner diameter.
Model Sensitivities to Parameters
The values used for some models parameters are substantially uncertain. Therefore, in a set of parameter sensitivity studies, we studied the effects of varying selected parameters on model behaviors. The parameters that we considered were the following: v1, the voltage associated with the opening of half the population of the calcium channels (see Eq. 2); v6, which determines the voltage associated with the opening of half the population of the potassium channels (see Eq. 25); Φn, which determines the rate at which the potassium channels open (see Eq. 23); kCa, the rate constant for cytosolic calcium extrusion (see Eq. 21); kψ, which determines the rate of formation of cross bridges (see Eq. 4); C, the cell capacitance (see Eq. 26); and gK and gCa, which are the whole-cell membrane conductances associated with the potassium and calcium currents (see Eq. 26). We varied these parameters individually, over wide ranges, with transmural pressure set to 100 mmHg. We determined the amplitude and frequency of the vasomotion, average AA inner radius, average membrane voltage potential, and average cytosolic calcium concentration. The results of this sensitivity study are summarized in Table 7. We conducted simulations for 20 sets of parameters, labeled A1, A2, … B1, B2, etc. in Table 7 under column “Case.” Cases labeled with the same letter (e.g., A1, A2, and A3) correspond to simulations in which the same parameter was varied; the number distinguishes cases in which different values were assigned to that parameter.
Table 7.
Determinants of vasomotion
| Case | Parameter | Value | Oscillation | Amplitude, μm | Frequency, mHz | Voltage, mV | Radius, μm | Cai, nM |
|---|---|---|---|---|---|---|---|---|
| Base case | Y | 0.495 | 175 | −37.7 | 9.99 | 191 | ||
| A1 | v1 (−22.5 mV) | −30.0 | N | −21.8 | 7.45 | 443 | ||
| A2 | −25.0 | Y | 0.102 | 267 | −28.7 | 7.89 | 284 | |
| A3 | −20.5 | Y | 2.74 | 66.7 | −46.8 | 16.4 | 111 | |
| A4 | −19.0 | N | −60.0 | 21.3 | 33.6 | |||
| B1 | v6 (−15.0 mV) | −5.00 | N | −14.2 | 7.41 | 411 | ||
| B2 | −25.0 | Y | 1.12 | 100 | −47.4 | 13.0 | 118 | |
| C1 | ϕn (0.9 s−1) | 0.300 | Y | 3.54 | 85.7 | −40.0 | 13.9 | 175 |
| C2 | 1.10 | Y | 0.255 | 233 | −32.2 | 8.57 | 237 | |
| C3 | 2.6 | N | −23.3 | 7.54 | 330 | |||
| D1 | kCa (190 s−1) | 95.0 | Y | 0.540 | 133 | −42.8 | 8.28 | 300 |
| D2 | 250 | Y | 0.297 | 200 | −32.2 | 10.2 | 178 | |
| E1 | kψ (0.25 s−1) | 0.200 | Y | 0.660 | 167 | −37.3 | 9.97 | 195 |
| E2 | 0.330 | Y | 1.19 | 171 | −37.9 | 15.5 | 191 | |
| F1 | C | ×0.25 | Y | 0.283 | 300 | −32.3 | 11.4 | 185 |
| F2 | (7.85 × 10−14 C/mV) | ×1.25 | Y | 0.350 | 200 | −32.0 | 8.55 | 235 |
| G1 | gK (314 pS) | ×2 | Y | 0.685 | 150 | −43.3 | 11.5 | 154 |
| G2 | ×0.5 | N | −16.4 | 7.48 | 395 | |||
| H1 | gCa (157 pS) | ×2 | N | −15.0 | 7.31 | 809 | ||
| H2 | ×1.5 | Y | 0.198 | 257 | −25.1 | 7.99 | 376 | |
| H3 | ×0.5 | N | −65.6 | 22.6 | 14.9 |
The model's oscillatory behavior is caused by the interactions between cytosolic calcium and potassium currents, with the depolarization of the cell membrane by the calcium current, followed by hyperpolarization by the potassium calcium. Thus variations in model parameters that determine the rate of oscillations in these currents may affect the dynamics of the model. Results in Table 7 show that, in case C2, the large φn value accelerated the kinetics of potassium channel opening, with the effect that oscillations persist but at a frequency 1.33 times of that found in the base case. Oscillation frequency is also increased by decreasing the cell capacitance C (F1), or vice versa.
When calcium extrusion rate kCa is increased (D2), cytosolic calcium concentration decreases, and vascular radius increases. Similarly, when cross-bridge formation rate constant kψ increases, vasodilation is predicted. This is because the model predicts that, for model parameters considered, the time-averaged values of cross-bridge formation rate, given by kψψ/(ψm + ψ), is lower than cross-bridge degeneration rate, kψω. Thus Eq. 4 yields a smaller ω for a larger first-order rate constant kψ and vasodilation results.
With v1 set to a large negative value (−30.0 mV) in case A1, the equilibrium distribution of open calcium channel states is shifted so that cytosolic calcium concentration increases, the calcium transport overrides the potassium transport, cell membrane is depolarized, and oscillations vanish. An opposite effect was obtained when the magnitude of v1 was reduced to −19.0 mV (case A4), or when the whole-cell membrane conductances associated with the calcium current (gCa) were reduced (case H3). In both cases, oscillations again vanish, but with cell-membrane hyperpolarization and vasodilation. When v6, which is associated with the equilibrium distribution of open potassium channel states, is set to a large negative value (B2), the outward-directed potassium current increases, which hyperpolarizes the cell. The same effect is achieved by increasing gK, the whole-cell membrane capacitances associated with the potassium current (G1).
DISCUSSION
We have identified a set of parameters that are consistent with the physical properties and dynamics of the AA in the rat kidney and applied those parameters to the model of arteriolar smooth muscle cell vasomotion by Gonzalez-Fernandez and Ermentrout (14). Using base-case parameters, the resultant model predicts that, given a transmural pressure of 100 mmHg at the entrance to the AA, the time-averaged inner diameter of the AA is ∼20 μm, consistent with experimental measurements (28). The model also predicts that the interactions among the calcium and potassium cell membrane transports spontaneously generate periodic membrane voltage oscillations and vasomotion, with an amplitude of ∼1 μm and a frequency of ∼175 mHz. Model simulations suggest that, owing to the asymmetry in vasoconstriction and vasodilation response times, the AA may be able to sense systolic pressure at heartbeat frequency and respond with a sustained vasoconstriction when systolic pressure is elevated.
Comparison with Previous Models
Our AA model is based on the vascular muscle cell model of Gonzalez-Fernandez and Ermentrout (14) (which we refer to as the “GE model”). The GE model was formulated for cerebral arterioles of the cat, which are substantially larger than the renal AA and which exhibit quantitatively different dynamic behaviors. The model cerebral arteriole has an average diameter of ∼540 μm, and the frequency of the vasomotion is ∼450 mHz. In contrast, the average diameter of the AA is ∼20 μm; and the frequency of the vasomotion is ∼175 mHz.
In the GE model, the myogenic response is incorporated by assuming that the voltage associated with the opening of half of the calcium channels (denoted v1) is a decreasing function of transmural pressure Δp (see Fig. 6 in Ref. 14). Reference 14 exhibits the model arteriole's responses to differing steady-state transmural pressure values, but it does not include the model's dynamic responses to variations in pressure. Our implementation of the GE model generates approximately the same vasoconstriction and vasodilation response times, which is inconsistent with experimental observations by Loutzenhiser and coworkers (28, 29).1 To obtain the appropriate asymmetry in response times, rate sensitivity was introduced into the model equations. We hypothesize that, during vasoconstriction, v1 first undergoes a transient overshoot response before returning to the target value. This overshoot response shortens the response time and produces the desired rapid vasoconstriction. Rate sensitivity has been observed in many vascular beds (15, 23). In the renal microvasculature, spectral analysis of renal blood flow (RBF) dynamics reveals features characteristic of rate sensitivity, namely, a rise in gain and an increase in phase that are accentuated by inhibition of nitric oxide synthesis (38, 39). Although the rapid RBF response to a step change in pressure predicted by rate sensitivity is often not seen in barbituate-anesthetized rats, responses consistent with a rate-sensitive component emerge after inhibition of nitric oxide synthesis (24). During vasodilation, we have assumed that v1 undergoes a slow, two-phase response, which gives rise to a slow vasodilation. This behavior is consistent with observations in renal vessels (28) and with data from isolated hamster cheek pouch arterioles, which exhibit unidirectional rate sensitivity such that the responses to rapid decreases in pressure show much less rate dependency than responses to step increases in pressure (5). Nevertheless, further direct studies of rate sensitivity of renal arterioles will need to be conducted to evaluate our assumption of unidirectional rate sensitivity. Furthermore, the origin of the rate sensitivity has yet to be determined. One possibility is that rapid changes in wall tension following a rapid rise in intravascular pressure may open the sodium or calcium channels, which are tethered to the cytoskeleton and extracellular matrix; subsequent remodeling of the cytoskeleton or relaxation of the viscoelastic elements in the vessel wall may reduce the tension, thereby resulting in rate sensitivity.
Marsh and coworkers (30) adopted the smooth muscle cell model of Gonzalez-Fernandez and Ermentrout (14) to study the interactions between AA myogenic response and TGF. However, some of the model parameters used in Ref. 30 are not appropriate for the dimensions of the rat AA, which is at least an order of magnitude smaller than the arterial vessel considered by Gonzalez-Fernandez and Ermentrout. For example, the length of the parallel elastic component associated with a reference stress (denoted by a parameter x0) should be on the same order of magnitude as the circumference of the AA. However, x0 was taken to be 1,500 μm in Ref. 30. In contrast, x0 was set to 150 μm in our model. Also, in Ref. 30 myogenic responses were generated only in response to oscillatory transmural pressure, whereas it has long been observed that changes in mean pressure also induce myogenic responses (28). In contrast, our model exhibits myogenic responses as a function of both pressure and its rate of change.
Based on the kinetic attributes of the AA myogenic response and the steady-state pressure and AA diameters, Loutzenhiser et al. (28) developed a mathematical model of renal autoregulation. Both that model and the present model predict vascular responses that appear to be consistent with the dynamic features of renal autoregulation observed in the intact kidney. However, the model in Ref. 28 is a phenomenological model that predicts only AA diameters. In a follow-up study, Williamson et al. (41) developed a more extensive systems model to examine the impact of systolic-pressure sensitivity on renal autoregulation. Their results show that the asymmetry in time delays in the myogenic response is more important than differences in the time constants of vasoconstriction vs. vasodilation in accounting for the sensitivity to systolic pressure in the hydronephrotic kidney. The present model extends those efforts in that it incorporates ionic transport, cell membrane potential, muscle contraction of AA smooth muscle cells, and the mechanics of a thick-walled cylinder, while still capturing the important behaviors identified by Loutzenhiser and his colleagues (28).
Implications of Model Results
When presented with pressure oscillations of sufficiently high frequency (>1 Hz), our model generates a sustained vasoconstriction, the magnitude of which is determined by the peak pressure rather than the mean pressure. These results support the hypothesis that baseline myogenic tone is strongly influenced by systolic pressure (28, 29). This observation broadens the concept that the myogenic response functions to maintain an approximately constant RBF and glomerular filtration rate (GFR) as blood pressure is varied. Under physiological conditions, where mean and systolic blood pressures vary in tandem, a myogenic response determined by systolic pressure would also regulate RBF and GFR, which are determined primarily by mean perfusion pressure, not peak pressure. However, under some pathophysiological conditions, where changes in systolic and mean blood pressures can be decoupled, an elevation in systolic pressure would result in a myogenic vasoconstriction, even if mean perfusion pressure is unchanged or decreased. Thus the myogenic response serves not only to maintain an approximately constant RBF, but it also protects the glomerulus from systolic pressure peaks. This behavior is of potential importance because studies have identified strong correlations between systolic pressure and renal injury (18).
Model Limitations and Potential Extensions
Because, as previously noted, this AA wall model is intended to be incorporated into future multiscale models of integrated renal hemodynamic control, we sought to develop a model that is computationally efficient. Thus some degree of simplification was necessary, and certain details, such as the possible involvement of epithelial sodium channels (ENaC) in the initiation of the myogenic response, signaling pathways underlying the vascular smooth muscle constriction, or signaling mechanisms that modulate the myogenic response, while important, were neglected or represented phenomenologically to keep computational costs low.
In the present model, the initiating event of the myogenic response is based on the assumption that the voltage associated with the opening of half of the calcium channels (denoted v1) is a decreasing function of transmural pressure Δp (see Fig. 6 in Ref. 14). Although this assumption is adequate for our purposes here, a number of other factors have been shown to be essential elements in the myogenic response, including TRP cation channels (1, 36) and cytochrome P-450 metabolites (35). However, it has been difficult to determine to what extent these factors are involved in the sensory event that initiates the myogenic response, or whether they are essential downstream mediators. One intriguing explanation of the origin of the myogenic response is the involvement of a stretch- or tension-induced membrane depolarization mediated by ENaC that may be part of a complex membrane mechanotransducer (12). It has been proposed that ENaC play a role in mechanotransduction events in a variety of organisms (12) and are essential elements in the renal myogenic response (16, 21, 22), although the available data for involvement in renal autoregulation are by no means conclusive (40). As new data emerge, the present model could be modified to include this alternative mechanism, which would replace the assumption of a pressure-dependent shift in the voltage dependency of calcium channels with a pressure-dependent membrane depolarization driven by an increase in membrane sodium conductance.
To enable the myogenic mechanism to respond to systolic pressure, we incorporated measured asymmetrical time delays and constructed an asymmetrical multicomponent dynamic pattern of calcium channel activation based on unilateral rate sensitivity. Although this description yields behaviors consistent with the observations of Loutzenhiser et al. (28, 29), it must be viewed as an emergent hypothesis that needs experimental verification. Furthermore, if the initiating event in the myogenic response does, in fact, involve ENaC that respond to systolic pressure, then the dynamics of the response of the ENaC to an abrupt increase in tension would have to exhibit unilateral rate sensitivity and time delays similar to those we have assumed for calcium channel activation.
The present model only represents the myogenic response of an isolated segment of the AA near its origin. The transmural pressure is specified a priori, the AA responds with a change in diameter, and the rise in segmental resistance is assumed to alter downstream pressure. Thus, at present, the model does not account for the interactions between the AA myogenic response and the fluid dynamics of the blood flowing though the segment.
Despite its limitations, the present model of a small segment of the AA wall can be used as an essential component in models of integrated renal hemodynamic regulation. For example, a model of the entire AA can be constructed by connecting instances of the AA wall segment model in series. Each segment model can be coupled to its neighbors through gap junctions, which allows representation of the electrotonic conduction along the AA, a phenomenon that is central to coordination of the responses of the individual cells. An appropriate fluid dynamics model would need to be included to relate fluid pressure, fluid flow, and tubular resistance. Also, many of the parameters of the present AA wall segment model will depend upon the location within the AA because of the decrease in intravascular pressure along the vessel. Using an approach similar to Ref. 30, the AA tubular model could then be combined with a model of glomerular filtration (e.g., Ref. 6) and a model of the TGF mechanism (e.g., Ref. 26) to study the interactions between the myogenic and TGF mechanisms in the context of renal autoregulation.
APPENDIX
Model Equations
Ion transport and membrane potential.
The smooth muscle cells of the AA can undergo contractions that are determined by the free cytosolic calcium concentration Cai. The sum of Cai and bound buffer CaB gives the total calcium concentration CaT, i.e.,
| (17) |
The free cytosolic calcium and the unbound buffer B combine to yield CaB in a reversible reaction that can be represented by
| (18) |
Because the kinetics of the calcium-buffer system is substantially faster than other relevant membrane transporters, the above reaction is assumed to be at equilibrium. Thus
| (19) |
By differentiating Eq. 17 with respect to time and using Eq. 19, one obtains
| (20) |
The rate of change of CaT can be described by the following first-order kinetics
| (21) |
where Vcell is the cell volume; β is the fraction of cell volume occupied the cytosol; F is the Faraday constant; zCa = 2 is the valence of the calcium ion; and kCa is the first-order rate constant for cytosolic calcium extrusion. Equation 1 is obtained by equating the right-hand sides of Eqs. 21 and 20.
The opening of potassium channels induces a transmembrane K+ efflux, which polarizes the cell membrane. To represent the K+ flux, we describe the rate of change of the fraction of K+ channel open states, denoted n, by first-order kinetics (31)
| (22) |
where n∞ denotes the equilibrium distribution of open K+ channel states. The rate constant λn is given by
| (23) |
where φn determines the rate at which the potassium channels open. This distribution depends on the membrane voltage v and the free cytoplasmic calcium concentration Cai
| (24) |
where
| (25) |
The potential v3, which determines the voltage at which half of the potassium channels are open, is a function of Cai; v4 and Ca4 are measures of the spread of the distributions of n∞ and v3, respectively.
The rate of change of the membrane potential v is the sum of transmembrane currents
| (26) |
where C denotes the cell capacitance. The transmembrane leak, potassium, and calcium currents, denoted IL, IK, and ICa, respectively, are given by IL = gL(v − vL), IK = gKn(v − vK), and ICa = gCam∞(v − vCa), respectively, where gL, gK, and gCa are associated with the respective whole-cell membrane conductances, and vL, vK, and vCa denote the respective Nernst reversal potentials.
Hoop stresses.
To approximate experimental measurements (8–11, 32), the hoop stresses associated with the parallel elastic, contractile, and series elastic components, denoted by σx, σy, and σu, respectively, are given in Ref. 14 by
| (27) |
| (28) |
| (29) |
where σy0 is the reference stress that depends on the fraction of cross bridges formed, ω
| (30) |
On the right-hand side of Eq. 27, the first term represents the stiff collagen fibers that come into play for large expansions; the second term represents the compliant elastin fibers that play a role in smaller deformations; the third term represents the large stiffness that arises when the vessel radius is substantially reduced; and the fourth term serves to fit σx to experimental data (32).
GRANTS
This research was supported by the National Science Foundation, through grants DMS-0715021 (to A. T. Layton) and by the National Institutes of Health, through National Institute of Diabetes and Digestive and Kidney Diseases Grants DK-89066 (to A. T. Layton) and DK-42091 (to H. E. Layton).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
Footnotes
Symmetric response times are expected for the model equations. Despite their nonlinearity, our numerical experience suggests that the model equations have a unique solution for parameters that are physiologically relevant. Thus the equations are reversible in time, which, in this context, means that if a pressure increase from Δp1 to Δp2 causes the vascular radius to decrease from r1 to r2 in a time interval Δt, then the reversed pressure change would induce a vasodilation from r2 to r1 in the same time Δt.
REFERENCES
- 1. Beech DJ. Emerging functions of 10 types of TRP cationic channel in vascular smooth muscle. Clin Exp Pharmacol Physiol 32: 597–603, 2005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Bidani AK, Griffin KA. Long-term renal consequenecs of hypertension for normal and diseased kidneys. Curr Opin Nephrol Hypertens 11: 73–80, 2002 [DOI] [PubMed] [Google Scholar]
- 3. Bidani AK, Griffin KA. Pathophysiology of hypertensive renal damage: implications for therapy. Hypertension 44: 1–7, 2004 [DOI] [PubMed] [Google Scholar]
- 4. Cupples WA, Novak P, Novak V, Salevsky FC. Spontaneous blood pressure fluctuations and renal blood flow dynamics. Am J Physiol Renal Fluid Electrolyte Physiol 270: F82–F89, 1996 [DOI] [PubMed] [Google Scholar]
- 5. Davis MJ, Sikes PJ. Myogenic responses of isolated arterioles: test for a rate-sensitive mechanism. Am J Physiol Heart Circ Physiol 259: H1890–H1900, 1990 [DOI] [PubMed] [Google Scholar]
- 6. Deen WM, Robertson CR, Brenner BM. A model of glomerular ultrafiltration in the rat. Am J Physiol 223: 1178–1183, 1972 [DOI] [PubMed] [Google Scholar]
- 7. Dillon PF, Askoy MO, Driska SP, Murphy RA. Myosin phosphorylation and the cross-bridge cycle in arterial smooth muscle. Science 211: 495–497, 1981 [DOI] [PubMed] [Google Scholar]
- 8. Dillon PF, Murphy RA. Tonic force maintenance with reduced shortening velocity in arterial smooth muscle. Am J Physiol Cell Physiol 242: C102–C108, 1982 [DOI] [PubMed] [Google Scholar]
- 9. Dobrin PB. Vascular mechanics. In: Handbook of Physiology. The Cardiovascular System. Peripheral Circulation and Organ Blood Flow. Bethesda, MD: Am Physiol Soc, 1983, sect. 2, vol. III, pt. 1, chapt. 3, p. 65–102 [Google Scholar]
- 10. Dobrin PB, Canfield TR. Identification of smooth muscle series elastic component in intact carotid artery. Am J Physiol Heart Circ Physiol 232: H122–H130, 1977 [DOI] [PubMed] [Google Scholar]
- 11. Driska SP, Damon DM, Murphy RA. Estimates of cellular mechanics in arterial smooth muscle. Biophys J 24: 525–540, 1978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Drummond HA, Grifoni SC, Jernigan NL. A new trick for an old dogma: ENaC proteins as mechanotransducers in vascular smooth muscle. Physiology (Bethesda) 23: 23–31, 2008 [DOI] [PubMed] [Google Scholar]
- 13. Ehrenstein G, Lecar H. Electrically gated ionic channels in lipid bilayers. Q Rev Biophys 10: 1–34, 1977 [DOI] [PubMed] [Google Scholar]
- 14. Gonzalez-Fernandez JM, Ermentrout B. On the origin and dynamics of the vasomotion of small arteries. Math Biosci 119: 127–167, 1994 [DOI] [PubMed] [Google Scholar]
- 15. Grande PO, Lundvall J, Mellander S. Evidence for a rate-sensitive regulatory mechanism in myogenic microvascular control. Acta Physiol Scand 99: 432–447, 1977 [DOI] [PubMed] [Google Scholar]
- 16. Guan Z, Pollock JS, Cook AK, Hobbs JL, Inscho EW. Effect of epithelial sodium channel blockade on the myogenic response of rat juxtamedullary afferent arterioles. Hypertension 54: 1062–1069, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Harder DR, Gilbert R, Lombard JH. Vascular muscle cell depolarization and activation in renal arteries on elevation of transmural pressure. Am J Physiol Renal Fluid Electrolyte Physiol 253: F778–F781, 1987 [DOI] [PubMed] [Google Scholar]
- 18. He J, Whelton PK. Elevated systolic blood pressure and risk of cardiovascular and renal disease: overview of evidence from observational epidemiologic studies and randomized controlled trials. Am Heart J 138: 211–219, 1999 [DOI] [PubMed] [Google Scholar]
- 19. Holstein-Rathlou NH, Marsh DJ. Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol Rev 74: 637–681, 1994 [DOI] [PubMed] [Google Scholar]
- 20. Holstein-Rathlou NH, Wagner AJ, Marsh DJ. Tubuloglomerular feedback dynamics and renal blood flow autoregulation in rats. Am J Physiol Renal Fluid Electrolyte Physiol 260: F53–F68, 1991 [DOI] [PubMed] [Google Scholar]
- 21. Jernigan NL, Drummond HA. Vascular ENaC proteins are required for renal myogenic constriction. Am J Physiol Renal Physiol 289: F891–F901, 2005 [DOI] [PubMed] [Google Scholar]
- 22. Jernigan NL, Drummond HA. Myogenic vasoconstriction in mouse renal interlobar arteries: role of endogenous beta and gamma ENaC. Am J Physiol Renal Physiol 291: F1184–F1191, 2006 [DOI] [PubMed] [Google Scholar]
- 23. Johansson B, Mellander S. Static and dynamic components in the vascular myogenic response to passive changes in length as revealed by electrical and mechanical recordings from the rat portal vein. Circ Res 36: 76–83, 1975 [DOI] [PubMed] [Google Scholar]
- 24. Just A. Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am J Physiol Regul Integr Comp Physiol 292: R1–R17, 2007 [DOI] [PubMed] [Google Scholar]
- 25. Kamm KE, Stull JT. The function of myosin and myosin light chain kinase phosphorylation in smooth muscle. Ann Rev Pharmacol Toxicol 25: 593–620, 1985 [DOI] [PubMed] [Google Scholar]
- 26. Layton HE, Pitman EB, Moore LC. Bifurcation analysis of TGF-mediated oscillations in SNGFR. Am J Physiol Renal Fluid Electrolyte Physiol 261: F904–F919, 1991 [DOI] [PubMed] [Google Scholar]
- 27. Lecar H, Ehrenstein G, Latorre R. Mechanism for channel gating in excitable bilayers. Ann NY Acad Sci 264: 304–313, 1975 [DOI] [PubMed] [Google Scholar]
- 28. Loutzenhiser R, Bidani A, Chilton L. Renal myogenic response: kinetic attributes and physiologic role. Circ Res 90: 1316–1324, 2002 [DOI] [PubMed] [Google Scholar]
- 29. Loutzenhiser R, Bidani A, Wang X. Systolic pressure and the myogenic response of the renal afferent arteriole. Acta Physiol Scand 181: 404–413, 2004 [DOI] [PubMed] [Google Scholar]
- 30. Marsh DJ, Sosnovtseva OV, Chon KH, Holstein-Rathlou NH. Nonlinear interactions in renal blood flow regulation. Am J Physiol Regul Integr Comp Physiol 288: R1143–R1159, 2005 [DOI] [PubMed] [Google Scholar]
- 31. Mooris C, Lecar H. Voltage oscillations in the barnacle giant muscle fiber. Biophys J 35: 193–213, 1981 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Murphy RA. Mechanics of vascular smooth muscles. In: Handbook of Physiology. The Cardiovascular System. Vascular Smooth Muscle. Bethesda, MD: Am Physiol Soc, 1980, sect. 2, vol. II, chapt. 13, p. 325–442 [Google Scholar]
- 33. Murphy RA. Muscle cells of hollow organs. News Physiol Sci 3: 124–128, 1988 [Google Scholar]
- 34. Rembold CM, Murphy RA. Latch-bridge model in smooth muscle: (Ca2+)i can quantitatively predict stress. Am J Physiol Cell Physiol 259: C251–C257, 1990 [DOI] [PubMed] [Google Scholar]
- 35. Roman RJ. P-450 metabolites of arachidonic acid in the control of cardiovascular function. Physiol Rev 82: 131–185, 2002 [DOI] [PubMed] [Google Scholar]
- 36. Scotland RS, Chauhan S, Davis C, de Felipe C, Hunt S, Kabir J, Kotsonis P, Oh U, Ahluwalia A. Vanilloid receptor TRPV1, sensory C-fibers, and vascular autoregulation: a novel mechanism involved in myogenic constriction. Circ Res 95: 1027–1034, 2004 [DOI] [PubMed] [Google Scholar]
- 37. Smeda JS, Daniel EE. Elevations in arterial pressure induce the formation of spontaneous action potentials and alter neurotransmission in canine ileum arteries. Circ Res 62: 1104–1110, 1988 [DOI] [PubMed] [Google Scholar]
- 38. Wang X, Loutzenhiser RD, Cupples WA. Frequency modulation of renal myogenic autoregulation by perfusion pressure. Am J Physiol Regul Integr Comp Physiol 293: R1199–R1204, 2007 [DOI] [PubMed] [Google Scholar]
- 39. Wang X, Salevsky FC, Cupples WA. Nitric oxide, atrial natriuretic factor, and dynamic renal autoregulation. Can J Physiol Pharmacol 77: 777–786, 1999 [PubMed] [Google Scholar]
- 40. Wang X, Takeya K, Aaronson PI, Loutzenhiser K, Loutzenhiser R. Effects of amiloride, benzamil, and alterations in extracellular Na+ on the rat afferent arteriole and its myogenic response. Am J Physiol Renal Physiol 295: F272–F282, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Williamson GA, Loutzenhiser R, Wang X, Griffin K, Bidani AK. Systolic and mean blood pressures and afferent arteriolar myogenic response dynamics: a modeling approach. Am J Physiol Regul Integr Comp Physiol 295: R1502–R1511, 2008 [DOI] [PubMed] [Google Scholar]