SAINT: Probabilistic Scoring of Affinity Purification - Mass Spectrometry Data

Abstract

We present SAINT (Significance Analysis of INTeractome), a computational tool that assigns confidence scores to protein-protein interaction data generated using affinity-purification coupled to mass spectrometry (AP-MS). The method utilizes label-free quantitative data and constructs separate distributions for true and false interactions to derive the probability of a bona fide protein-protein interaction. We demonstrate that SAINT is applicable to data of different scales and protein connectivity and allows for the transparent analysis of AP-MS data.

The analysis of protein complexes and protein interaction networks is of central importance in biological research. A combination of affinity purification and mass spectrometry (AP-MS) has been increasingly used for both small scale and large scale analysis of protein complexes and interaction networks ^1–4. However, the development of computational tools for the processing of AP-MS data has not kept pace with improvement in experimental approaches. In addition to the general challenge of false positive protein identifications in MS-based proteomic data⁵, unfiltered AP-MS datasets contain a large number of non specifically binding proteins; filtering these contaminants represents the foremost computational challenge.

While early methods filtered the noise using binary data (presence or absence of a protein), more recently proposed methods take into account quantitative information embedded in the mass spectrometric data (e.g. label-free quantification, such as spectral counts). For example, one recently described method converts the normalized spectral abundance factor (NSAF) into the posterior probability of a true interaction between a bait-prey pair using simple heuristics, which we term PP-NSAF hereafter ⁶. Another method, CompPASS computes scores that adjust observed spectral counts relative to the reproducibility of detection across biological replicates and to the frequency of observing prey proteins in purifications of different baits⁷. Although both approaches are effective in analyzing the datasets for which they were developed, these scores are an empirical transformation of spectral counts without a probability model for the measurement errors in the data in a transparent manner.

In a recent work we introduced an advanced approach for statistical analysis of interaction data from AP-MS experiments utilizing label-free quantification, which we termed Significance Analysis of INTeractome (SAINT) ⁸. Like PP-NSAF and CompPASS, our original SAINT approach was designed for the analysis of a specific dataset, the yeast kinase and phosphatase interactome. Here we present a generalized SAINT framework that can compute interaction probabilities in a variety of datasets. The method incorporates negative controls commonly generated as a part of the experimental study, but can also be applied to large datasets in the absence of such data. Here we illustrate the methodology and its advantages through the analysis of datasets of different sizes and network density levels: from a large, sparsely connected network involving human deubiquitinating enzymes to a smaller, highly interconnected network for chromatin remodeling proteins, and even to the analysis of a single bait, the protein CDC23.

The aim of SAINT is to convert the label free quantification (spectral count X_ij) for a prey protein i identified in a purification of bait j into the probability of true interaction between the two proteins, P(True|X_ij). The spectral counts for each prey-bait pair are modeled with a mixture distribution of two components representing true and false interactions. Note that these distributions are specific to each bait-prey pair. The parameters for true and false distributions, P(X_ij|True) and P(X_ij|False), and the prior probability π_T of true interactions in the dataset, are inferred from the spectral counts for all interactions involving prey i and bait j. SAINT normalizes spectral counts to the length of the proteins and to the total number of spectra in the purification.

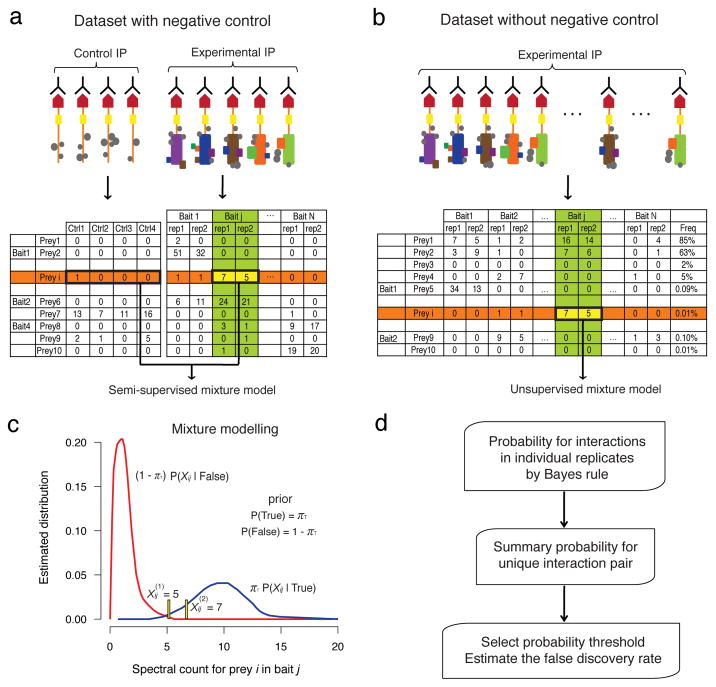
In addition to the experimental data for bait proteins, AP-MS data often contain negative controls (Fig. 1a). When these are available, SAINT estimates the spectral count distribution for false interactions directly from the negative controls, which makes the modeling approach semi-supervised (see Methods). SAINT modeling can also be performed without negative control data, given that a sufficient number of independent baits are profiled, and provided that these baits are not densely interconnected. In this case (illustrated in Fig. 1b), a prey detected in the purification of a bait is scored in reference to the quantitative information for the same prey across purifications of all other baits in the dataset. While this is possible for large datasets such as the yeast kinase and phosphatase network⁸ and the human deubiquitinating (DUB) enzyme interaction network⁷ (that each contain >75 baits; see below), this unsupervised approach involves additional assumptions and separate treatment of high and low frequency prey proteins (see Methods).

Figure 1. Probability model in SAINT.

a–b Interaction data in the presence (a) and absence (b) of control purifications. Top: schematic of the experimental AP-MS procedure; Bottom: illustration of a spectral count interaction table. c. Modeling spectral count distributions for true and false interactions. For the interaction between prey i and bait j, SAINT utilizes all relevant data for the two proteins, as shown in the column of the bait (green) and the data in the row of the prey (orange) in a and b. d. Probability is calculated for each replicate by application of Bayes rule, and a summary probability is calculated for the interaction pair (i,j).

One challenge in modeling AP-MS data is the limited number of replicates available for each bait. SAINT addresses this problem by inferring individual bait-prey interaction parameters via joint modeling of the entire bait-prey data. To this end, SAINT defines a protein-specific abundance parameter and establishes a multiplicative model in the mixture component distributions. In other words, if prey i and bait j interact, then the “interaction abundance” (the spectral count of the prey i in purification with bait j) is assumed to be proportional to α_i×α_j. Under this assumption, the protein-specific abundance parameters α_i and α_j can be learned not only from the interaction between the two proteins themselves, but also from other bona fide interactions that involve either one of them. The same principle applies to false interactions. Hence SAINT builds a large number of mixture distributions by pooling data (separate mixture distributions for individual prey-bait pairs), but all models are interconnected through the shared abundance parameters.

The probability distributions P(X_ij|True) and P(X_ij|False) are then used to calculate the posterior probability of true interaction P(True|X_ij) (Fig. 1c and 1d, Methods). For baits profiled in replicates, the next step involves computing a combined probability score from independent scoring of each replicate (see Methods). Finally, SAINT probabilities can be used to estimate the false discovery rate (FDR). By ordering interactions in a decreasing order of probabilities, a threshold can be selected that considers the average of the complement probabilities as the Bayesian FDR⁹. Although the accuracy of FDR estimates remains to be validated, the availability of an objective reliability measure that has been widely used is an advantage over other methods.

The performance of the generalized SAINT model was first investigated using a human dataset centered around four key protein complexes involved in chromatin remodeling, Prefoldin, hINO80, SRCAP, and TRRAP/TIP60 (referred to as the TIP49 dataset)⁶. While the original publication focused the analysis on the interaction network observed between a core set of 65 proteins, the entire dataset provided by the authors of the study is analyzed here. The dataset consists of 27 baits (35 purifications) and 1207 preys which yielded 5521 unfiltered interactions. 35 negative controls were included in the dataset, allowing semi-supervised modeling (Fig. 1a; Supplementary Table 1).

We applied SAINT to this data and compared the results to PP-NSAF⁶ and CompPASS Z and D^N scores^7,10, which we re-implemented in-house (see Methods). We note that PP-NSAF⁶ removes all interactions involving prey proteins for which the sum of squared NSAF values across the negative control purifications is higher than that in the experiments containing bait proteins. CompPASS is the only method that does not incorporate negative controls in scoring.

SAINT selected 1375 interactions at the probability threshold 0.9, which was approximately equivalent to an estimated FDR of 2%. In PP-NSAF, since arbitrary cutoffs were set to define high, moderate, and low probability interaction sets, the same number of top scoring interactions was selected from the method (corresponding to a PP-NSAF probability 0.2 or higher). In CompPASS, the same number of interactions corresponded to a D^N-score threshold of 1.48 (Supplementary Table 1).

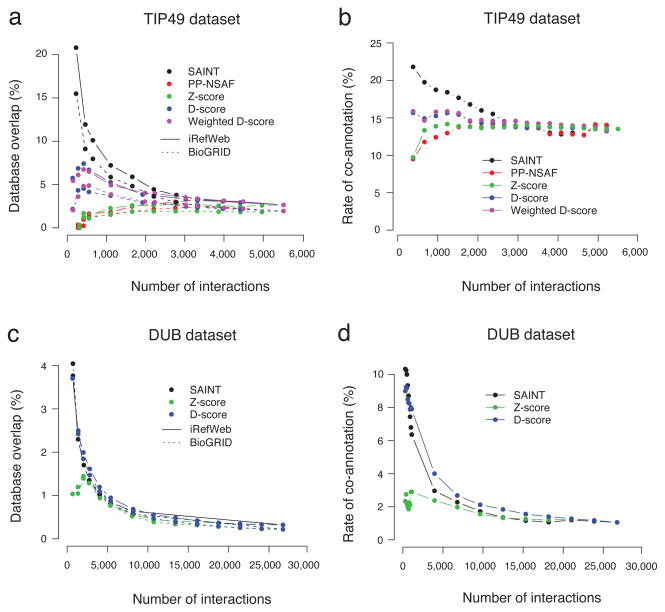
We evaluated the performance of each algorithm firstly by benchmarking the selected interactions against two interaction databases BioGRID¹¹ and iRefWeb¹² (Fig. 2a), and secondly by assessing the co-annotation rate of interaction partners to common Gene Ontology (GO) terms in Biological Processes (Fig. 2b; Supplementary Table 1). SAINT filtered interactions (with controls) consistently showed the highest overlap with previously reported interactions and co-annotation rates to terms relevant to chromatin remodelling, including histone acetylation, protein amino acid acetylation, chromatin organization and modification, and cellular macromolecular complex assembly. Variation of the SAINT probability thresholds (0.8 ~ 0.95) did not qualitatively change this conclusion (data not shown). Note that omission of negative controls from SAINT modeling decreased the literature overlap (Supplementary Fig. 1). Explicit incorporation of the negative control data improves the robustness of modeling, especially in small to medium datasets.

Figure 2. Analysis of TIP49 and DUB datasets.

a. Benchmarking of filtered interactions in the TIP49 dataset by the overlap with interactions previously reported in BioGRID and iRefWeb databases. b. Co-annotation of interaction partners to common GO terms in Biological Processes in the TIP49 dataset. c. Benchmarking against BioGRID and iRefWeb in the DUB dataset. d. Co-annotation to GO terms in the DUB dataset.

The performance of SAINT for large scale datasets without negative controls (Fig. 1b) was tested on the human deubiquitinating enzymes (DUB) dataset ⁷ (this dataset was used in the development of CompPASS). High confidence interactions from SAINT were compared to the high confidence set from CompPASS (see Supplementary Table 2). Due to the absence of negative controls, it was not possible to apply PP-NSAF to this dataset. SAINT probabilities and D^N scores were notably correlated (Pearson correlation r=0.79). At probability 0.8 threshold, SAINT selected 1300 interactions, while CompPASS D^N≥1 (threshold value used in ⁷) reported 1377 interactions. Of these, 1051 interactions were common to both methods. Reflecting the similarity of selected interactions, SAINT and CompPASS recovered previously reported interactions at comparable rates (Fig. 2c). In the top 1000 interactions, SAINT showed higher overlap with literature data. The co-annotation of interaction partners to the common GO terms also showed similar results between the two methods (Fig. 2d), including relevant terms such as positive and negative regulation of ubiquitin-protein ligase activity during mitotic cell cycle, proteasome, etc. (Supplementary Table 2). While SAINT and CompPASS recovered largely overlapping interactions, SAINT removed the interactions identified with 1–2 spectral counts, which were still scored by CompPASS if they were specific to a single bait protein and detected in duplicates.

Another advantage of SAINT over other methods is that it is applicable to the analysis of small-scale datasets for which control purifications are available; this extends to the case of a single bait. We illustrate this by using a recent dataset¹³ containing 3 experimental purifications of the bait CDC23 and 3 control purifications. In the original analysis, the authors of the study identified true interactions using ion intensity-based quantification followed by a simple t-test. We applied the SAINT approach to the same dataset by using spectral counts (the data was researched in-house as described in Methods). The results obtained by SAINT were nearly identical to the initial report (Supplementary Table 3), the sole exception being the single peptide hit C11orf51, which was reported as a new interactor in the original analysis¹³, but which was removed by SAINT.

In summary, SAINT is a probability-based model that is generally applicable to mass spectrometry-based interaction data. The SAINT model presented here is based on label-free quantification using spectral counts, a parameter that is easily extracted from most AP-MS datasets. However, SAINT can also be extended to model other types of quantitative parameters such as peptide ion intensity ¹⁴ or other continuous variables ¹⁵, which can be accommodated by simply substituting the likelihood with an appropriate continuous distribution.

Supplementary Material

1

Supplementary Figure 1. Literature overlap for the TIP49 dataset using SAINT with and without control purification data.

2

Supplementary Table 1. Supplementary data for the TIP49 dataset. 1A) List of all detected interactions and scores from PP-NSAF, CompPASS, and SAINT. 1B) All interactions in control purifications were included in a separate table after merging of 35 technical replicate purifications into 9 purifications. 1C) Table of technical replicates of control purifications. 1D) GO terms enrichment in top scoring interactions for each scoring method.

3

Supplementary Table 2. Supplementary data for the DUB dataset. 2A) List of all detected interactions and scores from CompPASS and SAINT. 2B–D) GO terms enrichment in top scoring interactions for each scoring method.

4

Supplementary Table 3. Supplementary data for the CDC23 dataset. List of all detected interactions with SAINT scores and results reported by t-test.