Abstract
We study the cosegmentation problem where the objective is to segment the same object (i.e., region) from a pair of images. The segmentation for each image can be cast using a partitioning/segmentation function with an additional constraint that seeks to make the histograms of the segmented regions (based on intensity and texture features) similar. Using Markov Random Field (MRF) energy terms for the simultaneous segmentation of the images together with histogram consistency requirements using the squared L2 (rather than L1) distance, after linearization and adjustments, yields an optimization model with some interesting combinatorial properties. We discuss these properties which are closely related to certain relaxation strategies recently introduced in computer vision. Finally, we show experimental results of the proposed approach.
1. Introduction
Cosegmentation refers to the simultaneous segmentation of similar regions from two (or more) images. It was recently proposed by Rother et al. [1] in the context of simultaneously segmenting a person or object of interest from an image pair. The idea has since found applications in segmentation of videos [2] and shown to be useful in several other problems as well [3; 4]. The model [1] nicely captures the setting where a pair of images have very little in common except the foreground. Notice how the calculation of image to image distances (based on the entire image) can be misleading in these cases. As an example, consider Fig. 1, where approximately the same object appears in the pair of images. The background and the object's spatial position in the respective image(s) may be unrelated, and we may want to automatically extract only the coherent regions from the image pair simultaneously. This view of segmentation is also very suitable for biomedical imaging applications where it is important to identify small (and often inconspicuous) pathologies, either for evaluating the progression of disease or for a retrospective group analysis. Here, standard segmentation techniques, which are usually designed to reliably extract the distinct regions of the image, may give unsatisfactory results. However, if multiple images of a particular organ (e.g., brain) are available, the commonality shared across the images may significantly facilitate the task of obtaining a clinically usable segmentation. For instance, since the primary brain structures remain relatively unchanged from one subject to the next, extracting this coherence as the foreground leaves the variation (i.e., patient specific pathology) as the “residuals” in the background.
Figure 1.

The same object in different positions in two images with different backgrounds.
Segmentation of objects and regions in multiple images has typically been approached in a class-constrained fashion. That is, given a large set of images of the object (or an object class) of interest, how can we solve the problem of segmenting or recognizing the object in a set of unannotated images? Of course, one option is to use a set of hand-segmented images or a manually specified model(s) – an approach employed in several papers, see [5; 6; 3] and references therein. Such training data has also been successfully used for performing segmentation and recognition in parallel [7; 8], and for segmentation in a level-sets framework [9]. A number of ideas have been proposed for the unsupervised setting as well: [10] suggested using a database of (yet to be segmented) images using a generative probabilistic model, and [11] learned the figure-ground labeling by an iterative refinement process. In [1], the object of interest is segmented using just one additional image. The authors approach the problem by observing that similar regions (that we desire to segment) in a pair of images will have similar histograms, noting that such a measure has been successfully used for region matching [12]. A generative model was proposed – assuming a Gaussian model on the target histogram (of the to-be-segmented foreground); they suggested maximizing the posterior probability that the foreground models in both images are the same. The formulation results in a challenging optimization problem, and requires an iterative minimization. Some clever observations allow the solution of subproblems using graph-cuts, where it is shown that the objective function value improves (or in the worst case, does not deteriorate) at each iterative step. However, the approximation factor guarantees associated with graph-cuts obtained for each iteration (subproblem) do not carry over to the original optimization. Recently, [13] proposed constructing a Joint Image Graph for soft image segmentation and calculating point correspondences in the image pair. Because the underlying discrete problem is hard, the authors used a relaxation method followed by an iterative two step approach to find the solution.
In this paper, inspired by [1], we also seek to match the histograms1 of the segmented regions. But rather than a generative model (with predefined distribution families) for the histograms, we consider the matching requirement as an algebraic constraint. Our successive formulation includes histogram constraints as additional, appropriately regularized, terms in the segmentation objective function. We analyze the structure of the model using the squared L2 distance (SSD) for measuring histogram similarity, instead of the L1-norm [1]. After linearization and adjustments of the objective function, the constraint matrix of the resultant linear program exhibits some interesting combinatorial properties, especially in terms of the LP solutions of the ‘relaxation’. We observe this by analyzing the determinant of the submatrices of the constraint matrix, which suggests a nice 2-modular structure [14]. The form of the objective function (after linearization) also corroborates the fact that if we choose SSD to specify histogram variations, the problem permits roof-duality relaxation [15; 16] recently introduced in computer vision [17; 18; 19]. Either way, the primary benefit is that unlike the (harder) L1-norm based problem, the LP solution of the new relaxed LP contains only multiples of “half-integral” values. Demonstrating that the cosegmentation problem exhibits these desirable characteristics (without major changes to the underlying objective function) is a primary contribution of this paper. These properties allow a simple rounding scheme that gives good solutions in practice and enables bounding the sub-optimality due to rounding under some conditions. We discuss these aspects in §3.1-§3.3. Finally, we present experimental results on a set of image pairs in §4 and concluding remarks in §5.
2. Histogram matching
Let the two input images be Ii = [Ii(p)], i ∈ {1, 2}, p ∈ {1,⋯, n}, where each image has n pixels. Let the intensity histogram bins be given by sets H1,⋯, Hβ, where Hb corresponds to the b-th bin. For each image Ii, a coefficient matrix Ci of size n × β is such that for pixel j and histogram bin Hb,
| (1) |
The entry Ci(p, b) is 1 if pixel intensity Ii(p) belongs to
(i.e., the intensity of Ii(p) is in bin b), where i refers to the first or the second image. Summing over the columns of Ci gives the histogram for each image as a vector. Now, consider X1, X2 ∈ 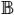 n as a pair of {0, 1} assignment vectors for images I1 and I2, that specifies the assignment of pixels to foreground and background regions by a segmentation method. For i ∈ {1, 2}, Xi(p) = 1 if Ii(p) is classified as foreground and 0 otherwise. We want to cosegment (i.e., by assigning to foreground) two regions from the image pair with the requirement that the two histograms of the foreground pixels are similar. The histogram, H{i} for image Ii, for the pixels assigned to the foreground is
n as a pair of {0, 1} assignment vectors for images I1 and I2, that specifies the assignment of pixels to foreground and background regions by a segmentation method. For i ∈ {1, 2}, Xi(p) = 1 if Ii(p) is classified as foreground and 0 otherwise. We want to cosegment (i.e., by assigning to foreground) two regions from the image pair with the requirement that the two histograms of the foreground pixels are similar. The histogram, H{i} for image Ii, for the pixels assigned to the foreground is
| (2) |
Since Xi (p) is 0 if pixel p is a background pixel, we can simply focus on the histogram of the foreground pixels and penalize the variation. We note that an expression similar to (2) was discussed in a technical report accompanying [1] to obtain a supermodularity proof.
Modeling image segmentation problems as maximum a posteriori (MAP) estimation of Markov Random Fields with pairwise interactions has been very successful [20; 21] and gives good empirical results. It also seems suitable for the segmentation objective here. In this framework, given an image I, each pixel (random variable) p ∈ I, can take one among a discrete set of intensity labels, 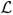 = {
= {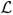 1,
1, 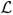 2,⋯,
2,⋯, 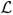 k}. The pixel must (ideally) be assigned a label fp ∈
k}. The pixel must (ideally) be assigned a label fp ∈ 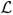 similar to its original intensity, to incur a small deviation (or data) penalty, D(p, fp); simultaneously two adjacent (and similar) pixels, p, q, must be assigned similar labels to avoid a high separation (or smoothness) penalty W(p, q) : p ∼ q (where ∼ indicates adjacency in a chosen neighborhood system). This gives the following objective function for arbitrary number of labels:
similar to its original intensity, to incur a small deviation (or data) penalty, D(p, fp); simultaneously two adjacent (and similar) pixels, p, q, must be assigned similar labels to avoid a high separation (or smoothness) penalty W(p, q) : p ∼ q (where ∼ indicates adjacency in a chosen neighborhood system). This gives the following objective function for arbitrary number of labels:
| (3) |
where Y(p, q) = 1 indicates that p and q are assigned to different labels and X̂(·, ·) gives the pixel-to-label assignments. Proceeding from (2) and allowing for cases where the histograms do not match perfectly, we can specify the following simple binary model where X, Y ∈ {0, 1} (labels are foreground or background) using an error tolerance, ε
| (4) |
Here, Di(p) is a simplified form of the function Di(p, fp) for the figure-ground segmentation case. We set Di(p) = Di(p, fg) − Di(p, bg) where ‘fg’ (and ‘bg’) indicates foreground (and background). The objective also has a constant term given by ΣpDi(p, bg)2 that makes it positive.
3. Successive model
The previous model may be modified by including the histogram constraint as an additional (regularized) term in the objective function:
| (5) |
where λ is the regularizer controlling the relative influence of the histogram difference in the objective and R(C1, C2) measures the difference of the two foreground histograms. Including this term (or the constraints in (4)), however, makes the optimization more challenging. Further analysis shows that the difficulty of the resultant optimization model can be attributed not only to the inclusion of the extra penalty in the objective but to the choice of the norm in this additional term. Using the squared L2 distance (rather than L1) has significant advantages as we will discuss shortly. First, using squared L2 distances, we can represent the form of histogram differences as
| (6) |
This squared term can be linearized as follows. Consider two corresponding bins and in the two images. Let and , and the number of foreground pixels after the segmentation in those bins is νb and ν̂b respectively. Then, the squared term estimates the sum of (νb − ν̂b)2 over b, i.e., Σb(νbνb−2νbν̂b+ν̂bν̂b). We may use an auxiliary variable, Zi(p, q), such that Zi(p, q) = 1 if both nodes p and q belong to bin and are also part of the foreground in image Ii, and 0 otherwise. Then, summing over all such Zi's : i ∈ {1, 2}, gives the terms νbνb and ν̂bν̂b. Similarly, we may use another auxiliary variable, V(p, q), which is set to 1 if node p (and node q) belongs to bin (and bin ), and is part of the foreground in image I1 (and image I2). To specify the linearized representation, let us first introduce some notation. Let denote those pairs (p, q) that satisfy Ci(p, b) = 1 and Ci(q, b) = 1 for some bin and image i (i.e., intra-image links). Also, denotes those pairs (p, q) that satisfy C1(p, b) = 1 and C2(q, b) = 1 for bins and (i.e., inter-image links). To summarize, this procedure introduces ‘lifting’ variables for linearization (see [22; 17] for other examples) and allows rewriting the model as
| (7) |
3.1. Properties of the constraint matrix in (7)
The preferred alternative to solving the {0, 1} integer program (IP) in (7) directly (using branch-bound methods) is to relax the {0, 1} requirement to [0, 1], and then obtain an integral solution from the [0, 1] solution via rounding. In general, little can be said about the real valued solution. In some special cases, the situation is better and the cosegmentation problem described in (7) belongs to this category.
If the model has only (monotone) constraints of the form in the first set of inequalities in (7), the constraint matrix is totally unimodular (i.e., the determinants of each of its square submatrices are in {0, ±1}). By the Hoffman-Kruskal theorem [23], the optimal vertex solution of the linear program is integral. In cosegmentation, the constraints, Xi(j) + Xi(l) ≤ Zi(j, l) + 1, are non-monotone, and spoil unimodularity. Fortunately, the model still retains a desirable structure – first, we derive this by analyzing the modularity properties of the constraint matrix. Later, we discuss how the objective function may also be interpreted to recognize the nice structure of the model. These properties will help show that the values in the optimal LP solution cannot be arbitrary reals in [0, 1]. We first provide some definitions.
Definition 1 (Nonseparable matrix) A matrix is nonseparable if there do not exist partitions of the columns and rows to two (or more) subsets 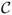 1,
1, 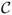 2 and ℛ1, ℛ2 such that all nonzero entries in each row and column appear only in the submatrices defined by the sets ℛ1 ×
2 and ℛ1, ℛ2 such that all nonzero entries in each row and column appear only in the submatrices defined by the sets ℛ1 × 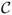 1 and ℛ2 ×
1 and ℛ2 × 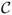 2.
2.
Let the constraint matrix of (7) be denoted as A. Below, we outline the key properties of the constraint matrix for the cosegmentation problem.
Lemma 1 A is a nonseparable matrix.
Proof: The entries in X refer to the pixels of an image. For two pixels that are adjacent w.r.t. the chosen neighborhood system 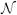 (e.g., four neighborhood), the columns of their corresponding X entries will be non-zero in at least one row (for the constraint where they appear together). Then, they must be in the same partition (either ℛ1 or ℛ2). Other ‘neighbors’ of these pixels must also be in the same partition. Because each pixel is reachable from another via a path in
(e.g., four neighborhood), the columns of their corresponding X entries will be non-zero in at least one row (for the constraint where they appear together). Then, they must be in the same partition (either ℛ1 or ℛ2). Other ‘neighbors’ of these pixels must also be in the same partition. Because each pixel is reachable from another via a path in 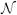 , the same logic applied repeatedly shows that the X columns (correspond to pixels) must be in the same partition. Each Y and Z variable appears in at least one constraint (non-zero entry in A) together with X, and so must belong in the same partition as X. Each V variable appears in two constraints, with X1 (·), and X2 (·), and so must also be in the same partition. Therefore, A is non-separable.
, the same logic applied repeatedly shows that the X columns (correspond to pixels) must be in the same partition. Each Y and Z variable appears in at least one constraint (non-zero entry in A) together with X, and so must belong in the same partition as X. Each V variable appears in two constraints, with X1 (·), and X2 (·), and so must also be in the same partition. Therefore, A is non-separable.
Theorem 1 The determinant of all submatrices of A belongs to {−2, −1, 0, 1, 2}, i.e., its absolute value is bounded by 2.
Proof: We prove by induction. Since the entries in A are drawn from {−1, 0, 1}, the 1 × 1 matrix case is simple. Now assume it holds for any m − 1 × m − 1 submatrix and consider m × m submatrices. By construction, A (and any non-singular square submatrix) has at most three non-zero entries in a row. Let Ā be a m × m non-singular submatrix of A. To obtain the result, we must consider the following three cases.
Case 1: Ā has one non-zero entry in any row/column.
Case 2: Ā has two non-zero entries in every row and column.
Case 3: Ā has three non-zero entries in any row.
It is easy to verify that the structure of A rules out other possibilities. For presentation purposes, we will start with Case 3 and consider Case 2 last.
Case 3: Ā has three non-zero entries in any row. First, observe that the rows with three non-zero entries must come from the first three constraints in (7). In each such constraint, there is at least one variable, Yi(j, l), Yi(l, j), or Zi(j, l), that does not occur in any other constraint. Therefore, the corresponding columns of that variable must have only one non-zero entry, say at position (p, q). We may permute Ā so that (p, q) moves to location (1, 1). Let M[u,υ] denote the matrix obtained from M by deleting row u and column υ. The determinant of Ā is expressed as Ā(1, 1) det(Ā[1,1]), where Ā[1,1] is m − 1 × m − 1. Now, Ā(1, 1) ∈ {± 1, 0} and det(A[1,1]) ∈ {±2, ±1, 0}, so the product of these terms is in {±2, ±1, 0}.
Case 1: Ā has 1 non-zero entry in any row. This can be shown using the same argument as in case 3 above.
Case 2: Ā has 2 non-zero entries in every row and column. This case was proved by Hochbaum et al. [24] (Lemma 6.1) and the same idea can be applied here. Wlog, we may assume that the two non-zero entries in row i of Ā are in columns i and (i + l)mod m (due to Lemma 1). Hence, det(Ā) = Ā(1, 1) det(Ā[1,1]) − (−1)mĀ(m, 1) det(Ā[m,1]). The submatrix determinants equal 1 since they are both triangular matrices (with non-zero diagonal elements). Thus, det(Ā) ∈ {±2, ±1, 0}.
Corollary 1 The model in (7) has super-optimal half integral solutions, i.e., each variable in the optimal LP solution is in {0, , 1}.
Corollary 1 shows that A has 2-modular structure with half-integral solutions [14]. This property leads to a two-approximation for a wide variety of NP-hard problems including vertex cover and many variations of 2-SAT [24]. Notice that if the objective function has only positive terms, we can round all the variables up to 1, leave the integral variables unchanged, and still ensure that the value of the objective is within a factor of two of the optimal solution [24]. This is not applicable in our case due to the negative term in the objective function. However, we can still obtain approximations if the half integral solution satisfies some conditions, as we show in §3.3.
3.2. Pseudo-Boolean optimization
In the last section, we analyzed the constraint matrix of the LP to derive desired properties. An analogous approach is to analyze the objective function in (5), which is given by the MRF terms (submodular) and the histogram variation (non-submodular). To facilitate this discussion, first recall that a Pseudo-Boolean (PB) function has the form:
where 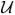 = {1, 2,…, n}, x = (x1, x2, ⋯, xn) ∈
= {1, 2,…, n}, x = (x1, x2, ⋯, xn) ∈ 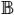 n denotes a vector of binary variables,
n denotes a vector of binary variables, 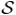 is a subset of
is a subset of 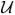 , and c
, and c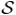 denotes the coefficient of
denotes the coefficient of 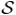 . That is, a function f :
. That is, a function f : 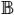 n ↦ ℝ is called a pseudo-Boolean function. If the cardinality of
n ↦ ℝ is called a pseudo-Boolean function. If the cardinality of 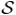 is upper bounded by 2, the corresponding form is
is upper bounded by 2, the corresponding form is
These are Quadratic Pseudo-Boolean functions (QPB). The histogram term in (6) from our model can also be written in this form. If the objective permits a representation as a QPB, an upper (or lower) bound can be derived using roof (or floor) duality [16], recently utilized in several vision problems [18; 19; 17]. Obtaining a solution then involves representing each variable as a pair of literals, xi and x̄i, each representing a node in a graph where edges are added based on the coefficients of the terms in the corresponding QPB. A max-flow/min-cut on this new graph yields a part of the optimal solution, i.e., the {0, 1} values in the solution (called ‘persistent’) are exactly the same as an optimal solution to the problem instance. The unassigned variables correspond to half-integral values as discussed in the previous section. Independent of the method employed, once such a super-optimal/half-integral solution [24] is found, the challenge is to derive an integral solution via rounding.
3.3. Rounding and approximation
The approximation depends critically on how the variables are rounded. If we fix the {0, 1} variables, and round 's to 1, a good approximation may be obtained. However, such a solution may not be feasible w.r.t. the constraints in a worst case setting (although in practice, a simple rounding heuristic exploiting half-integral solutions may work). We discuss this issue next where we fix the X variables. Note that “fixing” the set of {0, 1} variables (as in [25; 24]) is the same as “persistence” in the pseudo-Boolean optimization literature, i.e., only the valued variables are modified.
We refer to the block of X variables in the solution vector as X for convenience; X includes X1 and X2. The corresponding block in the optimal LP solution is given as , and (in the present context we will refer to X's as sets). Clearly, , where , and refers to the 0, 1 and entries in X* respectively. Let refer to those entries that are in histogram bin b in image i (for presentation purposes, we assume Hb in image 1 corresponds to Hb in image 2, and so we drop the image superscript). A subset of the constraints in (7) relating and are
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
First, consider the -valued entries. Since , and are all , and (7) is a minimization, is 0 and V*(q, r) is at optimality. Setting , and to 1 satisfies (9)-(12), regardless of the value of V*(·, ·), but (8) is violated if is unchanged. On the other hand, if we round (or ) to 0, (8) is satisfied, but (9) or (11) is violated. Therefore, to ensure a feasible solution, we must round a few variables (V and X) to 0, and set a few Z variables (which were 0 in the optimal solution) to 1. In the general case, this might increase the objective function arbitrarily. However, under some conditions, we can still bound the gap.
For convenience, let , and . In the rounding, we do not change the {0, 1} X* variables; only the half-integral variables are rounded to 1 or 0. Assume that a rounding scheme, ℛ, sets entries to 1 and entries to 0, so . Consider the histogram mismatch penalty in the the objective first. In the optimal solution, let this term be for Hb. In terms of ai, di and ci,
Let the increase in due to rounding be ρ = ρZ + ρV, where ρZ (and ρV) is the increase due to Z (and V). These can be expressed as
For i ∈ {1, 2}, we can prove the following result:
Lemma 2 If a1 ≥ αa2, ai ≥ αdi, d1 ≥ d2, then where . For α = 3, .
In Lemma 2, the increase is bounded by a multiple of the lower bound if the conditions are satisfied. Notice that ξ decreases with an increase in α. What remains to be addressed is (1) to specify what the rounding scheme ℛ is, and (2) the loss due to rounding for the MRF terms in the objective in (7). First, consider ℛ: how to round to {0, 1}. To do this, we solve the original MRF problem in (7) (but without the histogram constraints) on both images using max-flow/min-cut. Let γMRF be the value of such a solution and be the part of γMRF corresponding only to variables in . Clearly, . We round variables based on their assignment in the MRF solution. Let be the optimal LP solution. Again, can be written as . Since γMRF is the smallest possible solution for the original (unconstrained) MRF, . The solution after rounding is . We can now state the following result:
Theorem 2 If a1 ≥ αa2, ai ≥ adi, d1 ≥ d2 where α = 3, then .
4. Experimental results
We performed evaluations of our cosegmentation algorithm on several image pairs used in [1] (see http://research.microsoft.com/∼carrot/software.htm) together with additional image pairs that we collected from miscellaneous sources. The complete data will be made publicly available after publication. The image sizes were 128 × 128, and we used the RBF kernel to calculate the data D(·) and smoothness costs W(·, ·) in (7). In the current implementation, histogram consistency was enforced using RGB intensities and gradients only, but this can be extended to use texture features. Notice that the size of our problem is dependent on the number of bins used. Using few bins makes the problem size large (as a function of the number of pairs in each bin). Also, such a histogram is insufficient to characterize the image properly: dissimilar pixels may now belong to the same bin. This makes histogram constraints counterproductive. On the other hand, too many bins do not enforce the consistency properties strongly. We found using 30-50 bins per color channel for our experiments achieves a nice balance between these competing effects, and solving the LP on a modern workstation using CPLEX takes 15-20s. In this section, we cover (a) qualitative results of segmentation, (b) error rate, i.e., percentage of misclassified pixels (using hand-segmented images as ground truth), and (c) empirical calculation of the loss in optimality due to rounding. For (a) and (b), we also illustrate results from a graph-cuts based MRF segmentation method (GC) [20] applied on the images independently as well as results from the cosegmentation algorithm of [1].
For comparison with [1], we used the trust region graph cuts approach (TRGC) using an implementation shared with us by the authors of [1]. In TRGC, the energy is iteratively minimized by expressing the new configuration of the non-submodular part of the function as a combination of an initial configuration of the variables and the solution from the previous step. Therefore, it requires an initial segmentation of the images. For this purpose, we used the solution of graph cuts based MRF segmentation (without histogram constraints). Also, since it is difficult to optimize both images simultaneously using the L1 norm, the approach in [1] keeps one image fixed and then optimizes the second image w.r.t. the first, and repeats this process. In our experiments, we found that either (a) the solution converged in under five iterations or (b) in some cases a poor segmentation generated in one of the early iterations adversely affected the subsequent iterations. To avoid the second problem, the number of iterations was kept small. We evaluated various values of the regularizer λ, and report the settings that correspond to the best results.
In Fig. 2, we show cosegmentation results of the three approaches for a set of image pairs with a similar object in the foreground but different backgrounds. The first two columns correspond to the MRF solution (without histogram constraints), columns three and four illustrate solutions obtained using our approach, and the last two columns show the segmentations from [1]. In the first row (Stone), the stone in image-2 is larger (which gives dissimilar foreground histograms), but the algorithm successfully segments the object in both images. Notice that our method compares well to [1] for this image pair. For the next image pair (Banana), our algorithm is able to recognize the object in both images but shows a significant improvement in image-2 compared to GC with the same parameter settings and is comparable to the results of TRGC. For the third image pair (Woman), our algorithm segments roughly the same foreground as GC for image-1. For image-2, several regions in the background with similar intensities as the foreground are incorrectly labeled by GC. Using the histogram constraints eliminates these regions from the segmentation yielding a cleaner and more accurate segmentation. On this image pair, our solution is better than TRGC. In the fourth (Horse) and fifth (Lasso) image pairs, GC does not perform well on image-1, but yields similar results as our method on image-2. Note that the object (foreground) in Lasso image-1 is difficult to discern from the background making it a challenging image to segment. However, using the histogram constraints, we are able to obtain a reasonable final segmentation. When compared to TRGC, our segmentation seems to correctly identify more foreground pixels for Lasso image-1. Table 1 shows the error rate (i.e., the average pixel misclassification error for each image pair). These were generated by comparing the segmentation with hand segmented images. In general, the misclassification error rate was 1 – 5% as shown in Table 1.
Figure 2.

The images in columns (a) and (b) are solutions from independent graph-cuts based segmentations on both images, the pair of images in columns (c) and (d) are solutions from our cosegmentation algorithm applied on the images simultaneously, and images in (e) and (f) are solutions obtained from the algorithm in [1], The segmentation is shown in blue.
Table 1.
Misclassification errors (% of pixels misclassified) in the segmentation and empirical approximation estimates of the solution.
| Instance | our error rate (λ = 0.01) | approximation | GC error rate | error rate [1] |
|---|---|---|---|---|
| Stone | 1.56% | 1.04 | 3.57% | 1.92% |
| Banana | 3.02% | 1.02 | 7.75% | 3.33% |
| Woman | 2.14% | 1.06 | > 10% | ≈ 10% |
| Horse | 4.80% | 1.02 | 5.70% | 4.92% |
| Lasso | 2.87% | 1.03 | 7.9% | 3.72% |
Values for λ
The specific value of λ used in our experiments was determined empirically by iterating over four possible values: starting from λ = 10−4 and increasing it by an order of magnitude until λ = 1.0. The extracted foregrounds were then compared using mutual information, and λ = 0.01 was found to work best for our experiments. We show a plot of this behavior in Fig. 4. As the images suggest, λ values at either end of the range [100, 10−4] are not ideal for cosegmentation. When λ is too large (≥ 1.0), the foreground becomes smaller and less smooth. This is because the histogram term overwhelms the MRF terms and returns only those foreground pixels where the histogram bins match perfectly. We found that if λ ≤ 10−4, the results are similar to those obtained by graph-cuts segmentation. Also, Fig. 4 shows that the segmentations are relatively stable for wide range of λ values. This makes it relatively easy to select a reasonable λ value using our approach. We note that in our experiments, cosegmentation results using the L1 norm seem to be more sensitive to the value of λ.
Half-integrality/inconsistent pixels
In the proposed model, the number (or proportion) of variables assigned values varies as a function of λ. In practice, a higher value of λ leads to more “inconsistent” pixels (terminology borrowed from [17; 18]). In our case, for λ = 0.01, the number of ( ) pixels was 0-20%. The cumulative increase in the objective function due to these variables (i.e., rounding loss) was 0-6% of the lower bound (shown in Table 1), suggesting that our worst case estimate in Thm. 2 is conservative. In addition, some new results indicate that even further performance improvements are possible [26; 18].
5. Conclusions
We propose a new algorithm for the cosegmentation problem. The model uses an objective function with MRF terms together with a penalty on the sum of squared differences of the foreground regions' histograms. We show that if SSD is used as the penalty function for histogram mismatch, the optimal LP solution is comprised of only {0, , 1} values. Half integrality leads to a simple rounding strategy that gives good segmentations in practice and also allows an approximation analysis under some conditions. The proposed approach also permits general appearance models and requires no initialization.
Figure 3.
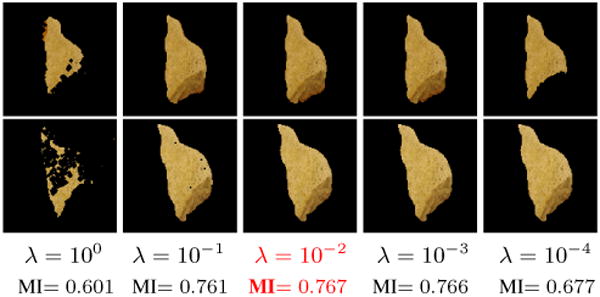
The extracted foreground (after Mi-based affine registration) for the pair of stone images as a function of λ.
Acknowledgments
The authors are grateful to Dorit S. Hochbaum and Sterling C. Johnson for a number of suggestions and improvements. V. Singh was supported in part through a UW-ICTR CTSA grant, and by the Wisconsin Comprehensive Memory Program. C. R. Dyer was supported in part by NSF grant IIS-0711887.
Footnotes
We consider intensity histograms in our implementation, though the proposed model can be directly extended for other types of histograms (such as ones incorporating texture features) as well, as noted in [1].
The data term is Xi(p)Di(p, fg) + (1 − Xi(p))Di(p,bg) = Di(p, bg) + (Di(p, fg) − Di(p, bg)) Xi(p).
Contributor Information
Lopamudra Mukherjee, Email: mukherjl@uww.edu.
Vikas Singh, Email: vsingh@biostat.wisc.edu.
Charles R. Dyer, Email: dyer@cs.wisc.edu.
References
- 1.Rother C, Minka T, Blake A, Kolmogorov V. Cosegmentation of image pairs by histogram matching – incorporating a global constraint into MRFs. Proc. of Conf. on Computer Vision and Pattern Recognition; 2006. [Google Scholar]
- 2.Cheng DS, Figueiredo Mario AT. Cosegmentation for image sequences. Proc. of International Conf. on Image Anal. and Processing; 2007. [Google Scholar]
- 3.Cao L, Fei-Fei L. Spatially coherent latent topic model for concurrent object segmentation and classification. Proc. of International Conf. on Computer Vision; 2007. [Google Scholar]
- 4.Sun J, Kang SB, Xu ZB, Tang X, Shum HY. Flash Cut: Foreground Extraction with Flash and No-flash Image Pairs. Proc. of Conf. on Computer Vision and Pattern Recognition; 2008. [Google Scholar]
- 5.Cootes T, Taylor C, Cooper D, Graham J. Active shape models – their training and applications. Computer Vision and Image Understanding. 1995;61(1):38–59. [Google Scholar]
- 6.Borenstein E, Sharon E, Ullman S. Combining top-down and bottom-up segmentation. Proc. of Conf. on Computer Vision and Pattern Recognition; 2004. [Google Scholar]
- 7.Yu S, Shi J. Object-specific figure-ground segmentation. Proc. of Conf. on Computer Vision and Pattern Recognition; 2003. [Google Scholar]
- 8.Yu SX, Gross R, Shi J. Concurrent object recognition and segmentation by graph partitioning. Advances in Neural Information Processing Systems. 2002 [Google Scholar]
- 9.Riklin-Raviv T, Kiryati N, Sochen N. Prior-based segmentation by projective registration and level sets. Proc. of International Conf. on Computer Vision; 2005. [Google Scholar]
- 10.Winn J, Jojic N. Locus: Learning object classes with unsupervised segmentation. Proc. of International Conf. on Computer Vision; 2005. [Google Scholar]
- 11.Borenstein E, Ullman S. Learning to segment. Proc. of European Conf. on Computer Vision; 2004. [Google Scholar]
- 12.Wang JZ, Li J, Wiederhold G. SIMPLIcity: semantics-sensitive integrated matching for picture libraries. Trans on Pattern Anal and Machine Intel. 2001;23(9) [Google Scholar]
- 13.Toshev A, Shi J, Daniilidis K. Image matching via saliency region correspondences. Proc. of Conf. on Computer Vision and Pattern Recognition; 2007. [Google Scholar]
- 14.Kotnyek B. PhD thesis. London School of Economics and Political Science; 2002. A generalization of totally unimodular and network matrices. [Google Scholar]
- 15.Hammer PL, Hansen P, Simeone B. Roof duality, complementation and persistency in quadratic 0–1 optimization. Mathematical Programming. 1984;28(2):121–155. [Google Scholar]
- 16.Boros E, Hammer PL. Pseudo-Boolean optimization. Discrete Applied Math. 2002;123(1-3):155–225. [Google Scholar]
- 17.Raj A, Singh G, Zabih R. MRFs for MRIs: Bayesian reconstruction of MR images via graph cuts. Proc. of Conf. on Computer Vision and Pattern Recognition; 2006. [Google Scholar]
- 18.Rother C, Kolmogorov V, Lempitsky V, Szummer M. Optimizing binary mrfs via extended roof duality. Proc. of Conf. on Computer Vision and Pattern Recognition; 2007. [Google Scholar]
- 19.Kohli P, Shekhovtsov A, Rother C, Kolmogorov V, Torr P. On partial optimality in multi-label mrfs. Proc. of International Conf. on Machine learning; 2008. [Google Scholar]
- 20.Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts. Trans on Pattern Anal and Machine Intel. 2001;23(11):1222–1239. [Google Scholar]
- 21.Ishikawa H, Geiger D. Segmentation by Grouping Junctions. Proc. of Conf. on Computer Vision and Pattern Recognition; 1998. [Google Scholar]
- 22.Kahl F, Henrion D. Globally optimal estimates for geometric reconstruction problems. International Journal of Computer Vision. 2007;74(1):3–15. [Google Scholar]
- 23.Korte B, Vygen J. Combinatorial Optimization: Theory and Algorithmsn. Birkhäuser; p. 101. [Google Scholar]
- 24.Hochbaum DS, Megiddo N, Naor J, Tamir A. Tight bounds and 2-approximation algorithms for integer programs with two variables per inequality. Math Programming. 1993;62(1):69–83. [Google Scholar]
- 25.Hochbaum DS. Efficient bounds for the stable set, vertex cover and set packing problems. Discrete Applied Math. 1983;6:243–254. [Google Scholar]
- 26.Boros E, Hammer PL, Tavares G. Preprocessing of unconstrained quadratic binary optimization. Technical report, Rutgers University. 2006 [Google Scholar]


