A Comprehensive Examination of the Contributions to Binding Entropy of Protein-Ligand Complexes

Abstract

The process of ligand binding is very complex due to the intricacy of the interrelated processes that are difficult to predict and quantify. One of the most important requirements in computer-aided drug design is the ability to reliably evaluate the binding free energies. However, deeper understanding of the origin of the observed binding free energies requires the ability to decompose these free energies to their contributions from different interactions. Furthermore, it is important to evaluate the relative entropic and enthalpic contributions to the overall free energy. Such an evaluation is useful for assessing temperature effects and exploring specialized options in enzyme design. Unfortunately, calculations of binding entropies have been much more challenging than calculations of binding free energies. This work is probably the first to present microscopic evaluation of all of the relevant components to the binding entropy, namely, configurational, polar solvation and hydrophobic entropies. All of these contributions are evaluated by the restraint release (RR) approach. The calculated results shed an interesting light on major compensation effects in both the solvation and hydrophobic effect, and despite some overestimate, can provide very useful insight. The present study also helps in analyzing some problems with the widely used MM/PBSA approach.

I. INTRODUCTION

The discovery of new chemical entities (NCEs) is still a major challenge in pharmaceutical research. Structure based drug design plays an increasingly important role in this endeavor. This requires a detailed knowledge of the binding site, preferably in complex with a lead inhibitor, to draft a new inhibitor de novo (lead discovery) or to improve upon an existing entity (lead optimization) to enhance the favorable interactions with the target enzyme, to obtain a better drug. To better understand the thermodynamical description of binding/biomolecular recognition processes and to make predictions about ligand binding, the accurate determination of absolute binding free energy (binding affinity) remains a key element of computer-aided drug design.^1–3 The binding affinity, K_a, is determined by the corresponding binding free energy. The binding free energy reflects entropic and enthalpic contributions and understanding the origin of these contributions is fundamentally important. Considering only the binding free energy in evaluating and analyzing the potency of an enzyme inhibitor may present an incomplete picture, since different inhibitors may bind with equal affinities even though the contributions from enthalpy and entropy are completely different.⁴ It is true that within a series of closely related inhibitors, enthalpy-entropy compensation for binding to the enzyme is a typical, although our knowledge of this phenomenon is not yet complete.⁵ However, improving the existing affinity to achieve an extremely high binding affinity may be advanced by obtaining a synergy of favorable enthalpic and entropic contributions to the binding affinity.^6–8

The two major contributions to the binding entropy are the change in conformational entropy and the change in solvation entropy. The conformational entropy change is usually unfavorable, as the process of binding leads to the loss of conformational degrees of freedom for both the ligand and the protein. Conversely, the solvation entropy is almost always favorable, resulting from partial or complete desolvation of the binding cavity upon binding. This contribution also involves changes in hydrophobic and polarization entropy.

Estimates of binding entropies date back to Page and Jencks who estimated the loss of translational and rotational entropy upon binding^9,10 to Janin and Chothia who estimated the contributions of surface area burial due to the hydrophobic effect. ^11,12 Attempts to move to a more quantitative level leads to significant controversy with respect to the estimation of protein-ligand binding entropy, either by computationally expensive conformational sampling-based methods^13–15 or the methods of scoring functions.^16,17 In principle, one may try to estimate the binding entropies directly by evaluating the change of binding free energy with temperature¹⁸ but such an approach is extremely expensive. Alternatively, it is tempting to try to use the quasiharmonic (QH)¹⁹ approximation in entropy calculation. However, this approach encountered convergence problems when applied to protein-protein complexes.^20,21 Moreover, using QH approach to account for all components associated with the receptor at present seems to be associated with large errors, since the system cannot be described reliably by this approximation.²² Related attempts have been made with normal mode analysis,^20,23,24 however this approach cannot account for the anharmonicity or the effects of solvent. Note that at physiological temperature, the overall protein flexibility is dominated by such anharmonic motions²⁵ and may, to a large extent, be driven by solvent fluctuations.²⁶ One may also try to estimate the entropic effects using knowledge-based scoring functions ^17,27–36 by using some empirical measures for binding entropy.³⁷ However, it is unlikely that such approaches will have a clear connection to the relevant physical basis of the entropic effects.

Specific examples of systematic attempts to explore similar aspect of the binding entropy include the important work of Hermans and Wang, who used a restraint release approach (with some limitations that will be discussed in Results and Discussion section) to study binding of benzene to enzyme T4 lysozyme. ³⁸ The same system was studied by Carlsson and Åqvist who explored several methods to calculate the overall entropy.³⁹ Using the “Mining Minima” approach, Luo and Gilson examined the binding of adenine to synthetic adenine receptors and computed the translational/rotational entropy change upon binding.⁴⁰ Erickson suggested a value of 11 kcal/mol for the loss of translational and rotational entropy upon protein-protein association.⁴¹ From free energy calculations and MD simulations of anthracycline antibiotics to DNA, Baginski et al. reported a rotational-translational entropy change between 4 kcal/mol and 9 kcal/mol.⁴² Applying MD simulations, Swanson et al. calculated the translational and rotational entropy changes of 10.6 and 2.0 cal/mol.K, respectively due to binding of 4-hydroxy-2-butanone to FK506 binding protein.⁴³ Employing quasiharmonic analysis and MD simulations, Luo and Sharp analyzed and calculated the entropic contribution upon binding of antibody FAB fragment to digoxigenin and streptavidin to biotin.⁴⁴ From MD simulations of ligand-avidin/streptavidin complexes, Lazaridis et al. estimated association entropies that ranged between −1.5 kcal/mol and −7.5 kcal/mol for four different ligands.⁴⁵ However, none of these interesting studies considered the contributions from solvation entropies including the hydrophobic effects, making it hard to compare them to the relevant observed values.

Here, we address the challenge of calculating the absolute binding entropies by our restraint release approach, that was used to study the configurational entropies in the enzyme catalysis ^46–48 and, more recently, in calculating the solvation entropies of monovalent and divalent ions.²² Here, we combine the two applications in the calculation of absolute binding entropies. To the best of our knowledge, this study provides the first simulation based estimate of separate contributions from the configurational and solvation entropies to the overall binding entropy.

II. METHODS AND CONCEPTS

II.1. Simulation Protocols

In this section, we will review the methods used in the present study and provide relevant background to the readers.

The starting coordinates of the protein in complex with their respective ligands were obtained from Protein Data Bank (PDB).⁴⁹ The PDB IDs and resolutions of the x-ray crystallographic structures used in this study are as follows: Bacteriophage T4 lysozyme [3DMX, 1.8Å], B. subtilis Chorismate Mutase [2CHT, 2.2Å], Bovine Trypsin [1K1L, 2.5Å] and Bovine Trypsin [1S0R, 1.02Å]. The crystal waters were removed in each case. All hydrogen atoms and water molecules were added using MOLARIS.⁵⁰

The charge distribution of the ligands was obtained from ab initio quantum calculations by the Gaussian03 package⁵¹ DFT (B3LYP/6–31G**) calculations using the PCM solvation model. The structure of the ligands were partially optimized in the gas phase and used to derive the relevant charges.

The simulation system (that includes the protein, bound ligand, water and langevin dipoles) was initially equilibrated for 2ps at 300K with a time steps of 0.5fs using the program ENZYMIX.⁵⁰ The spherical inner part of the system with radius 18Å was constrained by a weak harmonic potential of the form, V' = Σ_iA(r⃗_i − r⃗_i⁰)², with A=0.01 kcal mol⁻¹Å⁻² to keep the protein atoms near the corresponding observed positions. The protein atoms outside this sphere were held fixed and their electrostatic effects excluded from the model. The rms deviation of the relaxed structure from the crystal structure was typically within 0.8Å on an average.

To determine the ionization state of the protein residues around the inhibitor, we used the approach as described in ref^50,52. This was done using the ‘titra_pH’ routine of the POLARIS program package.^50,53 If the probability of a group to be charged at pH 7 was ≥ 50%, it was considered to be charged. For details, see ref ⁵².

II.2. Entropy Calculation

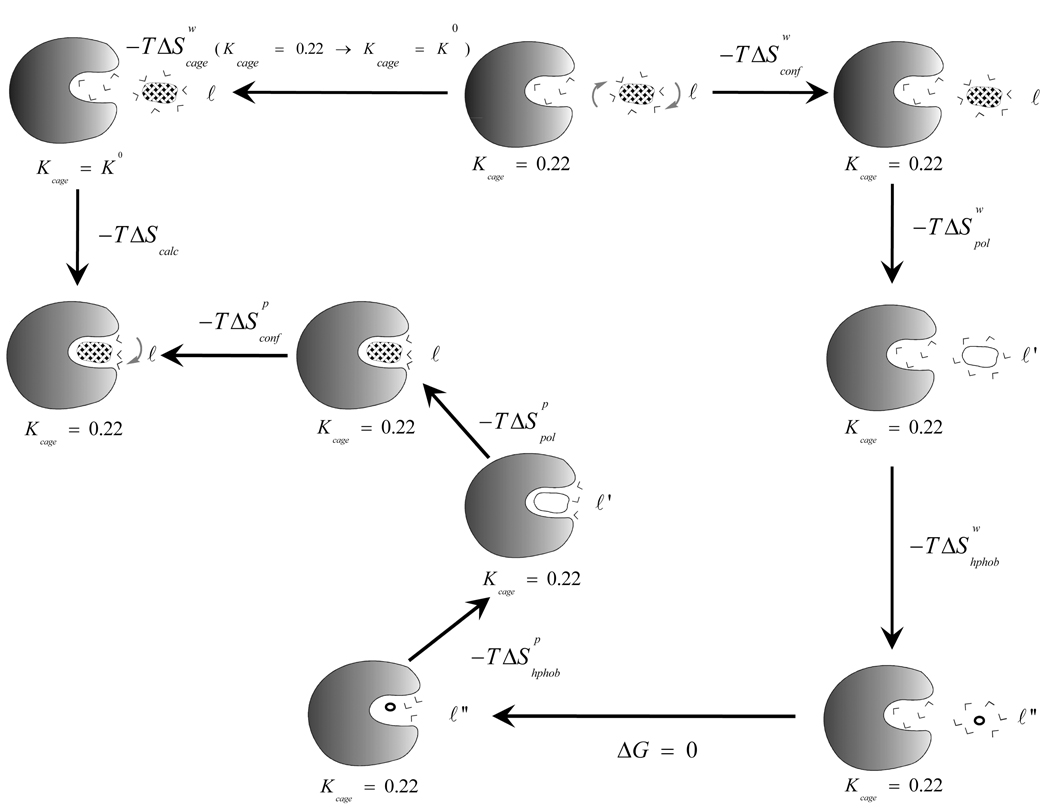
To evaluate the importance of a specific contribution to binding, it is essential to define the relevant thermodynamics cycle. This is particularly important in considering entropy contributions, whose definition and estimates involve in many cases incomplete thermodynamics cycles. Our approach in calculations of binding entropies of biomolecular complexes involves the thermodynamic cycle of Figure 1. This cycle considers separately the different components of the binding process, namely, the configurational (ΔS_conf), the hydrophobic (ΔS_hphob) and the polarization (ΔS_pol) contributions to the overall binding entropy.

Figure 1.

The thermodynamics cycle used in calculating the binding entropy. ℓ and ℓ' represents the charged and uncharged forms of the ligand, respectively, while ℓ" represents the ligand being reduced to “nothing”. p and w designate protein and water, respectively. The calculations use K_cage= 0.22 kcal mol⁻¹ Å⁻² throughout the cycle, except when it is set to K⁰ = 0.026 kcal mol⁻¹ Å⁻², that corresponds to a molar volume (1660 Ų). Also, note that the calculations of the polarization and hydrophobic entropies involve a strong constraint on the ligand.

The different terms in the cycle were evaluated according to the procedure described in the next section.

II.2.1. Evaluating the Configurational Entropy

The configurational entropies were explicitly evaluated using our restraint release (RR) approaches.^47,48 The RR approach imposes strong harmonic Cartesian restraints on the position of the ligand atoms in water (unbound,UB) and the same within the protein active site (bound,B), and then evaluates the free energy associated with the release of these restraints by means of a FEP approach. This is done while changing the restraint coordinate and looking for the set that minimizes the restraint (see below).

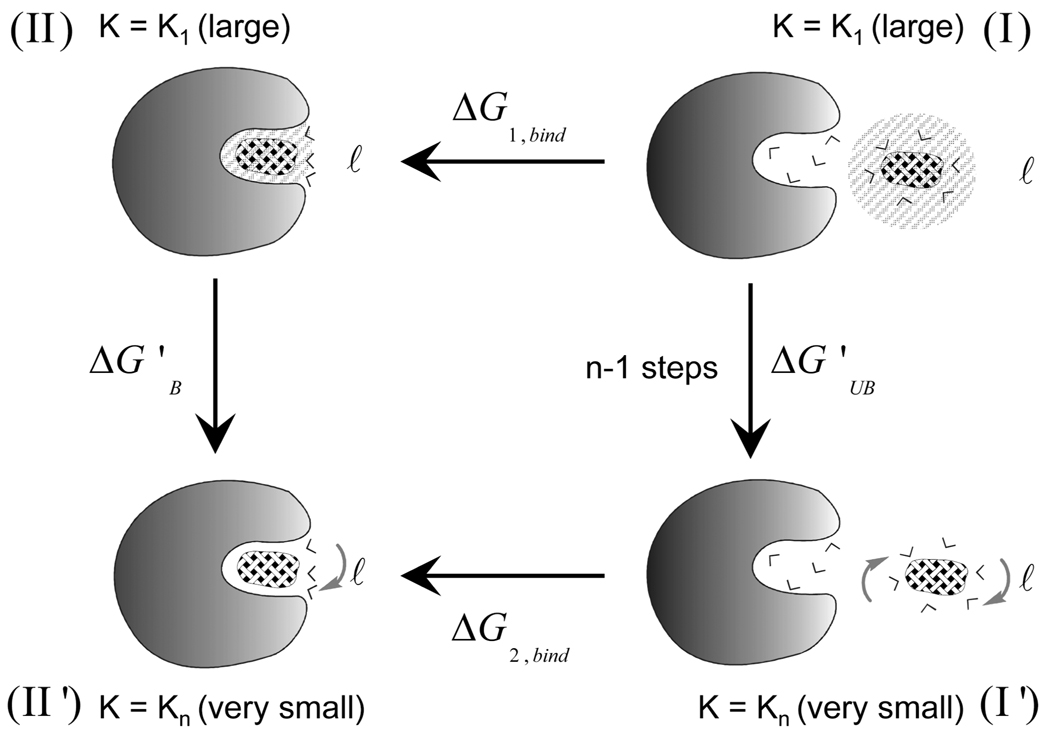
In order to clarify different contributions in Figure 1, we begin with the simple thermodynamics cycle of Figure 2 that considers the configurational contribution to the binding entropy. The figure considers the binding free energy, ΔG', in the following two limiting conditions:

Figure 2.

The thermodynamics cycle used to calculate configurational entropy.

In the upper part of the cycle, we consider the binding process when the ligand is subjected to a very large Cartesian constraint in both the bound (B) and the unbound (UB) state. Since the ligand is practically frozen in both cases, the corresponding binding entropy is approximately zero (−TΔS_1,bind ≈ 0). In the lower part of the cycle, we consider the case where these constraints are released. Thus, we obtain

$$-T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}^{\mathit{\text{conf}}}=-T\mathrm{\Delta }{S}_{2,\mathit{\text{bind}}}=-T\mathrm{\Delta }S{\text{'}}_B-T\mathrm{\Delta }{S}_{1,\mathit{\text{bind}}}+T\mathrm{\Delta }S{\text{'}}_{\mathit{\text{UB}}}\simeq -T\mathrm{\Delta }S{\text{'}}_B+T\mathrm{\Delta }S{\text{'}}_{\mathit{\text{UB}}}$$ (1)

The above mentioned constraint, that determines ΔS'_UB and ΔS'_B, is given by:

$$U_{\mathit{\text{rest}},j}^N=(K_j/2){\displaystyle \sum _i{(R_i^N-{\overline{R}}_i^N)}^2}$$ (2)

where i runs over the solute coordinates and ${\overline{R}}_i^N$ are reference coordinates that define the minimum of the restraint potential at the given state (N = I, or N = II for the unbound and bound state, respectively). The index j corresponds to the initial and final values of K.

The constraint release free energies (ΔG_RR = ΔG') are evaluated by FEP approach (e.g., ref ⁵⁴) using the following standard expression:

$$\mathrm{\Delta }G{\text{'}}_N(K_1\to K_2)={\displaystyle \sum _{m=0}^{n-1}}\mathrm{\Delta }\mathrm{\Delta }G{\text{'}}_N(m\to m+1)$$ (3)

where,

$$\mathrm{\Delta }\mathrm{\Delta }G{\text{'}}_N(m\to m+1)=-{\beta }^{-1}\text{ ln}{\langle \text{exp}\left\{-\beta (U_{m+1}^N-U_m^N\right\}\rangle }_{U_m^N}$$

and

$$U_m^N=(1-{\lambda }_m)U_{\mathit{\text{rest}},1}^N+{\lambda }_m{U}_{\mathit{\text{rest}},2}^N+E$$

Also, β = 1/ (k_BT); k_B is the Boltzmann constant and λ_m is changed from 0 to 1 in n increments. Here, E designates the unconstrained potential surface of the system (for details see ref⁴⁸) and U_rest,j corresponds to the use of K _j.

The results of the FEP calculations depend on the position of the restraint coordinates. All RR free energies contain a residual contribution from the enthalpy of the system. However, this contribution approaches zero for restraint coordinates that give the lowest RR energy, for details see refs^22,48. Accordingly, when we use the restraint position that gives the minimal absolute value of the restraint release free energy, we satisfy −TΔS_RR = ΔG_RR. Accordingly, we can write:

$$-T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}^{\mathit{\text{conf}}}=\text{min}(\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^B)-\text{min}(\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^{\mathit{\text{UB}}})$$ (4)

where ‘min’ indicates the minimum value of the indicated ΔG_RR.

Generally, one is interested in the entropic contribution for a 1 M standard state. This can be obtained, in principle, by choosing a simulation sphere of a volume which is equal to the molar volume (v₀ = 1,660 ų) while allowing K₂ to approach zero. However, such an approach is expected to encounter major convergence problems since the ligand is unlikely to sample the large simulation sphere in a reasonable simulation time. A faster convergence would be obtained by allowing the ligand to move in a smaller effective volume, v_cage by imposing an additional constraint. This is done by using a mapping potential of the form:

$$U_m^N=(1-{\lambda }_m)U_{\mathit{\text{rest}},1}^N+{\lambda }_m{U}_{\mathit{\text{rest}},2}^N+(K_{\mathit{\text{cage}}}/2){(R_{\ell ,i}-{\overline{R}}_{\ell ,i})}^2+E$$ (5)

where R_ℓ,i is the position of a specified central atom of the ligand. Using $U_m^N$ leaves v_cage unaffected by the change of λ_m. Now, we can let K₂ approach zero without a divergence in ΔS' since the volume of the system is restricted by the K_cage term.

The entropy associated with the release of K_cage is evaluated analytically and is given by:

$$-T\mathrm{\Delta }{S}_{\mathit{\text{cage}}}=-{\beta }^{-1}\text{ln}(v_0/v_{\mathit{\text{cage}}})$$ (6)

where

$$v_{\mathit{\text{cage}}}={\left(\frac{2\pi }{\beta K_{\mathit{\text{cage}}}}\right)}^{3/2}$$ (7)

Following the above considerations, we can write:

$$-T\mathrm{\Delta }{S}^{\mathit{\text{conf}}}=\text{min}(\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^B)-\text{min}(\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^{\mathit{\text{UB}}})-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{cage}}}$$ (8)

where ΔΔS_cage is the change in ΔS_cage for the bound and unbound ligand state.

In calculating ΔΔS_cage we exploit the fact that the ligand cannot move inside the protein by more than at most 4Å in each direction, and use a restraint of $K_{\mathit{\text{cage}}}^B=0.22{\text{ kcal mol}}^{-1}{\mathrm{\AA }}^{-2}$ (this corresponds to allowing the center of mass to move in a volume of 4³Å³). Thus, we run the calculations both in the protein as well as in water with K_cage= 0.22 kcal mol⁻¹ Å⁻², however in the case of calculations in water, we analytically evaluate (using Eq. 6 and 7) the contribution of changing K_cage = 0.22 kcal mol⁻¹ Å⁻² to K_cage = K⁰ = 0.026 kcal mol⁻¹ Å⁻² (that corresponds to the molar volume). In this case, $\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{cage}}}\to \Delta S_w^{\mathit{\text{cage}}}$.

Furthermore, instead of starting with a large value of K₁ we can save major amount of computer time by replacing Eq (8) by:

$$-T\mathrm{\Delta }{S}^{\mathit{\text{conf}}}=-T\mathrm{\Delta }{S}^B{(K=K{\text{'}}_1)}_{\mathit{\text{QH}}}+\text{min}[\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^B(K=K{\text{'}}_1\to K=0)]+T\mathrm{\Delta }{S}^{\mathit{\text{UB}}}{(K=K{\text{'}}_1)}_{\mathit{\text{QH}}}-\text{min}[\mathrm{\Delta }{G}_{\mathit{\text{RR}}}^{\mathit{\text{UB}}}(K=K{\text{'}}_1\to K=0)]+T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{cage}}}$$ (9)

where the −TΔS(K = K'₁)_QH designates the entropy computed by the QH approximation,^55,56 where K'₁ is the initial value of the restraint. In general, the QH approximation tends to be valid when restraints are significant however, starts to be problematic when the restraints become small, resulting in a range of very shallow and anharmonic potential energy surfaces.

The practical RR calculations involved the following steps: We started with an initial relaxation of the B and UB systems using MD runs of 40ps at 300K with time steps of 1 fs. These runs were used to generate 8 different sets of R̅ s, the constraint coordinates. The RR contributions for each of these sets for the B and the UB systems were then evaluated. This was done by evaluating the QH contribution with K'₁ = 10.0 kcal mol⁻¹ Å⁻² followed by the RR-FEP contribution for changing K from 10 to 0.003 kcal mol⁻¹ Å⁻² (see supporting information). The calculations were performed with an 18Å simulation sphere of explicit water molecules subject to the surface constraint all-atom solvent (SCAAS) boundary conditions.⁵⁰ The RR-FEP involved the release of the position restraints in 4 FEP stages. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time steps. The minimum value (min) was then taken from 8 series of runs.

II.2.2. Evaluating the polar part of the solvation entropy

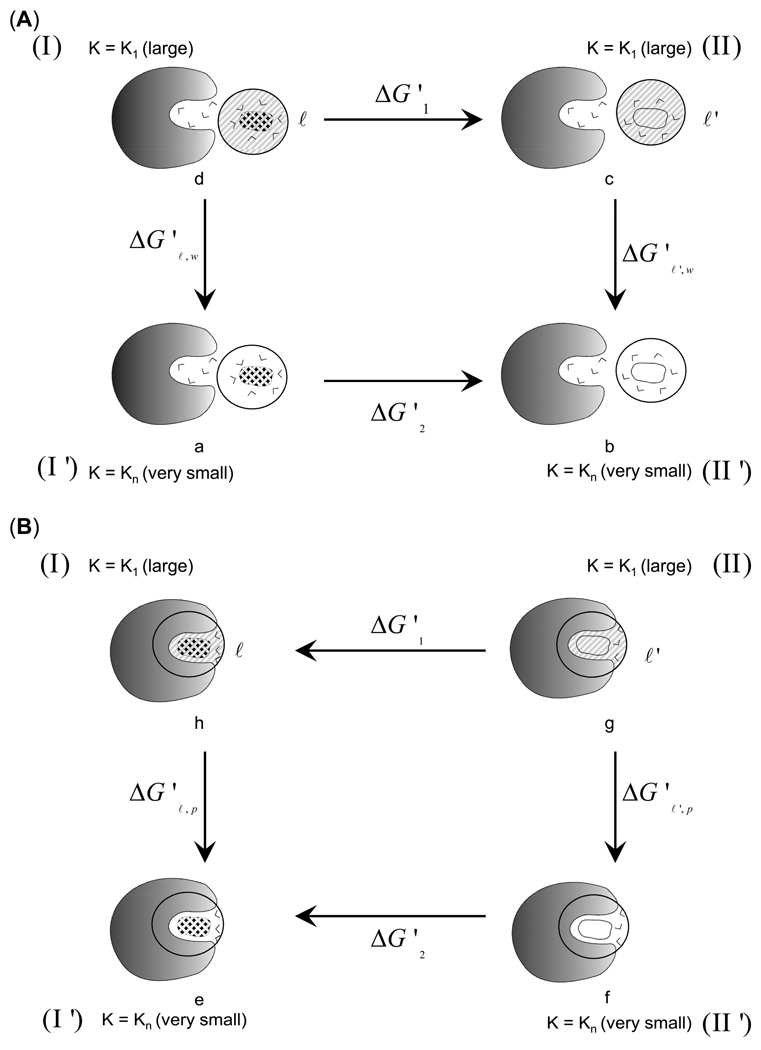
The solvation entropy can be roughly separated into polarization and hydrophobic entropies. The polarization entropy reflects mainly the orientational freedom of the ‘solvent dipole’ due to the presence of the solute charges.²² In order to calculate the entropy loss upon ordering of the solvent molecules in the vicinity of the charged or polar ligand, while moving from water to protein, we devised the following thermodynamics cycle of Figure 3.

Figure 3.

The thermodynamics cycles for the calculation of the entropy loss upon ordering of the solvent molecules in the vicinity of a charged solute. The shaded area designates large constraint and fixed solvent whereas the white areas designates free solvent molecules. (A) The cycle (a→b→c→d) provides the polarization entropy in water ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^w$). (B) The cycle (e→f→g→h) provides the corresponding entropy contribution in protein ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^p$). The difference between the entropy values obtained from the two cycles provide the overall entropy loss due to the electrostatically-induced ordering of solvent molecules upon moving the solute (ℓ) from water to the protein ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^{w\to p}$).

The polarization entropy for the ligand (ℓ) in water is given by:

$$-T\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^w=-T\mathrm{\Delta }S{\text{'}}_2=-T\mathrm{\Delta }S{\text{'}}_{\ell \text{'},w}-(-T\mathrm{\Delta }S{\text{'}}_{\ell ,w})-T\mathrm{\Delta }S\text{'}\simeq -T\mathrm{\Delta }S{\text{'}}_{\ell \text{'},w}+T\mathrm{\Delta }S{\text{'}}_{\ell ,w}$$ (10)

Here, we used the fact that −TΔS'₁ = 0 since it involves very strong constraints. The same treatment is applied to the polarisation entropy in the protein and therefore, we use:

$$-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^{w\to p}=-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^p-(-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^w)$$ (11)

II.2.3. Evaluating the Hydrophobic entropy

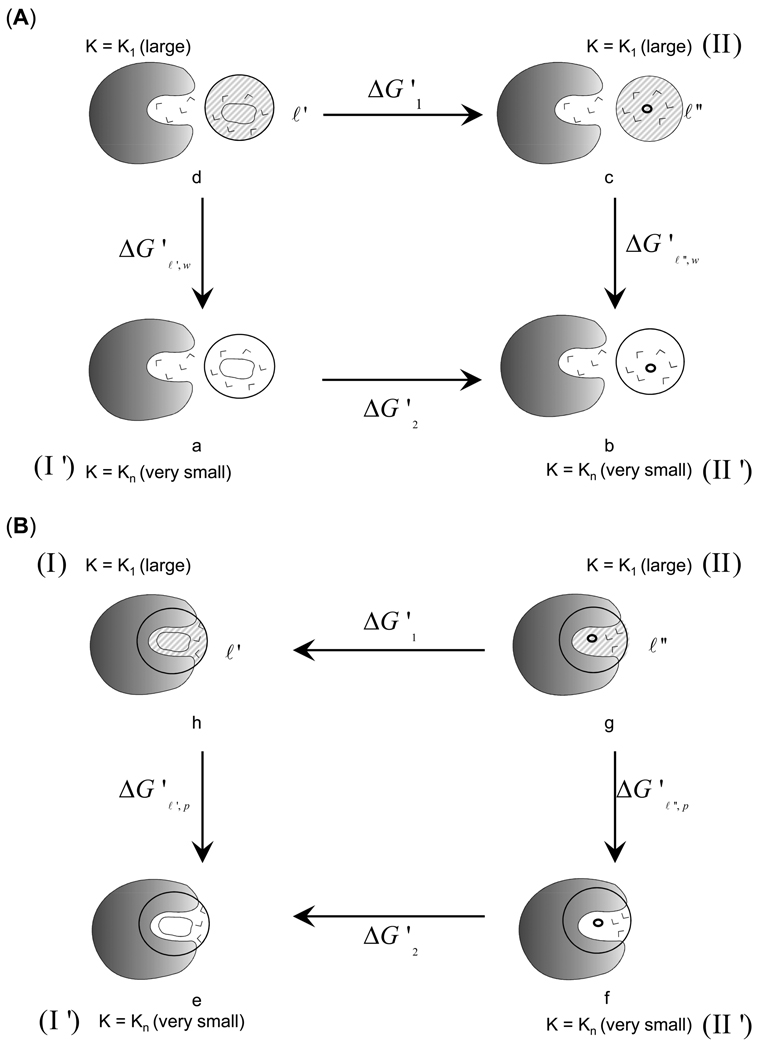
The hydrophobic entropy term is a measure of the decrease in the number of configurations available for the solvent molecules (dipoles) near the non-polar solute surface relative to the configurations available in the bulk solvent. The thermodynamics cycles of Figure 4 allow the evaluation of the loss of configurational entropy upon moving the non-polar ligand (ℓ), which is obtained by “uncharging” the ligand (ℓ) by setting all the residual charges to zero, from water to the protein active site. One way is to directly determine the entropic contributions of binding of the non-polar ligand in water to the protein active site in one step. However, from our experience we know that mutating the non polar ligand to “nothing” i.e. a zero-sized ligand (ℓ") by making use of the following thermodynamics cycles provide more stable results. The resulting non-polar ligand was allowed to shrink to “nothing” in water and in protein as depicted in Figure 4(A) and 4(B), respectively. Consequently, one may obtain $-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^w\text{ and }-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^p$ which is represented by ΔG'₂ in Figure 4(A) and 4(B) for contributions in water and the protein, respectively.

Figure 4.

The thermodynamics cycle used for the evaluation of the entropic contribution from hydrophobic effect. (A) The upper cycle (a→b→c→d) provides the hydrophobic contribution in water ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^w$). The cycle involves the release of the constraint for the non-polar-ligand (ℓ') and “nothing” (ℓ"), see text for details. (B) The lower cycle (e→f→g→h) provides the corresponding contribution in the protein ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^p$). The difference between the entropy values obtained from the two cycles provides the loss in entropy upon moving the non-polar ligand (ℓ') from water to protein ($-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^{w\to p}$).

Applying the same consideration as in the previous section (namely that −TΔS'₁=0), we may write:

$$-T\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^w=-T\mathrm{\Delta }S{\text{'}}_2=-T\mathrm{\Delta }S{\text{'}}_{\ell ",w}-(-T\mathrm{\Delta }S{\text{'}}_{\ell \text{'},w})$$ (12)

Similarly,

$$-T\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^p=-T\mathrm{\Delta }S{\text{'}}_2=-T\mathrm{\Delta }S{\text{'}}_{\ell ",p}-(-T\mathrm{\Delta }S{\text{'}}_{\ell \text{'},p})$$

Now, we can write

$$-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^{w\to p}=-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^p-(-T\mathrm{\Delta }\mathrm{\Delta }{S}_{\mathit{\text{hphob}}}^w)$$ (13)

II.2.4. Evaluating the entropy due to water displacement

In considering the solvation entropy one should also include the effect of removing water from the active site upon ligand binding. This effect has been included implicitly in the hydrophobic calculations since we consider the mobility of the water molecules in the cases with and without the ligand (ℓ and ℓ "). The effect of moving water from the protein site to the bulk has been accounts for, at least in part, by keeping the same number of solvent molecules in the constraint region for ℓ' and ℓ". Further validation of this approach is clearly needed.

All calculations were performed using the MOLARIS software package, and the ENZYMIX force field.^50,57 The calculations are done on the University of Southern California High Performance Computing and Communication (USC-HPCC) Linux computer, using the Dual Intel P4 3.0 GHz 2GB memory nodes.

I. RESULTS AND DISCUSSION

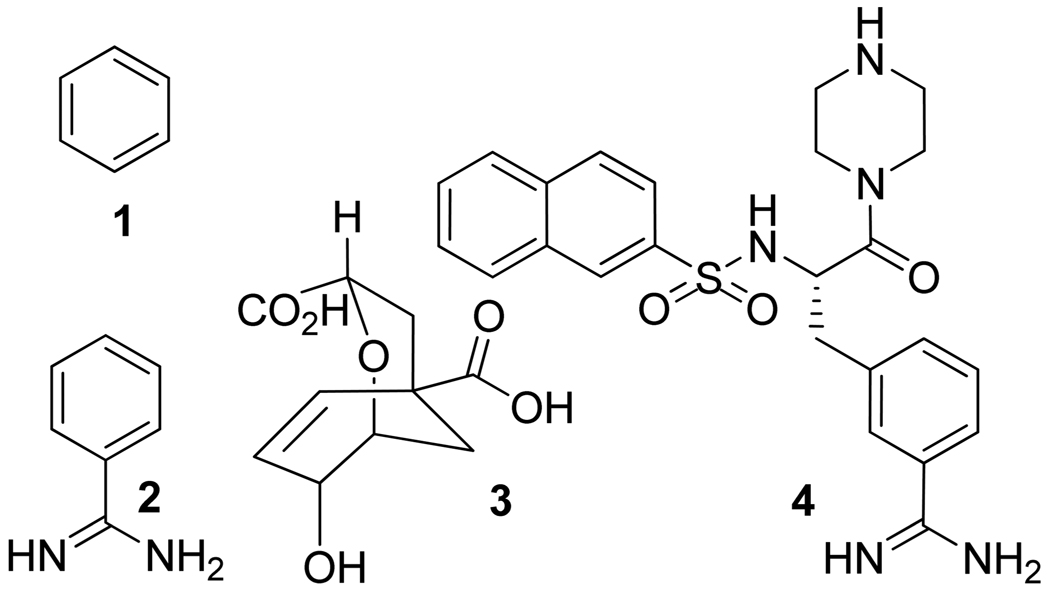
In the present work, we evaluate binding entropy in three characteristically distinct protein-ligand complexes: Bacteriophage T4 lysozyme-benzene, Chorismate mutase-transition state analog and complexes of Trypsin with benzamidine and a substituted benzenecarboximidamide. The first system is an engineered Bacteriophage T4 lysozyme protein in which the single-point mutation L99A results in a buried hydrophobic cavity able to bind benzene (compound 1; Figure 5) and other similarly sized hydrophobic molecules.^58,59 This system is a good benchmark for computational studies of protein-ligand binding entropies because high-resolution structures of the enzyme have been determined by x-ray crystallography both in its apo and complexed forms.⁵⁹ Furthermore, the T4 lysozyme-L99A mutant is an excellent subject for modeling by dynamic simulations because the C-terminal domain containing the cavity is locally stable throughout many nanoseconds of dynamics, even though the molecule undergoes a significant global conformational change in which the two domains and the connecting helix move relative to each other. ^60,61 The second system belongs to Chorismate mutases that are known to occupy a central role in the shikimate pathway leading to the aromatic amino acids, PHE and TYR, in bacteria, fungi and plants. These enzymes are absent in mammals and therefore, are potential targets for the development of antibiotics and herbicides. The crystal structures reveal extensive shape and charge complementarity between the highly charged active site residues and the negatively charged transition state analog (compound 3; Figure 5) that makes this system particularly interesting. The third system is Trypsin in complex with a small and rigid inhibitor (compound 2; Figure 5) and also, a larger and more flexible inhibitor (compound 4; Figure 5). The availability of several crystal structures in complex with different ligands to this enzyme, in addition to, the extensive thermodynamic data, wherein both enthalpic and entropic contributions are known, to allow comparison of the estimated binding energetics to the experimental data, makes it a good benchmark.⁶² Trypsin-like serine proteinases are of significance as either potential targets in the blood coagulation cascade or as functional model systems for the analysis of protein-ligand interactions and the structural and energetic features responsible for specificity and selectivity.

Figure 5.

Structural formulae of ligands used in this study.

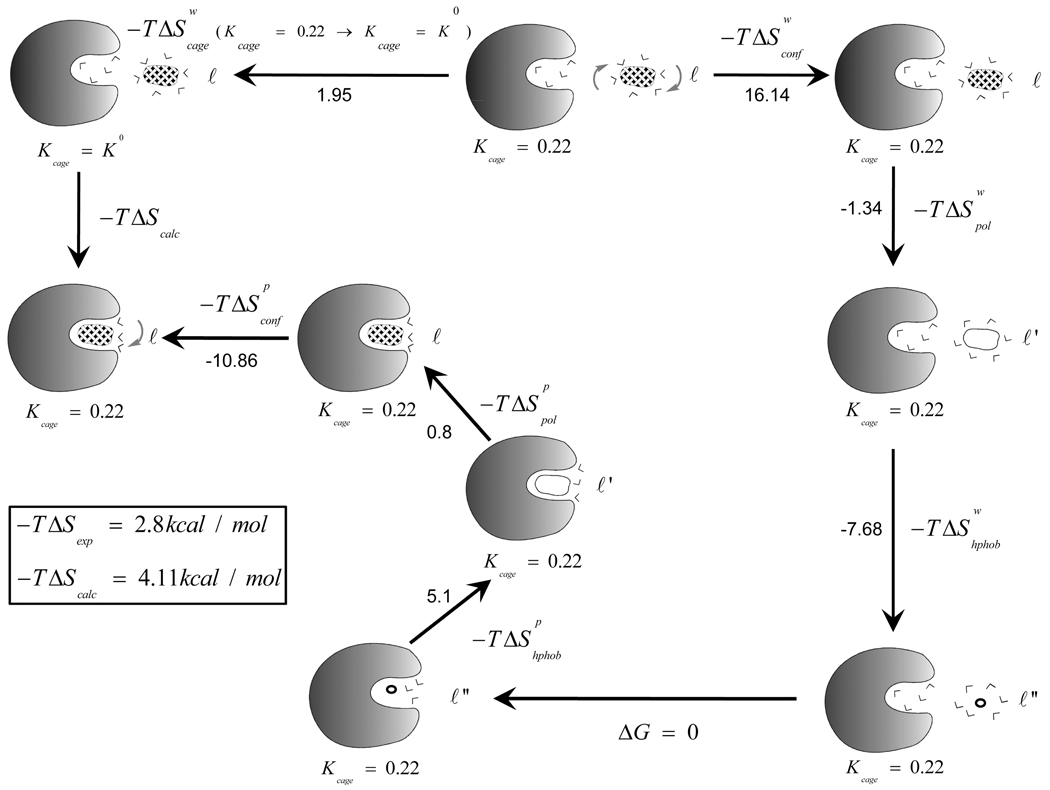
Our calculations are demonstrated in the specific case of benzene binding to T4 lysozyme and are summarized in Figure 6 and in Tables 1–5. The figure and the tables illustrate our overall strategy. The same approach has been used for the other systems (see supplementary material) and the corresponding results are summarized in Table 6.

Figure 6.

The thermodynamics cycle used to calculate the overall binding entropy of compound 1 binding to bacteriophage T4-lysozyme.

Table 1.

The configurational entropy calculation for binding of compound 1 to bacteriophage T4 lysozyme using the RR approach.^a

Protein	1	2	3	4	5	6	7	8
RR10→0.003	−5.47	−5.55	−5.44	−5.35	−5.69	−5.6	−5.88	−5.46
RR1→0.003	−3.91	−3.55	−3.2	−3.02	−4.18	−3.9	−3.29	−3.06
RR0.3→0.003	−2.5	−2.09	−2.15	−1.95	−2.78	−2.53	−2.3	−2.14
RR0.03→0.003	−0.76	−0.64	−0.6	−0.61	−0.64	−0.6	−0.96	−0.62
QH10	−5.7	−5.5	−5.42	−5.61	−5.24	−5.79	−5.66	−5.6
RR10→0.003+ QH10	−11.17	−11.05	−10.86	−10.96	−10.93	−11.39	−11.54	−11.06
Water
RR10→0.003	−11.71	−12.03	−12.06	−12.37	−10.6	−12.98	−10.63	−12.26
RR1→0.003	−9.44	−9.77	−9.83	−10.12	−9.27	−10.51	−9.15	−9.96
RR0.3→0.003	−6.97	−7.23	−7.35	−7.53	−6.76	−7.99	−6.63	−7.5
RR0.03→0.003	−2.56	−2.64	−2.6	−3.41	−2.49	−3.34	−2.75	−2.61
QH10	−6.27	−6.24	−5.87	−5.68	−5.77	−6.5	−5.51	−6.36
RR10→0.003+ QH10	−17.98	−18.27	−17.93	−18.05	−16.37	−19.48	−16.14	−18.62
–T ΔScalc	5.28

^aEnergy values are given in kcal/mol. The table includes the results from eight sets (1–8) of simulations with different restraint coordinates. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time step. The value in bold signifies the best estimate of –TΔS obtained by taking the corresponding values from the run with R that gives the smallest |ΔG'| and thus, the value that satisfies Eq. 9. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions and these contributions approach zero for restraint coordinates that gives the lowest RR contribution.

Table 5.

Calculation of the hydrophobic entropy term of the non-polar ligand in protein. ^a

Uncharged Ligand	1	2	3	4	5	6	7	8
RR10→0.003	−127.04	−120.04	−125.53	−127.32	−126.88	−126.45	−125.78	−128.3
RR1→0.003	−58.3	−54.15	−58.52	−58.41	−58.63	−59.2	−58.23	−61.1
RR0.3→0.003	−28.53	−22.46	−29.07	−29.99	−28.48	−28.13	−27.94	−28.88
RR0.03→0.003	−6.1	−4.2	−5.96	−5.45	−5.67	−5.20	−5.28	−6.28
QH10	−231.14	−226.33	−227.8	−225.4	−227.67	−229.12	−227.23	−226.19
RR10→0.003+QH10	−358.18	−346.37	−353.33	−352.72	−354.55	−355.57	−353.01	−354.49
Nothing
RR10→0.003	−143.98	−122.27	−126.66	−128.47	−127.82	−129.9	−129.52	−134.64
RR1→0.003	−67.71	−59.08	−58.81	−60.1	−59.1	−61.93	−61.22	−64.82
RR0.3→0.003	−36.19	−29.51	−29.83	−30.2	−32.29	−31.18	−32.24	−33.63
RR0.03→0.003	−7.12	−7.36	−8.01	−7.34	−6.84	−7.2	−7.52	−9.12
QH10	−240.8	−229.2	−236.66	−230.79	−232.17	−234.6	−236.18	−231.84
RR10→0.003+ QH10	−384.78	−351.47	−363.32	−359.26	−359.99	−364.5	−365.7	−366.48
–T ΔScalc	5.1

^aEnergy values are given in kcal/mol. The table includes the results from eight sets (1–8) of simulations with different restraint coordinates. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time step. The value in bold signifies the best estimate of –TΔS obtained by taking the corresponding values from the run with R that gives the smallest |ΔG'| and thus, the value that satisfies Eq. 9. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions and these contributions approach zero for restraint coordinates that gives the lowest RR contribution.

Table 6.

Calculated and observed binding entropies for the macromolecular systems studied in this work. ^{a *}

Enzyme/Ligand	$-T\mathrm{\Delta }{S}_{\mathit{\text{conf}}}^w$	$-T\mathrm{\Delta }{S}_{\mathit{\text{conf}}}^p$	$-T\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^w$	$-T\mathrm{\Delta }{S}_{\mathit{\text{pol}}}^p$	$-T\mathrm{\Delta }{S}_{\mathit{\text{hphop}}}^w$	$-T\mathrm{\Delta }{S}_{\mathit{\text{hphop}}}^p$	$-T\mathrm{\Delta }{S}_{\mathit{\text{cage}}}^w$	$-T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}^{\mathit{\text{calc}}}\mathbf{*}$	$-T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}^{\mathit{\text{exp}}}$
T4 lysozyme /167	16.14	−10.86	−1.34	0.8	−7.68	5.1	1.95	4.11	2.81
Trypsin/262	20.45	−19.13	−0.33	2.63	−8.93	6.78	1.95	3.42	1.84
Chorismate mutase/368	33.78	−27.57	−21.21	20.88	−13.98	12.6	1.95	6.45	4.4
Trypsin/469	57.12	−50.97	−13.13	14.43	−16.93	14.85	1.95	7.32	5.83

^aEnergy values are given in kcal/mol.

^*For details, see supplementary information.

In order to analyze the significance of our results, it is useful to start with other related studies. For example, Hermans and Wang used a restraint release approach (although using only internal coordinates and without the idea of looking for the optimal constraint coordinates). ³⁸ They estimated the binding entropy of benzene to T4-lysozyme as ~ 7 kcal/mol. However, the calculations only considered the orientational entropies. Carrlson and Åqvist also studied the same complex using unstrained MD simulations. They estimated the binding entropy of 8.3 kcal/mol for the orientational entropy using Schlitter’s formula, 8.5 kcal/mol using quasiharmonic approximation, 6.0 kcal/mol using uniform distribution of the ligand center of mass and Euler angels, and 5.4 kcal/mol using Gaussian distribution of the ligand center of mass and Euler angels.³⁹

The difference between the above studies and the present work is the fact that we also calculated the polarization and hydrophobic effect which is needed for a comparison with the experimentally observed binding entropies. Our calculated configurational entropy is similar to the estimates of Refs^38,39 and overall, we overestimate the observed binding entropy. In this respect we note, however, that one could have expected even larger values from the regular assumptions about the hydrophobic contribution. However, we obtain an interesting compensation by having hydrophobic contribution both in the protein and in the water. This “strange” finding must reflect some real trend since the contribution from the configurational entropy is already positive and a large hydrophobic contribution would have led to even larger overestimate of the observed −TΔS_bind.

At this point, it might be useful to comment about the widely used Molecular Mechanics Poisson–Boltzmann/Surface Area (MM/PBSA) approach.^63,64 This method, is in some way, an inconsistent adaptation of the earlier scaled Protein Dipoles Langevin Dipoles-Linear Response Approximation (PDLD/S-LRA version),^50,53,57 as it does not use the two-state charging procedure and as a consequence, have inconsistent electrostatic results. More importantly, the MM/PBSA uses normal mode analysis plus estimates for translational entropy that gives extremely large entropy contributions to the binding free energy. Unfortunately, the entropies calculated by this method were never validated by comparing to the experimental entropies, and as shown here, the entropic contributions to the binding are typically quite small. The typical error of about 10 kcal/mol in the MM/PBSA is apparently the reason for obtaining reasonable absolute binding free energy. This can be serious as the coincidental agreement makes it difficult to realize the errors in the MM/PBSA.

IV. CONCLUSIONS

Reliable estimation of the entropic contributions to protein-ligand binding is important because it allows a detailed understanding of the thermodynamical driving forces at the molecular level. However, consistent evaluation of binding entropies is very challenging and in fact, has never been accomplished in a way that provides an insight on the different entropic components. More specifically, previous efforts^18,38,39 have provided about the configurational entropy contribution to the binding free energies but have not evaluated the microscopic and entropic contributions from polar solvation and hydrophobic effects. The present work extends the utility of our RR approach to evaluate the polar and hydrophobic contributions and thus, provide the first microscopic estimate of the magnitude of all the contributions to binding entropy.

Although the overall trend from the present study captures the corresponding observed trend, we still overestimate the total binding entropy. The origin of the overestimate is probably associated with the convergence problems and/or with the inclusion of a limited part of the protein. While efforts to reduce the overestimate are underway it is quite possible that scaling the calculated results will yield a powerful prediction tool. We believe that such calculations can provide a deeper understanding of the binding process and offer the opportunity to optimize the entropic/enthalpic contributions to maximize affinity during drug design and optimization process. Finally, the results may have implications in formulation of improved empirical models for ligand screening and design. For example, this should help in rationalizing the Linear Interaction Energy (LIE) ^65,66 and the microscopic Linear Response Approximation (LRA/β version) ⁵⁷ as well as PDLD/S-LRA/β non-electrostatic term and in exploring the problems with the MM/PBSA entropic terms.

Table 2.

Calculation of the entropy loss upon ordering of the solvent molecules in the vicinity of the polar form of compound 1 in water.^a

Charged ligand	1	2	3	4	5	6	7	8
RR10→0.003	−107.55	−113.88	−121.93	−124.38	−105.51	−116.25	−119.22	−122.79
RR1→0.003	−87.12	−93.05	−101.75	−101.94	−87.29	−95.83	−101	−101.05
RR0.3→0.003	−73.17	−75.1	−84.77	−84.74	−72.76	−78.05	−83.68	−80.83
RR0.03→0.003	−38.88	−36.54	−44.27	−41.33	−36.17	−40.07	−39.74	−39.32
QH10	−186.95	−186.5	−192.19	−194.35	−194.17	−194.94	−192.19	−189.4
RR10→0.003+QH10	−294.5	−300.38	−314.12	−318.73	−299.68	−311.19	−311.41	−312.19
Uncharged ligand
RR10→0.003	−108.91	−113.68	−116.26	−124.45	−115.32	−123.86	−116.07	−126.5
RR1→0.003	−88.59	−92.79	−96.19	−102.13	−97.09	−103.42	−97.69	−104.62
RR0.3→0.003	−74.71	−74.8	−79.25	−84.73	−82.38	−85.83	−80.6	−84.66
RR0.03→0.003	−36.64	−37.26	−40.15	−45.58	−39.43	−43.26	−42.51	−39.72
QH10	−186.93	−186.86	−191.86	−194.67	−195.02	−196.1	−191.49	−190.92
RR10→0.003+QH10	−295.84	−300.54	−308.12	−319.12	−310.34	−319.96	−307.56	−317.42
–T ΔScalc	1.34

^aEnergy values are given in kcal/mol. The table includes the results from eight sets (1–8) of simulations with different restraint coordinates. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time step. The value in bold signifies the best estimate of –TΔS obtained by taking the corresponding values from the run with R that gives the smallest |ΔG'| and thus, the value that satisfies Eq. 9. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions and these contributions approach zero for restraint coordinates that gives the lowest RR contribution.

Table 3.

Calculation of the entropy loss upon ordering of the solvent molecules in the vicinity of the polar form of compound 1 in protein. ^a

Charged Ligand	1	2	3	4	5	6	7	8
RR10→0.003	−77.93	−80.48	−75.66	−68.98	−69.27	−84.88	−83.91	−83.68
RR1→0.003	−37.23	−40.25	−35.31	−30.34	−30.19	−37.84	−40.15	−34.67
RR0.3→0.003	−17.33	−18.21	−16.7	−14.13	−13.88	−18.71	−19.19	−16.75
RR0.03→0.003	−2.65	−2.76	−2.38	−2.38	−2.46	−3.03	−2.75	−3.22
QH10	−107.56	−105.78	−106.2	−110.01	−105.71	−105.71	−106.08	−108.08
RR10→0.003+QH10	−185.49	−186.26	−181.86	−178.99	−174.98	−190.59	−189.99	−191.76
Uncharged Ligand
RR10→0.003	−86.81	−73.04	−75.06	−73.25	−69.45	−87.29	−88.42	−83.36
RR1→0.003	−40.12	−33.01	−35.19	−31.91	−31.67	−39.98	−41.88	−34.67
RR0.3→0.003	−19.53	−15.51	−16.74	−14.22	−14.92	−20.11	−20.53	−16.03
RR0.03→0.003	−3.68	−2.17	−2.8	−2.19	−2.27	−3	−3.98	−3.1
QH10	−108.04	−106.13	−107.57	−109.3	−106.33	−106.52	−107.22	−108.35
RR10→0.003+ QH10	−194.85	−179.17	−182.63	−182.55	−175.78	−193.81	−195.64	−191.71
–T ΔScalc	0.8

^aEnergy values are given in kcal/mol. The table includes the results from eight sets (1–8) of simulations with different restraint coordinates. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time step. The value in bold signifies the best estimate of –TΔS obtained by taking the corresponding values from the run with R that gives the smallest |ΔG'| and thus, the value that satisfies Eq. 9. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions and these contributions approach zero for restraint coordinates that gives the lowest RR contribution.

Table 4.

Calculation of the hydrophobic entropy term of the non-polar ligand in water. ^a

Uncharged Ligand	1	2	3	4	5	6	7	8
RR10→0.003	−108.91	−113.68	−116.26	−124.45	−115.32	−120.77	−116.07	−126.5
RR1→0.003	−88.59	−92.79	−96.19	−102.13	−97.09	−101.81	−97.69	−104.62
RR0.3→0.003	−74.71	−74.8	−79.25	−84.73	−82.38	−82.6	−80.6	−84.66
RR0.03→0.003	−36.64	−37.26	−40.15	−45.58	−39.43	−39.65	−42.51	−39.72
QH10	−186.93	−186.86	−191.86	−194.67	−195.02	−194.41	−191.49	−190.92
RR10→0.003+QH10	−295.84	−300.54	−308.12	−319.12	−310.34	−315.18	−307.56	−317.42
Nothing
RR10→0.003	−115.21	−117.82	−121.57	−125.66	−117.99	−123.86	−120	−125.18
RR1→0.003	−98.08	−100.68	−102.77	−102.98	−99.73	−103.42	−100.56	−104.42
RR0.3→0.003	−80.58	−81.68	−82.54	−82.98	−81.69	−85.83	−82.71	−85.32
RR0.03→0.003	−37.18	−37.69	−40.75	−41.62	−40.03	−43.26	−40.61	−42.19
QH10	−188.31	−188.81	−193.1	−195.61	−196.57	−196.1	−193.7	−195.57
RR10→0.003+ QH10	−303.52	−308.13	−314.67	−321.27	−314.56	−319.96	−313.7	−320.75
–T ΔScalc	7.68

^aEnergy values are given in kcal/mol. The table includes the results from eight sets (1–8) of simulations with different restraint coordinates. The simulations consisted of 41 windows, each with a simulation time of 40ps at 300K with 1fs time step. The value in bold signifies the best estimate of –TΔS obtained by taking the corresponding values from the run with R that gives the smallest |ΔG'|and thus, the value that satisfies Eq. 9. As discussed in the main text, this variational minimization reflects the fact that all the RR free energies contain enthalpic contributions and these contributions approach zero for restraint coordinates that gives the lowest RR contribution.