Variance Component Methods for Analysis of Complex Phenotypes

Introduction

Variance component methods have a long history in both human quantitative genetics and agricultural genetics and animal breeding. They are designed for genetic analysis of continuously varying quantitative traits like body mass index (BMI), cholesterol levels, or IQ. They can be used to assess the strength of genetic effects on a trait, to localize genes influencing a trait though either linkage or association methods, to assess whether associated variants are likely to be the functional variants behind a given localization signal, to explore whether related traits have shared genetic influences in multivariate analyses, and to characterize the genetic effects on a trait through analyses of gene-gene and gene-environment interaction. An excellent reference for a thorough explanation of classical variance component methods in genetics is Falconer and Mackay 1996.

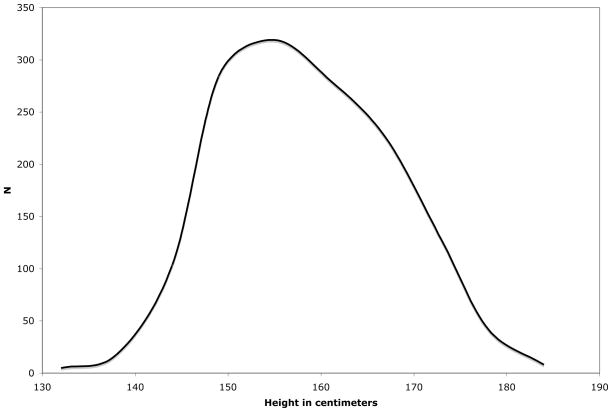
Conceptually, the idea behind variance component methods is very simple – to decompose the overall variance in a phenotype into particular sources. Assuming that the trait of interest is normally distributed, a common assumption in variance component analyses, the distribution of a trait or phenotype can be described in terms of the mean and variance of the trait. Figure 1 shows the distribution of height in the 1411 participants of the San Antonio Family Heart Study (SAFHS) (Mitchell et al. 1996). The height of study participants ranges from 132.4 cm to 190.5 cm and the mean is 161.64 cm. Most people are about average and a few people are very short or very tall. The variance describes the spread of the trait values around the mean. The variance in height in the SAFHS is 85.65. Asking what the sources of variance in a trait are is essentially asking what makes people different from each other.

Figure 1.

Distribution of height in the San Antonio Family Heart Study.

The most basic way to group these sources of variance is to divide the overall phenotypic variance (σ²_p) into genetic (σ²_g) and environmental (σ²_e) components:

$${{\sigma }^2}_{\text{p}}={{\sigma }^2}_{\text{g}}+{{\sigma }^2}_{\text{e}}.$$ (1)

Each of these can be further subdivided. Genetic variance is often subdivided into additive and dominance variance and sometimes epistatic variance, which arises from interactions among genes. Environmental variance is typically divided into shared and unshared or unique. Shared environmental variance may reflect influences that are common to members of a nuclear family, to spouses, to sibships, or to larger community units that extend beyond the nuclear family. Unshared or unique environmental variance is specific to each individual and may include things such as measurement error.

Heritability and Covariates

Heritability is a measure of the strength of genetic effects on a trait. In its most general sense, heritability (h²) is defined as the proportion of the phenotypic variance in a trait that is attributable to genetic effects:

$${\text{h}}^2={{\sigma }^2}_{\text{g}}/{{\sigma }^2}_{\text{p}}.$$ (2)

This is broad sense heritability and includes dominance and epistatic interaction effects. However, most human family studies deal with additive genetic or narrow sense heritability, which is the proportion of the phenotypic variance attributable to additive genetic effects or

$${\text{h}}^2={{\sigma }^2}_{\text{a}}/{{\sigma }^2}_{\text{p}}.$$ (3)

The overall phenotypic variance is estimated from the observed distribution of trait values in a sample and is decomposed into genetic and environmental components using the observed covariance in the trait among family members (Ω) and structuring matrices that predict the covariances among family members if they are due to additive genetic effects or to environmental effects.

$$\mathrm{\Omega }=2\mathrm{\Phi }{{\sigma }^2}_{\text{a}}+\text{I}{{\sigma }^2}_{\text{e}}$$ (4)

Here Ω is an N-by-N matrix, where N is the number of individuals in the data set, whose elements are the observed covariances in phenotype for each pair of individuals in the data set (see Chapter 2, Sinsheimer for a definition of covariance). The right side of the equation consists of possible sources of covariance among individuals and structuring matrices describing what the covariances among individuals should be if they are due to that component. In this case, equation 4 describes a very simple model including only aggregate additive genetic effects of an unspecified number of loci at unknown locations in the genome (σ²_a) and unique, unshared environmental effects (σ²_e). Each variance component is accompanied by a structuring matrix that predicts the covariance among individuals attributable to that component. In the case of the additive genetic component, the structuring matrix is the coefficient of relationship, 2Φ, which is also twice the kinship coefficient. The coefficient of relationship can be specified for any two individuals on the basis of their family relationship and requires only knowledge of the pedigree connections between individuals, not their genotypes. It is one half for first degree relatives and goes down by a factor of one half with each degree of relationship, being one quarter for second degree relative pairs, one eighth for third degree pairs, and so on (Table 1). For pairs with more complex types of relationships who are related through multiple lines of descent, as may occur with inbreeding or with marriage loops in a pedigree, this coefficient can also be calculated by tracing the paths between them through all common ancestors multiplying by one half for each step along the path and summing across the multiple paths. The coefficient of relationship is also the expected proportion of DNA shared on average by a given relative pair across the whole genome. The basic idea behind this model is intuitively obvious - to the extent that additive genetic effects influence a trait of interest, regardless of how many genes influence the trait, close relatives should be more correlated in their phenotype than are more distant relatives who should be more correlated than are unrelated individuals. The structuring matrix for the environmental component is an identity matrix, which is ones down the diagonal (i.e. for the individual with themselves) and zeros everywhere else. This implies that the environmental component is unique to each individual and unshared or uncorrelated between individuals. Based on the observed covariances in phenotype among individuals in the data set and on these structuring matrices, maximum likelihood techniques are used to estimate the additive genetic and environmental variance components (see Chapter 2, Sinsheimer for more on maximum likelihood). Returning to our example of height in the SAFHS, the maximum likelihood estimate of the additive genetic variance, given the observed covariances among individuals and the kinship coefficients among family members, is 45.39, providing an additive genetic heritability of 45.39/85.65 = 0.53. As a proportion, heritability varies between zero and one, with higher values indicating stronger genetic effects.

Table 1.

Family relationships and coefficient of relationship.

Degree of relationship	Types of relative pairs	Coefficient of relationship (2Φ)
1	Parent-child, sibling	½ = 0.5
2	Grandparent-grandchild, half sibling, avuncular (aunt or uncle with niece or nephew)	¼ = 0.25
3	Great grandparent –grandchild, half avuncular, grand avuncular, first cousins	1/8 = 0.125
4	Great great grandparent – grandchild, half grand avuncular, great grand avuncular, first cousins once removed	1/16 = 0.0625

It is important to note that genes are not the only thing shared by family members and that some study designs are susceptible to confounding familial effects with genetic ones, inflating estimates of the additive genetic variance and therefore heritability through unaccounted for effects of shared environment. In twin studies, a common assumption is that environmental sharing is the same for monozygotic and dizygotic pairs. If this is true, estimating the heritability of a trait by taking the difference in the covariances of the two types of twin pairs results in the environmental variance canceling out. In studies of extended pedigrees, the comparable assumption is that shared environment is unlikely to mimic genetic sharing, which falls off by a factor of one half with each degree of relationship as shown in Table 1. Studies of nuclear families that do not include twins do not have either of these protections and are somewhat more vulnerable to the problem of overestimation of heritability due to the effects of correlations among family members that are due to shared environment rather than shared genes.

One approach to the problem of shared environmental effects is to incorporate them directly into the variance component model. This is easily done, provided one can specify a structuring matrix that indicates which individuals in the study share the relevant environment. In its simplest form, this could be a matrix of zeroes and ones specifying for each pair of individuals in the study whether they do or do not share the environmental factor. Household is often used in this way, with a matrix indicating which individuals lived in the same household at the time of study, as a proxy for many difficult to measure factors such as diet. One might also use this kind of matrix to model childhood rearing environment (i.e. which individuals lived together as children) or to allow for correlations between spouses. Although a simple share/don’t share matrix of zeroes and ones is the most common type of environmental sharing incorporated into human variance component studies, there is no reason such a matrix can’t contain continuously varying measures of sharing. One example of this would be a distance matrix where individuals in the same household have complete sharing (ones in our zero/one matrix) and individuals in different household have values decaying toward zero and depending on how far apart the households are. This type of household matrix might be useful as a proxy for environmental exposures such as pollutants.

Another important source of trait variation to consider is known environmental factors that can be measured in each study participant. It is more powerful to incorporate a direct measure of an environmental factor than to use indirect measures of whether individuals share or don’t share this environmental factor. Using the examples above, if we could measure diet or pollution exposure for each individual, that would be preferable to using household membership as a proxy for sharing of these factors among family members. Accounting for the effects of measured environmental factors reduces the unexplained trait variance and effectively magnifies a genetic signal. Covariates are dealt with in variance component analyses as a modification to the trait mean, rather than a component of the variance. Essentially, covariate-specific trait means are used in the calculation of covariances among relatives. In the case of height, it is well known that men are, on average, taller than women. Including sex as a covariate in our example analysis from the SAFHS, we learn that females in this study are, on average, 13.4 cm shorter than males and after taking into account mean differences in height between males and females, we reduce the residual trait variance to 39.68 of which 69% can be attributed to additive genetic effects. If we consider the heritability to be a sort of signal-to-noise ratio for genetic effects, including this one covariate increased our ratio by 0.16, from 0.53 to 0.69. Another covariate we might choose to include for height is age, as people do lose some height as they get older, or birth cohort as there are known secular trends in height.

The selection of covariates can have a large effect on the outcome of variance component analyses. Accounting for non-genetic sources of variance can magnify the genetic signal, as demonstrated above. However, one must consider that it is also possible to choose as covariates traits that absorb genetic variance as well as environmental. For example, many individuals with type 2 diabetes also have hypertension, abdominal obesity, high triglyceride levels and low HDL cholesterol levels: a clustering of phenotypes described as metabolic syndrome. Because of this, one might choose to include the known correlates blood pressure, triglyceride levels, and HDL levels as covariates in genetic analyses of type 2 diabetes. However, because these traits are themselves genetically influenced, including them as covariates raises the possibility that one is correcting out not only environmental factors but also genetic ones, potentially decreasing the magnitude of the genetic signals for type 2 diabetes. If hypertension, abdominal obesity, high triglyceride levels, low HDL cholesterol levels and diabetes commonly occur together because they are influenced by the same genes, including blood pressure and lipid measurements as covariates in an analysis of type 2 diabetes will likely reduce the power to find genes that influence both these phenotypes and diabetes. There are instances when one may decide to take this route as a deliberate choice, for example if one is interested in genetic effects on type 2 diabetes that are independent of obesity. However, in general, one should be very cautious about including as a covariate anything that might share overlapping genetic influences with the trait of interest. One way to assess this is to examine the genetic correlations among traits (discussed below in the section on Multivariate Analysis).

Liability Threshold Model

Although variance component methods were designed for continuously varying quantitative traits, an extension of this basic model can be used to analyze discrete or categorical traits by assuming that there is an unobserved, continuous, quantitative trait underlying the observed categorical one. This imagined underlying quantitative trait is referred to as the liability and is assumed to be normally distributed. A threshold is placed on this imaginary distribution so that a portion of the distribution equal to the trait prevalence is above the threshold. So if 12% of the population is affected, the threshold is placed such that 12% of the liability distribution is above the threshold. Covariates, such as age and sex, are modeled as effects on this threshold and allow for different prevalences of the trait in males and females or by age or with smoking or medication use. One conceptual advantage of this model is that it acknowledges differences within affected and unaffected individuals. Some affected individuals are mildly affected and can be thought of as having a liability that is just over the threshold whereas others are severely affected with a very high liability. Similarly, as the threshold moves with age, some young individuals with higher liabilities who are now unaffected may become affected as they get older.

Of course, it is impossible to directly measure an individual’s liability since liability is an unobserved and imaginary trait. We only know which side of the threshold an individual is on given their affection status and where the threshold is for someone of their age, sex, and covariate status. The analysis is thus performed by integrating over the possible liability threshold values each individual could have given their observed dichotomous trait status and age, sex, and other covariates. The success of this analysis once again depends on contrasting relatives who are more and less alike in their phenotypes, so it requires the presence of individuals on both sides of the threshold and could not be done with a sample that contains, for example, only affected individuals. The power of the approach depends in part on the prevalence of the trait. Imagine a relatively rare disease, such as schizophrenia which has a prevalence of roughly 1%. Knowing someone is affected localizes their liability to a relatively small portion of the curve, the top 1%. But knowing that someone is unaffected tells you almost nothing about their liability, they are somewhere in the bottom 99%. The power of the liability threshold is greatest when the prevalence approaches 50% and affected and unaffected individuals are equally informative (Williams and Blangero 2004).

Linkage

The basic model for linkage analysis within a variance components framework is a simple extension of equation (4), adding in a new locus-specific variance component (σ²_qtl) and a structuring matrix for it (Π) that is a function of observed allele sharing among family members at genotyped markers in a region of interest (Goldgar 1990; Amos 1994; Almasy and Blangero 1998):

$$\mathrm{\Omega }=\mathrm{\Pi }{{\sigma }^2}_{\text{qtl}}+2\mathrm{\Phi }{{\sigma }^2}_{\text{a}}+\text{I}{{\sigma }^2}_{\text{e}}.$$ (5)

The elements of the Π matrix are the proportion of alleles shared identical by descent (IBD) by each relative pair at a particular location in the genome, which is estimated based on the genotypes at surrounding markers. To be IBD, two alleles must not only be the same (e.g. both 116 base pairs for a microsatellite or both G alleles for a SNP), they must be copies of the same ancestral chromosome. This is the heart of how linkage differs from association. Linkage analysis is not based on which allele any given person or pair of relatives have at a given marker; the genotypes are merely used to mark the flow of chromosomes through pedigrees and to determine how correlated a relative pair is for their alleles on that segment of chromosome. In the region of a gene influencing a trait of interest, relatives who are more correlated in their trait values should have higher IBD allele sharing and relatives who are less correlated phenotypically should have lower IBD sharing. This is true regardless of the type and complexity of the underlying genetic model. Imagine a gene with extensive allelic heterogeneity. This same quantitative trait locus (QTL) influences the trait of interest in many families, but there are many functional variants. This QTL can still be detected by linkage because although there may be a different allele in each family, within a family relatives who share the same allele will be more phenotypically alike than relatives who are discordant at the QTL, regardless of which functional allele they carry and whether that particular allele increases or decreases trait values.

IBD sharing is usually represented as a proportion – 0 for pairs that share no alleles, ½ for pairs that share exactly one allele, and 1 for pairs that share both alleles – and the Π matrix contains the estimated IBD sharing at a given location for each pair of individuals in the sample. In practice, when parents are ungenotyped or homozygous, we may not be able to determine whether a pair shares 0, 1, or 2 alleles. In this case, the estimated IBD sharing is a weighted average of the probability of sharing 1 allele and the probability of sharing 2 alleles:

$$1/2\text{pr}(\text{share}1\text{allele})+\text{pr}(\text{share}2\text{alleles}).$$ (6)

The power of variance component linkage analysis is a function of the proportion of variance due to the QTL (σ²_q), the sample size, and the family configuration. For a fixed sample size, linkage power is maximized when the individuals are concentrated into as few pedigrees as possible; larger pedigrees provide more power per person sampled (Blangero et al. 2003). Analytical power formulae can be written down for fixed pedigree configurations (Williams and Blangero 1999), but in practice most studies contain a mixture of different types of pedigrees and power is estimated by simulation. It can be shown that power is greater for quantitative traits than for discrete traits derived from a quantitative measure (e.g. as obesity is from BMI), when QTL effect and sample size and configuration are held constant, unless the quantitative trait is very poorly measured with a high degree of error.

Ascertainment

A common rule of thumb often taught is that the ascertainment scheme used to select families for study must be taken into account in segregation analyses but not in linkage analyses. However, not taking into account the way in which families were ascertained can hurt power in variance component analyses. As described above, the analyses depend on the trait mean and variance, which is being estimated from the sample. If the trait of interest is genetically influenced, family members are correlated with each other for their trait values. So selecting families through an individual with an extreme phenotype, e.g. a BMI > 35, affects the distribution of trait values not only in those probands but also in their family members. In such a sample, the estimated mean will be higher than the population mean and the variance will be lower than the population variance, as individuals from the lower end of the trait distribution are likely to be underrepresented. Consequently, an individual with a BMI of 40, who would be very extreme compared to the population distribution, is less extreme relative to the sample trait distribution, effectively undervaluing this individual in the analysis. Additionally, correlations among relatives will be underestimated.

The most straightforward ascertainment correction involves conditioning the likelihood of each pedigree on the proband’s phenotype (Boehnke and Lange 1984). However, this is only an exact correction when each family was ascertained based on the phenotype of a single individual. When families were ascertained through multiple individuals, e.g. affected sibling pairs, it is possible to condition on both individuals’ phenotypes, but this correction is no longer guaranteed to recover the correct population mean and variance and may, in some cases, further reduce analytical power. Another approach that can be used is to fix the trait mean and variance based on measures from epidemiological studies in the same population, rather than estimating them. However, if this is done, one must also fix any covariate effects rather than estimating them. When faced with a complicated ascertainment scheme where it is difficult to identify probands and no appropriate epidemiological data is available for fixing the mean and variance, the good news is that failing to employ an ascertainment correction should be conservative. It reduces power but should not increase false positive rate.

Non-normality

Likelihood-based variance component methods typically assume that a trait is normally distributed, like a bell curve. Skewness and kurtosis describe two ways that a distribution may be non-normal. It may not be symmetrical around the mean with more of the trait values falling to one side than to the other, in which case it is skewed. Or it may have tails that have too many or too few individuals, which is kurtosis. Examining Figure 1, we can see that the distribution of height is slightly skewed, but there is no significant kurtosis. The specific type of non-normality that can be problematic for variance component analyses is leptokurtosis, when the tails of a distribution are too full and there are more trait values far from the mean than would be expected in a normal distribution. It has been shown that the evidence for linkage can be inflated if such data is analyzed assuming a normal distribution. The increase in false positive rate depends on the degree of kurtosis and on the heritability of the trait, but could be two or even three times what is expected.

Fortunately, this situation is easily corrected and one only need be aware of the issue and take appropriate steps when analyzing leptokurtic traits. Two commonly used corrections are using the t-distribution instead of the normal or calculating a correction constant. The correction constant can be calculated directly for pedigrees of fixed structure, but more commonly it is derived from comparing LOD scores obtained in simulations under the null of no linkage to the observed LOD score distribution for the trait at hand. These corrections are discussed more fully in Blangero et al 2000 and Blangero et al 2001. Some investigators also choose to use transformations to normalize their data. These transformations could range from taking the natural log of the trait values to rank ordering the trait values and replacing them with a corresponding value from a normal distribution. The use of such transformations is somewhat controversial, with some arguing that changing the distribution of the trait may change the properties and detectability of the underlying genetic signal. One potential safeguard against this is to choose transformations that maintain or enhance the trait heritability. If the goal of the study is gene localization, choosing a transformation that maximizes heritability should not bias any eventual linkage or association results.

Multivariate Analysis

Joint analysis of multiple related phenotypes can be used to answer questions about the nature of the relationship between the traits and to increase power to localize genes influencing the traits (Lange and Boehnke 1983; Almasy et al 1997). For example, when two traits are known to be correlated, we often would like to know whether this is because they are influenced by the same genes. Identifying networks of related risk factors that share overlapping genetic effects may provide insight into the biology of a disease phenotype. Similarly, showing that two heritable risk factors for the same disease have no overlapping genetic effects suggests that there are at least two independent pathways contributing to disease risk.

As with the variance for a single trait, the overall phenotypic correlation between two traits (ρ_p) can be broken down into a genetic (ρ_g) and an environmental component (ρ_e):

$${\rho }_p=\sqrt{h_1^2}\sqrt{h_2^2}{\rho }_g+\sqrt{1-h_1^2}\sqrt{1-h_2^2}{\rho }_e$$ (7)

where h²₁ and h²₂ are the heritabilities of trait 1 and trait 2. In practice, the genetic and environmental correlations are obtained by estimating the genetic and environmental variance components for each trait (σ²_a and σ²_e) and the covariance between them, using the observed covariances among family members for the two traits and the same structuring matrices as before, 2Φ and I.

The additive genetic correlation, ρ_g, varies between −1 and 1 and is a measure of pleiotropy, the extent of common genetic effects on the two traits. If ρ_g = 0, the two traits are influenced by independent genetic factors. If ρ_g = −1 or 1, the genetic influences on the two traits are identical with the sign indicating whether variants that increase levels of one trait also increase levels of the other (+1) or whether factors that increase levels of one trait decrease levels of the other (−1). Likelihood ratio tests can be used to obtain a p-value testing the hypothesis of pleiotropy (i.e. whether ρ_g is different from 0). This test of pleiotropy is one way to assess whether a measured co-factor may have overlapping genetic influences with the focal trait in an analysis before deciding whether to use it as a covariate.

The linkage models discussed above are also easily expanded to bivariate or multivariate analyses via a QTL variance for each trait and the locus-specific correlations between them (Almasy et al 1997). For a specific test of pleiotropy, one may choose to fix the locus-specific correlation to 1 or −1, implying that the same functional variant (or variants) in the region affect both traits. In the case where there are multiple functional variants that comprise a QTL, one may observe a genetic correlation < | 1 | if some variants influence both traits and some influence only one or if there are gene-environment interactions influencing one trait but not the other.

Association

The simplest association analysis for quantitative traits is to test whether the mean trait values differ by genotype, sometimes called a measured genotype test (Boerwinkle et al. 1986). This tested is implemented in the same way as are covariate effects such as age and sex. The genotype of each individual is scored, a regression coefficient is estimated, and a likelihood ratio test is used to assess whether the regression coefficient is different from zero.

Often an additive model of gene action is assumed. For a marker with only two alleles, such as a SNP, an additive model requires a single genotype score with genotypes AA, Aa, and aa being scored as 0, 1, and 2, respectively. This model effectively constrains the trait mean for heterozygotes to be at the midpoint of the mean for the two homozygotes and provides a one degree of freedom association test. Recessive and dominant models, in which the heterozygote mean is constrained to be equal to that of one of the homozygotes and the genotypes are scored 0 or 1, also provide one degree of freedom tests but are less commonly used. Means may also be estimated separately for each genotype using two 0/1 genotype scores to differentiate the three genotype classes. This does not require any assumptions about the underlying model of gene action. However, it results in a two degree of freedom test and it may lead to parameter estimates that are biologically implausible for many phenotypes (e.g. a situation of overdominance where the mean for the heterozygote is outside the range of the homozygote means). These fixed effects regression-based association tests for differences in trait mean by genotype are identical to ones that might be performed with any statistical analysis software. The advantage to implementing them within a variance component framework is that the non-independence among family members is accounted for through the additive genetic component in the random effects model of the variance. Ignoring this non-independence among family members could bias the p-values of the association tests.

Although the measured genotype test implemented in a variance component framework takes into account the non-independence among family members, it is still susceptible to the effects of population stratification. A variety of transmission disequilibrium tests for quantitative traits have also been implemented in a variance component framework. These tests protect against association due to population stratification by separating the genotype score for association with a marker into between- and within-family components and using only the within-family component for the test of association (Fulker et al. 1999; Abecasis et al. 2000a; Abecasis et al. 2000b; Siegmund et al. 2001).

Gene-Gene and Gene-Environment Interactions

The above models are easily expanded to incorporate or test gene-gene and gene-environment interactions. On the level of aggregate genetic effects at unspecified points in the genome, gene-environment interactions (described in Chapter 11 Loos) can be thought of as due to either differences in magnitudes of genetic effects between environments or differences in which genes influence a trait in different environments. Differences in magnitudes of genetic effects are modeled for dichotomous environments (e.g. smokers and non-smokers) by specifying environment-specific variance components (σ²_a, σ²_e, and σ²_q if it is a linkage model). Differences in which genes influence a trait in different environments are modeled with correlations between the genetic and environmental variance components in the two environments (ρ_g and ρ_e). A simple test of overall, non-locus-specific, gene-environment interaction can be achieved by comparing the likelihood of a model where separate additive genetic components are allowed to differ between environments to the likelihood of a model where the additive genetic variances are constrained to be equal for a simple one degree of freedom test. The same type of test can also be used in linkage by testing equality of the QTL-specific variances in the two environments. On the level of association, the analogous test would be to model the difference in mean trait values by genotype separately for smokers and non-smokers and perform a likelihood ratio test using models where regression coefficients for the SNP effect are estimated separately versus constrained to be equal. In the simple non-locus-specific, additive genetic model, gene-environment interaction is also present when the genetic correlation between environments is different from one, implying different genes influencing the trait in the two environments. Variance component models for gene-environment interaction are described more fully in Blangero 1993. In the case of an environmental factor that varies continuously, the genetic and environmental variance components can be modeled as a function of the environmental measure, with genetic or environmental variances increasing or decreasing per unit of change in the environmental measure, as described in Diego et al 2003.

Gene-gene interactions, or epistasis, can be modeled on the level of linkage by adding a variance component for epistatic interaction between two loci with an appropriate structuring matrix to a two QTL linkage model that also contains QTL-specific variance components for the independent effects of each of the loci (Mitchell et al 1997):

$$\mathrm{\Omega }={\mathrm{\Pi }}_1{{\sigma }^2}_{\text{q1}}+{\mathrm{\Pi }}_2{{\sigma }^2}_{\text{q}2}+{\mathrm{\Pi }}_1\odot {\mathrm{\Pi }}_2{{\sigma }^2}_{\text{epi}}+2\mathrm{\Phi }{{\sigma }^2}_{\text{a}}+\text{I}{{\sigma }^2}_{\text{e}}.$$ (8)

For additive-additive interaction, the structuring matrix for the epistatic component would be the Hadamard product of the IBD matrices for each of the individual QTLs, Π₁⊙Π₂. A focal test of gene-gene interaction is then provided by testing whether the new epistatic component of variance, σ²_epi, is > 0. Additive-dominance, dominance-additive, and dominance-dominance epistasis are not often used in human genetic studies but also can be modeled with the appropriate structuring matrices. For additive components this is the IBD sharing matrix, Π, whereas for dominance components it is a locus-specific version of Jaquard’s Δ₇, the probability that each pair of individuals shares both alleles identical by descent. On the level of association, gene-gene interaction can be modeled similar to gene-environment interaction, by estimating multiple regression coefficients (as above in gene-environment interaction) and evaluating whether the displacement among trait means by genotype at one locus differs by genotype at a second locus.

Identifying Potentially Functional Variants

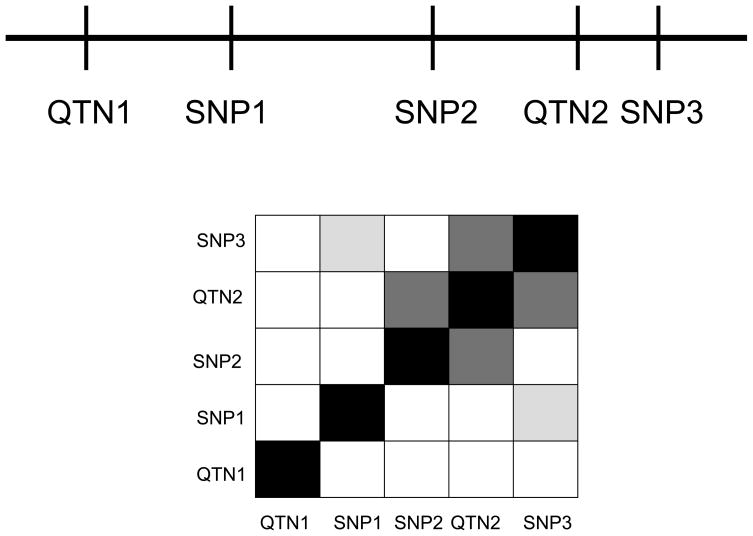
Ideally, localization of a QTL to a region or gene through linkage or association will be followed by identification of the specific DNA variants that influence a phenotype. Confirmation of functional variants will of course involve laboratory studies of function, such as expression constructs, and potentially animal models. However, statistical genetic techniques may aid in prioritizing variants for these studies. Suppose that there are two functional variants within a particular QTL, a promoter variant that has a relatively small effect on the mean trait values in the population (QTN1 in Figure 2) and a coding change that has a large population-level effect (QTN2). (Remember that the effect size on the population level is a function of both the frequency of a variant and the shift in phenotype values it causes in each individual who carries it. A variant may have a larger population level effect either by being common or by causing a large displacement in the mean phenotype value.) Suppose also that there are many other SNPs in and around this gene that do not affect our phenotype (SNPs 1-3 in Figure 2). Some of these non-functional polymorphisms are in greater or lesser degrees of linkage disequilibrium (LD) with one or the other of the two functional variants. If we rank SNPs for functional studies in order of their p-values for association with the phenotype, non-functional SNPs that are in strong LD with the coding variant of large effect (SNPs 2 and 3 in Figure 2) will be higher on our list of candidates than QTN1, the promoter variant that is truly functional but has a smaller effect size. This is because the effective effect size for association studies for a given genotyped marker (σ²_mark) is a function of the proportion of variance attributable to a functional variant (σ²_qtn), which we call a QTN or quantitative trait nucleotide, and the correlation between that QTN and the genotyped marker:

$${{\sigma }^2}_{\text{mark}}=\rho {{\sigma }^2}_{\text{qtn}}$$ (9)

where ρ is the correlation between genotypes at the marker and at the QTN, which is also the square root of the common measure of linkage disequilibrium r-squared. If our functional variants account for 1% of the trait variance, in the case of the weaker QTN1, or 2%, in the case of the stronger QTN2, non-functional SNPs with r-squared of > 0.25 with QTN2 will have a σ²_mark that is greater than the σ²_qtn of QTN1 and will produce stronger p-values in an association analysis.

Figure 2.

A chromosomal region with two functional variants (QTN1 and QTN2) and three SNPs and the linkage disequilibrium between these pairs of markers. Darker boxes indicate stronger disequilibrium.

Bayesian methods of multi-marker association analysis have been proposed to screen out SNPs whose strong p-value in an association analysis is due to LD with another genotyped variant (Blangero et al. 2005). This approach involves obtaining a goodness of fit statistic for models including each variant individually and then pairs of variants and then three variants at a time and so with the addition of variants continuing until no n+1 variant model fits better than the best n variant model. Then the Bayesian Information Criterion (BIC) is used to compare these non-nested models. Rather than selecting one model as the ‘best’, all of the models within a certain window of BIC values are retained and Bayesian Model Averaging is used to obtain a posterior probability for each SNP. Returning to the example above, with a coding variant of large effect and a promoter variant of smaller effect and other SNPs in LD with them, both of the functional variants and all of the markers in LD with them will do well in the models with individual markers. However, in the two locus models, once one of the functional variants is in the model the SNPs in LD with that variant will provide no additional information. Unless another SNP is in complete LD with one of the functional variants (r-square = 1), the models with the true functional variant will provide a better fit than the models with variants that are only in LD with the functional variant. This approach depends on having assayed all of the variants in a region that are present in the samples being analyzed, such that the functional variants are among the genotyped markers, as we will soon have given the growing access to high-throughput sequencing as a routine part of studies. It also depends on the LD between the functional variants and surrounding markers. The degree of LD that can be distinguished depends on the sample size and configuration, but it is not out of the question to be able to pick out a functional variant from markers with an r-squared of 0.95 with that variant.

Summary and conclusions

Variance component methods have a long history in quantitative human, animal, and plant genetics. They can be used to assess the strength of genetic effects on a phenotype of interest, to explore which phenotypes are influenced by the same genes, and to localize, identify, and characterize the genetic variants influencing a trait. They have been used in many successful studies of quantitative risk factors related to human disease (e.g. Comuzzie et al 1997; Curran et al 2005; Goring et al 2007; Mitchell et al 1996; Soria et al 2005).