Motor Learning Reduces Eye Movement Variability through Reweighting of Sensory Inputs

Abstract

Motor learning can improve both the accuracy and precision of motor performance. We analyzed changes in the average trajectory and the variability of smooth eye movements during motor learning in rhesus monkeys. Training with a compound visual–vestibular stimulus could reduce the variability of the eye movement responses without altering the average responses. This improvement of eye movement precision was achieved by shifting the reliance of the movements from a more variable, visual signaling pathway to a less variable, vestibular signaling pathway. Thus, cerebellum-dependent motor learning can improve the precision of movements by reweighting sensory inputs with different variability.

Introduction

The motor control achieved by the nervous system is remarkable in many ways, yet movements are not perfect and are prone to error. By studying repeated trials of a movement, two types of motor errors can be distinguished (Schmidt and Lee, 2005). Constant errors are systematic deviations of the mean movement trajectory, averaged across multiple trials, from the ideal trajectory. In addition, noise in sensorimotor signaling pathways causes movement trajectories to vary from trial to trial, creating variable errors (Faisal et al., 2008; Müller and Sternad, 2009). Thus, constant and variable errors reflect the accuracy and precision of movements, respectively.

Motor learning can reduce both types of errors (Logan, 1988; Segalowitz and Segalowitz, 1993; Gribble et al., 2003; Deutsch and Newell, 2004; Mosier et al., 2005; Ashby et al., 2007; Hung et al., 2008; Cohen and Sternad, 2009; Ranganathan and Newell, 2010). It is relatively easy to imagine how synaptic plasticity mechanisms such as long-term potentiation and long-term depression could adjust the average movement trajectory to reduce constant errors. It is less intuitive how such plasticity mechanisms could reduce the variability of movements, but recent theoretical and behavioral studies suggest that optimal utilization of sensory inputs with different amounts of uncertainty can reduce movement variability (Clark and Yuille, 1990; Rossetti et al., 1995; van Beers et al., 1999; Hillis et al., 2002; Todorov and Jordan, 2002; Sober and Sabes, 2003; Faisal and Wolpert, 2009).

Here, we analyzed the effects of motor learning on the constant and variable errors associated with smooth eye movements. Smooth eye movements can be elicited by visual inputs, vestibular inputs, or both. In primates, a visual target can drive smooth pursuit eye movements that track the visual stimulus (Lisberger, 2010). Vestibular stimuli elicit eye movements in the opposite direction from head movements, known as the vestibulo-ocular reflex (VOR) (Angelaki et al., 2008). Whether driven by visual or vestibular sensory input, the function of smooth eye movements is to stabilize visual images on the retina; therefore, retinal image motion represents a performance error.

Cerebellum-dependent learning can modify the smooth eye movement responses to visual and vestibular stimuli. Training with a moving visual stimulus can reduce retinal image motion by increasing the gain of the tracking eye movement responses (Collewijn et al., 1979; Nagao, 1988; Kahlon and Lisberger, 1996). Moreover, the pairing of visual and vestibular stimuli can induce a learned change in the average eye movement response to the vestibular stimulus (Boyden et al., 2004). This latter form of motor learning, known as VOR adaptation or VOR learning, is assessed by measuring the eye movement responses to vestibular stimuli presented in total darkness, to isolate the VOR from visually driven eye movements. However, when there is no image to stabilize on the retina, eye movement performance errors are ill-defined. Thus, in the present study, we assessed the functional significance of VOR learning by measuring its effect on the eye movement responses to the compound visual–vestibular stimuli used for training. Moreover, we extended previous studies of oculomotor learning by measuring the effect of learning on both the average trajectory and the variability of the smooth eye movement responses.

Materials and Methods

General procedures.

Experiments were conducted on two male rhesus monkeys (monkey E and monkey C) trained to perform a visual fixation task to obtain liquid reinforcement. Previously described surgical procedures were used to implant orthopedic plates for restraining the head (Lisberger et al., 1994; Raymond and Lisberger, 1996), a coil of wire in one eye for measuring eye position (Robinson, 1963), and a stereotaxically localized recording cylinder. During experiments, each monkey sat in a specially designed primate chair to which his implanted head holder was secured. Vestibular stimuli were delivered using a servo-controlled turntable (Ideal Aerosmith) that rotated the animal, the primate chair, and a set of magnetic coils (CNC Engineering) together about an earth-vertical axis. Visual stimuli were reflected off mirror galvanometers onto the back of a tangent screen 114 cm in front of the eyes. The animal was rewarded for tracking a small visual target subtending 0.5° of visual angle. A juice reward was delivered if the animal maintained gaze within a 2° × 2° window around the target for 1200–1800 ms. Where noted, a 20° × 30° visual background, consisting of a high-contrast black-and-white checkerboard pattern, was presented and moved exactly with the target. All surgical and behavioral procedures conformed to guidelines established by the U.S. Department of Health and Human Services (National Institutes of Health) Guide for the Care and Use of Laboratory Animals as approved by Stanford University.

Behavioral experiments.

Motor learning was induced by presenting compound visual–vestibular stimuli for 1 h. For low-frequency training, the vestibular component of the stimulus had a 0.5 Hz sinusoidal velocity profile with peak velocity of ±10°/s or, in some cases where noted, ±20°/s. For high-frequency training, the vestibular component of the stimulus had a 5 Hz sinusoidal velocity profile with peak velocity of ±10°/s. The visual–vestibular stimuli are described as ×G, where G is the eye velocity gain (relative to head movement) required to stabilize the visual stimulus on the retina. If the visual stimulus moved exactly with the head, the eye movement gain required to stabilize the image on the retina was zero, and so the visual–vestibular stimulus is described as ×0. If the visual stimulus moved at the same speed as the head but 180° out of phase, the eye movement gain required to stabilize the image on the retina was 2 (eye velocity equal to twice head velocity), and so the stimulus is described as ×2. Training and testing were done with ×0 or ×2 visual–vestibular stimuli, using coherent target and background motion as the visual stimulus. Testing was also done with ×G visual–vestibular stimuli (G = 0, 0.1 … 1.9, 2), with the visual motion stimulus provided by the target alone. In addition, VOR performance was tested before, after, and at 15 min intervals during training by delivering the vestibular stimulus in total darkness. Experiments were separated by at least 24 h to allow the eye movement gains to readapt to their normal value before the next experiment.

Data analysis.

Data analysis was performed in Matlab, Excel, and GraphPad Prism. Voltages related to the position and velocity of the eye, head, and visual stimulus were recorded during the experiment at 500 Hz/channel. Eye velocity traces were edited to remove the rapid deflections caused by saccades. For the eye movement responses to stimuli that included a visual stimulus, the analysis was limited to portions of the data in which gaze position was within 3° of the visual target position. For eye movement responses to the vestibular stimulus in the dark, the analysis was limited to portions of the data in which gaze position was within 15° of straight-ahead gaze. Eye and head velocity traces were subjected to a least-square fit of sinusoids. The gain of the eye movement response was calculated as the ratio of peak eye velocity to peak head velocity, derived from the fitted sinusoidal functions: F(t) = Asin(ωt + θ), ω = 2πf. Variability of the eye movements was quantified as the SD of the raw eye velocity trace from the sinusoidal fit of the average eye movement response.

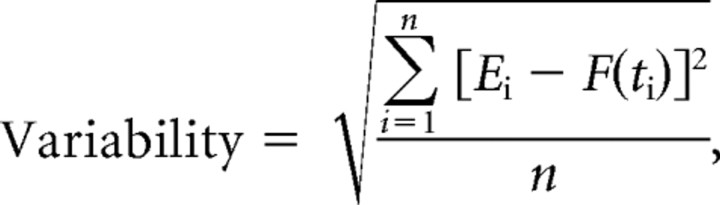where E_i is the eye velocity measured at the ith 2 ms sample of eye velocity (sampling rate 500 Hz).

A second, alternative method was used to quantify variability, with similar results. Eye movement responses to each cycle of a stimulus were aligned on head velocity. The variability of the eye movements was quantified as the SD of the raw eye velocity traces from the average eye velocity response.

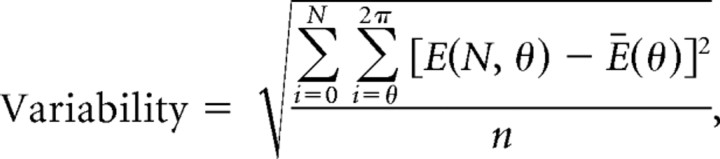where E(N, θ) is the measured eye velocity at phase θ of the stimulus, during the Nth stimulus cycle. Bin size for θ was determined by the resolution of the sampling rate (2π/500 Hz).

Model construction.

We modeled the variability of the eye movement responses to a range of visual–vestibular stimuli as the sum of the variability arising from the following four sources: visual (VAR_vis), vestibular (VAR_ves), motor (VAR_m), and constant (C).

Variability in the visual, vestibular, and motor pathways was assumed to be signal-dependent, i.e., proportional to the amplitude of the visually driven component of the eye velocity (E_vis), the vestibularly driven component of the eye velocity (E_ves), and the motor command for the total eye velocity (E_m). Constant variability (C) captured other, signal-independent sources of variability.

E_m was the measured eye movement amplitude. The vestibularly driven component of the eye movement (E_ves) was estimated as the gain of the eye movement response to the vestibular stimulus alone (VOR gain, 0.9 before learning) multiplied by the amplitude of the vestibular stimulus (10°/s or 20°/s). The visually driven component of the eye movement (E_vis) was estimated as the absolute value of the difference between the total eye movement (E_m) and the vestibularly driven component of the eye movement (E_ves).

To extract parameters k_vis, k_ves, and k_m, linear regression was applied to the eye movement data from compound visual–vestibular stimuli (Table 1). Independent estimates of k_vis + k_m and of k_ves + k_m (Table 1) were obtained from the eye movement responses to a series of visual stimuli alone (smooth pursuit) or a series of vestibular stimuli alone [VOR in the dark (VORD)], using the following equations:

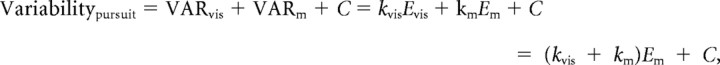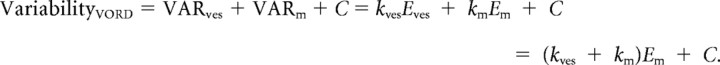Table 1.

Comparison of model parameters obtained from different experimental data sets

Fit coefficient	Compound visual–vestibular stimuli		Individual stimuli
	10°/s	20°/s	Visual	Vestibular
kvis	0.0193	0.0191
kves	0.0044	0.0044
km	0.0067	0.0070
kvis+ km	0.0260	0.0261	0.0282
kves+ km	0.0111	0.0114		0.0107

Values for the parameters k_vis, k_ves, and k_m obtained using linear regression on the eye movement data from compound visual–vestibular stimuli with peak head velocity of 10°/s or 20°/s and those obtained from the eye movement.

Results

We measured the eye movement responses to compound visual–vestibular stimuli and changes in the average trajectory and variability of these responses during a 60 min training period. The vestibular stimulus had a sinusoidal velocity profile, with a peak velocity of ±10°/s and a frequency of 0.5 Hz (except where noted). The visual stimulus either moved exactly with the head, so that an eye movement response with velocity of zero was required to stabilize the visual image on the retina (×0 stimulus), or the visual stimulus moved at the same speed as the head, but in the opposite direction, so that the eye movement required to stabilize the visual image would have twice the speed of the head movement (×2 stimulus) (Fig. 1). Eye movement responses were fit with a sinusoid and characterized by their gain (the ratio between eye velocity and head velocity) and their variability.

Figure 1.

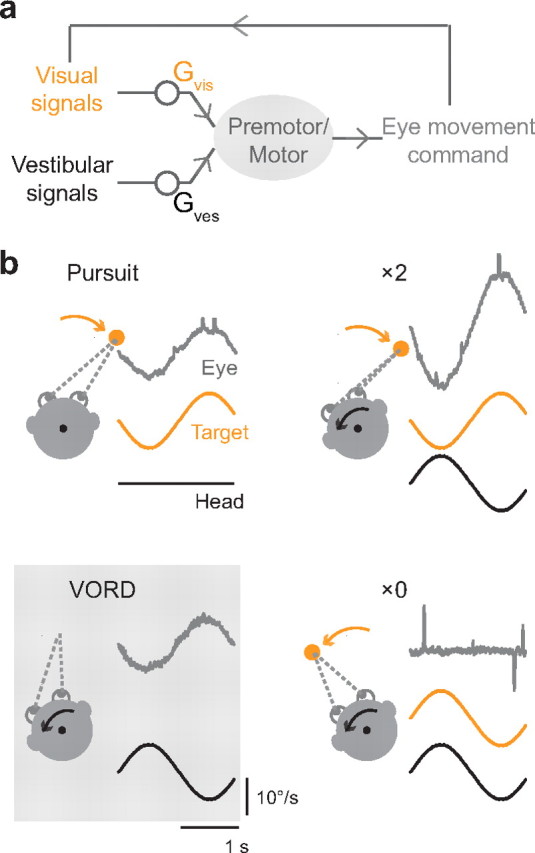
Control of smooth eye movements by visual and vestibular stimuli. a, Schematic of sensory-motor pathways controlling smooth eye movements. Both visual and vestibular signals can drive smooth eye movements. The eye movement output can influence the visual input. b, Representative eye velocity responses (gray traces) to a visual stimulus alone (pursuit, upper left), a vestibular stimulus alone in the dark (VORD, lower left), and compound visual–vestibular stimuli with the visual stimulus moving exactly opposite the head (×2, upper right) or with the head (×0, lower right). Orange and black arrows and traces represent the velocity of the visual stimulus (target) and vestibular stimulus (head), respectively.

Training did not improve movement accuracy

The visual component of the compound visual–vestibular stimulus had an immediate and substantial effect on the eye movement responses. Right from the start of training, the average eye movement responses to the ×2 stimulus and ×0 stimulus were different from each other and from the response to the vestibular stimulus alone (Fig. 2a). The gains of the eye movement responses to the ×2 and ×0 stimuli were close to the ideal values of 2 and 0, respectively (Fig. 2a). In other words, the eye movement responses were fairly accurate at the start of training.

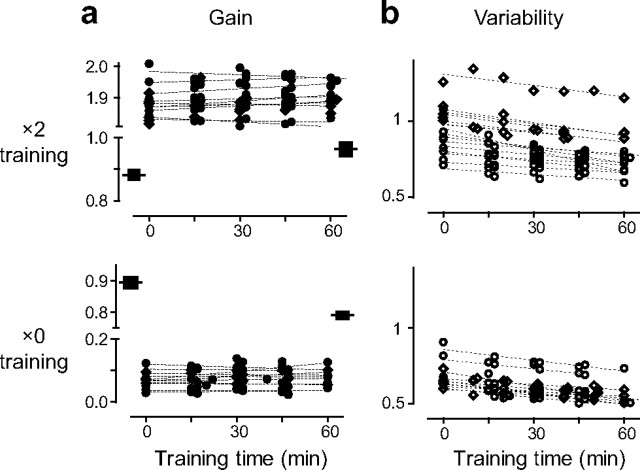
Figure 2.

Effect of training on the eye movement responses to low-frequency visual–vestibular stimuli. a, b, Gain (a) and variability (b) of eye movement responses to the 0.5 Hz visual–vestibular stimuli in monkey E (circles) and monkey C (diamonds) as a function of training time. Dashed lines are the linear fits of data points from an individual experimental session. The black boxes in a represent the mean and SEM of the eye movement responses to the vestibular stimulus alone (the VOR gain) pretraining and posttraining.

Training with the 0.5 Hz visual–vestibular stimuli did not yield any improvement in the accuracy of the eye movement responses (Fig. 2a). During 60 min of training, there was no significant change in the gain of the eye movement responses to the visual–vestibular stimuli (p > 0.5, paired t test) (Fig. 2a; supplemental Table, available at www.jneurosci.org as supplemental material). However, as reported previously, the eye movement responses to the vestibular stimulus alone were modified by the training. Training with the ×2 visual–vestibular stimulus induced a learned increase in the gain of the eye movement response to the vestibular stimulus alone (the VOR gain), and training with the ×0 visual–vestibular stimulus induced a learned decrease in the VOR gain (p < 0.001, paired t test) (Fig. 2a, black boxes). These learned changes in the VOR gain measured in the dark indicated that plasticity had indeed been induced in the neural circuitry controlling smooth eye movements. However, in the absence of a visual stimulus, eye movements have no benefit for visual acuity, raising the question of whether the plasticity induced by training with low-frequency visual–vestibular stimuli has any functional relevance. Therefore, we examined the effect of training on the variable errors associated with the eye movement responses to compound visual–vestibular stimuli.

Training reduced movement variability

Although training had no effect on the average eye movement gain, the variability of the eye movement responses was significantly reduced during training. The variability of the eye movements was measured by calculating the root mean square deviation of the raw eye velocity trace, after removal of saccadic eye movements, from the sinusoidal fit to the average eye movement response. Similar results were obtained when variability was quantified as the SD of the eye velocity response across stimulus cycles (see Materials and Methods) (supplemental Fig. 1, available at www.jneurosci.org as supplemental material).

The variability of the eye movement responses was significantly reduced during training with the 0.5 Hz visual–vestibular stimuli (p < 0.001, paired t test) (Fig. 2b; supplemental Table, available at www.jneurosci.org as supplemental material). In all of the training sessions with the ×2 stimulus (10 in monkey E and 7 in monkey C), eye movement variability decreased (Fig. 2b, top). Likewise, in all of the training sessions with the ×0 visual–vestibular stimulus (7 in monkey E and 5 in monkey C), variability decreased (Fig. 2b, bottom). Thus, training with 0.5 Hz visual–vestibular stimuli could reduce variable errors in the eye movement responses without affecting the constant errors.

Higher variability of visually driven eye movements

The eye movement responses to the visual–vestibular training stimuli had both vestibularly driven and visually driven components. Therefore, the reduction in variability during training could, in principle, result from a reduction in the variability of visually driven eye movements or vestibularly driven eye movements. However, training had no effect on the variability of the eye movement responses to the vestibular stimulus alone (p > 0.30, paired t test) (Fig. 3a) or the variability of the eye movement response to the visual stimulus alone (p > 0.28, paired t test) (Fig. 3b). Therefore, the reduced variability of the eye movement responses to the visual–vestibular training stimuli could not be accounted for by a reduction in the variability within the vestibular signaling pathway, the visual pathway, or the shared motor pathway (Fig. 1a). Rather, it seems to result from a change in the relative reliance of the eye movement responses on the visual versus vestibular pathways.

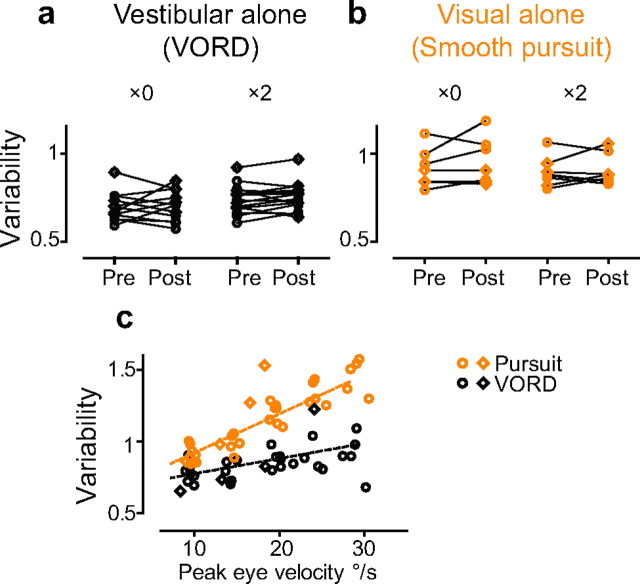
Figure 3.

Variability of eye movement responses to vestibular and visual stimuli. a, b, Variability of eye movement responses to a vestibular stimulus alone (a, 0.5 Hz, 10°/s) and a visual stimulus alone (b, 0.5 Hz, 10°/s) before (Pre) and after (Post) training with a ×0 or ×2 visual–vestibular stimulus. c, Variability of eye movement responses to vestibular (black) or visual (orange) stimuli with a range of peak velocities, plotted as a function of the peak eye velocity elicited, measured in monkey E (circles) and monkey C (diamonds) in the absence of visual–vestibular training.

Visually driven eye movements were more variable than vestibularly driven eye movements. We compared the eye movement responses to a series of 0.5 Hz, sinusoidally moving visual targets, with different peak velocities from 10 to 30°/s, and to a series of vestibular stimuli with the same motion profiles (Fig. 3c). Regardless of the sensory modality controlling the eye movement, the variability increased with the amplitude of the eye movements (Fitts, 1992; Harris and Wolpert, 1998). In addition, eye movements of similar amplitude were significantly more variable when driven by a visual stimulus than a vestibular stimulus (p < 0.0001, ANOVA) (Fig. 3c). Thus, a change in relative reliance on these two sensory inputs could produce the observed change in the variability of the eye movement responses during training. More specifically, a reduced reliance on the more variable, visual signaling pathway could reduce the overall variability of the eye movement responses to the compound visual–vestibular stimuli.

Model of eye movement variability

A simple model that incorporated four sources of variability was used to describe the observed variability of the eye movements. The variability of the smooth eye movements was modeled as the sum of the variability in a visual pathway, a vestibular pathway, and a shared motor pathway, plus a constant variability (see Materials and Methods for details) (Fig. 4).

Figure 4.

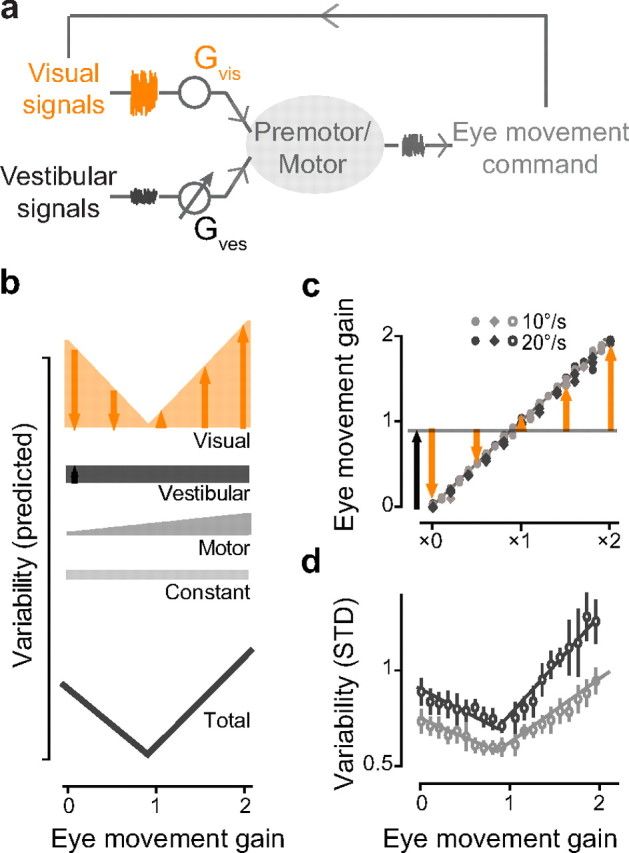
Model of multiple sources of eye movement variability. a, Schematic of sensory-motor pathways controlling smooth eye movements, indicating the gain and noise associated with each pathway. b, Predicted variability of eye movement responses to visual–vestibular stimuli that elicit eye movement responses of different gains. The total variability of an eye movement response is modeled as the sum of the variability in the visual pathway (orange), in the vestibular pathway (black), and in the shared motor pathway (dark gray), plus a constant variability (light gray). c, Gain of the eye movement responses to a range of visual–vestibular stimuli (from ×0 to ×2), with peak velocity of the vestibular stimulus 10°/s (light gray) or 20°/s (dark gray) in monkey E (circles) and monkey C (diamonds). Black and orange arrows represent the estimated amplitude of vestibularly driven and visually driven components of the eye movement responses, respectively. d, Measured variability of the eye movement responses shown in c. Eye movement responses were binned according to their gain (bin size = 0.1), and the mean and SEM of variability were plotted for each bin. Solid lines are the fits to the model described in text.

E_vis and E_ves represent the amplitudes of the visually driven and vestibularly driven components of the eye movement responses, respectively. E_m represents the motor command for the net eye movement. k_vis, k_ves, and k_m are coefficients reflecting the variability of the corresponding eye movements. C reflects any constant sources of variability.

Since visually driven eye movements had higher variability than vestibularly driven eye movements (Fig. 3c), one would expect the total variability of the eye movements to be higher when reliance on the visual input is greater, and lower when reliance on the visual input is less. During compound visual–vestibular stimuli, reliance on the visual signal should be minimal when the eye movement gain required to stabilize the visual stimulus is equal to the gain of the eye movement response to the vestibular stimulus alone (the VOR gain). Reliance on the visual signal should increase as the eye movement response to the compound visual–vestibular stimulus deviates from the VOR gain. Before training, the VOR gain was ∼0.9, hence reliance on visual signals and variability should be lowest for visual–vestibular stimuli that elicit eye movements with a gain close to 0.9, and progressively larger for visual–vestibular stimuli that elicit larger or smaller eye movement gains (Fig. 4b, orange). Variability from the vestibular pathway is assumed to be constant across all visual–vestibular stimuli with the same vestibular stimulus (Fig. 4b, black). As suggested by the data in Figure 3c, variability from the shared motor pathway (Fig. 4b, gray) is assumed to be proportional to the total eye velocity. When these three sources of variability are summed, the curve relating predicted variability to the gain of the eye movement response to a visual–vestibular stimulus has an asymmetric V shape, with a steeper slope for eye movement gains above the VOR gain (0.9) than below (Fig. 4b, bottom).

We tested this prediction by measuring the variability of eye movement responses to visual–vestibular stimuli that elicited eye movement responses with a range of gains (Fig. 4c). The eye movement responses were assessed for two series of 0.5 Hz sinusoidal visual–vestibular stimuli, with peak velocity of the vestibular stimulus of 10 °/s or 20 °/s. As predicted by the model in Figure 4a,b, the measured variability was well described by an asymmetric V-shaped curve (R² > 0.8) (Fig. 4d). Eye movement variability was minimal when the gain of the eye movement response to the compound visual–vestibular stimulus was close to the VOR gain (∼0.9). Furthermore, it increased linearly as the gain of the eye movement response deviated from the VOR gain, with a steeper slope for eye movement gains above than below this value.

The simple model described by Variability = k_visE_vis + k_vesE_ves + k_mE_m + C could account quantitatively as well as qualitatively for the variability of eye movements elicited by the range of visual–vestibular stimuli tested. Values for the parameters k_vis, k_ves, and k_m obtained using linear regression on the eye movement data from compound visual–vestibular stimuli with peak head velocity of 10°/s were remarkably similar to the values obtained with a peak head velocity of 20°/s (Table 1). Moreover, the fits for k_vis, k_ves, and k_m obtained from the compound visual–vestibular stimuli (Table 1; Fig. 4c,d) were consistent with those obtained from the eye movement responses to visual or vestibular stimuli presented alone (see Materials and Methods for details) (Table 1; Fig. 3c).

Furthermore, this model can account for the effects of motor learning on eye movement variability. During ×0 training, the VOR gain decreased (Fig. 2a, black boxes), which shifts the V-shaped curve describing total eye movement variability leftwards (Fig. 5, cyan trace), reflecting less reliance on the visual input during visual–vestibular stimuli that elicit low eye movement gains, such as ×0 stimuli, and hence lower variability for those stimuli (p < 0.0001, paired t test) (Fig. 5ii). On the other hand, during ×2 training, the VOR gain increased (Fig. 2a, black boxes), shifting the V-shaped curve describing eye movement variability rightwards (Fig. 5, red trace), reflecting less reliance on the visual signals during visual–vestibular stimuli that elicit high eye movement gains, such as ×2 stimuli, and hence lower variability for those stimuli (p < 0.0001, paired t test) (Fig. 5iv).

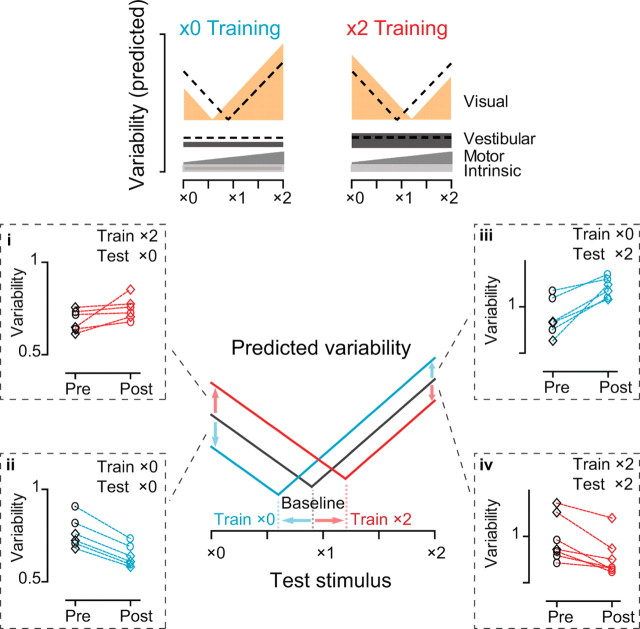
Figure 5.

Effect of training on the variability of eye movement responses to a range of 0.5 Hz visual–vestibular stimuli. Top, Predicted effect of ×0 training (left) and ×2 training (right) on the different sources of eye movement variability for a range of visual–vestibular stimuli (×0 to ×2). Dashed lines represent the baseline, pretraining variability. The lowest point of each curve reflects the VOR gain. Bottom, Predicted (center) and measured (dashed boxes) variability of eye movements pretraining (black), post-×0 training (cyan) and post-×2 training (red). The training and testing stimuli are indicted in the upper right corner of each dashed box.

The model predicts that the reduced variability of the eye movement responses to the visual–vestibular stimulus used for training would come at the expense of increased variability of the eye movement responses to other visual–vestibular stimuli. For example, the model predicts that after ×0 training, variability of the eye movement responses to a ×2 stimulus would increase, since the low gain of the eye movement response to the vestibular stimulus would render high-gain eye movements more dependent on the more variable, visual signals (Fig. 5, cyan curve). As predicted, when the eye movement responses to ×2 stimuli were measured after ×0 training, the variability increased (p < 0.01, paired t test) (Fig. 5iii), even though there was no significant change in the gain of the eye movement response to the ×2 stimulus (p > 0.3, paired t test) (supplemental Fig. 2, available at www.jneurosci.org as supplemental material). Likewise, ×2 training increased the variability of the eye movement responses to a ×0 stimulus (p < 0.05, paired t test) (Fig. 5i) without affecting their average gain (p > 0.6) (supplemental Fig. 2, available at www.jneurosci.org as supplemental material), as one would predict if ×2 training shifted the V-shaped curve describing eye movement variability to the right, rendering low-gain eye movements more dependent on the visual stimulus (Fig. 5, red curve).

High-frequency training improved movement accuracy but not variability

The stimulus frequency used above (0.5 Hz) is well within the dynamic range of both visually and vestibularly driven eye movements. We also tested the effects of motor learning using a stimulus frequency above the effective range for visually driven eye movements. Visual stimuli are not very effective at driving eye movements at frequencies above ∼1 Hz, whereas vestibular stimuli can reliably drive eye movements at stimulus frequencies up to well above 10 Hz (Fuchs, 1967; Jäger and Henn, 1981; Boyle et al., 1985; Ramachandran and Lisberger, 2005). We tested the effects of training on the eye movement responses to 5 Hz visual–vestibular stimuli.

The 5 Hz visual–vestibular stimuli drove robust eye movement responses, which seemed to be controlled almost entirely by the vestibular stimulus, with little effect of the visual stimulus apparent at the beginning of training. At the start of training, the gain (Fig. 6a) and phase (supplemental Fig. 3b, available at www.jneurosci.org as supplemental material) of the eye movement responses to both the ×2 and ×0 high-frequency visual–vestibular stimuli were similar to the eye movement responses to the same vestibular stimulus delivered in the dark. Thus, the high-frequency visual stimulus had little immediate influence on eye movement performance. Consequently, the average eye movement trajectory deviated substantially from the ideal trajectory required to stabilize the visual image on the retina during the ×2 and ×0 stimuli. The gain measured at the start of training was ∼0.9 during both the ×2 and ×0 high-frequency visual–vestibular stimuli, whereas the ideal eye movement gain was 2 for the ×2 stimulus, and 0 for the ×0 stimulus.

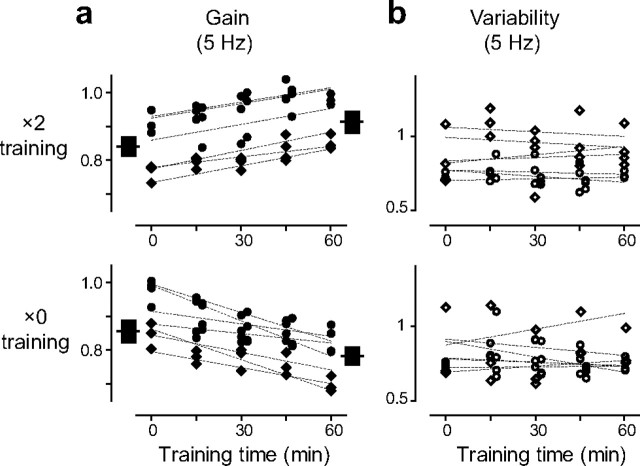
Figure 6.

Effect of training on the eye movement responses to high-frequency visual–vestibular stimuli. a, b, Gain (a) and variability (b) of eye movement responses during training with 5 Hz visual–vestibular stimuli in monkey E (circles) and monkey C (diamonds). Dashed lines are the linear fits of data points from an individual experimental session. The black boxes in a represent the mean and SEM of the eye movement responses to the vestibular stimulus alone (the VOR gain) pretraining and posttraining.

Despite the ineffectiveness of the visual stimuli to influence the ongoing eye movements, over a longer period, the visual stimuli did influence the eye movement responses to the high-frequency visual–vestibular stimuli. During 60 min of training with the 5 Hz visual–vestibular stimuli, significant learned changes in the average gain of the eye movement responses were induced (Fig. 6; supplemental Table, available at www.jneurosci.org as supplemental material). The direction of these changes depended on the motion of the visual stimulus: the gain of the eye movement response to the ×2 stimulus gradually increased during training toward the ideal value of 2, and the gain of the eye movement response to the ×0 stimulus gradually decreased toward the ideal value of 0 (p < 0.001, paired t test) (Fig. 6a). These changes in the responses to the visual–vestibular stimuli paralleled the learned changes in the VOR gain measured in the dark (p > 0.16, paired t test) (Fig. 6a, black boxes). Thus, high-frequency training can improve the accuracy of the eye movement responses to the visual–vestibular training stimuli. On the other hand, there was no significant change in the variability of the eye movement responses during high-frequency training (p < 0.19, paired t test) (Fig. 6b).

Thus, the effects of training were dramatically different for low- versus high-frequency stimuli. Training with low-frequency visual–vestibular stimuli reduced the variability of the eye movements without altering the average eye movement response. Training with high-frequency stimuli altered the average eye movement trajectory, with no significant effect on the variability of the eye movements.

Discussion

Our results suggest that a function of motor learning is to optimize the weighting of sensory pathways with different variability to improve the precision of movements. Training with visual–vestibular stimuli recruits plasticity mechanisms in the oculomotor circuit that shift the reliance of eye movements onto vestibular signals rather than visual signals. Since the vestibular signaling pathway is less noisy than the visual pathway, motor learning achieves a more optimal combination of the two sensory inputs controlling eye movements, which reduces the variability of motor performance.

A previous analysis of visually driven smooth pursuit eye movements suggested that most of the movement variability arose from noise in the visual signal processing pathways, and not from noise in the motor system itself (Osborne et al., 2005). Consistent with this, we found that eye movement responses with similar average trajectories were less variable when controlled by vestibular rather than visual stimuli. Several factors may contribute to the noisiness of the visual pathway controlling eye movements. Visually driven eye movements are under closed-loop control, whereas the control of eye movements by vestibular input is open-loop (Fig. 1a). In addition, visual motion signals are processed through multiple synapses in subcortical and cortical pathways before impinging on the oculomotor circuitry (Mustari et al., 2009; Lisberger, 2010). In contrast, vestibular primary and secondary afferents synapse directly on premotor neurons in the vestibular nuclei (Angelaki et al., 2008).

Although visual and vestibular sensory inputs can both drive smooth eye movements, they operate over different, yet overlapping dynamic ranges. Visual inputs fail to control eye movements effectively at frequencies above ∼1 Hz (Fuchs, 1967; Boyle et al., 1985), whereas vestibular inputs drive robust eye movements at frequencies >10 Hz (Ramachandran and Lisberger, 2005). Therefore, a properly calibrated VOR gain is critical for the accuracy of high-frequency eye movements, as measured by their ability to stabilize images on the retina during compound visual–vestibular stimuli (Fig. 6). At lower frequencies, when vision adequately controls eye movements, the role of the VOR has been less clear. In particular, since there is no change in the average trajectory of eye movement responses to low-frequency visual–vestibular stimuli (Fig. 2a), it was not apparent whether VOR learning had any functional relevance in that frequency range. The present results resolve this puzzle by demonstrating that VOR learning reduces the variability of eye movement responses to the compound visual–vestibular stimuli used for training.

During low-frequency visual–vestibular stimuli, visually driven eye movements can compensate for an improperly calibrated VOR; hence the constant errors were small, even from the start of training. However, the reliance on visual signals makes the eye movements variable; hence as the VOR gain approaches the ideal during training, the reliance on visual signals is reduced and the variability decreases. Thus, motor learning reduced the variability of smooth eye movements by increasing reliance on the less noisy, vestibular signaling pathway and decreasing reliance on the noisier, visual signaling pathway. This reweighting of sensory inputs with different variability appears to be the sole mechanism for the reduced variability of the eye movements, since there was no change in the variability of eye movements driven by the visual or vestibular stimulus alone after low- or high-frequency training (Fig. 3; supplemental Fig. 4, available at www.jneurosci.org as supplemental material).

The reduced variability of the eye movement responses to the training stimulus came at the expense of increased variability of the responses to certain other visual–vestibular stimuli. In other words, the prior expectation for the appropriate eye movement gain, which is acquired during training and embodied in the VOR gain, reduces the variability of the responses to the training stimulus but can increase the variability of the eye movement responses to other, less probable visual–vestibular stimuli. This variance–variance tradeoff is reminiscent of the variance-bias tradeoff, which is a hallmark of Bayesian estimation (Körding and Wolpert, 2004; T. Verstynen, P. N. Sabes, unpublished observations).

Previous studies of many motor learning tasks have reported parallel changes in the average trajectory and variability of movements during learning, which yielded parallel reductions in constant and variable errors (Logan, 1988; Segalowitz and Segalowitz, 1993; Gribble et al., 2003; Deutsch and Newell, 2004; Mosier et al., 2005; Ashby et al., 2007; Hung et al., 2008; Cohen and Sternad, 2009; Ranganathan and Newell, 2010). Here, we report that learning can reduce constant or variable errors in eye movement performance separately, depending on the exact testing conditions. Whereas training altered the variability but not the gain of the eye movement responses to low-frequency visual–vestibular stimuli, it altered the gain but not the variability of the eye movement responses to the high-frequency stimuli. At 5 Hz, smooth eye movements are almost completely reliant on the vestibular input before and after learning. Therefore, learning does not alter the relative reliance on vestibular versus visual inputs, and hence there is no reduction in variability during learning.

The different effects of high- versus low-frequency training on oculomotor performance can be explained by the same underlying mechanism, namely, a change in synaptic weights in the neural circuitry controlling the VOR gain. This same circuit-level change could influence the average trajectory or variability of the eye movement responses, depending on the operating state of the broader oculomotor circuit, in particular, the recruitment of the visual pathway. Notably, electrophysiology or imaging studies during motor performance might detect different neural correlates of learning, associated with the recruitment of the apparently unmodified visual pathway, despite similar plasticity in the vestibular pathway during high- versus low-frequency training. Thus, the finding of different neural correlates of learning need not indicate different neural plasticity mechanisms.

Thus, our results suggest that a function of cerebellum-dependent learning is to improve movement precision by optimizing the weighting of sensory pathways with different variability. Many previous studies have reported changes in the average movement trajectory during motor learning, which improve movement accuracy. Recently, theoretical and behavioral studies have highlighted the variability of movements as another critical parameter of motor performance (Körding and Wolpert, 2006; Faisal et al., 2008). Since movements are often guided by multiple sensory inputs with different uncertainty or variability, it has been suggested that optimal utilization of sensory inputs can minimize the effects of noise on the movement (Clark and Yuille, 1990; Rossetti et al., 1995; van Beers et al., 1999; Hillis et al., 2002; Todorov and Jordan, 2002; Sober and Sabes, 2003; Faisal and Wolpert, 2009). Our results from the oculomotor system support this idea. We found that learning can reduce the variability of smooth eye movement performance. This reduction in variability is achieved by increasing reliance on a less variable, vestibular signaling pathway and decreasing reliance on a more variable, visual signaling pathway. The mechanism for this reweighting of sensory inputs is a well studied form of cerebellum-dependent learning, namely VOR learning.