Optimizing magnetite nanoparticles for mass sensitivity in magnetic particle imaging

Abstract

Purpose: Magnetic particle imaging (MPI), using magnetite nanoparticles (MNPs) as tracer material, shows great promise as a platform for fast tomographic imaging. To date, the magnetic properties of MNPs used in imaging have not been optimized. As nanoparticle magnetism shows strong size dependence, the authors explore how varying MNP size impacts imaging performance in order to determine optimal MNP characteristics for MPI at any driving field frequency f₀.

Methods: Monodisperse MNPs of varying size were synthesized and their magnetic properties characterized. Their MPI response was measured experimentally using a custom-built MPI transceiver designed to detect the third harmonic of MNP magnetization. The driving field amplitude H₀=6 mT μ₀⁻¹ and frequency f₀=250 kHz were chosen to be suitable for imaging small animals. Experimental results were interpreted using a model of dynamic MNP magnetization that is based on the Langevin theory of superparamagnetism and accounts for sample size distribution and size-dependent magnetic relaxation.

Results: The experimental results show a clear variation in the MPI signal intensity as a function of MNP diameter that is in agreement with simulated results. A maximum in the plot of MPI signal vs MNP size indicates there is a particular size that is optimal for the chosen f₀.

Conclusions: The authors observed that MNPs 15 nm in diameter generate maximum signal amplitude in MPI experiments at 250 kHz. The authors expect the physical basis for this result, the change in magnetic relaxation with MNP size, will impact MPI under other experimental conditions.

INTRODUCTION

Magnetic nanoparticles (MNPs) are attractive agents for biomedicine due to strong intrinsic magnetism that, through interaction with a magnetic field, enables their detection or influence from deep within a living subject. Rightly, MNPs have been studied extensively as potential contrast agents or tracer materials in molecular imaging applications based on magnetic resonance imaging (MRI), as well as carriers for magnetically assisted drug delivery^{1, 2, 3} and hyperthermia.⁴ Recently, a new imaging modality called magnetic particle imaging (MPI) was introduced as a technique for visualizing MNPs in humans and animals. MPI is fast, quantitative, sensitive, and features good spatial resolution, a combination that is difficult to realize in MR imaging of MNPs, because MPI directly probes the large MNP moment rather than its indirect effect on proton relaxation, as does MR imaging. Noteworthy recent MPI studies include in vivo, real-time imaging of MNPs passing through a beating mouse heart⁵ and compact, single-sided scanners that can image a patient without first inserting them into a costly and potentially claustrophobic magnetic device.⁶

Despite much exciting progress in MPI scanner design and related image processing,⁷ relatively little effort has been spent developing MNPs that optimize imaging sensitivity. In fact, for MPI to successfully move beyond proof-of-principle experiments into the clinic or preclinical research laboratory, it will be critical to engineer MNP tracers that are optimized for MPI. Most recent studies have used commercially available MNP agents, including Resovist^® (Bayer Schering Pharma, Berlin) and Feridex I.V.^® (AMAG Pharmaceuticals, Lexington, MA; trade name Endorem^™ in Europe); these are far from being magnetically optimized for MPI and thus inhibit MPI from reaching its full potential in terms of both spatial resolution and mass sensitivity. For example, in Resovist^®, which to date has been the most popular material for MPI studies, it has been shown that only 3% of the total sample mass contributes noticeably to the MPI signal.⁸ More efficient tracers are highly desirable for molecular imaging applications that depend on active targeting, where for the highest sensitivity, each unit of tracer must generate the maximum achievable MPI signal voltage. Furthermore, for quantitative imaging, the signal intensity, and therefore MNP properties, must be uniform and reproducible. For the pioneering MPI scheme developed by Gleich et al.,⁸ signal is generated by harmonics in superparamagnetic nanoparticle magnetization and the critical metric for efficiency is harmonic amplitude per unit particle mass.

With recent advances in techniques for chemical MNP synthesis and phase transfer, it is possible to control final particle size and shape to produce highly uniform MNPs^{9, 10, 11, 12, 13, 14, 15} that are stable in water, biocompatible, and not toxic,^{16, 17} as required for any in vivo biomedical application. In this paper, we show that the MPI’s mass sensitivity can be maximized by engineering biocompatible MNPs with optimum physical diameter. Our experimental results are explained using a model of MNP magnetization based on the Langevin theory of superparamagnetism, which provides a basis for synthesizing optimal materials with signal efficiency that exceeds, considerably, that of available commercial options.

METHODS

Langevin model of nanoparticle magnetization

Here we adapt a model of dynamic MNP magnetization developed in a previous work for MPI at 50 kHz.¹⁸ Our model describes how a system of MNPs, with a distribution of diameters, will respond to an ac magnetic field to generate harmonics and therefore a MPI signal. We model MNP susceptibility χ using the complex convention¹⁹ first developed to describe the permittivity of polar dielectrics in solution by Debye, such that

$$\chi ={\chi }^{\prime }-i{\chi }^{″}=\frac{{\chi }_0}{1+{\left(\omega \tau \right)}^2}-i\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}{\chi }_0,$$ (1)

where ω is the angular frequency of the applied magnetic field, τ is the time required for the MNP magnetic moment to reverse its direction, and χ₀ is the equilibrium susceptibility. For this approximation to be strictly valid, relaxation should be rotational and domain processes excluded and all particles should have identical size and shape.^{20, 21} Thus, for a driving field of the form

$$H\left(t\right)=H_0\text{\hspace{0.17em}cos}\omega t=\text{Re}\left[H_0{e}^{i\omega t}\right],$$ (2)

the MNP magnetization is

$$M\left(t\right)=\text{Re}\left[\chi H_0{e}^{i\omega t}\right]=H_0\left({\chi }^{\prime }\text{\hspace{0.17em}cos}\omega t+{\chi }^{″}\text{\hspace{0.17em}sin}\omega t\right)$$ (3)

and M(t) contains both in-phase and out-of-phase terms due to the complex form of Eq. 1. The nonlinear equilibrium susceptibility χ₀ of superparamagnetic MNPs can be described by the Langevin function L, such that²²

$${\chi }_0=\frac{M\left(H_0\right)}{H_0}=\frac{M_s}{H_0}\mathcal{L}\left(\alpha \right),$$ (4)

where

$$\alpha =\frac{{\mu }_0{H}_0{M}_s\pi d^3}{6k_{b}T},$$

μ₀ is 4π×10⁻⁷ (Henry m⁻¹), H₀ is the equilibrium magnetic field strength in T μ₀⁻¹, k_b is the Boltzmann constant, 1.38×10⁻²³ (JK⁻¹), T is the temperature in Kelvin, and we have expressed the magnetic moment of each particle in terms of the diameter d of its magnetic volume and volume saturation magnetization M_s in kA m⁻¹ (446 for bulk magnetite).

MNP susceptibility depends on the effective relaxation time τ for the MNP moment to reverse in an alternating magnetic field

$$\tau ={\tau }_B{\tau }_N∕\left({\tau }_B+{\tau }_N\right),$$ (5)

which includes two distinct relaxation processes, each with a characteristic time. The Neél relaxation time τ_N describes the magnetic reversal of an “unblocked” volume

$${\tau }_N=\frac{\sqrt{\pi }}{2}{\tau }_0\frac{\text{exp}\left[K\rho \right]}{{\left(K\rho \right)}^{1∕2}},$$ (6)

where K (Jm⁻³) is the magnetocrystalline anisotropy constant, a material property

$$\rho =\frac{\pi d^3}{6k_{b}T},$$

and the attempt time τ₀ is ∼10⁻¹⁰ s.²³ Typically, τ_N dominates in small particles. The Brownian relaxation time, τ_B describes the physical rotation of a “blocked” magnetic volume

$${\tau }_B=\frac{3\eta \pi d_H^3}{6k_{b}T},$$ (7)

where d_H is the MNP hydrodynamic diameter and η (Pa s) is the viscosity of the suspending fluid (0.89 for water). τ_B typically dominates in larger particles.

Finally, we can modify Eq. 3 to describe the magnetization M(t) of MNPs having a distribution of diameters g(d) in an alternating field of the form given in Eq. 2, such that

$$M\left(t\right)=M_s{\int }_0^{\infty }\left(\frac{1}{1+{\left(\omega \tau \right)}^2}\mathcal{L}\left(\alpha \text{\hspace{0.17em}cos}\omega t\right)+\frac{\omega \tau }{1+{\left(\omega \tau \right)}^2}\mathcal{L}\left(\alpha \text{\hspace{0.17em}sin}\omega t\right)\right)g\left(d\right)dd.$$ (8)

The diameter distribution g(d) can be approximated by a log-normal distribution function²⁴

$$g\left(d\right)=\frac{1}{\sigma d\sqrt{2\pi }}\text{exp}\frac{-\text{ln}{\left(d∕d_0\right)}^2}{2{\sigma }^2},$$ (9)

where exp(σ) is the geometric standard deviation of the distribution and d₀ is the median diameter.

Magnetite MNP synthesis

For this work, magnetite MNPs were synthesized by the pyrolysis of iron (III) oleate in 1-octadecene (technical grade, 90%, Aldrich).^{25, 26} Iron (III) oleate was formed in a separate reaction, prior to nanoparticle formation, by dissolving 10 mmol of iron (III) chloride (anhydrous, Aldrich) in 50 ml methanol along with 30 mmol of oleic acid (technical grade, 90%, Aldrich). To this mixture was added, dropwise, 30 mmol of sodium hydroxide dissolved in 100 ml of methanol. The resulting waxy precipitate was washed five times with methanol, dried, dispersed in hexane, and washed five times with water in a separatory funnel. Finally, the product is dried again for storage and later use.

In a typical reaction, to produce 15 nm magnetite nanoparticles, 12 mmol of oleic acid (technical grade, 90% Aldrich, St. Louis, MO) was added to 0.5 mmol of the iron (III) oleate complex dissolved in 2.5 g of 1-octadecene. After purging under argon for 30 min, the mixture was heated, also under argon atmosphere, and refluxed for 24 h. Finally, the reaction mixture was cooled to room temperature and the nanoparticles were collected and washed thoroughly in a 1:1 mixture of chloroform and methanol.

Phase transfer

We chose to use a synthetic route based on organic solvents and surfactants because it leads to highly crystalline MNPs with narrow size distributions (typical σ of 0.1, corresponding to a 95% confidence interval of ±∼2 nm) and controllable size. However, since organic solvents are not suitable for use in biological imaging, the as-synthesized MNPs must be transferred to the water phase.²⁷ To ensure biocompatibility, organic residue must be removed and the final MNPs must be stable and not cytotoxic. General guidelines for determining iron oxide MNP toxicity are well-established²⁸ and we have previously studied the toxicity of iron oxide MNPs made in our laboratory by similar methods.^{16, 17} Here we use the amphiphilic polymer poly(maleic anhydride-alt-1-octadecene)-poly(ethylene glycol) (PMAO-PEG) to affect phase transfer and dissolve the final MNPs in 1× phosphate buffered saline solution for testing. Details of the phase transfer as well as cytotoxicity and viability studies for MNPs made by the present method will be published elsewhere.¹⁷

Magnetite MNP characterization

As-synthesized samples were dispersed on carbon TEM grids by a controlled evaporation of the solvent. Bright field images (Fig. 1) were then obtained using a FEI Tecnai TEM (Hillsboro, OR) equipped with a Gatan CCD camera (Pleasanton, CA), operating at 200 KeV.

Figure 1.

Bright field TEM image of as-synthesized magnetite nanoparticles.

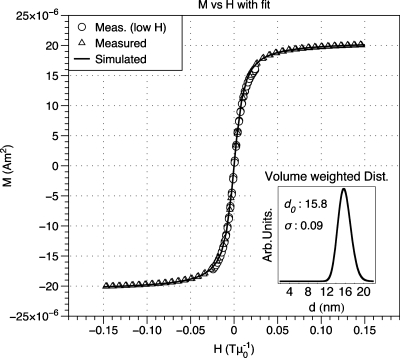
Following phase transfer to aqueous solution, iron concentration was measured with an inductively coupled plasma-atomic emission spectrophotometer (Jarrel Ash 955). The iron concentration in synthesized samples ranged from 0.5 to 3.6 mgFe ml⁻¹. Magnetization vs field data M(H) was acquired with a LakeShore (Weterville, OH) vibrating sample magnetometer at room temperature. Sample UW170_16 showed a slight open loop at room temperature and for this sample, M(H) data were acquired above the blocking temperature at 575 K using a Quantum Design (San Diego, CA) PPMS VSM oven. Saturation magnetization M_s (kA m⁻¹) was determined from M(H) data and the measured sample concentration by assuming density equal to stoichiometric magnetite (5180 kg m⁻³). The median diameter and diameter distribution of each sample were determined from M(H) data according to the Chantrell method (Fig. 2).²⁴

Figure 2.

Example of Chantrell fitting. Simulated data that were reconstructed from fit parameters are overlaid on measured data. Inset: Volume-weighted diameter distribution and fit parameters.

MPI signal testing

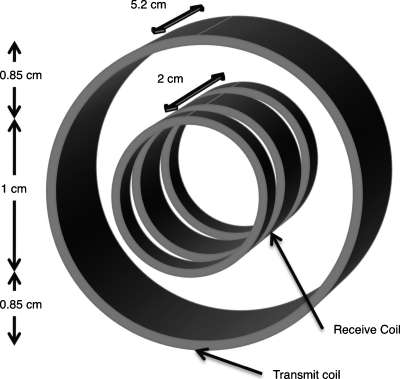
MPI signal was measured using a custom-built narrow-band transceiver designed to detect the third harmonic of MNP magnetization.²⁹ Figure 3 shows a schematic diagram of transmit and receive coil arrangement in the MPI transceiver. During transceiver operation, an air-cooled, wire-wound solenoid transmit coil excites sample harmonics that are then detected by a receiver coil. The transmit coil consists of 94 turns of 550 μm diameter copper wire and has a diameter and a length of 2.71 and 5.2 cm, respectively. The receiver coil is positioned inside the transmit coil and contains 140 total turns of 114 μm diameter copper wire. The receiver coil is designed to inductively isolate receive and transmit channels. It features three coaxial solenoids connected in series: Two outer coils each with 35 counterwound turns are positioned on either side of a central solenoid with 70 turns. The entire receiver coil has a diameter of 1 cm and a total length of 2 cm, with 3 mm spacing between the central and outer windings. During operation, the outer windings inductively decouple the receiver from the transmitter to reduce the level of harmonic noise that is detected. Additional use of radio-frequency (RF) traps and capacitive decoupling increases electrical isolation between the transmitter and receiver to well over 120 dB. For this study, the transmit coil was driven at 250 kHz by a commercial RF amplifier (Hotek Technologies, Tacoma, WA, Model AG1017L). To narrow receiver bandwidth and provide optimal power transfer for harmonic detection, the receiver coil is tuned and matched to 50 Ω at 750 kHz. Induced harmonics are also amplified using ∼24 dB of gain before detection with a commercial spectrum analyzer (Rohde & Schwarz, Munich, Germany, Model FSL303).

Figure 3.

Schematic diagram of MPI transceiver coils. The central receive coil is wound with opposite sense from the two adjacent coils to inductively decouple the transmit and receive channels.

During testing, the transmitter coil was driven with 10 W of RF power to produce a sinusoidal excitation field with amplitude H₀ ∼ 6 mT μ₀⁻¹. To assess measurement variability, MPI signal testing was performed in triplicate. For each MNP sample, three cuvettes were filled with 100 μl of sample at the measured concentration listed in Table 1. Sample cuvettes were then inserted into the transceiver coils and the signal was recorded. The normalized signal listed in Table 1 is the average of the three tested samples.

Table 1.

Properties of magnetite MNPs used in MPI signal testing.

Sample	MPI signal (mV∕mgFe)	mgFe∕ml	Ms (kA∕m)	d0 (nm)	σ
Feridex IV	10	2.21	223	6.9	0.40
UW056_42	3	0.24	225	5.6	0.42
UW075_28	1	1.68	155	7.5	0.28
UW124_18	72	0.68	322	12.4	0.18
UW140_12	136	1.56	384	14.0	0.12
UW143_17	163	2.72	203	14.3	0.17
UW150_22	291	1.17	347	15.0	0.22
UW158_09	233	3.45	293	15.8	0.09
UW163_07	216	2.94	300	16.3	0.07
UW170_16	91	1.66	309	17.0	0.16

Numerical simulations

MPI signal was simulated using MATHEMATICA software according to the model described in Sec. 2A. M(t) data were generated at a sampling rate of 4 MHz, sufficient to resolve the MPI signal at 750 kHz, by numerical integration of Eq. 1. The integration was limited to physically relevant diameters in order to reduce computing time. For each distribution, the integration bounds were chosen such that g(d) [Eq. 5] >0.01 at the boundary d values. For all fields H₀ up to saturation, this condition yielded the same precision in M(t) to at least four significant figures, as setting the bounds from ∼0 to 1000 nm. The step size was chosen to ensure similar accuracy in M(t) at a range of fields up to saturation. We defined the MPI signal to be the emf induced in a receive coil by M₃, the third harmonic of M(t), determined by discrete Fourier transform of M(t). According to the theory of reciprocity, this can be related to the axial field B_axial (TA⁻¹), produced by unit current in the receive coil

$${\text{emf}}_V=6\pi f_0{M}_3{B}_{\text{axial}},$$ (10)

where f₀ is the driving field frequency.³⁰

RESULTS

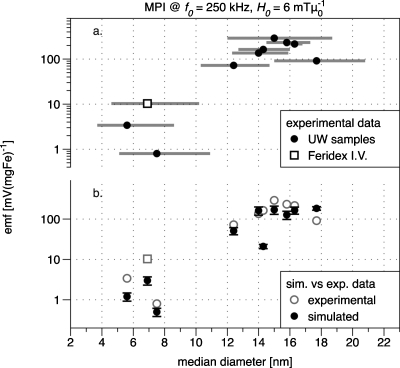
MPI signal is plotted against the measured median diameter d₀ in Fig. 4a and characteristics of the measured MNP samples are provided in Table 1. All data have been normalized by iron concentration to allow comparison between samples. The signal voltage per mg iron has 12% average uncertainty due to errors in the iron concentration and MPI signal voltage measurements. The error bars are smaller than the dot size in Fig. 4a. Size-dependent signal generation can be seen in the figure, with a maximum value for sample UW150_22 (median diameter equal to 15 nm).

Figure 4.

(a) MPI signal testing results. Symbols represent MNP samples (particle details are listed in Table 1). The error bars in x are not uncertainty, but rather delineate the first standard deviation of the sample diameter distribution. (b) Simulated data for each experimental sample with measured points duplicated (in gray) for reference (see the text for simulation parameters).

Figure 4b shows simulated data for each experimental sample. Normalized MPI signal voltage was calculated per mg iron, assuming stochiometric magnetite of density 5180 kg m⁻³. Measured values of d₀, σ, and M_s were used as listed in Table 1; K was assumed to be the bulk value (11 kJ m⁻³), f₀ was 250 kHz, and H₀ was 6 mT μ₀⁻¹. Values of M_s listed in Table 1 have 20% average uncertainty due mainly to error in the sample volume used to measure M(H). The hydrodynamic diameter d_H=d+2δ was used to determine the Brownian component of the effective relaxation time τ [Eq. 5], where δ is the thickness of the polymer layer surrounding the magnetic core; in all simulations, δ was 10 nm, the length of the PMAO-PEG layer as measured by dynamic light scattering of MNPs before and after phase transfer.

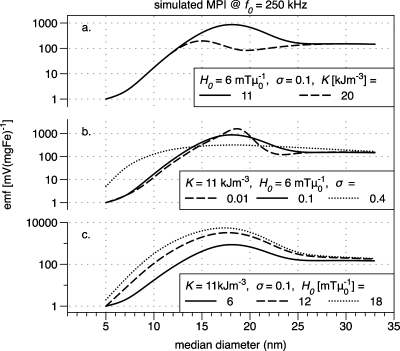
Figure 5 shows simulated data for magnetite MNPs to illustrate how changes in the anisotropy K, the standard deviation of the diameter distribution σ, and the driving field amplitude H₀ affect the signal voltage as a function of MNP size. In Fig. 5a, the range of K values is the expected range for magnetite nanoparticles, from the bulk value 11 kJ m⁻³ to a larger value 20 kJ m⁻³ that is in the middle of the range of values observed for particles smaller than 20 nm diameter in experimental and theoretical literature.^{23, 31, 32, 33, 34}

Figure 5.

Simulated MPI data for (a) different anisotropy constants K, (b) different diameter distribution widths (σ), and (c) different driving field amplitudes H₀.

DISCUSSION

By controlling MNP synthesis to produce a series of samples with closely spaced diameters and narrow size distributions, we have demonstrated that MPI signal varies dramatically with MNP diameter, as predicted by the model presented in Sec. 2A. The observed normalized MPI signal is seen to vary over three orders of magnitude in the measured samples, with some particles exhibiting a 30-fold sensitivity increase over commercial counterparts with comparable iron concentration.

Our experimental device was designed to test the feasibility of generating harmonics for MPI imaging of small volumes, suitable for small animals. The driving field frequency, f₀=250 kHz throughout this work, was chosen accordingly. The field strength used in experiment (6 mT μ₀⁻¹) was chosen to limit coil heating, while the simulated fields in Fig. 5c were also chosen as relevant for imaging small animals at 250 kHz, where 12 mT μ₀⁻¹ is the magnetic simulation threshold estimated by Schaefer et al.³⁵ Goodwill and Conolly³⁶ estimate that similar parameters are relevant for rodents in their excellent paper on x-space MPI.

A striking feature of Fig. 4 is the observed peak in harmonic signal as a function of MNP diameter. This peak confirms our prediction that there is an optimum MNP size for MPI at 250 kHz. Comparing experimental data with the simulated data of Fig. 4b, we see quantitative agreement to within a factor of 2 for most samples. The exceptions include the two smallest samples, UW056_42 and Feridex I.V.^™, which also feature the largest σ; sample UW143_17, which has an unusually low measured M_s relative to its neighbors; and UW170_16, the largest sample. In fact, we expect some difficulty in modeling samples UW056_42 and Feridex, which are doubly tricky due to small median diameters and very broad distributions. Their measured distribution functions g(d) each include diameters as small as 1 nm, which is of the order of a single unit cell for magnetite. Such a particle is almost entirely surface and with the associated break in symmetry, we would expect unique physical properties. On the other hand, the broad distribution functions of both small samples include large particles up to 80 nm, which should be ferrimagnetic and not expected to obey the Langevin approximation we have used. Finally, it is worth mentioning here that we have assumed a simple log-normal distribution for all MNP samples in this work. This assumption serves well for narrow to moderate distributions but could likely be improved for very broad distributions.³⁷

In the simulated points of Fig. 4b, the signal voltage increases with diameter up to 15 nm, corresponding to the experimental data. However, a peak diameter is not clearly visible. In fact, given our assumption that K is equal to the bulk value (11 kJ m⁻³), we would expect to need samples up to at least 20 nm in diameter to clearly resolve the peak [shown in Fig. 5a]. Our experimental data show a peak near 15 nm, from which we might infer that our MNPs have anisotropy greater than 11 kJ m⁻³. In fact, for K=20 kJ m⁻³, the simulated data of Fig. 5a show a peak at 15 nm. This is consistent with theoretical studies showing that nanoparticles can have an effective anisotropy greater than the bulk due to broken symmetry at their surfaces.^{23, 31} Experimentally determined values for K have been reported with substantial variation from the bulk value up to 25 kJ∕m⁻³. In addition, the measured effective anisotropy can depend on particle concentration and the method of preparation.^{23, 32, 34, 38} It is therefore difficult to estimate K precisely for our samples, while measurements are beyond the scope of this work.

The same effects that yield increased K lead to a reduction in M_s with decreasing MNP size. We observe this trend in our samples: The average measured M_s is 70% (308 kA m⁻¹) of the bulk (446) value for magnetite for the samples with d₀>10 nm; it is 45% (201) for samples with d₀<10 nm. Similar size dependence of M_s has been shown previously in magnetite nanoparticles prepared by thermal decomposition.³⁸ It is also known that interparticle magnetic interactions produce an effective anisotropy, as well as enhanced MPI signal for MNPs with high iron concentrations (>0.2 mol∕l)³⁹ However, our maximum concentration of 3.65 mgFe∕ml (0.065 molFe∕l) is quite low and it is unlikely that the small variations in our sample concentrations contributed to the observed differences in MPI signal.

The simulated results in Fig. 5 provide insight into how the MPI signal strength will vary with sample properties and the driving field amplitude H₀. More generally, our model and simulated results provide a physical understanding of the peak observed in our experiments. The decrease in MPI signal for MNPs larger than 15 nm in diameter is due to increased relaxation time τ. In small particles less than ∼10 nm in diameter, magnetic relaxation is dominated by the Neél process wherein the moment is thermally activated and typically reverses in nanoseconds. Brownian relaxation dominates in large particles greater than ∼20 nm in diameter. The moment of such particles is blocked or fixed along an easy axis, so that the entire particle must physically rotate to align with an external field. The Brownian relaxation constant varies linearly with hydrodynamic volume and is substantially slower than Neél relaxation, its period ranging from microseconds to milliseconds depending on the thickness of the hydrodynamic layer that is made up of the surface coating(s) on the nanoparticles. Because the Neél relaxation time τ_N [Eq. 6] depends exponentially on the magnetic volume, relaxation slows dramatically with increasing diameter in the critical region between 10 and 20 nm for magnetite. If the effective relaxation time τ is longer than the period of the driving field, one would expect the MNP moment to lag behind the driving field, the in-phase component of susceptibility to decrease, and the out-of-phase component to become more prominent. For the simulated data of Fig. 5, this transition corresponds to descent from the peak in MPI signal to the shoulder as the diameter increases. We note that the peak height varies with K, but the height of the shoulder, where relaxation is Brownian, does not. Important works by Rauwerdink and Weaver^{40, 41} have explored how magnetization harmonics in the Brownian regime are affected by sample properties and environmental factors. As expected, larger H₀ yield increased harmonic amplitude, especially for intermediate sizes where Néel relaxation dominates. The peak signal is seen to shift to slightly smaller diameters with increasing field.

Our experimental data show that a detectable third harmonic can be produced by fields as small as 6 mT μ₀⁻¹. Furthermore, the measured decrease in MPI signal for larger sized MNPs implies that the 6 mT μ₀⁻¹ excitation field generated by our MPI transceiver during these experiments is not large enough to shorten the effective relaxation time τ. Therefore, the finite relaxation time must be considered as in Sec. 2A. We can estimate the field at which shortening is expected to occur; according to Shliomis, this should be when H_a⪢H_K, where H_a is the applied field and H_K is the anisotropy field.⁴² For bulk magnetite, which has cubic symmetry, H_K=4 K∕(3 μ₀ M_s)=34 mT μ₀⁻¹.²² Given that such a field amplitude is likely to cause magnetostimulation, magnetic relaxation effects will be relevant in future MPI investigations.

Our model provides a quantitative and qualitative guide for optimizing MNPs for MPI, though there is room for further improvement. Most notably, it would benefit to have an experimentally determined K value for each MNP sample. Such data would allow simulation using only experimentally determined MNP properties and help confirm the validity of the assumptions that underpin our model. Several methods have been used by other groups to measure K, though none of them are trivial. Most common are ac susceptibility,⁴³ magnetic resonance,⁴⁴ and Mössbauer spectroscopy.³⁴ To date, our own efforts to determine K experimentally by ac susceptibility have been inconclusive. Additionally, in the simulations presented here, we have used a simplified excitation field to model the response of MNPs at the sensitive or zero-field point of an MPI system. During actual imaging, MNPs will be subjected to additional gradient fields and∕or intermodulation⁴⁵ that should also be modeled. These will affect the harmonic spectrum and may also alter the shape of the peak we observed here for M₃. Furthermore, additional particle samples of larger size would help to resolve the experimental peak diameter definitively.

Though here we have discussed MPI at 250 kHz, we are aware that for lower frequencies, where much recent MPI research has focused, the time window for MNP relaxation is longer. This is expected to permit the use of larger particles whose Brownian relaxation can occur within the period of the driving field and whose M(H) curve approaches the ideal step function. The equations of Sec. 2A. should be relevant for determining MPI signal at least to the limit where MNPs are superparamagnetic at room temperature, about 30 nm diameter. At lower frequencies, optimizing MNP size will also require balancing large core size against the tendency to agglomerate, as well as changes to the hydrodynamic volume, and hence the relaxation and by extension MPI signal, once MNPs encounter patient blood. Furthermore, our model can be extended easily to simulate higher harmonics in order to optimize MPI spatial resolution. Here we have assumed in our optimization that only M₃ will be detected and maximum sensitivity per gram of MNPs is the critical metric. When considering spatial resolution, the relevant metrics are both harmonic amplitude and the number of detectable harmonics per gram of MNP or, equivalently, the width of the time derivative of Eq. 1, where a narrow width is desirable.³⁶

Finally, given that our best-performing sample had a relatively broad size distribution of 0.22, we expect even better performance would be achieved for MPI at 250 kHz by a sample with ideal diameter and distribution d₀∼15 nm and σ∼0.1 based on our experimental results. For such a sample, we expect increased signal voltage by a factor of 2.

CONCLUSIONS

We have shown with experiments that magnetite MNPs chosen for their optimized magnetic properties can show 30-fold improvement in normalized MPI signal over commercial samples, where the frequency of the driving field f₀ is 250 kHz and the MPI signal is measured at 3f₀. We have also observed a peak in MPI signal as a function of MNP size, with the ideal diameter ∼15 nm. A rigorous model of MNP magnetization based on the Langevin theory predicts a similar peak and gives some physical understanding of the underlying cause: The transition between Néel and Brownian relaxation results in a reduction in the MPI signal. Based on the physical insight provided by our model, we would expect similar results for MPI at other driving frequencies: Wherever the effective magnetic relaxation time τ of some samples under test approaches 1∕2πf₀ in magnitude, there should be an optimum MNP size. The results presented here motivate further work to optimize MNPs for different imaging conditions and thereby improve image quality in a wide range of MPI applications.