Heteronuclear proton assisted recoupling

Abstract

We describe a theoretical framework for understanding the heteronuclear version of the third spin assisted recoupling polarization transfer mechanism and demonstrate its potential for detecting long-distance intramolecular and intermolecular ¹⁵N–¹³C contacts in biomolecular systems. The pulse sequence, proton assisted insensitive nuclei cross polarization (PAIN-CP) relies on a cross term between ¹H–¹⁵N and ¹H–¹³C dipolar couplings to mediate zero- and/or double-quantum ¹⁵N–¹³C recoupling. In particular, using average Hamiltonian theory we derive effective Hamiltonians for PAIN-CP and show that the transfer is mediated by trilinear terms of the form N^±C^∓H_z (ZQ) or N^±C^±H_z (DQ) depending on the rf field strengths employed. We use analytical and numerical simulations to explain the structure of the PAIN-CP optimization maps and to delineate the appropriate matching conditions. We also detail the dependence of the PAIN-CP polarization transfer with respect to local molecular geometry and explain the observed reduction in dipolar truncation. In addition, we demonstrate the utility of PAIN-CP in structural studies with ¹⁵N–¹³C spectra of two uniformly ¹³C,¹⁵N labeled model microcrystalline proteins—GB1, a 56 amino acid peptide, and Crh, a 85 amino acid domain swapped dimer (MW = 2 × 10.4 kDa). The spectra acquired at high magic angle spinning frequencies (ω_r/2π > 20 kHz) and magnetic fields (ω_0H/2π = 700–900 MHz) using moderate rf fields, yield multiple long-distance intramonomer and intermonomer ¹⁵N–¹³C contacts. We use these distance restraints, in combination with the available x-ray structure as a homology model, to perform a calculation of the monomer subunit of the Crh protein.

INTRODUCTION

Magic angle spinning (MAS) nuclear magnetic resonance (NMR) has become a valuable tool to probe the structure and dynamics of biomolecular systems that exhibit low solubility or lack long range order and therefore cannot be addressed with the traditional tools of structural biology, solution NMR or x-ray diffraction. Recent applications of MAS NMR to such systems have provided insight into protein folding and misfolding,¹ amyloid aggregation,^{2, 3} and membrane protein function.⁴

MAS NMR experiments are preferred for structural studies of these types of systems since they average second rank tensor interactions such as the chemical shift anisotropy and dipolar interactions⁵ and therefore yield high resolution spectra. In both membrane and amyloid systems spectra resolution of ≤1 ppm is now common and in some cases even better line-widths are observed. However, even though MAS provides high resolution by attenuating the shift anisotropy, it concurrently suppresses dipolar couplings that are the source of distance information and structural data. Therefore, to measure distances it is necessary to reintroduce both ¹³C–¹³C ⁶ and ¹³C–¹⁵N ^{7, 8, 9, 10, 11} dipolar couplings via carefully designed rf irradiation during a mixing period. Subsequently, structure calculations utilize these internuclear distance constraints to generate a three-dimensional fold that is often refined with backbone chemical shifts, chemical shift anisotropies, and torsion angles. This protocol has yielded several MAS NMR structures with a precision ≤1 Å.^{3, 12, 13, 14, 15}

Most heteronuclear experiments require ¹⁵N–¹³C dipolar couplings to be reintroduced with a train of π pulses at the ¹³C and/or ¹⁵N frequencies while simultaneously decoupling the ¹H spins from the ¹⁵N–¹³C spin dynamics. This is the basic approach employed in the development of the majority of heteronuclear recoupling sequences including rotational echo double resonance (REDOR),⁷ transferred echo double resonance (TEDOR),⁸ frequency selective (FS)-REDOR,⁹ z-filtered (ZF-) and band-selective (BASE-)TEDOR,⁹ and frequency selective (FS-)TEDOR¹⁶ which enable accurate N–C distance measurements, and have been especially important in the determination of high resolution 3D structures.^{15, 17} Nevertheless, efficient heteronuclear recoupling in larger biomolecular systems remains challenging.

One of the most significant challenges encountered in these approaches to heteronuclear recoupling is the requirement to accommodate high power rf irradiation on all three channels during the mixing periods. In particular, the NMR probes must be capable of performing stable irradiation during mixing periods of up to tens of milliseconds in order to probe structurally relevant but weak ¹⁵N–¹³C dipolar couplings corresponding to medium to long distance contacts (3.5–8 Å). This is an important concern since inadequate power settings during recoupling sequences result in significant polarization losses. The requirement of high power proton decoupling during recoupling is particularly acute for longer mixing times in temperature sensitive samples. This specific problem has been partially alleviated with the development NMR probes that reduce the electric field in the sample, more efficient cooling systems, and low power methods applicable at > 50 kHz spinning frequencies; however, sample heating still remains a significant concern. Even with improved experimental efficiency, it is generally very difficult to transfer polarization between spins that are far apart in the presence of closer spins since the stronger coupling dominates the transfer.^{18, 19}

Recently, a number of different methods were demonstrated as useful for providing long-range distance restraints for protein structure determination.^{14, 20, 21, 22} Among them there are two promising approaches: proton assisted recoupling (PAR) and proton assisted insensitive nuclei cross polarization (PAIN-CP), which are based on a more general third spin assisted recoupling (TSAR) mechanism.^{14, 22} Notably, these new recoupling methods have been used to solve the largest solid-state nuclear magnetic resonance (SSNMR) protein structure reported to date (i.e., 17.6 kDa MMP-12).¹² These techniques have also been applied to the challenging case of ¹⁵N–¹⁵N correlation spectroscopy and also demonstrated as one of the few pulse sequences able to provide long distance restraints in uniformly ¹³C and ¹⁵N labeled proteins in the ω_r/2π > 50 kHz spinning frequency regime.²³ We remark that the TSAR mechanism was also used to obtain ¹⁵N–¹⁵N correlations for static samples.²⁴

In this manuscript, we explain in detail the TSAR mechanism involved in the heteronuclear recoupling sequence PAIN-CP. In particular, we show that analytical expressions derived using average Hamiltonian theory (AHT) facilitates a clear understanding of the associated spin physics. The use of protons as assisting spins to transfer magnetization from ¹⁵N's to ¹³C's is extensively discussed in the context of zero-quantum (ZQ) and double-quantum (DQ) mechanisms. Analytical expressions permit one to fully understand the structure of the polarization transfer optimization maps, the influence of different second-order cross terms, and to reproduce numerical simulations even in presence of chemical shift interactions. In the context of uniformly ¹⁵N, ¹³C labeled systems, we discuss the presence of long distance ¹⁵N–¹³C transfers, attenuation of the dipolar truncation phenomenon, and the influence of PAR-relayed transfer. Finally, this new methodology is applied to two model proteins, GB1 and the dimeric Crh proteins. We demonstrate the feasibility of obtaining long distance (up to 7 Å) transfers on [U-¹⁵N, ¹³C] Crh and heterogeneously labeled 50%-[U-¹⁵N]/50%-[U-¹³C] Crh. We also show that the number of distance restraints from PAIN-CP experiments is sufficient to calculate 3D structures and provides a good method for studying protein–protein interactions.

PRINCIPLES OF PAIN-CP RECOUPLING

PAIN-CP pulse sequence

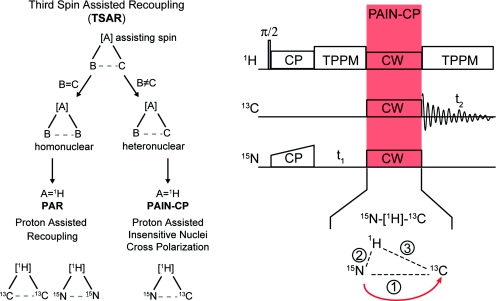
Figure 1 illustrates the pulse sequence used throughout this work to record heteronuclear 2D correlation spectra. Following the initial cross-polarization (CP) step and the ¹⁵N indirect t₁ evolution, CW irradiation, which constitutes the PAIN-CP recoupling block, is applied simultaneously on the ¹⁵N, ¹³C, and ¹H channels, followed by ¹³C detection in the presence of heteronuclear decoupling. As we shall see in the following, the PAIN-CP mechanism relies on second-order recoupling involving ¹⁵N–¹H and ¹H–¹³C dipolar interactions, and is classified as ¹⁵N–[¹H]–¹³C TSAR recoupling.

Figure 1.

(left) Third spin assisted recoupling (TSAR) is a second-order mechanism where polarization is transferred from spin B to C using the cross term between the couplings to an assisting spin A. In the context of biological NMR, this mechanism can be used to design methods that transfer polarization between homonuclear and heteronuclear spins, referred as the PAR and PAIN-CP pulse sequence respectively. (right) PAIN-CP pulse sequence for obtaining 2D ¹⁵N–¹³C heteronuclear correlation spectra. The PAIN-CP mixing consists of continuous wave (CW) irradiations on ¹⁵N, ¹³C, and ¹H channels that reintroduce second-order cross term between ¹⁵N–¹H and ¹H–¹³C dipolar couplings (terms 2 and 3) in order to transfer polarization from ¹⁵N to ¹³C. Note that the TSAR mechanism can be utilized both in MAS and static NMR spectroscopy.

Second-order effective Hamiltonian—PAIN-CP subspace

The PAIN-CP experiment can be analyzed using average Hamiltonian theory²⁵ that allows one to define a PAIN-CP subspace, which greatly facilitates understanding the TSAR mechanism. Accordingly, we consider a three-spin system consisting of two low-γ spins—a ¹⁵N and ¹³C—and an assisting ¹H spin subject to three CW rf fields of strengths ω_1N/2π, ω_1C/2π, and ω_1H/2π, respectively. The internal Hamiltonian can therefore be written as

$$\begin{array}{ccc}\hfill \mathrm{H}& =& \stackrel{1}{\overbrace{{\omega }_{NC}2N_z{C}_z}}+\stackrel{2}{\overbrace{{\omega }_{NH}2N_z{H}_z}}+\stackrel{3}{\overbrace{{\omega }_{HC}2H_z{C}_z}}\hfill \\ & & +\stackrel{4}{\overbrace{{\omega }_N{N}_z}}+\stackrel{5}{\overbrace{{\omega }_C{C}_z}}+\stackrel{6}{\overbrace{{\omega }_H{H}_z}}\hfill \\ & & +{\omega }_{1N}{N}_x+{\omega }_{1C}{C}_x+{\omega }_{1H}{H}_x,\hfill \end{array}$$ (1)

where ω_N, ω_C, and ω_H denote shift tensors and resonant offsets of the ¹⁵N, ¹³C, and ¹H nuclei, respectively, and ω_NC, ω_NH, and ω_HC denote heteronuclear dipolar couplings. Note that rotation at the magic angle induces a time dependence to the spatial anisotropy of the interactions.

We introduce the indices p in order to reduce the dependence on four different averaging frequencies in the experiment (ω_r/2π the frequency of the spinning rotor, ω_1N/2π, ω_1C/2π, and ω_1H/2π the strength of the ¹⁵N, ¹³C and ¹H CW fields, respectively) to a single frequency dependence. Let us assume that we can find the integers $p_N^1,p_N^2,p_C^1,p_C^2,p_H^1,p_H^2$ such that

$$\frac{{\omega }_{1N}}{2\pi }=\frac{p_N^1}{p_N^2}\left(\frac{{\omega }_r}{2\pi }\right)=p_N\left(\frac{{\omega }_r}{2\pi }\right)$$ (2)

$$\frac{{\omega }_{1C}}{2\pi }=\frac{p_C^1}{p_C^2}\left(\frac{{\omega }_r}{2\pi }\right)=p_C\left(\frac{{\omega }_r}{2\pi }\right)$$ (3)

$$\frac{{\omega }_{1H}}{2\pi }=\frac{p_H^1}{p_H^2}\left(\frac{{\omega }_r}{2\pi }\right)=p_H\left(\frac{{\omega }_r}{2\pi }\right)$$ (4)

where $\frac{p_N^1}{p_N^2},\frac{p_C^1}{p_C^2},\frac{p_H^1}{p_H^2}$ denote irreducible ratios. We assume that the four frequencies are commensurate which is not a demanding constraint and allows us to reduce the problem to single frequency dependence. Average Hamiltonian theory is then applicable over a period nτ_r, where n = lcm(p_N²,p_C²,p_H²), given that n is sufficiently small to ensure rapid convergence and τ_r is a rotor period. Equation 1 can be rewritten in the interaction frame defined by the three CW irradiations using spherical tensor notations (see SI Sec. 1 for details) (Ref. ²⁶) and conventional expressions of time-dependent interactions during MAS to yield

$$\begin{array}{ccc}\hfill & & \tilde{\mathrm{H}}=\stackrel{1}{\overbrace{\sum _{m_1=-2}^2\sum _{\genfrac{}{}{0pt}{}{q_{1N}=-1}{q_{1N\ne 0}}}^1\sum _{\genfrac{}{}{0pt}{}{q_{1H}=-1}{q_{1H\ne 0}}}^1{\omega }_{NH}^{m_1}\mathrm{sgn}\left(q_{1N}\right)\mathrm{sgn}\left(q_{1H}\right)T_{1q_{1N}}^N{T}_{1q_{1H}}^H\exp \left\{-i\left(n{X}_1\right)\frac{{\omega }_{r}t}{n}\right\}}}\hfill \\ \hfill & & +\stackrel{2}{\overbrace{\sum _{m_2=-2}^2\sum _{\genfrac{}{}{0pt}{}{q_{2H}=-1}{q_{2H\ne 0}}}^1\sum _{\genfrac{}{}{0pt}{}{q_{2C}=-1}{q_{2C\ne 0}}}^1{\omega }_{HC}^{m_2}\mathrm{sgn}\left(q_{2H}\right)\mathrm{sgn}\left(q_{2C}\right)T_{1q_{2H}}^H{T}_{1q_{2C}}^C\exp \left\{-i\left(n{X}_2\right)\frac{{\omega }_{r}t}{n}\right\}}}\hfill \\ \hfill & & \stackrel{3}{\overbrace{\sum _{m_3=-2}^2\sum _{\genfrac{}{}{0pt}{}{q_{3C}=-1}{q_{3C\ne 0}}}^1\sum _{\genfrac{}{}{0pt}{}{q_{3H}=-1}{q_{3H\ne 0}}}^1{\omega }_{NC}^{m_3}\mathrm{sgn}\left(q_{3N}\right)\mathrm{sgn}\left(q_{3C}\right)T_{1q_{3N}}^N{T}_{1q_{3C}}^C\exp \left\{-i\left(n{X}_3\right)\frac{{\omega }_{r}t}{n}\right\}}}\hfill \\ \hfill & & +\stackrel{4+5+6}{\overbrace{\sum _{\lambda \in \left\{N,C,H\right\}}\sum _{m_{\lambda }=-2}^2\sum _{\genfrac{}{}{0pt}{}{q_{\lambda }=-1}{q_{\lambda \ne 0}}}^1{\omega }_{\lambda }^{m_{\lambda }}\left(\mathrm{sgn}\left(q_{\lambda }\right)∕\phantom{\mathrm{sgn}\left(q_{\lambda }\right)\sqrt{2}}\sqrt{2}\right)T_{1q_{\lambda }}^{\lambda }\exp \left\{-i\left(n{X}_{\lambda }\right)\frac{{\omega }_{r}t}{n}\right\}}}\hfill \end{array}$$ (5)

where we use the following substitutions:

$$\begin{array}{c}{X}_1=m_1+p_N{q}_{1N}+p_H{q}_{1H}\hfill \\ X_2=m_2+p_H{q}_{2H}+p_C{q}_{2C}\hfill \\ X_3=m_3+p_N{q}_{3N}+p_C{q}_{3C}\hfill \\ X_{\lambda }=m_{\lambda }+p_{\lambda }{q}_{\lambda }\hfill \end{array}$$ (6)

and sgn(q) is a sign function of q and λ represents the indices N, C, and H.

We assume that the rf fields are chosen so that neither Hartmann–Hahn (H–H)²⁷ nor rotary resonance (R³)²⁸ conditions are matched (i.e., X₁ ≠ 0, X₂ ≠ 0, X_C ≠ 0, X_N ≠ 0, X_H ≠ 0). The first-order AHT contribution is thus zero. In order to describe the TSAR recoupling mechanism, we calculate the second-order cross term between terms 1 and 2 in Eq. 5

$${\overline{\tilde{H}}}_{1\times 2}^{\left(2\right)}=\sum _{\genfrac{}{}{0pt}{}{m_1,q_{1N},q_{1H},}{m_2,q_{2C},q_{2H}}}\left[\begin{array}{c}{\displaystyle \frac{1}{2iT}{\omega }_{NH}^{m_1}\mathrm{sgn}\left(q_{1N}\right)\mathrm{sgn}\left(q_{1H}\right){\omega }_{HC}^{m_2}\mathrm{sgn}\left(q_{2H}\right)sg\left(q_{2C}\right)T_{1q_{1N}}^N{T}_{1q_{2C}}^C\left[T_{1q_{1H}}^H,T_{1q_{2H}}^H\right]}\\ {\displaystyle {\int }_0^{T}d{t}_2{\int }_0^{t_2}d{t}_1\left(\exp \left\{-i{\omega }_r\left(X_1{t}_2+X_2{t}_1\right)\right\}-\exp \left\{-i{\omega }_r\left(X_2{t}_2+X_1{t}_1\right)\right\}\right)}\end{array}\right].$$ (7)

The above expression is nonvanishing if and only if

$$q_{1H}=-q_{2H}\Rightarrow \left[T_{1q_{1H}}^H,T_{1q_{2H}}^H\right]=-\mathrm{sgn}\left(q_{1H}\right)T_{10}^H$$ (8)

$$X_2=-X_1\ne 0.$$ (9)

Which implies that:

$$\left(m_1+m_2\right)+p_N{q}_{1N}+p_C{q}_{2C}=0.$$ (10)

Equation 10 has several solutions given that (m₁ + m₂) ∈ {0, ±1, ±2, ±3, ±4}.

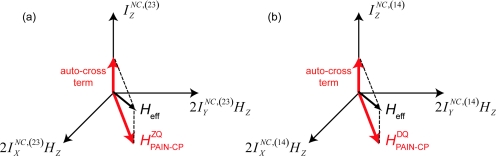
To simplify further discussion we introduce the following notation to describe the resulting PAIN-CP recoupling cases: δp_m = p_N – p_C = m and σp_m = p_N + p_C = m. Equation 10 leads to five types of heteronuclear TSAR recoupling that we described below. Solutions 1–3 and 4–5 lead, respectively to ZQ and DQ heteronuclear polarization transfer, which can be visualized using the appropriate TSAR subspace presented in Figs. 2a, 2b. Note that the third term of Eq. 5, which corresponds to the ¹⁵N–¹³C dipolar interaction, can potentially be recoupled to the first order (i.e., X₃ = 0) depending on the PAIN-CP condition chosen (vide infra).

Figure 2.

(a)–(b) Visualization of the PAIN-CP spin dynamics subspace. The space can be seen as a coupled basis between a ZQ/DQ fictitious spin I (involving the nitrogen spin N and the carbon spin C) and a proton spin H (assisting spin). The red arrows indicate the transverse PAIN-CP recoupling axis and the longitudinal off resonance contribution (from autocross terms, see Sec. 2C) which result in a tilting of the effective recoupling axis. [see SI Sec. 1 for fictitious ZQ/DQ spin operator notations] (Ref. ²⁶).

Solution 1: ZQ PAIN-CP with δp₀

For q_1N = −q_2C and |p_N − p_C| = 0, the effective Hamiltonian is composed of ZQ TSAR terms of the form $T_{1\pm 1}^N{T}_{1\mp 1}^C{T}_{10}^H$, with no restriction on p_H. The analytical expression for this solution (p_N = p_C) can be derived straightforwardly since it is analogous to the homonuclear TSAR case (presented previously in Ref. 14)

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_{ZQ,\delta p_0}^{\left(2\right),\mathrm{PAIN}\text{-}\mathrm{CP}}& =& 2{\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\left(T_{11}^N{T}_{1-1}^C\right)T_{10}^H\hfill \\ & & +2{\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}*}\left(T_{1-1}^N{T}_{11}^C\right)T_{10}^H\hfill \\ & =& \mathrm{Re}\left({\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_X^{NC,\left(23\right)}{H}_Z\hfill \\ & & +\mathrm{Im}\left({\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_Y^{NC,\left(23\right)}{H}_Z.\hfill \end{array}$$ (11)

Where the effective TSAR coupling is equal to

$$\begin{array}{ccc}\hfill {\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}-\mathrm{CP}}& =& \left({\displaystyle \frac{\mathrm{Re}\left({\omega }_{NH}^1{\omega }_{HC}^{-1}\right)}{{\omega }_r}\lambda \left(1,p_C,p_H\right)}\right.\hfill \\ & & \left.{\displaystyle +\frac{\mathrm{Re}\left({\omega }_{NH}^2{\omega }_{HC}^{-2}\right)}{{\omega }_r}\lambda \left(2,p_C,p_H\right)}\right)\hfill \\ & & +i\left({\displaystyle \frac{\mathrm{Im}\left({\omega }_{NH}^1{\omega }_{HC}^{-1}\right)}{{\omega }_r}\sigma \left(1,p_C,p_H\right)}\right.\hfill \\ & & \left.{\displaystyle +\frac{\mathrm{Im}\left({\omega }_{NH}^2{\omega }_{HC}^{-2}\right)}{{\omega }_r}\sigma \left(2,p_C,p_H\right)}\right)\hfill \end{array}$$ (12)

with

$$\begin{array}{ccc}\hfill \lambda \left(m,p_C,p_H\right)& =& \left(\frac{-\left(p_C+p_H\right)}{m^2-{\left(p_C+p_H\right)}^2}\right.\left.+\frac{-\left(p_H-p_C\right)}{m^2-{\left(p_H-p_C\right)}^2}\right)\hfill \\ \hfill \sigma \left(m,p_C,p_H\right)& =& \left(\frac{m}{m^2-{\left(p_H+p_C\right)}^2}\right.\left.-\frac{m}{m^2-{\left(p_H-p_C\right)}^2}\right).\hfill \end{array}$$ (13)

Solution 2: ZQ PAIN-CP with δp_±1 or δp_±2

For q_1N = −q_2C and |p_N − p_C| = 1 or 2, the effective Hamiltonian is composed of ZQ TSAR terms of the form $T_{1\pm 1}^N{T}_{1\mp 1}^C{T}_{10}^H$, with no restriction on p_H, but also of ZQ CP terms of the form $T_{1\pm 1}^N{T}_{1\mp 1}^C$ since X₃ = 0.

Assuming δp = p_N − p_C = 1, the effective Hamiltonian can be written

$$\overline{\tilde{H}}={\overline{\tilde{H}}}_{ZQ,\delta p_1}^{\left(1\right),\mathrm{CP}}+{\overline{\tilde{H}}}_{ZQ,\delta p_1}^{\left(2\right),\mathrm{PAIN}\text{-}\mathrm{CP}}$$ (14)

with

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_{ZQ,\delta p_1}^{\left(1\right),\mathrm{CP}}& =& -{\omega }_{NC}^{-1}{T}_{11}^N{T}_{1-1}^C-{\omega }_{NC}^{+1}{T}_{1-1}^N{T}_{11}^C\hfill \\ \hfill & =& -\mathrm{Re}\left({\omega }_{NC}^{-1}\right)2I_X^{NC,\left(23\right)}-\mathrm{Im}\left({\omega }_{NC}^{-1}\right)2I_Y^{NC,\left(23\right)}\hfill \end{array}$$ (15)

and

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_{ZQ,\delta p_1}^{\left(2\right),\mathrm{PAIN}\text{-}\mathrm{CP}}& =& 2{\omega }_{ZQ,\delta p_1}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\left(T_{11}^N{T}_{1-1}^C\right)T_{10}^H\hfill \\ & & +2{\omega }_{ZQ,\delta p_1}^{\mathrm{PAIN}\text{-}\mathrm{CP}*}\left(T_{1-1}^N{T}_{11}^C\right)T_{10}^H\hfill \\ & =& \mathrm{Re}\left({\omega }_{ZQ,\delta p_1}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_X^{NC,\left(23\right)}{H}_Z\hfill \\ & & +\mathrm{Im}\left({\omega }_{ZQ,\delta p_1}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_Y^{NC,\left(23\right)}{H}_Z\hfill \end{array}$$ (16)

and

$$\begin{array}{ccc}\hfill {\omega }_{ZQ,\delta p_1}^{\mathrm{PAIN}\text{-}\mathrm{CP}}& =& \frac{{\omega }_{NH}^{-2}{\omega }_{HC}^{+1}}{{\omega }_r}\psi \left(1,p_C,p_H\right)\hfill \\ & & +\frac{{\omega }_{NH}^{+1}{\omega }_{HC}^{-2}}{{\omega }_r}\psi \left(-2,p_C,p_H\right)\hfill \end{array}$$ (17)

with

$$\psi \left(m,p_C,p_H\right)=\frac{p_H}{p_H^2-{\left(p_C-m\right)}^2}.$$ (18)

Similar expressions can be derived for δp = p_N − p_C = −1, −2, 2.

Solution 3: ZQ PAIN-CP with δp_±3 or δp_±4

For q_1N = −q_2C and |p_N − p_C| = 3 or 4, the effective Hamiltonian is composed of ZQ TSAR terms of the form $T_{1\pm 1}^N{T}_{1\mp 1}^C{T}_{10}^H$, with no restriction on p_H. Following solution 1 and 2, the expression of the effective Hamiltonian can be derived straightforwardly.

Solution 4: DQ PAIN-CP with σp₁ or σp₂:

For q_1N = q_2C and (p_C + p_N) = 1, 2, the effective Hamiltonian is composed of DQ TSAR terms of the form $T_{1\pm 1}^N{T}_{1\pm 1}^C{T}_{10}^H$ with no restriction on p_H, but also of DQ CP terms of the form $T_{1\pm 1}^N{T}_{1\pm 1}^C$ since X₃ = 0. Following solution 1 and 2, the expression of the effective Hamiltonian can be derived straightforwardly.

Solution 5: DQ PAIN-CP with σp₃ or σp₄

For q_1N = q_2C and (p_C + p_N) = 3, 4, effective Hamiltonian is composed of DQ TSAR terms of the form $T_{1\pm 1}^N{T}_{1\pm 1}^C{T}_{10}^H$ with no restriction on p_H. Following solution 1 and 2, the expression of the effective Hamiltonian can be derived straightforwardly.

To summarize, heteronuclear TSAR recoupling can be achieved with several rf settings classified according to solutions 1 through 5. At this point, it is important to note that solutions 1, 3 and 5 rely on a TSAR recoupling term alone for driving the polarization transfer, whereas solutions 2 and 4 also reintroduce a ¹⁵N–¹³C CP term. The overall spin dynamics during the polarization transfer varies depending on the recoupling condition chosen: ZQ/DQ transfer, scaling factor, local geometry dependency, etc. Moreover, it is worth noting that some of the rf settings correspond to unfavorable conditions as they satisfy both ZQ and DQ PAIN-CP recoupling conditions. For instance, rf irradiation characterized by p_C = 1 and p_N = 1 satisfies both solution 1 and 4.

Second-order effective Hamiltonian autocross terms

In this section, we evaluate the second-order cross terms other than the TSAR terms. An important class of these cross-terms, referred to as autocross terms, yields nonzero contributions that can be expressed as a function of p_C, p_N, and p_H rf field strengths (in units of the MAS frequency). Such terms yield longitudinal T₁₀ operators (along the z axis in the TSAR subspace, see Fig. 2a, 2b that induce tilt of the effective recoupling axis and thus influence the choice of rf settings used for the PAIN-CP experiment.

The autocross term of term 1 in Eq. 5 (i.e., ¹H–¹⁵N dipolar coupling) can be written as follows:

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_{1\times 1}^{\left(2\right)}& =& \frac{1}{{\omega }_r}\left[{\omega }_{NH}^1{\omega }_{HN}^{-1}\chi \left(1,p_N,p_H\right)\right.\hfill \\ & & \left.+{\omega }_{NH}^2{\omega }_{HN}^{-2}\chi \left(2,p_N,p_H\right)\right]T_{10}^N\hfill \\ & & +\frac{1}{{\omega }_r}\left[{\omega }_{NH}^1{\omega }_{HN}^{-1}\kappa \left(1,p_N,p_H\right)\right.\hfill \\ & & \left.+{\omega }_{NH}^2{\omega }_{HN}^{-2}\kappa \left(2,p_N,p_H\right)\right]T_{10}^H\hfill \end{array}$$ (19)

with

$$\begin{array}{ccc}\hfill \chi \left(m,p_N,p_H\right)& =& -\frac{1}{2}\left(\frac{\left(p_H+p_N\right)}{m^2-{\left(p_H+p_N\right)}^2}\right.\hfill \\ & & \left.-\frac{\left(p_H-p_N\right)}{m^2-{\left(p_H-p_N\right)}^2}\right)\hfill \\ \hfill \kappa \left(m,p_N,p_H\right)& =& -\frac{1}{2}\left(\frac{\left(p_H+p_N\right)}{m^2-{\left(p_H+p_N\right)}^2}\right.\hfill \\ & & \left.+\frac{\left(p_H-p_N\right)}{m^2-{\left(p_H-p_N\right)}^2}\right).\hfill \end{array}$$ (20)

Similarly, one can derive ${\overline{\tilde{\mathrm{H}}}}_{2\times 2}^{\left(2\right)}$—the second order contribution of term 2 in Eq. 5 with itself (i.e. ¹H–¹³C dipolar coupling)—by replacing the index N with C in Eqs. 19, 20.

In order to obtain a more complete expression of the longitudinal contribution, one should also evaluate the cross term of the chemical shift tensors of the ¹⁵N's, ¹³C's, and ¹H's with themselves

$$\begin{array}{ccc}& & {\overline{\tilde{H}}}_{4\times 4}^{\left(2\right)}+{\overline{\tilde{H}}}_{5\times 5}^{\left(2\right)}+{\overline{\tilde{H}}}_{6\times 6}^{\left(2\right)}\hfill \\ & & =\frac{1}{{\omega }_r}\left[\frac{{\left({\omega }_N^0\right)}^2}{2p_N}+\xi \left(1,p_N\right){\omega }_N^1{\omega }_N^{-1}+\xi \left(2,p_N\right){\omega }_N^2{\omega }_N^{-2}\right]T_{10}^N\hfill \\ & & +\frac{1}{{\omega }_r}\left[\frac{{\left({\omega }_C^0\right)}^2}{2p_C}+\xi \left(1,p_C\right){\omega }_C^1{\omega }_C^{-1}+\xi \left(2,p_C\right){\omega }_C^2{\omega }_C^{-2}\right]T_{10}^C\hfill \\ & & +\frac{1}{{\omega }_r}\left[\frac{{\left({\omega }_H^0\right)}^2}{2p_H}+\xi \left(1,p_H\right){\omega }_H^1{\omega }_H^{-1}+\xi \left(2,p_H\right){\omega }_H^2{\omega }_H^{-2}\right]T_{10}^H\hfill \end{array}$$ (21)

where

$$\xi \left(m,p\right)=\frac{p}{\left(p^2-m^2\right)}.$$ (22)

Autocross terms arising from J couplings are also present, but can generally be neglected as being small compared to dipolar autocross terms considered above. Autocross terms of the form ${\overline{\tilde{\mathrm{H}}}}_{\mathrm{j}\times \mathrm{j}}^{\left(2\right)}$ yield longitudinal T₁₀ operators that can be rearranged as combinations of ZQ/DQ fictitious spin operators. More precisely the relevant Hamiltonian can be written as three commuting terms

$$\begin{array}{c}\hfill {\overline{\tilde{H}}}_{\mathrm{AUTO}}^{\left(2\right)}={\omega }_{ZQ}^{\mathrm{AUTO}}{I}_Z^{NC,\left(23\right)}+{\omega }_{DQ}^{\mathrm{AUTO}}{I}_Z^{NC,\left(14\right)}+{\omega }_H^{\mathrm{AUTO}}{H}_Z.\end{array}$$ (23)

The longitudinal contribution relevant for description of the TSAR mechanism corresponds to one of the two first terms depending if the TSAR conditions chosen is ZQ or DQ. Analytical expressions of ${\omega }_{ZQ}^{\mathrm{AUTO}}$ and ${\omega }_{DQ}^{\mathrm{AUTO}}$ can be derived depending on the PAIN-CP conditions. For instance, for the solution 1 (ZQ δp₀ PAIN-CP), we obtain

$${\omega }_{ZQ,\delta p_0}^{\mathrm{AUTO}}=\frac{1}{{\omega }_r}\left[\begin{array}{c}\stackrel{\mathrm{ZQ}\mathrm{TSAR}\mathrm{autocross}\mathrm{terms}}{\overbrace{\left({\omega }_{NH}^1{\omega }_{HN}^{-1}-{\omega }_{CH}^1{\omega }_{HC}^{-1}\right)\chi \left(1,p,p_H\right)+\left({\omega }_{NH}^2{\omega }_{HN}^{-2}-{\omega }_{CH}^2{\omega }_{HC}^{-2}\right)\chi \left(2,p,p_H\right)}}\\ \underset{\mathrm{ZQ}\mathrm{CS}\mathrm{autocross}\mathrm{terms}}{\underbrace{\frac{{\left({\omega }_N^0\right)}^2-{\left({\omega }_C^0\right)}^2}{2p}+\xi \left(1,p\right)\left({\omega }_N^1{\omega }_N^{-1}-{\omega }_C^1{\omega }_C^{-1}\right)+\xi \left(2,p\right)\left({\omega }_N^2{\omega }_N^{-2}-{\omega }_C^2{\omega }_C^{-2}\right)}}\end{array}\right]$$ (24)

$${\omega }_{DQ,\delta p_0}^{\mathrm{AUTO}}=\frac{1}{{\omega }_r}\left[\begin{array}{c}\stackrel{\mathrm{DQ}\mathrm{TSAR}\mathrm{autocross}\mathrm{terms}}{\overbrace{\left({\omega }_{NH}^1{\omega }_{HN}^{-1}+{\omega }_{CH}^1{\omega }_{HC}^{-1}\right)\chi \left(1,p,p_H\right)+\left({\omega }_{NH}^2{\omega }_{HN}^{-2}+{\omega }_{CH}^2{\omega }_{HC}^{-2}\right)\chi \left(2,p,p_H\right)}}\\ \underset{\mathrm{DQ}\mathrm{CS}\mathrm{autocross}\mathrm{terms}}{\underbrace{\frac{{\left({\omega }_N^0\right)}^2+{\left({\omega }_C^0\right)}^2}{2p}+\xi \left(1,p\right)\left({\omega }_N^1{\omega }_N^{-1}+{\omega }_C^1{\omega }_C^{-1}\right)+\xi \left(2,p\right)\left({\omega }_N^2{\omega }_N^{-2}+{\omega }_C^2{\omega }_C^{-2}\right)}}\end{array}\right].$$ (25)

Numerical simulations of all the PAIN-CP conditions

In this section we illustrate the recoupling conditions introduced in the previous section (solution 1–5) using numerical simulations. Based on the polarization transfer maps reported in the SI (Figs. SI 1, SI 2, SI 3, and SI 4),²⁶ we were able to choose combinations of ¹⁵N, ¹³C, and ¹H power levels in order to obtain appropriate PAIN-CP polarization transfer for each of the cases mentioned above.

Figure 3 demonstrates the wide latitude of conditions available for implementing a heteronuclear TSAR polarization transfer. The polarization transfer can be either ZQ (noted δp_x) or DQ (noted σp_x). As explained in the previous section, direct polarization transfer that uses the NC coupling [cross-polarization (CP)] can also occur when typical Hartmann and Hahn conditions are matched (δp₁, δp₋₁, δp₂, δp₋₂, σp₁, and σp₂). For the other cases, we can insure that the polarization transfer is quenched when the couplings to the ¹H are removed (black dashed lines in Fig. 3). Note that the CP transfer, when active, may appear more efficient than the second-order TSAR contribution (blue circles versus black dashed line), but this is only true for one-bond NC transfer. As we shall see in the following, this is the reverse situation for polarization transfer over longer distances. Finally, we remark that the various PAIN-CP settings highlighted here are for illustrative purposes only, and that care should be taken when making any sort of quantitative comparisons only based on the settings presented here. Other points in the maps (see SI)²⁶ may have slightly different behaviors (buildup time, transfer efficiency, etc.). In general, it is important to simulate the polarization transfer in the desired regime before setting up PAIN-CP experiments (examples of SPINEVOLUTION scripts may be found in the SI).²⁶ Moreover, the PAIN-CP settings chosen here are based on three spin optimization maps. Effect of additional ¹H's and multiple ¹³C sites (relayed transfer, dipolar truncation, etc.) on the spin dynamics will be considered in the following. Notably the buildup curves and maps presented above will change upon the introduction of other protons (e.g., H_α proton). We deliberately choose to present a simple three-spin case here to clearly describe the PAIN-CP principles. Note that such a spin system is realized experimentally with a ²H, ¹³C, ¹⁵N labeled protein with back-exchanged amide protons.

Figure 3.

Heteronuclear polarization transfer for the PAIN-CP conditions highlighted in the text. Simulations with all the dipolar couplings included (blue circle), and ¹H–X (black dashed line) or ¹⁵N–¹³C (red solid line) couplings removed are considered. The spin system (top left) consists of three spin and the magnetization starts on the nitrogen and is detected on the carbon. The simulations include typical anisotropic chemical shift interactions (see Sec. 2C). The rf power levels of the three CW irradiations are chosen based on optimization maps (indicated by stars on Fig. SI 2–5) (Ref. ²⁶) and correspond to settings resulting in adequate polarization transfer efficiency. The rf power level settings (in units of the MAS frequency) are shown directly on the figure. The panels with the grey and with the white background indicate respectively conditions without and with concurrent ¹⁵N–¹³C CP active during the experiment.

DETAILS OF THE PAIN-CP MECHANISM

Numerical versus analytical simulations for directly bonded ¹⁵N/¹³C spins

In Sec. 2 we derived analytical expressions that provide considerable insight into the heteronuclear PAIN-CP spin dynamics. Notably we have seen that the polarization transfer can be visualized in an appropriate PAIN-CP subspace (Fig. 2). In this section we compare analytical and numerical simulations in order to discuss further the influence of other interactions and higher order terms. As we will see numerical simulations are in excellent agreement with the analytical expressions derived in Sec. 2 clearly indicating that the second-order AHT derivation is sufficient to explain in detail the structure of the PAIN-CP optimization maps.

Figures 45 show simulations of the PAIN-CP polarization transfer for two typical spin geometries encountered in proteins. The first system—NH_NC_α (Fig. 4)—is composed of three spins: one ¹⁵N with a ¹H and a directly attached C_α carbon. The second system—NH_NC—is also composed of three spins: one ¹⁵N with a ¹H and a directly attached carbonyl ¹³C. Both figures compare analytical and numerical simulations of the δp₀ PAIN-CP polarization transfer and highlight the impact of the ¹³C CSA on the PAIN-CP polarization transfer maps. The analytical simulations are performed based on the analytical expressions derived in sec. 2. The spin dynamics in the TSAR subspace are described by the following equation:

$$\begin{array}{ccc}\hfill {\overline{\tilde{H}}}_{ZQ,\delta p_0}^{\left(2\right),\mathrm{PAIN}\text{-}\mathrm{CP}}& =& \mathrm{Re}\left({\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_X^{NC,\left(23\right)}{H}_Z\hfill \\ & & +\mathrm{Im}\left({\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}\right)2I_Y^{NC,\left(23\right)}{H}_Z\hfill \\ & & +{\omega }_{ZQ,\delta p_0}^{\mathrm{AUTO}}{I}_Z^{NC,\left(23\right)}.\hfill \end{array}$$ (26)

Figure 4.

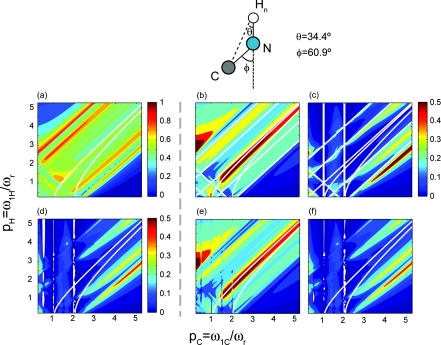
¹⁵N–¹³C PAIN-CP polarization transfer after 3 ms irradiation for δp₀, i.e., p_N = p_C = p, as a function of the proton and carbon/nitrogen rf field strengths in unit of the MAS spinning frequency. The spin system is composed of three spins: a nitrogen N, an amide proton H_n, and a carbon C_α. The chosen geometry and chemical shifts are those of a typical NH_nC_α system found in a protein [see Sec. 3C for details]. ¹⁵N, ¹³C, and ¹H spins are irradiated on resonance. ¹⁵N–¹³C analytical polarization transfer maps with (a) only the TSAR term [see Eqs. 11, 12, 13], (b) with the TSAR term and the TSAR autocross terms [see Eqs. 23, 24], (c) the TSAR term, the TSAR autocross terms and CS autocross terms [see Eqs. 23, 24]. ¹⁵N–¹³C numerical polarization transfer maps with (d) all interactions included, (e) only dipolar couplings included, (f) all interactions included except the ¹⁵N–¹³C coupling.

Figure 5.

¹⁵N–¹³C PAIN-CP polarization transfer after 3 ms irradiation for δp₀, i.e., p_N = p_C = p, as a function of the proton and carbon/nitrogen rf field strengths in unit of the spinning frequency. The spin system is composed of three spins, a nitrogen N, an amide proton H_n, and a carbonyl carbon C. The chosen geometry and the chemical shifts are those of a typical C′NH_n system found in protein (see Sec. 3C for details). ¹⁵N, ¹³C, and ¹H spins are irradiated on resonance. ¹⁵N–¹³C analytical polarization transfer maps with (a) only the TSAR term [see Eqs. 11, 12, 13], (b) with the TSAR term and the TSAR autocross terms [see Eqs. 23, 24], (c) the TSAR term, the TSAR autocross terms and chemical shift autocross terms [see Eqs. 23, 24]. ¹⁵N–¹³C numerical polarization transfer maps with (d) all interactions included, (e) only dipolar couplings included, (f) all interactions included except the ¹⁵N–¹³C coupling.

The effective Hamiltonian can be decomposed into a transverse component (TSAR term) that drives the polarization transfer between ¹⁵N and ¹³C, and a longitudinal component arising from the autocross terms contributions.

If the magnetization starts on the ¹⁵N spin and is detected on the ¹³C, the polarization transfer efficiency for a given crystallite orientation can be written $\frac{1}{2}{\cos }^2\left({\theta }_{\mathrm{eff}}\right).\left[1-\cos \left({\omega }_{\mathrm{eff}}t\right)\right]$ where ω_eff represents the recoupling frequency along the effective tilted axis and θ_eff is the angle between the transverse TSAR component and the effective tilted component (when longitudinal cross terms are considered). Both parameters can be expressed as a function of ${\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}$ (PAIN-CP recoupling frequency, abbreviated ω _{PAIN - CP} ) and ${\omega }_{ZQ}^{\mathrm{AUTO}}$ (autocross terms contribution, abbreviated ω_AUTO) using the following expressions: tan(θ _eff)=ω _AUTO ∕ω _AUTO ω _{PAIN - CP} ω _{PAIN - CP} and ${\omega }_{\mathrm{eff}}^2={\omega }_{\mathrm{PAIN}\text{-}\mathrm{CP}}^2+{\omega }_{\mathrm{AUTO}}^2$. The scaling factor cos ²(θ_eff) accounts for the fact that the effective recoupling axis is not perpendicular to the z-axis of the PAIN-CP subspace (which stands as both the initial magnetization axis and the detection axis). The polarization transfer efficiency can then easily be computed for a random distribution of crystallites.¹⁴

More specifically Figs. 4a, 5a show that the PAIN-CP polarization transfer occurs when only the PAIN-CP term is included, and is potentially active over a wide range of rf settings. The structure of the polarization transfer maps does vary significantly with the inclusion of autocross terms coming from the NH and HC dipolar interactions (Figs. 4b, 5b. In this case the polarization transfer is only possible for rf settings that minimize the longitudinal component of the effective Hamiltonian compared to the transverse component. This is notably achieved for conditions located just below the diagonal of the PAIN-CP maps. The two white lines displayed on the contour plots in Figs. 45 represent points where χ(1, p_N/C, p_H) = 0 and χ(2, p_N/C, p_H) = 0 (i.e., autocross terms for spatial components m = 1 and m = 2 are equal to 0). These two conditions are also described by equations $p_H=\sqrt{p_C^2-1}$ and $p_H=\sqrt{p_C^2-4},$ respectively. It appears that the best PAIN-CP conditions are closer to $p_H=\sqrt{p_C^2-1}$ since the contribution of the spatial component m = 1 dominates. This can also be seen in Fig. SI 5 that compares the relative contribution of each component to the PAIN-CP transfer.²⁶

Overall the analytical maps displayed in Figs. 4b, 5b are very similar to each other, which is understandable since the two spin system geometries are similar and only dipolar interactions have been included. These two analytical maps perfectly match the numerical simulations (Figs. 4e, 5e where only dipolar interactions are included.

The structure of the maps varies significantly upon the inclusion of the autocross terms involving chemical shifts tensors. However, it is important to point out that the analytical expressions obtained through a second order AHT derivation [Eqs (11)–(14) and (23)–(24)] are sufficient to describe and understand the spin dynamics at stake for both spin systems since we obtained an excellent agreement between the analytical and numerical simulations [see panels (d) and (f) of Figs. 45 respectively]. The favorable PAIN-CP settings are represented by rf settings that minimize the longitudinal contribution (resulting from the various autocross terms). The corresponding analytical expression [Eqs 23, 24] is quite complex and involves internuclear distances, interdipolar angles, chemical shifts, CSA's, etc. As a consequence, the significant difference in CSA's magnitude between aliphatic and carbonyl yield important shifts for the rf settings that maximize the polarization transfer optima. We remark that this deviation is more pronounced at higher magnetic fields.

Precise settings for optimum PAIN-CP transfer thus vary upon the type of NC transfer (nitrogens to aliphatic carbons NCx versus nitrogen to carbonyls NC) and upon the recoupling conditions chosen (i.e. δp₀, δp_±1, δp_±2, δp_±3, δp_±4, σp₁, σp₂, σp₃, σp₄ PAIN-CP). Because of the large number of factors involved it is always beneficial to confirm the expected behavior by simulating PAIN-CP transfer prior conducting an experiment. As a guideline, examples of SPINEVOLUTION scripts can be found in the SI.²⁶

The next sections investigate the effect of multiple protons and of the carrier offset on the PAIN-CP transfer. We show their impact on the two main applications for which PAIN-CP should prove a valuable tool: spectral assignment and detection of long range ¹⁵N–¹³C contacts.

Influence of the carrier offset: Broadband versus band-selective PAIN-CP transfer

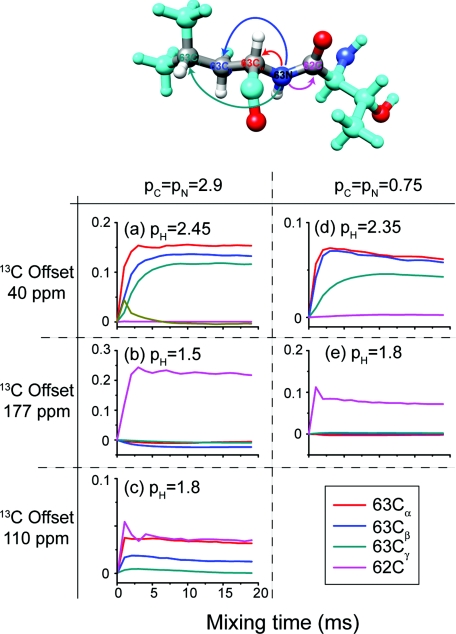
In this section we illustrate that, depending on the aim of the experiment, the δp₀ PAIN-CP experiment can be implemented in a broadband or band-selective manner by adjusting the ¹³C offset frequency and the N/C/H PAIN-CP rf power levels. Figure 6 shows ¹⁵N–¹³C polarization transfer simulations for the residue L63 of the Crh protein. The settings were chosen based on optimization maps with the ¹³C carrier offset at 40 ppm (Fig. SI 1),²⁶ 177 ppm (Fig. 5) and 110 ppm (Fig. SI 6).²⁶

Figure 6.

¹⁵N–¹³C δp₀ PAIN-CP polarization transfer at ω_H0/2π = 750 MHz and ω_r/2π = 20 kHz for three different ¹³C offset frequencies, 40 ppm (a) and (b); 177 ppm (c) and (d); 110 ppm for (e) and (f). The left column correspond to favorable low power PAIN-CP settings whereas the right column to higher power PAIN-CP settings. The spin system is extracted from the Crh x-ray structure (PDB ID: 1mu4) (Ref. ³⁰) and is composed of L63N, four carbons (L63C_α, L63C_β, L63C_γ, T62C), and the four protons mainly involved in the spin dynamics (L63H, L63H_α, L63H_β2, L63Hγ). The ¹³C chemical shifts are taken from the protein assignment (Ref. ³¹). The L63N and the protons are irradiated on resonance. The simulation includes typical CSA tensor parameter for nitrogen (99 ppm, 0.19), carbonyls (−76 ppm, 0.9) and proton (5 ppm, 0.7).

Note that with the offset on resonance with carbonyls or aliphatics, we can make the PAIN-CP transfer band-selective [see Figs. 6a, 6b, 6c, 6d]. This is particularly important for assignments (experiments with short mixing time), but also to favour long distance transfers (by minimizing the number of sites to which initial ¹⁵N magnetization is distributed). We remark that even though it is possible to perform broadband ¹⁵N–¹³C PAIN-CP transfer, it may be often more “cost-effective” to perform two separate band-selective experiments, i.e., carbonyl PAIN-CP and aliphatic PAIN-CP. This is especially relevant for high field experiments (≥14 Tesla = 600 MHz).

The flexibility of PAIN-CP is illustrated in Fig. 7, which shows experimental results obtained on the tripeptide [U-¹³C,¹⁵N]-N-f-MLF-OH at ω_0H/2π = 750 MHz with various rf power levels and offsets. These data illustrate the great potential of the PAIN-CP experiment to perform protein resonance assignments using sequential contacts as well as protein structure determination using long distance contacts.

Figure 7.

Figure illustrating the flexibility of PAIN-CP pulse sequence. Using an appropriate combination of rf strength, offset and mixing time PAIN-CP can accomplish: (a) selective N–C′ recoupling, (b) selective N–C_α recoupling, (c) broadband ¹⁵N–¹³C recoupling with contacts ranging from one-bond to long range, (d) band-selective ¹⁵N–¹³C recoupling to aliphatic carbons (with contacts ranging from one-bond to long range), (e) band-selective ¹⁵N–¹³C recoupling to aliphatic carbons except Cα's (with contacts ranging from two bond to long range). All spectra were obtained on NAc-[U-¹³C,¹⁵N]-f-MLF-OH at ω_0H/2π = 750 MHz and ω_r/2π = 20 kHz using eight scans per t₁ point. Specific δp₀ PAIN-CP settings were: (a) 8 ms mixing time with ω_1C/N∕2π ∼15 kHz, ω_1H∕2π ∼57 kHz with the ¹³C offset in the middle of C′ region, (b) 1 ms mixing time with ω_1C/N∕2π ∼4 kHz, ¹H 43 kHz with the ¹³C offset in the middle of the C_α region, (c) 3 ms mixing time with ω_1C/N∕2π ∼53 kHz, ω_1H∕2π ∼78 kHz with the ¹³C offset in the middle between C′ and C_α region, (d) 9 ms mixing time with ω_1C/N∕2π ∼15 kHz, ω_1H∕2π ∼time with ω_1C/N∕2π ∼15 kHz, ω_1H∕2π ∼57 kHz with the ¹³C offset at 28.8 ppm.

Influence of the ¹H–¹H couplings on the PAIN-CP transfer

The effect of the ¹H–¹H dipolar couplings on the PAIN-CP transfers is illustrated in Fig. SI 7 which shows comparison of the aliphatic PAIN-CP (identical spin system and settings as in the Fig. 10a with and without the ¹H–¹H couplings included in the simulation.²⁶ The presented simulations illustrate that ¹H–¹H couplings do not critically affect the PAIN-CP polarization transfer, except for the Crh protein L63N to T62Cα polarization transfer which involves the shorter ¹H–¹H distance (2.1 Å). In this case, the overall polarization transfer involves a direct PAIN-CP mechanism as well as a non-negligible part relayed through the ¹H–¹H dipolar coupling between L63H and T62Hα.

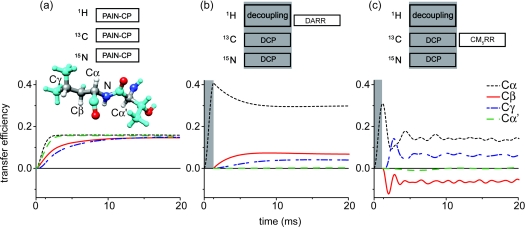
Figure 10.

Backbone nitrogen to sidechain carbons polarization transfer: (a) ¹⁵N–¹³C δp₀ PAIN-CP at ω_r/2π = 20 kHz with p_C = p_N = 2.6 and p_H = 2.4. (b) NCACX with DCP (ω_1C/2π = 25 kHz, ω_1N/2π = 35 kHz and 100 kHz ¹H decoupling) followed by DARR (ω_1H/2π = 10 kHz) mixing at ω_r/2π = 10 kHz. (c) NCACX with DCP (ω_1C/2π = 30 kHz, ω_1N/2π = 50 kHz and 100 kHz ¹H decoupling) followed by CM₅RR (ω_1C/2π = 100 kHz, phase ±11.46°) mixing at ω_r/2π = 20 kHz. Simulations were performed at ω_0H/2π = 750 MHz. The spin system [inset of panel (a)] is extracted from the Crh x-ray structure (PDB ID: 1mu4) (Ref. ³⁰) and is composed of L63N, four aliphatic carbons L63C_α, L63C_β, L63C_γ, T62C_α (grey atoms) and the four protons mainly involved in the spin dynamics (T62H_α, L63H, L63H_α, L63H_β2, L63H_γ - white atoms). The chemical shifts are taken from the protein assignment (Ref. ³¹). L63N and the protons are irradiated on resonance. The ¹³C carrier frequency is set on resonance with L63C_α. The simulation includes typical CSA tensor parameter for nitrogen (−115 ppm, 0.2), aliphatic carbons (20–25 ppm, 0.0), and proton (5.7 ppm, 0.65).

More generally, the influence of the ¹H–¹H couplings will vary upon the rf settings chosen but will not dominate the spin dynamics of the heteronuclear TSAR transfer.

Contribution of the ¹³C–¹³C relayed transfer to a global heteronuclear proton assisted recoupling

We remark that ¹³C–¹³C PAR can also occur during a ¹⁵N–¹³C PAIN-CP experiment as triple channel irradiation leading to efficient heteronuclear TSAR effect can potentially yield effective homonuclear TSAR effect.¹⁴ In Fig. SI8,²⁶ we show simulations on the tripeptide [U–¹³C,¹⁵N] N-f-MLF-OH of long distance transfers in leucine between a ¹⁵N spin and two ¹³C δ spins 3.5 and 4.4 Å. In the absence of ¹³Cγ, NCδ2 transfer (shorter distance) reaches ∼15% efficiency in ∼15 ms and NCδ1 transfer (longer distance) reaches ∼10% efficiency in ∼20 ms. In presence of ¹³Cγ spin (located almost on the straight line connecting N and Cδ1, ∼3 Å from the nitrogen), both transfers reach ∼10% efficiency in about 10 ms with the initial rate regime substantially accelerated for NCδ1 and almost unchanged for NCδ2. This illustrates that in specific cases (i.e. given a favorable geometry e.g. N, Cγ, Cδ1) the long distance heteronuclear transfer (e.g. N–Cδ1) can contain a contribution from a relayed transfer mechanism through an intermediate spin located in between (here Cγ), which manifest itself in acceleration of the polarization transfer compared to the three spin case.

PAIN-CP FOR ASSIGNMENT OF UNIFORMLY LABELED BIOMOLECULAR SYSTEMS

Sequential contacts: Short mixing carbonyl PAIN-CP

Figure 8 illustrates the potential of PAIN-CP to perform sequential resonance assignments. With the offset on the ¹³C = O region, the ¹⁵N magnetization N_i is distributed to mainly the C_i−1 = O (directly bonded carbon in a previous residue) but also to the C_i (two-bond polarization transfer) and C_i−2. Note that this behavior is complementary to double cross polarization (DCP) and TEDOR experiments in which the mixing time can be chosen to observe exclusively N_i–C_i−1 polarization transfer. Consequently, a comparison of PAIN-CP and DCP/TEDOR spectra may provide a facile approach for extracting additional assignment constraints. Note that the spin system (Fig. 8) is only composed of carbonyls since it was demonstrated in Sec. 3C that under similar experimental conditions (i.e., ¹³C carrier on the carbonyls), almost no polarization transfer to the aliphatic carbons was achieved.

Figure 8.

¹⁵N–¹³C δp₀ PAIN-CP polarization transfer for p_C = p_N = 0.75 and p_H = 1.8 (a) and p_C = p_N = 2.9, p_H = 1.5 (b). ¹⁵N–¹³C δp₀ DCP polarization transfer for p_C = 3.5, p_N = 2.5 and p_H = 10 (c) and p_C = 3.5, p_N = 2.5, p_H = 5 (d). Both sets of simulations were performed at ω_0H/2π = 750 MHz and ω_r/2π = 20 kHz. The spin system is extracted from the Crh x-ray structure (PDB ID: 1mu4) (Ref. ³⁰) and is composed of L63N, three carbonyls (V61C′, T62C′, and L63C′), and the four protons mainly involved in the spin dynamics (T62H, T62Hα, L63H, and L63Hα). The chemical shifts are taken from the protein assignments (Ref. ³¹). The ¹³C carrier offset is set at 177 ppm, L63N, and the protons are irradiated on resonance. The simulation includes typical CSA tensor parameter for nitrogen (99 ppm, 0.19), carbonyls (−76 ppm, 0.9) and proton (5 ppm, 0.7).

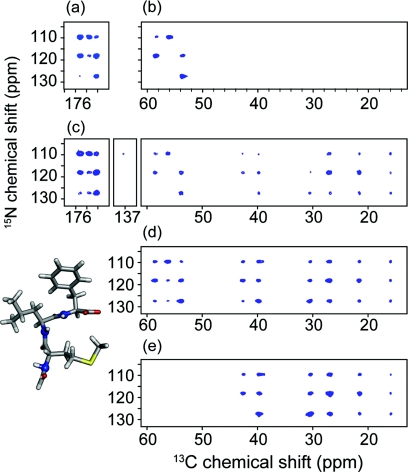
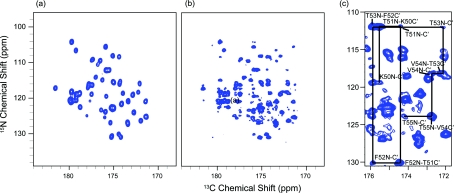
The complementary nature of PAIN-CP and TEDOR (or DCP) is illustrated in Fig. 9 which shows a carbonyl δp₀ PAIN-CP and a carbonyl TEDOR spectra of the [1,3]-¹³C GB1 protein. The PAIN-CP spectrum contains all the cross peaks present in the TEDOR spectrum (corresponding to covalently bonded N_i–C_i−1 spins) and additional weaker cross peaks corresponding to two bond N_i–C_i contacts (r_NC ∼2.3 Å).

Figure 9.

(a) ¹⁵N–¹³C TEDOR and (b) ¹⁵N–¹³C δp₀ PAIN-CP 2D correlation experiments of [1,3]-¹³C GB1. (c) Expansion of the PAIN-CP spectrum. The TEDOR experiment was performed at ω_0H/2π = 750 MHz and ω_r/2π = 12.5 kHz; PAIN-CP was performed at ω_0H/2π = 900 MHz and ω_r/2π = 20 kHz. The TEDOR mixing was optimized to 1.4 ms to maximize the one-bond transfer, and the PAIN-CP mixing time was set to 5 ms according to simulations reported in Fig. 8.

We note that spectral crowding (in part due to the J_C′Cα dominated carbonyl linewidths) renders PAIN-CP 2D experiments rather challenging in larger [U–¹³C,¹⁵N] proteins. Consequently, the full potential of the PAIN-CP selectivity combined with long distance transfers should be fully realized in J-decoupled and higher dimensionality (nD with n ≥ 3) solid-state NMR experiments at high magnetic fields.

Sequential contacts: Short mixing aliphatic PAIN-CP

Figure 10a illustrates the potential of the aliphatic PAIN-CP experiment for performing resonance assignment. By setting the ¹³C offset in the aliphatic region one can achieve selective transfer from nitrogens to aliphatic carbons. In contrast to a DCP or TEDOR experiments, PAIN-CP is able to transfer magnetization from N_i not only to the directly bonded C_αi, but also to the C_αi-1 on a similar time scale with similar efficiency (see the back short dash and green long dash lines). Thus, similar to the carbonyl case, it may be beneficial to compare a short mixing time DCP and PAIN-CP NC_α experiments. Besides NC_α contacts, short mixing time aliphatic PAIN-CP yields contacts between backbone N_i and sidechain C_βi, C_γi, etc. in a single step. As for carbonyl PAIN-CP, the use of higher dimensionality (nD with n ≥ 3) and J decoupled experiments will likely be mandatory in order to fully exploit its potential for resonance assignment and structure determination.

Correlations between backbone ¹⁵N and sidechain ¹³C are also the basis of NCACX experiments that are routinely employed for protein assignments.²⁹ A typical NCACX experiment consists of two steps: first the polarization is transferred from the backbone N_i to the directly bonded C_α,i carbon using the DCP sequence with high power ¹H decoupling; second the polarization is then transferred along the carbon chain using a ¹³C–¹³C recoupling sequence. NCACX experiments thus provide correlations between backbone ¹⁵N and sidechain ¹³C, which often display a better spectral dispersion than the C_α's. In the following we choose to compare the type of NC correlations that can be obtained with PAIN-CP to two variants of the NCACX experiments: the first uses Dipolar assisted rotational resonance (DARR), the second uses cosine modulated rotary resonance (CMRR) as the ¹³C–¹³C recoupling step, respectively.

Figure 10 shows the results of the simulations performed with the spin system displayed in (a), at ω_H0/2π = 750 MHz and ω_r/2π = 20 kHz. Note that the spinning frequency was lowered in the NCACX with DARR case to 10 kHz in order to retain sufficient polarization transfer efficiency (both for DCP and DARR polarization transfer). PAIN-CP clearly appears as a good alternative to the NCACX experiments since it provides an efficient polarization transfer to the side-chain carbons in rather short times (3 to 5 ms for optimum intraresidue transfers depending on the relaxation). This is especially important in the context of NCACX experiments that are known to be rather insensitive. We remark that the PAIN-CP polarization transfer to the side-chain carbons can be achieved using moderate rf levels even at higher spinning frequencies.

With the DARR pulse sequence (see Fig. 10b, we expect around 5–7% polarization transfer efficiency to Cβ's and Cγ's. This appears to be less transfer than in the PAIN-CP case. In contrast, DARR is very easy to implement. At the same time both PAIN-CP and DARR lead to ZQ transfer and thus do not allow for easy discrimination between Cα, Cβ, and Cγ resonances (since all cross peaks have the same sign). In order to decrease the level of ambiguity, DQ sequences can be used for the ¹³C–¹³C recoupling step. The alternating sign of the cross peaks in DQ experiments allows for distinguishing odd and even step relayed transfers. In Fig. 10c we simulate such an experiment using the DQ CM₅RR (Ref. ¹⁸) sequence for the ¹³C–¹³C recoupling step and DCP with some typical rf settings. CMRR was shown to perform very well on protein samples—it does not require concurrent ¹H irradiation and leads to efficient ¹³C–¹³C relayed transfer mechanism.^{14, 18} Figure 10c clearly demonstrates that CMRR can be used to obtain >10% polarization transfer for both Cβ's and Cγ's with very short mixing times (∼0.8 and 1.3 ms, respectively). We remark that the first DCP step is less efficient in (c), since it is much difficult to find efficient DCP conditions at higher MAS frequencies (here 20 kHz) if the maximum ¹H decoupling field is 100 kHz (which is a rule-of-thumb maximum decoupling level used for protein studies in many SSNMR labs). With the C/N power levels used in the simulation much higher ¹H decoupling (>150 kHz, data not shown) is required to reach ∼40% NCα polarization transfer.

PAIN-CP FOR MEDIUM/LONG DISTANCE TRANSFER IN UNIFORMLY LABELED SYSTEMS: APPLICATION TO PROTEIN–PROTEIN INTERACTION AND PROTEIN STRUCTURE DETERMINATION

Long distance transfer and local geometry dependency

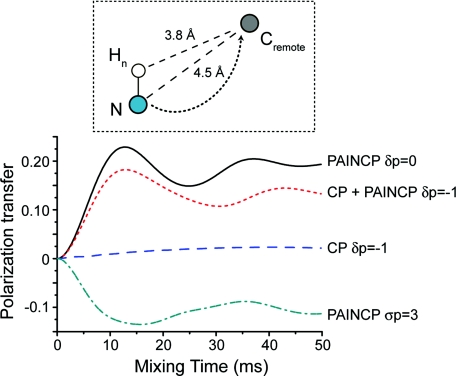
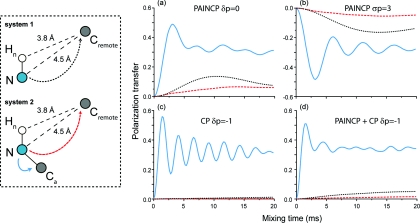
PAIN-CP is ideally suited to detect long distance transfer both in the context of intra- and intermolecular contacts. We illustrate this in Fig. 11 that compares simulations of various PAIN-CP settings and a ¹⁵N–¹³C CP experiment for a long distance NC transfer. The spin system is composed of three spins: nitrogen (where the magnetization is initially located), a remote carbon (r_NC = 4.5 Å) and a proton directly bonded to the nitrogen. PAIN-CP appears superior for ¹⁵N–¹³C magnetization transfer in presence of protons. Since the PAIN-CP transfer does not rely on the very weak NC couplings but involves the product of the NH and HC couplings, with optimized settings we can achieve more than 10% polarization transfer in tens of milliseconds mixing time. The ZQ δp₀ PAIN-CP condition appears the most efficient, but the DQ version is also a viable alternative. The polarization transfer efficiency difference can be explained by the influence of the ¹³C/¹⁵N chemical shift interactions on a ZQ versus DQ ¹⁵N–¹³C magnetization transfer.

Figure 11.

ZQ/DQ heteronuclear polarization transfers between long distant spins for various ¹⁵N–¹³C PAIN-CP/CP conditions. The spin system is composed of three spins (a directly bonded NH pair and a remote carbon with r_NC = 4.5 Å). The initial magnetization is placed on the nitrogen and is detected on the carbon. The simulations include typical CSAs (see Sec. 3). The irradiation is on resonance for all spins. The rf power levels are same as in Fig. 3: p_C = p_N = 2.9 p_H = 2.45 for ¹⁵N–¹³C δp₀ PAIN-CP; p_C = 0.36, p_N = 2.64, p_H = 2.05 for ¹⁵N–¹³C σp₃ PAIN-CP; p_C = 3.5, p_N = 2.5, p_H = 10 for σp_-1¹⁵N–¹³C CP; p_C = 3.5, p_N = 2.5, p_H = 1.9 for ¹⁵N–¹³C CP + δp₋₁ PAIN-CP.

In the discussion above we assumed a model spin system with a particular geometry to analyze the heteronuclear TSAR transfer mechanism. Although, this is a useful point of departure, the details of the spin system geometry and the averages over the powder Euler angles will influence the TSAR polarization transfer process.

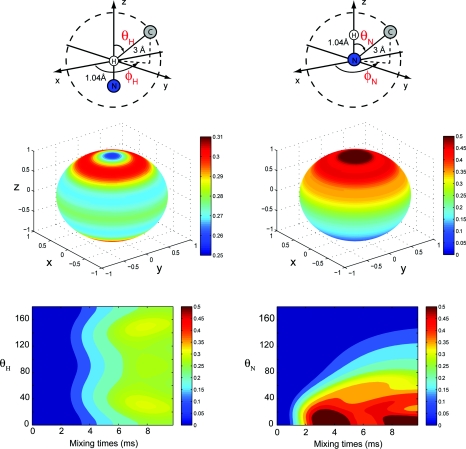
Figure 12 illustrates δp₀ PAIN-CP polarization transfer for a three spin system similar to the one in Fig. 11 as a function of local geometry. The simulated system is composed of a directly bonded ¹⁵N–¹H spin pair and a ¹³C located on a sphere of constant radius centered either on the ¹H spin (left column) or on the ¹⁵N spin (right column). Following the analytical derivation reported in De Paëpe et al.,¹⁴ the effective TSAR recoupling frequency is evaluated as

$$\begin{array}{ccc}\hfill {\omega }_{ZQ,\delta p_0}^{\mathrm{PAIN}\text{-}\mathrm{CP}}& =& \left[\begin{array}{c}\underset{{\omega }_{\mathrm{PAIN}\text{-}\mathrm{CP}}^1}{\underbrace{\frac{1}{{\omega }_r}\left(\mathrm{Re}\left({\omega }_{NH}^1{\omega }_{HC}^{-1}\right)\lambda \left(1,p_C,p_H\right)+i\mathrm{Im}\left({\omega }_{NH}^1{\omega }_{HC}^{-1}\right)\sigma \left(1,p_C,p_H\right)\right)}}\hfill \\ +\underset{{\omega }_{\mathrm{PAIN}\text{-}\mathrm{CP}}^2}{\underbrace{\frac{1}{{\omega }_r}\left(\mathrm{Re}\left({\omega }_{NH}^2{\omega }_{HC}^{-2}\right)\lambda \left(2,p_C,p_H\right)+i\mathrm{Im}\left({\omega }_{NH}^2{\omega }_{HC}^{-2}\right)\sigma \left(2,p_C,p_H\right)\right)}}\hfill \end{array}\right].\hfill \\ & \approx & \frac{1}{{\omega }_r}{d}_{NH}{d}_{HC}\mathrm{f}\left(p_C,p_H,\alpha ,\beta ,\theta ,\varphi \right)\hfill \end{array}$$ (27)

Figure 12.

The spin system used in the simulations is composed of one ¹⁵N spin, one ¹H spin (which are fixed in space), and one ¹³C spin which position is defined on a 3 Å radius sphere by the θ and ϕ spherical coordinates with origin at the ¹H or ¹⁵N in the left/right column, respectively. The spherical map represents the ¹⁵N–¹³C polarization transfer efficiency as a function of the position of the ¹³C spin for a PAIN-CP mixing time of 10 ms using p_C = p_N = 2.9 and p_H = 2.55. The map below represents the ¹⁵N–¹³C polarization efficiency for ϕ = 0 as a function of the mixing time and the θ angle.

It is thus composed of two terms ${\omega }_{\mathrm{PAIN}\text{-}\mathrm{CP}}^1$ and ${\omega }_{\mathrm{PAIN}\text{-}\mathrm{CP}}^2$ proportional to the product of the dipolar couplings d_NH and d_HC, a complicated function of the spherical coordinates

(ϕ and θ) that defines the local geometry of the system, and of the Euler powder angles (α and β). Note that the Euler angle γ is absent from the recoupling frequency, and thus the TSAR mechanism appears as a γ-compensated recoupling mechanism.¹⁴

As shown in the left column of Fig. 12, the polarization transfer from ¹⁵N to ¹³C (after 10 ms of PAIN-CP irradiation) does not depend on the ϕ coordinate and only slightly with respect to the θ angle (∼5% variation). A substantial polarization transfer is present over the entire sphere with slight improvement occurring close to the poles and the equator.

On the other hand, we observe very anisotropic polarization transfer in the case where the ¹³C is on a sphere at fixed distance from the ¹⁵N (right column). In particular we have a significant polarization transfer for θ_N close to zero (i.e., the proton is between the nitrogen and the carbon). For this configuration the ¹H–¹³C distance is minimized yielding a maximum of polarization transfer. This clearly illustrates the difficulty of extracting precise N–C distances from PAIN-CP data but also potential of exploiting the spin system geometry for probing long distance N–C transfer.

Intramolecular contacts in uniformly ¹³C, ¹⁵N labeled Crh protein

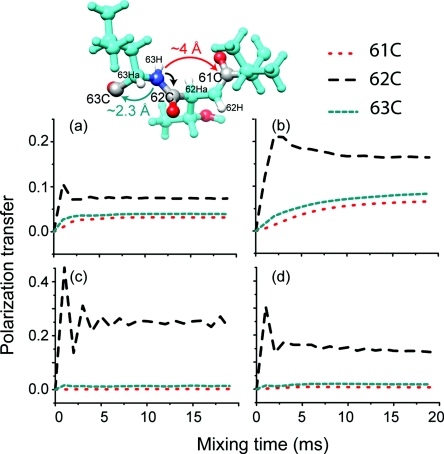
Polarization transfer when both long and short distances (weak and strong dipolar couplings) are present is usually dominated by the stronger coupling. The reason is that (except for REDOR/TEDOR) the heteronuclear recoupling sequences yield noncommuting terms which lead to a truncation phenomenon and favor transfer over short distances (largest NC couplings). This effect is quite significant for first order recoupling sequences (e.g., CP, which is based on the direct reintroduction of the NC dipolar couplings) and is clearly illustrated in Fig. 13 where no polarization transfer over long distance can be achieved in the CP case.

Figure 13.

Long distance ¹⁵N–¹³C polarization transfers for various ¹⁵N–¹³C PAIN-CP/CP conditions. The spin system is composed of four nuclear spins (a nitrogen with directly attached proton, directly bonded C_α and a remote carbon with r_NC = 4.5 Å). The magnetization starts on the nitrogen and is detected on the carbon. The simulations include typical CSAs (see Sec. 3B). The triple irradiation is performed on resonance for each spin. The rf power levels are the same as settings used in Fig. 3: p_C = p_N = 2.9 p_H = 2.45 for δp₀ PAIN-CP in (a); p_C = 0.36, p_N = 2.64, p_H = 2.05 for σp₃ PAIN-CP in (b); p_C = 3.5, p_N = 2.5, p_H = 10 for δp₋₁¹⁵N–¹³C CP in (c), and p_C = 3.5, p_N = 2.5, p_H = 1.9 for ¹⁵N–¹³C CP + δp₋₁PAIN-CP in (d).

Figure 13 shows that the heteronuclear TSAR mechanism described here is an excellent solution for detecting long distance NC contacts even in presence of directly bonded NC spins. Contrary to the ¹⁵N–¹³C CP case in (c) where the long distance transfer is essentially quenched in presence of the directly bonded carbon, the heteronuclear TSAR mechanism suffers only a small reduction of the long distance polarization transfer in the same situation. For δp₀ PAIN-CP (a) and σp₃ PAIN-CP (b), we can still transfer about 10% of the initial ¹⁵N magnetization in 15 ms of irradiation. We remark that ¹⁵N–¹³C CP experiment (performed with very high power proton decoupling) remains the best option for one bond NC transfer with more than 50% efficient transfer with ∼2 ms of irradiation.

Note that care should be taken when interpreting ¹⁵N–¹³C CP experiments employing moderate CW ¹H irradiation. As seen in the previous section, contributions from the PAIN-CP term can also be present in such cases. This is illustrated in Fig. 13d where the one-bond NC transfer is less intense than in the ¹⁵N–¹³C CP only case in Fig. 13c, whereas long distance NC transfer is still detectable in less than 20 ms. In this specific case, the one-bond transfer is mainly performed through the NC dipolar couplings while the long distance NC transfer relies primarily on the PAIN-CP terms. In both cases, the transfer is only possible when the chosen ¹H irradiation minimizes the TSAR autocross terms introduced in the previous sections.

As a consequence, for [U–¹³C,¹⁵N] systems, there are many good alternatives for obtaining one bond NC polarization transfer but rather few reliable methods for obtaining long distance NC polarization transfer. The only alternatives to transfer magnetization between NC spins distant by more than one bond is to use band-selective techniques,⁹ 3D BASE TEDOR¹⁰ or the NHHC²¹ experiment, which first transfers magnetization from nitrogens to protons, then from protons to surrounding protons, and finally back to carbons.²¹ PAIN-CP nicely complements these experiments as it is more sensitive than NHHC, requires small number of experiments to probe multiple distance restraints compared to frequency selective methods, and still leads to faster polarization buildup compared to TEDOR (helping to minimize polarization losses due to relaxation). Finally it is worth noting that PAIN-CP significantly outperforms TEDOR for detecting long distance NC contacts in systems with high density of nitrogen atoms (i.e. including many amino acids containing nitrogens in the side chain).

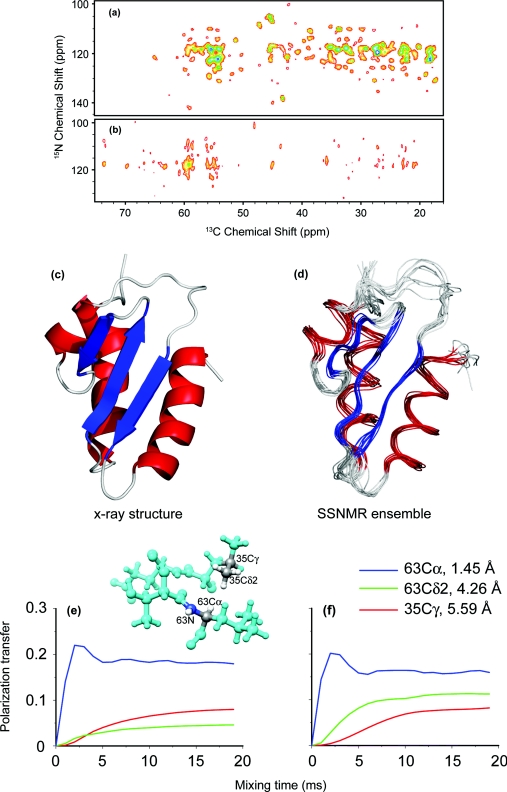
Figure 14a shows the 2D ¹⁵N–¹³C correlation spectrum of the Crh protein, a dimeric crystalline model protein of 2*85 residues, with a known x-ray structure³⁰ and solid-state NMR chemical shifts.³¹ The spectrum was recorded using 10 ms of PAIN-CP mixing time (ω_0H/2π = 750 MHz, ω_r/2π = 20 kHz). The spectrum displays a large number of cross peaks, including many long distance contacts. Figures 14e, 14f, complement the experimental data presented in panel (a) by illustrating the beneficial effect of the fast methyl rotation on long distance PAIN-CP transfer (a notable feature of TSAR based methods¹⁴). The efficiency of the simulated polarization transfer appears significantly improved by the fast methyl rotation and the corresponding buildup time and efficiency at the plateau are fully consistent with the three distance classes: i.e., the shortest distance contacts builds up to ∼20% efficiency in 2 ms, the 4.26 Å distance to ∼10 % in 7 ms, and the longest distance contacts (5.59 Å) to 7.5% in 10 ms.

Figure 14.

2D ¹⁵N–¹³C correlation PAIN-CP spectra on [U–¹³C,¹⁵N] (a) and heterogeneously 50%/50% [U–¹³C]/[U–¹⁵N] labeled (b) Crh. (a) was obtained at ω_0H/2π = 750 MHz, ω_r/2π = 20 kHz with 15 ms mixing time. (b) was obtained at ω_0H/2π = 900 MHz, ω_r/2π = 20 kHz. The spectrum in (b) is a sum of experiments with mixing time of 5 and 10 ms. (c) Crh x-ray structure [PDB entry: 1MU4 (Ref. ³⁰)] and (d) solid-state NMR structures of an isolated monomer. ¹⁵N–¹³C PAIN-CP buildup curves for the spin system [see panel (e)] composed of one nitrogen, three carbons, and five protons without (e) and with fast methyl rotation (f). The magnetization starts on the L63N spin and is distributed to the L63Cα (directly bonded), the L35Cδ2 (4.26 Å distant), the L35Cγ (5.59 Å distant). The three rf power levels of the CW irradiations are chosen based on optimization maps (see Fig. SI 2) (Ref. ²⁶). The rf power level settings (in units of the MAS frequency) are p_C = p_N = 2.9 p_H = 2.45 (δp₀ PAIN-CP).

Intermolecular contacts in heterogeneously labeled Crh protein

Following the work of Etzkorn et al.,³² we investigated intermonomer contacts in the domain-swapped protein dimer of Crh. Specifically we used heterogeneously labeled mixtures composed respectively of ¹⁵N and ¹³C labeled spin species to detect exclusively intermolecular ¹⁵N–¹³C correlations.^{32, 33} Occurrence of numerous intermolecular cross peaks in Fig. 14b confirms the suitability of the heteronuclear TSAR mechanism for characterizing the dimer interface. Such approach should be of importance for investigating protein–protein interactions, as for example, intermonomer contacts in fibrillar proteins. We remark that the PAIN-CP is strongly complementary to TEDOR experiments for probing interfaces between heterogeneously labeled protein domains. Since PAIN-CP depends on the strength and geometry of CH/NH couplings and TEDOR on the strength of NC couplings these two techniques should yield complementary sets of cross peaks and information about the nature of the interface.

Application to protein structure determination

To evaluate the potential of the PAIN-CP for structural characterization of a large biological system, we performed a 10 ms PAIN-CP experiment on the [U–¹³C,¹⁵N]-Crh [Fig. 14a]. The spectrum exhibits a large number of additional ¹⁵N–¹³C correlations compared to the intra-residue 2D NCACB reported in Bockmann et al.³¹ Using the x-ray structure of the Crh protein (PDB entry: 1MU4) (Ref. ³⁰) and a distance cut-off of about 6 Å, we can classified the cross peaks in sequential, medium-range and long-range ¹⁵N–¹³C contacts. 123 long-range ¹⁵N–¹³C contacts could be assigned in the PAIN-CP spectrum, demonstrating the ability of PAIN-CP experiment to detect long-range contacts (within a 6 Å distance range) in a uniformly ¹³C/¹⁵N labeled protein. Furthermore we modified the structure calculation protocol previously reported by adding the ¹⁵N–¹³C correlations identified in the 10 ms mixing PAIN-CP data to the previously assigned ¹³C–¹³C PAR distance restraints¹⁴ as internuclear ¹⁵N–¹³C restraints with a distance range of 7 Å. The addition of the PAIN-CP distance restraints improves the precision (from 1.36 to 1.06 Å), as well as the accuracy (from 1.7 to 1.5 Å) of the Crh structures calculated compared to the calculation using only the PAR restraints, as is shown by the high-resolution bundle of NMR structures in Fig. 14d.

CONCLUSIONS

We have introduced and characterized the heteronuclear version of the TSAR mechanism applied to ¹⁵N–¹³C polarization transfer in biomolecular systems. The PAIN-CP sequence relies on a three spin process involving second order cross terms between ¹H–¹⁵N and ¹H–¹³C dipolar couplings that promotes polarization transfer between ¹⁵N and ¹³C via trilinear operators such as N^±C^∓H_Z. The analytical expressions derived from AHT permit visualization of the subspace in which the TSAR spin dynamics evolves (either ZQ or DQ) and indicates that the processes are influenced by the presence of autocross term involving chemical shift tensors, ¹H–X dipolar couplings. We show that the autocross terms may be compensated to a large extent for specific combinations of ¹⁵N, ¹³C, and ¹H rf fields. In addition, we demonstrate that dipolar truncation is significantly reduced in the heteronuclear TSAR mechanism which allowed us to record high quality spectra of the uniformly labeled protein. Finally, we demonstrate that this methodology can be used to probe molecular interfaces in heterogeneously labeled protein systems.