The effect of correlated bath fluctuations on exciton transfer

Abstract

Excitation dynamics of various light harvesting systems have been investigated with many theoretical methods including various non-Markovian descriptions of dissipative quantum dynamics. It is typically assumed that each excited state is coupled to an independent thermal environment, i.e., that fluctuations in different environments are uncorrelated. Here the assumption is dropped and the effect of correlated bath fluctuations on excitation transfer is investigated. Using the hierarchy equations of motion for dissipative quantum dynamics it is shown for models of the B850 bacteriochlorophylls of LH2 that correlated bath fluctuations have a significant effect on the LH2 → LH2 excitation transfer rate. It is also demonstrated that inclusion of static disorder is crucial for an accurate description of transfer dynamics.

INTRODUCTION

Excitation transfer plays a fundamental role in photosynthetic organisms.^{1, 2} Photosynthesis begins with the absorption of a photon that creates an excited state on a pigment molecule, such as the bacteriochlorophyll (Bchl) found in phototrophic bacteria.³ The excitation is transferred multiple times between the pigments of light harvesting (LH) complexes until it arrives at a reaction center (RC) pigment–protein complex. At the RC the photon energy is used for charge separation that establishes a voltage difference across the cell membrane.^{4, 5}

While photosynthetic systems have been studied extensively, many questions in relation to excitation transfer in biological contexts remain to be fully addressed.^{6, 7, 8, 9, 10} One of the remaining fundamental questions is how different manifestations of environmental noise affect excitation transfer.^{11, 12} It has been shown that in photosynthetic systems environmental fluctuations broaden excited state energies that enhance transfer between pigments and are also responsible for the degree of quantum coherence between electronically excited pigments.^{11, 13} Even with the dephasing effects of the environment taken into account, quantum coherence can last up to hundreds of femtoseconds and, thus, play a role in excitation transfer.^{8, 14}

Developing a theory of excitation transfer and dynamics that correctly takes environmental effects into account has been a topic of great interest for many years.^{15, 16, 17, 18, 19, 20, 21, 22, 23, 24} Much effort has been spent to determine the key parameters that describe the system and correctly reproduce experimentally observable properties such as optical spectra.^{25, 26, 27, 28, 29, 30} Although many parameters can be measured directly or calculated, the parameters that determine the effect of the environment on the system remain difficult to determine. These parameters are usually determined from fits of optical spectra calculated by various theoretical models to experimentally measured spectra.^{13, 31, 32, 33, 34, 35}

In the last two decades computational power and theoretical developments have made it possible to include more detail and make fewer assumptions when modeling photosynthetic light harvesting systems. As a result, it is currently possible to calculate excitation dynamics for biologically relevant systems where non-Markovian dynamic disorder and quantum coherence effects cannot be neglected.^{6, 8, 36, 37, 38} Although many methods take into account non-Markovian effects,^{18, 39, 40} here the hierarchy equations of motion (HEOM) are employed, which do not require the secular approximation or the assumption of 0 K. One of the aspects that still requires further investigation is the effect or importance that correlated bath fluctuations play for excitation transfer.^{6, 13, 41, 42}

For multi-pigment systems, the assumption is usually made that pigments are independently coupled to the environment.^{6, 8, 37} This assumption has been partly examined by the inclusion of phenomenologically assigned correlated bath fluctuations between multiple pigments in model and biological systems.^{12, 20, 30, 41, 42, 43, 44, 45, 46, 47, 48, 49} It was found that environmental fluctuations that are correlated between pigments have a significant effect on 2D spectra^{30, 42, 44} and on excitation transfer between these pigments.^{13, 20, 41, 43, 45, 47, 48, 49} The effect, however, on the rate of excitation transfer between clusters of pigments, where there are correlated environmental fluctuations within a pigment cluster, but not between pigment clusters, remains to be investigated.

First, the effect that correlated bath fluctuations within a cluster of pigments can have on intercluster excitation transfer is examined. Second, the effect of correlated bath fluctuations and the influence of structural, or static, disorder on linear absorption spectra and excitation transfer is investigated. In Sec. 2 we present the hierarchy equations of motion that are used to calculate excitation dynamics and absorption spectra, which is then followed by our results for the effect of correlation in a model Bchl dimer and in light harvesting complex 2 (LH2).

METHODS

In this section the structure of the LH2 pigment–protein complex is described and the coupling between the excited states of the Bchls of interest is given. A model Hamiltonian which describes the excited states of the Bchls of interest, and how they are coupled to a thermal bath, is then introduced. The HEOM,^{6, 18, 37, 50, 51, 52} which describe the excitation dynamics of the system using the model Hamiltonian, is also given. Next, a description of how static disorder is taken into account is provided, which is followed by a brief derivation on how the linear absorption spectrum is calculated from the HEOM. Finally, the various cases of correlated bath fluctuations that are investigated in this work are specified.

LH2 B850

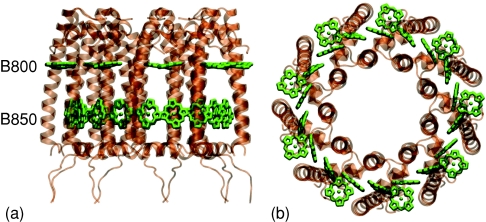
LH2 is a pigment–protein complex, shown in Fig. 1, that consists of a cyclic array of nine transmembrane α, β-polypeptide heterodimers. Each polypeptide pair contains three Bchls: a dimer of Bchls bound near the outer membrane surface and a single Bchl near the inner membrane. Two rings, one of 18 Bchls and one of 9 Bchls, are formed and are, respectively, responsible for the 850 and 800 nm absorption peaks of LH2. The ring of 18 closely packed Bchls, responsible for the 850 nm absorption peak, is known as the B850 ring and the ring of 9 Bchls, responsible for the 800 nm absorption peak, is known at the B800 ring.

Figure 1.

(a) Side view and (b) top view of the LH2 pigment–protein complex showing the B800 and B850 Bchl rings.

The coupling between neighboring Bchls in the B850 ring are given by two terms: the coupling between Bchls within the same α, β dimer V and the coupling between Bchls of neighboring α, β dimers V′. The site energies and nearest neighbor interaction energies for the Q_y state of the B850 Bchls are taken to be³⁵E_n = 12 390 cm⁻¹, V = 315 cm⁻¹, and V′ = 245 cm⁻¹. The coupling between non-nearest neighbor Bchls is determined using the induced dipole–induced dipole approximation which states

$$V_{nm}=C\frac{{\widehat{\mathbf{d}}}_n·{\widehat{\mathbf{d}}}_m-3\left({\widehat{\mathbf{d}}}_n·{\widehat{\mathbf{r}}}_{nm}\right)\left({\widehat{\mathbf{d}}}_n·{\widehat{\mathbf{r}}}_{nm}\right)}{{\left|{\mathbf{r}}_{nm}\right|}^3},$$ (1)

where the coupling constant is C = 348 000 ų cm⁻¹,⁵³ the unit vector ${\widehat{\mathbf{d}}}_n$ defines the orientation of the transition dipole moment of the Q_y excitation of Bchl n, and r_nm is the vector connecting the Mg atoms Bchls n and m.

Model Hamiltonian

A model Hamiltonian can be constructed to give a reduced description of the system of interest.^{6, 7, 8, 41, 54, 55, 56} In the case of the B850 ring of LH2 this includes only the Q_y excited state of the B850 Bchls.^{20, 56, 57, 58, 59, 60, 61, 62} The Hamiltonian is^{6, 53, 63, 64}

$${\widehat{H}}_S=\sum _{n=1}^N{E}_n|n⟩⟨n|+\sum _{m,n=1}^N{V}_{mn}|m⟩⟨n|,$$ (2)

where |n⟩ refers to the Q_y excited state of the nth Bchl. ${\widehat{H}}_S$ can be diagonalized to give the zero temperature excitons |α⟩ with energies ϵ_α

$${\widehat{H}}_S=\sum _{\alpha }{ϵ}_{\alpha }|\alpha ⟩⟨\alpha |.$$ (3)

To immerse the system in a dynamic environment a linear coupling to a bath of harmonic oscillators is introduced, as done in the spin-boson (Caldeira–Leggett) model.^{5, 9, 65} The Hamiltonian of the bath is

$${\widehat{H}}_B=\sum _j\left(\frac{p_j^2}{2m_j}+\frac{m_j}{2}{\omega }_j^2{q}_j^2\right),$$ (4)

and the Hamiltonian of the interaction between system and bath is

$${\widehat{H}}_I=\sum _{a=1}^M{\widehat{F}}_a\sum _j{c}_{aj}{q}_j,$$ (5)

where a runs over the number, M, of system-bath coupling terms ${\widehat{F}}_a$ and c_aj is the coupling strength of oscillatory mode j to the coupling terms ${\widehat{F}}_a$. The system-bath coupling terms ${\widehat{F}}_a$ set how thermal fluctuations are correlated between Bchls and are specified in detail below. The introduction of the interaction Hamiltonian shifts the minimum positions of the harmonic oscillators making up the bath degrees of freedom. To counteract this shift, a renormalization term is introduced

$${\widehat{H}}_{\text{ren}}=\sum _{a,b=1}^M{\widehat{F}}_a{\widehat{F}}_b\sum _j\frac{c_{aj}{c}_{bj}}{2m_j{\omega }_j^2}.$$ (6)

Including the renormalization term, the effective system Hamiltonian is ${\widehat{H}}_{\text{eff}}={\widehat{H}}_S+{\widehat{H}}_{\text{ren}}$. The total Hamiltonian is then given by

$${\widehat{H}}_T={\widehat{H}}_{\text{eff}}+{\widehat{H}}_B+{\widehat{H}}_I.$$ (7)

Hierarchy equations of motion

The dynamics of a quantum system can be obtained from the time evolution of the density matrix ρ_T that describes all the degrees of freedom. The time evolution of the density matrix is calculated using⁶⁶

$${\dot{\rho }}_T\left(t\right)=-\frac{i}{\hslash }{\mathcal{L}}_T\left(t\right){\rho }_T\left(t\right),$$ (8)

where L_T·=[H_T,·]. The solution is

$${\rho }_T\left(t\right)=\exp \left(-\frac{i}{\hslash }{\int }_0^{t}d\tau {\mathcal{L}}_T\left(\tau \right)\right){\rho }_T\left(0\right).$$ (9)

The total density matrix describes both system and bath degrees of freedom. By taking the trace over the bath degrees of freedom one can obtain the time evolution of the system density matrix ρ(t), averaged over all bath fluctuations. The result is formally expressed as

$$\rho \left(t\right)={\mathrm{tr}}_{\mathrm{B}}\left\{\mathcal{U}\exp \left(-\beta H_B\right)\right\}\rho \left(0\right)∕{\mathrm{tr}}_{\mathrm{B}}\left\{\exp \left(-\beta H_b\right)\right\},$$ (10)

where β = 1∕k_BT and the time evolution operator U is

$$\mathcal{U}=\exp \left(-\frac{i}{\hslash }{\int }_0^{t}d\tau {\mathcal{L}}_T\left(\tau \right)\right).$$ (11)

The HEOM arise when taking the time derivative of the bath averaged time evolution operator.^{6, 18, 37, 50, 51} The time derivative of the bath averaged time evolution operator allows the introduction of auxiliary density matrices that take into account the non-Markovian behavior of the system. Once the bath average is taken, the effect of the thermal fluctuations enters only through the bath correlation function C_a(t),

$$\begin{array}{c}\hfill C_a\left(t\right)={〈u_a\left(t\right)u_a\left(0\right)〉}_B=\frac{1}{\pi }{\int }_0^{\infty }d\omega J_a\left(\omega \right)\frac{\exp \left(-i\omega t\right)}{1-\exp \left(-\beta \hslash \omega \right)},\end{array}$$ (12)

where u_a(t) = ∑_jc_ajq_j(t). The spectral density J_a(ω) is used to characterize the oscillatory modes of the thermal bath. The hierarchy equations of motion has only been derived for few spectral densities, such as the Drude spectral density

$$J_a\left(\omega \right)=2\frac{{\lambda }_a{\gamma }_a}{\hslash }\frac{\omega }{{\omega }^2+{\gamma }_a^2},$$ (13)

that is employed accordingly here. The parameter λ_a = 160 cm⁻¹ is the bath reorganization energy and 1∕γ_a = 100 fs is the bath response time; the two values hold for LH2.³⁵ The corresponding correlation function is then⁶⁷

$$C_a\left(t\right)=\sum _{k=0}^{\infty }{c}_{ak}\exp (-{\nu }_{ak}t),$$ (14)

where ν_a0 = γ_a is the Drude decay constant and for k ⩾ 1, ν_ak = 2πk∕βℏ are the Matsubara frequencies.⁵⁰ The coefficients c_ak of the correlation function are⁶

$$\begin{array}{c}\hfill c_{ak}=\left\{\begin{array}{cc}\hfill {\displaystyle ({\lambda }_a{\gamma }_a∕\hslash )\left[\cot \left(\frac{\beta \hslash {\gamma }_a}{2}\right)-i\right],}& \hfill \mathrm{for}k=0,\\ \hfill (4{\lambda }_a{\gamma }_a∕\beta {\hslash }^2)\left[{\nu }_{ak}∕\left({\nu }_{ak}^2-{\gamma }_a^2\right)\right],& \hfill \mathrm{for}k\ge 1.\end{array}\right.\end{array}$$ (15)

The summation in Eq. 14 is truncated at a level K using the Markovian approximation⁵⁰ ν_aKexp ( − ν_aKt) ≈ δ(t).

Accurate spectral densities have been determined for the B850 ring of LH2,^{9, 10, 68, 69} however, these contain multiple sharp peaks. The spectral densities can be composed into a series of Lorentzians,⁷⁰ where each Lorentzian peak introduces two additional exponential terms^{67, 71} into the correlation function. Each additional exponential term effectively doubles the size of the system, making it computationally intractable due to the poor scaling of the method.^{6, 51, 67} The Drude spectral density employed here was previously determined to accurately reproduce the experimental spectra of LH2³⁵ and makes the calculation using the HEOM possible.

The derivation of the HEOM for the correlation function in Eq. 14 has been presented in a previous paper.⁶ The hierarchy of density matrices ${\widehat{\rho }}_{\mathbf{n}}$ are indexed by a vector n = (n₁₀, …, n_1K, …, n_M0, …, n_MK), n = (n₁, …, n_M), where each n_a is given by n_a = (n_a0, …, n_aK). The density matrix with index n = (0, …, 0) is the system density matrix of primary interest. The equations of motion governing the time evolution of the hierarchy of density matrices are

$$\begin{array}{ccc}\hfill {\dot{\widehat{\rho }}}_{\mathbf{n}}& =& -\frac{i}{\hslash }[{\widehat{H}}_{\text{eff}},{\widehat{\rho }}_{\mathbf{n}}]-\sum _{a=1}^M\sum _{k=0}^K{n}_{ak}{\nu }_{ak}{\widehat{\rho }}_{\mathbf{n}}\hfill \\ & & -\sum _{a=1}^M\left(\frac{2{\lambda }_a}{\beta {\hslash }^2{\gamma }_a}-\sum _{k=0}^K\frac{c_{ak}}{{\nu }_{ak}}\right)[{\widehat{F}}_a,[{\widehat{F}}_a,{\widehat{\rho }}_{\mathbf{n}}]]\hfill \\ & & -i\sum _{a=1}^M\left[{\widehat{F}}_a,\sum _{k=0}^K{\widehat{\rho }}_{{\mathbf{n}}_{ak}^{+}}\right]\hfill \\ & & -i\sum _{a=1}^M\sum _{k=0}^K{n}_{ak}\left(c_{ak}{\widehat{F}}_a{\widehat{\rho }}_{{\mathbf{n}}_{ak}^{-}}-{\widehat{\rho }}_{{\mathbf{n}}_{ak}^{-}}{\widehat{F}}_a{c}_{ak}^{*}\right).\hfill \end{array}$$ (16)

The density matrices ρ_n are coupled to those with indices ${\mathbf{n}}_{ak}^{\pm }=\left(n_{10},...,n_{ak}\pm 1,...,n_{MK}\right)$. Each density matrix in the hierarchy is assigned to a tier L, which is numbered by

$$L=\sum _{a=1}^M\sum _{k=0}^K{n}_{ak}.$$ (17)

There are infinitely many density matrices in the hierarchy to treat, making an exact integration of Eq. 16 intractable. To integrate Eq. 16 all density matrices with L greater than a cut-off value L_trunc are truncated. Different truncation schemes have been used with the simplest one being to set all the truncated density matrices to zero. This is referred to as the time-nonlocal truncation and has been shown to introduce spurious peaks in calculations of absorption spectra.^{37, 71} A different truncation scheme is to treat all density matrices with L > L_trunc with the Markovian approximation. This so-called time-local truncation introduces the following approximation for all the density matrices with L = L_trunc,^{37, 52}

$$\sum _{k=0}^K{\widehat{\rho }}_{{\mathbf{n}}_{ak}^{+}}\approx -i\left({\widehat{Q}}_a^K\left(t\right){\rho }_{\mathbf{n}}-{\rho }_{\mathbf{n}}{{\widehat{Q}}_a^K\left(t\right)}^{†}\right),$$ (18)

where

$$\begin{array}{ccc}\hfill {\widehat{Q}}_a^K\left(t\right)& =& {\int }_0^t\left(\sum _{k=0}^K{c}_{ak}\exp \left(-{\nu }_{ak}\tau \right)\right)\exp \left(-\frac{i}{\hslash }{H}_{\text{eff}}\tau \right){\widehat{F}}_a\hfill \\ & & \times \exp \left(\frac{i}{\hslash }{H}_{\text{eff}}\tau \right)d\tau .\hfill \end{array}$$ (19)

The time-local truncation has been shown to improve the convergence of absorption spectra of molecular aggregates with respect to the level of truncation^{37, 71} and is employed in the present work.

Static disorder

The total Hamiltonian H_T, stated in Eq. 7, describes in principle all possible influences of the thermal bath on the system. However, the ensemble average over the spectral density in Eq. 13 assumes that the system dynamics is slower than the thermal fluctuations. This precludes the proper description of long time fluctuations that can arise from large scale deformations of the protein complex.

To take the unaccounted for disorder (often termed “static” disorder) into account the excited state energy levels are taken to be Gaussian distributed with means E_n and widths σ_n for each pigment n.^{6, 29, 32, 34, 37, 72, 73} Thus to include the static disorder, one replaces E_n by E_n + δE_n where δE_n is drawn from a Gaussian distribution with zero mean and standard root mean squared deviation σ_n; for the case of LH2 we assume σ_n = 220 cm⁻¹, a value taken from previous fits to experimental absorption spectra.³⁵ An average over many realizations of static disorder is thus taken for a more realistic view of the excitation dynamics present in the system.

Absorption line shape

The absorption line shape I(ω) can be calculated through Fourier transform of the transition dipole–transition dipole autocorrelation function,^{20, 55, 56} namely through

$$I\left(\omega \right)\propto \mathrm{Re}{\int }_0^{\infty }d\tau \exp \left(i\omega \tau \right)⟨\widehat{\mu }\left(0\right)\widehat{\mu }\left(t\right)⟩,$$ (20)

where $\widehat{\mu }={\sum }_n{\mu }_n\left(|0⟩⟨n|+|n⟩⟨0|\right)$ is the total transition dipole operator. In the current study, it is assumed that the transition dipole strength μ_m is identical for all Bchls, and is set to μ. The transition dipole–transition dipole autocorrelation function is given by

$$〈\widehat{\mu }\left(0\right)\widehat{\mu }\left(t\right)〉={\mathrm{tr}}_{\mathrm{S}}\left\{{\mathrm{tr}}_{\mathrm{B}}\left\{\widehat{\mu }\left(0\right)\widehat{\mu }\left(t\right)\right\}\right\}.$$ (21)

The total transition dipole operator does not depend on the bath degrees of freedom q_j and, hence, the trace over the bath degrees of freedom can be carried out to give

$${\mathrm{tr}}_{\mathrm{S}}{\mathrm{tr}}_{\mathrm{B}}\left\{\widehat{\mu }\left(0\right)\widehat{\mu }\left(t\right)\right\}={\mathrm{tr}}_{\mathrm{S}}\left\{\widehat{\mu }\left(0\right){\mathrm{tr}}_{\mathrm{B}}\left\{\widehat{\mu }\left(t\right)\right\}\right\}.$$ (22)

The time evolution of the total transition dipole operator $\widehat{\mu }\left(t\right)$ is given by

$$\widehat{\mu }\left(t\right)=\exp \left(-\frac{i}{\hslash }{\widehat{H}}_{\text{tot}}t\right)\widehat{\mu }{\rho }_g\exp \left(\frac{i}{\hslash }{\widehat{H}}_{\text{tot}}t\right),$$ (23)

where ${\rho }_g=\exp (-\beta {\widehat{H}}_B)∕{\mathrm{tr}}_{\mathrm{B}}\left\{\exp (-\beta {\widehat{H}}_B)\right\}$ is the equilibrium state of the bath. It can be seen then that ${\mathrm{tr}}_{\mathrm{B}}\left\{\widehat{\mu }\left(t\right)\right\}$ is simply the time evolution of the system density matrix $\widehat{\rho }\left(t\right)$ from the initial state $\widehat{\rho }\left(0\right)=\widehat{\mu }$. The absorption line shape can thus be calculated using

$$I\left(\omega \right)\propto \mathrm{Re}{\int }_0^{\infty }d\tau \exp \left(i\omega \tau \right){\mathrm{tr}}_{\mathrm{S}}\left\{\widehat{\rho }\left(0\right)\widehat{\rho }\left(\tau \right)\right\},$$ (24)

where $\widehat{\rho }\left(0\right)=\widehat{\mu }$ and $\widehat{\rho }\left(\tau \right)$ is evaluated using Eq. 16.

Correlated bath fluctuations

To proceed with the integration of the HEOM, the system-bath interaction terms ${\widehat{F}}_a$ need to be specified. Two systems are examined with different forms of correlated bath fluctuations. First a model two-site system is examined with uncorrelated, perfectly correlated, and anticorrelated bath fluctuations. The case of the B850 ring of LH2 is then investigated with the already mentioned models of correlation between neighboring Bchls; a distance-based correlation is also considered.

Model dimer

The model dimer consists of the two B850 Bchls in an αβ subunit. Three different system-bath coupling mechanisms for the Bchl dimer are investigated. The first corresponds to each Bchl independently coupled to the thermal bath. In this case M = 2 and ${\widehat{F}}_a=|a⟩⟨a|$. A change in the position of oscillator q_j can thus affect the energy level of each excited state |a⟩ independently, as given by the individual coupling terms c_aj. The interaction Hamiltonian H_I is thus

$${\widehat{H}}_I=\sum _{a=1}^2|a⟩⟨a|\sum _j{c}_{aj}{q}_j.$$ (25)

The other two cases considered are perfectly correlated, denoted as “+”-correlated, fluctuations between the Bchls and perfectly anticorrelated, denoted as “−”-correlated, bath fluctuations. For “+”-correlated fluctuations any change in the position of oscillator q_j affects each excited state |a⟩ in exactly the same way, both will either increase or decrease in energy by the same amount. For “−”-correlated fluctuations, any change in the position of oscillator q_j will change the energy level of each excited state |a⟩ in exactly opposite ways, i.e., where one increases by a certain amount the other will decrease by the same amount. For both “+” and “−”-correlated cases there is only a single system-bath interaction term, i.e., M = 1 holds in Eqs. 5, 6. In the case of “+”-correlated fluctuations F₁=(|1⟩⟨1|+|2⟩⟨2|) holds and the interaction Hamiltonian becomes

$${\widehat{H}}_I=\left(|1⟩⟨1|+|2⟩⟨2|\right)\sum _j{c}_j{q}_j,$$ (26)

where c_j has replaced c_aj since we only have a single bath coupling term. For “−”-correlated fluctuations F₁=(|1⟩⟨1|−|2⟩⟨2|) holds and the interaction Hamiltonian becomes

$${\widehat{H}}_I=\left(|1⟩⟨1|-|2⟩⟨2|\right)\sum _j{c}_j{q}_j.$$ (27)

To investigate the effect of intradimer correlated fluctuations on the interdimer excitation transfer, a four Bchl system is constructed from the nearest dimers of two LH2s in steric contact.

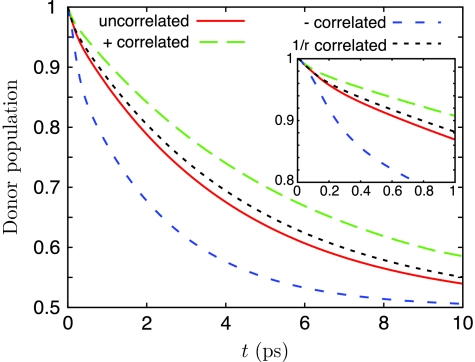
Figure 6.

Donor B850 population for uncorrelated, “+”-correlated, “−”-correlated, and (1∕r)-based correlated bath fluctuations, for the pair of LH2s shown in Fig. 3.

LH2

For the B850 ring, four cases of correlation are investigated, the three cases discussed above and a distance-based correlation. In all the cases the system-bath coupling terms ${\widehat{F}}_a$ are normalized such that $\mathrm{tr}{\widehat{F}}_a{\widehat{F}}_a=1$ to ensure that the total reorganization energy on each Bchl is kept constant. For perfectly correlated and perfectly anticorrelated bath fluctuations the system-bath coupling terms are

$${\widehat{F}}_a^{\pm }=\frac{1}{\sqrt{2}}\sum _{n=1}^{18}\left(|n⟩⟨n|\pm |n+1⟩⟨n+1|\right),$$ (28)

where cyclic counting is employed such that 18 + n ≡ n.

The distance-based correlation is employed to mimic coupling due to Coulomb interactions between charges. The assumption here is that the fluctuations in the environment surrounding a Bchl n will also affect Bchl m ≠ n via Coulomb interaction, such that the coupling is inversely proportional to the distance between Bchls m and n. The system-bath coupling terms in this case are

$${\widehat{F}}_a^C=C_a\sum _{n=1}^{18}\left[\frac{r_0}{r_{an}}+\left(1-\frac{r_0}{r_{an}}\right){\delta }_{an}\right]|n⟩⟨n|,$$ (29)

where r_an is the distance from Bchl a to Bchl n, r₀ is a scaling factor that we set to 1 Å and

$$C_a={\left(1+r_0^2\sum _{n\ne a}{r}_{an}^{-2}\right)}^{-1∕2}.$$ (30)

The maximum correlation with the distance-based system-bath coupling terms is then ∼0.1 for neighboring Bchls. Mixed quantum mechanical∕molecular mechanical calculations on LH2 have calculated the maximum correlation between B850 Bchls to be near this value.⁶⁸

RESULTS

The effect of correlated bath fluctuations is presented here for the Bchl dimer and for the B850 ring of LH2. First, the effect on the absorption spectrum and excitation transfer for different cases of correlation are presented for the Bchl dimer, in the presence and absence of static disorder. Second, the effect on the absorption spectrum and excitation transfer of different cases of correlation are presented for the B850 Bchls in LH2. All calculations for the model dimer and for the B850 ring were performed at T = 300 K.

Bchl dimers

To examine the effect of bath correlation on absorption spectra and excitation transfer, first a dimer of B850 Bchls is studied. The system Hamiltonian of the dimer is given by Eq. 2 with coupling V = 180 cm⁻¹ between the Bchls chosen as the average of the inter- and intradimer couplings in LH2. All calculations for the dimer were done with cut-offs of L_trunc = 13 and K = 1 using the time-local truncation^{37, 52} and the Markovian temperature correction.⁵⁰ Averages over static disorder were performed over 5000 realizations of disorder.

Dimer spectrum

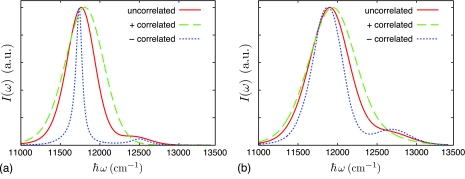
The dimer spectrum excluding static disorder is shown in Fig. 2a. As expected, perfectly correlated bath fluctuations have a Gaussian absorption spectrum. For both anticorrelated and uncorrelated bath fluctuations the absorption spectrum symmetry is lost and an enhanced tail on the blue edge of the spectrum appears. For anticorrelated fluctuations this tail is more prominent and the absorption spectrum is also significantly narrower than in the other cases. A general trend can be seen as the correlation shifts from positively correlated, to uncorrelated, to negatively correlated: the spectrum width decreases and the high-energy tail becomes more prominent.

Figure 2.

Spectra of a dimer with uncorrelated, “+”-correlated, and “−”-correlated bath fluctuations without static disorder (a) and with static disorder (b).

The inclusion of diagonal static disorder of σ = 220 cm⁻¹, shown in Fig. 2b, still preserves the tail features of each spectrum and the aforementioned trend for the spectrum width. In each case of correlation, the inclusion of static disorder increases the width of the spectrum; the most significant increase in spectrum width is seen in the case of “−”-correlated bath fluctuations.

Interdimer transfer

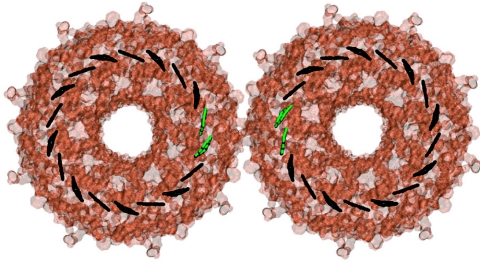
The two nearest B850 Bchl pairs from two LH2s in steric contact (see Fig. 3) serve as a model for the excitation transfer between B850 rings. The interdimer coupling between Bchls is chosen to be the highest and next-highest intercomplex coupling values of 10 and 5 cm⁻¹, respectively. The system of four Bchls is small enough that the computationally intensive HEOM can be treated in the presence of static disorder.

Figure 3.

Two LH2 complexes shown with their respective B850 rings in black. Highlighted in green is the nearest pair of Bchls from each ring. The excitation transfer for the Bchls in green is shown in Fig. 4. The excitation transfer for all Bchls is shown in Fig. 6.

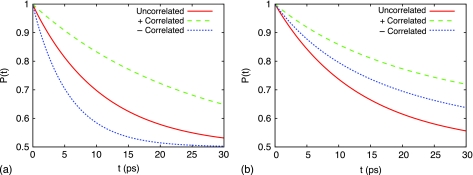
Figure 4a shows the time-dependent population of the donor pair of Bchls. It can be seen that in the absence of static disorder, perfectly correlated bath fluctuations significantly slow the excitation transfer from the donor Bchl pair to the acceptor pair; in contrast, perfectly anticorrelated bath fluctuations enhance excitation transfer. The transfer times τ can be determined from a fit of exp ( − 2t∕τ) to the donor population, and are presented in Table 1 for the pair of Bchl dimer.

Figure 4.

Donor population for uncorrelated, “+”-correlated, and “−”-correlated bath fluctuations (a) excluding and (b) including static disorder.

Table 1.

Interdimer transfer times from fits of a single exponential curve to P(t) for each case of correlation as shown in Fig. 4 for the pair of Bchl dimers. All values are in ps.

	“−”-Correlated	Uncorrelated	“+”-Correlated
Without static disorder	11.3	21.7	49.5
With static disorder	41.7	27.7	65.5

The inclusion of static disorder has a greater impact on excitation transfer in the presence of correlation than in the absence of correlation, as can be seen by comparing Figs. 4a, 4b. The fits of single exponential functions to the time evolution of the donor population shows that there is a 265% increase in the transfer time for “−”-correlated fluctuations when static disorder is included, compared to 28% and 32% increases for uncorrelated and “+”-correlated fluctuations, respectively.

In the presence of static disorder, a dimer with perfectly correlated bath fluctuations exhibits the slowest interdimer excitation transfer. Transfer between dimers with perfectly anticorrelated bath fluctuations is comparably faster; the fastest excitation transfer occurs when each Bchl has independent bath fluctuations.

LH2

For LH2, only the B850 ring of pigments are considered. Due to the large system size, it is computationally unfeasible to account for static disorder in this case. Also due to the large system size, the cut-off was reduced to L_trunc = 4, still employing time-local truncation.

LH2 spectrum

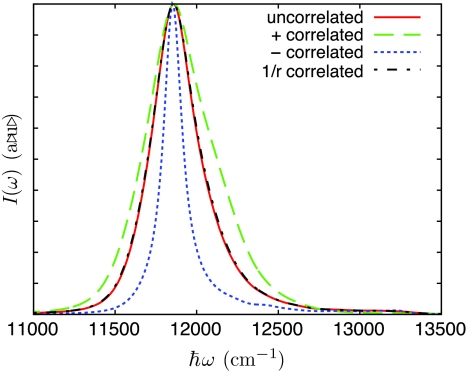
The linear absorption spectrum for a single B850 ring, shown in Fig. 3, was calculated for the cases of (I) uncorrelated bath fluctuations, (II) perfectly correlated fluctuations between each nearest-neighbor pair, (III) perfectly anticorrelated fluctuations between each nearest-neighbor pair, and (IV) (1∕r)-based correlation. It can be seen that the (1∕r)-based correlation yields an absorption spectrum nearly identical to that calculated for uncorrelated bath fluctuations.

The trend of a narrowing spectral width as correlation between pigments goes from positive to negative, found for a Bchl dimer, is also seen in Fig. 5 for the B850 ring of LH2. The increase in the number of pigments masks the signature of correlation from the high-energy tail region, however, there is still a small increase in the tail peak with decreasing correlation. As the spectral features of the Bchl dimer were preserved and in some cases enhanced by the inclusion of static disorder, it is expected that the same holds for the LH2 spectrum.

Figure 5.

Linear absorption spectrum for the B850 ring of LH2 for uncorrelated, “+”-correlated, and “−”-correlated and (1∕r) -correlated bath fluctuations.

Inter-LH2 transfer

To test the effect of differently correlated bath environments on excitation transfer, the time evolution of the system density matrix ρ(t) was calculated for the B850 rings of two LH2s that are in steric contact (see Fig. 3). The increase in system size made the cut-off of L_trunc = 4 computationally too demanding and, thus, was reduced to L_trunc = 3. Although this reduction in the cut-off does have an affect on the excitation relaxation dynamics, it was seen, based on shorter calculations (data not shown) of the donor populations at t = 1 ps, that there was less than 2% difference between L_trunc = 4 and L_trunc = 3 for any of the cases of correlated fluctuations. The comparison between the different cases of correlation thus remains valid even for the reduced truncation.

The evolution of the donor population is shown in Fig. 6 for the different cases of correlation. In contrast to the linear absorption spectra, there is an observable difference in the excitation transfer between uncorrelated bath fluctuations and (1∕r)-correlated bath fluctuations. Perfect correlation between neighboring Bchls hinders excitation relaxation from the initial state, which reduces transfer between B850 rings. In contrast, anticorrelated bath fluctuations of neighboring Bchls assists relaxation from the initial state. This can be seen from the faster initial decline (see inset of Fig. 6) of the donor population for “−”-correlated bath fluctuations compared to the other cases of correlation. The transfer times based on fits of single exponentials to the donor populations shown in Fig. 6 are given in Table 2.

Table 2.

Inter-LH2 transfer times determined from fits of a single exponential curve to P(t) for each case of correlation as shown in Fig. 6 for the pair of B850 rings. All values are in ps.

“−”-Correlated	Uncorrelated	(1∕r)-Correlated	“+”-Correlated
4.7	8.03	8.89	11.17

The effect of correlation on excitation transfer between two B850 rings is similar to that on excitation transfer between two Bchl dimers. As nearest-neighbor correlation decreases from perfectly correlated, to partially correlated (1∕r-correlated) to negatively correlated, the transfer time also decreases. This trend is identical to that which is observed for the transfer between two Bchl dimers excluding the effect of static disorder.

CONCLUSION

The effect of correlated dynamic disorder on excitation transfer between clusters of Bchls was investigated for a model Bchl dimer system and for the B850 ring of light harvesting complex LH2. In either case the extremes of perfectly correlated and perfectly anticorrelated coupling to heat baths were studied and compared to that of completely uncorrelated bath coupling. The aim was to investigate how fluctuations of a heat bath that are correlated between Bchls in a cluster affect excitation transfer to another cluster of Bchls. It was shown that for both the Bchl dimer and the B850 ring, correlated bath fluctuations broaden the absorption spectrum and suppress excitation transfer as compared to uncorrelated bath fluctuations. In contrast, negatively correlated intracluster bath fluctuations tend to narrow the absorption spectrum and enhance intercluster excitation transfer.

Hennebicq et al.⁷⁴ studied the effect of correlated fluctuations between a donor and acceptor pair where, in contrast to the present investigation, the correlations were between the donor and acceptor pigments. They found that in the weak coupling limit, for an over-damped Brownian oscillator the effect of same or opposite sign correlations was to effect a respective decrease or increase of the reorganization energy. The effect of an increase in reorganization energy is to damp out the coherent oscillations within the donor cluster of pigments and induce quick relaxation from the initial state into the steady state.

The respective changes in the transfer rate between clusters of pigments with intracluster fluctuations can be understood based on the differences in the absorption spectra for each case of correlation. In the case of perfectly anticorrelated fluctuations, the absorption spectrum is narrowest with the effect that most of the excitation is carried by a single, partially coherent, delocalized state. Furthermore, the exciton state carrying most of the excitation is one of the lower energy states with a high transfer rate to the acceptor.⁶ As the correlation increases from negative to positive values, the absorption spectrum broadens and the excitation is shared between more of the higher energy exciton states, which have lower transfer rates, and thus the overall transfer is slowed down.

The inclusion of static disorder was also shown to have a significant impact on the absorption spectra and excitation transfer in the case of the Bchl dimer. Due to the large size of the B850 ring and the poor scaling of the hierarchy equations of motion, only a dimer system could be modeled with static disorder. It was shown that the inclusion of static disorder slows down excitation transfer and broadens the spectra for all cases of correlation investigated. In particular, the enhancing effect of negative correlation on excitation transfer is countered by the inclusion of static disorder: the narrow absorption band is clearly broadened such that the low-energy exciton state with the higher transfer rate carries less of the excitation. This effect is not as prominent in the cases of uncorrelated and positively correlated fluctuations.

Since the absorption spectra and excitation migration of B850 rings follow the same correlation-based trends as seen for the Bchl dimers excluding static disorder, it is expected that static disorder should have a similar effect on the B850 rings as it has on Bchl dimers. Our results indicate that the inclusion of intra-LH2 correlated bath fluctuations, whether positive or negative, would likely slow inter-LH2 excitation transfer.

There are many questions that remain unanswered, such as how the interplay of the various parameters affect excitation transfer in the presence of correlated fluctuations. Similarly, it would be interesting to understand what the effect of correlated static disorder could be.