Discovering amino acid patterns on binding sites in protein complexes

Abstract

Discovering amino acid (AA) patterns on protein binding sites has recently become popular. We propose a method to discover the association relationship among AAs on binding sites. Such knowledge of binding sites is very helpful in predicting protein-protein interactions. In this paper, we focus on protein complexes which have protein-protein recognition. The association rule mining technique is used to discover geographically adjacent amino acids on a binding site of a protein complex. When mining, instead of treating all AAs of binding sites as a transaction, we geographically partition AAs of binding sites in a protein complex. AAs in a partition are treated as a transaction. For the partition process, AAs on a binding site are projected from three-dimensional to two-dimensional. And then, assisted with a circular grid, AAs on the binding site are placed into grid cells. A circular grid has ten rings: a central ring, the second ring with 6 sectors, the third ring with 12 sectors, and later rings are added to four sectors in order. As for the radius of each ring, we examined the complexes and found that 10Å is a suitable range, which can be set by the user. After placing these recognition complexes on the circular grid, we obtain mining records (i.e. transactions) from each sector. A sector is regarded as a record. Finally, we use the association rule to mine these records for frequent AA patterns. If the support of an AA pattern is larger than the predetermined minimum support (i.e. threshold), it is called a frequent pattern. With these discovered patterns, we offer the biologists a novel point of view, which will improve the prediction accuracy of protein-protein recognition. In our experiments, we produced the AA patterns by data mining. As a result, we found that arginine (arg) most frequently appears on the binding sites of two proteins in the recognition protein complexes, while cysteine (cys) appears the fewest. In addition, if we discriminate the shape of binding sites between concave and convex further, we discover that patterns {arg, glu, asp} and {arg, ser, asp} on the concave shape of binding sites in a protein more frequently (i.e. higher probability) make contact with {lys} or {arg} on the convex shape of binding sites in another protein. Thus, we can confidently achieve a rate of at least 78%. On the other hand {val, gly, lys} on the convex surface of binding sites in proteins is more frequently in contact with {asp} on the concave site of another protein, and the confidence achieved is over 81%. Applying data mining in biology can reveal more facts that may otherwise be ignored or not easily discovered by the naked eye. Furthermore, we can discover more relationships among AAs on binding sites by appropriately rotating these residues on binding sites from a three-dimension to two-dimension perspective. We designed a circular grid to deposit the data, which total to 463 records consisting of AAs. Then we used the association rules to mine these records for discovering relationships. The proposed method in this paper provides an insight into the characteristics of binding sites for recognition complexes.

Background

Protein-protein interactions have become important in drug design. Proteins are the major catalytic agents, signal transmitters, and transporters in cells [1]. The interactions are usually involved in signalling cascades and biochemical pathways. When two proteins interact, only a small portion of the surfaces of two proteins are involved. The contacting surfaces are called binding sites. These binding sites determine the functions of proteins. There are seven characteristics of binding sites: residue propensity, hydrophobicity, accessible surface area, shape index, electrostatic potential, curvedness, and conservation scores [2]. Experiments in labs on protein-protein interaction are timeconsuming and very expensive. Some methods for accurately predicting protein-protein interaction have been developed [2–8]. These methods provide tools for predicting the interaction of proteins and protein sequence alignments. If one protein sequence is homologous with another, it may be classified into a same group, further exploiting the known protein so to predict the structures and functions of the unknown protein. In addition, analysis of physicochemical properties of the protein interface also can help us to find out some similar biological functions and characteristics in cell processes.

Protein-protein recognition is defined as: A protein recognizes another protein if they interact and their assembly becomes a transient complex. As for classifying transient complexes and permanent complexes, some literatures applied machine learning to predict results, such as Support Vector Machine [3] and Neural Network [4, 7]. Furthermore, there are also some studies in data mining to predict protein-protein interaction [9]. Fabian et al. [10] used a nonredundant set of 621 protein interfaces to characterize protein-protein interaction. They used the residue frequencies and the propensity of residueresidue to estimate many pairing preferences, which are: residue-residue contacts, amino acid composition, residue-residue contact, specific residueresidue contacts, hydrophobic-hyrdrophobic, hyrdrophobic-charged, oppositely charged residues, and so on. In [12], the three-dimensional data of residues on binding sites from RS-PDB database [13] is used to mine the characteristics of binding site residue compositions from protein-ligand complexes. However, those methods did not further analyze which residues on the proteins more frequently bind with the residues on ligands. Our goal is to apply the association rule mining technique to mine patterns of binding site residues in recognition complexes. Some commonly used methods for mining frequent patterns are Apriori [14], FP-growth [15], and Gradational decomposition algorithm [16]. A pattern is a set of residues which is supported by at least a predefined number of transactions. And a pattern is supported by a transaction if the pattern is a subset of the transaction. Patterns are further analyzed to obtain the hidden relations of residues.

Methodology

Datasets

For the experiment, we adopted the dataset from [17] which consisted of 209 identified transient recognition complexes, including 34 antibody-antigen complexes and 60 enzyme-inhibitor complexes. First, we obtain binding sites from the BOND website ( http://bond.unleashedinformatics.com/), which offers detailed AA numbers of a pair of interaction proteins. Second, we retrieved the protein three-dimensional structure coordinates from PDB [18, 19], which provides a large number of accurate three-dimensional protein complex structures. Since we could not find the matching binding sites on the BOND website from the 209 recognition complexes, we could not integrate them with PDB. After filtering the inadequate data, there are 78 transient recognition complexes for the experiment, as shown in Table 1(see Table 1). The proposed method is divided into two parts respectively: first, forming a circular grid, and then applying the mining association rule. The first part is also subdivided into five steps. As for the association rule, we will use the data mining technique to mine these AA relations.

Circular Grid

Step 1: The three-dimensional coordinate of binding site residues in proteins are obtained by combining the information of PDB file and BOND file. We manually examine and correct the name and number of AAs in the BOND file whether they can match the same AAs in the PDB file for getting the correct three-dimensional coordinates. Moreover, in order to simplify the calculation, we adopt the coordinate of C_a atom of residues. Three points are needed to decide a projected plane. The mid-point of each residue pair on binding sites is computed. The three points are determined as follows: the first point is the mean of all the mid-points. The second point is a mid-point which is farthest from the first point. The third point is a mid-point which is farthest from the second point. Euclidean distance is adopted. Step 2: Project all of the Ca atoms of residues on the binding sites to the plane, which will be different for each protein complex. Step 3: Rotate the residues on the plane twice. First, we rotate the plane parallel with the YZ plane. Second, we rotate the plane again, making it parallel with the XY plane, while eliminating the Z coordinate of residues. Then, we just take the (x, y) results and calculate, as shown in Figure 1.The counter clockwise rotation formula is given in Supplementary material.

Figure 1.

The rotation illustration.

Step 4: All of residues on the plane will then be put into a circular grid, which consists of ten rings: a central ring, the second ring with 6 sectors, the third ring with 12 sectors, and the later rings, which are added to four sectors in order. As for the radius of each ring, it is an arbitrary parameter in our program, but we complete a small calculation on it to obtain its proper value. For each recognition complex, we calculate the center of all residues on binding sites and then find out the longest distance from the center for each complex. Next, we average the longest distances and divide the result by 10. Finally, we double the average as a radius. Therefore, the radius of each ring is 10 Å. After that, we draw a central ring with the radius from the center, the second ring with double radius from the center, and so on. The radian of a sector of each ring (r_i) has the formula as follows: The radian of a sector of each ring = 2 * PI / r_iwhere r_i = {1, 6, 12, 16, 20, 24, 28, 32, 36 , 40}, PI = 3.1415926535. Figure 2 illustrates the partitioning of protein complex 1BKD into circular sectors. Step 5: Finishing the above work, we refer each sector as a transaction record. A transaction record is a data mining term, which is also called an itemset. In this study a transaction is the set of AAs in a sector on the binding sites, like the transaction X = {R_leu, L_asp, …}. In the transaction, we add a prefix to an item (i.e., an AA). Prefix L is added to the AAs on the convex side of the protein complex; and prefix R is for the concave side. After we retrieve these transactions from each sector, there are total 463 transactions, which consist of 78 recognition complexes. An example of an itemset generated from a protein complex is shown in Figure 3.

Figure 2.

The illustration of protein complex 1BKD. The left picture shows the result of above steps.

Figure 3.

The illustration of itemset generation.

Association Rules

Here, we briefly introduce association rule mining. For a market example, the association rule {Milk, Cheese} → {Bread} means: if Milk and Cheese are bought, then customers are likely to buy Bread.A transaction supports an itemset if the itemset is contained in the transaction. A set of items is referred to an itemset, and in this paper the items consist of residues. The support of an itemset is the number of transactions that contain the itemset. If the support of an itemset is larger than the predetermined minimum support, it is called a frequent itemset. The support of a rule X→ Y is the support of X ∪ Y. The confidence of a rule X→ Y is the conditional probability that a transaction having X also contains Y. An association rule meets the requirements of userdefined minimum support and minimum confidence.In order to discover hidden relationships and characteristics of amino acids on the binding site, we apply association rule mining on the 463 transactions. The analytic results can help biologists to better understand the amino acids on the binding site of recognition protein complexes.

Results

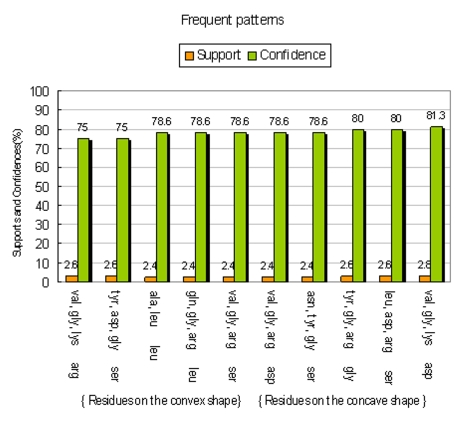
In the first experiment, we try to find the frequent appearance residues on the binding sites of all recognition complexes. Table 2 (see Table 2) shows the result of applying association rule mining on the 463 AA transactions. In Table 2 (see Table 2), we discovered that no matter which side residues form on a protein, {arg} binds at the highest frequency; or, we can say {arg} appears most on the binding sites in the recognition complexes.In the second experiment we take the shape of binding sites into account. In data mining terminology, we put {arg} to the consequent and observe the antecedent {antecedent} → {consequent}, as illustrated in Figure 4. We set the minimum support at 1.5% and the minimum confidence at 80%. The results we mined, such as {phe, ser} →{arg}, are shown in Figure 5. Figure 6 shows {arg} on the concave shape of binding sites in a protein and the mining AA patterns on the convex shape of binding sites in another protein. The minimum support and the minimum confidence is the same above. Furthermore, we are also interested in the higher frequency AA patterns on the binding sites in recognition complexes. Figure 7 describes AAs on the convex binding sites in a protein, which contact more frequently with the AA patterns on the concave binding sites in another protein. The minimum support is 2% and the minimum confidence is 75%. For the same above-mentioned experiment, we also mined the opposite side to discover different situations (Figure 8). The minimum support is also 2% and the minimum confidence is also 75%. All of above experiments show if we set various Supports and Confidences properly, and we will discover more surprising facts in the dataset of recognition protein complexes.

Figure 4.

The illustration for convex and concave shape of binding sites.

Figure 5.

The relations between {arg} on the convex side in a protein and AA patterns on the concave side in another protein.

Figure 6.

The relations between {arg} on the concave side in a protein and AA patterns on the convex side in another protein.

Figure 7.

Frequent patterns are consisted of AAs on the convex and AA patterns on the concave. For an example, {val, ile} → {gly}, {gly} is on the convex of binding sites in a protein, and {val, ile} is on the convex of binding sites in another protein.

Figure 8.

Frequent patterns are consisted of AAs on the concave of binding sites in a protein and AA patterns on the convex of binding sites in another protein.

Conclusion

In this study, we present a mining method for the relationship among AAs on the convex or concave binding sites in protein complexes, and take the advance of data mining to discover several interesting AA patterns. Furthermore, we analyzed them on different binding sites to make the results more biochemically meaningful. Before using the association rule mining techniques, we had the difficult task of integrating BOND files with PDB structure files, which contain three-dimensional coordinates of AAs. Taking advantage of the twodimensional circular grid, the distance range of each mining AA patterns came within 10Å, making the discovery of AA patterns more meaningful. By analyzing the frequency of residues by using different radii, we found {cys} always appears fewest on the binding sites in recognition complexes. As for the probability of appearance, {pro}, {his}, {trp}, and {met} are also rated low. Oppositely, {arg} and {asp} appear most on the binding sites in recognition complexes. Perhaps the protein complex dataset is not large enough since it only generates 438 transactions. As a result, we are unable to find more patterns or hidden relationships among the AAs on the binding sites. However, our experimental results can be exploited as an attribute of feature vectors to improve the prediction of protein-protein recognition or protein-protein interactions accurately.