Abstract
We used FRET to examine the kinetics and thermodynamics of structural changes associated with ADP release in myosin V, which is thought to be a strain sensitive step in many muscle and non-muscle myosins. We also explore essential dynamics using FIRST/FRODA starting with three different myosin V X-ray crystal structures to examine intrinsic flexibility and correlated motions. Our steady-state and time resolved FRET analysis demonstrates a temperature dependent reversible conformational change in the nucleotide binding pocket. Our kinetic results demonstrate that the nucleotide binding pocket goes from a closed to an open conformation prior to the release of ADP while the actin binding cleft remains closed. Interestingly, we find that the temperature dependence of the maximum actin-activated myosin V ATPase rate is similar to the pocket opening step, demonstrating this is the rate limiting structural transition in the ATPase cycle. Thermodynamic analysis demonstrates the transition from the open to closed nucleotide binding pocket conformation is unfavorable because of a decrease in entropy. The intrinsic flexibility analysis is consistent with conformational entropy playing a role in this transition as the MV.ADP structure is highly flexible compared to the MV.APO structure. Our experimental and modeling studies support the conclusion of a novel post-power-stroke actomyosin.ADP state in which the nucleotide binding pocket and actin binding cleft are closed. The novel state may be important for strain sensitivity as the transition from the closed to open nucleotide binding pocket conformation may be altered by lever arm position.
Keywords: Myosin, Actin, Motility, Motor Proteins, FRET
Myosins are molecular motors capable of converting chemical energy into mechanical work through a cyclic interaction with actin filaments in what is known as the mechanochemical ATPase cycle. There is substantial evidence to support the lever arm hypothesis of force generation in which small conformational changes in the nucleotide-binding region are coupled to a large rotation in the lever arm or light chain binding region [1, 2]. The swing of the lever arm generates nanometer displacements of actin filaments in muscle contraction and walking of myosin along actin in non-muscle cells. In addition, coupling between the active site and the actin binding region is critical to allow myosin to cyclically attach and detach from the actin filament. A large cleft in the 50 kDa region separates the actin binding region into an upper and lower 50 kDa subdomain. Considerable evidence suggests this cleft favors a closed conformation in the high actin affinity states and an open conformation in the low actin affinity states [3–6]. However, it is unclear how conformational changes in the nucleotide binding pocket are communicated to the lever arm and actin binding cleft. In addition, determining mechanisms of subdomain coupling is critical for understanding how myosin motors adapt their mechanochemical cycle to external loads, a requirement for motor function in a cellular environment.
Several studies have demonstrated the lever arm swing during the mechanical cycle of myosin, including muscle fiber studies [7, 8] and single molecule proccessive walking experiments [9–12]. High resolution crystal structures have captured the lever arm in the pre- and post-power stroke conformation while there is still debate as to what step in the ATPase cycle (before, during, or after phosphate release) the power stoke occurs. However, electron microscopy and image reconstructions studies have observed movements of the lever arm in a subset of myosins when comparing the actomyosin nucleotide-free (APO) and ADP states [13–15] . The observed structural changes along with other biochemical and biophysical studies lead to the hypothesis that the ADP release step may play a role in strain sensitivity [16]. Indeed, a strain sensitive step was originally proposed by Huxley to explain the non-linear force velocity relationship in muscle contraction [17] and later ADP release was found to be the step that limits contractile speed in muscle by White and coworkers [18]. The ADP release step is thought to be strain sensitive in that if the lever arm is exposed to negative strain, force in the direction opposing motion, the ADP release rate will be reduced while if it is exposed to positive strain the ADP release rate is enhanced [16]. In addition, gating between the two heads of the myosin V dimer is thought to occur during the ADP release step and allows for processive walking in which myosin V can take multiple steps along actin prior to detachment. Single molecule studies have provided direct evidence for strain dependent ADP release in the myosin V dimer providing support for the head gating hypothesis [19–22]. Therefore it is critical to understand the structural changes in the nucleotide binding region associated with ADP binding and release to understand this mechanism.
The current study utilizes a method of FRET between dmantADP or IAEDANS actin and FlAsH labeled myosin V [4, 23] to examine the conformation of the nucleotide binding region and the upper 50 kDa subdomain during the ADP binding and release steps. Our studies demonstrate that the conformational change measured by FRET correlates well with the rate limiting step in the actomyosin V ATPase cycle. Our results allow us to propose a model in which strain dependent ADP release is mediated by the conformational change in the nucleotide binding pocket characterized by our FRET studies.
Results
Conformational dynamics of the nucleotide-binding pocket
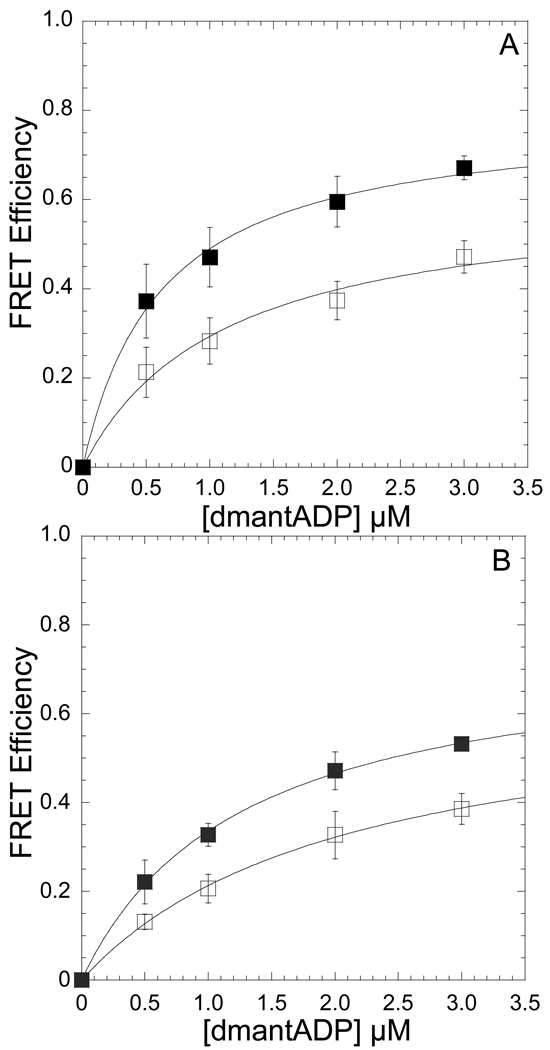
We measured the efficiency of energy transfer by acceptor enhancement with a method described in our previous work [4, 23]. MV FlAsH (0.5 µM) or acto-MV FlAsH served as an acceptor for mant labeled nucleotides (dmantADP or dmantATP). The FRET efficiency as a function of increasing donor concentration was fit to a hyperbolic function to measure the efficiency for 100% bound nucleotide. The efficiencies with MV FlAsH (Figure 1A) and acto-MV FlAsH (Figure 1B) were measured at 4°C and 35°C with this method and distances between the acceptor and donor fluorophores were calculated at both temperatures (Table 1). We also measured the distance between the dmantADP and FlAsH sites with time-resolved FRET. The dmantADP fluorescence lifetime was examined in the acto-MV FlAsH.dmantADP and the acto-MV.dmantADP (7.5 µM: 2.0 µM) complexes. The fluorescence decays were best fit by a double exponential function and the average intensity weighted lifetime was determined at 4, 25, and 35 °C and used to calculate the FRET efficiency by donor quenching. The temperature dependent distances measured by time-resolved FRET (21.0 ± 0.2, 22.8 ± 0.2, and 25.2 ± 1.2 Å, at 4, 25, and 35 °C) were similar to the steady state FRET results.
Figure 1. Conformation of the nucleotide-binding pocket as function of temperature monitored by FRET between dmantADP and MV FlAsH.
The emission of 0.5 µM MV FlAsH (A) or acto-MV FlAsH (B) was measured in the presence of increasing concentrations of dmantADP at 4 and 35 °C. The FRET efficiency was monitored by the enhancement in the acceptor fluorescence and the maximum FRET efficiency was determined by fitting the data to a hyperbolic binding function. Error bars represent the standard deviation from at least three separate experiments done with three different protein preparations.
Table 1.
Summary of FRET measurements with dmant labeled nucleotides and MV or acto-MV FlAsH.
|
Nucleotide-State |
FRET Efficiency (4°C) |
FRET Efficiency (35°C) |
r (Å) (4°C) |
r (Å) (35°C) |
cFRODA (Å) |
|---|---|---|---|---|---|
| aMV FlAsH:dmantADP | 0.79 ± 0.03 | 0.62 ± 0.06 | 22.8 ± 0.7 | 25.6 ± 1.1 | 27.5 ± 1.0 |
| aActo-MV FlAsH:dmantADP | 0.76 ± 0.02 | 0.66 ± 0.03 | 22.9 ± 0.4 | 25.0 ± 0.5 | NA |
| bMV FlAsH:dmantATP | 0.81 ± 0.05 | 0.74 ± 0.03 | 22.5 ±1.1 | 23.3 ± 0.6 | 23.6 ± 0.6 |
FRET efficiency/distance determined from data in Figure 1
FRET efficiency/distance determined from stopped-flow fluorescence transients
Distance distribution from FIRST/FRODA analysis
All error bars represent standard deviation of the mean
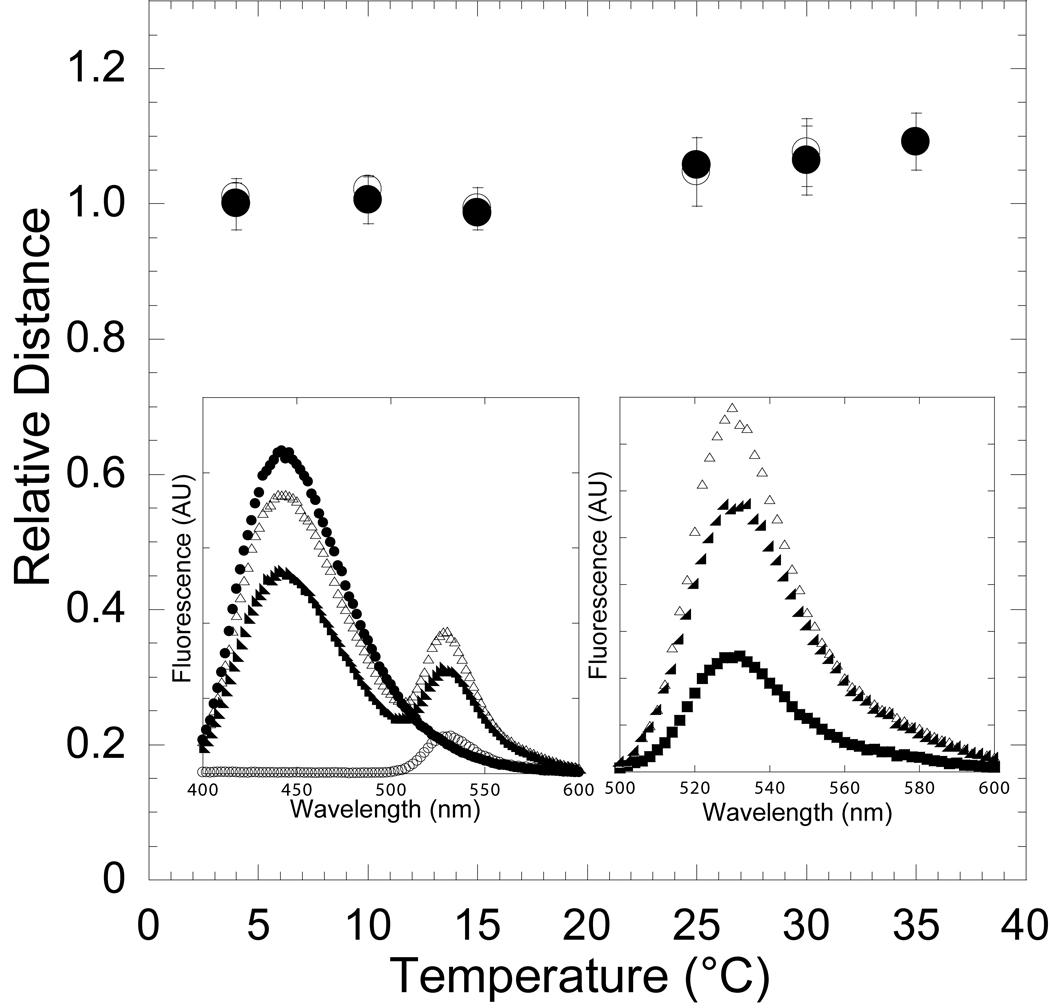
In an effort to demonstrate that the conformational change in the nucleotide binding pocket monitored by FRET was reversible we performed temperature ramping FRET experiments. We examined the energy transfer between MV FlAsH (0.5 µM) and dmantADP (3 µM) in the presence and absence of actin (1–5 µM). The FRET of the same sample was measured at 4, 10, 15, 25, 30 and 35°C and then measured at 30, 25, 15, 10 and 4 °C to demonstrate reversibility. The FRET at each temperature was averaged over at least three experiments done with different protein preparations. The data was corrected for dmantADP quantum yield and fraction bound differences at each temperature. The distance between the FlAsH and dmantADP sites was found to be reversible both in the presence and absence of actin (Figure 2).
Figure 2. Reversibility of the temperature-dependent conformational change in the nucleotide-binding pocket in the presence of ADP.
The FRET of the acto-MV FlAsH:dmantADP complex was measured at 4, 10, 15, 25, 30, and 35 °C (closed circles) and then measured at 30, 25, 15, 10, and 4 °C (open circles) to demonstrate reversibility. The distance between the donor-acceptor pair was determined at each temperature and is shown relative to the distance at 4 °C. Error bars represent the standard deviation from at least three separate experiments done with three different protein preparations. The inset shows the fluorescence spectra of 0.5 µM acto-MV FlAsH in the presence of 3 µM dmantADP at 4 °C (closed circles) and 35 °C (closed triangles), acto-MV FlAsH in the presence of 3 µM unlabeled ADP (open circles), and 3 µM dmantADP (closed squares)(left panel). The MV FlAsH fluorescence after subtracting the dmantADP fluorescence component is shown for each sample (right panel).
We also measured the FRET efficiency and hence the distance between the FlAsH and dmant sites in the presence of dmantATP at 4 °C and 35 °C. We performed these FRET experiments in the stopped-flow to avoid the effects of ATP turnover that would complicate the interpretation of steady-state experiments. MV FlAsH (0.5 µM) was mixed with excess dmantATP (3 µM) and the fluorescence increase (excitation at 365 nm) in the acceptor (515 long pass filter) was monitored as a function of time. The fluorescence transients were fit to a single exponential at both 4 and 35 °C and the amplitude of the transients relative to the acceptor alone fluorescence (MV FlAsH mixed with unlabeled ATP) was used to calculate FRET efficiency. As a control the fluorescence transients of unlabeled MV and dmantATP were examined. We observed a small fluorescence increase at both 4 and 35 °C (<10% of the FRET signal), which was subtracted from the FRET signal in the efficiency calculations. No fluorescence change was observed from mixing MV FlAsH with unlabeled ATP. The FRET efficiency and distance was similar at both 4 and 35 °C in the presence of dmantATP and similar to our measurements at 4 °C in the presence of dmantADP. (Figure 2, Table 1).
Conformational dynamics of the actin-binding cleft
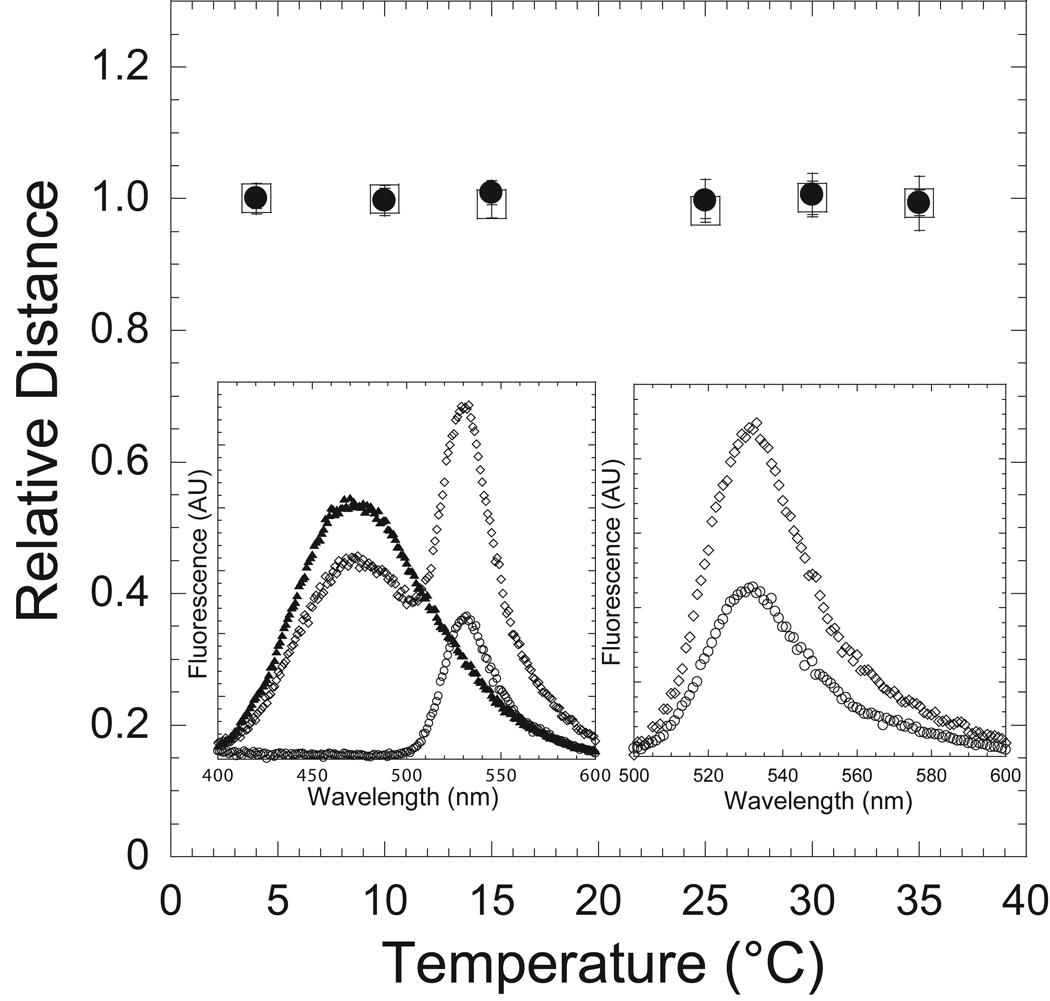
To monitor the changes in the actin binding cleft, the efficiency of energy transfer between the MV FlAsH (0.5µM) and IAEDANS-actin (1µM) was measured as a function of temperature in the nucleotide-free (APO) state and in presence of ADP (200 µM). FRET measurements were examined by steady-state acceptor enhancement as discussed above. The FRET efficiency and distance between the FlAsH and IAEDANS probes was temperature independent and similar in both the ADP and APO states (Figure 3). The calculated distances at 4 and 35 °C (64.8 ± 2.3, 64.8 ± 3.7 in the APO state, 65.5 ± 0.6, 65.6 ± 1.8 in the ADP state, respectively) were also similar to our previous results at 25 °C [4].
Figure 3. Conformation of the actin-binding cleft as a function of temperature in the ADP and APO actomyosin states.
MV FlAsH complexed with IAEDANS-actin in the presence (circles) and absence (squares) of ADP was examined as a function of temperature as in Figure 2. The FRET was monitored by acceptor enhancement and the calculated distance is shown as a function of temperature (relative to the distance at 4 °C). Error bars represent the standard deviation from at least three separate experiments done with three different protein preparations.
Kinetics of dmantADP binding to and dissociation from acto-MV FlAsH
We examined the association and dissociation kinetics with MV FlAsH (3 separate protein preparations) and dmantADP in the presence of actin using stopped-flow rapid mixing techniques. In the association experiments we examined the kinetics of the FRET signal observed upon dmantADP binding to nucleotide-free acto-MV FlAsH (0.5 µM actin; 0.25 µM MV FlAsH). The FRET signal was isolated by exciting dmantADP at 365 nm and measuring the emitted fluorescence from FlAsH with a 515 nm long pass filter. There was no fluorescence observed from the donor only control, dmantADP mixed with acto-MV unlabeled, and acceptor only control, ADP mixed with acto-MV FlAsH [4]. The following scheme (scheme 1) was used to model the dmantADP binding to acto-MV FlAsH at all temperatures.
scheme 1.
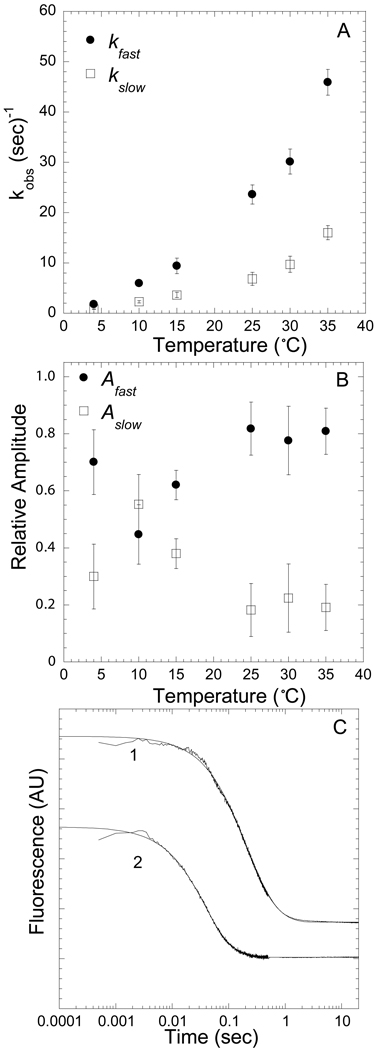
The “strong” and “weak” AM.dmantADP states in scheme 1 refer to the affinity of ADP for myosin. We observed a two exponential rise in fluorescence in the association reaction at all dmantADP concentrations (1.25 – 7.5 µM) and temperatures (4, 10, 15, 25, 30, 35 °C) measured (Figure 4C). The fast phase of the two exponential rise was dependent on dmantADP concentrations (Figure 5B) while the slow phase was independent of dmantADP concentrations at all temperatures. We modeled the two step binding as the initial weak association step (Kligand) followed by a slower conformational change (Kpocket) representing closure of the nucleotide binding pocket. The initial weak association step (Kligand) likely includes two equilibria, a collision complex followed by formation of a weakly bound complex. Under these conditions ([dmantADP]⋙ [actomyosin]) we fit the fast and slow observed rates as well as the amplitude of the slow phase with the following three equations [24, 25].
| (1) |
| (2) |
| (3) |
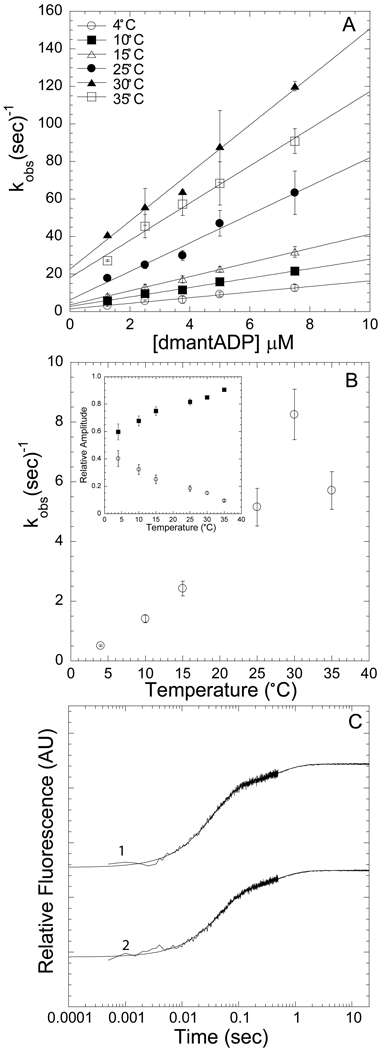
Figure 4A demonstrates the temperature dependence of the fast phase (formation of the “weak” actomyosin.ADP state). A linear fit of the fast phase as a function of dmantADP concentrations was used to calculate the second-order rate constant at each temperature. The slow phase, which was independent of dmantADP concentrations, was also dependent on temperature (Figure 4B). The amplitudes of the fast and slow components were also temperature dependent with a reduction in the slow phase amplitude as a function of temperature (Figure 4B inset). For each of the three protein preparations we fit the associated fluorescence transients with equations 1, 2, and 3 to determine the unknown rate constants (k+pocket and k−pocket). The values for k+ligand and k−ligand (determined from the slope and y-intercept of the fast phase, respectively, as shown in Figure 4A) were held fixed in equations 1, 2, and 3.
Figure 4. Kinetics of dmantADP binding to actomyosin V FlAsH.
We observed a fast and a slow phase with all association reactions measured. A) The fast phase, which was dependent on ligand concentration and temperature, was fit to a linear relationship to obtain the second-order binding constant at each temperature (symbols for 4, 10, 15, 25, 30, 35 °C are in order top to bottom). B) The slow phase was independent of ligand concentration but was temperature dependent. Inset demonstrates the relative amplitudes of the fast (closed squares) and slow (open diamonds) phases at each temperature. C) Representative fluorescence transients are shown on a log scale, 0.25 µM actomyosin V FlAsH and 7.5 µM dmantADP or 2.5 µM dmantADP at 15 °C [biexponential fits: 21.8 ± 0.2 and 2.1 ± 0.1 sec−1 (χ2 = 0.73, R2 = 0.99); 28.7 ± 0.3 and 2.0 ± 0.1 sec−1 (χ2 = 0.96, R2 = 0.99)]. Error bars in A and B represent the standard error from three separate protein preparations.
Figure 5. Kinetics of dmantADP dissociation from ActoMV FlAsH.
Pre-equilibrated acto-MV FlAsH.dmantADP was mixed with excess ATP and all traces were fit to a biexponential function. A) The slow and fast phases are plot as function of temperature. B) The amplitudes of the slow and fast phases are plot as a function of temperature. C) Representative fluorescence transients of dmantADP dissociation from acto-MV FlAsH are plot on a log scale and are fit to a biexponential function. [top trace, 15 °C − 6.0 ± 0.1 and 2.2 ± 0.1 sec−1 (χ2 = 0.37, R2 = 0.99) bottom trace, 25 °C – 27.7 ± 0.3 and 9.7 ± 0.4 sec−1 (χ2 = 0.95, R2 = 0.99). Error bars in A and B represent the standard error from three separate protein preparations.
We also examined the FRET signal observed during the dissociation of dmantADP from acto-MV FlAsH by mixing the acto-MV FlAsH.dmantADP complex (0.5 µM actin, 0.25 µM MV FlAsH, 1.5 µM dmantADP) with excess ATP (1 mM). The fluorescence transients were bi-phasic and fit to a two exponential equation at all temperatures (Figure 5C). The fast and the slow phases were both temperature dependent (Figure 5A), with the fast phase being more steeply dependent on temperature. The relative amplitudes of the fast and slow components were temperature dependent with the slow phase being more dominant at low temperature and the fast phase more dominant at higher temperatures (Figure 5B). Although the rate constants for the fast and slow phase only differ by 3–4 fold the traces were fit with fairly high precision as demonstrated by a χ2 less than one and a R2 near one. We fit the dissociation fluorescence transients of each protein preparation to the following three equations to determine the rate constants of the collision complex and pocket conformational change steps (scheme 1) as derived in Hannemann et al.[24].
| (4) |
| (5) |
| (6) |
The rate constants determined from fitting the dissociation experiments from three separate protein preparations were averaged with the rate constants determined from the association analysis. The overall affinity was calculated with equation 7,
| (7) |
and similar KD values we obtain with titration experiments. A summary of the average values for each of the rate and equilibrium constants are shown in Table 2. The errors are shown as standard error of the mean.
Table 2.
Rate and equilibrium constants measured by FRET.
| Rate Constant | 4°C | 10°C | 15°C | 25°C | 30°C | 35°C |
|---|---|---|---|---|---|---|
| ak+ligand (µM−1·s−1) | 1.5 ± 0.1 | 2.5 ± 0.1 | 3.8 ± 0.1 | 7.6 ± 0.7 | 9.9 ± 0.6 | 12.8 ± 0.9 |
| bk−ligand (s−1) | 1.7± 0.2 | 3.4 ± 0.4 | 5.6 ± 1.3 | 15.4 ± 3.2 | 22.2 ± 1.7 | 38.9 ± 2.5 |
| 1/Kligand (µM) | 1.1 ± 0.2 | 1.4 ± 0.2 | 1.5 ± 0.4 | 2.0 ± 0.5 | 2.2 ± 0.3 | 3.0 ± 0.6 |
| bk+pocket (s−1) | 0.3 ± 0.1 | 1.3 ± 0.4 | 1.2 ± 0.3 | 1.3 ± 0.4 | 2.3 ± 1.0 | 2.0 ± 0.9 |
| bk−pocket (s−1) | 0.7 ± 0.2 | 2.4 ± 0.6 | 3.3 ± 0.7 | 6.3 ± 1.1 | 9.7 ± 1.9 | 12.5 ± 2.6 |
| Kpocket = kon /koff | 0.4 ± 0.2 | 0.5 ± 0.2 | 0.4 ± 0.1 | 0.2 ± 0.1 | 0.2 ± 0.1 | 0.2 ± 0.1 |
| cKD overall (µM) | 0.8 ± 0.2 | 0.9 ± 0.2 | 1.1 ± 0.3 | 1.7 ± 0.4 | 1.8 ± 0.3 | 2.6 ± 0.5 |
| dKD overall (µM) | 0.8 ± 0.1 | 1.0 ± 0.1 | 1.3 ± 0.1 | 1.3 ± 0.1 | 1.5 ± 0.1 | 1.7 ± 0.1 |
Thermodynamic Analysis
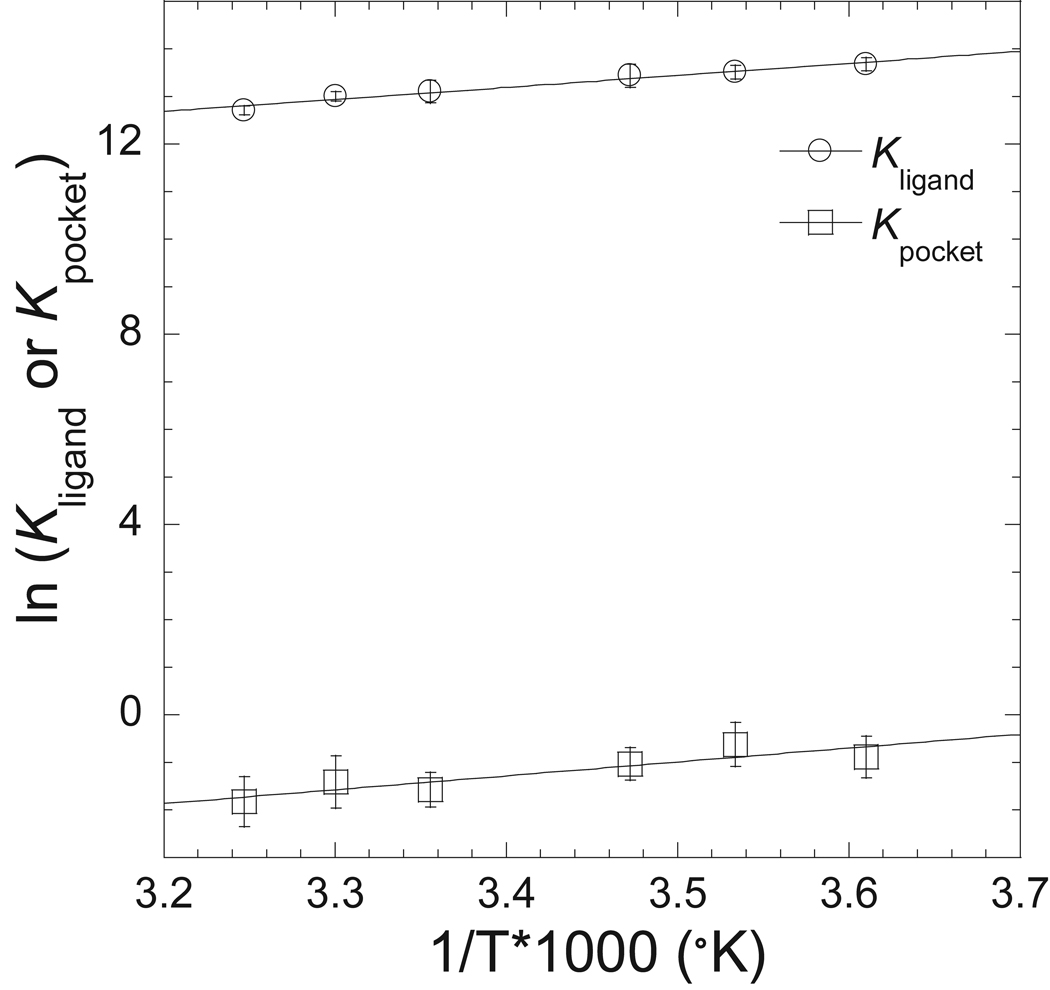
We further analyzed the kinetic data to determine the thermodynamic parameters of the proposed two actomyosin.ADP states, one with a closed pocket (high FRET) and another with an open pocket (low FRET). The temperature dependence of the equilibrium constants for each reaction step, Kligand and Kpocket, were plotted in the form of a van’t Hoff plot to deteremine the enthalpic and entropic component for each step (Figure 6). We found that both the collision complex step (Kligand) and pocket conformational change step (Kpocket) could be fit to linear dependence on temperature. Therefore the van’t Hoff plots were fit to equations 13 and 14 to determine the standard enthalpic and entropic contributions to the free energy change associated with the Kligand and Kpocket steps. The results are summarized in Table 3.
Figure 6. Thermodynamics of the two acotmyosin.ADP states.
The equilibrium constants for the association and pocket conformational changes steps are shown with van’t Hoff plots. The data is fit to a linear relationship to determine the enthalpic and entropic contributions to free energy changes. A summary of the calculated values is shown in Table 3.
Table 3.
Thermodynamic parameters calculated from van’t Hoff plots.
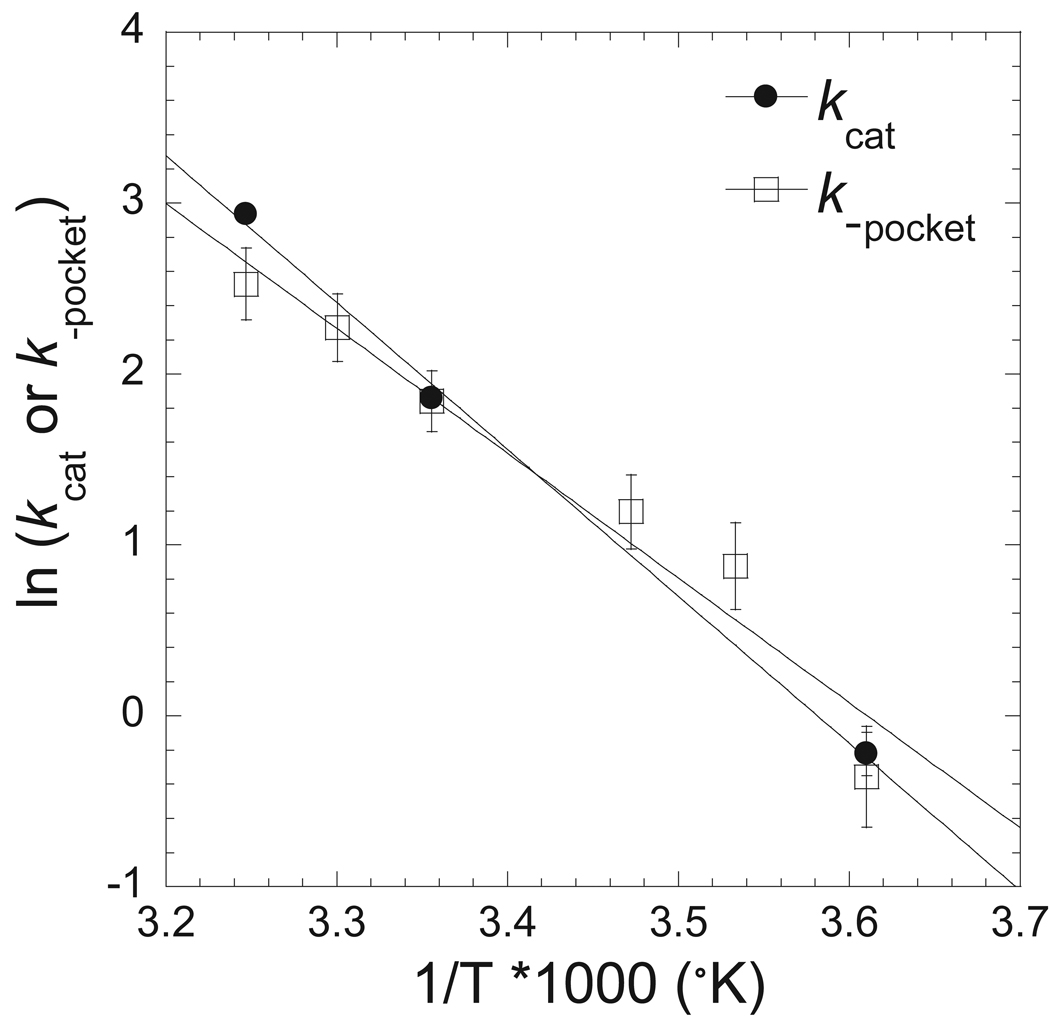
In order to establish the importance of the pocket conformational change step in the actomyosin ATPase cycle we performed actin-activated ATPase assays at a range of temperatures (4°C, 25°C, and 35°C) (Table 4). Our results demonstrate that the maximum rate of actin-activated ATPase activity correlates well with the rate of the pocket opening measured by FRET (Figure 7). We also examined the FRET change associated with the dmantADP release steps in a sequential mix single turnover experiment. We mixed MV FlAsH (0.5 µM) with dmantATP (0.4 µM), allowed the reaction to age for two seconds, and then mixed with actin (final concentrations: 0.25 µM MV FlAsH, 0.2 µM dmantATP, and 25 µM actin). The fluorescence transients were measured at each temperature and were best fit by a single exponential function (Table 4). The single turnover rate was similar to the maximum actin-activated ATPase rate. Therefore, we propose that pocket opening is the rate limiting step in the actomyosin V ATPase cycle at all measured temperatures.
Table 4.
Temperature dependence of MV FlAsH actin-activated ATPase activity.
| Temperature (°C) |
aV0 | bkcat | cKATPase | dk−pocket |
|---|---|---|---|---|
| 4 | 0.04 ± 0.04 | 0.8 ± 0.1 | 2.5 ± 0.5 | 0.8 ± 0.1 |
| 25 | 0.08 ± 0.02 | 6.4 ± 0.3 | 1.4 ± 0.3 | 7.7 ± 0.1 |
| 35 | 0.23 ± 0.22 | 18.8 ± 0.4 | 2.5 ± 0.2 | 19.0 ± 0.1 |
ATPase activity in the absence of actin. Errors represent the standard deviation from 3 separate measurements done with three separate protein preparations.
Maximum actin-activated ATPase activity determined from fit of data to the Michaelis-Menton relationship. Error bars represent the standard error of the fit of data from three separate protein preparations.
Actin concentration at which the ATPase activity is one-half maximal. Error bars represent the standard error of the fit of data from three separate protein preparations.
The rate of dmantADP release measured by single turnover (sequential mixing with dmantATP and then actin).
Figure 7. Correlation of maximal ATPase and pocket conformational change rates as a function of temperature.
The rate constant for pocket opening and maximal ATPase rate are shown as a function of temperature in an Eyring plot. The data is fit to a linear relationship with a similar slope for kcat (slope) and k−pocket (slope) providing evidence that the pocket opening step is rate limiting in myosin V.
Discussion
Myosin motors are capable of altering their kinetic and mechanical cycles in response to external loads while the structural details of this mechanism are currently unclear. Our studies have characterized a key conformational change in the nucleotide binding pocket which is intimately associated with the rate limiting step in the actomyosin V ATPase cycle. The conformational change may be associated with the strain sensitive step in the ATPase cycle which is proposed to be critical for gating the two heads of the dimer in myosin V and limiting maximal sliding velocity in muscle. We interpret our results in the context of defining the coupling mechanism between the load sensing lever arm and nucleotide binding pocket (NBP) that is required for strain sensitivity in myosin motors.
Temperature dependence of the NBP conformation
It is well established that ADP release is the rate-limiting step in the actomyosin V ATPase cycle [26, 27] and there is substantial evidence for multiple actomyosin.ADP states in the kinetic pathway of myosin V [24, 26, 28]. Our results demonstrate the NBP opens during the transition from the strong ADP binding to the weak ADP binding actomyosin.ADP state (k−pocket) and that this conformational change limits the release of ADP (see Scheme 1 where weak and strong refer to the ADP affinity for myosin). Determining the distance change associated with the open and closed NBP conformations would require defining the FRET efficiency of each conformation when both states are populated in the presence of ADP. Ideally, time-resolved FRET would be able to delineate the two different conformations and the average distance associated with each conformation. We obtained an average distance by time-resolved FRET that was similar to our steady state measurements, while the data was not at high enough resolution to fit to a two component FRET model with high certainty. Overall, our FRET results suggest the closed NBP is more populated at low temperature (0–15 °C) and is similar to the closed pocket conformation in the presence of ATP. This is consistent with our previous results that demonstrated the conformation of the NBP remains closed during phosphate release and opens during the rate limiting transition between the two actomyosin.ADP states in single turnover experiments [23]. In the current study, we performed single turnover and actin-activated ATPase experiments as a function of temperature and found both single turnover and maximum ATPase rates were similar to the pocket opening step (k−pocket).
We refer the closed NBP conformation as the conformation in which the upper 50kDa subdomain is rotated toward the NBP which has been demonstrated in the MV.ADP.BeFX crystal structure. The open NBP conformation in which the upper 50 kDa subdomain is rotated away from the NBP was demonstrated in the MV.ADP and MV.APO (nucleotide-free) crystal structures. The motion of the upper 50 kDa subdomain was proposed to be coupled to the movement of switch I in the active site [3, 29] and biochemical evidence [30] support this conclusion. The average distance between the mant and FlAsH sites in the closed conformation (presence of ATP or low temperatures in the presence of ADP) is 22–23 Å while the average distance of the open conformation is 25–26 Å. Thus the pocket appears to be capable of at least a 2–4 Å conformational change when comparing the open and closed states, which is consistent with the crystal structures of myosin V [3, 29] and our simulations (Table 1). Measurements of the pocket conformational change in smooth muscle myosin were similar but the magnitude of the distance change between the ATP and ADP states in the absence of actin was greater (~8 Å) [31]. The differences between these two studies may reflect the different donor/acceptor probe positions or different structural dynamics of myosin II and myosin V.
Computational simulations of the NBP
In order to gain insight into the closed NBP conformation of myosin V in the presence of ADP, which is more populated at low temperature, we investigated the intrinsic flexibility of each of the three crystal structures of myosin V using FIRST/FRODA analysis (see Methods for details). We measured the distance distributions between proline 294, which is near the center of the FlAsH labeling site, and lysine 171, which is near the mant motif based on aligning the structure of myosin V with the structure of myosin II bound to mantADPBeFX [32]. The distance distributions demonstrate that the 294-171 distance in the MV.ADP.BeFx structure does not overlap with the distance distributions of MV.ADP structure (Figure S1), which suggests the MV.ADP structure is not capable of converting to the closed pocket conformation without significantly breaking constraints. In addition, in the MV.ADP state structure we observed very few modes of pocket opening/closing that agree with experiment suggesting that this structure represents the weak open pocket MV.ADP state and that the strong closed pocket MV.ADP state has not been revealed by crystallography. Two other studies came to a similar conclusion in regard to the MV.ADP crystal structure [24, 33]. Our results provide support for a strong MV.ADP conformation that has an ATP-like closed NBP, while it has a closed actin binding cleft (see below).
Conformational dynamics of the actin binding cleft
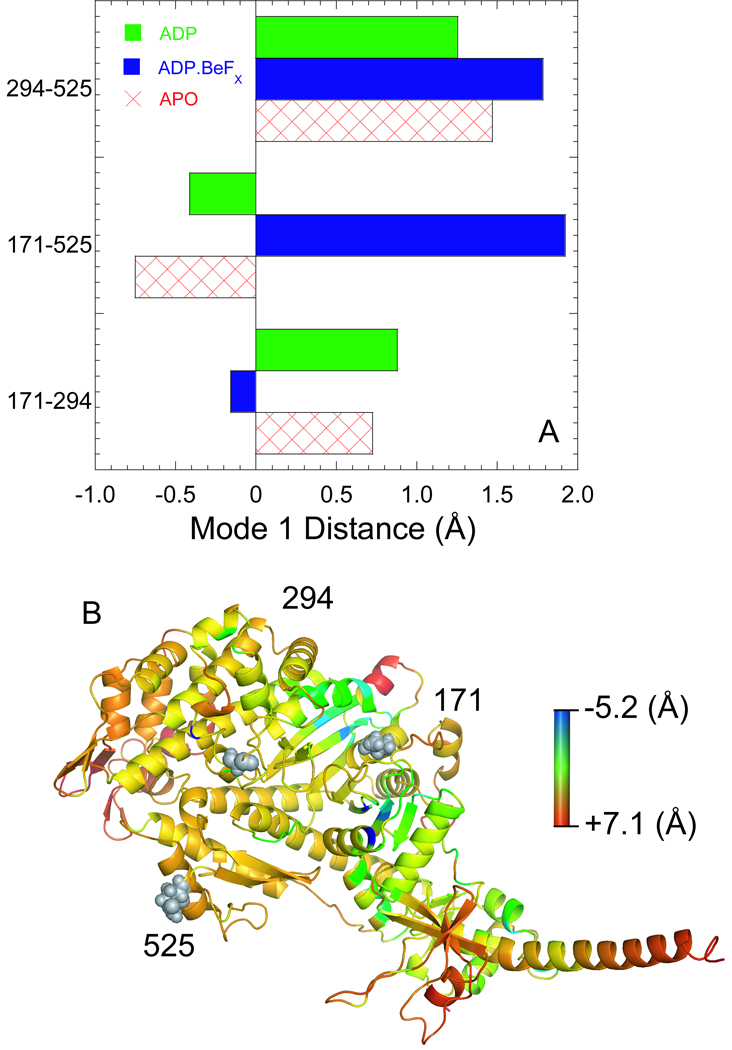
We demonstrate that the nucleotide pocket opening step (k−pocket) during the transition from the strong to the weak actomyosin.ADP state occurs while the actin binding cleft remains closed. The MV FlAsH:IAEDANS actin complex in the presence and absence of ADP was found to have a similar distance at all temperatures measured (4–35°C). We performed principle component analysis (PCA) to examine motions of the NBP (171–294) and actin binding cleft (294–525 & 171–525) in the MV.ADP and MV.ADP.BeFX (MV.ATP-state), and MV.APO structures (Fig. 8A). We chose the residue glutamine 525 because it is located near the actin binding interface near the IAEDANS label at cysteine 374 on actin. In the ATP-state we observed a dominant mode of motion that consisted of no motion of the pocket while the cleft was capable of larger motions (294–525 and 171–525). Our simulations in the MV.ADP state demonstrated less dynamics of the actin binding cleft while the motions of the NBP are increased compared to the MV.ATP state. These results suggest the motions of the cleft and pocket depend on the nucleotide-state where residue pair distances are coupled in phase within the APO and ADP states, and weak out of phase motion is found in the ATP state. For example when the NBP opens the cleft also opens in the MV.ADP state while the opposite is true for M.ATP, when the NBP closes the actin binding cleft opens. Our results demonstrate the transition from a closed to open NBP conformation (k−pocket) is likely to occur without disrupting the strong binding complex between actin and myosin. Thus, the conformational changes in the pocket are uncoupled from the conformational changes in the actin binding region during this step as would be expected for a strain sensitive transition that does not lead to detachment from actin, which was also suggested from mechanical studies (see below).
Figure 8. Intrinsic flexibility and dynamiccs of the MV crystal structures.
A) We performed PCA analysis using FRODA to examine the relative motions of three residue pairs (294-171, 171–525, and 294–525) in all three crystal structures. The correlated motions were similar in the MV.ADP and MV.APO states although different in magnitude, while they were quite different in magnitude and direction in the MV.ADP.BeFX state. B) The residue root mean square deviation (RMSD) determined by FRODA was examined in the MV.APO and MV.ADP crystal structures. The MV.APO residue RMSD was subtracted from the MV.ADP residue RMSD and the relative flexibility change is shown in a ribbon diagram The color scale is shown with red representing the most positive change in RMSD (MV.ADP more flexible than MV.APO) and blue representing the most negative change in RMSD (MV.APO more flexible than MV.ADP).
Energetics of ADP release in myosin V
Kinetics and thermodynamics of the ADP release steps in myosin V have been examined by several labs using different kinetic or structural techniques [22, 24, 26, 28, 33–36]. Previous studied found evidence for two actomyosin.ADP states with stopped-flow studies of dmantADP and myosin V, and the equilibrium and rate constants they measured at 25 °C are similar to our measurements [24, 33]. However, one of these studies concluded that the slow phase associated with dmantADP release represented an off pathway intermediate since it was slower than the maximum actin-activated ATPase rate. Our current results differ from these studies in that the pocket opening step is similar to the maximum ATPase rate and the single turnover rate with dmantATP. The results may differ because our results are based on FRET changes while the previous results examined the fluorescence of the dmant fluorophore which may monitor only local changes in the pocket. Therefore, our results which utilize FRET to characterize the structural changes in the NBP associated with the transition from the strong (closed) to the weak (open) actomyosin.ADP state demonstrate this is the rate limiting conformational change in the actomyosin V ATPase cycle.
Another study explored the thermodynamics of the actomyosin.ADP states using kinetic competition with ATP induced dissociation monitored by pyrene actin fluorescence, which allowed them to use unlabeled ADP [28]. This study was able to delineate the thermodynamics of collision complex formation and transition into the bound actomyosin.ADP states. However, this study did not differentiate between weak and strong actomyosin.ADP states but their results are in general agreement with our studies. We summarize our thermodynamics analysis in Figure 9. Although we did not examine the collision complex step, Robblee et al. [28] demonstrated a favorable enthalpy driven collision complex formation with unfavorable entropy contributions. We observed that formation of the weak actomyosin.ADP state is associated with a favorable change in entropy suggesting an increase in conformational entropy in the weak (open pocket) actomyosin.ADP state compared to the APO and collision complex states. Our results are supported by the FIRST/FRODA analysis demonstrating an increase in overall flexibility (increase in conformational entropy) in the MV.ADP crystal structure compared to the APO structure (Figure 8B). We demonstrate that formation of the strong actomyosin.ADP state (closed pocket) is unfavorable largely because of an unfavorable change in entropy, which suggests that the closed pocket conformation is more rigid (less conformational entropy) than the open pocket conformation. The FIRST/FRODA calculations were performed in the absence of actin and we acknowledge that structural changes at the actomyosin interface could have a significant impact the conformational entropy estimations. Robblee et al. demonstrated an increase in entropy in the actomyosin.ADP states compared to the collision complex state. Studies in skeletal muscle myosin II also demonstrated a favorable increase in entropy upon ADP binding, although it is unclear if myosin II significantly populates the closed pocket actomyosin.ADP state in the absence of strain [37]. While conformational entropy is only one component that contributes to the overall entropy (i.e solvent and ligand), evidence for protein conformational entropy playing a significant role in ligand binding was provided by NMR and thermodynamics studies of calmodulin complexed with target peptides [38].
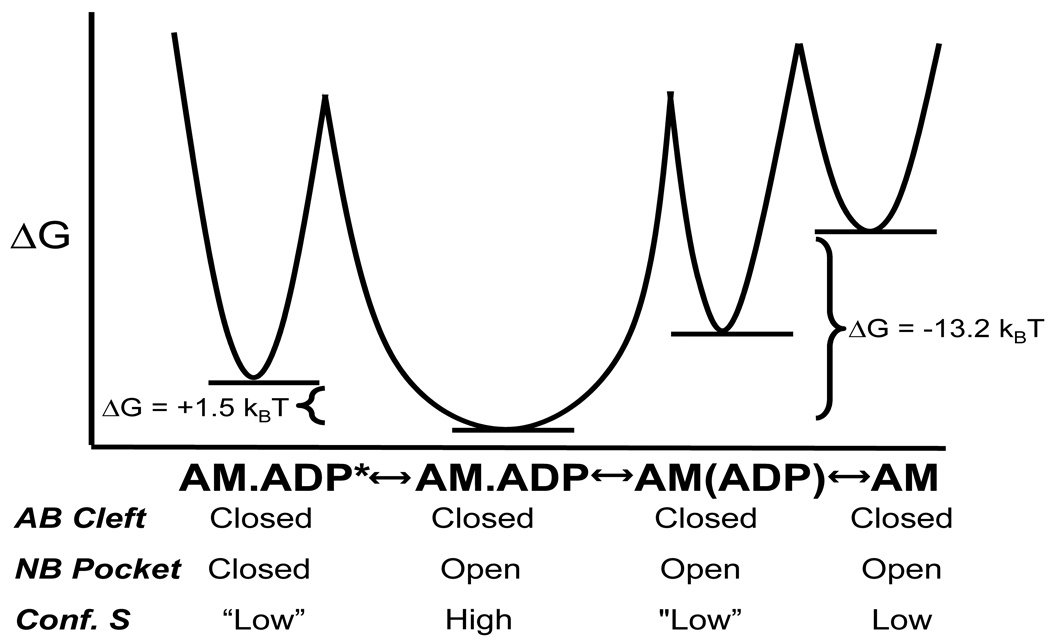
Figure 9. Energetics of the two actomyosin.ADP states.
The free energies (units are the product of kB, Boltzmann constant, and the temperature, 298° K) of the two actomyosin.ADP states, the collision complex state, and the APO state from the thermodynamic measurements are shown in a reaction coordinate diagram. The conformation of the nucleotide binding pocket (NB pocket) and actin binding cleft (AB cleft) from the FRET measurement is shown for each state. The proposed conformational entropy (conf. S) examined from the thermodynamic analysis and computation simulations is also shown for each state (the AM.ADP* and AM.(ADP) is shown is quotes because this state was not examined by FIRST/FRODA simulations).
Coupling between the lever arm and nucleotide binding pocket
Many studies with non-muscle and muscle myosin suggest that there is coupling between the lever arm and nucleotide-binding regions. A series of studies by the De La Cruz and Ishiwata groups has provided significant evidence demonstrating that load impacts the ADP release steps in myosin V [19–21]. Further optical trapping studies with single headed myosin V demonstrate that the second substep in the mechanical transients, proposed to be the lever arm swing during ADP isomerization step [22], is temperature dependent which is consistent with our results of a temperature dependent conformational change in the NBP. The rate of ADP release is also altered by strain between the two heads of the dimer of myosin V, as demonstrated with solution kinetic and processive walking studies using fluorescently labeled nucleotides [34, 35, 39]. Strain sensitive ADP release has been found in other non-muscle and muscle myosins. Optical trapping studies demonstrated that myosin 1C can stay associated with actin for long periods of time because the ADP release step is extremely strain sensitive [40]. Studies of White and coworkers found that the maximal contractile velocity in muscle is limited by ADP release [18]. Although the phenomena of strain dependent ADP release is well documented the specific load dependent conformational changes in the nucleotide binding pocket have not been elucidated.
Overall our results which demonstrate a temperature dependent conformational change in the NBP allow us to speculate on the structural mechanism of strain dependent ADP release that may be common to all myosin motors. In the presence of backward load such as the lead head of the myosin dimer prior to release of the trail head, a negatively strained cross-bridge in muscle, or a resistive load in a force producing myosin the nucleotide binding pocket would favor a closed conformation which would slow the ADP release step. However, in the presence of assistive load the nucleotide binding pocket would favor an open conformation enhancing the rate of ADP release. In the proposed mechanism the lever arm position would impact the nucleotide-binding pocket conformation and therefore future studies will need to focus on identifying the specific mechanism of coupling between the lever arm and nucleotide binding pocket.
Materials and Methods
All reagents were the highest purity commercially available. ATP and ADP were prepared fresh from powder. N-Methylanthraniloyl (mant)-labeled 2’-deoxy-ADP and 2’-deoxy-ATP (dmantADP and dmantATP) were purchased from Axxorra (San Diego, CA). The dmantATP and dmantADP concentrations were determined from absorbance measurements at 255 nm using ε255 of 23,300 M−1·cm−1. ATP and ADP concentrations were determined by absorbance at 259 nm using an ε259 of 15,400 M−1·cm−1. Nucleotides were prepared prior to use in the presence of equimolar MgCl2. 1, 5 IAEDANS (5((((2-iodoacetyl) amino) ethyl) amino)-naphthalene-1-sulfonic acid) was purchased from Invitrogen (Carlsbad, CA) and FlAsH (fluorescein biarscenical hairpin-binding dye) was generously provided by Roger Tsien and Stephen Adams (University of California, San Diego).
Myosin V cDNA Construction, Expression, and Purification
Site-directed mutagenesis was performed on a construct of chicken myosin V containing a single IQ motif (WT MV) (residues 1–792). Residues 292–297 were substituted with with a tetracysteine motif (Cys-Cys-Pro-Gly-Cys-Cys) to generate the MV construct for FlAsH labeling [4, 23]. The MV labeled with FlAsH, referred to as MV FlAsH, was generated as described [4, 23]. The baculovirus system was used to express MV, which contained a C-terminal Myc tag (EQKLISEEDL) followed by a FLAG tag (DYKDDDDK) for purification purposes [4, 23, 42]. All myosin V constructs were coexpressed with chicken calmodulin. The purity was greater than 95% based on Coomassie-stained SDS gels. Myosin concentrations were determined using the Bio-Rad microplate assay using bovine serum albumin (BSA) as a standard or absorbance (ε280 = 103,600 M−1·cm−1). Actin was purified from rabbit skeletal muscle using an acetone powder method [43]. F-actin was labeled with IAEDANS as described [44] and the concentration was determined by absorbance (ε290 = 14,300 M−1·cm−1 for actin after correcting for IAEDANs absorbance at 290 nm, and ε336 = 5700 M−1·cm−1 for IAEDANS). All experiments were performed in KMg50TCEP buffer (50 mM KCl, 1 mM EGTA, 1 mM MgCl2, 1 mM TCEP, and 10 mM imidozole- HCl, pH 7.0, 25 °C).
Fluorescence Spectroscopy
A Quantamaster fluorometer (Photon Technology International, Lawrenceville, NJ), equipped with a 75-watt xenon arc lamp as an excitation source and excitation/emission monochrometers, was used to measure steady-state fluorescence of dmantATP/ADP, MV FlAsH, and IAEDANS actin. The dmantATP/ADP and IAEDANS actin were excited at 365 nm, and the emission spectra measured from 400 nm to 600 nm. Slit widths were set at a resolution of 0.5 nm. All fluorescence spectra were corrected for variations in the wavelength sensitivity of the detector system, the presence of Raman scatter, and background fluorescence in the appropriate buffer solution.
Fluorescence lifetime experiments were performed with a Timemaster Fluorescence Spectrometer (Photon Technology International, Birmingham, NJ), equipped with a pulsed LED light source. IAEDANS or dmantATP/ADP fluorescence was excited using a 365 nm LED and the fluorescence emission was measured through a emission monochrometer with 10 nm slit widths. Fluorescence decays were analyzed by Global analysis software provided with the instrument.
FRET Measurements
FRET was used to measure the distance between donor fluorophore, dmantATP/ADP, IAEDANS actin, and the acceptor fluorophore, FlAsH-labeled MV, using the Förester energy transfer theory [4, 23, 45]. The steady-state efficiency (E) of energy transfer was measured by examining the increase in the acceptor emission. The efficiency of transfer is given by the following equation.
| (Eq. 8) |
where is the fluorescence intensity of the acceptor in the absence of the donor, is the fluorescence intensity from the acceptor in the presence of the donor, corrected by subtracting the fluorescence from unbound donor fluorophore. The extinction coefficients for MV FlAsH and dmantATP/ADP at 365nm, εA365 and εD365 are 1259 M−1·cm−1 and 5304 M−1·cm−1, respectively, and extinction coefficients for MV FlAsH and IAEDANS actin at 365 nm, εA365 and εD365 are 1259 M−1·cm−1 and 5700 M−1·cm−1, The FRET efficiency (E) examined by lifetime measurements between the donors of IAEDANS actin or dmantATP/ADP and the acceptor MV FlAsH was calculated from the observed fluorescence lifetimes of 2.5 µM donor (IAEDANS actin or dmantATP/ADP) in the presence of 2.5 µM or 7.5 µM, respectively, of unlabeled MV (τD) or MV FlAsH (τDA):
| (Eq. 9) |
The average amplitude weighted lifetimes (‹τ›) were calculated from the sum of the individual component lifetimes (τi) weighted by their respective amplitudes (Ai) as determined from fits to the fluorescence emission decay data (F(t) = Σ Ai τi). The Förster critical distance at which energy transfer is equal to 50% (R0) was calculated from Equation 10.
| (Eq. 10) |
where η is the refractive index of the buffer (≈ 1.4 for solutions of protein), QD is the quantum yield of donor fluorophore (dmantATP/ADP or IAEDANS actin) , 2 κ2 is the orientation factor assuming free rotation of the donor and acceptor fluorophore (2/3), QD is the quantum yield of the donor probe, and J is the spectral overlap integral in cm3·M−1 given by Equation 11 [4, 23, 44]..
| (Eq. 11) |
The QD of dmantADP bound to MV or acto-MV (0.44, 0.44, 0.42, 0.44, 0.43, and 0.44 at 4, 10, 15, 25, 30, 35 °C) and IAEDANS actin:MV (0.42, 0.42, 0.41, 0.38, 0.38, and 0.39 at 4, 10, 15, 25, 30, 35 °C) were determined by a comparative method using the QD value of IAEDANS actin or dmantATP at 25 °C as a standard. In equation 11, FD(λ) is the normalized total integrated intensity of the unquenched donor group and εA is the extinction coefficient of the acceptor. J was numerically integrated at 1-nm intervals, where λ is the wavelength in centimeters. The distance (r) between the donor and acceptor fluorophores was calculated with Equation 12.
| (Eq. 12) |
Stopped-flow Measurements and Kinetic Modeling
Transient kinetic experiments were performed in an Applied Photophysics (Surrey, UK) stopped-flow apparatus with a dead time of 1.2 ms. A monochrometer with a 2-nm band pass was used for fluorescence excitation, and cut-off filters were used to measure the emission. All optical filters were provided with the stopped-flow instrument. The dmantATP/ADP was excited at 365 nm, in the presence and absence of MV FlAsH or unlabeled MV, and the FRET emission was measured with a 515 nm long pass filter. Nonlinear least-squares fitting of the data was done with software provided with the instrument or Kaleidagraph (Synergy Software, Reading, PA). Uncertainties reported are standard error of the fits unless stated otherwise.
Kinetic modeling and simulations were performed with Pro-K software (Applied Photophysics) using the reaction scheme that has been used in kinetics studies of myosin V [4, 23, 26]. All concentrations mentioned in the stopped-flow experiments are final concentrations unless stated otherwise.
The thermodynamic parameters were calculated using the Gibbs free-energy equation.
| (Eq. 13) |
where R is the gas constant, T is the absolute temperature in Kelvin, and K is the equilibrium constant for the reaction. The van’t Hoff plots were used to determine the enthalpic (ΔH) and entropic (ΔS) components of the free energy change associated with the two actomyosin.ADP states.
| (Eq. 14) |
The slope of the van’t Hoff plots was used to determine the standard enthalpy change of each reaction. The standard entropy change was calculated from the following equation
| (Eq. 15) |
where ΔH° is determined from the van’t Hoff plots and ΔG° is determined from equation 14 at 298 °K.
ATPase assays were performed in the stopped-flow at 4, 25, and 35 °C using the NADH coupled assay. The steady-state ATPase rate of 0.05 µM MV FlAsH in the presence and absence of a range of actin concentrations was examined. The data was fit to a Michelis-menton equation to determine kcat, KATPase, and V0 as described [4, 23, 26, 27].
Geometrical simulation (FIRST/FRODA)
FRODA trajectories were generated using the FIRST/FRODA software, version 6.2 [46]. The geometrical simulation paradigm [47, 48] represents the molecular structure as a distance constraint network. Developed by Thorpe and co-workers, FRODA is a Framework Rigidity Optimized Dynamic Algorithm to explore allowed motions at the all-atom level of resolution while maintaining imposed native interactions. Determined from a starting input structure, native interactions include covalent bonds, hydrogen bonds (H-bonds) and hydrophobic tethers. The input structures employed here are the same that were used in previous work [4]. As previously described [4], the known X-ray crystal structures (1OE9, 1W7J, 1W7I) were processed using MOE (Molecular Operational Environment) software from Chemical Computing Group. All missing residues and atoms where computationally added, with missing loop regions determined by homology modeling, and the energy of each structure minimized. Hydrophobic tethers are determined by the default geometrical criteria of FRODA, and H-bonds are determined by a combination of default geometric criteria and a user-defined H-bond energy cutoff.
Rather then solving equations of motion that enforce distance constraints, a rigid cluster decomposition is performed using FIRST [49] , and subsequently, each rigid cluster is held together by stiff springs placed between pairs of atoms within the cluster with natural lengths set equal to the distance defined by the input structure. Between atoms from different rigid clusters: hydrophobic tethers are enforced using distance inequalities, and, a short-range repulsive force prevents atoms (and rigid clusters) from passing through one another subject to the appropriate molecular van der Waals radii criteria. The initial energy of the system is therefore zero, indicating all geometrical attributes (packing, bonding, hydrophobic interactions) are valid and native-like. Thereafter, rigid cluster center of mass coordinates and orientations are randomized slightly in a Monte Carlo (MC) move. After each randomization step, the energy of the system is relaxed back to zero energy without causing any atomic clashing, and all rigid clusters are maintained within tight distance constraint tolerances. This procedure produces a trajectory that preserves all rigid clusters, while allowing relative positions of atoms in different rigid clusters to change within flexible regions without having any atom or rigid cluster pass through each other. This method is very efficient in generating a native state conformational ensemble.
The simulations performed in this work differ from our previous study [4] in two respects. First, a ‘momentum’ bias toward moving rigid clusters in the direction that was successful in the previous MC step is implemented in the latest version of FRODA (used here). This new feature allows conformational space to be explored more efficiently and robustly. When specifying the constraint network, FRODA requires a cutoff for the H-bond energy, such that any H-bond with energy less than a specified cutoff is modeled as distance constraints. In previous work, the H-bond energy cut-off was adjusted to fix the number of independent degrees of freedom in each structure, ranging from 200 to 1200 in steps of 200. Here, a series of trajectories were generated using the same energy cutoff across all three input structures. The cutoff energy ranged from 0.0 kcal/mol to −5.0 kcal/mol, while default settings for hydrophobic tethers were used. As the energy cutoff is lowered, less H-bonds are modeled as distance constraints, resulting in the protein becoming more flexible. Whereas in our previous study [4] residue mobility characteristics of the three structures were compared under the condition that each had the same number of independent degrees of freedom (but with variable energy cutoffs), here a constant energy cutoff is applied across all structures, which results in a variable number of independent degrees of freedom.
Samples from a FRODA trajectory are taken to form a set of conformations that represent the native state ensemble. Each conformational ensemble was constructed by selecting every 50th structure from a given simulation containing 100,000 structures, thus yielding 2,000 samples for statistical analysis. Principle Component Analysis (PCA) was performed using carbon alpha atoms described by Cartesian coordinates. The structures comprising of each trajectory were optimally aligned to remove overall rigid body translation and rotation motions from the intrinsic atomic fluctuations. PCA analysis was performed based on individual trajectories subject to a specific H-bond energy cutoff) and combined trajectories (using multiple H-bond cutoffs) to test sensitivity in the H-bond energy cutoff. Consistent results are obtained regardless of the H-bond energy cutoff between −0.5 kcal/mol to −3.0 kcal/mol, which agrees with the FRODA default cutoff of −1.0 kcal/mol.
The results we report are based on another type of PCA, compatible with our focus on residues 171, 294 and 525. A covariance matrix is constructed based on the distances between the carbon alpha atoms of these three residues. This analysis yields 3 PCA modes that characterize the correlated displacements of these three selected residues. We note that no linear transformation was needed to remove overall rotations and translations of the protein because atomic pair distances are invariant under global rigid body motions.
Supplementary Material
Acknowledgements
We thank William Unrath and Lorna Silipino for outstanding technical assistance, Michael Rose and Mingxuan Sun for help with initial studies, as well as Joe Muretta and Enrique De La Cruz for helpful discussions. CMY is supported by grants from NIH (EY018141 and HL093531) and DJJ is supported by NIH (GM073082) and a subcontract from Pennsylvania State University through HL093531.
Abbreviations
- dmantATP
N- methylanthraniloyl (mant)-labeled 2’deoxy ATP
- dmantADP
N- methylanthraniloyl (mant)-labeled 2’deoxy ADP
- IAEDANS-Actin
(5((((2-iodoacetyl) amino) ethyl) amino)-naphthalene-1-sulfonic acid) labeled actin
- MV FlAsH
myosin V 1IQ labeled with the fluorescein biarscenical hairpin-binding dye
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
See Supplemental Figure S1. Distance distribution plots.
References
- 1.Sweeney HL, Houdusse A. Structural and functional insights into the Myosin motor mechanism. Annu Rev Biophys. 2010;39:539–557. doi: 10.1146/annurev.biophys.050708.133751. [DOI] [PubMed] [Google Scholar]
- 2.Malnasi-Csizmadia A, Kovacs M. Emerging complex pathways of the actomyosin powerstroke. Trends Biochem. Sci. 2010;35:684–690. doi: 10.1016/j.tibs.2010.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Coureux PD, Wells AL, Menetrey J, Yengo CM, Morris CA, Sweeney HL, Houdusse A. A structural state of the myosin V motor without bound nucleotide. Nature. 2003;425:419–423. doi: 10.1038/nature01927. [DOI] [PubMed] [Google Scholar]
- 4.Sun M, Rose MB, Ananthanarayanan SK, Jacobs DJ, Yengo CM. Characterization of the pre-force-generation state in the actomyosin cross-bridge cycle. Proc. Natl. Acad. Sci. USA. 2008;105:8631–8636. doi: 10.1073/pnas.0710793105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Conibear PB, Bagshaw CR, Fajer PG, Kovacs M, Malnasi-Csizmadia A. Myosin cleft movement and its coupling to actomyosin dissociation. Nat. Struct. Biol. 2003;10:831–835. doi: 10.1038/nsb986. [DOI] [PubMed] [Google Scholar]
- 6.Yengo CM, De La Cruz EM, Chrin LR, Gaffney DP, 2nd, Berger CL. Actin-induced closure of the actin-binding cleft of smooth muscle myosin. J. Biol. Chem. 2002;277:24114–24119. doi: 10.1074/jbc.M111253200. [DOI] [PubMed] [Google Scholar]
- 7.Irving M, St Claire Allen T, Sabido-David C, Craik JS, Brandmeier B, Kendrick-Jones J, Corrie JE, Trentham DR, Goldman YE. Tilting of the light-chain region of myosin during step length changes and active force generation in skeletal muscle. Nature. 1995;375:688–691. doi: 10.1038/375688a0. [DOI] [PubMed] [Google Scholar]
- 8.Goldman YE. Wag the tail: structural dynamics of actomyosin. Cell. 1998;93:1–4. doi: 10.1016/s0092-8674(00)81137-x. [DOI] [PubMed] [Google Scholar]
- 9.Dunn AR, Spudich JA. Dynamics of the unbound head during myosin V processive translocation. Nat. Struct. Mol. Biol. 2007;14:246–248. doi: 10.1038/nsmb1206. [DOI] [PubMed] [Google Scholar]
- 10.Forkey JN, Quinlan ME, Shaw MA, Corrie JE, Goldman YE. Three-dimensional structural dynamics of myosin V by single-molecule fluorescence polarization. Nature. 2003;422:399–404. doi: 10.1038/nature01529. [DOI] [PubMed] [Google Scholar]
- 11.Shiroguchi K, Kinosita K., Jr Myosin V walks by lever action and Brownian motion. Science. 2007;316:1208–1212. doi: 10.1126/science.1140468. [DOI] [PubMed] [Google Scholar]
- 12.Toprak E, Enderlein J, Syed S, McKinney SA, Petschek RG, Ha T, Goldman YE, Selvin PR. Defocused orientation and position imaging (DOPI) of myosin V. Proc. Natl. Acad. Sci. USA. 2006;103:6495–6499. doi: 10.1073/pnas.0507134103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Whittaker M, Wilson-Kubalek EM, Smith JE, Faust L, Milligan RA, Sweeney HL. A 35-A movement of smooth muscle myosin on ADP release. Nature. 1995;378:748–751. doi: 10.1038/378748a0. [DOI] [PubMed] [Google Scholar]
- 14.Jontes JD, Ostap EM, Pollard TD, Milligan RA. Three-dimensional structure of Acanthamoeba castellanii myosin-IB (MIB) determined by cryoelectron microscopy of decorated actin filaments. J. Cell Biol. 1998;141:155–162. doi: 10.1083/jcb.141.1.155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Volkmann N, Liu H, Hazelwood L, Krementsova EB, Lowey S, Trybus KM, Hanein D. The structural basis of myosin V processive movement as revealed by electron cryomicroscopy. Mol. Cell. 2005;19:595–605. doi: 10.1016/j.molcel.2005.07.015. [DOI] [PubMed] [Google Scholar]
- 16.Nyitrai M, Geeves MA. Adenosine diphosphate and strain sensitivity in myosin motors. Philos Trans R Soc Lond B Biol Sci. 2004;359:1867–1877. doi: 10.1098/rstb.2004.1560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Huxley AF. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 18.Siemankowski RF, Wiseman MO, White HD. ADP dissociation from actomyosin subfragment 1 is sufficiently slow to limit the unloaded shortening velocity in vertebrate muscle. Proc. Natl. Acad. Sci. USA. 1985;82:658–662. doi: 10.1073/pnas.82.3.658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Oguchi Y, Mikhailenko SV, Ohki T, Olivares AO, De La Cruz EM, Ishiwata S. Robust processivity of myosin V under off-axis loads. Nat Chem Biol. 6:300–305. doi: 10.1038/nchembio.322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Oguchi Y, Mikhailenko SV, Ohki T, Olivares AO, De La Cruz EM, Ishiwata S. Load-dependent ADP binding to myosins V and VI: implications for subunit coordination and function. Proc. Natl. Acad. Sci. USA. 2008;105:7714–7719. doi: 10.1073/pnas.0800564105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Uemura S, Higuchi H, Olivares AO, De La Cruz EM, Ishiwata S. Mechanochemical coupling of two substeps in a single myosin V motor. Nat. Struct. Mol. Biol. 2004;11:877–883. doi: 10.1038/nsmb806. [DOI] [PubMed] [Google Scholar]
- 22.Sellers JR, Veigel C. Direct observation of the myosin-Va power stroke and its reversal. Nat. Struct. Mol. Biol. 17:590–595. doi: 10.1038/nsmb.1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sun M, Oakes JL, Ananthanarayanan SK, Hawley KH, Tsien RY, Adams SR, Yengo CM. Dynamics of the upper 50-kDa domain of myosin V examined with fluorescence resonance energy transfer. J. Biol. Chem. 2006;281:5711–5717. doi: 10.1074/jbc.M508103200. [DOI] [PubMed] [Google Scholar]
- 24.Hannemann DE, Cao W, Olivares AO, Robblee JP, De La Cruz EM. Magnesium, ADP, and actin binding linkage of myosin V: evidence for multiple myosin V-ADP and actomyosin V-ADP states. Biochemistry. 2005;44:8826–8840. doi: 10.1021/bi0473509. [DOI] [PubMed] [Google Scholar]
- 25.Lemaire PA, Tessmer I, Craig R, Erie DA, Cole JL. Unactivated PKR exists in an open conformation capable of binding nucleotides. Biochemistry. 2006;45:9074–9084. doi: 10.1021/bi060567d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.De La Cruz EM, Wells AL, Rosenfeld SS, Ostap EM, Sweeney HL. The kinetic mechanism of myosin V. Proc Natl Acad Sci U S A. 1999;96:13726–13731. doi: 10.1073/pnas.96.24.13726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.De La Cruz EM, Sweeney HL, Ostap EM. ADP inhibition of myosin V ATPase activity. Biophys. J. 2000;79:1524–1529. doi: 10.1016/S0006-3495(00)76403-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Robblee JP, Cao W, Henn A, Hannemann DE, De La Cruz EM. Thermodynamics of nucleotide binding to actomyosin V and VI: a positive heat capacity change accompanies strong ADP binding. Biochemistry. 2005;44:10238–10249. doi: 10.1021/bi050232g. [DOI] [PubMed] [Google Scholar]
- 29.Coureux PD, Sweeney HL, Houdusse A. Three myosin V structures delineate essential features of chemo-mechanical transduction. EMBO J. 2004;23:4527–4537. doi: 10.1038/sj.emboj.7600458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kintses B, Gyimesi M, Pearson DS, Geeves MA, Zeng W, Bagshaw CR, Malnasi-Csizmadia A. Reversible movement of switch 1 loop of myosin determines actin interaction. EMBO J. 2007;26:265–274. doi: 10.1038/sj.emboj.7601482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Robertson CI, Gaffney DP, 2nd, Chrin LR, Berger CL. Structural rearrangements in the active site of smooth-muscle myosin. Biophys J. 2005;89:1882–1892. doi: 10.1529/biophysj.105.059840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bauer CB, Kuhlman PA, Bagshaw CR, Rayment I. X-ray crystal structure and solution fluorescence characterization of Mg.2'(3')-O-(N-methylanthraniloyl) nucleotides bound to the Dictyostelium discoideum myosin motor domain. J. Mol. Biol. 1997;274:394–407. doi: 10.1006/jmbi.1997.1325. [DOI] [PubMed] [Google Scholar]
- 33.Rosenfeld SS, Houdusse A, Sweeney HL. Magnesium regulates ADP dissociation from myosin V. J. Biol. Chem. 2005;280:6072–6079. doi: 10.1074/jbc.M412717200. [DOI] [PubMed] [Google Scholar]
- 34.Forgacs E, Cartwright S, Sakamoto T, Sellers JR, Corrie JE, Webb MR, White HD. Kinetics of ADP dissociation from the trail and lead heads of actomyosin V following the power stroke. J. Biol. Chem. 2008;283:766–773. doi: 10.1074/jbc.M704313200. [DOI] [PubMed] [Google Scholar]
- 35.Forgacs E, Cartwright S, Kovacs M, Sakamoto T, Sellers JR, Corrie JE, Webb MR, White HD. Kinetic mechanism of myosinV-S1 using a new fluorescent ATP analogue. Biochemistry. 2006;45:13035–13045. doi: 10.1021/bi060712n. [DOI] [PubMed] [Google Scholar]
- 36.Oke OA, Burgess SA, Forgacs E, Knight PJ, Sakamoto T, Sellers JR, White H, Trinick J. Influence of lever structure on myosin 5a walking. Proc. Natl. Acad. Sci. USA. 107:2509–2514. doi: 10.1073/pnas.0906907107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Smith SJ, White HD, Woledge RC. Microcalorimetric measurement of the enthalpy of binding of rabbit skeletal myosin subfragment 1 and heavy meromyosin to F-actin. J. Biol. Chem. 1984;259:10303–10308. [PubMed] [Google Scholar]
- 38.Frederick KK, Marlow MS, Valentine KG, Wand AJ. Conformational entropy in molecular recognition by proteins. Nature. 2007;448:325–329. doi: 10.1038/nature05959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sakamoto T, Webb MR, Forgacs E, White HD, Sellers JR. Direct observation of the mechanochemical coupling in myosin Va during processive movement. Nature. 2008;455:128–132. doi: 10.1038/nature07188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Laakso JM, Lewis JH, Shuman H, Ostap EM. Myosin I can act as a molecular force sensor. Science. 2008;321:133–136. doi: 10.1126/science.1159419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Howard J. Mechanics of Motor Proteins and the Cytoskeleton. Sunderland, MA: Sinauer Associates; 2001. Motility Models: From Crossbridges to Motion; pp. 263–283. [Google Scholar]
- 42.Sweeney HL, Rosenfeld SS, Brown F, Faust L, Smith J, Xing J, Stein LA, Sellers JR. Kinetic tuning of myosin via a flexible loop adjacent to the nucleotide binding pocket. J. Biol. Chem. 1998;273:6262–6270. doi: 10.1074/jbc.273.11.6262. [DOI] [PubMed] [Google Scholar]
- 43.Pardee JD, Spudich JA. Purification of muscle actin. Methods Enzymol. 1982;85(Pt B):164–181. doi: 10.1016/0076-6879(82)85020-9. [DOI] [PubMed] [Google Scholar]
- 44.Yengo CM, Chrin LR, Berger CL. Interaction of myosin LYS-553 with the C-terminus and DNase I-binding loop of actin examined by fluorescence resonance energy transfer. J. Struct. Biol. 2000;131:187–196. doi: 10.1006/jsbi.2000.4296. [DOI] [PubMed] [Google Scholar]
- 45.Lakowicz JR. Principles of Fluorescence Spectroscopy. 3rd Edition. New York, NY: Springer; 2006. [Google Scholar]
- 46. http://flexweb.asu.edu/.
- 47.Wells S, Menor S, Hespenheide B, Thorpe MF. Constrained geometric simulation of diffusive motion in proteins. Phys. Biol. 2005;2:S127–S136. doi: 10.1088/1478-3975/2/4/S07. [DOI] [PubMed] [Google Scholar]
- 48.Farrell DW, Speranskiy K, Thorpe MF. Generating stereochemically acceptable protein pathways. Proteins. 78:2908–2921. doi: 10.1002/prot.22810. [DOI] [PubMed] [Google Scholar]
- 49.Jacobs DJ, Rader AJ, Kuhn LA, Thorpe MF. Protein flexibility predictions using graph theory. Proteins. 2001;44:150–165. doi: 10.1002/prot.1081. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.