Abstract
Over the past three decades we have steadily increased our knowledge on the genetic basis of many severe disorders. Nevertheless, there are still great challenges in applying this knowledge routinely in the clinic, mainly due to the relatively tedious and expensive process of genotyping. Since the genetic variations that underlie the disorders are relatively rare in the population, they can be thought of as a sparse signal. Using methods and ideas from compressed sensing and group testing, we have developed a cost-effective genotyping protocol to detect carriers for severe genetic disorders. In particular, we have adapted our scheme to a recently developed class of high throughput DNA sequencing technologies. The mathematical framework presented here has some important distinctions from the ’traditional’ compressed sensing and group testing frameworks in order to address biological and technical constraints of our setting.
Index Terms: compressed sensing, DNA, genotyping, group testing
I. INTRODUCTION
Genotyping is the process of determining the genetic variation in a certain trait in an individual. This process plays a pivotal role in medical genetics to detect individuals that carry risk alleles* for a broad range of devastating disorders, from Cystic Fibrosis to mental retardation. These disorders lead to severe incapacities or lethality of the affected individuals at an early age, but have a very low prevalence in the population. In the past years, extensive efforts were made to identify the genetic basis of many disorders. These efforts have not only led to deeper insights regarding the molecular mechanisms that underlie those genetic disorders, but have also contributed to the emergence of large scale genetic screens, where individuals are genotyped for a panel of risk alleles in order to detect genetic disorders and provide early intervention where possible.
The human genome is diploid, and with a few exceptions, each gene has two copies. Consequently, many of the mutations that cause severe genetic diseases are recessive; where the dysfunction of the mutated allele can be compensated by the activity of the normal allele. Therefore, recessive genetic disorders appear only in individuals carrying two non-functional alleles. When genotyping an individual for a recessive disorder, there are three possible outcomes: (a) normal - an individual with two functional alleles (b) carrier - an individual with one functional allele and one non-functional allele (c) affected - an individual with two non-functional alleles. There are no phenotypic differences between a carrier and a normal individual, and they are both healthy. However, a mating between two carriers may give rise to an affected offspring, as explained by Mendel’s rules (Table I): A mating between two normal individuals always gives rise to a normal offspring. A mating between a normal and a carrier has 50% chance of giving a normal offspring and 50% chance of giving a carrier, but no chance of giving an affected offspring. A mating between two carriers has 25% chance of giving an affected offspring, 50% of giving a carrier, and 25% of giving a normal offspring. We do not consider the possibility of matings between affected individuals, since they rarely survive to reproductive age. This picture reveals that only families with two parental carriers are at risk for having an affected offspring, and that other mating combinations are safe.
TABLE I.
The Genotype of the Offsprings as a function of mating combination
| Offsprings | |||
|---|---|---|---|
| Mating: | Normal | Carrier | Affected |
| Normal × Normal | 100% | 0% | 0% |
| Normal × Carrier | 50% | 50% | 0% |
| Carrier × Carrier | 25% | 50% | 25% |
In order to eradicate severe genetic disorders, many countries have employed wide-scale carrier screening programs, in which individuals are genotyped for a small panel of risk genes that are highly prevalent in the population [1], [2]. The common practice is to offer the screening program to the entire population regardless of their familial history, either before mate selection (premarital screens), or prenatally in order to provide a reproductive choice for the parents.
One possible genotyping method is to sequence the genomic region that harbors the mutation site, and analyzing whether the DNA sequence is wild-type (WT) or mutated. This approach has gained popularity due to its high accuracy (sensitivity and specificity), applicability to a wide variety of genetic disorders, and technical simplicity. However, the current DNA sequencing platforms utilized in medical diagnosis provide only serial processing of a single specimen/region combination at a time. Therefore, while the genetic basis of many disorders is known, the cumbersome costs of large genotyping panels has hinder its routine application in the clinic.
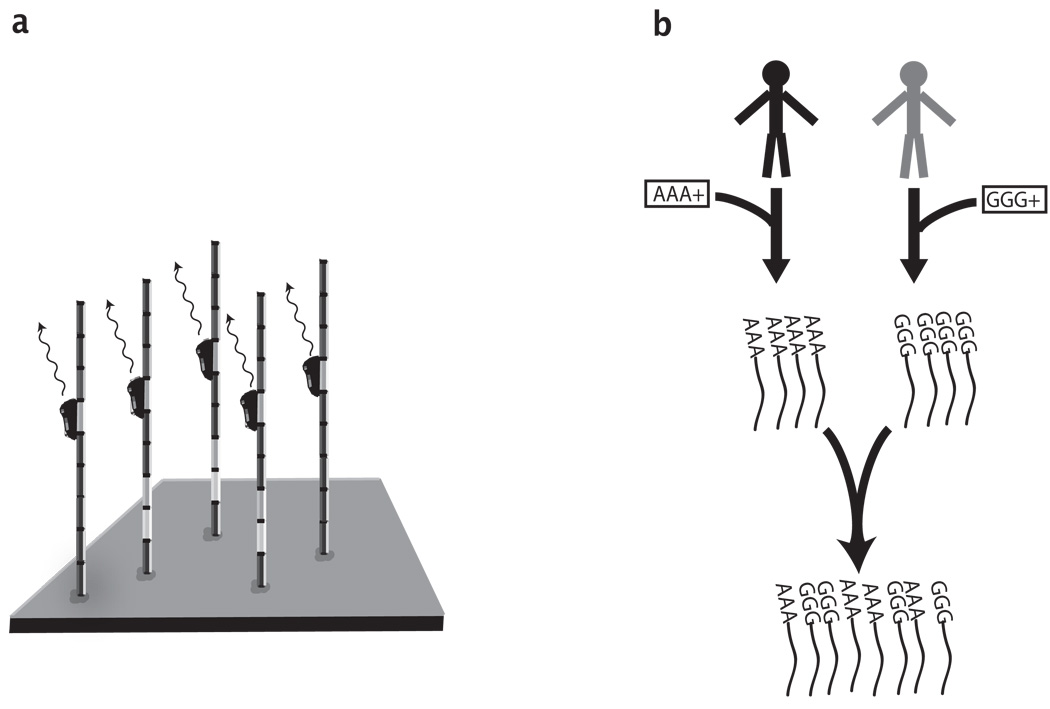
Recently, a new class of DNA sequencing methods, dubbed next-generation sequencing technologies, has emerged, revolutionizing molecular biology and genomics [3]. These sequencing platforms process short DNA fragments in parallel and provide millions of sequence reads in a single batch, each of which corresponds to a DNA molecule within the sample. While there are several types of next generation sequencing platforms and different sets of sequencing reactions, all platforms achieve parallelization using a common concept of immobilizing the DNA fragments onto a surface, so that each fragment occupies a distinct spatial position. When the sequencing reagents are applied to the surface, they generate optical signals according to the DNA sequence, which are then captured by a microscope and processed. Since the fragments are immobilized, successive signals from the same spatial location convey the DNA sequence of the corresponding fragment (Fig. 1a). Using this approach millions of DNA fragments can be simultaneously sequenced to lengths of tens to hundreds of nucleotides. For tutorials on next generation sequencing, the interested readers are referred to [4], [5].
Fig. 1.
Common techniques in next generation sequencing (a) Schematic Overview of High throughput DNA Sequencing. The DNA fragments (vertical rods) are immobilized onto a surface and occupy distinct spatial locations. The sequencing reagents (black ovals) generate optical signals according to the DNA composition of each fragment. A series of signals from the same spatial location conveys the sequence of a single DNA fragment. (b) DNA Barcoding. DNA barcoding starts with synthesizing short DNA sequences. In the example, there are two barcodes: ’AAA’ and ’GGG’. The barcodes are then concatenated in a simple chemical reaction to the DNA fragments of each sample (black lines). When the barcoded samples are mixed and sequenced, the barcodes retain the origin of the sequences. In this example, every sequence read will start with a short tag of 3 nucleotides, either ’AAA’ or ’GGG’.
Harnessing next generation sequencing platforms to carrier screens will dramatically increase their utility. The main challenge is to fully exploit the wide capacity of the sequencers. Allocating one sequencing batch to genotype a single individual would utilize only a small fraction of the sequencing capacity, and in fact, would be even less cost-effective than the serial approach. Therefore, multiplexing large number of specimens in a single batch is essential to utilize the full capacity of the platforms. However, a significant problem arises from when specimens are simply pooled and sequenced together; the sequencing results reflect only the allele frequencies of the specimens in the pools, and do not provide any information about the genotype of a particular specimen.
A simple solution to overcome the specimen-multiplexing problem is to append unique identifiers, dubbed DNA barcodes, to the specimens prior to sequencing [6] [7]. Each barcode is an artificially synthesized short DNA molecule with a unique sequence. When the barcode is concatenated to the DNA fragments of a specimen, it labels them with a unique identifier. The sequencer reads the entire fused fragment, and reports both the sequence of the interrogated region and the sequence of the associated barcode. By decoding the portion of the sequence corresponding to the barcode, the experimenter links the genotype to a given specimen (Fig. 1b). While this method has been quite successful for multiplexing small number of specimens, the process of synthesizing and concatenating a large number of barcodes is both cumbersome and expensive, and therefore not scalable.
Drawing inspiration from compressed sensing [8], [9], we ask: since only a small fraction of the population are carriers of a severe genetic disease, can one employ a compressed genotyping protocol to identify those individuals? We propose a compressed genotyping protocol in which pools of specimens are loaded to a next-generation sequencing platform, which will realize the sequencing capacity, while reducing the number of barcodes, and maintaining a faithful detection of the carriers. While our main motivation is to apply this approach to carrier screens, the concepts and ideas presented here can be used also for other genotyping tasks, such as whole-genome discovery of rare genetic variations.
A. Related work
Our work is closely related to group testing and compressed sensing, which deals with efficient methods for extracting sparse information from a small number of aggregated measurements. Much of the literature of group testing (thoroughly reviewed in: [10], [11]) is dedicated to the prototypical problem, which describes a set of interrogated items that can either be in an active state or an inactive state and a test procedure, which is performed on pools of items, and returns ’inactive’ if all items in the pool are inactive, or ’active’ if at least one of the items in the pool is active. Mathematically, this type of test can be thought of as an OR operation over the items in the pool, and is called superimposition [12]. In general, there are two types of test schedules: adaptive schedules, in which items are analyzed in successive rounds and re-pooled from round to round according to the accumulated results, and non-adaptive schedules, where the items are pooled and tested in a single round. While in theory adaptive schedules require fewer tests, in practice they are more labor intensive and time consuming due to the re-pooling steps and the need to wait for the test results from the previous round. For that reason, non-adaptive schedules are favored, and have been employed for several biological applications including finding sequence-tagged sites in yeast artificial chromosomes [13], and mapping protein interactions [14].
The theory of group testing offers a large number of highly efficient pooling designs for the prototypical problem. These designs reduce the number of pools with respect to the number of items while ensuring exact recovery of the active items [10]–[12], [15]–[17]. In practice, however, the relevance and the feasibility of many of those theoretical objects are questionable as technical limitations constrain the pooling design [18]–[21]. For instance, some biological assays suffer from a dilution noise - a decreased accuracy when the assay conducted on a large number of specimens [22], which restricts the ratio between items and pools [23]. Other complications can be restricted amounts of specimens’ material, which limit the number of times an item can be sampled or tedious designs that are time consuming. Du and Hawng also recognized the limited applicability of the prototypical problem to some practical settings, and pointed out in their monograph on group testing theory: “Recent application of group testing theory in clone library screening shows that the easiness of collecting test-sets can be a crucial factor… the number of tests is no longer a single intention to choose an algorithm” [10]. Later in this sequel, we will discuss the exact technical limitations of our setting, and introduce a new class of designs that reduces the number of pools, while satisfying the technical constraints. We will also compare the performance of our design to the theoretical oriented designs, which focus only on the maximal reduction in the number of pools.
Compressed sensing [8], [9] is an emerging signal processing technique that describes conditions and efficient methods for capturing sparse signals by measuring a small number of linear projections. This theory extends the framework of group testing to the recovery of hidden variables that are real (or complex) numbers. Additional difference from group testing is the measurement process that reports the linear combination of the aggregated data points, and not their superimposition. However, some combinatorial concepts from group testing were found useful also for constructing sparse compressed sensing designs [24]–[27]. These designs enable very fast encoding and recovery of the compressed signal. Inspired from the rigor of compressed sensing, a wide variety of applications has been devised, for example: single pixel cameras [28], fast MRI [29], and ultra wideband converters [30]. A closely related application to our subject is highly efficient microarrays with a small number of DNA probes [31], [32].
Our approach combines lessons from group testing and compressed sensing, but also possesses some notable differences. The most obvious distinction is that we seek an ’on a budget’ design that not only reduces the number of queries (termed ’measurements’ in compressed sensing, or ’tests’ in group testing), but also minimizes the weight - the number of times a specimen is sampled. This constraint originates from the properties of next generation sequencers, and prevents maximal query reduction. We will discuss the consequences of this constraint and provide some theoretical bounds and efficient designs. Additional unique feature of our setting is the measurement process, called ’compositional channel’. This process neither reports the superimposition results of the specimens in the query, nor their linear combination; rather it reports the results of a sampling with replacement procedure of the items in the query. We will compare this process to the measurement processes in group testing and compressed sensing.
The theoretical framework presented here was built on our recent experimental results in genotyping thousands of bacterial colonies for a biotechnological application using combinatorial pooling [21]. Prabhu et al. [33] has also developed a closely related theoretical approach to detect extremely rare genetic variations using error correcting codes. A somewhat similar compressed sensing approach to the setting proposed here has been independently developed by Shental et al. [34]. Some of the results presented in that paper are based on our earlier work in [35].
The manuscript is divided as follows: In section II, we set up the basic formulation of compressed genotyping. In section III, we present the concept of light-weight designs and provide a lower theoretical bound. Then, we show how a design based on the Chinese Reminder Theorem comes close to this bound. In section IV, we present a Bayesian reconstruction approach based on belief propagation, and in section V, we provide several simulations of carrier screens. Section VI presents some open problems and possible future directions and section VII concludes the manuscript.
II. THE GENOTYPING PROBLEM - PRELIMINARIES
A. Notations
We denote matrices as an upper-case bold letter and the (i, j) element of the matrix X as Xij. The shorthand X̅ denotes a matrix that its row vectors are normalized. 𝕀(X) is an indicator function that returns a matrix in the same size of X with:
For example:
The operation | · | denotes the cardinality of a set or the length of a vector. For graphs, ∂a refers to the subset of nodes that are connected to node a, and the notation ∂a\b means the subset of nodes that are connected to a except node b. We use natural logarithms.
B. Genotype representation
We will represent the genotype of a specimen by the number of it non-functional allele copies. Since the human genome is diploid, a genotype has three possible values: 0 if the specimen is normal, 1 if the specimen is a carrier, and 2 if the specimen is affected. The symptoms of severe genetic diseases are always overt, and therefore affected individuals never participate in carrier screens. Thus, the genotype is either 0 or 1 in our setting. x, the genotype vector, represents the genotype of n individuals. For example:
In that case, the 3th specimen is a carrier, and the other 4 specimens are normal.
Our main interest in a carrier screen is to recover x with a small number of queries. Since the number of carriers is extremely low in rare genetic diseases, x is highly sparse. For example, consider a screen for ΔF508, the most prevalent mutation in Cystic Fibrosis (CS) among people of European descent; the ratio between k, the number of non-zero entries (carriers) in x, to n is around 1:30 [36] [37]. Cystic Fibrosis is one of the most prevalent genetic diseases, and therefore a ratio of 1/30 is almost the lowest expected sparsity for a carrier screen.
C. A Cost-effective Genotyping Strategy
We envision a compressed genotyping strategy that is based on a non-adaptive query schedule using next-generation sequencing. Φ denotes the query design, a t × n binary matrix; the columns of Φ represent specimens, and each row determines a pool of specimens to be queried. For example, if the first row of Φ is (1, 0, 1, 0, 1…), it specifies that the 1st, 3rd, 5th, … specimens are pooled and queried (sequenced) together. Since pooling is carried out using a liquid handling robot that takes several specimens in every batch, we only consider balanced designs, where every specimen is sampled the same number of times. Let w be the weight of Φ, the number of times a specimen is sampled, or equivalently, the number of 1 entries in a given column vector. Let ri be the compression level of the ith query, namely the number of 1 entries in the ith row, which denotes the number of specimens in the ith pool.
1) First objective - minimize t
In large scale carrier screens, n is typically between thousands to tens of thousands of specimens. We restrict ourselves to query designs with rmax ≲ 1000 specimens, due to technical / biological limitations (in DNA extraction and PCR amplification) when processing pools with larger number of specimens. Interestingly, similar restrictions are also found in other practical group testing studies [18], [20]. When rmax ≲ 1000, a single query does not saturate the sequencing capacity of next generation platforms. In order to fully exploit the capacity, we will pool queries together into query groups until the size of each group reaches the sequencing capacity limit, and we will sequence each query in a distinct reaction. Before pooling the queries, we will label each query with a unique DNA barcode in order to retain its identity (for an in-depth protocol of this approach see [21]). Thus, the number of queries, t, is proportional to the number of DNA barcodes that should be synthesized, and one objective of the query design, similar to those found in group testing and compressed sensing, is to minimize t.
In practice, once the DNA barcodes are synthesized, there is enough material for a few dozens experiments, and one can re-use the same barcode reagents for every query group as these are sequenced in distinct reactions. Hence, the number of queries in the largest query group, τmax, dictates the synthesis cost for a small series of experiments. While this does not change the asymptotic cost (e.g. for synthesizing barcodes for a large series of experiments), it has some practical implications, and we will include it in our analysis.
2) Second objective - minimize w
There are three reasons to minimize the weight of the design. First, the weight determines the number of times the liquid handling robot samples a specimen. Thus, minimizing the weight reduces robot time, and therefore the overhead of the pooling procedure. Second, each time a robot samples a specimen, it consumes some material. In many cases, the material is rather limited, and therefore w must be below a certain threshold. The third reason to minimize w is to reduce the overall sequencing capacity. Each time an aliquot of a specimen is added to a pool, we need a few more sequence reads to report the genotype of the specimen. While the sequencing capacity of a single batch of next generation platforms is high, it is not limited. We will see in the next subsection that the sequencing coverage, the ratio between the number of sequence reads to the number of specimens, determines the quality of the results. Thus, minimizing w will improve the quality of the results.
Next generation sequencers are usually composed of several distinct biochemical chambers, called ’lanes’, that can be processed in a single batch. We assume that the sequencing capacity needed for n specimens corresponds to one lane†. Since the pooling step generates nw aliquots of specimens in total, one needs w lanes to sequence the entire design, where each lane gets a different query group.
We do not intend to specify a global cost function that includes the costs of barcode synthesis, robotic time, sequencing lanes, and other reagents. Clearly, these costs vary with different genotyping strategies, sequencing technologies, and so on. Rather, we will present heuristic rules that would be applicable in most situations. First, w should not exceed the maximal number of lanes that can be processed in a single sequencing batch, as launching a run is expensive and time consuming. The number of lanes in the most widespread next-generation sequencing platform is 8 [39], and therefore, we favor designs with w ≤ 8. Second, we assume that the cost of adding a sequencing lane is about two to three orders more than the cost of synthesizing an additional barcode. We will use that ratio to evaluate the performance of the query design.
To conclude, the query design that we seek is a t × n binary matrix that: (a) provides sufficient information to recover x (b) minimizes t (c) keeps the weight w balanced and small. Table II presents the notations we used in that part.
TABLE II.
Summary of Query Design Parameters
| Notation | Meaning | Typical Values | Comments |
|---|---|---|---|
| Φ | Query design | ||
| n | Number of specimens | Thousands | |
| t | Number of queries (pools) | ||
| w | Weight | ≤ 8 | Number of times a specimen is sampled |
| rmax | Max. level of compression | ≲ 1000 | Maximal number of specimens in a pool |
| τmax | Number of queries in the largest query group | Up to a few hundreds | Corresponds to barcode synthesis reactions for a single experiment |
D. The Compositional Channel - A Model for High Throughput Sequencing
The sequencer captures a random subset of DNA molecules from the input material and reports its composition. In essence, this process is a sampling with replacement; the sequencer takes βi molecules from substantial number of input molecules of the i-th query, and reports αi the number of sequence reads from the non-functional allele, and βi. Let yi be the ratio of the sequence reads from the non-functional allele to the total number of reads in the query. yi = αi / βi. The result of the sampling procedure is given by the following equation:
| (1) |
where
and Φ̅i is the i-th row vector in Φ̅. The reason that p is divided by 2 is that every specimen has two copies of each gene. One implication of Eq. (1) is that higher βi gives more accurate estimation on the number of carriers in the query. The number of sequence reads for each query is a stochastic process that determined by many technical factors, and βi is a random variable with Poisson distribution. We will use the following shorthand β = [β1, …, βt].
We will term the measurement process in Eq. (1) compositional channel. The reason for that name is that the sequencing process places 2-dimensional input vectors in 1-dimensional simplex, which is reminiscent of the concept of compositions in data analysis [40].
The sequencer may also produce errors when reading the DNA fragments. For simplicity, we assume that the sequencing errors are symmetric; the probability of the sequencer to report a normal allele as non-functional allele is equal to the probability of reporting a non-functional allele as normal. Let Λ be the error probability. In the presence of error, the sequencing results are given by:
| (2) |
where
and
The value of Λ dependents on the sequence differences between the normal allele and the non functional allele and the specific chemistry that is utilized by the sequencing platform. Once these are determined, one can infer Λ with high accuracy [41]. For single nucleotide substitutions, the most subtle mutations, we expect Λ = 1%, and when the sequence differences are more profound, like the three base-pair deletion in the Cystic Fibrosis mutation ΔF508, we expect Λ = 0 [38], [41].
1) Comparison between the compositional channel and the superimposed channel
The superimposed channel has been extensively studied in the group testing literature, and describes a measurement process that only returns the presence or absence of the tested feature among the members in the pool. The superimposed channel is given by:
| (3) |
The information degradation of the superimposed channel is more severe than the degradation of the compositional channel. Since in the latter case, the observer can still evaluate the ratio of carriers in the query.
Consider the following data degradation procedure that gets y = [y1, …, yt]T, the sequencing results of Eq. (1), and returns y′super, a degraded version of the results:
| (4) |
In essence, this procedure returns the presence or absence of carriers for each query.
Proposition 1: With high probability, y′super = ysuper, if βi ≫ 2n log n and Λ = 0.
In other words one can process the data of a compositional channel in Eq. (1) as if it was obtained from a superimposed channel in Eq. (3), once the sequencing coverage is high enough. The proof for the proposition is given in appendix B.
Group testing theory suggests a sufficient condition, called d-disjunction, for Φ that ensures faithful and tractable reconstruction of any d sparse vector that was obtained from a superimposed channel [12]. According to Proposition (1) d-disjunction is also a sufficient condition to recover up to d carriers when βi is high, and no sequencing errors. In that case, one can use group testing designs to employ the queries and guarantee the recovery of x.
2) Comparison between the compositional channel and the real-adder channel
The real adder channel describes a measurement process that reports the linear combination of the data points, and is given by:
| (5) |
This type of channel serves as the main model for compressed sensing, and it captures many physical phenomena and signal processing tasks. A closely related models were studied in group testing for finding counterfeit coins with a precise spring scale [42] and in multi-access communication [43] [44] [45]. Rewriting Eq. (2) reveals that the compositional channel is reminiscent of the noisy version of the adder channel:
| (6) |
However, there are two key differences between the compositional channel and the real-adder channel: (a) unlike the models in compressed sensing, ε is not i.i.d, and does depend on x. To emphasize that, consider a query with one carrier that is mixed with 99 normal specimens, and β = 5000. The sequencing results will follow a binomial distribution with . Accordingly, the variance of the results will be p(1 − p)β = 1/200 * 199/200 * 5000 = 24.8. Now, consider a query with 50 carriers and 50 normal specimens; the variance is 100/200 * 100/200 * 5000 = 1250, which is 50 times higher then the previous case. Notice that the only difference in the two cases is the composition of the query. (b) the observer can evaluate the reliability of each single query since he knows β. Thus, in the recovery procedure, the observer can give more weight to queries with higher number of reads, and vice verse. On the contrary, adder channel models assume that the observer only knows the noise distribution. The vast majority of the compressed sensing recovery algorithms does not have an inherent mechanism that takes into account the reliability of each measurement. Rather, they are built with a ’top-down’ approach that minimizes a global cost function.
To summarize that part, we presented the compositional channel as a model for next generation sequencing. We showed that the channel is reminiscent of to the channel models in group testing and compressed sensing, but not identical. We further showed that disjunctness is a sufficient decoding condition when the sequencing coverage is high. Table III summarizes the different channel models in this section.
TABLE III.
Comparison of Different Channels Models
| Channel model | Measurement process | Example |
|---|---|---|
| Superimposition | OR operation | Antibody reactivity |
| Compositional | Binomial sampling | Next generation sequencing |
| Real Adder | Additive | Spring scale |
III. QUERY DESIGN
A. Light-Weight Designs
We are seeking non-trivial d-disjunct matrices that reduce the number of barcodes with a minimal increase of the weight.
Definition 2: Φ is called d-disjunct if the Boolean sum of d column vectors does not contain any other column vector.
Definition 3: Φ is called reasonable if it does not contain a row with a single 1 entry, and its weight is more than 0. We are only interested in reasonable designs.
Definition 4: λij is the dot-product of two column vectors of Φ, and λmax ≜ max(λij).
Lemma 5: The minimal weight of a reasonable d-disjunct matrix is: w = d + 1.
Proof: Let ci be a column vector in Φ, and assume w ≤ d. According to definition (3), every 1 entry in ci intersects with another column vector. Thus, by choosing at most other w vectors, one can cover ci. According to definition (2), Φ cannot be d-disjunct, and w ≥ d + 1. The existence d-disjunct matrices with w = d + 1 was proved by Kautz and Singleton [12].
Definition 6: Φ is called light-weight d-disjunct in case w = d + 1.
Lemma 7: Φ is a light-weight (w−1)-disjunct iff λmax = 1 and Φ is reasonable.
Proof: First we prove that if Φ is a light-weight (w − 1)-disjunct then λmax = 1. Assume λmax occurs between ci and cj. According to definition (3), there is a subset of at most w − λmax + 1 column vectors in which ci is included in its Boolean sum. On the other hand, the Boolean sum of any w − 1 column vectors does not include ci. Thus, λmax < 2, and according to definition (3), λmax > 0. Thus, λmax = 1. In the other direction, Kautz and Singelton [12] proved that d = ⌊(w − 1)/λmax⌋, and Φ is light-weight according to definition (6).
Lemma 8: The number of columns of Φ is bounded by:
| (7) |
Proof: see Kautz and Singelton [12].
Theorem 9: The minimal number of rows, t, in a light-weight d-disjunct matrix is
Proof: plug lemma (7) to lemma (8):
Corollary 10: The minimal number of barcodes is in a light-weight weight design.
Proof: There are w query groups, and the bound is immediately derived from theorem (9).
A light weight design is characterized by λmax = 1, and rows. Low λmax does not only increase the disjunction of the matrix but also eliminates any short cycle of length 4 in the factor graph built upon Φ, which enhances the convergence of the reconstruction algorithm. We will discuss this property in section IV.
Notice that the light weight design is an extreme case of the sparse designs suggested in compressed sensing [46]–[48]. The weight of those designs usually scale with the number of specimens. For instance, in the sparse design of Chaining Pursuit, w ~ O(d log n) [47]. The light weight design is far more restricted, and w has no dependency per-se on n. We will show in section III-D that such dependency in other designs reduces their applicability to our setting.
B. The Light Chinese Design
We suggest a light weight design construction based on the Chinese Remainder Theorem. This construction reduces the number of queries to the vicinity of the lower bound derived in the previous section, and can be tuned to different weights and numbers of specimens. The repetitive structure of the design simplifies its translation to robotic instructions, and permits easy monitoring.
Constructing Φ starts by specifying: (a) the number of specimens, and (b) the required disjunction, which immediately determines the weight. Accordingly, a set of w positive integers Q = {q1, …, qw}, called query windows, is chosen with the following requirement:
| (8) |
where lcm denotes the least common multiplier. We map every specimen x to a residue system (r1, r2, ⋯, rw) according to:
| (9) |
Then, we create a set of w all-zero sub-matrices Φ(1), Φ(2), ⋯ called query groups with sizes qi × n. The submatrices captures the mapping in Eq. (9) by setting when this clause: x ≡ r (mod qi) is true. Finally, we vertically concatenate the submatrices to create Φ:
| (10) |
For instance, this is‡ Φ for n = 9, and w = 2, with {q1 = 3, q2 = 4}:
Definition 11: Construction of Φ according to Eq. ( 8 – 10 ) is called light Chinese design.
Theorem 12: A light Chinese design is a light weight design.
Proof: Let x ≡ vx (mod qi) and x ≡ ux (mod qj), where i ≠ j. According to the Chinese Remainder Theorem there is a one-to-one correspondence ∀x : x ↔ (ux, vx). Thus, every two positive entries in cx are unique. Consequently, |cx ∩ cy| < 2, and λmax < 2. Since specimens in the form r, r + qi, r + 2qi, … are pooled together Φ, λmax = 1. According to lemma (7) Φ is light-weight.
C. Choosing the Query Windows
The set of query windows, Q, determines the number of rows in Φ as:
| (11) |
Since , where gcd is the greatest common divisor, minimizing the elements in Q subject to the constraint in Eq. (8) implies that q1, …, qw should be pairwise co-prime and . Let , the definition of the problem we seek to solve is as follows: given a threshold, κ, and w, a valid solution is a set, R, that contains w co-prime numbers, all of which are larger than κ. We seek for the optimal solution, Q, being the solution satisfying that the sum of Q is minimal.
We begin by introducing a bound on max(Q) − κ, a value we will name δ, or the discrepancy of the optimal solution. In order to give an upper bound on δ, let us first consider a bound that is not tight, δ0, the discrepancy of the solution Q0 that is composed of the w smallest primes greater than κ. Primes near κ have a density of 1/log(κ), so δ0 ≈ w log(κ). δ0 is known to be an upper bound on δ because if any value greater than κ + δ0 appears in the Q, then there is also a prime q, κ < q ≤ max(Q0) that is not used. There is at most one value in Q that is not co-prime with q and if it exists it is larger than q. Replace it by q in Q (or replace max(Q) with q if all numbers in Q are co-prime with q) to reach a better solution, contradicting our assumption that Q is the optimal solution.
This upper bound can improved as follows. We know that Q ⊂ (κ, κ + δ0]. In this interval, there is at most one value that divides any number greater or equal to δ0. Consider, therefore, the solution Q1 composed of the w smallest numbers larger than κ that have no factors smaller than δ0. In order to assess the discrepancy of this solution, δ1, note that the density of numbers with no factors smaller than δ0 is at least 1/log(δ0). This can be shown by considering the (lower) density that is the density of the numbers with no factors smaller than pδ0, where pi indicates the i’th smallest prime. This density is given by:
| (12) |
where e is Euler’s constant and we make use of , a well-known property of the prime harmonic series. Like δ0, the bound δ1 is also an upper bound on δ. To show this, consider that the optimal solution Q may have z values larger than κ + δ1 in it. If so, there are at least z members of Q1 absent from it. Replace the z members of Q with the absent members of Q1 to reach an improved solution. We conclude that z = 0 and δ1 ≥ δ.
Theorem 13: For κ → ∞ and large w, δ ≈ w log(w).
Proof: Consider repeating a similar improvement procedure as was used to improve from δ0 to δ1 an arbitrary number of times. We define Qi+1 as the set of w minimal numbers that are greater than κ and have no factors smaller than δi, where δi is the discrepancy of solution Qi. This creates a series of upper bounds for δ that is monotone decreasing, and therefore converges. Because each δi+1 satisfies δi+1 ≈ w log(δi), we conclude that the limit will satisfy δ∞ ≈ w log(δ∞), meaning δ ≤ δ∞ ≈ w log(w). This gives an upper bound on δ. To prove that this bound is tight, we will show that, asymptotically, it is not possible to fit w co-prime numbers on an interval of size less than w log(w). To do this, note first that at most one number in the set can be even. Fitting w − 1 odd numbers requires an interval of size at least 2w (up to a constant). The remaining numbers can contain at most one value that divides by 3. The rest must be either 1 or 2 modulo 3. This indicates that they require an interval of at least . More generally, if S contains w values, with each of the first w prime numbers dividing at most one of said values, then the interval length of S must be at least on the order of:
This gives a lower bound on δ equal to the previously calculated upper bound, meaning that both bounds are tight.
Corollary 14:
Proof:
Since the number of positive entries in each submatrix is the same and equals to n the query groups are formed by partitioning Φ to the submatrices. Consequently, τmax = max(Q).
Importantly, the maximal compression level, rmax, is never more than , and the light Chinese design is practical for genotyping tens of thousands of specimens. The tight bound on δ also implies a tight bound on the sum of Q. Let . We give a tight bound on σQ that, asymptotically, reaches a 1:1 ratio with the optimal value.
Theorem 15: The number of queries in the light Chinese design is
Proof: Proof that this is a lower bound is by induction on w. Specifically, let us suppose the claim is true for Qw−1 and prove for Qw, where Qw is the optimal solution with w elements (There is no need to verify the “start” of the induction, as any bounded value of w can be said to satisfy the approximation up to an additive error). To prove a lower bound, σQw cannot be better than σQw−1 + w log(w), as the discrepancy of Qw is known and the partial solution Qw \ max (Qw) can not be better than Qw−1. To prove that this is also an upper bound, consider that the discrepancy of Qw is known to be approximately w log(w), so any prime larger than approximately pw cannot be a factor of more than one member of the interval (κ, max(Qw)]. Furthermore, the optimal solution for Qw can not be significantly worse than the optimal solution for Qw−1 plus the first number that is greater than max(Qw−1) and has no factors smaller than pw. As we have shown before, this number is approximately max(Qw−1) + log(w). However, we already know the discrepancy of Qw−1 is approximately (w − 1) log(w − 1), so this new value is approximately κ + (w − 1) log(w − 1) + log(w) ≈ κ + w log(w). Putting everything together, we get that σQw ≤ σQw−1 + w log(w) ≤ Σi≤w i log(i), proving the upper bound. The value Σi≤w i log(i) is between , so asymptotically σQ converges to .
We will now consider algorithms to actually find Q. First, consider an algorithm that begins by setting τmax to the w prime number after κ, and then runs an exhaustive search through all sets of size w that contain values between κ and τmax. This is guaranteed to return the optimal result, and does so in complexity O((τ−κ)w), which is asymptotically equal to O((w log(κ))w). Though this complexity is hyper exponential, and so unsuitable for large values of w it may be used for smaller w.
The upper bound described above suggests a polynomial algorithm for Q since it is a bound that utilizes sets chosen such that none of their elements have prime factors smaller than κ. This implies the following simplistic algorithm that calculates a solution that is asymptotically guaranteed to have a 1:1 ratio with the optimal σQ.
Let Q be the set of the w smallest primes greater than κ.
repeat
δ ← max(Q) − κ
Q ← the w smallest numbers greater than κ that have no factors smaller than δ
until δ = max(Q) − κ
output Q.
In practice, this is never the optimal solution, as for example, it contains no even numbers. In order to increase the probability that we reach the optimal solution (or almost the optimal solution), we opt for a greedy version of this algorithm. The greedy algorithm begins by producing the set of smallest numbers greater than κ that have no factors smaller than δ (as in the upper bound). It continues by producing the set of smallest co-prime numbers greater than κ that have at most one distinct factor smaller than δ (as in the calculation of the lower bound). Then, it attempts to add further elements with a gradually increasing number of factors. If these attempts cause a decrease in δ, it repeats the process with a lower value of δ until reaching stabilization.
Q ← initial solution.
repeat
δ ← max(Q) − κ
the number of distinct primes smaller than δ in the factorization of x.
Sort the numbers κ+1, …, max(Q) by increasing n(x) [major key] and increasing value [minor key].
for all i in the sorted list do
if i is co-prime to all members of Q and i < max(Q) then
replace max(Q) by i in Q.
else if i is co-prime to all members of Q except one, q, and i < q then
replace q with i in Q.
end if
end for
until δ = max(Q) − κ
output Q.
Because this greedy algorithm only improves the solution from iteration to iteration, using the output of the first algorithm described as the initial solution for it guarantees that the output will have all asymptotic optimality properties proved above. In practice, on the range κ = 100 … 299 and w = 2 … 8 it gives the exact optimal answer in 91% of the cases and an answer that is off by at most 2 in 96% of the cases. (Understandably, no answer is off by exactly 1.) The worst results for it appear in w = 8, where only 82% of the cases were optimal and 88% of the cases were off by at most 2.
Notably, due to the fact that κ + 1 does not always appear in either the optimal solution or the solution returned by the greedy algorithm, sub-optimal results tend to appear in streaks: a sub-optimal result on a particular κ value increases the probability of a sub-optimal result on κ+1 (A similar property also appears when increasing w), and we denote an interval of consecutive κ values where the greedy algorithm returns sub-optimal results to be a “streak”. The number of streaks is, perhaps, a better indication for the quality of the algorithm than the total number of errors. For the parameter range tested (totaling 1400 cases), the greedy algorithm produced 61 sub-optimal streaks (of which in only 23 streaks the divergence from the optimal was by more than 2). The worst w was 6, measuring 14 streaks. The worst-case for divergence by more than 2 was w = 8, with 8 streaks.
In terms of the time complexity of this solution, this can be bounded as follows. First, we assume that the values in the relevant range have been factored in advance, so this does not contribute to the running time of the algorithm. (This factorization is independent of κ and w, except in the very weak sense that κ and w determine what the “relevant” range to factor is.) Next, we note that the initial δ is determined by searching for w primes, so we begin with a δ value on the order of w ln(κ). Each iteration decreases δ, so there are at most w log(κ) iterations. In each iteration, the majority of time is spent on sorting δ numbers. Hence, the running time of the algorithm is bounded by δ2 log(δ) or w2 log2(κ)(log(w) + log(log(κ))). Clearly, this is a polynomial solution. In practice, it converges in only a few iterations, not requiring the full δ potential iterations. In fact, in the tested parameter range the algorithm never required more than three iterations in any loop, and usually less. (Two iterations in the greedy allocation loop is the minimum possible, and an extra iteration over that was required in only 4% of the cases.)
In some cases, it is beneficial to increase the number of barcodes from κ to κ1 in order to achieve higher probability of faithful reconstruction of signals that are not d sparse. This is achieved by finding w integers in the interval (κ, κ1) that follow Eq. (8) and maximize . We give more details about this problem in appendix C.
Lastly, we note that even though these approximation algorithms are necessary for large values of w, for small w an exhaustive search for the exact optimal solution is not prohibitive, even though the complexity of such a solution is exponential. One can denote the solution as Q = {κ + s1, κ + s2, …, κ + sw} in which case the values {s1, …, sw} are only dependent on the value of κ modulo primes that are smaller than the maximal δ or approximately w log(w). This means that the {s1, …, sw} values in the optimal solution for any (κ, w) pair is equal to their values for (κ mod P, w), where P is the product of all primes smaller than δ. Essentially, there are only P potential values of δ that need to be considered. All others are equivalent to them.
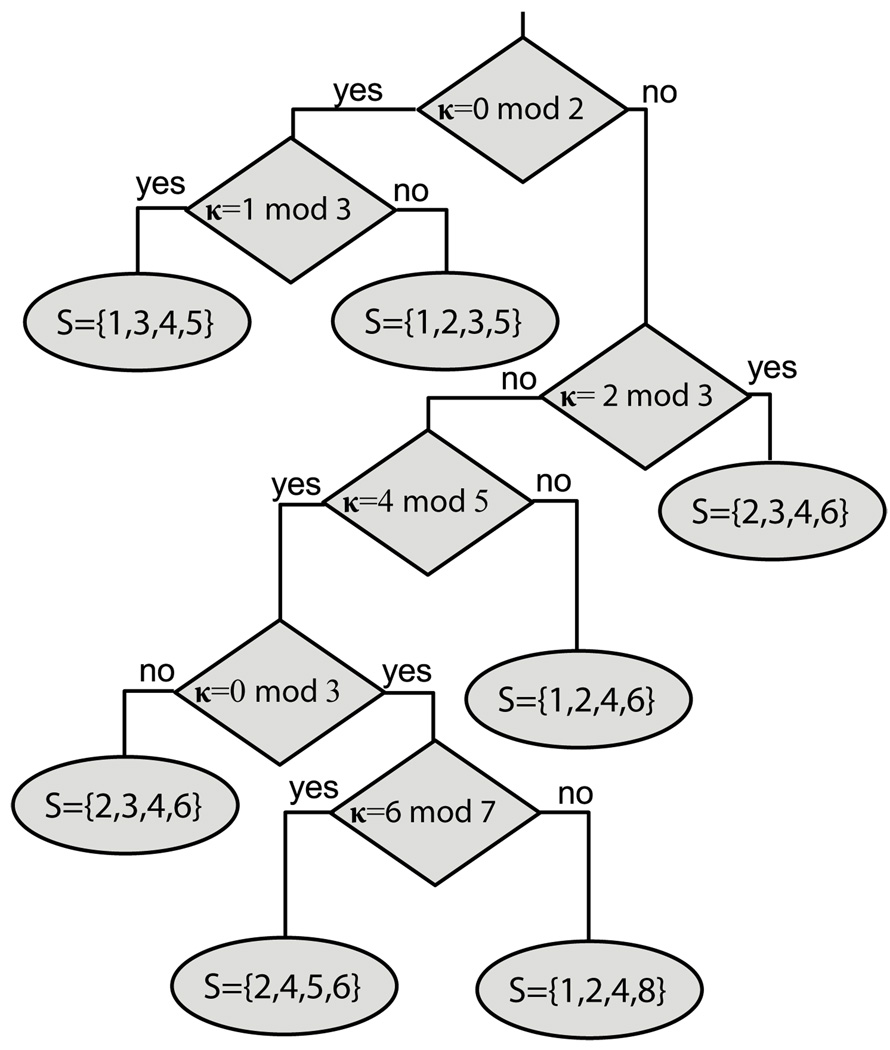
In practice, the number of different κ values that need to be considered is significantly smaller than this. As an example, Fig. 2 gives the complete optimal solution for any value of κ with w = 4. The figure shows that the set S = {s1, …, sw} for any κ has only 7 possible values, and that determining which set produces the optimal solution for any particular value of κ can be done by at most 5 Boolean queries regarding the value of κ modulo specific primes.
Fig. 2.
An Optimal Solution using Tree Search
D. Comparison to other designs
It is well established in group testing theory and in compressed sensing that certain designs can reach to the vicinity of the lower theoretical bound of t ~ O(d log n) [16], [49]. The scale in light weight designs raises the question whether other designs are more cost effective for compressed genotyping with thousands of specimens.
We compared the performance of the light Chinese design to other two designs: Chinese Remainder Sieve (CRS) [50], and Shifted Transversal Design (STD) [51]. CRS, to the best of our knowledge, shows the maximal reduction of t for the general case. Interestingly, it is also based on the Chinese Remainder Theorem, but without the assertion in Eq. (8). Instead, to create a d-disjunct matrix, CRS allows Q to contain any series co-prime numbers whose product is more than nd. The number of queries in CRS for a given d is:
| (13) |
and the weight is:
| (14) |
Notice that the weight scales with the number of specimens, implying that more sequencing lanes and robotic logistic are required with the growth of n even if d is constant. STD is also a number theoretic design, which has been used for several biological applications [18], [19].
From the results in table IV we see that CRS and STD are not applicable to the biological and technical constraints in the genotyping setting of w ≤ 8 and rmax ≲ 1000 (labeled in the table with †) when the number of specimens is 5000 or more. Moreover, the reduction in the number of barcodes, τmax, and the number of queries in CRS and STD is no more than ten fold than the light Chinese design, but their weights are least 2.5 fold greater than the weights in the light Chinese design. The estimated cost ratio between a single barcode synthesis to a sequencing lane is around 1 : 100. Therefore, the light Chinese design is more cost effective to our setting.
TABLE IV.
Comparison between light Chinese design to other designs
| n | d | CRS | STD | Light Chinese Design | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t | w | τmax | rmax | t | w | τmax | rmax | t | w | τmax | rmax | ||||
| 5000 | 3 | 149 | 10† | 29 | 1000 | 110 | 10† | 11 | 455 | 293 | 4 | 77 | 64 | ||
| 4 | 237 | 12† | 37 | 714 | 169 | 13† | 13 | 385 | 370 | 5 | 77 | 64 | |||
| 5 | 336 | 15† | 47 | 1000 | 272 | 16† | 17 | 295 | 449 | 6 | 79 | 64 | |||
| 40000 | 3 | 209 | 12† | 37 | 8000† | 169 | 13† | 13 | 3077† | 811 | 4 | 205 | 199 | ||
| 4 | 335 | 14† | 47 | 5714† | 221 | 13† | 17 | 2353† | 1020 | 5 | 209 | 199 | |||
| 5 | 472 | 17† | 59 | 5714† | 272 | 16† | 17 | 2353† | 1231 | 6 | 211 | 199 | |||
Additional interesting design is the Subset Containment Design [17]. This design has queries, specimens, and a weight of , where q and k are design parameters. Since the weight of the design is controllable, we evaluated the performance of this design when the w = d + 1 as in the light Chinese design. In that case, k = d + 1. Since , then , and the number of queries scales with . Thus, for our setting, the light Chinese design outperforms the subset containment design.
IV. DECODING
A. Formulating the decoding setting
Now, we will turn to address the other part of the compressed genotyping protocol, which is how to reconstruct x given y and Φ. The MAP decoding of x is:
| (15) |
For simplicity, we assume that we do not have any prior knowledge, besides the expected carrier rate in the screen. Notice that in some cases, the observer has information about kinship between the specimens or their familial history regarding genetic diseases. Incorporating this information will remain outside the scope of this manuscript. Let φ(0) be the expected rate of normal specimens and φ(1) the expected rate of carriers. For instance, for Cystic Fibrosis ΔF508 screen φ(0) = 29/30, and φ(1) = 1/30. The prior probability for a particular (x1, …, xn) ∈ x configuration is:
| (16) |
The probability of particular sequencing results is:
| (17) |
we use x∂a to denote a configuration of the subset of specimens in the a query, and ya denotes the sequencing results of the a-th query. The probability distribution Pr(ya | x∂a) is given by the compositional channel model in Eq. (2). We will use the following shorthand to denote this probability distribution:
| (18) |
| (19) |
The factorization above is captured by a factor graph with two types of factor nodes: φ nodes that denote the prior expectations, and Ψ nodes that denote the probability of the sequencing data. Each φ node is connected to a single variable nodes, whereas the Ψ nodes are connected to the variables according to the query design in Φ, so each variable node is connected to w different Ψ nodes. An example of a factor graph with 12 specimens, and Q = {3, 4} is given in Fig. 3.
Fig. 3.
Example of a Factor Graph in Compressed Genotyping
B. Bayesian decoding using belief propagation
Belief propagation (sum-product algorithm) [52], [53] is a graphical inference technique that is based on exchanging messages (beliefs) between factor nodes and variable nodes that tune the marginals of the variable nodes to the observed data. When a factor graph is a tree this process returns the exact marginals. Clearly, any reasonable query design induces a factor graph with many loops, implying that finding xMAP is NP-hard [54]. Belief propagation can still approximate the marginals even if the graph has loops as long as the local topology of the graph is tree-like and there are no long-range correlations between the variable nodes [55], [56]. Approximating NP-hard problems with belief propagation was successfully tested in a broad spectrum of tasks including decoding LDPC codes [52], finding assignments in random k-SAT problems [57], and even solving Sudoku puzzles [58]. Recently, several independent studies investigated the performance of belief propagation as a recovery technique for compressed sensing [31], [48], [59] and group testing [15]. Mezard et al. [15] studied the decoding performance of belief propagation in the prototypical problem of group testing. One advantage of their decoding technique is a pre-processing stripping procedure that identifies ’sure zeros’, variables nodes that are connected to at least one ’inactive’ test node and removes them from the graph. The stripped graph is much smaller, leading to faster convergence of the belief propagation. Our algorithm is reminiscent of Mezard et al. approach. We first employ a stripping procedure to reduce the size of the graph, and then we use belief propagation to calculate the marginals of the remained variable nodes.
1) stripping
The stripping procedure iterates between three step: (a) evaluating whether the sequencing data in a Ψ node indicates ’no carriers’ (b) removing the node and its connected variable nodes (c) extrapolating the sequencing results in the other factor nodes so they will reflect removing normal specimens from the queries.
In order to evaluate whether the sequencing data indicates ’no carriers’, we calculate the relative ratio of the two competing hypothesis: H0 - there are no carriers in the pool; and H1 - there is at least one carrier in the pool. H0 and H1 for that query are given by:
| (20) |
| (21) |
where pk denotes the probability of having k carriers in the pool, and qk denotes the likelihood of the data given that there are k carriers in the pool. pk and qk are Poisson probabilities given by:
| (22) |
| (23) |
and:
| (24) |
| (25) |
Where ni is the number of specimens in the i-th query. Once the ratio Pr(H0)/Pr(H1) crosses a user-determined threshold, we apply the stripping procedure to the factor node, and to its connected variable nodes.
We then update the observed data of the factors nodes that were connected to each stripped variable node. Let:
| (26) |
| (27) |
| (28) |
The new number of reads (β′) and the new fraction of non-functional reads in the factor node are set to:
| (29) |
| (30) |
where yi is the previous fraction of reads from the non-functional allele, and β is the previous number of reads in that factor node.
2) Belief Propagation
The marginal probability of xi is given by the Markov property of the factor graph:
| (31) |
The approximation of belief propagation in loopy graphs is that the beliefs of the variables in the subset ∂a\xi regarding xi are independent. Since λmax = 1 in light-weight designs, the resulted factor graph does not have any short cycles of girth 4, implying that the beliefs are not strongly correlated, and that the assumption is approximately fulfilled. The algorithm defines μa→xi (xi) as:
| (32) |
and
| (33) |
were u ∈ ∂xj denotes the subset of queries with xj. Eq. (32) describes message from a factor node to a variable node, and Eq. (33) describes message from a variable node to a factor node. By iterating between the messages the marginals of the variable nodes are gradually obtained, and in case of successful decoding the algorithm reaches to a stable point, and reports x*:
| (34) |
This approach encounters a major obstacle - calculating the factor to node messages requires summing over all possible genotype configurations in the pool, which may exponentially grow with the compression level, rmax, or . To circumvent that, we use Monte-Carlo sampling instead of an exact calculation to find the factor to node messages of each round. This is based on drawing random configurations of x∂a according to the probability density functions (pdf) that are given by the μxj→a(xj) messages and evaluating Ψa(x∂a). An additional complication are strong oscillations that hinder the convergence of the algorithm. We attenuate the oscillations by a damping procedure [60] that averages the variable to factor messages of the m round with the messages of the m − 1 round:
| (35) |
The damping extent can by tuned with γ ∈ [0, 1] ; γ = 1 means no updates, and with γ = 0, we restore the algorithm in Eq. (33). Appendix D presents a full layout of the belief propagation reconstruction algorithm.
V. NUMERICAL RESULTS
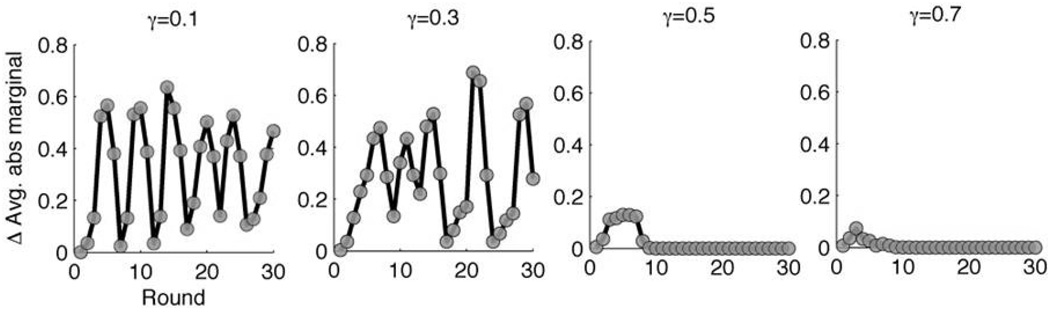
To demonstrate the power of our method, we simulated several settings with: n = 1000, β = 103, w = 5, d = 4 and Q = {33, 34, 35, 37, 41}. Fig. 4 shows the effect of damping on the belief propagation convergence rates. In this example, the actual number of carriers in the screen, d0, was 43, and we ran the decoder for 30 iterations. We evaluated different extents of damping: γ ∈ [0.1, …, 0.9], and we measured for each iteration the averaged absolute difference of the marginals from the previous step. We found that with γ < 0.5, there are strong oscillations and the algorithm did not converge, whereas with γ ≥ 0.5, there are no oscillations, and the algorithm correctly decoded x.
Fig. 4.
The Effect of Damping on Oscillations
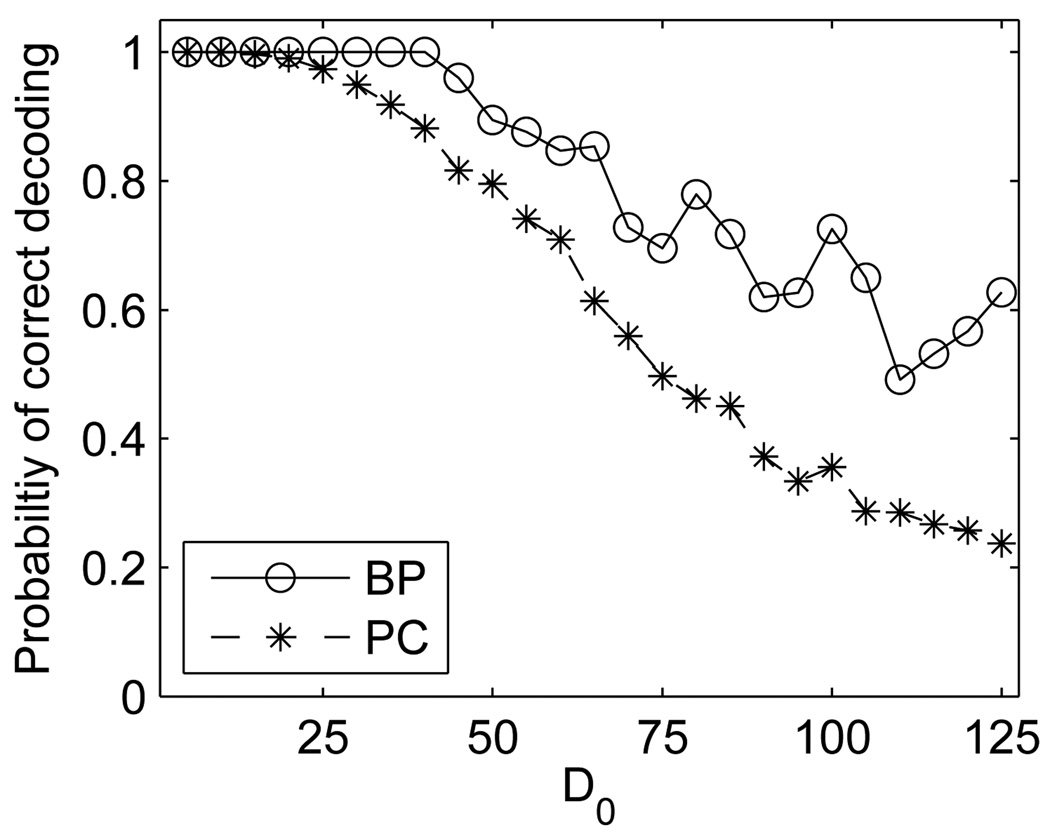
We also tested the performance of the reconstruction algorithms for increasing number of carriers in the screen, ranging from 5 to 150, with no sequencing errors (Fig. 5). In order to benchmark the approximation results by the belief propagation, we compared its performance to pattern consistency (PC) decoding, a baseline group testing decoder [21]. The belief propagation reconstruction outperformed the pattern consistency decoder and reconstructed the genotypes with no error even when the number of carriers was 40, which is a quite high number for severe genetic diseases. The ability of the belief propagation to faithfully reconstruct cases with d0 ≫ d-disjunction of the query design is not surprising, since d-disjunction is a conservative sufficient condition even for a superimposed channel.
Fig. 5.
Decodability as a Function of Number of Carriers
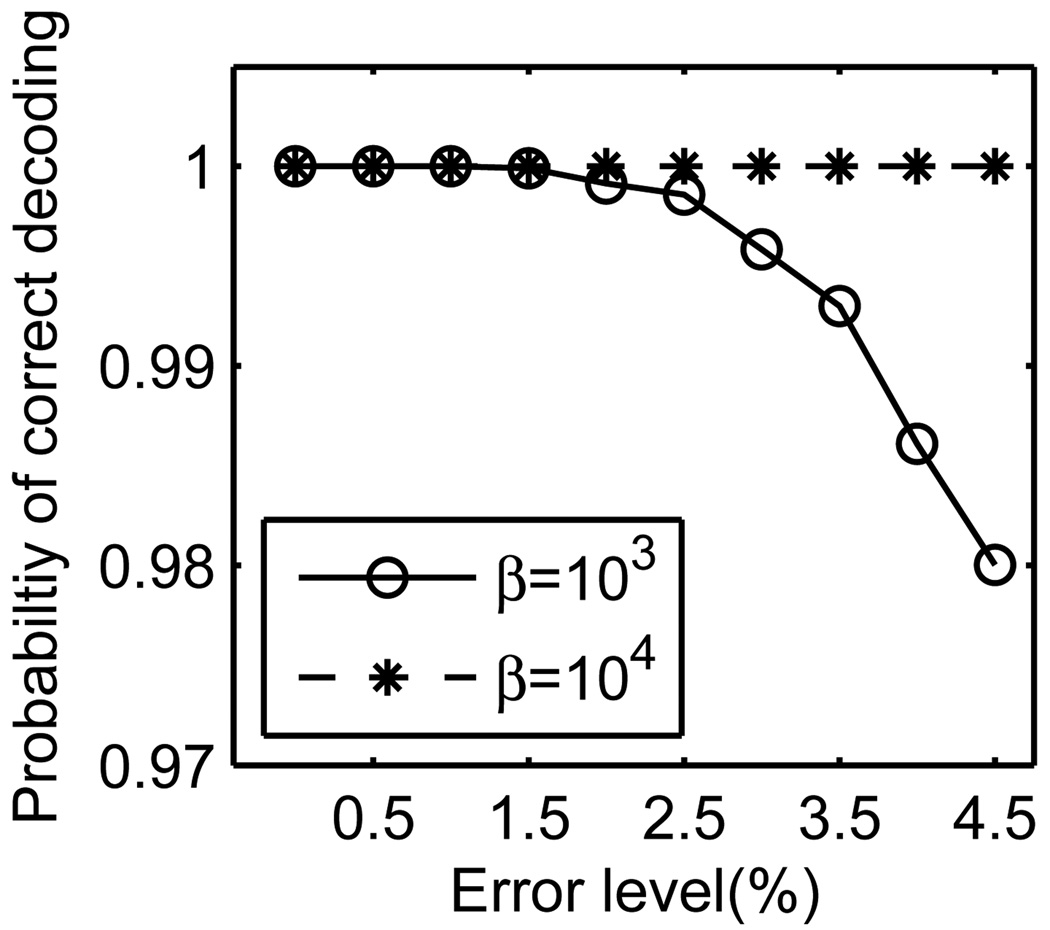
We continue to evaluate the performance of the algorithm in a biologically-oriented setting - detecting carriers for Cystic Fibrosis W1282X mutation, where the carrier rate in some populations is about 1.8% [37]. The relatively high rate of the carriers challenges our scheme with a difficult genetic screening problem. Moreover, the sequence difference between the wild-type allele and the mutant allele is only a single base substitution, increasing the probability of sequencing errors. To simulate that, we introduced increasing levels of sequencing errors with 0% ≤ Λ ≤ 4.5%, and tested the performance of the reconstruction algorithms when β = 103 and β = 104 (Fig. 6). The belief propagation algorithm reported the correct genotype for all specimens even when the error rate was 1.5% and β = 103. Importantly, the decoding mistakes at higher error rates were false positives, and did not affect the sensitivity of the method. When we increased the number of reads for each query to β = 104, the belief propagation decoder reported the genotype of all the specimens without any mistake. As we mentioned earlier, the expected sequencing error rate for single nucleotide mutations is around 1%, implying that the parameters used in the simulation are quite conservative.
Fig. 6.
Simulation of Cystic Fibrosis Screen - The Effect of β and Sequencing Errors
VI. FUTURE DIRECTIONS AND OPEN QUESTIONS
Tighter sufficient decoding condition
Currently, we rely on the disjunctness for evaluating the decoding performance. Even for group testing tasks, d-disjunct is a weak lower bound, and in practice the decoding performance is much better. The compositional channel gives richer information than the superimposed channel, and we can easily recover x’s that are not d-sparse. For instance, we showed that we can recover with 100% accuracy even 40 carriers with a 4-disjunct design (Fig. 5). The sufficient recovery conditions in compressed sensing (e.g. RIP-p [24]) also do not fit ’as-is’ to our setting. First, these conditions mainly discuss additive i.i.d noise, while the noise in compositional channel does dependent on the input. Second, the input vectors in compressed sensing are real, x ∈ ℝn, whereas in our setting the input vector is in the binary domain, x ∈ {0, 1}n. A tighter condition is important for developing more efficient query designs, and to predict the performance of the design without tedious simulations.
Incorporating prior information to the query design
Our query design assumes that the prior probability of the specimens to be carriers is i.i.d. There are several situations in which the experimenter knows the kinship information between the specimens, their medical history, or their ethnic background. In those cases, the prior probabilities are neither identical nor independent. For example, consider a design for Cystic Fibrosis that includes four specimens: two Caucasian brothers, and two unrelated Afro-American individuals. The two brothers have higher prior probability based on their ethnicity, and if one brother is a carrier, it increases the likelihood of the other brother to be a carrier. An open question is how to incorporate this information in the encoding stage in order to maximize the information. Kainkaryam et al. [20] studied a similar problem in the context of drug screening, and proposed a genetic algorithm for near-optimal pooling designs. However, his approach is computational intensive and not feasible for large scale designs.
Expanding the mathematical setting to full range of genetic diseases
While the genotype representation presented in section II is valid for the vast majority of rare genetic diseases, the genetics of a small subset of diseases does not fit to our description. First, some diseases, such as Spinal Muscular Atrophy, involve copy number variation. In those cases, the gene is not diploid, and the entries of x are no longer binary. Second, some diseases have a spectrum of alleles with different levels of clinical outcomes. For instance, the gene FMR1, that causes Fragile X mental retardation [61], has dozens of possible alleles. Thus, the genotype of a single individual should be represented by a vector and not a scalar, and we need to recover a (sparse) matrix and not a vector. A fully inclusive treatment should include those cases as well.
Pooling imperfections
Throughput the sequel, we assumed that Φ is exactly known. However, the pooling procedure may be imperfect and introduce some noise to Φ. For example, it may happen that unequal amount of DNA are taken from each individual, or that small amounts of material from one pool contaminate the following pool to be sequenced, etc. Such problems introduce multiplicative noise to Φ, which may hinder accurate reconstruction [62]. While the experimenter can not completely eliminate those imperfections, he can invest more efforts to reduce their extent. The main question is if the pooling imperfections cause a phase transition, i.e, if below a certain threshold their effect is minor, and above the threshold the recovery procedure will fail. Knowing the value of that threshold is important when designing optimized experiments.
VII. CONCLUSION
In this paper, we presented a compressed genotyping framework that harnesses next generation sequencers for large scale genotyping screens of severe genetic diseases using ideas and concepts from group testing and compressed sensing. We discussed the unique setting of our problem compared to group testing and compressed sensing. We showed that in addition to the traditional objective of minimizing the number of queries, our setting favors light weight designs, in which the weight does not depend on the number of specimen. In addition, we showed that the sequencing process creates a different measurement channel called the compositional channel. For constructing light weight designs, we proposed a simple method based on the Chinese Remainder Theorem, and we showed that this method reduces the number of queries to the vicinity of the theoretical bound. For the decoding part, we presented a Bayesian framework that is based on stripping procedure and loopy belief propagation. We expect that our framework can be useful for other compressed sensing applications.
ACKNOWLEDGMENT
The authors thank Oded Margalit and Oliver Tam for useful comments. Y.E is a Goldberg-Lindsay Fellow and ACM/IEEE Computer Society High Performance Computing PhD Fellow of the Watson School of Biological Sciences. G.J.H is an investigator of the Howard Hughes Medical Institute. P.P.M is a Crick-Clay Professor.
Biographies

Yaniv Erlich (Student, IEEE) earned his B.Sc. degree in neuroscience from Tel-Aviv University, Israel, in 2006. Since 2006, he is a PhD student in the Watson School of Biological Sciences in Cold Spring Harbor Laboratory, NY. He studies genomics and bioinformatics under the guidance of Prof. Gregory Hannon. His research interests are algorithm development for genomics, human genetics, and genetic diseases. He has two patents in the area of high throughout sequencing. During his studies he won several awards including Wolf Foundation Scholarship for excellence in exact sciences, ACM/IEEE-CS High Performance Computing PhD Fellowship, and the Goldberg-Lindsay PhD Fellowship.

Assaf Gordon has been a senior programmer at Greg Hannon’s lab in Cold Spring Harbor Laboratory, NY, since May 2008. His research intrests includes developing tools for high throughput sequencing, analysis, and annotation of genomics data. He pulished papers in small RNA biogenesis, and algorithm development for high throughput sequencing. He has more than 10 years experience in software development in various companies and for the Linux community.

Michael Brand holds an M.Sc. in Applied Mathematics from the Weizmann Institute of Science and a B.Sc. in Engineering from Tel-Aviv University. He has published papers in Strategy Analysis, Data Mining, Optimization Theory and Object Oriented Design, and has recently published the book ”The Mathematics of Justice: How Utilitarianism Bridges Game Theory and Ethics”. During the past twenty years he has worked as a researcher and an algorithm developer, most recently in speech research as the Chief Scientist of Verint Systems Ltd. and as a machine vision researcher in Prime Sense Ltd.

Gregory J. Hannon is a Professor in the Watson School of Biological Sciences at Cold Spring Harbor Laboratory. He received a B.A. degree in biochemistry and a Ph.D. in molecular biology from Case Western Reserve University. From 1992 to 1995, he was a postdoctoral fellow of the Damon Runyon-Walter Winchell Cancer Research Fund, where he explored cell cycle regulation in mammalian cells. After becoming an Assistant Professor at Cold Spring Harbor Laboratory in 1996 and a Pew Scholar in 1997, in 2000, he began to make seminal observations in the emerging field of RNA interference. In 2002 Dr. Hannon accepted a position as Professor at CSHL where he continued to reveal that endogenous non-coding RNAs, then known as small temporal RNAs and now as microRNAs, enter the RNAi pathway through Dicer and direct RISC to regulate the expression of endogenous protein coding genes. He assumed his current position in 2005 as a Howard Hughes Medical Institute Professor and continues to explore the mechanisms and regulation of RNA interference as well as its applications to cancer research.

Partha Mitra (Member, IEEE) received his PhD in theoretical physics from Harvard in 1993. He worked in quantitative neuroscience and theoretical engineering at Bell Laboratories from 1993–2003 and as an Assistant Professor in Theoretical Physics at Caltech in 1996 before moving to Cold Spring Harbor Laboratory in 2003, where he is currently Crick-Clay Professor of Biomathematics. Dr. Mitras research interests span multiple models and scales, combining experimental, theoretical and informatic approaches toward achieving an integrative understanding of complex biological systems, and of neural systems in particular.
APPENDIX A
GLOSSARY OF GENETIC TERMS
Allele - Allele is a possible variation of a gene. Consider a gene that encodes eye color. One alleles can be ’brown’, and another allele can be ’blue’.
Barcoding - An artificial reaction in which a short and unique DNA sequence is concatenated to the specimen’s DNA in order to label its identity. The short DNA sequence does not encode any relevant genetic information and it is synthesized in the lab according to the experimenter needs.
DNA - A long molecule that is composed of four building blocks, called nucleotides. The specific DNA composition encodes a trait.
DNA sequencing - Chemical reactions that convert a DNA molecule into signals that identify its composition.
Gene - Gene is a DNA sequence in the genome that confers a specific function. There are about 20,000 genes in the human genome.
Genotyping - The process of determining the alleles in a certain trait of an individual.
Lane - High throughput sequencers are composed of several distinct chambers called lanes. Thus, one can sequence in each lane a different sample while keeping the samples separated for each other.
Mutation - An alteration at a specific site in the genome. It is usually refers to a change that disrupts the normal gene activity.
Nucleotide - The building blocks of the DNA. There are four types of nucleotides that are labeled by A,C,G, and T.
Ploidy - The number of copies of a gene in the genome. In human, most of the genes are diploid, meaning that every gene appears in two copies. The two copies (alleles) can be identical or different from each other.
Recessive mutation - A mutation that causes a loss-of-function in an allele that can be compensated by the activity of a normal allele. In order for a recessive mutation to be overt, both alleles must contain the mutation.
Single Nucleotide Polymorphism (SNP) - The most common type of mutation. A change in a specific nucleotide.
Wild Type (WT) - The allele that is found in the vast majority of the population. In the context of genetic diseases, it refers to the allele with the normal activity.
APPENDIX B
PROOF FOR PROPOSITION 1
The main problem of reducing the compositional channel to a superimposed channel is insufficient sequencing coverage. In that case, the sequencing results of a query that contains carrier/s returns no reads from the non-functional allele, or α = 0. Consequently, the degradation procedure in Eq. (4) will return 0 from the query instead of 1. Since we assume in Eq. (3) that there are no error in the superimposed channel, we want to find a sufficient condition for β, the number of sequence reads, that will reduce probability of insufficient sequencing coverage to zero. Proposition (1) claims that β ≫ 2n log n is a sufficient condition.
Proof: : Let p be the rate of non-functional alleles in the query. The probability of not having a single read from the non-functional allele when sampling β molecules is: Pr(failure) = (1 − p)β. The probability of this event not to occur in any of t queries is:
| (36) |
| (37) |
Thus, when pβ ≫ log t the probability of having sufficient sequence coverage for all queries goes to 1. In the worst case (and unlikely) situation, one has exactly a single carrier, and each pool contains the entire set of specimens. In that case, p = 1/2n. Thus, r ≫ 2n log t. Since t < n, r ≫ 2n log n is a sufficient condition.
APPENDIX C
THE PRODUCT MAXIMIZATION ALGORITHM
Handling large number of DNA barcodes is usually done with microtiter plates that are composed of many wells, each of which contains a different DNA barcode. The plates have several defined sizes, and the most common ones are: 96 wells, 384 wells, and 768 wells. Thus, another practical consideration is that the number of barcodes will not exceed the number of wells in the plate, i.e keeping τmax below a certain threshold. For that purpose, we developed the product maximization algorithm that limits τmax below a threshold and finds a set of numbers that their product is maximal, which increases the probability of correct decoding.
The product maximization problem is defined as follows. Given parameters κ, κ1 and w, find the set Q of size w whose elements are all in the range κ < x ≤ κ1 and such that for no pair x, y ∈ Q has lcm(x, y) ≤ κ2. For product maximization, typical values in practice have κ in the range [100, 300), w in the range [2, 8] and κ1 fixed at 384. The reason for this number is the number of wells in a microtiter plate, which is compatible with liquid handling robots. The empirical results below relate to this entire range, for all of which we have optimal solutions discovered by exhaustive searching.
The product maximization problem has ties to the sum minimization problem in both bound-calculation and solving algorithms. First, note that in this problem we cannot consider “asymptotic” behavior when w, κ and κ1 are large without specifying how the ratio is constrained.
If κ is constant and κ1 rises, the asymptotic solution will be the set {κ1, κ1 − 1, κ1 − 2, …, κ1 + 1 − w}. This set clearly has the maximum possible product, while at the same time satisfying the condition on the lcm because no two elements in the solution can have a mutual factor greater than w. This value will be the optimum as soon as (κ1 + 1 − w) (κ1 + 2 − w) > wκ2 (and possibly even before), so should be taken as an upper bound for to form a non-trivial case.
For any specific ratio , the condition lcm(x, y) > κ2 for x and y values close to κ1 is equivalent to . This allows us to reformulate the question as that of finding the set Q with w elements, all less than or equal to κ1, s.t. the gcd of any pair is lower than or equal to .
For the product maximization problem, we redefine the discrepancy to be δ = κ1 + 1 − min(Q). In order to compute the asymptotic bound for this discrepancy, let us first define pseudo-primes. Let the set of k-pseudo-primes, Pk, be defined as the set s.t. i ∈ Pk ⇔ i > k and ¬∃j < i, j ∈ Pk s.t. i is divisible by j. The set of 1-pseudo-primes coincides with the set of primes.
One interesting property of k-pseudo-primes is that they coincide with the set of primes for any element larger than k2. To prove this, first note that if i is a prime and i > k then i by definition belongs to Pk. Second, note that if i is composite and i > k2 then i has at least one divisor larger than k. In particular, it must have a smallest divisor larger than k, and this divisor cannot have any divisors larger than k, meaning that it must belong to Pk. Consequently, i ∉ Pk.
Both the reasoning yielding the upper bound and the reasoning yielding the lower bound for the sum minimization problem utilize estimates for the density of numbers not divisible by a prime smaller than some d. In order to fit this to the product maximization problem, where a gcd of ρ is allowed, we must revise these to estimates for the density of numbers not divisible by a ρ-pseudo-prime smaller than δ. Because the k-pseudo-primes and the primes coincide beginning with k2, this density is the same up to an easy-to-calculate multiplicative constant γk.
Knowing this, both upper and lower bound calculations can be applied to show that the asymptotic discrepancy of the optimal solution is on the order of γkw log(w). This discrepancy can be used, as before, to predict an approximate optimal product. However, the bound on the product is much less informative than the bound on the sum: the product can be bounded from above by and from below by (κ1 − δ)w, both converging to a ratio of 1:1 at κ1 rises.
The revised greedy algorithm for this problem is given explicitly below.
Let Q be the set of the w largest primes ≤ κ1.
repeat
δ ← κ1 + 1 − min(Q)
Q ← the w largest numbers ≤ κ1 that have no factors smaller than δ
until δ = κ1 + 1 − min(Q)
repeat
δ ← κ1 + 1 − min(Q)
the number of distinct primes smaller than δ in the factorization of x.
Sort the numbers min(Q), …, κ1 by increasing n(x) [major key] and decreasing value [minor key].
for all i in the sorted list do
if ∀q ∈ Q, lcm(q, i) > κ2 and i > min(Q) then
replace min(Q) by i in Q.
else if there is exactly one q ∈ Q s.t. lcm(q, i) ≤ κ2, and i > q then
replace q with i in Q.
end if
end for
until δ = κ1 + 1 − min(Q)
output Q.
Note that the greedy algorithm tries to lower the discrepancy of the solution even when there is no proof that a smaller discrepancy will yield an improved solution set. In the sum minimization problem, any change of Δ in any of the variables yields a change of Δ in the solution, so there is little reason to favor reducing the largest element of Q (and thereby reducing the discrepancy) over reducing any other element of Q. In product maximization, however, a change of Δ to min(Q) (and hence to the discrepancy) corresponds to a larger change to the product than a change of Δ to any other member of Q. This makes the greedy algorithm even more suited for the product maximization problem than for sum minimization.
Indeed, when examining the results of the greedy algorithm on κ = 384, with w ∈ [2, 8] and κ ∈ [100, 300) we see that the greedy algorithm produces the correct result in all cases w ∈ [2, 3, 4]. In w ∈ [6, 7, 8] the algorithm produces the optimal result in all but 2,3 and 3 cases, respectively. The only w for which a large number of sub-optimal results was recorded is w = 5 where the number of sub-optimal results was 49. Note, however, that in product maximization there is a much larger tendency for “streaking”. The 49 sub-optimal results all belong to a single streak, where the optimal answer is {379, 380, 381, 382, 383} and the answer returned from the greedy algorithm is {377, 379, 382, 383, 384}. The difference in the two products is approximately 0.008%.
In terms of streaks, the optimal answer was returned in all but one streak in w ∈ [5, 6] and in all but two streaks in w ∈ [7, 8]. In terms of the number of iterations required, the only extra iterations that were needed in the execution of the algorithm beyond the minimal required was a single extra iteration through the first “repeat” loop when w was 3. In all other cases, no extra iterations were used, demonstrating that this algorithm is in practice faster than is predicted by its (already low-degree polynomial) time complexity.
APPENDIX D
FULL LAYOUT OF BELIEF PROPAGATION RECONSTRUCTION
Inputs: Query design Φ, sequencing results y, prior expectations about the normal and carrier rates φ(0), φ(1), damping parameter γ, number of iterations mmax, and number of Monte Carlo rounds z.
Preprocessing: (a) find β - enumerate the number of reads in the query. (b) learn the genotype error pattern Λ - the sequencing errors rate is estimated using spiked-in controls [41].
Initialization Initialize the iteration counter m. Initialize μxi→a (xi) to the priors in φ.
- Send messages from factors to variables:
- for each factor a in {1, …, t} do
- for each variable xi in query a do
- for each state of variable xi in {0, 1} do
- Set Ψ0 ← 0
- for {1, …, z} Monte-Carlo round do
- r ← random configuration of ∂a\x according to pdfs in
- Ψ0 ← Ψ0 + Ψa(r, state of xi)
- end for
- μa→xi (state of xi) ← Ψ0/m
- end for
- Normalize μa→xi (xi)
- Send message μa→xi (xi)
- end for
- end for
-
Send messages from variables to factors:
- for each variable xi in {1, …, n} do
- for each factor a connected to xi do
- Set to all ones vector.
- for each possible state of variable xi in {0, 1} do
- for each factor j connected to xi except a do
- end for
- end for
- Include prior by
- Damp
- Normalize
- Send message
- end for
- end for
- m ← m + 1
Go back to step 4 if m < mmax.
Marginalize: For every variable node compute the marginal according to Eq. (31), and find the state of the variable with the highest probability.
Report: Report the highest state of each variable and construct x.
Footnotes
Appendix A contains a glossary of biological terms
Recent study has shown that when the number of specimens is a few thousand up to tens of thousands this assumption is valid [38]
when x = qi we set ri = qi, so the first row in every submatrix is 1
Contributor Information
Yaniv Erlich, Email: erlich@cshl.edu, Watson School of Biological Science, Cold Spring Harbor Laboratory, NY, 11724 USA.
Assaf Gordon, Email: gordon@cshl.edu, Watson School of Biological Science, Cold Spring Harbor Laboratory, NY, 11724 USA.
Michael Brand, Email: ieee@brand.scso.com, Lester Associates, Bentleigh East, 3165 Australia.
Gregory J. Hannon, Email: hannon@cshl.edu, Watson School of Biological Science, Cold Spring Harbor Laboratory, NY, 11724 USA.
Partha P. Mitra, Email: mitra@cshl.edu, Watson School of Biological Science, Cold Spring Harbor Laboratory, NY, 11724 USA.
REFERENCES
- 1.Zlotogora J. Population programs for the detection of couples at risk for severe monogenic genetic diseases. Hum. Genet. 2009 Aug;vol. 126:247–253. doi: 10.1007/s00439-009-0669-y. [DOI] [PubMed] [Google Scholar]
- 2.Rosner G, Rosner S, Orr-Urtreger A. Genetic testing in Israel: an overview. Annu Rev Genomics Hum Genet. 2009;vol. 10:175–192. doi: 10.1146/annurev.genom.030308.111406. [DOI] [PubMed] [Google Scholar]
- 3.Chi KR. The year of sequencing. Nat. Methods. 2008 Jan;vol. 5:11–14. doi: 10.1038/nmeth1154. [DOI] [PubMed] [Google Scholar]
- 4.Shendure J, Ji H. Next-generation DNA sequencing. Nat. Biotechnol. 2008 Oct;vol. 26:1135–1145. doi: 10.1038/nbt1486. [DOI] [PubMed] [Google Scholar]
- 5.Metzker ML. Emerging technologies in DNA sequencing. Genome Res. 2005 Dec;vol. 15:1767–1776. doi: 10.1101/gr.3770505. [DOI] [PubMed] [Google Scholar]
- 6.Craig DW, Pearson JV, Szelinger S, Sekar A, Redman M, Corneveaux JJ, Pawlowski TL, Laub T, Nunn G, Stephan DA, Homer N, Huentelman MJ. Identification of genetic variants using bar-coded multiplexed sequencing. Nat. Methods. 2008 Oct;vol. 5:887–893. doi: 10.1038/nmeth.1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cronn R, Liston A, Parks M, Gernandt DS, Shen R, Mockler T. Multiplex sequencing of plant chloroplast genomes using Solexa sequencing-by-synthesis technology. Nucleic Acids Res. 2008 Nov;vol. 36:e122. doi: 10.1093/nar/gkn502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Candes E, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. Information Theory, IEEE Transactions on. 2006 Feb;vol. 52(no. 2):489–509. [Google Scholar]
- 9.Donoho D. Compressed sensing. Information Theory, IEEE Transactions on. 2006 April;vol. 52(no. 4):1289–1306. [Google Scholar]
- 10.Du D, Hwang FK. COMBINATORIAL GROUP TESTING AND ITS APPLICATIONS. Singapore, Singapore: World Scientific; 1999. [Google Scholar]
- 11.Du D, Hwang FK. POOLING DESIGNS AND NONADAPTIVE GROUP TESTING. Singapore, Singapore: World Scientific; 2006. [Google Scholar]
- 12.Kautz W, Singleton R. Nonrandom binary superimposed codes. Information Theory, IEEE Transactions on. 1964 Oct;vol. 10(no. 4):363–377. [Google Scholar]
- 13.Bruno WJ, Knill E, Balding DJ, Bruce DC, Doggett NA, Sawhill WW, Stallings RL, Whittaker CC, Torney DC. Efficient pooling designs for library screening. Genomics. 1995 Mar;vol. 26:21–30. doi: 10.1016/0888-7543(95)80078-z. [DOI] [PubMed] [Google Scholar]
- 14.Jin F, Hazbun T, Michaud GA, Salcius M, Predki PF, Fields S, Huang J. A pooling-deconvolution strategy for biological network elucidation. Nat. Methods. 2006 Mar;vol. 3:183–189. doi: 10.1038/nmeth859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mézard M, Tarzia M. Statistical mechanics of the hitting set problem. Physical Review E. 2007;vol. 76(no. 4):041 124+. doi: 10.1103/PhysRevE.76.041124. [Online]. Available: http://dx.doi.org/10.1103/PhysRevE.76.041124. [DOI] [PubMed] [Google Scholar]
- 16.D’yachkov A, Macula J, J A, Rykov V. New constructions of superimposed codes. Information Theory, IEEE Transactions on. 2000 Jan;vol. 46(no. 1):284–290. [Google Scholar]
- 17.Macula AJ. A simple construction of d-disjunct matrices with certain constant weights. Discrete Math. 1996;vol. 162(no. 1–3):311–312. [Google Scholar]
- 18.Xin X, Rual JF, Hirozane-Kishikawa T, Hill DE, Vidal M, Boone C, Thierry-Mieg N. Shifted Transversal Design smart-pooling for high coverage interactome mapping. Genome Res. 2009 Jul;vol. 19:1262–1269. doi: 10.1101/gr.090019.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kainkaryam RM, Woolf PJ. poolHiTS: a shifted transversal design based pooling strategy for high-throughput drug screening. BMC Bioinformatics. 2008;vol. 9:256. doi: 10.1186/1471-2105-9-256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kainkaryam A, Woolf P. Multiplexed experiment design in high-throughput screening [Google Scholar]
- 21.Erlich Y, Chang K, Gordon A, Ronen R, Navon O, Rooks M, Hannon G. Dna sudokuharnessing high-throughput sequencing for multiplexed specimen analysis. Genome Research. 2009 doi: 10.1101/gr.092957.109. [Online]. Available: http://genome.cshlp.org/content/early/2009/05/15/gr.092957.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Atia G, Saligrama V. Boolean compressed sensing and noisy group testing. 2009 [Online]. Available: http://www.citebase.org/abstract?id=oai:arXiv.org:0907.1061. [Google Scholar]
- 23.D’yachkov AG, Rykov VV. Optimal superimposed codes and designs for renyi’s search model. Journal of Statistical Planning and Inference. 2002;vol. 100(no. 2):281–302. [Online]. Available: www.scopus.com. [Google Scholar]
- 24.Berinde R, Gilbert A, Indyk P, Karloff H, Strauss M. Combining geometry and combinatorics: A unified approach to sparse signal recovery. Communication, Control, and Computing; 2008 46th Annual Allerton Conference on; Sept. 2008; pp. 798–805. [Google Scholar]
- 25.Cormode G, Muthukrishnan S. Combinatorial algorithms for compressed sensing. Proceedings of Conference on Information Sciences and Systems (CISS) 2006 invited submission. [Online]. Available: ../papers/cs-ciss.pdf. [Google Scholar]
- 26.Sarvotham S, Baron D, Baraniuk R. Sudocodes - fast measurement and reconstruction of sparse signals. Information Theory, 2006 IEEE International Symposium on; 2006. Jul, pp. 2804–2808. [Google Scholar]
- 27.Gilbert A, Iwen MA, Strauss MJ. Group testing and sparse signal recovery. presented at the 42nd Asilomar Conference on Signals, Systems, and Computers; Monterey, CA. 2008. 2008‘. [Google Scholar]
- 28.Duarte MF, Davenport MA, Takhar D, Laska JN, Sun T, Kelly KF, Baraniuk RG. Single-pixel imaging via compressive sampling [building simpler, smaller, and less-expensive digital cameras] Signal Processing Magazine, IEEE. 2008;vol. 25(no. 2):83–91. [Online]. Available: http://dx.doi.org/10.1109/MSP.2007.914730. [Google Scholar]
- 29.Lustig M, Donoho D, Pauly JM. Sparse mri: The application of compressed sensing for rapid mr imaging. Magnetic Resonance in Medicine. 2007;vol. 58(no. 6):1182–1195. doi: 10.1002/mrm.21391. [Online]. Available: http://dx.doi.org/10.1002/mrm.21391. [DOI] [PubMed] [Google Scholar]
- 30.Mishali M, Eldar YC. From theory to practice: Sub-nyquist sampling of sparse wideband analog signals. CoRR. 2009 vol. abs/0902.4291. [Google Scholar]
- 31.Sheikh M, Milenkovic O, Baraniuk R. Designing compressive sensing dna microarrays. Computational Advances in Multi-Sensor Adaptive Processing, 2007. CAMPSAP 2007; 2nd IEEE International Workshop on; Dec. 2007; pp. 141–144. [Google Scholar]
- 32.Dai W, Milenkovic O, Sheikh M, Baraniuk R. Probe design for compressive sensing dna microarrays. Bioinformatics and Biomedicine, 2008. BIBM ’08; IEEE International Conference on; Nov. 2008; pp. 163–169. [Google Scholar]
- 33.Prabhu S, Pe’er I. Overlapping pools for high-throughput targeted resequencing. Genome Res. 2009 Jul;vol. 19:1254–1261. doi: 10.1101/gr.088559.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shental N, Amir A, Zuk O. Rare-Allele Detection Using Compressed Se(que)nsing. arXiv. 2009 Sep; doi: 10.1093/nar/gkq675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Erlich Y, Shental N, Amir A, Zuk O. Compressed sensing approach for high throughput carrier screen. 2009 [Online]. Available: http://hannonlab.cshl.edu/labmembers/erlich/publications/allerton2009/allerton_2009_Erlich_et_al_final.pdf. [Google Scholar]
- 36.Bobadilla JL, Macek M, Fine JP, Farrell PM. Cystic fibrosis: a worldwide analysis of CFTR mutations–correlation with incidence data and application to screening. Hum. Mutat. 2002 Jun;vol. 19:575–606. doi: 10.1002/humu.10041. [DOI] [PubMed] [Google Scholar]
- 37.Orgad S, Neumann S, Loewenthal R, Netanelov-Shapira I, Gazit E. Prevalence of cystic fibrosis mutations in Israeli Jews. Genet. Test. 2001;vol. 5:47–52. doi: 10.1089/109065701750168725. [DOI] [PubMed] [Google Scholar]
- 38.Druley TE, Vallania FL, Wegner DJ, Varley KE, Knowles OL, Bonds JA, Robison SW, Doniger SW, Hamvas A, Cole FS, Fay JC, Mitra RD. Quantification of rare allelic variants from pooled genomic DNA. Nat. Methods. 2009 Apr;vol. 6:263–265. doi: 10.1038/nmeth.1307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Bentley DR, Balasubramanian S, Swerdlow HP, Smith GP, Milton J, Brown CG, Hall KP, Evers DJ, Barnes CL, Bignell HR, Boutell JM, Bryant J, Carter RJ, Keira Cheetham R, Cox AJ, Ellis DJ, Flatbush MR, Gormley NA, Humphray SJ, Irving LJ, Karbelashvili MS, Kirk SM, Li H, Liu X, Maisinger KS, Murray LJ, Obradovic B, Ost T, Parkinson ML, Pratt MR, Rasolonjatovo IM, Reed MT, Rigatti R, Rodighiero C, Ross MT, Sabot A, Sankar SV, Scally A, Schroth GP, Smith ME, Smith VP, Spiridou A, Torrance PE, Tzonev SS, Vermaas EH, Walter K, Wu X, Zhang L, Alam MD, Anastasi C, Aniebo IC, Bailey DM, Bancarz IR, Banerjee S, Barbour SG, Baybayan PA, Benoit VA, Benson KF, Bevis C, Black PJ, Boodhun A, Brennan JS, Bridgham JA, Brown RC, Brown AA, Buermann DH, Bundu AA, Burrows JC, Carter NP, Castillo N, Chiara M, Catenazzi E, Chang S, Neil Cooley R, Crake NR, Dada OO, Diakoumakos KD, Dominguez-Fernandez B, Earnshaw DJ, Egbujor UC, Elmore DW, Etchin SS, Ewan MR, Fedurco M, Fraser LJ, Fuentes Fajardo KV, Scott Furey W, George D, Gietzen KJ, Goddard CP, Golda GS, Granieri PA, Green DE, Gustafson DL, Hansen NF, Harnish K, Haudenschild CD, Heyer NI, Hims MM, Ho JT, Horgan AM, Hoschler K, Hurwitz S, Ivanov DV, Johnson MQ, James T, Huw Jones TA, Kang GD, Kerelska TH, Kersey AD, Khrebtukova I, Kindwall AP, Kingsbury Z, Kokko-Gonzales PI, Kumar A, Laurent MA, Lawley CT, Lee SE, Lee X, Liao AK, Loch JA, Lok M, Luo S, Mammen RM, Martin JW, McCauley PG, McNitt P, Mehta P, Moon KW, Mullens JW, Newington T, Ning Z, Ling Ng B, Novo SM, O’Neill MJ, Osborne MA, Osnowski A, Ostadan O, Paraschos LL, Pickering L, Pike AC, Pike AC, Chris Pinkard D, Pliskin DP, Podhasky J, Quijano VJ, Raczy C, Rae VH, Rawlings SR, Chiva Rodriguez A, Roe PM, Rogers J, Rogert Bacigalupo MC, Romanov N, Romieu A, Roth RK, Rourke NJ, Ruediger ST, Rusman E, Sanches-Kuiper RM, Schenker MR, Seoane JM, Shaw RJ, Shiver MK, Short SW, Sizto NL, Sluis JP, Smith MA, Ernest Sohna Sohna J, Spence EJ, Stevens K, Sutton N, Szajkowski L, Tregidgo CL, Turcatti G, Vandevondele S, Verhovsky Y, Virk SM, Wakelin S, Walcott GC, Wang J, Worsley GJ, Yan J, Yau L, Zuerlein M, Rogers J, Mullikin JC, Hurles ME, McCooke NJ, West JS, Oaks FL, Lundberg PL, Klenerman D, Durbin R, Smith AJ. Accurate whole human genome sequencing using reversible terminator chemistry. Nature. 2008 Nov;vol. 456:53–59. doi: 10.1038/nature07517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Aitchison J. The statistical analysis of compositional data. London, UK, UK: Chapman & Hall, Ltd.; 1986. [Google Scholar]
- 41.Erlich Y, Mitra PP, delaBastide M, McCombie WR, Hannon GJ. Alta-Cyclic: a self-optimizing base caller for next-generation sequencing. Nat. Methods. 2008 Aug;vol. 5:679–682. doi: 10.1038/nmeth.1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mow WH. Recursive constructions of detecting matrices for multiuser coding: A unifying approach. Information Theory, IEEE Transactions on. 2009 Jan;vol. 55(no. 1):93–98. [Google Scholar]
- 43.Mathys P. A class of codes for a t active users out of n multiple-access communication system. Information Theory, IEEE Transactions on. 1990 Nov;vol. 36(no. 6):1206–1219. [Google Scholar]
- 44.Chang S-C, Weldon E. Coding for t-user multiple-access channels. Information Theory, IEEE Transactions on. 1979 Nov;vol. 25(no. 6):684–691. [Google Scholar]
- 45.Khachatrian G, Martirossian S. Code construction for the t-user noiseless adder channel. Information Theory, IEEE Transactions on. 1998 Sep;vol. 44(no. 5):1953–1957. [Google Scholar]
- 46.G C, S M. Towards an algorithmic theory of compressed sensing. dIMACS TR: 2005-25. 2005 [Online]. Available: ftp://dimacs.rutgers.edu/pub/dimacs/TechnicalReports/TechReports/2005/2005-25.pdf.
- 47.Gilbert AC, Strauss MJ, Tropp JA, Vershynin R. Algorithmic linear dimension reduction in the l1 norm for sparse vectors. CoRR. 2006 vol. abs/cs/0608079. [Google Scholar]
- 48.Baron D, Sarvotham S, Baraniuk RG. Bayesian compressive sensing via belief propagation. 2008 Dec; [Online]. Available: http://arxiv.org/abs/0812.4627. [Google Scholar]
- 49.Sarvotham S, Baron D, Baraniuk RG. Measurements vs. bits: Compressed sensing meets information theory. presented at the Proceedings of the 44th Allerton Conference on Communication, Control, and Computing.2006. [Google Scholar]
- 50.Eppstein D, Goodrich MT, Hirschberg DS. Improved combinatorial group testing for real-world problem sizes. ACM Computing Research Repository. 2005 May [Google Scholar]
- 51.Thierry-Mieg N. A new pooling strategy for high-throughput screening: the Shifted Transversal Design. BMC Bioinformatics. 2006;vol. 7:28. doi: 10.1186/1471-2105-7-28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kschischang F, Frey B, Loeliger H-A. Factor graphs and the sum-product algorithm. Information Theory, IEEE Transactions on. 2001 Feb;vol. 47(no. 2):498–519. [Google Scholar]
- 53.Pearl J. Probabilistic Reasoning in Intelligent Systems : Networks of Plausible Inference. Morgan Kaufmann; 1988. Sep, [Online]. Available: http://www.amazon.ca/exec/obidos/redirect?tag=citeulike09-20\&path=ASIN/1558604790. [Google Scholar]
- 54.Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics) Springer; 2006. Aug, [Online]. Available: http://www.amazon.ca/exec/obidos/redirect?tag=citeulike09-20\&path=ASIN/0387310738. [Google Scholar]
- 55.Frey BJ, MacKay DJC. A revolution: belief propagation in graphs with cycles; NIPS ’97: Proceedings of the 1997 conference on Advances in neural information processing systems 10; Cambridge, MA, USA: MIT Press; 1998. pp. 479–485. [Google Scholar]
- 56.Mzard M, Montanari A. Information, Physics, and Computation. Oxford Graduate Texts: Oxford University Press; 2009. ser. [Google Scholar]
- 57.Kroc L, Sabharwal A, Selman B. sac09. Honolulu, HI: 2009. Mar, Message-passing and local heuristics as decimation strategies for satisfiability; pp. 1408–1414. [Google Scholar]
- 58.Moon T, Gunther J. Multiple constraint satisfaction by belief propagation: An example using sudoku. Adaptive and Learning Systems, 2006 IEEE Mountain Workshop on; July 2006; pp. 122–126. [Google Scholar]
- 59.Huang D, Milenkovic O. Superimposed coding for iterative detection of dna microarray spot failures. Genomic Signal Processing and Statistics, 2008. GENSiPS 2008. IEEE International Workshop on; June 2008; pp. 1–4. [Google Scholar]
- 60.Pretti M. A message-passing algorithm with damping. Journal of Statistical Mechanics: Theory and Experiment. 2005 November;vol. 2005(no. 11):P11 008+. [Online]. Available: http://dx.doi.org/10.1088/1742-5468/2005/11/P11008. [Google Scholar]
- 61.OWWST A decade of molecular studies of fragile X syndrome. Annu. Rev. Neurosci. 2002 Mar;vol. 25:315–338. doi: 10.1146/annurev.neuro.25.112701.142909. [DOI] [PubMed] [Google Scholar]
- 62.Herman MA, Strohmer T. General deviants: An analysis of perturbations in compressed sensing. CoRR. 2009 vol. abs/0907.2955. [Google Scholar]